Все формулы по тригонометрии
Все формулы по тригонометрии
Подождите пару секунд пока подгрузятся формулы
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$$$tgx= \frac{sinx}{cosx}$$
$$ctgx= \frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= \frac{1}{cos^2x}$$
$$ctg^2x+1= \frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}
\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}
\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}
\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}
\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$$$cos3x=4cos^3x-3cosx$$
$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}
\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= \frac{1-cos2x}{2}$$$$cos^2x= \frac{1+cos2x}{2}$$
$$tg^2x= \frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$
$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= \frac{3sinx-sin3x}{4}$$$$cos^3x= \frac{3cosx+cos3x}{4}$$
$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$
$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$
$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$
$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$
$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$
$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$
$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$
Формулы суммы тригонометрических функций
$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
Формулы разности тригонометрических функций
$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$
$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$
$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$
Формулы произведения тригонометрических функций
$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$
$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$
\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}
\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}
$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$
www.100formul.ru
Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
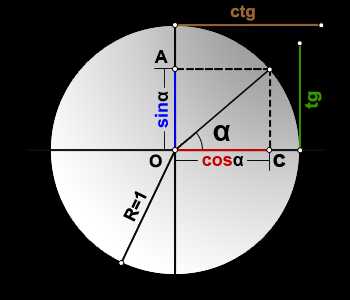
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
Значения функций для некоторых углов, α
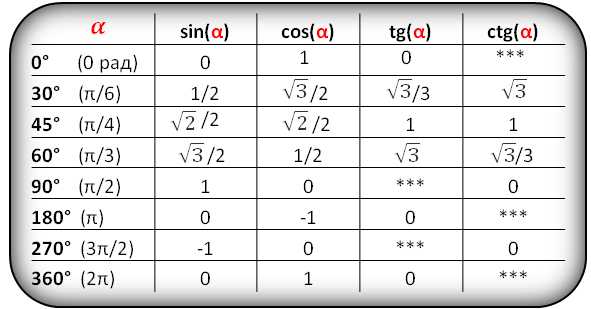
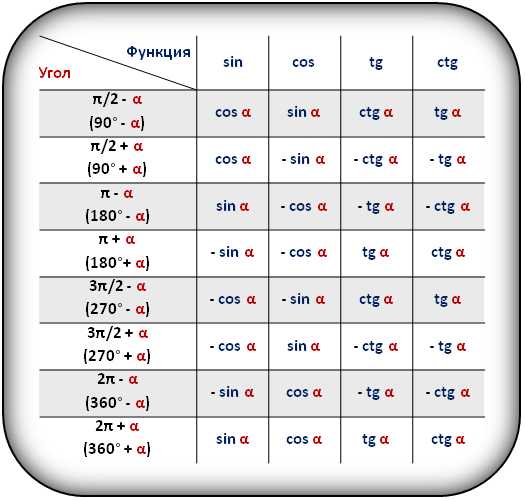
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
www-formula.ru
73 формулы тригонометрии
На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.
Все формулы тригонометрии
Основные тригонометрические тождества
{\tg \alpha = \dfrac {\sin \alpha}{ \cos \alpha} = \dfrac{1}{\ctg \alpha}}
{\ctg \alpha = \dfrac {\cos \alpha}{ \sin \alpha} = \dfrac{1}{\tg \alpha}}
{\sin ^2 \alpha + \cos ^2 \alpha = 1}
{1+\tg^2\alpha=\dfrac{1}{\cos^2\alpha}}
{1+\ctg^2\alpha=\dfrac{1}{\sin^2\alpha}}
{\tg\alpha \cdot \ctg\alpha=1}
Формулы двойного угла (аргумента)
{\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha}
{\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}}
{\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha}
{\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}}
{\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}}
{\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}}
Формулы тройного угла (аргумента)
{\sin(3\alpha)=3 \cdot \sin \alpha- 4 \cdot \sin ^3 \alpha}
{\cos(3\alpha)= 4 \cdot \cos ^3 \alpha- 3 \cdot \cos \alpha}
{\tg(3\alpha)= \dfrac{3 \cdot \tg \alpha- \tg ^3 \alpha}{1-3 \cdot \tg ^2 \alpha}}
{\ctg(3\alpha)= \dfrac{\ctg ^3 \alpha- 3 \cdot \ctg \alpha}{3 \cdot \ctg ^2 \alpha -1}}
Формулы понижения степени тригонометрических функций
Вторая степень
{\sin ^2 \alpha = \dfrac{1-\cos(2\alpha)}{2}}{\cos ^2 \alpha = \dfrac{1+\cos(2\alpha)}{2}}
{\tg ^2 \alpha = \dfrac{1-\cos(2\alpha)}{1+\cos(2\alpha)}}
{\ctg ^2 \alpha = \dfrac{1+\cos(2\alpha)}{1-\cos(2\alpha)}}
{(\sin \alpha- \cos \alpha)^2=1-\sin(2 \alpha)}
{(\sin \alpha+ \cos \alpha)^2=1+\sin(2 \alpha)}
Третья степень
{\sin ^3 \alpha = \dfrac{3 \cdot \sin(\alpha)-\sin(3 \alpha)}{4}}{\cos ^3 \alpha = \dfrac{3 \cdot \cos(\alpha)+\cos(3 \alpha)}{4}}
{\tg ^3 \alpha = \dfrac{3 \cdot \sin (\alpha)-\sin(3 \alpha)}{3 \cdot \cos (\alpha)+\cos(3 \alpha)}}
{\ctg ^3 \alpha = \dfrac{3 \cdot \cos (\alpha)+\cos(3 \alpha)}{3 \cdot \sin (\alpha)-\sin(3 \alpha)}}
Четвёртая степень
{\sin ^4 \alpha = \dfrac{3-4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}{\cos ^4 \alpha = \dfrac{3+4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}
Пятая степень
{\sin ^5 \alpha = \dfrac{10 \cdot \sin(\alpha)-5 \cdot \sin(3 \alpha)+\sin(5 \alpha)}{16}}{\cos ^5 \alpha = \dfrac{10 \cdot \cos(\alpha)+5 \cdot \cos(3 \alpha)+\cos(5 \alpha)}{16}}
Формулы половинного угла (аргумента)
{\sin \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1-\cos \alpha}{2}}}
{\cos \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}}
{\tg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1-\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1+\cos \alpha}}
{\ctg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1+\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1-\cos \alpha}}
Формулы понижения степени половинного угла (аргумента)
{\sin ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{2}}
{\cos ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{2}}
{\tg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{1+\cos \alpha}}
{\ctg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{1-\cos \alpha}}
Формулы сложения аргументов
{\sin(\alpha + \beta)=\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta}
{\cos(\alpha + \beta)=\cos \alpha \cdot \cos \beta- \sin \alpha \cdot \sin \beta}
{\tg(\alpha + \beta)= \dfrac{\tg \alpha + \tg \beta}{1-\tg \alpha \cdot \tg \beta}}
{\ctg(\alpha + \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta-1}{\ctg \alpha + \ctg \beta}}
Формулы вычитания аргументов
{\sin(\alpha- \beta)=\sin \alpha \cdot \cos \beta- \cos \alpha \cdot \sin \beta}
{\cos(\alpha- \beta)=\cos \alpha \cdot \cos \beta+ \sin \alpha \cdot \sin \beta}
{\tg(\alpha- \beta)= \dfrac{\tg \alpha- \tg \beta}{1+\tg \alpha \cdot \tg \beta}}
{\ctg(\alpha- \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta+1}{\ctg \alpha- \ctg \beta}}
Формулы суммы тригонометрических функций
{\sin \alpha+ \sin \beta=2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}
{\cos \alpha+ \cos \beta=2 \cdot \cos \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}
{\tg \alpha + \tg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}
{\ctg \alpha + \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}
{\sin (\alpha)+\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha+ \dfrac{\pi}{4} \Big)}
Формулы разности тригонометрических функций
{\sin \alpha- \sin \beta=2 \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha+ \beta}{2} \big)}
{\cos \alpha- \cos \beta=-2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big)}
{\tg \alpha- \tg \beta = \dfrac{\sin(\alpha- \beta)}{\cos \alpha \cdot \cos \beta}}
{\ctg \alpha- \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\sin \alpha \cdot \sin \beta}}
{\sin (\alpha)-\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha- \dfrac{\pi}{4} \Big)}
Формулы произведения тригонометрических функций
{\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}}
{\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}}
{\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}}
{\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}}
{\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}}
{\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}}
Формулы произведения тригонометрических функций в степени
{\sin ^2 (\alpha) \cdot \cos ^2 (\alpha) = \dfrac{1-\cos(4 \alpha)}{8}}
{\sin ^3 (\alpha) \cdot \cos ^3 (\alpha) = \dfrac{3 \cdot \sin(2 \alpha)- \sin(6 \alpha)}{32}}
{\sin ^4 (\alpha) \cdot \cos ^4 (\alpha) = \dfrac{3-4 \cdot \cos(4 \alpha)+ \cos(8 \alpha)}{128}}
{\sin ^5 (\alpha) \cdot \cos ^5 (\alpha) = \dfrac{10 \cdot \sin (2 \alpha)-5 \cdot \sin(6 \alpha)+\sin (10 \alpha)}{512}}
Все формулы тригонометрии на одном листе
На этой картинке собраны все формулы тригонометрии для печати. Листо можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Все формулы тригонометрии на одном листе
Просмотров страницы: 13 674
mnogoformul.ru
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | ||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | ||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | ||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | ||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | ||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | ||
| (7) | Тангенс двойного угла |
| ||
| (8) | Котангенс двойного угла |
| ||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | ||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | ||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | ||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | ||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | ||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | ||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | ||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | ||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | ||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | ||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | ||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | ||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | ||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | ||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | ||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | ||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | ||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | ||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
scolaire.ru
Тригонометрические формулы
Наиболее часто встречающиеся тригонометрические формулы:
\(\blacktriangleright\) Основные тождества:
\(\blacktriangleright\) Формулы сложения углов: \[\begin{array}{|l|r|} \hline &\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm{tg}\, (\alpha\pm \beta)=\dfrac{\mathrm{tg}\, \alpha\pm \mathrm{tg}\, \beta}{1 \mp \mathrm{tg}\, \alpha\cdot \mathrm{tg}\, \beta} & \mathrm{ctg}\, (\alpha\pm\beta)=-\dfrac{1\mp \mathrm{ctg}\, \alpha\cdot \mathrm{ctg}\, \beta}{\mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta}\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin{array}{|lc|cr|} \hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\ & & & \cos{2\alpha}=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\, \alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha = \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin {3\alpha}=3\sin \alpha -4\sin^3\alpha && & \cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы понижения степени: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin^2\alpha=\dfrac{1-\cos{2\alpha}}2 &&& \cos^2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы произведения функций: \[\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы суммы/разности функций: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= — \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}\]
\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}\]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos{(\alpha -\beta)}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\). Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\).

Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\). По теореме косинусов:
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
\(AB^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2=\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+\)
\(+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta=\big(\cos^2\alpha+\sin^2\alpha\big)+\big(\cos^2\beta+\sin^2\beta\big)-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=\)
\(=1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big) \ (2)\)
Таким образом, сравнивая равенства \((1)\) и \((2)\):
\(1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=1+1-2\cos(\alpha-\beta)\)
Отсюда и получается наша формула.
\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\):
1) \(\cos(\alpha+\beta)=\cos(\alpha-(-\beta))=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
2) \(\sin(\alpha+\beta)=\cos(90^\circ-(\alpha+\beta))=\cos((90^\circ-\alpha)-\beta)=\)
\(+\cos(90^\circ-\alpha)\cos\beta+\sin(90^\circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
3) \(\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
4) \(\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=\)
разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne
0\)
(при \(\cos\alpha=0 \Rightarrow
\mathrm{tg}\,(\alpha\pm\beta)=\mp \mathrm{ctg}\,\beta\), при \(\cos\beta=0 \Rightarrow
\mathrm{tg}\,(\alpha\pm\beta)=\pm \mathrm{ctg}\,\alpha\)):
\(=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}\)
Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\).
5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\), выводится формула котангенса суммы/разности двух углов.
\(\blacktriangleright\) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)
2) \(\cos2\alpha=\cos(\alpha+\alpha)=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha=\cos^2\alpha-\sin^2\alpha\)
Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\), получим еще две формулы для косинуса двойного угла:
2.1) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=\cos^2\alpha-(1-\cos^2\alpha)=2\cos^2\alpha-1\)
2.2) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=(1-\sin^2\alpha)-\sin^2\alpha=1-2\sin^2\alpha\)
3) \(\mathrm{tg}\,2\alpha=\dfrac{\sin2\alpha}{\cos2\alpha}=\dfrac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\)
разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm{tg}\,2\alpha=0\)):
\(=\mathrm{tg}\,2\alpha=\dfrac{2\mathrm{tg}\,\alpha}{1-\mathrm{tg}^2\,\alpha}\)
Таким образом, эта формула верна только при \(\cos\alpha\ne 0\), а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm{tg}\,2\alpha\)).
4) \(\mathrm{ctg}\,2\alpha=\dfrac{\cos^2\alpha-\sin^2\alpha}{2\sin\alpha\cos\alpha}=\dfrac{\mathrm{ctg}^2\,\alpha-1}{2\mathrm{ctg}\,\alpha}\)
По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\).
5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)
\(=\sin\alpha-2\sin^3\alpha+2\sin\alpha(1-\sin^2\alpha)=3\sin\alpha-4\sin^3\alpha\)
6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)
\(\blacktriangleright\) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac{1+\cos2\alpha}2\)
2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac{1-\cos2\alpha}2\)
Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\).
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
\(\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)\)
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\)
\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
Получим: \(\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)\)
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\). Тогда: \(\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2\). Подставим эти значения в предыдущие три формулы:
1) \(2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y\)
Получили формулу суммы косинусов.
2) \(2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x\)
Получили формулу разности косинусов.
3) \(2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x\)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
\(\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}\)
5) \(\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}\)
Аналогично выводится формула суммы котангенсов.
\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) \(\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=\)
(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\)):)
\(=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}\)
2) Так же, только делением на \(\sin^2\alpha\), выводится формула для косинуса.
\(\blacktriangleright\) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение \(a\sin x+b\cos x\). Домножим и разделим это выражение на \(\sqrt{a^2+b^2}\,\):
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\left(\dfrac a{\sqrt{a^2+b^2}}\sin x+ \dfrac b{\sqrt{a^2+b^2}}\cos x \right)=\sqrt{a^2+b^2}\big(a_1\sin x+b_1\cos x\big)\)
Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\), т.к. \(\left(\dfrac a{\sqrt{a^2+b^2}}\right)^2+\left(\dfrac b{\sqrt{a^2+b^2}}\right)^2=\dfrac{a^2+b^2}{a^2+b^2}=1\)
Таким образом, можно утверждать, что существует такой угол \(\phi\), для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\). Тогда наше выражение примет вид:
\(\sqrt{a^2+b^2}\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt{a^2+b^2}\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: \[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac a{\sqrt{a^2+b^2}}\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt{a^2+b^2}\,\cos (x-\phi)\]
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)\)
shkolkovo.net
Формулы тригонометрии
Формулы тригонометрии (тригонометрические формулы) или тригонометрические тождества описывают зависимости между синусом, косинусом, тангенсом и котангенсом и применяются при решении математических задач.
Ниже указаны основные тригонометрические тождества (равенства), формулы понижения степени, формулы двойного угла, косинус двойного угла, синус двойного угла, а также другие формулы. Дополнительно приведены значения тригонометрических функций для наиболее распространённых углов.
Основные тождества
… Подготовка формул …Формулы двойного угла
… Подготовка формул …Формулы тройного угла
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы половинного аргумента
Формулы понижения степени
половинного аргумента
… Подготовка формул …Формулы сложения
… Подготовка формул …Формулы вычитания
… Подготовка формул …Формулы преобразования суммы
в формулы произведения
… Подготовка формул …Формулы преобразования разности
в формулы произведения
… Подготовка формул …Формулы преобразования суммы
… Подготовка формул …Формулы преобразования произведения
в формулы суммы и разности
… Подготовка формул …Формулы преобразования произведения
функций в степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Универсальная
тригонометрическая подстановка
… Подготовка формул … Значения тригонометрических функций
| α | 0 | ||||||||||||||||
| α° | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | 0 | 1 | 0 | −1 | 0 | ||||||||||||
| cos α | 1 | 0 | −1 | 0 | 1 | ||||||||||||
| tg α | 0 | 1 | − | −1 | 0 | 1 | − | −1 | 0 | ||||||||
| ctg α | − | 1 | 0 | −1 | − | 1 | 0 | −1 | − |
Теория
Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.
Функция – это правило, описывающее зависимость одной величины от другой.
Тождество – это равенство, справедливое при любых значениях, входящих в него переменных
Скачать тригонометрические формулы
Вы можете скачать тригонометрические формулы в виде картинки:








doza.pro
Все формулы по тригонометрии
Все формулы по тригонометрии
Основные тригонометрические тождества
sin2x + cos2x = 1
tgx ctgx = 1
tg2x + 1 | = | 1 |
cos2x |
ctg2x + 1 | = | 1 |
sin2x |
Формулы двойного аргумента
sin2x = 2sinx cosx
sin2x | = | 2tgx | = | 2ctgx | = | 2 |
1 + tg2 x | 1 + ctg2x | tgx + ctgx |
cos2x = cos2 — sin2x = 2cos2x — 1 = 1 — 2sin2x
cos2x | = | 1 — tg2x | = | ctg2x — 1 | = | ctgx — tgx |
1 + tg2x | ctg2x + 1 | ctgx + tgx |
tg2x | = | 2tgx | = | 2ctgx | = | 2 |
1 — tg2x | ctg2x — 1 | ctgx — tgx |
ctg2x | = | ctg2x — 1 | = | ctgx — tgx |
2ctgx | 2 |
Формулы тройного аргумента
sin3x = 3sinx — 4sin3x cos3x = 4cos3x — 3cosx
tg3x | = | 3tgx — tg3x |
1 — 3tg2x |
ctg3x | = | ctg3x — 3ctgx |
3ctg2x — 1 |
Формулы половинного аргумента
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
tg | x | = | 1 — cosx | = | sinx |
2 | sinx | 1 + cosx |
ctg | x | = | 1 + cosx | = | sinx |
2 | sinx | 1 — cosx |
Формулы квадратов тригонометрических функций
sin2x | = | 1 — cos2x |
2 |
cos2x | = | 1 + cos2x |
2 |
tg2x | = | 1 — cos2x |
1 + cos2x |
ctg2x | = | 1 + cos2x |
1 — cos2x |
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
Формулы кубов тригонометрических функций
sin3x | = | 3sinx — sin3x |
4 |
cos3x | = | 3cosx + cos3x |
4 |
tg3x | = | 3sinx — sin3x |
3cosx + cos3x |
ctg3x | = | 3cosx + cos3x |
3sinx — sin3x |
Формулы тригонометрических функций в четвертой степени
sin4x | = | 3 — 4cos2x + cos4x |
8 |
cos4x | = | 3 + 4cos2x + cos4x |
8 |
Формулы сложения аргументов
sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ
tg(α + β) | = | tgα + tgβ |
1 — tgα tgβ |
ctg(α + β) | = | ctgα ctgβ — 1 |
ctgα + ctgβ |
sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ
tg(α — β) | = | tgα — tgβ |
1 + tgα tgβ |
ctg(α — β) | = | ctgα ctgβ + 1 |
ctgα — ctgβ |
Формулы суммы тригонометрических функций
sinα + sinβ | = 2sin | α + β | ∙ cos | α — β |
2 | 2 |
cosα + cosβ | = 2cos | α + β | ∙ cos | α — β |
2 | 2 |
(sinα + cosα)2 = 1 + sin2α
tgα + tgβ | = | sin(α + β) |
cosα cosβ |
ctgα + ctgβ | = | sin(α + β) |
sinα sinβ |
Формулы разности тригонометрических функций
sinα — sinβ | = 2sin | α — β | ∙ cos | α + β |
2 | 2 |
cosα — cosβ | = -2sin | α + β | ∙ sin | α — β |
2 | 2 |
(sinα — cosα)2 = 1 — sin2α
tgα — tgβ | = | sin(α — β) |
cosα cosβ |
ctgα — ctgβ | = – | sin(α — β) |
sinα sinβ |
Формулы произведения тригонометрических функций
sinα ∙ sinβ | = | cos(α — β) — cos(α + β) |
2 |
sinα ∙ cosβ | = | sin(α — β) + sin(α + β) |
2 |
cosα ∙ cosβ | = | cos(α — β) + cos(α + β) |
2 |
tgα ∙ tgβ | = | cos(α — β) — cos(α + β) | = | tgα + tgβ |
cos(α — β) + cos(α + β) | ctgα + ctgβ |
ctgα ∙ ctgβ | = | cos(α — β) + cos(α + β) | = | ctgα + ctgβ |
cos(α — β) — cos(α + β) | tgα + tgβ |
tgα ∙ ctgβ | = | sin(α — β) + sin(α + β) |
sin(α + β) — sin(α — β) |
studfiles.net
