Локальная и интегральная теоремы Лапласа
При достаточно большом 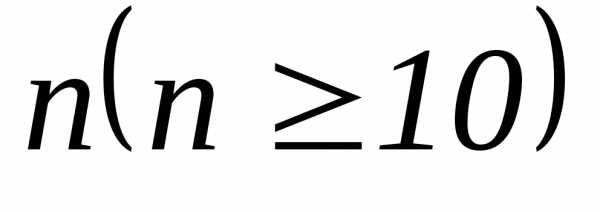 формула Бернулли дает громоздкие
вычисления. Поэтому в таких случаях
применяют локальную теорему Лапласа.
формула Бернулли дает громоздкие
вычисления. Поэтому в таких случаях
применяют локальную теорему Лапласа.
Теорема (локальная теорема Лапласа).
Если вероятностьpпоявления
события А в каждом испытании постоянна
и отлична от 0 и 1, то вероятность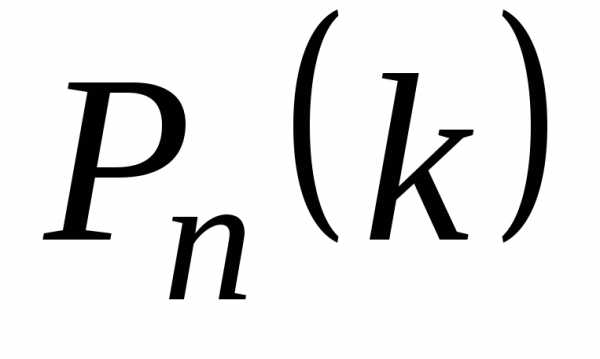 того, что событие А появится вnнезависимых испытаниях ровноkраз, приближенно равна значению функции:
того, что событие А появится вnнезависимых испытаниях ровноkраз, приближенно равна значению функции:
,
где
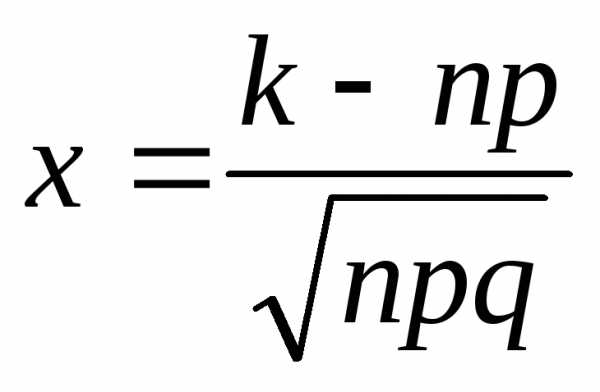 .
.
Имеются таблицы, в которых находятся
значения функции  ,
для положительных значенийx.
,
для положительных значенийx.
Заметим, что функция 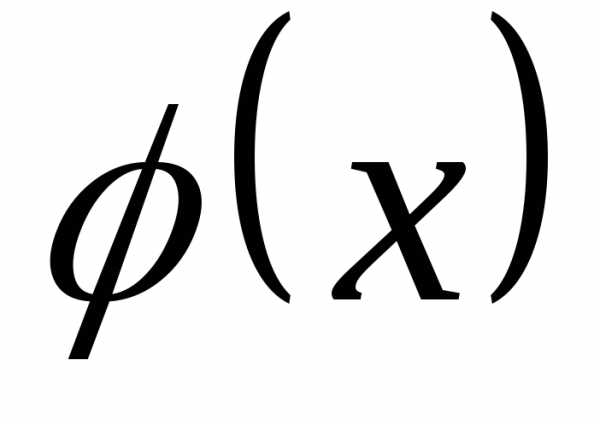 четна.
четна.
Итак, вероятность того, что событие А появится в nиспытаниях ровноkраз приближенно равна
 ,
где
,
где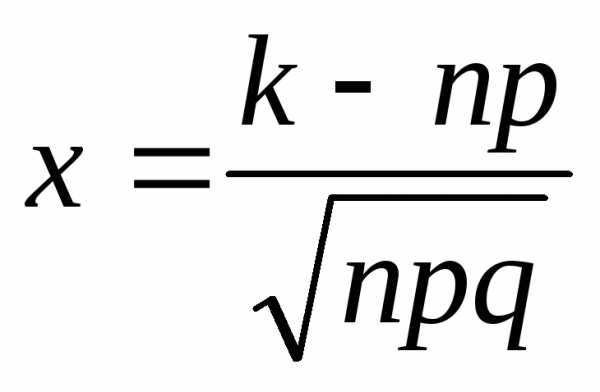 .
.
Пример. На опытном поле посеяли 1500 семян. Найти вероятность того, что всходы дадут 1200 семян, если вероятность того, что зерно взойдет, равна 0,9.
Решение.
Интегральная теорема Лапласа
Вероятность того, что в nнезависимых испытаниях событие А появится не менееk1 раз и не болееk2 раз вычисляется по интегральной теореме Лапласа.
Теорема (интегральная теорема Лапласа). Если вероятность р наступления события а в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А вnиспытаниях появится не менееk 1раз и не болееk2раз приближенно равна значению определенного интеграла:
,
где
.
Функция 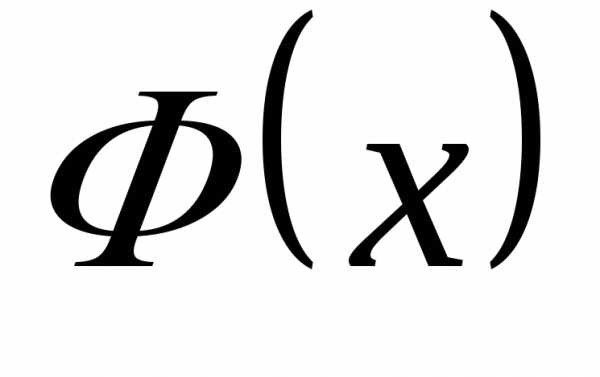 называется интегральной функцией
Лапласа, она нечетна и ее значение
находятся по таблице для положительных
значенийx.
называется интегральной функцией
Лапласа, она нечетна и ее значение
находятся по таблице для положительных
значенийx.
Пример.В лаборатории из партии семян, имеющих всхожесть 90%, высеяно 600 семян, давших всходы, не менее 520 и не более 570.
Решение.

Формула Пуассона
Пусть производится nнезависимых испытаний, вероятность появления события А в каждом испытании постоянна и равна р. Как мы уже говорили, вероятность появления события А вnнезависимых испытаниях ровноkраз можно найти по формуле Бернулли. При достаточно большомnиспользуют локальную теорему Лапласа. Однако, эта формула непригодна, когда вероятность появления события в каждом испытании мала или близка к 1. А при р=0 или р=1 вообще не применима. В таких случаях пользуются теоремой Пуассона.
Теорема (теорема Пуассона). Если вероятность р наступления события А в каждом испытании постоянна и близка к 0 или 1, а число испытаний достаточно велико, то вероятность того, что вnнезависимых испытаниях событие А появится ровноkраз находится по формуле:
 .
.
Пример. Рукопись объемом в тысячу страниц машинописного текста содержит тысячу опечаток. Найти вероятность того, что наудачу взятая страница содержит хотя бы одну опечатку.
Решение.

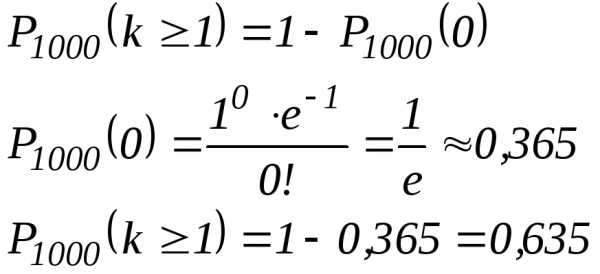
Вопросы для самопроверки
Сформулируйте классическое определение вероятности события.
Сформулируйте теоремы сложения и умножения вероятностей.
Дайте определение полной группы событий.
Запишите формулу полной вероятности.
Запишите формулу Бейеса.
Запишите формулу Бернулли.
Запишите формулу Пуассона.
Запишите локальную формулу Лапласа.
Запишите интегральную формулу Лапласа.
Тема 13. Случайная величина и ее числовые характеристики
Литература: [2],[8],[9],[10],[18],[22].
Одним из основных понятий в теории вероятностей является понятие случайной величины. Так принято называть переменную величину, которая принимает свои значения в зависимости от случая. Различают два вида случайных величин: дискретные и непрерывные. Случайные величины принято обозначать X,Y,Z.
Случайная величина Х называется непрерывной (дискретной), если она может принимать лишь конечное или счетное число значений. Дискретная случайная величина Х определена, если даны все ее возможные значения х1, х2, х3,…хn(число которых может быть как конечным, так и бесконечным) и соответствующие вероятности р1, р2, р3,…рn.
Закон распределения дискретной случайной величины Х обычно задается таблицей:
Х | х1 | х2 | х3 | … | хn | (1) |
Р | р1 | р2 | р3 | … | рn |
Первая строка состоит из возможных значений случайной величины Х, а во второй строке указаны вероятности этих значений. Сумма вероятностей, с которыми случайная величина Х принимает все свои значения, равна единице, то есть
р1+р2+ р3+…+рn=1.
Закон распределения дискретной случайной
величины Х можно изобразить графически.
Для этого в прямоугольной системе
координат строят точки М1(х1,р1),
М2(х2,р2), М3(х3,р3),…М
Пример. Дискретная величина Х задана следующим законом распределения:
Х | 48 | 53 | 57 | 61 |
Р | 0,2 | 0,4 | 0,3 | 0,1 |
Требуется вычислить: а) математическое ожидание М(Х), б) дисперсию D(X), в) среднее квадратическое отклонение σ.
Решение.
а) Математическое ожидание М(Х), дискретной случайной величины Х называется сумма попарных произведений всех возможных значений случайной величины на соответствующие вероятности этих возможных значений. Если дискретная случайная величина Х задана с помощью таблицы (1), то математическое ожидание М(Х) вычисляется по формулеМ(Х)=х1∙р1+х2∙р2+х3∙р3+…+хn∙pn. (2)
Математическое ожидание М(Х) называют также средним значением случайной величины Х. Применяя (2), получим:
М(Х)=48∙0,2+53∙0,4+57∙0,3 +61∙0,1=54.
б) Если М(Х) есть математическое ожидание случайной величины Х, то разность Х-М(Х) называется отклонением случайной величины Х от среднего значения. Эта разность характеризует рассеяние случайной величины.
Дисперсией (рассеянием) дискретной случайной величины Х называется математическое ожидание (среднее значение) квадрата отклонения случайной величины от ее математического ожидания. Таким образом, по самому определению имеем:
D(X)=M[X-M(X)]2. (3)
Вычислим все возможные значения квадрата отклонения.
[x1-M(X)]2=(48-54)2=36
[x2-M(X)]2=(53-54)2=1
[x3-M(X)]2=(57-54)2=9
[x4-M(X)]2=(61-54)2=49
Чтобы вычислить дисперсию D(X), составим закон распределения квадрата отклонения и затем применим формулу (2).
[x-M(X)]2 | 36 | 1 | 9 | 49 |
Р | 0,2 | 0,4 | 0,3 | 0,1 |
D(X)= 36∙0,2+1∙0,4+9∙0,3 +49∙0,1=15,2.
Следует отметить, что для вычисления дисперсии часто используют следующее свойство: дисперсия D(X) равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания, то есть
D(X)-M(X2)-[M(X)]2. (4)
Чтобы вычислить дисперсию по формуле (4), составим закон распределения случайной величины Х2:
Х2 | 482 | 532 | 572 | 612 |
Р | 0,2 | 0,4 | 0,3 | 0,1 |
Теперь найдем математическое ожидание М(Х2).
М(Х2)= (48)2∙0,2+(53)2∙0,4+(57)2∙0,3 +(61)2∙0,1=
=460,8+1123,6+974,7+372,1=2931,2.
Применяя (4), получим:
D(X)=2931,2-(54)2=2931,2-2916=15,2.
Как видно, мы получили такой же результат.
в) Размерность дисперсии равна квадрату
размерности случайной величины. Поэтому
для характеристики рассеяния возможных
значений случайной величины вокруг ее
среднего значения более удобно
рассматривать величину, которая равна
арифметическому значению корня
квадратного из дисперсии, то есть  .
Эту величину называют средним
квадратическим отклонением случайной
величины Х и обозначают через σ. Таким
образом
.
Эту величину называют средним
квадратическим отклонением случайной
величины Х и обозначают через σ. Таким
образом
σ= . (5)
. (5)
Применяя (5), имеем: σ=.
Пример. Случайная величина Х распределена по нормальному закону. Математическое ожидание М(Х)=5; дисперсияD(X)=0,64. Найти вероятность того, что в результате испытания Х примет значение в интервале (4;7).
Решение. Известно, что если случайная величина Х задана дифференциальной функциейf(x), то вероятность того, что Х примет значение, принадлежащее интервалу (α,β), вычисляется по формуле
. (1)
Если величина Х распределена по нормальному закону, то дифференциальная функция
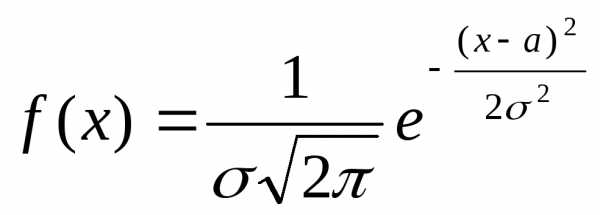 ,
,
где а=М(Х) и σ=. В этом случае получаем из (1)
. (2)
Формулу (2) можно преобразовать, используя функцию Лапласа.
Сделаем подстановку. Пусть  .
Тогда
.
Тогда илиdx=σ∙dt.
илиdx=σ∙dt.
Следовательно , гдеt1иt2соответствующие пределы для переменнойt.
Сократив на σ, будем иметь

Из введенной подстановки  следует, что
следует, что и
и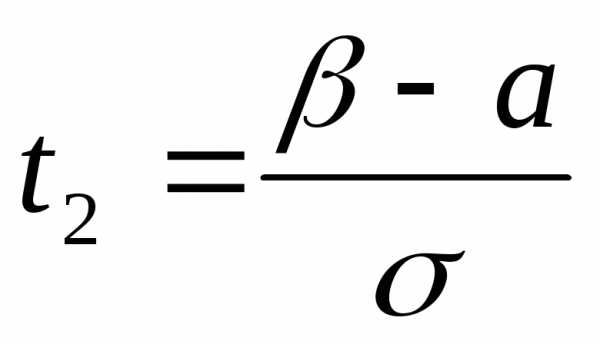 .
.
Таким образом,
(3)
По условию задачи имеем: а=5; σ= =0,8;
α=4; β=7. Подставив эти данные в (3), получим:
=0,8;
α=4; β=7. Подставив эти данные в (3), получим:
=Ф(2,5)-Ф(-1,25)=
=Ф(2,5)+Ф(1,25)=0,4938+0,3944=0,8882.
Пример. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Стандартная длина (математическое ожидание) а=40 см, среднее квадратическое отклонение σ=0,4 см. Найти вероятность того, что отклонение длины от стандартной составит по абсолютной величине не более 0,6 см.
Решение. Если Х – длина детали, то по условию задачи эта величина должна быть в интервале (а-δ,а+δ), где а=40 и δ=0,6.
Положив в формулу (3) α= а-δ и β= а+δ, получим
Итак,
. (4)
Подставив в (4) имеющиеся данные, получим:
Следовательно, вероятность того, что изготавливаемые детали по длине будут в пределах от 39,4 до 40,6 см, составляет 0,8664.
Пример. Диаметр деталей, изготавливаемых заводом, является случайной величиной, распределенной по нормальному закону. Стандартная длина диаметраа=2,5см, среднее квадратическое отклонение σ=0,01. В каких границах можно практически гарантировать длину диаметра этой детали, если за достоверное принимается событие, вероятность которого равна 0,9973?
Решение. По условию задачи имеем:
а=2,5; σ=0,01; .
Применяя формулу (4), получаем равенство:
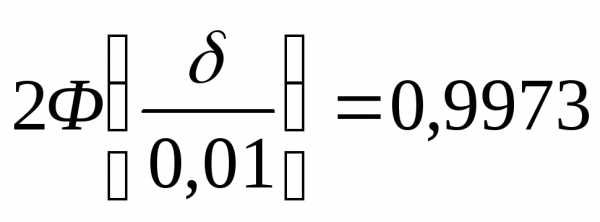 или
или .
.
По таблице 2 находим, что такое значение
функция Лапласа имеет при х=3. Следовательно,  ;
откуда σ=0,03.
;
откуда σ=0,03.
Таким образом, можно гарантировать, что длина диаметра будет изменяться в пределах от 2,47 до 2,53 см.
studfiles.net
Тема 5. Формула Пуассона. Локальная и интегральная формулы Муавра
Формула Пуассона
Использование
формулы Бернулли при больших значениях  и
и вызывают большие трудности. Например,
при 1000 подбрасываниях монеты необходимо
определить вероятность того, что «герб»
выпадет ровно 150 раз. В этом случае,
вызывают большие трудности. Например,
при 1000 подбрасываниях монеты необходимо
определить вероятность того, что «герб»
выпадет ровно 150 раз. В этом случае,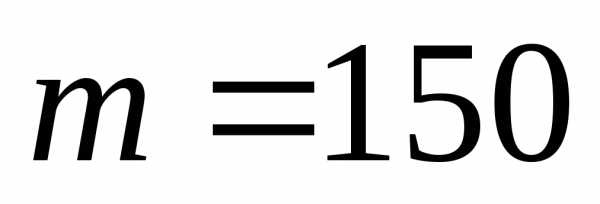 ,
, (выпадение «герба»),
(выпадение «герба»), (выпадение «решки»). Формула Бернулли
примет вид:.
(выпадение «решки»). Формула Бернулли
примет вид:.
Вычисления будут
очень громоздкими, поэтому возникает
необходимость в отыскании приближенных
формул для вычисления  ,
обеспечивающих необходимую точность.
Такие формулы дают нам предельные
теоремы; они содержат так называемые
асимптотические формулы, которые при
больших значениях испытаний дают сколь
угодно малую относительную погрешность.
Рассмотрим три предельные теоремы,
содержащие асимптотические формулы
для вычисления вероятности при.
,
обеспечивающих необходимую точность.
Такие формулы дают нам предельные
теоремы; они содержат так называемые
асимптотические формулы, которые при
больших значениях испытаний дают сколь
угодно малую относительную погрешность.
Рассмотрим три предельные теоремы,
содержащие асимптотические формулы
для вычисления вероятности при.
Теорема Пуассона. Если число испытаний неограниченно
увеличивается
и вероятность наступления события
наступления события в каждом испытании неограниченно
уменьшается
в каждом испытании неограниченно
уменьшается ,
но так, что их произведение является
постоянной величиной,
то вероятность
,
но так, что их произведение является
постоянной величиной,
то вероятность удовлетворяет
предельному равенству
удовлетворяет
предельному равенству

или
 ,
,  .
.
Формулу Пуассона
обычно используют в случае, когда λ 10.
10.
Пример 1. Завод отправляет в некоторый город 1500 автомобилей. Вероятность того, что в пути машина может получить повреждение, равна 0,002. Найти вероятность того, что в пути будет повреждено не более 4-х автомобилей.
Решение. Событие  – в пути будет повреждено не более 4-х
автомобилей, т.е. 0, 1, 2, 3, 4.
– в пути будет повреждено не более 4-х
автомобилей, т.е. 0, 1, 2, 3, 4.
, ,.
По формуле Пуассона
Локальная теорема Муавра – Лапласа
Теорема. Если вероятность 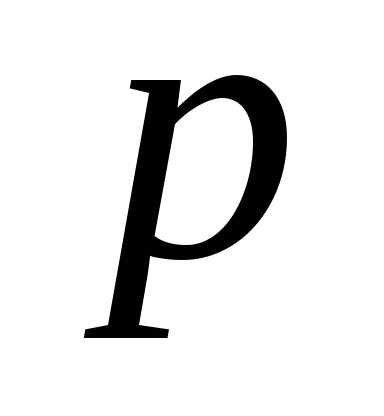 наступления события
наступления события в каждом испытании постоянна и отлична
от 0 и 1, а число независимых испытаний
достаточно велико, то вероятность
в каждом испытании постоянна и отлична
от 0 и 1, а число независимых испытаний
достаточно велико, то вероятность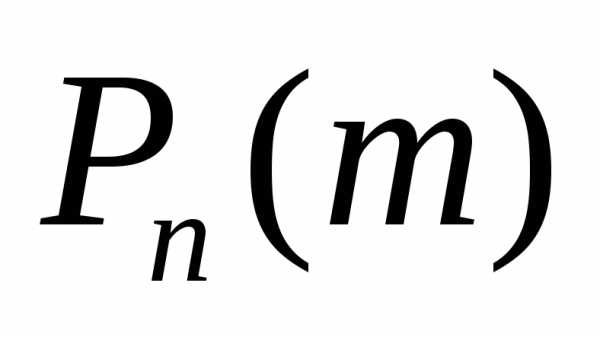 может быть вычислена по приближенным
формулам:
может быть вычислена по приближенным
формулам:
 ,
,
где 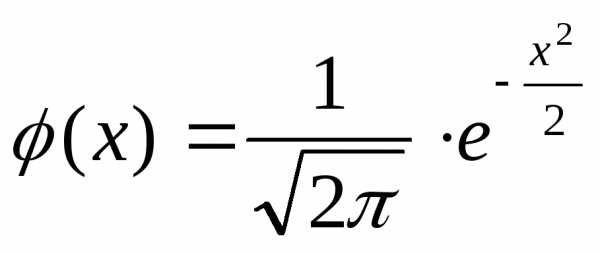 ,
, .
.
Функция  называется функцией Гаусса.
называется функцией Гаусса.
Свойства функции  .
.
1. Функция  — четная, т.е.
— четная, т.е. =
=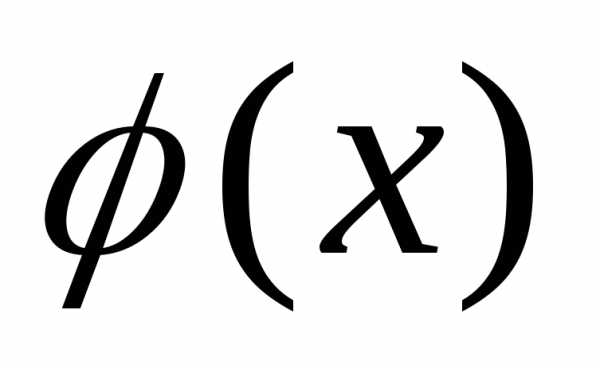 .
.
2. Функция  — монотонно убывает, при
— монотонно убывает, при можно считать, что
можно считать, что .
.
Пример 2. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение.  ,
,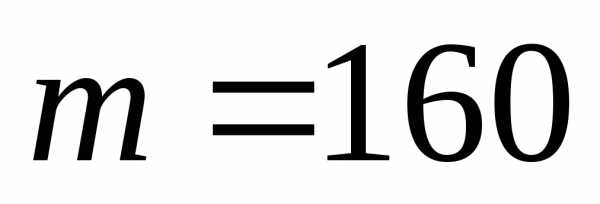 ,,
,, .
.
.
Учитывая, что , получим
3. Интегральная теорема Муавра – Лапласа
В тех случаях,
когда требуется вычислить вероятность
того, что в  независимых испытаниях событие
независимых испытаниях событие появится не менее
появится не менее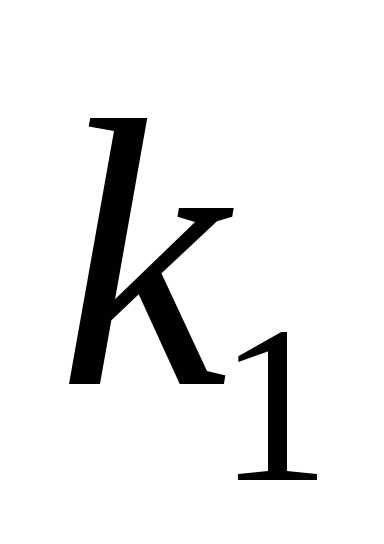 раз и не более
раз и не более раз, т.е.используют интегральную теорему Муавра
– Лапласа.
раз, т.е.используют интегральную теорему Муавра
– Лапласа.
Теорема. Если вероятность наступления  наступления события
наступления события в каждом испытании постоянна и отлична
от 0 и 1, то вероятностьможет быть найдена по приближенной
формуле
в каждом испытании постоянна и отлична
от 0 и 1, то вероятностьможет быть найдена по приближенной
формуле
,
где  ,специальная
функция, называемая нормированной
функцией Лапласа,
,специальная
функция, называемая нормированной
функцией Лапласа,
 ,
, 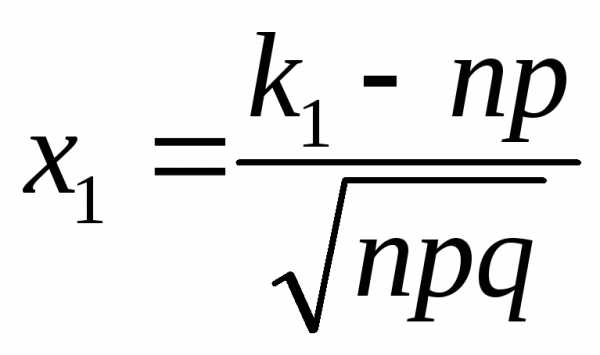 .
.
Свойства функции  .
.
1. Функция  — нечетная, т.е..
— нечетная, т.е..
2. Функция  монотонно возрастает, т.е. при
монотонно возрастает, т.е. при  можно считать, что
.
можно считать, что
.
Имеются таблицы
приближенных значений функции  ,
которыми удобно пользоваться для решения
задач.
,
которыми удобно пользоваться для решения
задач.
Пример 3. Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия бракуется, т.е. возвращается в цех. Какова вероятность того, что партия будет принята?
Решение.  ,
,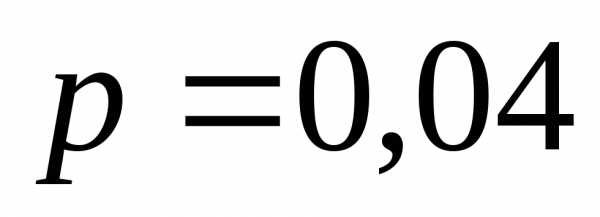 – вероятность бракованного изделия,
– вероятность бракованного изделия, – вероятность хорошего изделия.
– вероятность хорошего изделия.
Вероятность
принятия всей партии, т.е.можно найти по формуле: ,
, ,
,
,
,
,
,
.
studfiles.net
Локальная формула Муавра-Лапласа.
На
практике пуассоновским приближением
пользуются при  .
Если
.
Если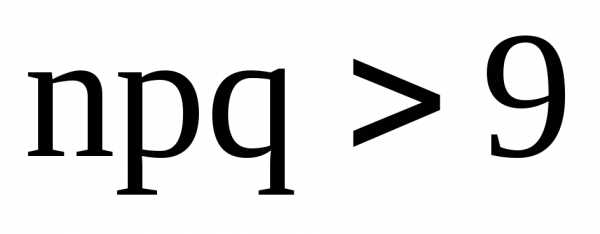 , то для расчетов используют приближение
в соответствии с теоремой Муавра-Лапласа.
, то для расчетов используют приближение
в соответствии с теоремой Муавра-Лапласа.
Пусть
0<p<1
и величина  ограничена при, тогда
ограничена при, тогда
Требование
ограниченности величины  означает, что при величина k
тоже должна расти вместе с величиной
n.
Точность формулы
означает, что при величина k
тоже должна расти вместе с величиной
n.
Точность формулы

растет
как с ростом величин n
и k
, так и по мере приближения величин p
и q
к 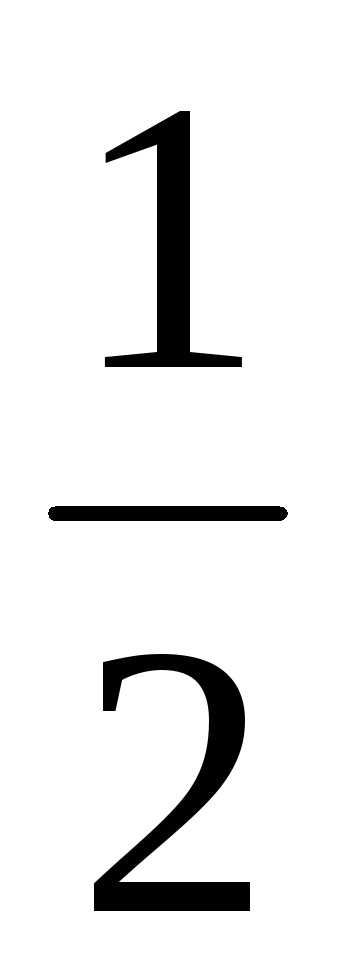 .
.
Пояснения к заданию е №2
Исследуйте для указанных значений параметров биноминального распределения точность асимптотической формулы Муавра-Лапласа.
Порядок выполнения задания.
1 Вычислите требуемые вероятности по формуле Бернулли.
2. Вычислите требуемые вероятности по интегральной формуле Муавра-Лапласа.
Сравните полученные результаты.
Пример выполнения задания.
Для
n=10,
20, 50 и для p=0.5,
0.3, 0.2 вычислите вероятность того, что
случайная величина, имеющая биномиальное
распределение, принимает значение,
равное  .
Проведите вычисления по формуле Бернулли
и по приближенной формуле Муавра-Лапласа.
Сравните результаты.
.
Проведите вычисления по формуле Бернулли
и по приближенной формуле Муавра-Лапласа.
Сравните результаты.
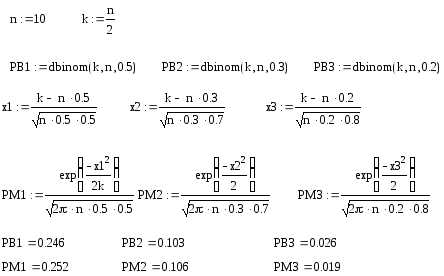 Фрагмент
рабочего документа Mathcad
с решением задачи приведен
ниже.
Фрагмент
рабочего документа Mathcad
с решением задачи приведен
ниже.


Приведенные утверждения полностью подтверждают теоретические утверждения: погрешность аппроксимации уменьшается с ростом n и по мере приближения p и q к 0.5 .
Интегральная формула Муавра-Лапласа.
Пусть 0<p<1 , тогда для случайной величины, имеющей биноминальное распределение с параметром р, при для любыхa и b справедлива формула
Это
означает следующее. Для вычисления
вероятности того, что число успехов в
n
испытаниях Бернулли заключено между  , можно использовать формулу
, можно использовать формулу
,
где .
В Mathcad для вычисления значений Ф(х) предназначена функция pnorm(x,k0,1)
Пояснения к заданию № 3.
Исследуйте для указанного биноминального распределения точность интегральной формулы Муавра – Лапласа.
Порядок выполнения задания.
Вычислите требуемые вероятности по формуле Бернулли.
Вычислите требуемые вероятности по интегральной формуле Муавра-Лапласа.
Вычислите требуемые вероятности по модифицированной интегральной формуле Муавра-Лапласа
Сравните полученные результаты.
Пример выполнения задания.
Вероятность рождения мальчика p=0.51 , а девочки q=1-p=0.49. Найти вероятность того, что среди 10000 новорожденных мальчиков будет не менее 4000 и не более 5000. Проведите вычисления по формуле Бернулли и по приближенным интегральным формулам Муавра-Лапласа. Сравните результаты.
 Фрагмент
рабочего документа Mathcad
с решением задачи приведен ниже.
Фрагмент
рабочего документа Mathcad
с решением задачи приведен ниже.
Приведенные вычисления полностью подтверждают теоретические утверждения : приближенные значения вероятностей совпадают с вероятностями, вычисленными по формуле Бернулли.
Порядок выполнения работы. Задание № 1
Исследуйте
для приведенного в задании эксперимента
точность фсимптотической формулы
Пуассона. Вычислите вероятность события  для биноминального распределения и
по приближенной формуле Пуассона
для биноминального распределения и
по приближенной формуле Пуассона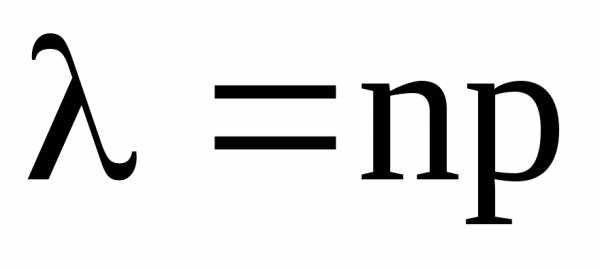 . Для сравнения выполните вычисления
для и
.
. Для сравнения выполните вычисления
для и
.
В а р и а н т ы 1-10. Провайдер обслуживает n абонентов сети Internet . Вероятность того, что любой абонент захочет войти в сеть в течение часа, равна р. Найти вероятность тоо, что в течение часа более k абонентов попытаются войти в сеть.
В а р и а н ты 11-20. Магазин продает в течение одного дня n коробок конфет, часть которых с сюрпризом. Вероятность того, что коробка с сюрпризом, равна р. Найти вероятность того, что в течение дня продано более k коробок с сюрпризом.
N | p | n | k | N | p | n | k |
1 | 1000 | 0.003 | 3 | 11 | 2000 | 0.0020 | 6 |
2 | 1100 | 0.0029 | 4 | 12 | 2100 | 0.019 | 3 |
3 | 1200 | 0.0028 | 5 | 13 | 2200 | 0.0018 | 4 |
4 | 1300 | 0.0027 | 5 | 14 | 2300 | 0.0017 | 6 |
5 | 1400 | 0.0026 | 4 | 15 | 2400 | 0.0016 | 8 |
6 | 1500 | 0.0025 | 3 | 16 | 2500 | 0.0015 | 5 |
7 | 1600 | 0.0024 | 3 | 17 | 2600 | 0.0014 | 4 |
8 | 1700 | 0.0023 | 6 | 18 | 2700 | 0.0013 | 3 |
9 | 1800 | 0.0022 | 9 | 19 | 2800 | 0.0012 | 3 |
10 | 1900 | 0.0021 | 9 | 20 | 2900 | 0.0011 | 4 |
studfiles.net
12. Локальная формула Муавра-Лапласа. Привести пример.
Если в схеме независимых испытаний Бернулли число испытаний n велико, а вероятности успеха и неудачи не малы (например, 0,1<p<0,9), то вероятность Pn(m) появления ровно m успехов в n испытаниях вычисляется по формуле (локальная теорема Муавра-Лапласа):
Pn(m)=где(х)=. Функция(х) – четная и для положительных значений х составлена таблица ее значений.
Пример. Вероятность поражения мишени стрелком при одном выстреле р=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
13. Интегральная формула Муавра-Лапласа. Привести пример. Если в схеме Бернуллиpсущественно отличается от 0 и 1, аnдостаточно велико, то вероятностьтого, что вnнезависимых испытаниях событие А наступит не менее раз, но менее раз, вычисляется поинтегральной формуле Муавра-Лапласа:
, где – функция Лапласа,, ,причём Ф(-х)=-Ф(х), Ф(х)≈0,5 при х≥5.
Формулы Муавра-Лапласа, как правило, используются, если 0,1<p<0,9, и дают хорошие результаты, если npq велико (>=20).
Пример. Вероятность появления события А в каждом из 600 независимых испытаний равна 0,6. Найдите вероятность того, что событие А в этих испытаниях наступит не менее 330 и не более 375 раз.
14. Случайная величина. Виды случайных величин. Закон распределения (распределение) СВ. Привести примеры. Под случайной величиной (СВ) понимают величину, которая в результате опыта принимает некоторое числовое значение, причём неизвестно заранее, какое именно.
Виды СВ: а) СВ называется дискретной, если множество ее возможных значений конечно или счетно (т.е. если все значения можно пересчитать).
Пример (а): Число очков, выпавших при однократном бросании игральной кости.
б) СВ называется непрерывной, если её функция распределения непрерывна на всей числовой оси. Непрерывная СВ принимает все значения из некоторого интервала или системы интервалов на числовой оси.
Пример (б): Прирост веса домашнего животного за месяц.
Законом распределения СВ называется любое правило, позволяющее определить её функцию распределения. О СВ говорят, что она распределена по данному закону или подчинена этому закону.
15. Дискретная случайная величина. Ряд распределения. Многоугольник распределения. Привести пример. СВ называется дискретной, если множество ее возможных значений конечно или счетно (т.е. если все значения можно пересчитать).
Ряд распределения – это закон распределения, заданный в виде таблицы, в которой перечислены все возможные значения СВ ξ и соответствующие им вероятности.
Многоугольник распределений – это как статистический аналог полигона.
Пример. В денежной лотерее разыгрывается 1 выигрыш в 1000 у.е., 10 выигрышей по 100 у.е. и 100 выигрышей по 1 у.е. при общем числе билетов 10 000. Найти закон распределения случайного выигрыша ξ для владельца одного лотерейного билета.
16. Функция распределения дискретной СВ и её основные свойства. Функцией распределенияслучайной величиныназывается функция,
определяющая вероятность того, что случайная величина примет значение, меньшее.
Свойства функции распределения:
а) функция распределения принимает значения только из отрезка [0,1]: 0 ≤ F(x) ≤ 1;
б) F(x) – неубывающая функция, т.е. еслиx2 > x1, то F(x2) > F(x1) ;
в) F(- ∞ ) = 0;F(+ ∞) = 1;
г) вероятность того, что случайная величина примет значение из интервала (причем), равна;
д) F(x) непрерывна слева, т. е.F(x) =F(x– 0).
17. Математическое ожидание дискретной СВ и его смысл. Основные свойства математического ожидания. Математическим ожиданиемДСВназывается среднее значение данной случайной величины
,
т. е. математическое ожидание – это сумма произведений значений случайной величины на соответствующие вероятности.
Свойства математического ожидания.
а), где;
б);
в);
г)если случайные величиныинезависимы, то.
studfiles.net
2.2. Формулы Лапласа
2.2.1 Локальная теорема Лапласа
Решим следующую задачу (задача Банаха).
Некто носит в кармане две коробки спичек
(по 60 спичек каждая) и всякий раз, когда
нужна спичка, наугад берет коробку и
вынимает спичку. Какова вероятность
того, что когда первая коробка будет
пуста, во второй все еще останется 20
спичек? Выбор коробки можно рассматривать
как независимое испытание, в котором с
вероятностью 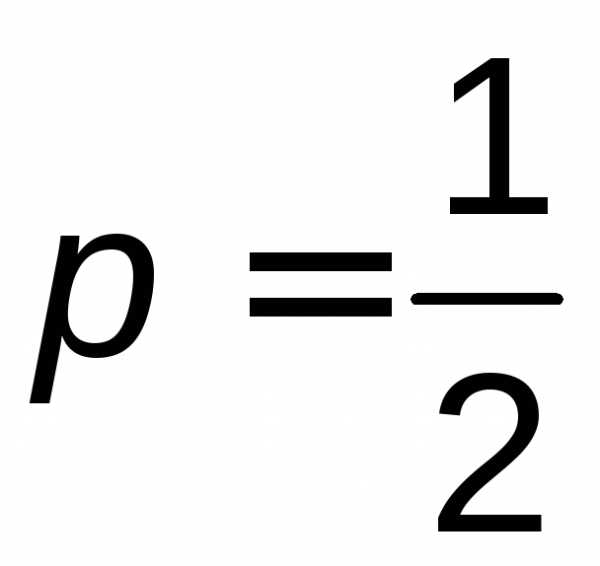 выбирается первая коробка. Всего опытов
производитсяn=
60+40=100, и в этих ста опытах первая коробка
должна быть выбрана 60 раз. Вероятность
этого равна:
выбирается первая коробка. Всего опытов
производитсяn=
60+40=100, и в этих ста опытах первая коробка
должна быть выбрана 60 раз. Вероятность
этого равна:
.
Из записи видно, что при больших nпользоваться формулой Бернулли
затруднительно из-за громоздких
вычислений. Существуют специальные
приближенные формулы, которые позволяют
находить вероятности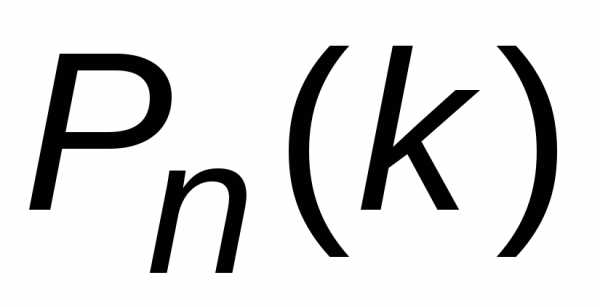 ,
еслиnвелико. Одну из
таких формул дает следующая теорема.
,
еслиnвелико. Одну из
таких формул дает следующая теорема.
Теорема 2.1. (Лапласа локальная). Если в схеме Бернулли, то вероятность того, что событиеAнаступит ровноkраз, удовлетворяет при большихnсоотношению
 где
где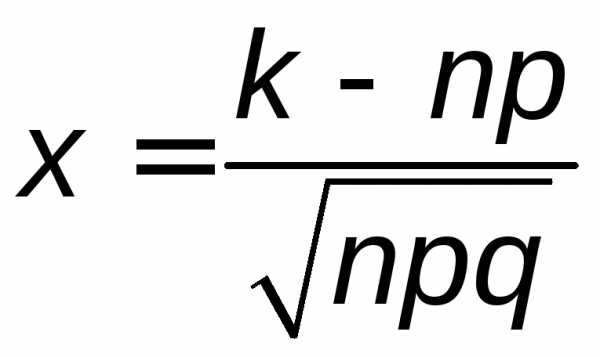 .
.
Для удобства вводится в рассмотрение
функция 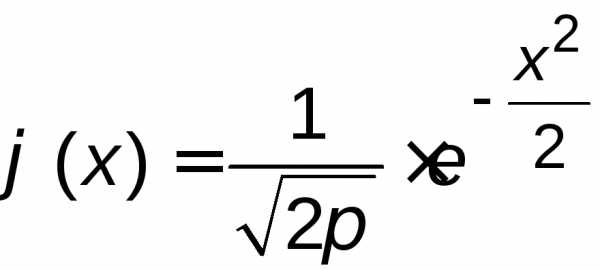 –
локальная функция Лапласа, с помощью
которой теорему Лапласа можно записать
так:
–
локальная функция Лапласа, с помощью
которой теорему Лапласа можно записать
так:
Существуют специальные таблицы функции 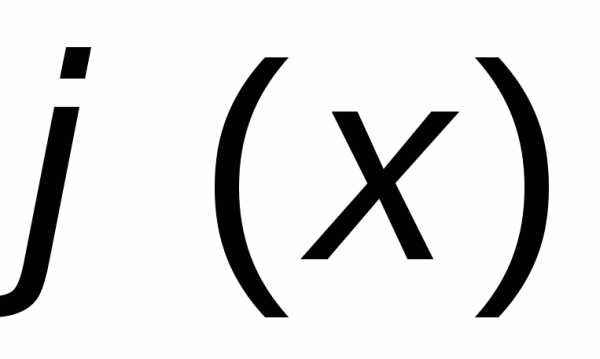 [4],
по которым для любого значения:
[4],
по которым для любого значения: можно найти соответствующее значение
функции. Получены эти таблицы путем
разложения функции
можно найти соответствующее значение
функции. Получены эти таблицы путем
разложения функции в ряд.
в ряд.
Геометрически этот результат означает,
что для больших nмногоугольник распределения хорошо
вписывается в график функции, стоящей
в формуле справа (рис. 2.3) и вместо
истинного значения вероятности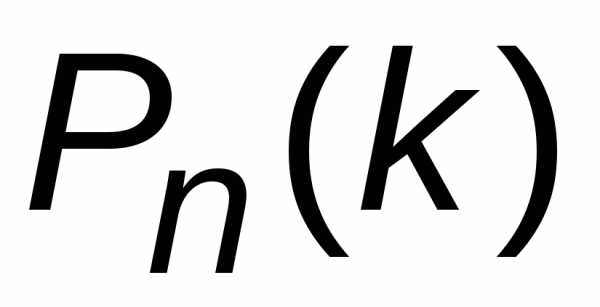 можно для каждогоkбрать значение функции в точкеk.
можно для каждогоkбрать значение функции в точкеk.
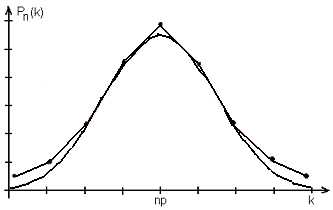
Рис. 2.3. Локальная функция Лапласа
Вернемся теперь к задаче. Используя формулу (2.1) находим:
,
где значение  определено по таблице [4].
определено по таблице [4].
2.2.2. Интегральная теорема Лапласа
Теорема 2.2 (Лапласа интегральная). Вероятность того, что в схемеnнезависимых испытаний событие наступит отk1доk2раз, приближенно равна
Pn (k1 k2)
k2) ,
,
где
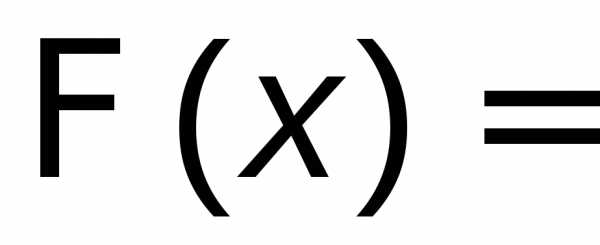
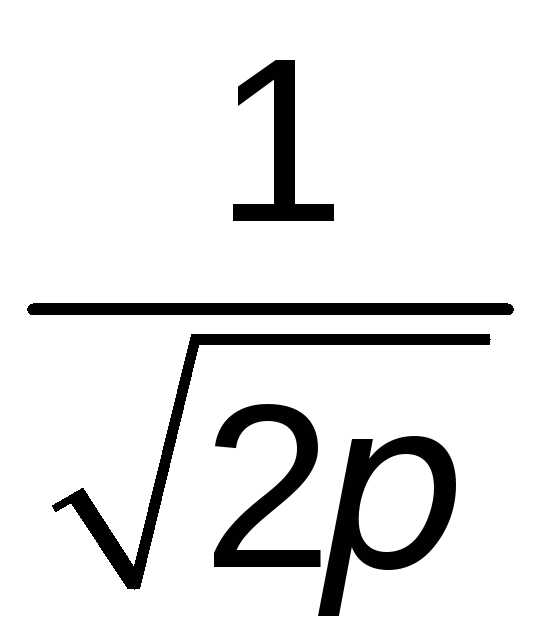

 –
интегральная функция Лапласа, для
которой составлены таблицы. ФункцияФ(х)нечетная:Ф(-х)=-Ф(х) иФ(х
–
интегральная функция Лапласа, для
которой составлены таблицы. ФункцияФ(х)нечетная:Ф(-х)=-Ф(х) иФ(х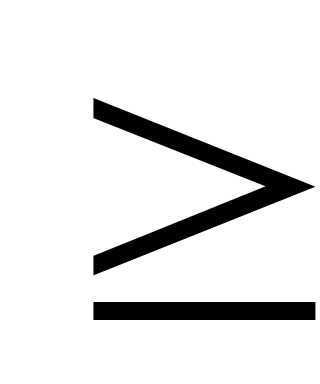 4)=0,5.
4)=0,5.
Рассмотрим пока без доказательства еще одно утверждение.
Отклонение относительной частоты  от вероятностиpвnнезависимых испытаниях равно
от вероятностиpвnнезависимых испытаниях равно
(
 .
.
Замечание.Обоснование этих фактов будет рассмотрено далее в разделе 7 (подразд. 7.2, 7.3). Теоремы Лапласа иногда называют теоремами Муавра–Лапласа.
Пример 2.3.
Вероятность появления события в каждом из 900 независимых испытаний равна 0.5. 1) найти вероятность того, что событие произойдет от 400 до 500 раз, 2) найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
Решение
1) Р900(400<k<500)==
2)  =
=
2.3. Формула Пуассона
Если зафиксировать число опытов n, а вероятность появления события в одном опытеризменять, то многоугольник распределения будет иметь различный вид в зависимости от величиныр(рис.2.4). При значенияхp, близких к 1/2, многоугольник почти симметричен и хорошо вписывается в симметричный график функции Лапласа. Поэтому приближенная формула Лапласа дает хорошую точность.

Рис. 2.4.
Для малых р(на практике меньших)
приближение плохое из-за несимметричности
многоугольника распределения. Поэтому
возникает задача найти приближенную
формулу для вычисления вероятностей в случае большихnи
малых р. Ответ на этот вопрос дает
формула Пуассона.
в случае большихnи
малых р. Ответ на этот вопрос дает
формула Пуассона.
Итак, рассмотрим схему независимых испытаний, в которой nвелико (чем больше, тем лучше), армало (чем меньше, тем лучше). Обозначимnр=λ. Тогда по формуле Бернулли имеем
.
Последнее равенство верно в силу того,
что  (второй замечательный предел). При
получении формулы наивероятнейшего
числа появления событияk0было рассмотрено отношение вероятностей.
Из него следует, что
(второй замечательный предел). При
получении формулы наивероятнейшего
числа появления событияk0было рассмотрено отношение вероятностей.
Из него следует, что
Таким образом, при kмного меньшихnимеем рекуррентное соотношение
.
Для k=0 учтем полученный ранее результат:, тогда
………………

Итак, если в схеме независимых испытаний nвелико, ар мало, то имеет местоформула Пуассона
Рn(к) ,
где λ=nр.
,
где λ=nр.
Закон Пуассона еще называют законом редких явлений.
Пример 2.4.
Вероятность выпуска бракованной детали равна 0,02. Детали упаковываются в коробки по 100 штук. Какова вероятность того, что а) в коробке нет бракованных деталей, б) в коробке больше двух бракованных деталей?
Решение
a) Так какnвелико, армало, имеем ; Р100(0);
б)Р100(k>2)=1-Р1-
Таким образом, в схеме независимых испытаний для вычисления вероятности Рn(k)следует пользоваться формулой Бернулли, еслиnневелико, а еслиnвелико, то в зависимости от величиныриспользуется одна из приближенных формул Лапласа или формула Пуассона.
studfiles.net
