| Слайд 1 Орг. момент Учитель читает стихи про карандаш. |
|
| Слайды 2-6
Устный счёт «Собери букет», «Испеки пирог». (таблица умножения на 8, 9) |
|
| Слайд 7 – Ребята, какая я невнимательная, забыла написать тему сегодняшнего урока. Как быть? Слайд 8 |
|
| – Прочитайте задание на слайде. – Открываем тетрадь. Прочитайте внимательно задания теста. – Выполните все задания теста. Время – 5минут! – Так какая тема сегодняшнего урока? |
|
| Слайд 9 – Совершенно верно, тема сегодняшнего урока: «Площадь прямоугольника». 1) Выяснить значения слова площадь; 2) Повторить способы сравнения площади фигур и познакомиться с новым способом; 3) Сформулировать правило нахождения площади прямоугольника и вывести формулу; 4) Уметь решать задачи на нахождение площади прямоугольника. |
|
| Слайд 10 – Какие ассоциации у вас возникают при слове «площадь»? Что сразу приходит на ум? – Пожалуйста, поделитесь своими мыслями. Учитель заслушивает все варианты ответа. (площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.) |
|
| Слайд 11
– Посмотрите, что изображено на слайде? – Да, это Красная площадь – центральная площадь Москвы. Возникновение Красной площади относится к концу 15 века, когда по приказу царя Ивана III были снесены деревянные постройки вокруг Кремля, угрожавшие постоянными пожарами. На их месте была организована площадь для мелкой торговли. Первоначально она так и называлась – Торговая. Красной площадь стали называть только в 17 веке. – А это что за площадь? Это одна из центральных площадей города Санкт-Петербурга. Она называется Сенатская площадь. Сенатская площадь была названа так после размещения на ней правительственного учреждения Сената. Сенатская площадь является одной из самых старых площадей Санкт-Петербурга. – Все узнали центральную площадь нашего города. Кто знает, как она называется? Совершенно верно, это площадь Ленинского комсомола. – Обратитесь за помощью к родителям, бабушкам и дедушкам, справочной литературе, сети Интернет, чтобы найти ответы на эти вопросы. А на ближайшем уроке окружающего мира мы вернёмся к этой теме. |
|
| Слайд 12 – Давайте прочитаем значения слова «площадь». Два ученика по слайду зачитывают по просьбе учителя. |
|
| Слайд 13 – Заглянем в толковый словарь русского языка В.И. Даля. – Внимательно прочитайте значение слова «площадь». Вдумайтесь в смысл! |
|
| Слайд 14
– Какие способы измерения площади фигур вам известны? Учитель заслушивает все варианты ответа. |
|
| Слайд 15
– Действительно, существует несколько способов: визуально, т.е. на глаз, способ наложения фигур и с использованием мерок. |
|
| Слайд 16
– Сравните на глаз площади треугольников. Что вы можете о них сказать? – Какова площадь круга: больше или меньше? |
|
– Что можете сказать о площади квадратов? – Почему площадь зелёного квадрата меньше? (полностью помещается в розовом квадрате) – Можно ли утверждать, что площадь треугольника больше площади самого маленького квадрата? – Почему? |
|
| Слайд 18 – Ещё один способ: подсчёт количества мерок, уложившихся в той или иной фигуре. – Сколько мерок уложилось в жёлтом прямоугольнике? – Площадь какого прямоугольника больше? – Что получится, если я буду использовать разные мерки для сравнения площадей этих прямоугольников: квадраты, круги, треугольники, овалы и т.д.? |
|
| Слайд 19 – Прочитаем вывод хором! Учитель говорит о том, что пришло время отдохнуть, напоминает о взаимной вежливости. |
|
| Слайд 20
Физ.минутка |
|
| Слайд 21 Учитель зачитывает по слайду. Гиперссылка = нажать на слово «единицы». – Если данная мерка – это один квадратный сантиметр, то чему тогда равна площадь каждого прямоугольника? (ответы детей)Гиперссылка = нажать на слово «мерка». |
|
| Слайд 22 – Есть ли такие единицы измерения площади, как квадратный дециметр, квадратный метр?Учитель заслушивает все варианты ответов. – Об этом мы узнаем на ближайших уроках математики. |
|
| Слайд 23 лежат конверты. Откройте их, достаньте геометрические фигуры. – Прочитайте задание на слайде. – Работа в парах: нужно сравнить площади этих фигур. – Как это сделать? Время для работы – одна минута! |
|
| – Ребята, вы молодцы! – Есть такое приспособление в математике!Слайд 24 Учитель зачитывает по слайду, раздаёт всем палетки. – Измерьте при помощи палетки площади данных фигур. – Что вы заметили? |
|
| Слайд 25 Дети сравнивают свои ответы с данным. – Молодцы! |
|
| Слайд 26 – Прочитайте вывод. |
|
| Слайд 27
– Как найти площадь прямоугольника? |
|
| Слайд 28 – Сначала нужно измерить стороны прямоугольника, т.е. узнать длину и ширину. |
|
| Слайд 29 – Прочитайте «про себя» правило нахождения площади прямоугольника. – Постарайтесь запомнить его, а дома выучить наизусть. |
|
| Слайд 30
– Постарайтесь запом |
xn--i1abbnckbmcl9fb.xn--p1ai
3 класс. Математика. Вычисление площади прямоугольника — Площадь прямоугольника
Комментарии преподавателя
Мы уже познакомились с понятием площадь фигуры, узнали одну из единиц измерения площади – квадратный сантиметр. На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см2, площадь второй фигуры 7 см2.
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см2.
Этот же прямоугольник можно разбить на 3 полоски по 4 см2.
Тогда площадь прямоугольника будет равна 4*3=12 см2.
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см2, а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
6*2=12 см2
Число 6 обозначает длину прямоугольника, а 2 – ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см2, а таких полосок 3. Следовательно, мы можем выполнить действие
2*3=6см2
Число 3 обозначает длину прямоугольника, а 2 – ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина – 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
9*2=18см2
Ответ: площадь прямоугольника 18см2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь – это произвед
www.kursoteka.ru
«Площади фигур». 3-й класс
Разделы: Начальная школа, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,8 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок комплексного применения знаний и умений
Цель урока: создавать условия для формирования умения решать задачи на нахождение площади фигур через совершенствование вычислительных навыков, знакомство со старинными мерами длины и площади, развитие логического мышления учащихся, кругозора, трудолюбия и аккуратности.
Задачи урока:
Образовательные:
- формировать целостный взгляд на мир средствами междисциплинарных связей на уроке; ориентировать на разнообразие способов решения задач и выбор наиболее рациональных из них; отрабатывать навыки решения задач с применением известных формул.
Развивающие:
- развивать творческую и мыслительную деятельность учащихся через решение геометрических заданий; формировать навыки самостоятельной и коллективной работы.
Воспитательные:
- прививать учащимся интерес к предмету через решение задач; формировать умение ясно и четко излагать свои мысли, правильно и рационально решать геометрические задачи; воспитывать веру в свои силы.
Методы: практический, частично-поисковый.
Организация пространства: работа фронтальная, групповая, индивидуальная, в парах (учащиеся располагаются за столами по 4 человека).
Оборудование: модели единиц площади (1см2, 1дм2, 1м2) на стенах класса, модели сложных фигур на листах А2, индивидуальные листы, презентация, листы А4, фломастеры.
Личностные УУД: осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Регулятивные УУД: определять и формулировать цель на уроке с помощью учителя; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.
Коммуникативные УУД: развивать коммуникативные навыки работы в группе.
Познавательные УУД: ориентироваться в своей системе знаний; понимать информацию, представленную в схематичной, модельной форме; выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; самостоятельно создавать способы решения проблем творческого и поискового характера.
Планируемые результаты:
Метапредметные
- использовать знаково-символические средства представления информации для создания способов решения практических задач.
Предметные результаты
- Уметь вычислять площади простых и сложных фигур разными способами;
- Уметь использовать наглядные модели (план, чертеж, схема), отражающие отношения между предметами для решения задач;
- Овладеть основами пространственного воображения, измерения, наглядного представления периметра и площади фигур.
Ход урока
I. Организационный момент
Учитель:
— Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В мир математики отправимся смело,
В мир примеров и разных задач.
А девизом нашего урока будут слова: (Хором.)Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно! (Слайд 2.)
II. Актуализация знаний учащихся
Учитель:
— Перед Вами древнерусская деревня. (Слайд 3.)
(Читает ученик.) Полторы тысячи лет прошло с тех пор, как на берегу реки на большой лесной равнине поселились славяне. Свое поселение они обнесли частоколом, высотой в целую сажень. Длина деревни достигала одной версты. В домах древних славян пол был углублен в землю почти на целый аршин. В углу находилась сложенная из камня печь - она обогревала дом, на ней же готовили еду. Вход в избу закрывала дверь толщиной в вершок.
— О каких величинах Вы услышали?
— Их использовали наши предки. Ребята познакомят с ними. (Слайды 4 — 9.) (Сообщения учащихся о старинных единицах длины и показ.)
1) Вершок – длина фаланги указательного пальца, мера длины, равная примерно 4-5 см.
2) Пядь — мера длины, равная расстоянию между концами вытянутых пальцев – большого и указательного.
3) Локоть – расстояние от концов пальцев до локтя согнутой руки.
4) При торговле с восточными народами стали применять аршин. В нем укладывается 16 вершков. Это примерно 71см. Первоначально “аршин” обозначал длину человеческого шага.
5) В Древней Руси применялись косая сажень – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки; маховая сажень – расстояние между концами пальцев разведенных в стороны рук.
6) Для измерения больших расстояний на Руси использовали версту.
Учитель:
— Сегодня мы пользуемся современными терминами, обозначающими меры длины. Где могут встретиться “локти”, “аршины”, “пяди”?
— Часто в своей речи мы используем пословицы, но, не зная толкования слова “пядь”, вряд ли бы сумели мы разобраться в значении выражений “Семи пядей во лбу”, “На свой аршин мерит”.
III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Подготовка: участник № 1 складывает лист формата А4 так, чтобы он разделился на 8 частей.
Учитель:
— Участники, по очереди запишите современные единицы, которые используем на уроках математики. № 1, разрежьте лист на отдельные листочки. Разделите листочки на группы. Назовите их. (Единицы длины и единицы площади.)
| см | дм | м | мм |
| см2 | дм2 | м2 | км |
— № 2, переверните листочки с единицами площади, перемешайте и раздайте их участникам своей группы.
— № 1, 3, 4, посмотрите на листочек и выберите, к какой модели сейчас отправитесь. (Участники № 1,3,4 групп получают листочки с записью единиц площади и отправляются к выбранным моделям: 1см2, 1дм2, 1м2, представленных на стенах класса.)
— Обсудите в группах, почему выбрали эту модель. Обсуждение и представление выбранной модели:
1) 1см2 — очень маленький, но играет важную роль в математике. Это квадрат со стороной 1см;
2) 1 дм2 — квадрат со стороной 1дм или 10см. В нем содержится 100 см2;
3) 1 м2 в 100 раз больше 1дм2 и в 10000 раз больше 1см2.
— Назовите одним словом. (Единицы площади.)
— Для измерения площади у русского народа были свои особые мерки: “копна”, “выть”, “соха”, “обжа”, “десятина”. От древних землемеров нам досталось только слово “площадь”.
— № 2, образуйте группу. Назовите ее. (Современные единицы длины.)
— Сформулируйте тему урока. Чему будем учиться?
— Еще 4-5 тысяч лет назад жители древнего города Вавилон умели определять площадь. Какая фигура служила эталоном при измерении площади?
— Квадрат, благодаря своим замечательным свойствам. Знаете их? Выясните в группах. (Обсуждение и обмен мнениями: 1) Равные стороны; 2) Прямые углы; 3) Совершенная форма; 4) Легко строить.)
— В Древнем Китае мерой площади была другая фигура. Догадайтесь, какая.
— Почему на уроке по нахождению площади фигур присутствуют единицы длины?
IV. Первичное закрепление в знакомой ситуации
а) Типовые задания
Устный счет “Калькулятор площади”. (Слайд 10 .)
Решение задач и объединение учащихся в группы в зависимости от ответа.
1. Длина прямоугольника 6см, ширина 2см. Чему равна третья часть площади прямоугольника?
2. Площадь коридора 18м2. Вычислите ширину, если длина 9м.
3. Найдите площадь прямоугольника, ширина которого 2см, и она в 3 раза меньше его длины.
4. Площадь фундамента дома квадратной формы 64м2. Чему равна сторона фундамента?
5. Найдите площадь прямоугольника, одна сторона которого 6см, другая – на 2см короче.
6. Во сколько раз площадь зала, равная 27м2, больше площади комнаты, равной 9м2?
Игра “Математическое лото”. (Слайд 11.)
Правила игры: 1 – придумать, 2 – решить, 3 – оценить.
Подготовка: участник № 3 складывает лист формата А4 так, чтобы он разделился на 8 частей. Получается таблица:
| a (длина) | ? | ||
| b (ширина) | ? | ||
| P (периметр) | ? | ? | |
| Ѕ (площадь) | ? | ? |
1. Составление задач. Передача листа-таблицы по команде для решения другой группе (по часовой стрелке).
2. Решение задач (заполнение таблицы). Передача листа-таблицы по команде для проверки следующей группе.
3. Проверка и оценка решения.
б) конструктивные задания (в измененной ситуации)
Учитель:
— Внимание на экран! (Слайд 12.)
Запишите, какими способами Вы найдете площади этих фигур.
— По сигналу встаньте, найдите пару и расскажите о своих способах. Если у Вас есть этот способ, поставьте “+”, если нет, дополните свой список. Запись известных способов:
1) Пользуясь формулой;
2) Палеткой;
3) Дополнить до прямоугольника или квадрата;
4) Разбить на квадратные мерки;
5) Разделить на отдельные квадраты и прямоугольники и найти их площади;
6) Из площади большой фигуры вычесть площадь маленькой фигуры.
— Расскажите в группе по одному способу, начиная с участника № 1. (Сбор информации, обмен знаниями и дополнение списка ответов в паре при перемещении по классу; обмен информацией в своей группе.)
— Подчеркните нерациональные способы. Почему Вы считаете их нерациональными? Покажите рациональные способы.
V. Физкультминутка
Учащиеся делятся на группы, получают карточки (“татарский танец”, “русская плясовая”, “полька”, “марш”), исполняют танцевальные движения под музыку.
VI. Творческое применение и добывание знаний в новой ситуации
а) Вычисление площади сложной фигуры на листе формата А2, представление работы групп.
б) Индивидуальная работа с планом классной комнаты, проверка ответов с партнером по плечу. (Слайд 13.)
в) Практическая работа по измерению площади, занимаемой группой, высказывание ответов.
VII. Информация о домашнем задании, инструктаж
1) Решите разноуровневые задания на карточке (Приложение);
2) Найдите площадь одной из комнат Вашей квартиры.
VIII. Итог урока
Учащиеся отвечают на вопросы:
- Что такое площадь?
- Как измерить площадь?
- Назовите единицы площади.
- По какой формуле находят площадь прямоугольника, квадрата?
- Какие площади у равных фигур?
- Какое свойство площади знаете?
- Людям каких профессий необходимо знание площади?
- Где Вы можете применить знания площади?
Проверка: зажигается звезда. (Слайд 14.)
Учитель:
— Послушайте притчу.
Шёл мудрец и встретил трех работников. “Что ты сегодня делал?” — спросил он каждого. Первый ответил: “Я целый день таскал ненавистные камни”. Второй ответил: “Я немного устал, но добросовестно выполнял свою работу”. Третий ответил: “Работа принесла мне радость и большое удовлетворение”.
— Кто из вас на уроке был первым работником, вторым работником, третьим работником? Очень хорошо, что работа на этом уроке принесла вам радость, вы открыли новые знания.
— Что для Вас было новым?
Использованная литература.
1. Федеральный государственный образовательный стандарт начального общего образования. Москва, 2010 г.
2. Концепция духовно-нравственного развития и воспитания личности гражданина России.
3. Овчинникова М.В. Методика изучения темы “Величины” на уроках математики в начальных классах: Методические рекомендации для студентов факультета “Начальное обучение. Дошкольное воспитание”. Ялта: ЦОП “Надежда”, 2000.
4. Райкина Т.Н. Математика. 3 класс. В 2 ч. Саратов: Лицей, 2009.
5. Жильцова Т.В., Обухова А.А. Поурочные разработки по наглядной геометрии: 1-4 класс. М.: ВАКО, 2004.
1.03.2014
xn--i1abbnckbmcl9fb.xn--p1ai
| 1. |
Площадь квадрата
Сложность: лёгкое |
1 |
| 2. |
Площадь прямоугольника
Сложность: лёгкое |
1 |
| 3. |
Найди сторону прямоугольника, зная его площадь
Сложность: лёгкое |
1 |
| 4. |
Найди площадь квадрата, зная его периметр
Сложность: среднее |
2 |
| 5. |
Найди периметр прямоугольника, зная его площадь
Сложность: среднее |
2 |
| 6. |
У какой клумбы больше площадь?
Сложность: среднее |
2 |
| 7. |
Площадь незакрашенной части прямоугольника
Сложность: среднее |
2 |
| 8. |
Изменится ли периметр и площадь клумбы
Сложность: сложное |
3 |
| 9. |
Площадь дорожки в саду
Сложность: сложное |
3 |
| 10. |
Сравни площади квадратов
Сложность: сложное |
3 |
www.yaklass.ru
Формулы геометрии. Площади фигур. — материалы для подготовки к ЕГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
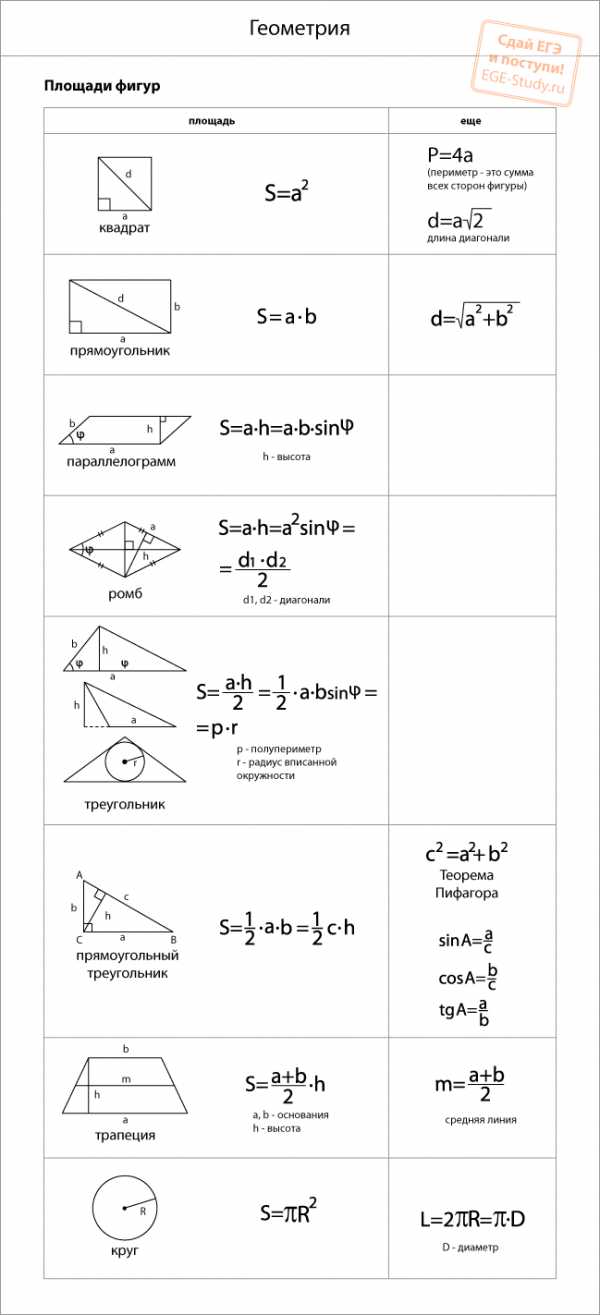
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
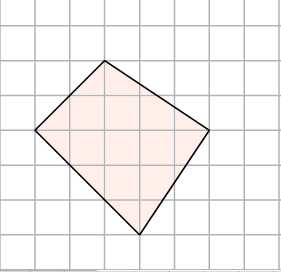
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
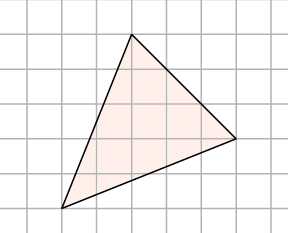
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
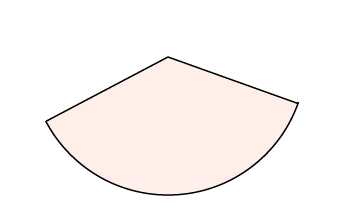
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Площадь прямоугольника. Видеоурок. Математика 3 Класс
Мы уже познакомились с понятием площадь фигуры, узнали одну из единиц измерения площади – квадратный сантиметр. На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см2, площадь второй фигуры 7 см2.
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см2.
Этот же прямоугольник можно разбить на 3 полоски по 4 см2.
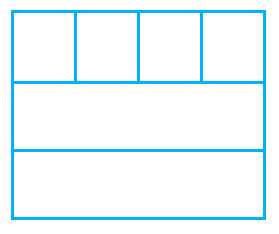
Тогда площадь прямоугольника будет равна 4*3=12 см2.
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см2, а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
6*2=12 см2
Число 6 обозначает длину прямоугольника, а 2 – ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см2, а таких полосок 3. Следовательно, мы можем выполнить действие
2*3=6см2
Число 3 обозначает длину прямоугольника, а 2 – ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина – 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем реше
interneturok.ru
Площадь геометрических фигур. 3-й класс
Разделы: Начальная школа
Цели:
1. Предметные:
- в совместной деятельности с учителем учиться находить площадь прямоугольника и пользуясь палеткой вычислять площади геометрических фигур, которые не являются многоугольниками;
- выполнять вычислении на основе знаний таблицы умножения и деления; решать простые и составные текстовые задачи.
2. Регулятивные: учиться определять цель учебной деятельности, составлять план действия по выполнению учебной задачи.
3. Познавательные: осуществлять поиск нужной информации, используя материалы учебника и сведения, полученные от учителя.
4. Коммуникативные: использовать простые речевые средства для общения на уроке, читать и понять текст учебника, участвовать в диалоге и в коллективном обсуждении, отвечать на вопросы
Ресурсы:
- учебник М.И.Моро, « Математика»;
- презентация «Площадь прямоугольника»;
- раздаточный материал (геометрические фигуры, палетка).
Ход урока
I. Организационный момент. Сообщение темы и целей урока.
Учитель: Здравствуйте, дети! Сегодня к нам на урок пришел гость. Вы его знаете?
Ученики: Да! Это Лунтик.
Учитель: Что вы знаете про него? (Ответы детей.) Ему все интересно, он хочет научиться всему. Лунтик очень хотел узнать, что мы будем делать на уроке.
Ученики (читают на слайде):
(Слайд 2)
- делить и умножать;
- решать задачи;
- геометрические фигуры разбирать;
- периметр фигур вычислять;
- ?
Учитель: Что вы можете сказать про эту фигуру?
Ученики: Квадрат, прямоугольник, квадраты, прямоугольник разделен на квадраты и т.д.
Учитель: Это и будет темой урока. Научимся вычислять площадь плоских геометрических фигур.
II. Устный счет.
Повторение знаний таблицы умножения и деления. (Слайды 3-5)
«Лунтик увидел бабочек и стал их ловить, хочет дружить с ними. Он еще не знает, что трогать их нельзя, что они погибнут. Природу надо беречь!»
Учитель: Давайте поможем бабочкам. Пусть они улетят и спрячутся от Лунтика. Если вы хорошо знаете таблицу умножения и деления, правильно решите примеры, то бабочки смогут улететь.
1) Реши задачи. (Слайд 6)
- Лунтик и Кузя нашли 9 платков. Это куски одеяла, которого унес ветер. Если Кузя отдаст 1 платок Лунтику, то у Лунтика платков будет в 2 раза больше. По сколько платков нашли Лунтик и Кузя?
- Пчеленок и его друг собирают мёд. Пчеленок пролетает за 1 минуту 8 метров, а его друг за 1 минуту 800 сантиметров. Кто первым прилетит к цветку?
2) Среди фигур найди прямоугольники. (Слайд 7) Докажи свой выбор.
3) Вычисли периметр данных фигур. (Слайд 8)
III. Новая тема. Постановка учебной задачи.
Учитель: На слайде изображены геометрические фигуры. Можно ли про них сказать, что они равны? Почему? (Слайд 9)
Практическая работа.
На партах в конвертах геометрические фигуры (работа в парах).
Задание: найти равные по площади геометрические фигуры.
Учитель: Как вы узнали, что они равные?
Ученики: Наложением друг на друга.
Учитель: Возьмите из конверта красный прямоугольник и красный квадрат. Можно ли сказать, что они равные? Почему?
Ученики: Нет. Потому, что наложением проверить невозможно.
IV. Решение учебной задачи.
Учитель: Можно сказать про эти два кусочка шоколада, что они равные. (Слайд 9)
— А если так, можно сказать, что они равные? (Слайд 10)
Ученики: Да, в каждой кусочке по 4 равных квадрата.
Практическая работа.
Учитель: Как мы можем узнать красные прямоугольники равны или нет?
Ученики: Разделить на равные квадраты. (Ученики с помощью перегибания делят прямоугольники (полоски бумаги) на 4 равные части.)
Учитель: Какой вывод можно сделать?
Ученики: Вывод: чтобы измерить площадь геометрических фигур, их нужно разделить на равные квадраты.
Учитель: Какие площади нужно измерять в быту?
Ученики: Полы, стены, участок земли, огорода и т.д.
V. Закрепление новой темы.
Решите задачу.
Лунтик и Кузя решили покрасить стены своего дома. У кого площадь стены больше?
Кому придется больше красок покупать? Как мы будем решать эту задачу?
Ученики: Площадь стен нужно разделить на равные квадраты.
Учитель: Сравните два домика. Площадь какого прямоугольника больше?
Ученики: В площадь синего прямоугольника поместились 16 квадратов, а в красного – 15.
Учитель: Какие приемы сравнения двух площадей вы узнали сегодня на уроке?
Ученики: Прием наложения фигур друг на друга и разделение фигур на равные квадраты.
Решите задачу.
Лунтик и Кузя решили поливать цветы. У кого площадь
клумбы больше? Кому надо больше таскать воду?
Учитель: Как можно измерить и сравнить площадь цветочных клумб? Какую форму они имеют?
Ученики: Клумбы имеют круглую и овальную форму. Измерить наложением не возможно, а разделить на квадраты можно.
Учитель: Какие квадраты получились?
Ученики: Полные и неполные.
Учитель: Посчитайте сколько квадратов в круге (первая клумба) и в овале (вторая клумба). Нужно считать целые квадраты и отдельно неполные. Число неполных квадратов делится на два. Складываются числа полных и половина числа неполных квадратов.
Ученики: В круге – 4 полных, 8 – неполных квадратов, всего 4 + 4 = 8 квадратов; в овале – 8 полных, 12 – неполных квадратов, всего 8 + 6 = 14 квадратов.
Информация.
Если фигура не является многоугольником, то его площадь можно
измерять с помощью палетки. На партах в конверте лежат палетки. Палетка – это лист
прозрачной бумаги, с нанесенным на ней сеткой из квадратов. Палетка
накладывается на фигуру и подсчитывается, сколько целых квадратов и отдельно неполных и
числа складываются.
Практическая работа.
На партах в конверте рисунки. Нужно измерить площадь
фигур с помощью палетки и записать ответ.
Учитель: Площади каких предметов, не имеющих форму многогранника нужно измерять в быту?
Ученики: Шкуры животных, кожа и т.д.
VI. Работа по учебнику.
1. №4. Прочитайте и составьте план действия по выполнению учебной задачи.
А) Анализ задачи (коллективная работа): О чем говорится в задаче?, Что нужно
узнать?, Что необходимо знать, чтобы сравнить?.
Б) Записываем условие задачи кратко или составляем схему (работа в группах).
В) Записываем основной вопрос задачи: Во сколько раз оставшаяся часть больше,
чем отпиленная?
Г) Записываем программу решения (самостоятельная работа).
Д) Записываем ответ.
2. №3, №4 (самостоятельная работа).
VII. Итог урока.
Учитель: Вам понравился урок? Нарисуйте свое настроение на уголке тетради.
— Что вы узнали сегодня на уроке? Чему научились?
Домашняя работа:
- Стр.51, №2.
- Измерить длину и ширину своей комнаты, записать в тетрадь.
16.06.2013
xn--i1abbnckbmcl9fb.xn--p1ai
