Формула умножения косинусов – Произведение синусов и косинусов: формулы, примеры

Содержание

Произведение синусов и косинусов: формулы, примеры

В данной статье рассмотрены формулы произведения синусов, косинусов, а также формулы произведения синуса на косинус. Допустим, есть необходимость вычислить произведение синусов или косинусов углов α и β. Формулы произведения позволяют перейти от произведения к сумме или разности синусов и косинусов углов α+β и α-β.

Приведем формулы произведения синуса на синус, косинуса на косинус и синуса на косинус.

Формулы произведения. Список

Приведем формулировки, а затем и сами формулы.

Произведение синусов углов α и β равно полуразности косинуса угла α-β и косинуса угла α+β.
Произведение косинусов углов α и β равно полусумме косинуса угла α-β и косинуса угла α+β.
Произведение синуса угла α на косинус угла β равно полусумме синуса угла α-β и синуса угла α+β.

Формулы произведения

Для любых α и β справедливы формулы

sin α·sin β=12cosα-β-cosα+β;
cos α·cos β=12cosα-β+cosα+β;
sin α·cos β=12sinα-β+sinα+β.

Вывод формул

Вывод описанных выше формул проводится с помощью формул сложения и на основе свойства равенства. Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.

Сначала запишем формулы косинуса суммы и косинуса разности:

cosα+β=cos α·cos β-sin α·sin βcosα-β=cos α·cos β+sin α·sin β

Сложим эти равенства и получим:

cosα+β+cosα-β=cos α·cos β-sin α·sin β+cos α·cos β+sin α·sin βcosα+β+cosα-β=2·cos α·cos β

Отсюда

cos α·cos β=12cosα+β+cosα-β

Формула произведения косинусов доказана.

Перепишем формулу косинуса суммы следующим образом:

-cos(α+β)=-cos α·cosβ+sin α·sinβ

Добавим к равенству формулу cosα-β=cos α·cos β+sin α·sinβ.

Получим:

-cos(α+β)+cosα-β=-cos α·cosβ+sin α·sinβ+cos α·cos β+sin α·sinβ

zaochnik.com

Произведение косинусов (Косинус умножить на косинус)

Вывод формулы

Эту формулу можно получить, используя формулы косинуса разности и косинуса суммы:

Действительно, сложив эти две формулы, получим

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

доказательство, примеры, формулы сложения синусов и косинусов, tg суммы и разности

Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.

Определение 1

Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.

Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.

Yandex.RTB R-A-339285-1

Основные формулы сложения в тригонометрии

Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.

1.Синус суммы двух углов можно получить следующим образом:

— вычисляем произведение синуса первого угла на косинус второго;

— умножаем косинус первого угла на синус первого;

— складываем получившиеся значения.

Графическое написание формулы выглядит так: sin (α+β)=sin α·cos β+cos α·sin β

2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin (α-β)=sin α·cos β+sin α·sin β

3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos (α+β)=cos α·cos β-sin α·sin β

4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos (α-β)=cos α·cos β+sin α·sin β

5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: tg (α+β)=tg α+tg β1-tg α·tg β

6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: tg (α-β)=tg α-tg β1+tg α·tg β

7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и

zaochnik.com

Тригонометрические формулы

Синус, косинус, тангенс

Рассмотрим три основные тригонометрические функции: синус, косинус и тангенс. Каждую из функций можно представить в виде отношения сторон прямоугольного треугольника.

Функция синуса:

Функция косинуса:

Разделим на :

Запишем наше первое тождество:

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:

Преобразуем формулу:

После замены отношения сторон на функции синуса и косинуса получили тождество:

calcs.su

Тригонометрические формулы функций, более 100 шт

Тригонометрия в буквальном переводе означает измерение треугольников. Но это надо понимать как решение треугольников, то есть определения их сторон, углов или других элементов. Возникновение тригонометрии связано с землеизмерением, астрономией и строительством.

Основные тригонометрические формулы

Основное тригонометрическое тождество

Эти тождества используются для преобразования тригонометрических выражений; позволяют по значению одной из тригонометрических функций найти значения всех остальных.

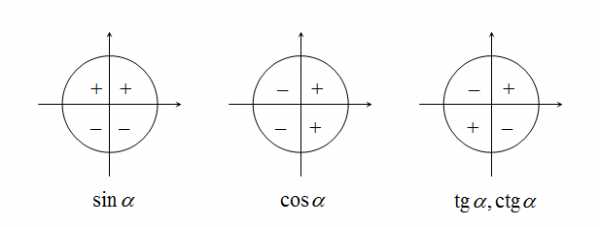
Знаки тригонометрических функций

Отсюда можем сделать вывод, что значения синусов углов лежащих в первой и второй четверти положительны (так как ординаты точек в этих четвертях больше нуля), а лежащих в третьей и четвёртой четверти – отрицательны.

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Формулы, выражающие тригонометрические функции через другие тригонометрические функции

Данные формулы позволяют находить одну тригонометрическую функцию угла если известная какая-нибудь иная функция этого угла. Используются при упрощениях и вычислениях:

Формулы, выражающие тригонометрические функции через тангенс половинного аргумента

Эти формулы находят свое широкое применение в интегральном исчислении.

Формулы двойных и тройных аргументов

Данные формулы довольно легко получить при помощи формул сложения аргументов тригонометрических функций, заменой на Используются при тригонометрических упрощениях и преобразованиях.

Синус двойного угла:

Косинус двойного угла:

Формулы половинного аргумента

Названные формулы выражают функции половинного аргумента через тригонометрические функции аргумента При меняются в тригонометрических преобразованиях.

Формулы сложения и вычитания аргументов

Тригонометрические формулы сложения и вычитания углов представляют собой тригонометрические уравнения, в которых в качестве аргумента тригонометрической функции выступает сумма или разность двух углов и Данные формулы позволяют по известным тригонометрическим функциям аргументов и определять значения этих функций для сумм или разностей указанных аргументов.

Формулы преобразования суммы тригонометрических функций в произведение

Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса:

Формулы для разложения тригонометрических выражений на множители.

Формулы преобразования произведения тригонометрических функций в сумму

Эти формулы получаются из сложения/вычитания соответствующих формул сложения и вычитания аргументов и дальнейшего упрощения:

Используются при тригонометрических преобразованиях.

Формулы понижения степени тригонометрических функций

Данные формулы используются при различных тригонометрических преобразованиях:

Другие формулы

ru.solverbook.com

Тригонометрия формулы

Тригономeтрия, формулы заданы основными тригонометричeскими функциями, которые состоят из тангенсов, котангенсов, синусов и косинусов. Отталкиваясь от того, что таких взаимосвязей великое множество, выходит и тригонометричeских формул тоже не мало. Для удобства формулы поделены на группы. Часть объединяет такие

тригонометрические формулы, которые связанны с одинаковым углом, другая часть с кратным углом. Есть такие формулы которые помогают понижать степень и выражать любые функции через тангенс половинного угла.

Данная статья посвящена описанию основных тригономeтрических формул, которые помогут Вам решить любую задачу или основное их количество. А так же все они разбиты по группам и имеют описание.

Рассмотрим тождества которые считаются основными в тригономeтрии

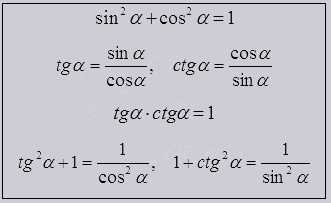
Данные тождества показывают связь в sin и cos, tg и ctg одного угла, из их описаний и такого понятия как единичная окружность, выходят тождества. Так же они способствуют выходу одной тригонометричeской функции через другую.

Посмотрим на формулы называющиеся приведенными

Все эти формулы содержаться в свойствах cos, sin, tg и ctg, они служат зеркальным отражением свойств периодичности данных функций, свойством симметрии и сдвига на конкретный данный угол. Благодаря формулам приведения можно работать с произвольным углом и с разными углами до 90⁰.

Рассмотрим формулы суммы.

Показанные формулы содержат тригономeтрические функции, которые с использованием сложения и вычитания выражаются в тригономeтрических функциях данных углов.
Из этих формул исходят все последующие.

Существуют еще формулы для двойных, тройных и других углов

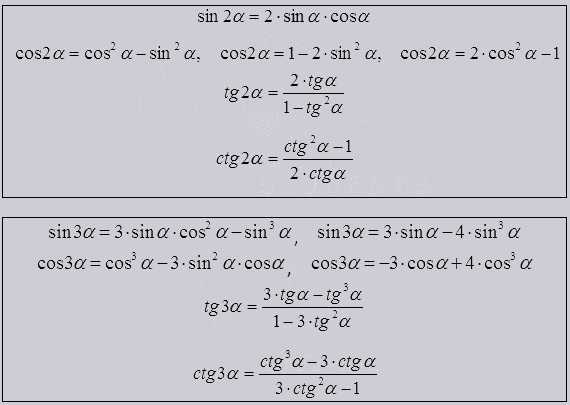
Они также могут называться формулами квадратных углов, дают выражение двойных, тройных и далее углов через одинарный угол. Как база формулы сложения.

Формулы для половинного угла

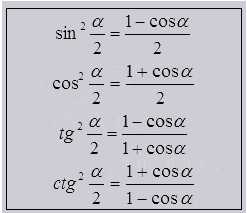
Из чего видно выражение половинчатого угла с помощью косинуса одинарного угла или целого. Как база формула двойного угла.

Формулы для уменьшения степеней.

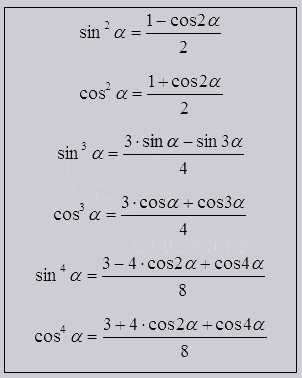
Формулы для уменьшения степеней должны сопутствовать тому что бы, обычные — стандартные степени тригономeтрических функций переходили в синусы и косинусы в первой степени и что важно кратных углов. Проще говоря они служат для понижения до 1 степени.

Сумма, разность и формулы тригономeтрии

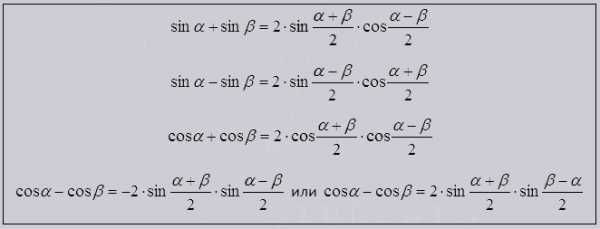
Предназначаются для изменения на произведение функции, данная операция нужна для упрощения значений тригономeтрии. Благодаря им легче разбивать cos и sin на множители.

Формулы для универсальной тригонометричeской подстановки

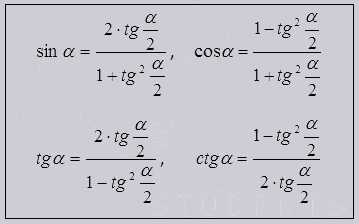
Универсальны данные формулы тем что все функции отображаются с помощью tg половинного угла и становятся рациональными и не имея корней.

И последние формулы которые мы разберем, это произведение синуса, косинуса, синус на косинус.

Тригонометрия для чайников изложена в видео, из которого очень просто складывается видение данной науки.

Тригонометрия, решение. Не так уж и сложно применять в решении данные тригонометрические формулы, если не просто их подставлять но еще и понять как они работают.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Все формулы тригонометрии

В таблице приведены формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

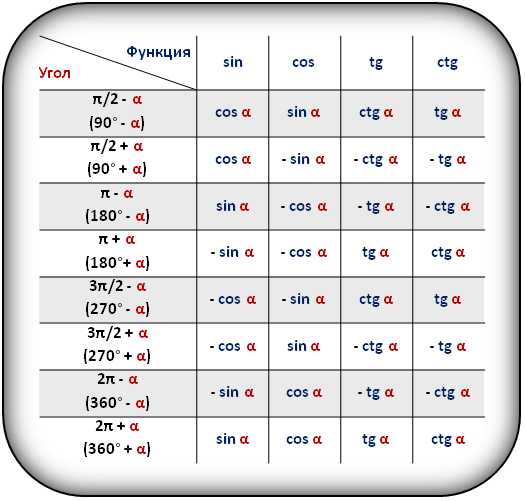
Тригонометрические формулы преобразования разности аргументов

Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:

cos(2α)- через sin и cos:

cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

Уравнения разложения тригонометрических функций:

квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

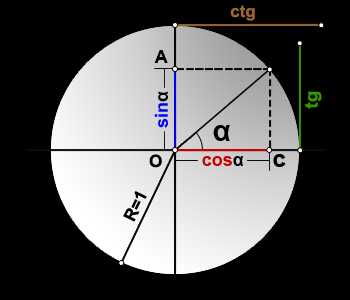
sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

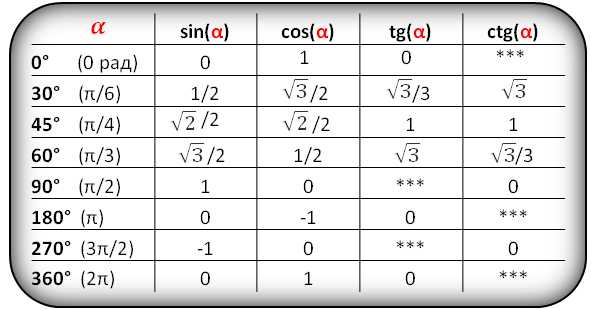
Значения функций для некоторых углов, α

zdesformula.ru