Объем шара, шарового сегмента, слоя и сектора. Видеоурок. Геометрия 11 Класс
Сколько чугуна нужно, чтобы отлить пушечное ядро? Что занимает больше места: арбузная корка или мякоть арбуза? Сколько воздуха поместится внутри воздушного шара? Чтобы ответить на все эти и многие другие вопросы, необходимо уметь находить объем шара. Сделать это не так просто. Разбить его на «кубики», треугольные призмы или другие фигуры, как это делалось раньше, не получится. Можно вычислить объем шара с помощью определенного интеграла. Но как же тогда вычисляли объем, например, древние греки – при отсутствии определенных интегралов? Метод, придуманный Архимедом, был очень красив и по сути своей являлся предшественником метода доказательства через интеграл. Он доказал формулу объема шара понятийно, представив половину шара через конус и цилиндр, объемы которых уже известны.
Идея Архимеда была такова.
Замечание: формулы объемов цилиндра и конуса Архимед уже знал.
Рассмотрим весы и такую конструкцию. На левой чаше – цилиндр радиуса и его высота . На правой чаше – конус радиуса и высотой (см. Рис. 1).
Рис. 1. Исходная конструкция
Разобьем каждую из этих фигур на равных слоев (цилиндриков). Будем считать, что конус тоже составлен из цилиндриков. (радиус у них у всех – , а высота слоя – , все колечки из одного и того же материала). Справа находится конус, составленный также из цилиндриков, высота каждого из которых – , а радиус уменьшается от до на в арифметической прогрессии, а также из полушар радиуса (см. Рис. 2).
Рис. 2. Разбиение фигур на «цилиндрики»
Докажем, что чаши уравновешены. Чтобы уравновесить чаши, необходимо добавить к каждому колечку конуса недостающее колечко так, чтобы суммарный их вес дал вес «цилиндрика» слева. Разумеется, можно приравнивать не массы, а объемы – в силу одинаковости материала. Но высоты у колечек одинаковы, значит, должны совпасть площади оснований.
У цилиндра площадь основания каждого колечка . У очередного слоя конуса – . Значит, на фигуру, стоящую правее от конуса, остается . Но если предположить, что справа находится «полушар», то радиус его сечения плоскостью, отстоящей от основания на как раз и будет равен (см. Рис. 3).
Рис. 3. Полушар со своими измерениями
Осталось устремить к нулю (что и дает, по сути, определенный интеграл).
Значит, объем полушара ищется как разность между объемами цилиндра и конуса.
Вычислим: , откуда . Что и требовалось доказать.
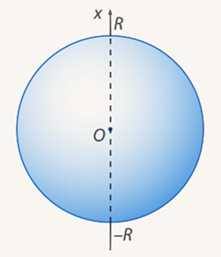
Рассмотрим произвольную ось , проходящую через центр шара – точку . Тогда объем шара можно найти по формуле:
, где – площадь сечения шара плоскостью, перпендикулярной оси и проходящей через точку этой оси с абсциссой . Почему именно от до ? Потому что если ось проходит через центр, то точки пересечения оси с границей шара находятся на расстоянии от начала координат: одна – в положительном направлении, а другая – в отрицательном (см. Рис. 4).
Найдем . Пусть – точка с абсциссой на оси. Рассмотрим такую точку , что она лежит на границе шара и при этом в плоскости сечения. В этом случае радиус сечения находится из треугольника по теореме Пифагора . А так как сечение – круг данного радиуса, то его площадь равна: (см. Рис. 5).

Рис. 5. Радиус сечения из треугольника
Тогда:
Предположим, что вы купили арбуз, имеющий форму шара. Арбуз этот состоит из мякоти (также в форме шара) и корки. При этом толщина корки в раза меньше радиуса мякоти . Какую часть от объема всего арбуза составляет объем мякоти ? (См. Рис. 3.)
Рис. 6. Купленный арбуз
Решение. Пусть радиус (толщина) корки , тогда радиус мякоти , а радиус всего арбуза . (См. Рис. 4.)
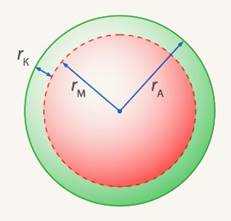
Рис. 7. Иллюстрация к условию
Имеем: объем мякоти а объем арбуза , значит, их отношение .
Ответ: .
Шаровой сегмент в пространстве чем-то похож на круговой сегмент в плоскости. Вспомним, что такое круговой сегмент. Фигура, которая образовалась при отсечении проведенной в круге хордой, называется сегментом. Хорда рассекает круг на два сегмента (см. Рис. 8).
Рис. 8. Два круговых сегмента – маленький и большой
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Не забывайте слово «шаровой»: хоть по контексту это обычно и понятно, но тем не менее сегмент – это плоская фигура. Соответственно, если проводить любую секущую плоскость, шар разбивается на два шаровых сегмента (см. Рис. 9).
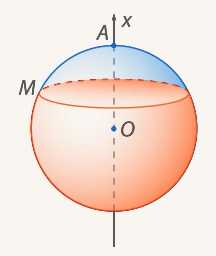
Рис. 9. Два шаровых сегмента – маленький и большой
Круг в сечении – основание сегмента (см. Рис. 10).
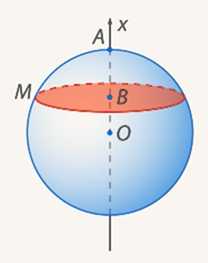
Рис. 10. Основание сегмента
interneturok.ru
Шар как геометрическая фигура
Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.
 Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.
Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.
Площадь поверхности шара можно найти по формулам:
S = 4 πr2
S = πd2,
где r – радиус шара, d – диаметр шара.
Объём шара находится по формуле:
V = 4 / 3 πr3,
где r – радиус шара.
Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле
Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.
Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.
Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.
Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.
Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Площадь поверхности шарового сегмента можно вычислить по формуле:
S = 2πRh,
где R – радиус большого круга, h – высота шарового сегмента.
Объём шарового сегмента можно найти по формуле:
V = πh2(R – 1/3h),
где R – радиус большого круга, h – высота шарового сегмента.
Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.
Объем шарового сектора находится по формуле:
V = 2/3 πR2H.
Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Шар и сфера — урок. Математика, 6 класс.

Шар — это геометрическое тело.
Предметы, имеющие форму шара, окружают нас очень часто.
Форму шара имеет мяч (футбольный, теннисный, баскетбольный).
Представление о шаре дают арбуз, апельсин, горошина.
Шарообразна и наша планета Земля.
Шар характеризует длина радиуса и диаметра.
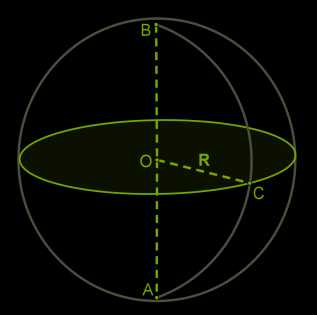
Рассмотрим чертёж.
Перед нами изображение шара с центром в точке \(O\). Все точки поверхности шара находятся на одинаковом расстоянии от его центра.
Это означает, что если мы выберем на поверхности три любые точки, например, точку \(A\), точку \(B\) и точку \(C\), соединим их с центром шара, то полученные отрезки будут равны (\(OA = OB = OC\)).
Такие отрезки называют радиусами.
\(OA\) — радиус шара, \(OB\) — радиус шара и \(OC\) — также радиус шара.
Так как центр шара можно соединить с бесконечно многими точками на поверхности шара, то можно провести бесконечно много радиусов.
Радиус шара — это отрезок, который соединяет точку поверхности шара и его центр.
На чертеже отрезок \(AB\) соединяет две точки поверхности шара и проходит через его центр.
Отрезок \(AB\) — это диаметр шара. Заметим, что отрезок \(AB\) состоит из двух отрезков \(OA\) и \(OB\).
Эти отрезки являются радиусами шара.
Поэтому диаметр шара в два раза больше его радиуса.
Диаметром шара называется отрезок, соединяющий две точки поверхности шара и проходящий через его центр.
Есть название и для поверхности шара. Её называют сферой.

Для шара можно вычислить объём по формуле:
Vшара=43⋅π⋅R3.
Для сферы можно вычислить поверхность по формуле:
Sсферы=4⋅π⋅R2.
www.yaklass.ru
Объём шара — Циклопедия
Шар 17. Стереометрия на ЕГЭ по математике. Объем шара // Анна Малкова [2:47] Объем шара // KhanAcademyRussian [6:01]Объём шара — это число, характеризующее шар в единицах измерения объёма.
Шар — это тело, ограниченное поверхностью вращения (сферой), образующей окружности вокруг оси лежащей в плоскости этой окружности и проходящей через её центр.
Введём обозначения:
R — радиус шара;
D — диаметр шара;
Sшар — площадь поверхности шара;
Vшар — объём шара.
[править] 1-й способ
[править] 2-й способ
[править] Другие формулы
- Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.177.
- Участник:Logic-samara
cyclowiki.org
Объем шара
На этом уроке мы дадим определение шара. Выведем формулу для вычисления объёма шара. А затем с её помощью выведем формулу для вычисления площади сферы.
Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое шар.
Определение:
Шар – это совокупность всех точек пространства, находящихся от данной точки на расстоянии, не больше данного. Причём, данная точка называется центром шара, а данное расстояние – радиусом шара.
Радиусом шара называют всякий отрезок, соединяющий центр шара с любой точкой шаровой поверхности.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.
Отрезок, соединяющий две точки шаровой поверхности и не являющийся диаметром шара, т.е. не проходящий через центр шара, называется хордой шара.
Понятно, что сечение шара плоскостью есть круг.
Сечение шара плоскостью, проходящей через его центр, называется большим кругом шара.
Итак, справедлива следующая теорема: объём шара радиуса равен .
Докажем теорему. Пусть нам дан шар радиуса с центром в точке . Выберем ось так, чтобы начало оси совпадало с центром шара.
Тогда отрезок это есть радиус шара .
Докажем, что объём шара равен .
На оси отметим произвольную точку и рассмотрим сечение шара плоскостью проходящее через эту точку перпендикулярно к оси . Заметим, что такое сечение шара плоскостью является кругом с центром в точке .
Отрезок .
Обозначим радиус этого круга через , а его площадь через , где – абсцисса точки .
Выразим площадь через и радиус шара .
Из прямоугольного треугольника по теореме Пифагора найдём радиус круга. Тогда имеем .
Площадь круга . Заменим радиус круга выражением . Тогда получаем, что .
Заметим, что эта формула верна для любого положения точки на диаметре . Иначе говоря, верна для всех , удовлетворяющих условию .
Так как мы с вами выразили площадь через , то можем вычислить объём шара с помощью основной формулы объёма тела. Вспомним её: объем тела равен .
Итак, применяя основную формулу для вычисления объёмов тел получаем, что объём шара равен .
Этим мы с вами доказали, что объём шара с радиусом равным можно вычислить по формуле .
Что и требовалось доказать.
Ранее мы с вами без доказательства привели формулу для вычисления площади сферы. Напомню, что площадь сферы можно вычислить по формуле: .
Теперь давайте выведем эту формулу, пользуясь формулой объёма шара.
Итак, рассмотрим сферу радиуса с центром в точке О и описанный около неё многогранник, имеющий граней.
Напомним, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.
Занумеруем грани в произвольном порядке и обозначим через – площадь -й грани.
Затем соединим центр О сферы отрезками со всеми вершинами многогранника. При этом получим эн пирамид с общей вершиной О, основаниями которых являются грани многогранника, а высотами – радиусы сферы, проведенные в точки касания граней многогранника со сферой.
Следовательно, объём -й пирамиды равен , а объём всего описанного многогранника равен: . Где – площадь поверхности многогранника.
Отсюда получаем: .
Теперь будем неограниченно увеличивать таким образом, чтобы наибольший размер каждой грани описанного многогранника стремился к нулю. При этом объём описанного многогранника будет стремиться к объёму шара. В самом деле, если наибольший размер каждой грани описанного многогранника не превосходит , то описанный многогранник содержится в шаре радиуса с центром в точке .
Но ведь с другой стороны, описанный многогранник содержит исходный шар радиуса . Значит, объём .
Так как выражение при , то и объем при ().
Переходя затем к пределу, получаем, что .
По определению площади сферы , следовательно, .
Что и требовалось доказать.
Задача: объём шара равен равен см3. Найдите диаметр шара.
Решение: запишем формулу для вычисления объёма шара.
По условию задачи объём шара равен см3.
Отсюда видим, что радиус шара равен (см). Напомним, что диаметр шара вдвое больше его радиуса. Тогда диаметр нашего шара равен (см).
Запишем ответ.
Задача: радиус шара увеличили в раза. Во сколько раз увеличился объём шара?
Решение: запишем формулу для вычисления объёма шара.
Так как по условию задачи радиус исходного шара увеличили в 2 раза, то радиус данного шара будет равен . Подставляя данный радиус в формулу для вычисления объёма шара видим, что объём исходного шара увеличился в 8 раз. Следовательно, ответ: объём шара увеличился в 8 раз.
Задача: в цилиндр вписан шар. Найдите отношение объёма шара к объёму цилиндра.
Решение: шар, вписанный в цилиндр, касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга, параллельной основаниям цилиндра. Отсюда следует, что , а высота цилиндра равна .
Объём шара вычисляется по формуле , а объём данного цилиндра можно вычислить по формуле , где – это площадь основания, - высота цилиндра. Так как высота данного цилиндра равна двум радиусам, а площадь основания равна , то объём цилиндра равен .
Найдём отношение объёма шара к объёму цилиндра. Получаем, что объём шара относится к объёму цилиндра, как .
Эту задачу называют «Задачей Архимеда». Во времена Архимеда формула объёма шара была неизвестна. Поэтому данная задача считалась очень трудной и, решив ее, Архимед испытал большую радость. На могиле Архимеда был поставлен памятник с изображением шара и описанного около него цилиндра.
Итоги:
На этом уроке мы дали определение шара. Вывели формулу для вычисления объёма шара. А затем с её помощью вывели формулу для вычисления площади сферы.
videouroki.net
2 Вывод рабочей формулы
Используя баллистический метод, получим формулу для определения скорости шаров в момент прохождения положения равновесия.
В этом методе мерой скорости служит величина угла отброса, рассчитываемая по угловой шкале.
В точке А (рисунок 5) шарик обладает потенциальной энергией равной
(2.1)
Систему маятник-Земля рассматриваем как замкнутую, пренебрегая трением в точке подвеса маятника и сопротивлением воздуха.
При перемещении шарика из положения А в положение С его потенциальная энергия перейдет в кинетическую.
(2.2)
Рисунок 5 – Отклонение шарика от положения равновесия.
Отсюда скорость шарика в точке С равна
. (2.3)
Используя соотношения в прямоугольном треугольнике и тригонометрическую формулу , выразим высотуh через длину нити l и угол
(2.4)
Подставив (2.4) в выражение для скорости (2.3), получаем
(2.5)
3 Порядок выполнения работы
1 Ознакомьтесь с лабораторной установкой.
2 Измерьте и запишите длину подвеса l в таблицу 1.
Таблица 1– Результаты измерений
Упражнение 1 Изучение упругого соударения шаров.
Поместите шары одинаковой массы на подвесы (). Запишите значения масс шаровв таблицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости угловой шкалы.
Отклоните первый шар на угол , а второй – на угол. Данные изапишите в таблицу. Значения угловизадает преподаватель.
Рассчитайте скорости первого и второго шаров до удара по формуле (2.5) (чтобы определить значениев формулу (2.5) подставляйте, для нахожденияв формулу (2.5) подставляйте). Результаты занесите в таблицу 1.
Отпустите шары. Измерьте значения углов ипосле удара, значения запишите в таблицу (один студент измеряет уголполного отклонения первого шара, второй студент измеряет уголполного отброса второго шара).
Рассчитайте скорости первого и второго шаров после удара по формуле (2.5). Результаты занесите в таблицу 1.
Проверьте выполнение закона сохранения импульса при упругом ударе .
Выберите направление координатной оси, найдите проекции скоростей ,,ина выбранную ось. Подставьте полученные значения в закон сохранения импульса. Убедитесь в справедливости закона сохранения импульса.
Рассчитайте относительное изменение импульсов до и после удара по формуле:
, где — импульс системы до удара,- импульс системы после удара.
Проверьте выполнение закона сохранения энергии используя формулу (1.20).
Пункты (1-8) выполните для двух других случаев: и
Упражнение 2 Изучение неупругого столкновения шаров.
Поместите на подвесы пластилиновые шары с одинаковыми массами (). Запишите значения масс шаровв таблицу 1.
Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости угловой шкалы.
Отклоните первый шар массой на угол. Второй шар массойнаходится в положении равновесия. Данные углазадает преподаватель. Значение. запишите в таблицу,=0.
Рассчитайте скорость первого шара до удара по формуле (2.5). Результат занесите в таблицу 1.
Отпустите первый шар. Измерьте значение угла после удара (при выполнении измерений за угол отклонения системы шаровпринимается угол , на который отклоняется центр масс системы двух шаров).
Рассчитайте скорость шаров после удара по формуле (2.5). Результат занесите в таблицу 1.
Проверьте выполнение закона сохранения импульса при неупругом ударе
.
Выберите направление координатной оси, найдите проекции скоростей ина выбранную ось. Подставьте полученные значения в закон сохранения импульса. Убедитесь в справедливости закона сохранения импульса.
Рассчитайте относительное изменение импульса ситемв до и после удара по формуле:
, где — импульс системы до удара,- импульс системы после удара.
Рассчитайте потери механической энергии системы тел по формуле (1.25).
studfiles.net
