Функция котангенс – Тангенс tg x котангенс ctg x

Функция y=сtgx, ее свойства и график . Видеоурок. Алгебра 10 Класс

Тема: Тригонометрические функции

Урок: Функция y=ctgt, её свойства и график

Зададим единственное число  Каждому действительному числу  соответствует единственная точка  на числовой окружности (рис. 1). Точка  имеет абсциссу и ординату, абсциссу называют косинусом числа  ординату – синусом числа  Отношение косинуса к синусу называется котангенсом числа

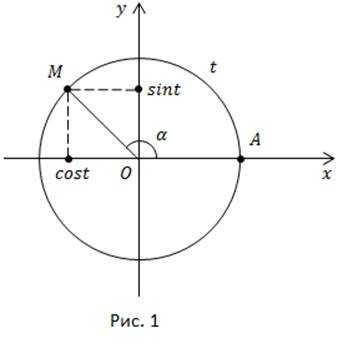
Каждому допустимому значению  соответствует единственная точка на окружности, единственная пара её координат, а значит и единственное значение дроби  т.е. единственное значение котангенса Таким образом, задаётся функция  или

Аргументом функции котангенс может быть число  или угол . Вспомним связь между числовым и угловым аргументами.

Радианом называется такой центральный угол, длина дуги которого равна  (рис. 2).

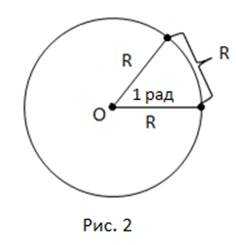
В окружности  штук радиан.

Если  то

Если есть угол  и окружность радиуса 1, то длина этой дуги или аргумент  связаны с  следующим образом:

Как определить значения котангенса для конкретных значений числового или углового аргумента? Они расположены на линии котангенсов – касательной к окружности в точке B (рис. 3).

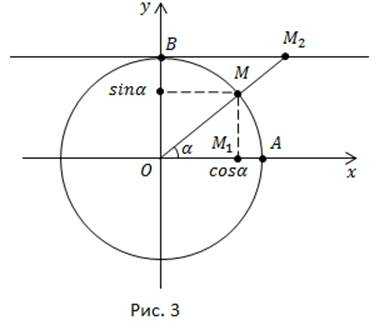
Возьмем аргумент  или угол  Аргументу  или углу в радианах соответствуют синус и косинус. Рассмотрим

Изобразим график функции  в координатной плоскости. По формулам приведения  Поэтому для построения графика функции достаточно график функции  симметрично отобразить относительно оси х и сдвинуть вдоль оси х на  влево (рис. 4).

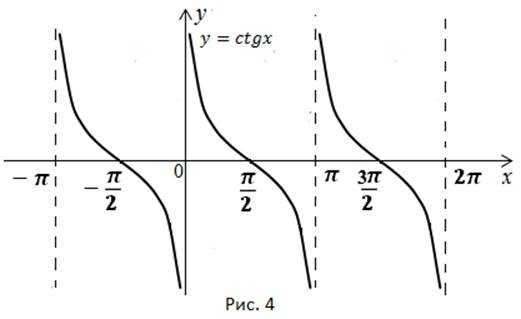
Исследуем график функции

1) Область определения:

2) Область значений:

a) Каждому допустимому  соответствует единственное значение

b) Любой  достигается при одном либо нескольких значениях

3) Функция нечетна:

График симметричен относительно начала координат.

4) Наименьший положительный период

Значение периода котангенса  также следует из формулы

  при том, что нам известен период тангенса.

5) Точки пересечения с осью x:

Точки пересечения с осью y отсутствуют (рис. 4).

6) Определим интервалы знакопостоянства (рис. 5):

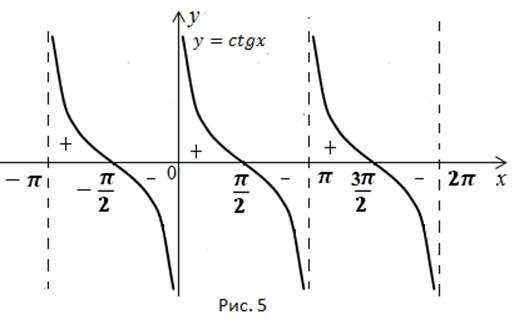
7) Функция монотонно убывает на каждом из интервалов

Покажем это:

Рассмотрим промежуток  длиной в период. Функция монотонно убывает от  до  

Действительно, если мы возьмем две точки из этого промежутка, такие, что то  большему значению аргумента соответствует меньшее значение функции (рис. 6).

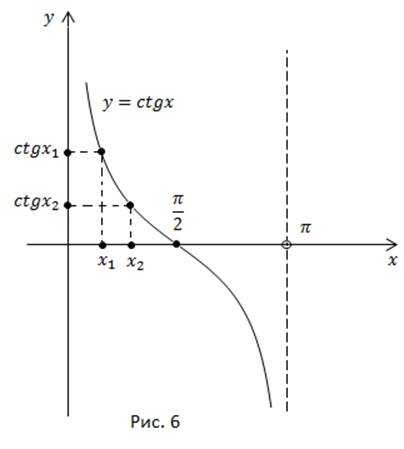
На каждом из отдельно взятых участков длиной в период функция также монотонно убывает.

8) Функция не имеет ни наибольшего, ни наименьшего значения.

Мы изучили функцию  её график и свойства. Все они будут использоваться в дальнейшем при решении различных задач, в том числе и при решении тригонометрических уравнений, к изучению которым мы приступим на следующем уроке.

 

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

 

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

№№ 20.2, 20.3(б, г), 20.5, 20.19.

 

Дополнительные веб-ресурсы

1. Математика (Источник).

2. Интернет-портал Problems.ru (Источник).

3. Образовательный портал для подготовки к экзаменам (Источник).

interneturok.ru

Котангенс — это… Что такое Котангенс?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Способы определения

Геометрическое определение

Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок.)

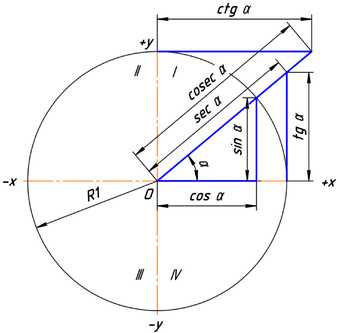
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности

R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4.
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
• Косинусом α называется отношение ОА/OB
  (прилежащего катета к гипотенузе)
• Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
• Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где B_n — числа Бернулли.

где E_n — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Свойства тригонометрических функций

Простейшие тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π

Формулы приведения

Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:

Формулы сложения

Другие тригонометрические тождества.

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

См. также Список интегралов от тригонометрических функций

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Сам термин тригонометрические функции введён Клюгелем в 1770.

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

функция котангенса — это… Что такое функция котангенса?



функция котангенса

мат. cotangent function

Большой англо-русский и русско-английский словарь. 2001.

• функция кососимметрическая
• функция кратности

Смотреть что такое «функция котангенса» в других словарях:

• Список математических аббревиатур — Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит …   Википедия

• Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения …   Википедия

• Тригонометрические функции —         один из важнейших классов элементарных функций.          Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги …   Большая советская энциклопедия

• Tan — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

• Tg — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

• Косинус — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

• Котангенс — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

• Секанс — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

• История тригонометрии — Геодезические измерения (XVII век) …   Википедия

• МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… …   Энциклопедия Кольера

• КОТАНГЕНС — КОТАНГЕНС, котангенса, муж. (лат. cotangens) (мат.). Тригонометрическая функция тангенс дополнительного угла. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

dic.academic.ru

Что такое тангенс и котангенс?

Тригонометрические функции

Данил, введи в гугле «тангенс и котангенс», поверь, найдешь немало информации.

в тригонометрии тангенс=синус разделить на косинус а второе наоборот..

Тангес острого угла в прямоугольном треугольнике называют отношение катете, лежащего против этого угла, к катету, прилежащему к этому углу. Котангес острого угла в прямоугольном треугольнике называют отношение катета, прилежащего к этому углу, к катету, лежащему против этого угла. tg A * ct A = 1

это тригонометрические функции, есть книжечка «Таблицы тригонометрических функций» Обязательно будешь учить в школе в старших классах, а пока ты в 5-м, молодец, что отличник, оставайся им до конца учёбы.

это такие отношения углов..

тригометрические функции и начинаются они так: 1 синус 2 косинус 3 тангенс 4 котангенс 5 сиктангенс и так далее

Тангенс — отношение синуса к косинусу (т. е. tg = sin/cos) или отношение противолежащего катета к прилежащему. Котангенс — отношение косинуса к синусу (т. е. ctg = cos/sin) или отношение прилежащего катета к противолежащему.

персонажи из пиворонпы

touch.otvet.mail.ru

Тригонометрические функции — это… Что такое Тригонометрические функции?

Рис. 1
Графики тригонометрических функций:      синуса      косинуса      тангенса      котангенса      секанса      косеканса

Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

К тригонометрическим функциям относятся:

прямые тригонометрические функции

• синус (sin x)
• косинус (cos x)

производные тригонометрические функции

• тангенс (tg x)
• котангенс (ctg x)

другие тригонометрические функции

• секанс (sec x)
• косеканс (cosec x)

В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.

Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.

Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.

Способы определения

Геометрическое определение

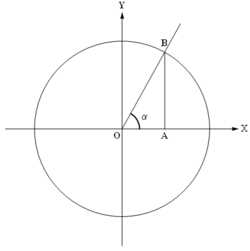Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок).

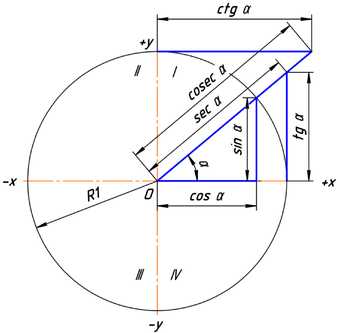Рис. 3
Численные значения тригонометрических функций угла в тригонометрической окружности с радиусом, равным единице

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
• Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
• Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
• Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).
• Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
• Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.

Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями , то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где

 — числа Бернулли,

 — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Значения тригонометрических функций прочих углов  

Свойства тригонометрических функций

Простейшие тождества

Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Это соотношение называется основным тригонометрическим тождеством.

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Непрерывность

Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции  — периодические с периодом 2π, функции и  — c периодом π.

Формулы приведения

Формулами приведения называются формулы следующего вида:

Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:

Некоторые формулы приведения:

Формулы сложения

Значения тригонометрических функций суммы и разности двух углов:

Аналогичные формулы для суммы трёх углов:

Формулы для кратных углов

Формулы двойного угла:

Формулы тройного угла:

Прочие формулы для кратных углов:

следует из формулы дополнения и формулы Гаусса для Гамма-функции

Формулы половинного угла:

Произведения

Формулы для произведений функций двух углов:

Аналогичные формулы для произведений синусов и косинусов трёх углов:

Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.

Степени

Суммы

Для функций от аргумента существует представление:

где угол находится из соотношений:

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

Тригонометрические функции комплексного аргумента

Определение

Формула Эйлера:

позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:

где

Соответственно, для вещественного x,

Комплексные синус и косинус тесно связаны с гиперболическими функциями:

Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:

• комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
• все нули комплексных синуса и косинуса лежат на вещественной оси.

Комплексные графики

На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.

История названий

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).

Сам термин тригонометрические функции введён Клюгелем в 1770 году.

См. также

Литература

• Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
• Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.

Ссылки

dvc.academic.ru

Котангенс — это… Что такое Котангенс?

Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.

Способы определения

Геометрическое определение

Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок.)

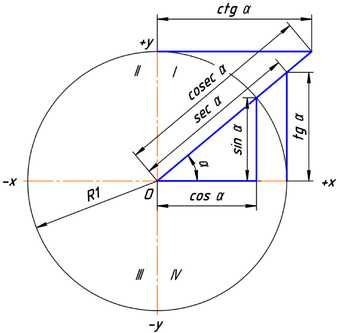
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4.
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
• Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
• Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
• Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
• Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
• Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где B_n — числа Бернулли.

где E_n — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Свойства тригонометрических функций

Простейшие тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π

Формулы приведения

Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:

Формулы сложения

Другие тригонометрические тождества.

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

См. также Список интегралов от тригонометрических функций

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Сам термин тригонометрические функции введён Клюгелем в 1770.

См. также

Ссылки

Wikimedia Foundation. 2010.

brokgauz.academic.ru

КОТАНГЕНС — это… Что такое КОТАНГЕНС?

КОТАНГЕНС — (лат. cotangens, вместо complementi tangens дополнение тангенса). В тригонометрии, тангенс дуги, дополняющей данную дугу. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КОТАНГЕНС в тригонометрии тангенс… …   Словарь иностранных слов русского языка

КОТАНГЕНС — (новолат. cotangens от complementi tangens тангенс дополнения), одна из тригонометрических функций …   Большой Энциклопедический словарь

КОТАНГЕНС — КОТАНГЕНС, котангенса, муж. (лат. cotangens) (мат.). Тригонометрическая функция тангенс дополнительного угла. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

КОТАНГЕНС — КОТАНГЕНС, а, муж. (спец.). Тригонометрическая функция, равная отношению косинуса к синусу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

КОТАНГЕНС — муж., мат. тангенс дополненья к прямому углу. Толковый словарь Даля. В.И. Даль. 1863 1866 …   Толковый словарь Даля

котангенс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 …   Словарь синонимов

котангенс — тангенс дополнения лат.: cotangens, complementi tangens новолат. лат …   Словарь сокращений и аббревиатур

Котангенс — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции  вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… …   Википедия

котангенс — (новолат. cotangens, от complementi tangens  тангенс дополнения), одна из тригонометрических функций. * * * КОТАНГЕНС КОТАНГЕНС (новолат. cotangens, от complementi tangens тангенс (см. ТАНГЕНС) дополнения), одна из тригонометрических функций (см …   Энциклопедический словарь

Котангенс — (новолат. cotangens, сокращение от complementi tangens Тангенс дополнения)         одна из тригонометрических функций (См. Тригонометрические функции), обозначение ctg. К. острого угла в прямоугольном треугольнике называется отношение катета,… …   Большая советская энциклопедия

dic.academic.ru