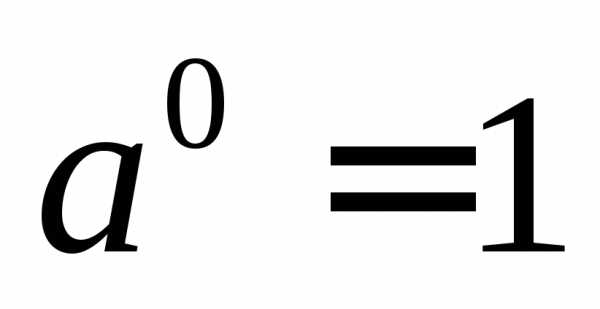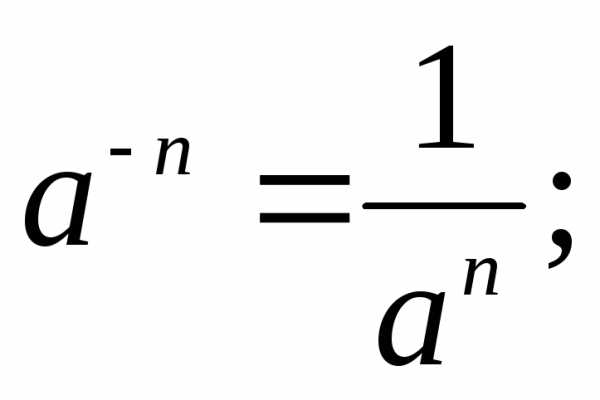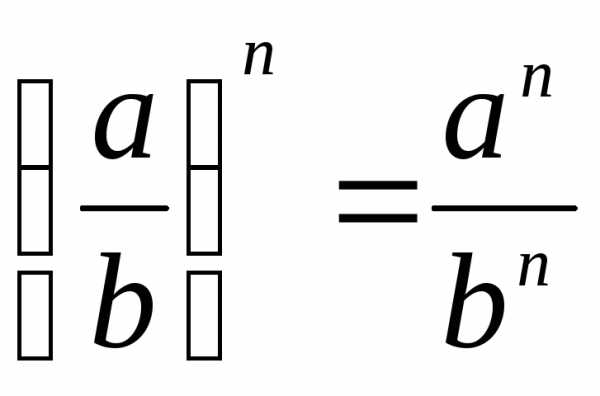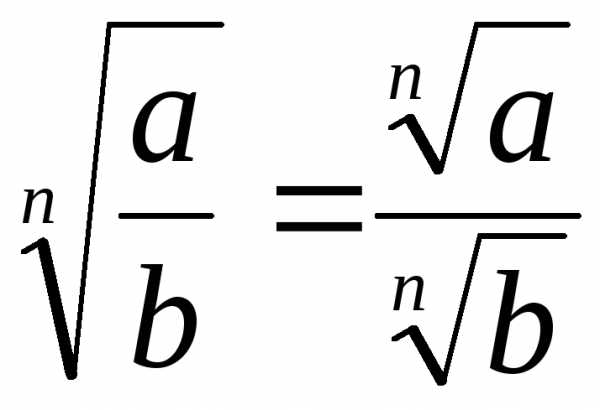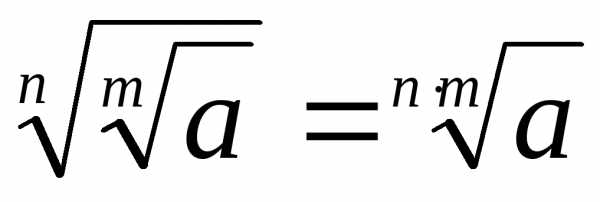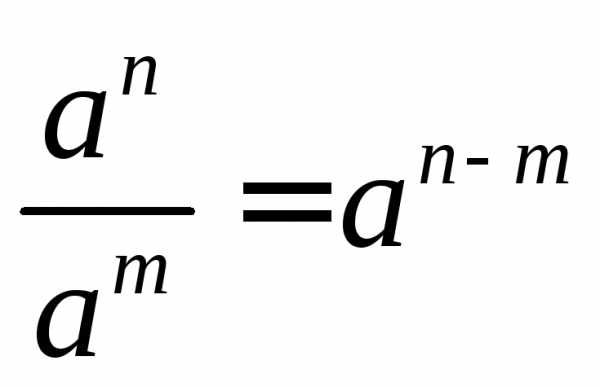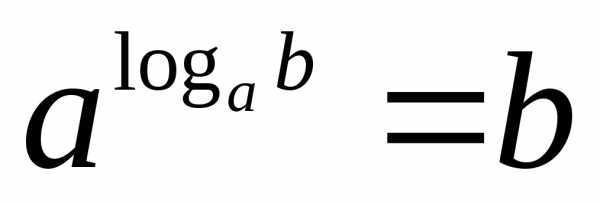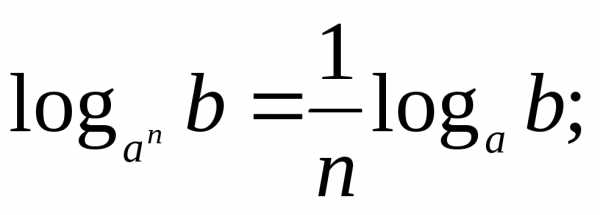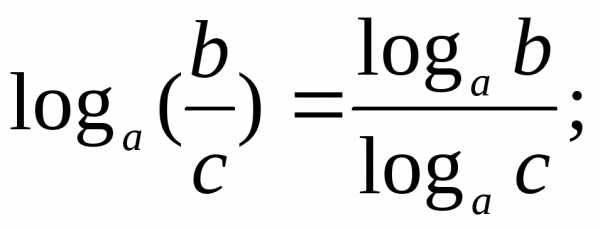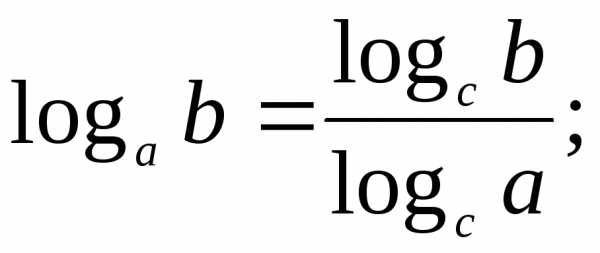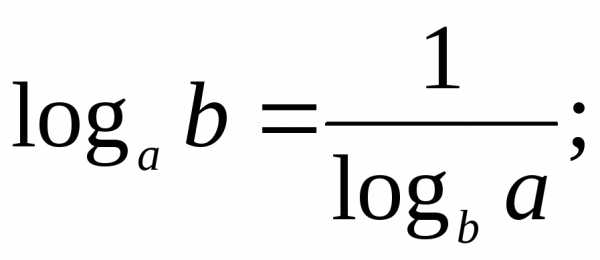Геометрическая прогрессия. Свойства геометрической прогрессии.
| Геометрическая прогрессия |· Числовая последовательность, первый член которой отличается от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией. Обозначается:
· Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу. Т.е. . Это число называется знаменателем геометрической прогрессии и обозначается q.
· Для того чтобы задать геометрическую прогрессию , достаточно знать ее первый член и знаменатель q.
· Если q>0 (), то прогрессия является монотонной последовательностью. Например, получаем геометрическую прогрессию: — монотонно убывающая геометрическая прогрессия.
· Если q<0, то прогрессия представляет собой знакочередующийся числовой ряд. Например, получаем геометрическую прогрессию: .
· Свойство геометрической прогрессии: , где
· Формула n-го члена геометрической прогрессии:
· Формула суммы первых n членов геометрической прогрессии
· Из определения знаменателя геометрической прогрессии следует:
primer.by
Геометрическая прогрессия, ее свойства — Алгебра — Мастер-класс
Геометрическая прогрессия, ее свойства.
Формула n-го члена геометрической прогрессии
Некоторые результаты естественных процессов образуют последовательность называется геометрической прогрессией.
Геометрическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же отличное от нуля число, которое называется знаменателем геометрической прогрессии. В геометрической прогрессии каждый член, начиная с второго, является срединно геометрическим между двумя соседними членами: .
Знаменатель геометрической прогрессии ( bn обозначается q и равна отношению любого члена прогрессии, начиная со второго, к предыдущему члену: . Вообще, если bi и bj — два данные члены геометрической прогрессии ( bn, причем i j, то .
Любой член геометрической прогрессии можно вычислить, зная первый член прогрессии
Свойства геометрической прогрессии с первым членом b1 и знаменателем q:
1. Если первый член геометрической прогрессии — число положительное (b1 > 0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является возрастающей; или если первый член геометрической прогрессии — число отрицательное (b1 0) и знаменатель прогрессии 0 > q 1, то такая геометрическая прогрессия является возрастающей.
2. Если первый член геометрической прогрессии — число отрицательное (b1 0) и знаменатель прогрессии q > 1, то такая геометрическая прогрессия является убывающей; или если первый член геометрической прогрессии — число положительное (b1 > 0) и знаменатель прогрессии 0 q 1, то такая прогрессия является убывающей; При q 0 геометрическая прогрессия не является ни убывающей, ни растущей.
3. Произведение двух членов конечной геометрической прогрессии, равноотстоящих от ее концов, равен произведению крайних членов.
na-uroke.in.ua
Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
О.Геометрической прогрессией
О.Это число называетсязнаменателем геометрической прогрессии q геометрической прогрессии.
Геометрическая
прогрессия задаётся своим первым членом
и знаменателем. Из определения
геометрической прогрессии следует,
что отношение любого её члена, начиная
со второго, к предыдущему члену равно q, т.е. при любом
натуральномnверно
равенство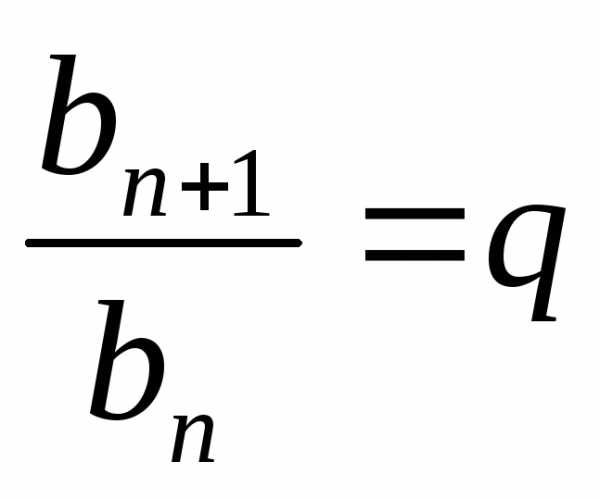 .
.
Формула n-го члена геометрической прогрессии.
Любой член
геометрической прогрессии можно
вычислить по формуле 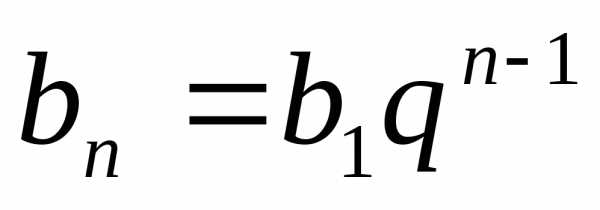 ,где
,где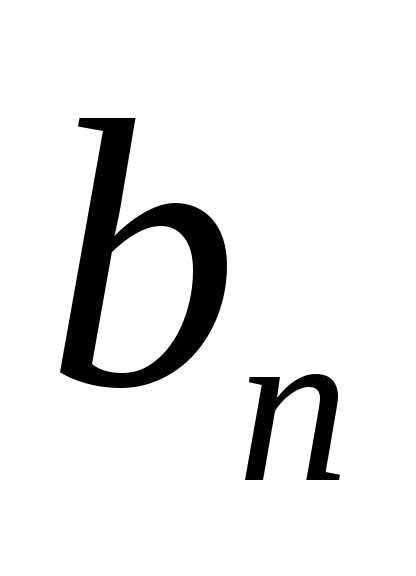 —
член прогрессии с номеромn,
—
член прогрессии с номеромn,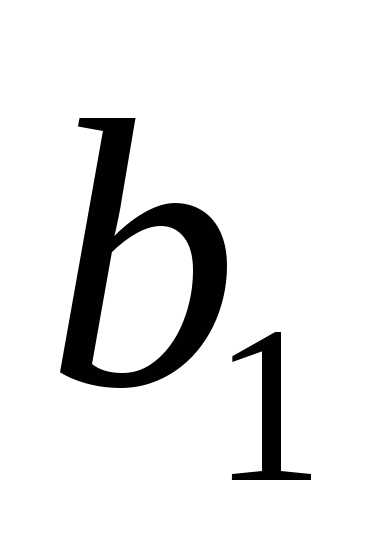 —
первый член иq– её
знаменатель.
—
первый член иq– её
знаменатель.
Возьмём произвольное натуральное n.Из определения геометрической прогрессии следует.
Эта цепочка состоит из nравенств, поэтому для любого конечногоnона может быть выписана. Следовательно, любой член геометрической прогрессии можно вычислить, зная его номер, первый член прогрессии и её знаменатель.
Характеристическое свойство геометрической прогрессии с положительными членами.
Если
последовательность положительных
чисел является геометрической
прогрессией, то все её члены, начиная
со
Доказательство.
Из определения
геометрической прогрессии следует,
что  .
.
Выразив из этого
равенства 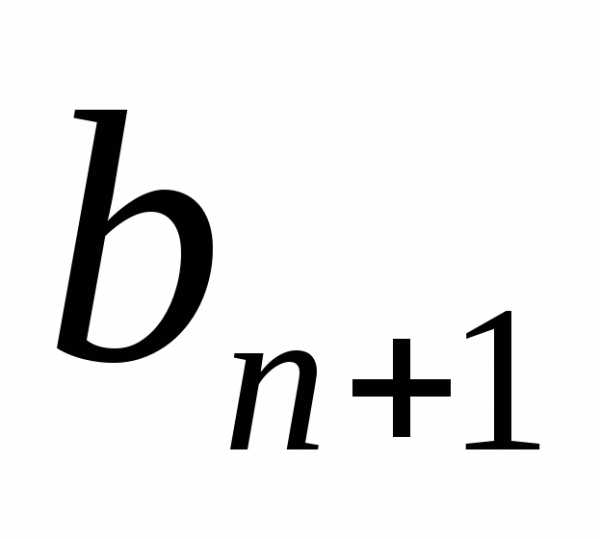 ,
получим.
,
получим.
Так как все члены прогрессии положительны, то последнее равенство равносильно следующему .
Теорема. (формула суммы n первых членов геометрической прогрессии).
Сумма n первых членов геометрической
прогрессии равна 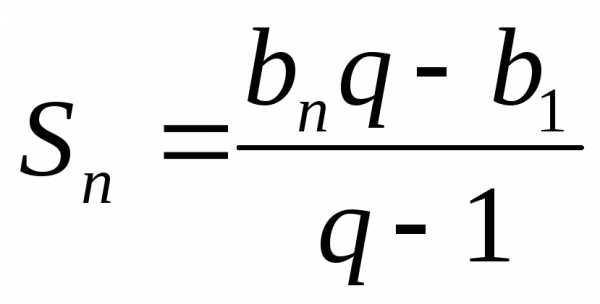 ,при
,при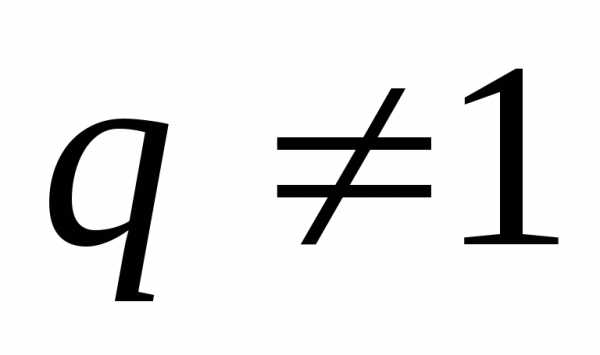
Доказательство.
Сумма nпервых членов геометрической прогрессии равна
. 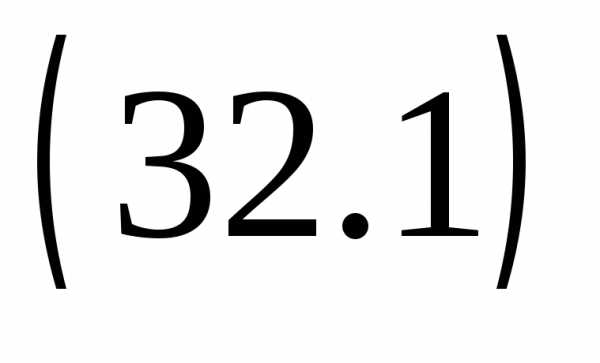
Домножим обе части этого равенства на знаменатель геометрической прогрессии .
Следовательно,
.
Вычтем полученное равенство из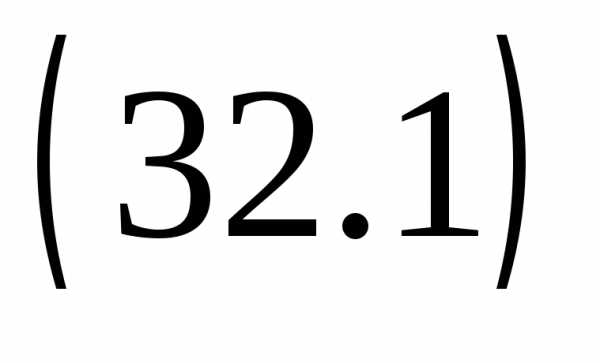 .
Получим:
.
Получим: .
.
Отсюда следует,
что
.
При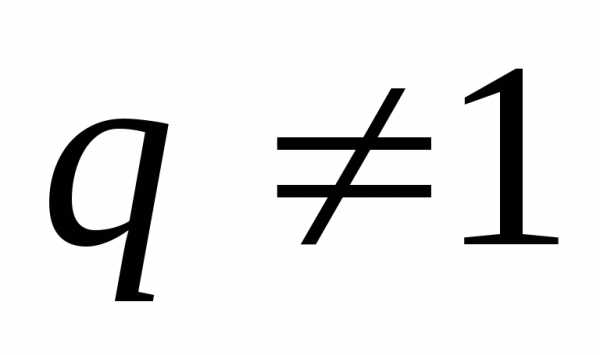 это равенство равносильно доказываемому.
Теорема доказана.
это равенство равносильно доказываемому.
Теорема доказана.
Следствие. 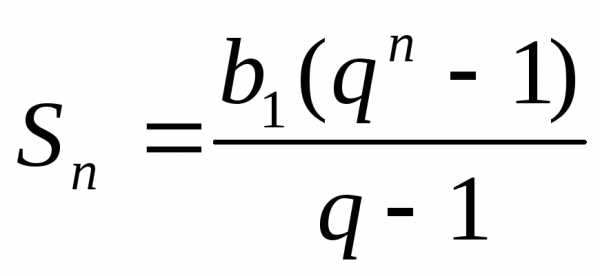 ,при
,при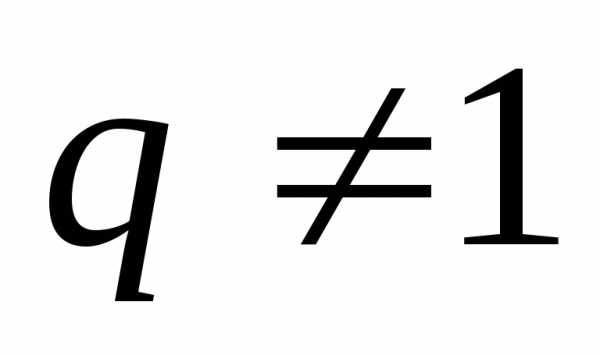
Доказательство.
Выразим 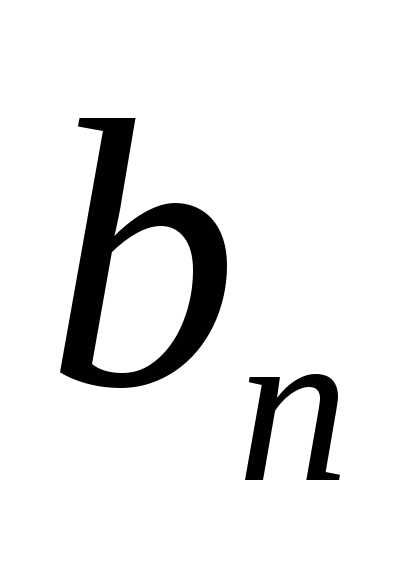 по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
Геометрическая
прогрессия называется бесконечно
убывающей, если её знаменательq по абсолютной величине меньше
единицы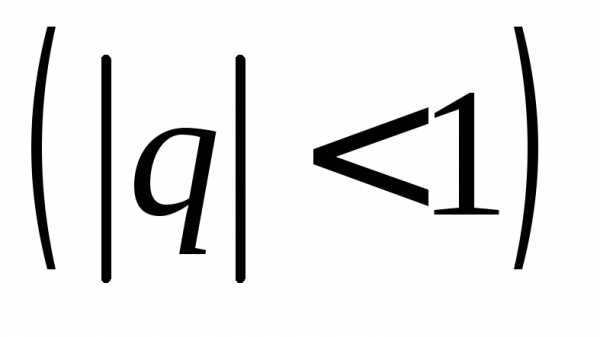 .
.
О.Суммой бесконечно убывающей геометрической прогрессииназывается число, к которому неограниченно приближается суммаnпервых членов бесконечно убывающей геометрической прогрессии при неограниченном увеличенииn.
Сумма
бесконечно убывающей геометрической
прогрессии равна 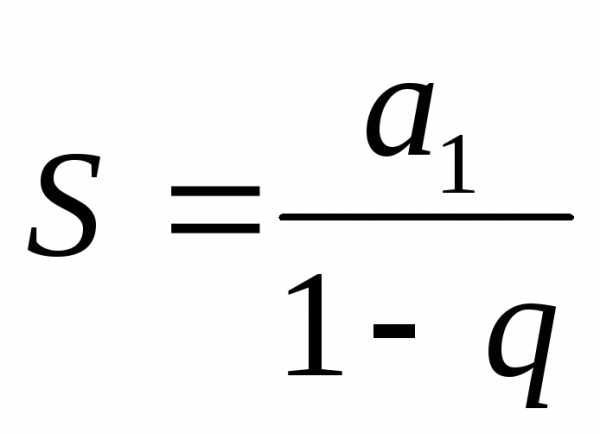
Приложение
Тригонометрическая окружность

Сборник формул
ТРИГОНОМЕТРИЯ Основные тригонометрические тождества Знаки тригонометрических функций по четвертям    Тригонометрические функции отрицательного аргумента Выражение одной функции через другую Обратные функции отрицательного аргумента Решение простейших тригонометрических уравнений Функция алгебраической суммы двух аргументов Преобразование Преобразование суммы функций в произведение произведения функций в сумму Функции половинного аргумента | АЛГЕБРА Корни квадратных уравнений Теорема Виета Разложение квадратного трехчлена на множители Логарифмы Степень двучлена Извлечение квадратного корня из квадрата. Определение модуля числа. |
studfiles.net
Геометрическая прогрессия — это… Что такое Геометрическая прогрессия?
У этого термина существуют и другие значения, см. Прогрессия.Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].
Описание
Любой член геометрической прогрессии может быть вычислен по формуле:
Если и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при — знакочередующейся[2].
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
Примеры
- Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата[3]:8-9.
- Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
- 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
- — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
Свойства
Доказательство
Пусть — последовательность :
- Полученное соотношение является характеристическим для арифметической прогрессии.
Доказательство
- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
- ,
Доказательство
- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
Доказательство
- Сумма первых членов геометрической прогрессии:
Доказательство
- Через сумму:
Примечания
См. также
dic.academic.ru
Геометрическая прогрессия
РЕФЕРАТ
по теме:
ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
работу выполнил:
студент Ставропольского
Государственного Университета
IV курса, Физ-Мат Факультета,
отделения МИИТ, гр. ”Б”
Неботов Виталий Дмитриевич
Ставрополь 1997 г.
СОДЕРЖАНИЕ :
Стр.
1. Вступительное слово…………………………………………………………………………3
2. Определение геометрической прогрессии…………………………………………..3
3. Свойства геометрической прогрессии…………………………………………………3
4. Сумма геометрической прогрессии…………………………………………………….4
5. Заключение……………………………………………………………………………………….5
6. Список использованной литературы……………………………………………………6
Геометрическая прогрессия играет большую и важную роль не только в школьном курсе алгебры, но и (как я мог убедится) в дальнейшем обучении в высших учебных заведениях. Важность этого на первый взгляд небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения, в частности он часто применяется в теории рядов, рассматриваемой на II-III курсах университета. Поэтому мне кажется крайне важным дать здесь полное описание этого курса, дабы внимательный читатель мог повторить уже известный ему (надеюсь — прим. автора) из школьного курса материал, или даже почерпнуть много нового и интересного.
Прежде всего необходимо дать определение геометрической прогрессии, ибо не определившись о предмете разговора невозможно продолжать сам разговор. Итак: числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и тоже не равное нулю число, называется геометрической прогрессией.
Внесу некоторую ясность в данное выше определение: во-первых, мы требуем от первого члена неравенства нулю для того, что при умножении его на любое число мы в результате снова получим ноль, для третьего члена опять ноль, и так далее. Получается последовательность нулей, которая не попадает под данное выше определение геометрической прогрессии и не будет являться предметом нашего дальнейшего рассмотрения.
Во-вторых, число на которое умножаются члены прогрессии опять же не должно быть равно нулю, по вышеизложенным причинам.
В-третьих, предоставляю возможность вдумчивому читателю самому найти ответ на вопрос, почему мы умножаем все члены прогрессии на одно и тоже число, а не, скажем, на разные. Ответ не так прост, как может показаться вначале.
Далее, из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. b2:b1 = b3:b2 = … = bn:bn-1 = bn+1:bn = … . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.
Несколько слов необходимо сказать и о способах задания геометрической прогрессии. Для того чтобы задать геометрическую прогрессию (bn), достаточно знать ее первый член b1 и знаменатель q. Например, условиями b1 = 2, q = -5 (q < 0) задается геометрическая прогрессия 2, -10, 50, -250, … . Эта прогрессия не является ни возрастающей ни убывающей последовательностью.
Следует заметить, что: последовательность называется возрастающей (убывающей) если каждый последующий член последовательности больше (меньше) предыдущего.
Таким образом, если q > 0 (q1), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -3, q = 4, тогда геометрическая прогрессия -3, -12, -48, -192, … есть монотонно убывающая последовательность.
Однако, если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.
Любая геометрическая прогрессия обладает определенным характеристическим свойством. Это свойство является следствием самого правила задания геометрической прогрессии: последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.
.
Пользуясь этим свойством можно находить любой член геометрической прогрессии если известны два рядом стоящие.
Для нахождения n-ного члена геометрической прогрессии есть еще одна формула. Для того чтобы найти любой член геометрической прогрессии необходимо, чтобы она была задана, т. е. были известны значения b1 и q:
.
Так как геометрическая прогрессия это числовая последовательность, то мы можем найти ее сумму. Для нахождения суммы геометрической прогрессии применяют следующую формулу:
Если в данную формулу подставить вместо bn его выражение в виде b1qn-1, то получим еще одну формулу для вычисления суммы геометрической прогрессии:
У геометрической прогрессии есть еще одно свойство, а именно: из определения знаменателя геометрической прогрессии следует, что b1bn = b2bn-1 = …, т. е. произведение членов, равно отстоящих от концов прогрессии, есть величина постоянная.
Наконец, нельзя не коснуться такого важного с научной точки зрения понятия, как бесконечной геометрической прогрессии при . Здесь наиболее важным понятием является понятие суммы бесконечной геометрической прогрессии: пусть (xn) — геометрическая прогрессия со знаменателем q, где Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию, называется предел суммыn первых ее членов при .
Найти эту сумму можно по следующей формуле:
Заканчивая описание геометрической прогрессии хочется лишний раз повторить, что за видимой простотой геометрической прогрессии скрывается большой прикладной потенциал этого раздела алгебры.
Список использованной литературы:
1. В. С. Крамор, Повторяем и систематизируем школьный курс
алгебры и начал анализа, Москва, Просвещение, 1990 г.
2. С. А. Теляковский, Алгебра, учебник для 8 класса средней школы,
Москва, Просвещение, 1987 г.
3. Личные заметки и наблюдения автора.
studfiles.net
Определение геометрической прогрессии: формула n-го члена прогрессии
Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число. Геометрическая прогрессия обозначается b1,b2,b3, …, bn, …
Свойства геометрической прогрессии
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .
Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).
Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. В таких случаях говорят, что прогрессия является постоянной последовательностью.
Формула n-го члена прогрессии
Для того, чтобы числовая последовательность (bn) являлась геометрической прогрессией необходимо, чтобы каждый её член, начиная со второго, являлся средним геометрическим соседних членов. То есть необходимо выполнение следующего уравнения — (b(n+1))^2 = bn * b(n+2), для любого n>0, где n принадлежит множеству натуральных чисел N.
Формула n-ого члена геометрической прогрессии имеет вид:
bn=b1*q^(n-1), где n принадлежит множеству натуральных чисел N.
Рассмотрим простой пример:
В геометрической прогрессии b1=6, q=3, n=8 найти bn.
Воспользуемся формулой n-ого члена геометрической прогрессии:
b8 = 6*3^7 = 13122.
Нужна помощь в учебе?
Предыдущая тема: Электронный учебник по геометрии: все темы школьной программы
Следующая тема:   Формула суммы n первых членов геометрической прогрессии + примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru

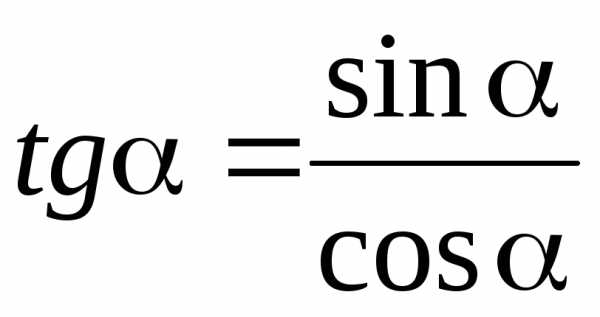
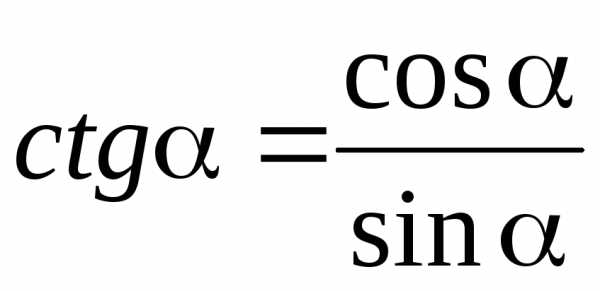
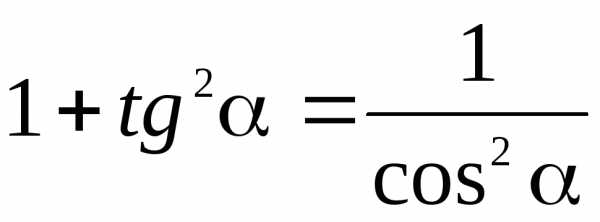
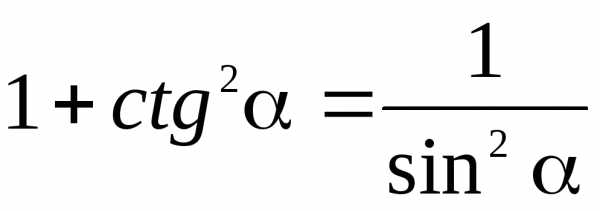



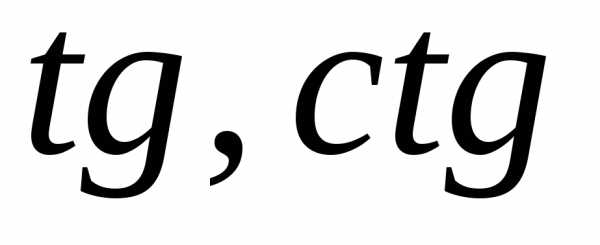

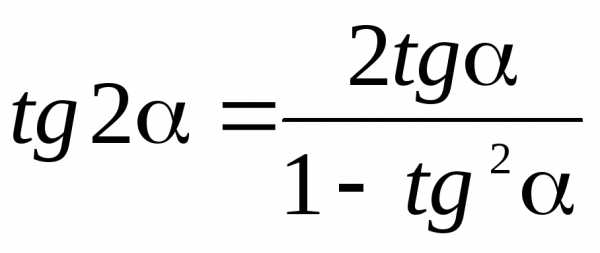 Функции
двойного аргумента
Функции
двойного аргумента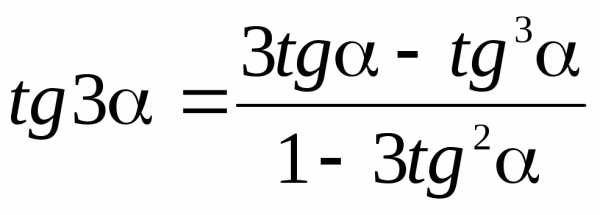 Функции
тройного аргумента
Функции
тройного аргумента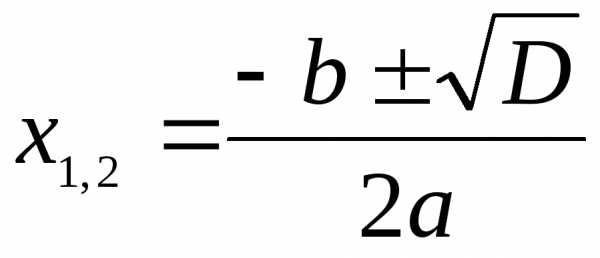
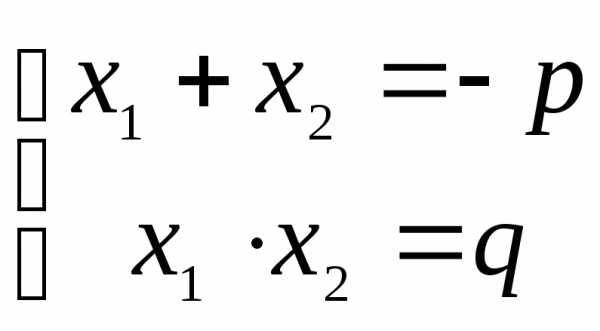
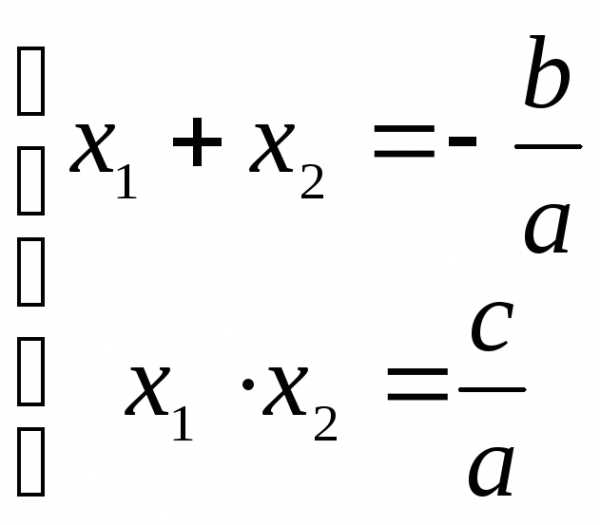
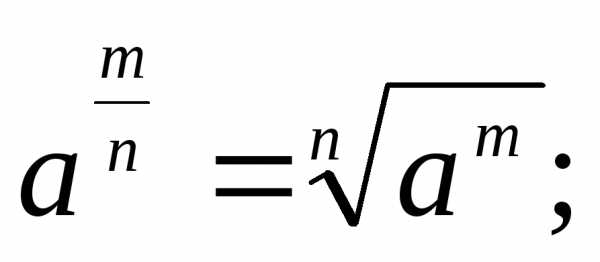 Степени
и корни
Степени
и корни