Проецирование прямой | Мир сварки
Проецирование прямой
Прямая линия в пространстве определяется положением двух ее точек, например А и В, достаточно выполнить комплексный чертеж этих двух точек, затем соединить одноименные проекции, получим соответственно горизонтальную, фронтальную и профильную проекции прямой.
Проекция прямой – всегда прямая, кроме тех случаев, когда прямая перпендикулярна к одной из плоскостей, и проекция этой прямой на эту плоскость будет изображаться в виде точки.
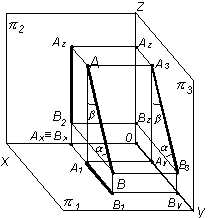
Чтобы положение прямой в пространстве было определенным, необходимо иметь не менее двух проекций отрезка (рис.1).
Рис.1. Проекции прямой |
Прямая общего положения – прямая, наклонная ко всем плоскостям проекций.
Прямая частного положения – прямая, параллельная хотя бы к одной из плоскостей проекций.
Условно частные положения прямых можно разбить на три группы.
Первая группа
Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций (рис.2).
Рис.2. Горизонтально проецирующая прямая |
Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций (рис.3).
Рис.3. Фронтально проецирующая прямая |
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций (рис.4).
Рис.4. Профильно проецирующая прямая |
Вторая группа
Прямые параллельны одной плоскости проекций, а к двум другим направлены под углом.
Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций (рис.5).
Рис.5. Горизонтальная прямая |
Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций (рис.6).
Рис.6. Фронтальная прямая |
Профильная прямая – прямая, параллельная профильной плоскости проекций (рис.7).
Рис.7. Профильная прямая |
Третья группа
Прямые, лежащие в плоскостях проекций (рис.8).
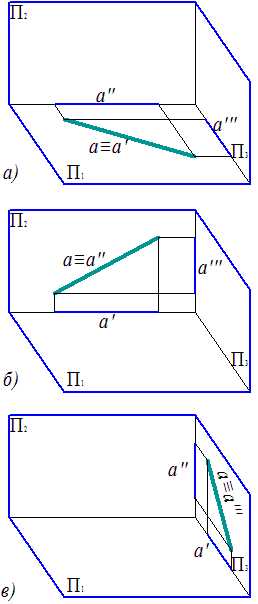 Рис.8. Прямая, лежащая в плоскостях проекций: а) в горизонтальной; б) в фронтальной; в) в профильной |
Пример проецирования прямой
Например:
Построить недостающую проекцию прямой (рис.9).
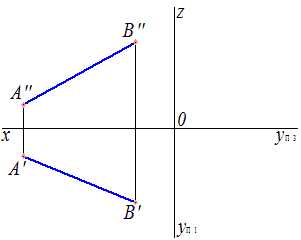 Рис.9 Проецирование прямой |
Для того, чтобы спроецировать прямую, необходимо спроецировать точки, принадлежащие этой прямой.
Находим точки пересечения координатных осей и проекционных линий (рис.10).
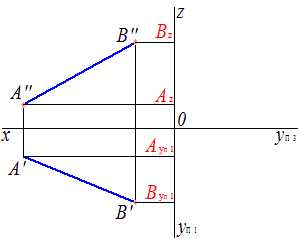 Рис.10 Проецирование прямой |
Переносим циркулем точки Ау и Ву с yП1 на yП3 (рис.11).
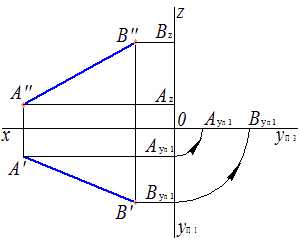 Рис.11 Проецирование прямой |
Соединяем проекционные линии из точек АуП3 и Аz, а также ВуП3 и B
z (рис.12), получаем точки А′″ и B′″.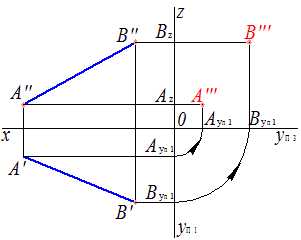 Рис.12 Проецирование прямой |
Соединяем точки А′″ и B′″ и получаем третью проекцию прямой (рис.13).
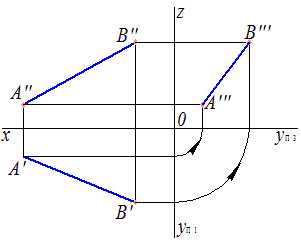 Рис.13 Проецирование прямой |
weldworld.ru
Проекции прямой
При проецировании прямой на какую-либо плоскость проекций проецирующие лучи, проходящие через точки прямой, образуют проецирующую плоскость, которая пересекает плоскость проекции по прямой (рис. 4.18). Следовательно, проекцией отрезка будет отрезок прямой. Чаще всего проекция отрезка меньше самого отрезка, так как его проекция (ab) является частью катета прямоугольной: треугольника (ВbМ), а отрезок (АВ) — частью гипотенузы. Так как Mb < MB, то и ab<AB. Отношение проекции отрезка к его натуральной величине называют коэффициентом искажения.
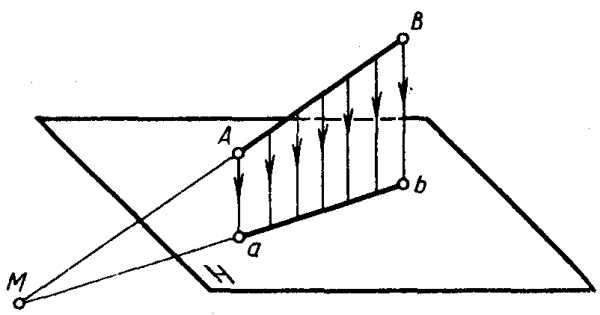
Рис. 4.17.
Коэффициент искажения обозначают буквой К,
К= аb/AB ≤1
Если отрезок прямой параллелен плоскости проекций, при проецировании образуется прямоугольник, в котором сам отрезок и его проекция являются противоположными сторонами этого прямоугольника. Следовательно ВС=bс. В этом случае коэффициент искажения К= аb/AB =1, т. е. отрезок проецируется без искажения.
Положение прямой в пространстве можно определить двумя ее точками, поэтому, чтобы задать прямую на эпюре, достаточно задать проекции двух ее точек (рис. 4.18), т.е. проекции отрезка этой прямой. Данные проекции отрезка прямой полностью определяют положение прямой в пространстве.
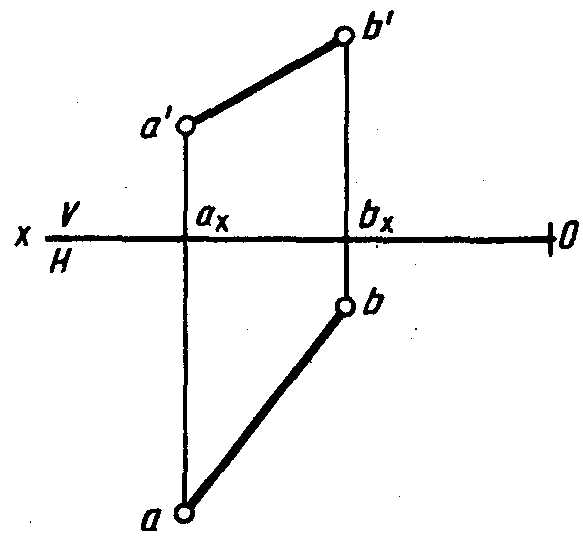
Рис. 4.18.
Сравнивая координаты точек А и В, являющихся концами отрезка, можно представить себе, как располагается отрезок в пространстве. Точка В находится выше точки А относительно плоскости Н, так как b’bх>а’ах, т. е. ZB>ZA, и точка В ближе к плоскости V, чем точка А, так как bbx<aax, т. е. YB<YA.
Различные случаи расположения прямых относительно плоскостей проекций
Прямая общего положения — прямая, не параллельная ни одной из плоскостей проекций (рис. 4.18), т. е. ни одна из проекций этой прямой не параллельна какой-либо оси проекций.
Горизонтальная прямая — прямая, параллельная плоскости Н. Все точки прямой находятся на одинаковом расстоянии от плоскости Н (рис. 4.19, а), т. е. координаты Z всех точек отрезка ВС равны между собой, ВЬ= = Сс — b’bx—c’cx — ZH = Zc- Фронтальная проекция горизонтальной прямой параллельна оси Ох (рис. 4.19,б). Положение второй проекции относительно оси Ох определяется положением самой прямой, Угол наклона горизонтальной прямой к плоскости V — р. На плоскость Н отрезок горизонтальной прямой проецируется в натуральную величину.
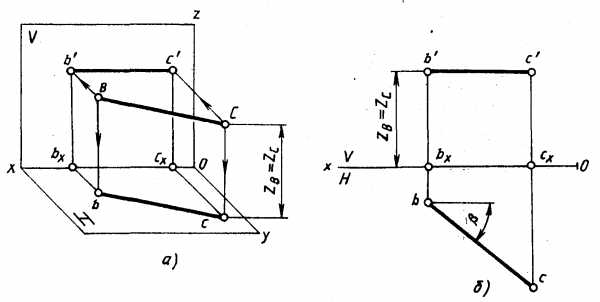
Рис. 4.19.
Фронтальная прямая — прямая, параллельная плоскости V. Все точки прямой находятся на одинаковом расстоянии от плоскости V (рис. 4.20, а), т. е. координаты Y всех точек отрезка CD равны между собой. Горизонтальная проекция фронтальной прямой параллельна оси Ох (рис. 4.20,б). Положение второй проекции относительно оси Ох определяется положением самой прямой. Угол наклона фронтальной прямой к горизонтальной плоскости H равен α. На плоскость V отрезок фронтальной прямой проецируется в натуральную величину.
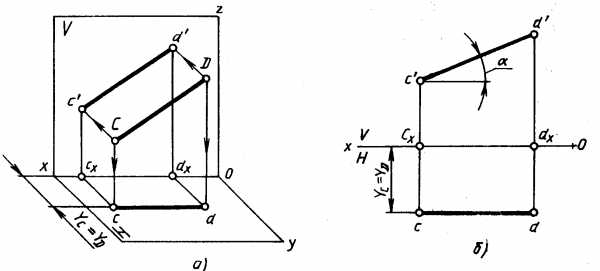
Рис. 4.20.
Профильная прямая — прямая, параллельная плоскости H. Все точки прямой находятся на одинаковом расстоянии от плоскости W (рис. 4.21,а), т. е. координаты X всех точек отрезка DE равны между собой. Фронтальная проекция профильной прямой параллельна оси Oz, а горизонтальная проекция — оси Оу (рис. 4.21,б). Положение профильной проекции определяется положением самой профильной прямой. Угол наклона профильной прямой к плоскости Н — α, к плоскости V — β. На плоскость W отрезок профильной прямой проецируется в натуральную величину.
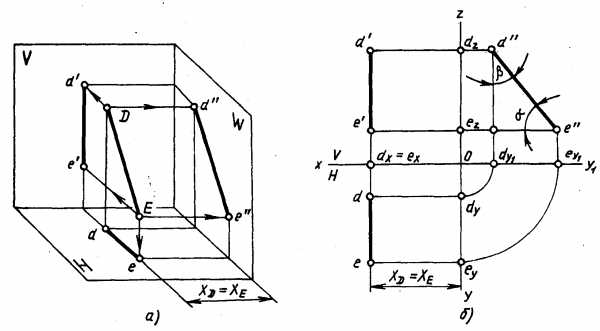
Рис. 4.21.
Прямые, перпендикулярные одной из плоскостей проекций, называют проецирующими прямыми.
Горизонтально-проецирующая прямая перпендикулярна плоскости H. Проекция такой прямой на плоскости Н является точкой, а ее фронтальная проекция перпендикулярна оси Ох и параллельна оси Оz (рис. 4.22). На плоскость V прямая проецируется в натуральную величину.
Фронтально-проецирующая прямая перпендикулярна плоскости V. Проекция этой прямой на плоскость V является точкой, а ее горизонтальная проекция перпендикулярна оси Ох и параллельна оси Оу (рис. 4.23). На плоскость Н прямая проецируется в натуральную величину.
Профильно-проецирующая прямая перпендикулярна плоскости W. Проекция этой прямой на плоскость W является точкой. Ее горизонтальная проекция перпендикулярна оси Оу и параллельна оси Ох, а фронтальная — перпендикулярна оси Oz и параллельна оси Ох (рис. 4.24). На плоскости Н и V прямая проецируется в натуральную величину.
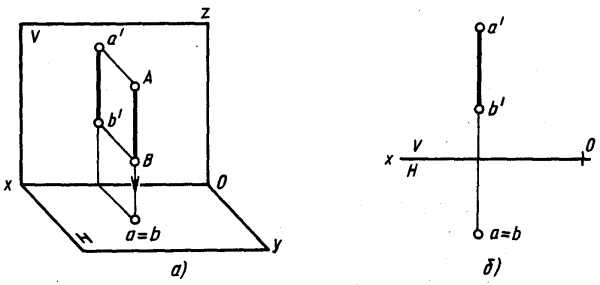
Рис. 4.22.
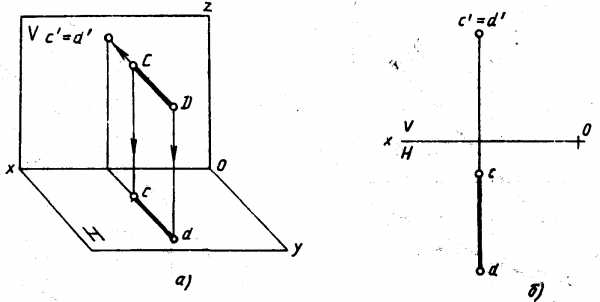
Рис. 4.23.
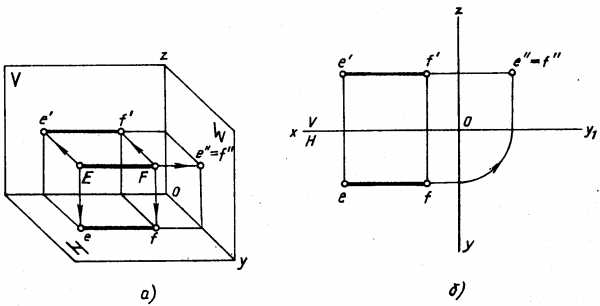
Рис. 4.24.
Точка, принадлежащая прямой. Если точка лежит на прямой, то ее проекции лежат на одноименных проекциях этой прямой и на одной линии проекционной связи. На рис. 4.25,а точка М лежит на прямой CD. Ее горизонтальная проекция т (рис. 4.25,б) лежит на горизонтальной проекции прямой cd, а фронтальная проекция т’ — на фронтальной проекции прямой c’d’.
Обычно по двум проекциям можно определить взаимное расположение точки и прямой. Точка 5 принадлежит прямой CD (рис. 4.25,б), так как ее проекции лежат на продолжении одноименных проекций прямой и на одной линии проекционной связи. Только одна проекция точки F (горизонтальная) лежит на одноименной проекции прямой ей, поэтому точка F не принадлежит прямой CD (рис. 4.25, а и б).
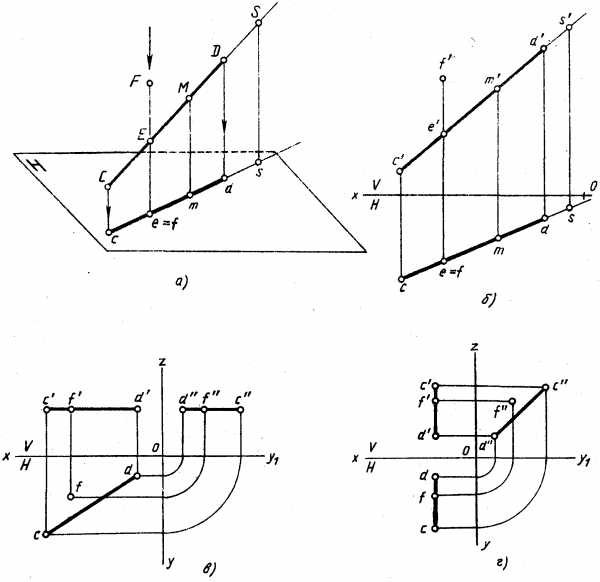
Рис. 4.25.
Если прямая параллельна одной из плоскостей проекций, о взаимном расположении прямой и точки можно получить представление на плоскости проекций, параллельной данной прямой. Для горизонтальной прямой — на плоскости, для фронтальной прямой — на плоскости V, для профильной прямой — на плоскости W.
На рис. 4.25, в и г показаны частные случаи расположения точки и прямой, когда только две проекции точки F лежат на одноименных проекциях прямой CD, и сама точка F не принадлежит прямой CD, так как третья проекция точки не лежит на проекции прямой.
studfiles.net
Лекция 2
2.2. Проецирование прямой
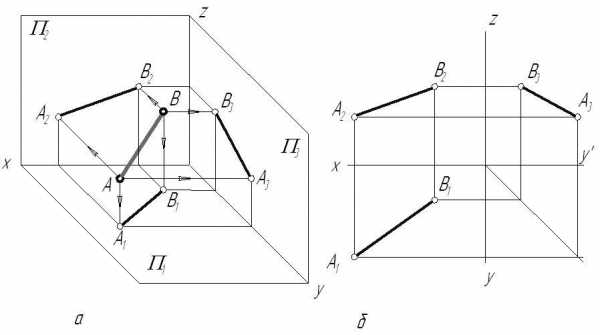
Рис. 2.5
Аксиома евклидовой геометрии гласит: «Через две точки проходит единственная прямая». В связи с этим построение проекций прямой линии на КЧ сводится к построению проекций двух точек ей принадлежащих.
Построим проекции прямой d, которой принадлежат точкиАиВ. Спроецировав их на плоскости проекций, а затем соединив между собой одноименные проекции, получаем проекции прямой (рис.2.5).
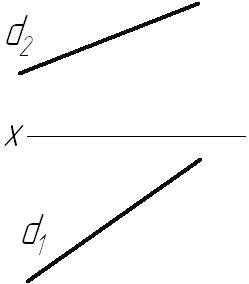
Рис. 2.6
На КЧ прямая может быть задана проекциями двух точек (отрезком) или, на основании инвариантного свойства 21, непосредственно своими проекциями (рис. 2.5 б, 2.6).
2.2.1. Положение прямой относительно плоскостей проекций
По расположению относительно плоскостей проекций различают прямые общего и частного положения.
Прямые не параллельные и не перпендикулярные ни одной из плоскостей проекций называются прямыми общего положения.
Признаки и свойства прямой общего положения:
На КЧ ни одна из проекций прямой общего положения, не параллельна осям проекций (или не перпендикулярна линиям связи) (рис. 2.5, 2.6).
Длина отрезка, принадлежащего прямой общего положения проецируется на любую плоскость проекций с искажением: каждая проекция отрезка короче его натуральной величины.
Прямые общего положения могут быть восходящими или нисходящими.
Прямая называется восходящей, если по мере удаления от наблюдателя она повышается.
Прямая называется нисходящей, если по мере удаления от наблюдателя она понижается.
Для того, чтобы определить по КЧ положение прямой, необходимо обратить внимание на то, как дальняя от наблюдателя точка отрезка прямой расположена относительно ближайшей точки: выше или ниже, правее или левее. На рисунке 2.5 изображена восходящая вправо прямая, т.к. наиболее удаленная точка Врасполагается правее и выше ближайшей точкиА.
Признак восходящих и нисходящих прямых:
На КЧ горизонтальная и фронтальная проекции имеют уклон в одну сторону относительно оси проекций (рис. 2.7 – прямая l).
У нисходящих прямых обе проекции наклонены в разные стороны относительно оси проекций (рис. 2.7 – прямая k).
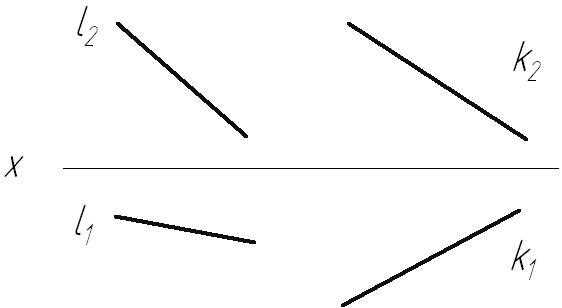
Рис. 2.7
Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.
Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня.
Существует три вида прямых уровня: горизонталь, фронталь и профильная прямая.
Горизонталь (h) – прямая, параллельная горизонтальной плоскости проекций.
Признаки и свойства горизонтали:
На КЧ фронтальная проекция горизонтали
 располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиямсвязи).
располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиямсвязи).На горизонтальную плоскость проекций без искажения проецируются отрезок, принадлежащий горизонтали (), и углы наклона его к фронтальной (
 )
и профильной (
)
и профильной ( )
плоскостям проекций.
)
плоскостям проекций.
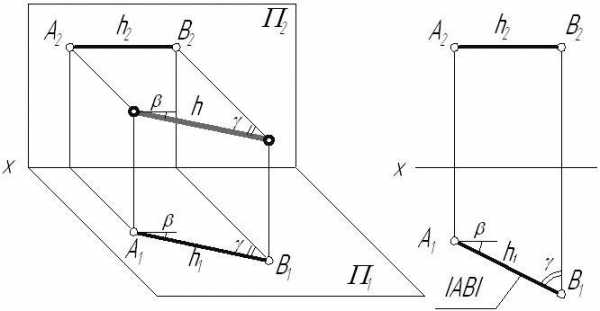
Рис. 2.8
Фронталь (f)–прямая, параллельная фронтальной плоскости проекций.
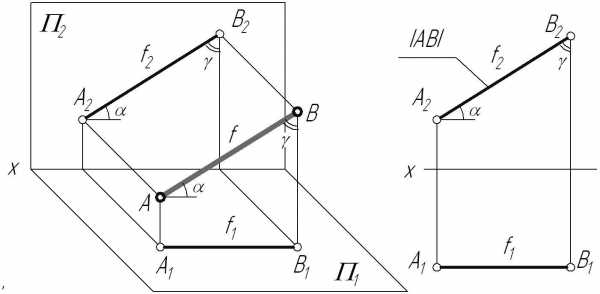
Рис. 2.9
Признаки и свойства фронтали:
На КЧ горизонтальная проекция фронтали
 располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиям связи).
располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиям связи).На фронтальную плоскость проекций проецируются без искажения отрезок, принадлежащий фронтали (), и углы наклона его к горизонтальной (
 )
и профильной (
)
и профильной ( )
плоскостям проекций.
)
плоскостям проекций.
Профильная прямая–прямая, параллельная профильной плоскости проекций.
Признаки и свойства профильной прямой:
На КЧ фронтальная
 и горизонтальная
и горизонтальная проекции отрезка профильной
прямой располагаются перпендикулярно
осих.
проекции отрезка профильной
прямой располагаются перпендикулярно
осих.На профильную плоскость проекций проецируются без искажения отрезок, принадлежащий профильной прямой (), и углы наклона его к фронтальной (
 )
и горизонтальной (
)
и горизонтальной ( )
плоскостям проекций.
)
плоскостям проекций.
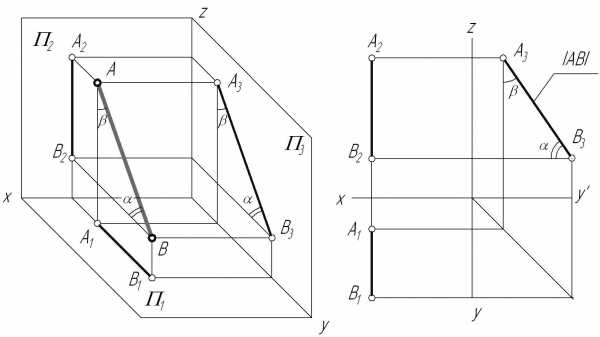
Рис. 2.10
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими прямыми.
Существует три вида проецирующих прямых: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая прямая.
Проекцией проецирующей прямой на плоскость проекций, к которой она перпендикулярна, является точка (след прямой). Все точки, принадлежащие проецирующей прямой, проецируются на ее след.
1. Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций.
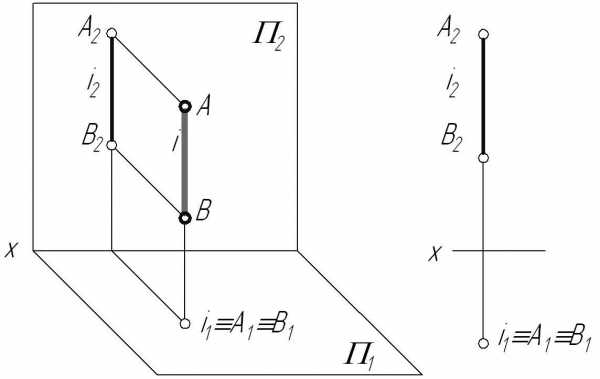 Рис.
2.11
Рис.
2.11
2. Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций.
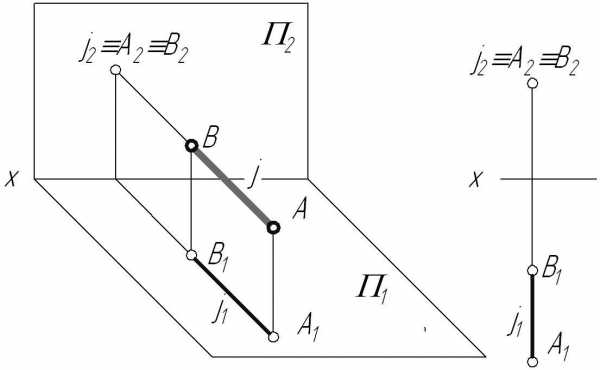
Рис. 2.12
3. Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций.
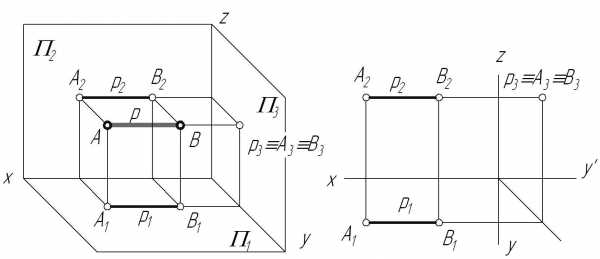
Рис. 2.13
К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня. На рис. 2.14 приведены примеры таких прямых: горизонтальhи профильно-проецирующая прямаяjрасполагаются на горизонтальной плоскости проекций, следовательно их фронтальные проекции находятся на оси0х; фронтальfи профильно-проецирующая прямаярлежат во фронтальной плоскости проекций, а значит их горизонтальные проекции на КЧ совпадают с осью0х.
Рис. 2.14
studfiles.net
Какое положение называется горизонтальным, что означает слово горизонталь
 Горизонтальность, горизонталь, горизонтальный – все эти слова обозначают положение предмета или любого объекта, в том числе живого, описываемого в переносном смысле, по отношению к земле. Если посмотреть с некоторой дистанции на беспорядочное скопление предметов, то можно увидеть, что объекты превращаются в горизонтальные цепочки, в конченом итоге — в горизонтальные линии.
Горизонтальность, горизонталь, горизонтальный – все эти слова обозначают положение предмета или любого объекта, в том числе живого, описываемого в переносном смысле, по отношению к земле. Если посмотреть с некоторой дистанции на беспорядочное скопление предметов, то можно увидеть, что объекты превращаются в горизонтальные цепочки, в конченом итоге — в горизонтальные линии.
Вконтакте
Одноклассники
Мой мир
Рассмотрим примеры, что значит по горизонтали?
- Мы смотрим вдаль – видим горизонт. Как расположена линия горизонта? Горизонтально. Чему? Земле.
- Мы легли отдыхать – приняли горизонтальное положение. В какой позиции находится наше тело? В горизонтальной. По отношению к чему? К дивану. К полу. К земле.
- Читаем письмо или книгу. Как расположены строки? По горизонтали. Относительно чего?
- Летит птица – горизонтально. Чему? Земле.
- Река течёт – горизонтально. Чему? Земле.
Здесь мы можем привести массу примеров, но теперь понятно, что горизонтальность означает параллельное положение линий, предметов, объектов или конструкций по отношению к земле или другому предмету (объекту, конструкции), но который должен быть расположен обязательно параллельно опять-таки земле. Чтобы было проще представить, что же такое горизонталь, горизонтальность или горизонт впредь предлагаем ориентироваться именно на расположение объекта по отношению в конечном счёте к поверхности земли.
Это интересно: разность чисел — что это, как ее найти?
Горизонтальная линия
 Рисуем горизонтальную линию на листе бумаги. Если лист бумаги лежит на столе – лист расположен горизонтально. Рисунок линии выполняется слева направо или справа налево – нарисована горизонтальная линия. Нарисовать на листе можно что угодно: вертикальные лини (сверху вниз или снизу вверх), диагональ, любой рисунок. При этом лист расположен всё равно горизонтально. Чему? Столу. Полу. Нижнему этажу дома. Земле.
Рисуем горизонтальную линию на листе бумаги. Если лист бумаги лежит на столе – лист расположен горизонтально. Рисунок линии выполняется слева направо или справа налево – нарисована горизонтальная линия. Нарисовать на листе можно что угодно: вертикальные лини (сверху вниз или снизу вверх), диагональ, любой рисунок. При этом лист расположен всё равно горизонтально. Чему? Столу. Полу. Нижнему этажу дома. Земле.
Горизонталь – самая знакомая из всех, базовая линия. Она в каких угодно смыслах служит основой любой композиции. Даже её визуальная тяжесть напоминает о том, что горизонтальная поверхность есть фундаментальная держащая основа. Она параллельна земле. Не зря изображение горизонтальной линии выражает вес, спокойствие, мир и стабильность.
Горизонтальность, как психологическое понятие
Горизонтальность линий в рисунках можно рассматривать через знание психологии. Прямые линии подразумевают некую разделительную черту. Человек, как зритель, может оставаться снаружи, заглядывая за неё, или перешагнуть этот горизонт, так сказать «переступить за черту». Прямые и чёткие линии выражают смелость и настойчивость, тонкие и изгибающиеся горизонтали – деликатность и мягкость.
Горизонталь – топографическое определение
Самое простое определение этому слову можно найти в многочисленных словарях и энциклопедиях разных направлений. Чаще всего такое название применяется в отношении изогипс, т. е., линий, соединяющих точки, находящиеся на одинаковой абсолютной высоте над уровнем моря или любой другой взятой за основу плоскости.
Вот как расшифровывает это понятие Энциклопедический толковый словарь И.А. Ефрона и Ф.А. Брокгауза:
- Горизонтали – (изогипсы) линии, соединяющие на местности точки, лежащие на одной и той же высоте над уровнем моря или какой-то основной плоскости, принятой за основание.
Вот что можно прочитать в Техническом железнодорожном словаре:
- Горизонтали – линии на карте или плане местности, полученные от пересечения земной поверхности горизонтальными плоскостями, стоящими друг от друга на одинаковом расстоянии.
Выдержка из Геологической энциклопедии:
- Горизонтали – это линии, соединяющие точки одной высоты над уровнем моря. С помощью горизонталей на топографических картах отображаются особенности рельефа различных участков земной коры.
И в конце приведём текст определения из Справочника технического переводчика (отрасль машиностроение):
- Горизонтали – линии на поверхности, параллельные горизонтальной плоскости проекций.
Определение в профессиональном росте
 У профессионалов есть такое понятие, как вектор карьеры. Многочисленные и очень сейчас популярные тренинги по достижению результатов в профессиональной деятельности и продвижении по лестнице к успешной карьере, выносят на обсуждение идеи, которые подразумевают рост потенциала человека как по вертикали, так и по горизонтали. По вертикали понятно, перешагивая ступени одну за другой, т. е., двигаясь вверх, индивид поднимается по вертикали. А что со вторым вариантом?
У профессионалов есть такое понятие, как вектор карьеры. Многочисленные и очень сейчас популярные тренинги по достижению результатов в профессиональной деятельности и продвижении по лестнице к успешной карьере, выносят на обсуждение идеи, которые подразумевают рост потенциала человека как по вертикали, так и по горизонтали. По вертикали понятно, перешагивая ступени одну за другой, т. е., двигаясь вверх, индивид поднимается по вертикали. А что со вторым вариантом?
Здесь надо вспомнить шутливый принцип канадского педагога Питера Лоуренса, говорящий о том, что при подъёме по вертикали есть предел, та ступень, выше которой человек подняться не в состоянии. Ну что ж, доля правды в этом есть. Но, мало кто согласен остановиться на том, в чём он хорош. Значит, есть смысл продолжить рост в другом направлении.
Рост по горизонтали означает углубление специалиста в экспертную область. Индивид становится отличным мастером и непревзойдённым экспертом в конкретном виде деятельности, конкретном направлении. Он делает свою работу, у него те же обязанности, но при этом освоены и применяются новые инструменты к выполнению возложенных задач. С некоторым временем его работа становится качественнее и выполняется виртуознее, за что профессионал больше ценится начальством и внешними партнёрами.
 Другой вариант развития профессиональной деятельности по горизонтали – это переход в параллельное направление, приобретение в нём новых навыков, в том числе и во многих других областях. Это необходимо, когда в компании практикуют перестановку сотрудников из одного блока в другой. Например, из финансового отдела в логистику. С одной стороны, специалист вносит в это новое подразделение знания из других областей, с другой – учится всё время новому. Сотрудник сильно развивается личностно, что непременно скажется на его профессиональных качествах.
Другой вариант развития профессиональной деятельности по горизонтали – это переход в параллельное направление, приобретение в нём новых навыков, в том числе и во многих других областях. Это необходимо, когда в компании практикуют перестановку сотрудников из одного блока в другой. Например, из финансового отдела в логистику. С одной стороны, специалист вносит в это новое подразделение знания из других областей, с другой – учится всё время новому. Сотрудник сильно развивается личностно, что непременно скажется на его профессиональных качествах.
Многие профессионалы вполне остаются довольны ростом по горизонтали и не нуждаются в росте по вертикали, мотивируя это таким немаловажным бонусом, как меньшая ответственность. Самое главное, что в этом случае человек должен понять, в какой своей роли он будет наиболее успешен, ценен для профессии и эффективен для результата. Здесь надо хорошо продумать свои шаги по карьерной лестнице и быть честным с собой самим. Тем более что не все хотят быть руководителями.
obrazovanie.guru
Вертикальная прямая (горизонтально-проецирующая) — Мегаобучалка
ЛЕКЦИЯ №2
ПРЯМЫЕ частного положения.
Прямые общего вида.
ПРЯМЫЕ частного положения
Относительно плоскостей проекций прямые могут располагаться по разному. Если они параллельны или перпендикулярны плоскостям проекций, то говорят , что это прямые частного положения.
Горизонталь
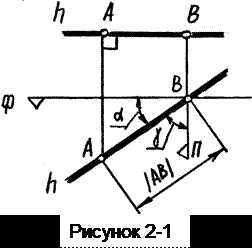 Прямая, параллельная горизонтальной плоскости, называется горизонталью,h // Г (рисунок 2-1). На фронтальной проекции (виде спереди) она всегда перпендикулярна вертикальным линиям связи, а на виде сверху составляет с ними некоторый угол α(реконструкцией чертежа определяем положение прямой в пространстве). На виде сверху отрезок АВ, взятый на прямой, изображается в натуральную величину; здесь же можно определить угол α наклона прямой к фронтальной плоскости и угол γ — наклона ее к профильной плоскости.
Прямая, параллельная горизонтальной плоскости, называется горизонталью,h // Г (рисунок 2-1). На фронтальной проекции (виде спереди) она всегда перпендикулярна вертикальным линиям связи, а на виде сверху составляет с ними некоторый угол α(реконструкцией чертежа определяем положение прямой в пространстве). На виде сверху отрезок АВ, взятый на прямой, изображается в натуральную величину; здесь же можно определить угол α наклона прямой к фронтальной плоскости и угол γ — наклона ее к профильной плоскости.
На горизонтальной проекции (виде сверху) горизонталь проецируется без искажения.
 4.2 Фронталь
4.2 Фронталь
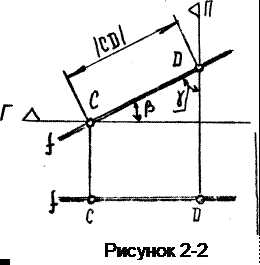
Прямая, параллельная фронтальной плоскости, называется фронталью. f // Ф (рисунок 2-2). На горизонтальной проекции (виде сверху) фронталь всегда перпендикулярна вертикальным линиям связи, а на фронтальной проекции (виде спереди) составляет с ними некоторый угол. Отрезок СD, взятый на прямой, на виде спереди изображается без искажений. Здесь же определяются углы наклона прямой к горизонтальной плоскости b и к профильной плоскости П γ.
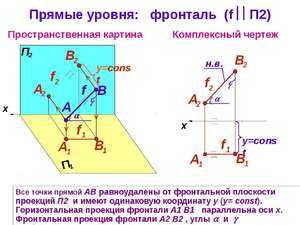
Фронталь проецируется без искажения на фронтальной проекции (виде спереди).
Профильная прямая
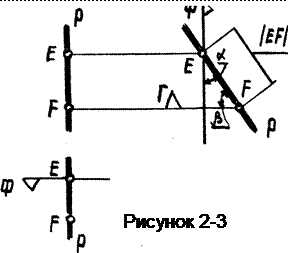 Прямая, параллельная профильной плоскости, называется профильной прямой р.р//П (рисунок 2-3). На видах спереди и сверху такая прямая всегда совпадает по направлению с вертикальными линиями связи. Эти виды не определяют наглядно положение прямой в пространстве, поэтому необходимо построить ее изображение на виде слева, где определяются углы наклона прямой к фронтальной a и горизонтальной b плоскостям уровня. Отрезок EF, взятый на прямой р, на виде слева изображается в натуральную величину.
Прямая, параллельная профильной плоскости, называется профильной прямой р.р//П (рисунок 2-3). На видах спереди и сверху такая прямая всегда совпадает по направлению с вертикальными линиями связи. Эти виды не определяют наглядно положение прямой в пространстве, поэтому необходимо построить ее изображение на виде слева, где определяются углы наклона прямой к фронтальной a и горизонтальной b плоскостям уровня. Отрезок EF, взятый на прямой р, на виде слева изображается в натуральную величину.
Положение прямой в пространстве определяется положением 2-х любых ее точек (например Е и F). Для построения точек Е и F на виде сверху необходимо наметить положение баз отсчета глубин, а затем, замерив глубины точек, отложить их на виде сверху. Удобно при выборе баз отсчета проводить их через одну из имеющихся точек. Так при выборе базы отсчета глубин ее проводят через дальнюю от наблюдателя точку — Е. Тогда задача построения 3-го вида упрощается — нужно строить на нем на одну точку меньше – F.
Профильная прямая проецируется без искажения на профильной проекции (виде слева).
Вертикальная прямая (горизонтально-проецирующая)
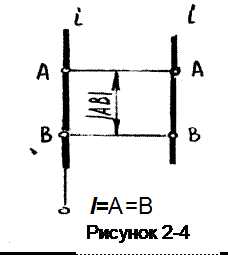 Это прямая, перпендикулярная горизонтальной плоскости Г.
Это прямая, перпендикулярная горизонтальной плоскости Г.
Отрезок, отложенный на данной прямой, на видах спереди и слева изображается в натуральную величину (рисунок 2-4), а на виде сверху — как точка, совпадающая с проекцией прямой i. Точки А и В называются горизонтально-конкурирующими (совпадающими).
megaobuchalka.ru
Прямая. Прямые уровня
Поскольку положение прямой в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно зафиксировать проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся проецирования точки.
2.1. Прямые частного и общего положения
2.1.1. Прямые уровня
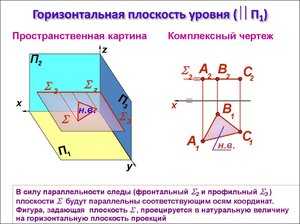
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.
а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.
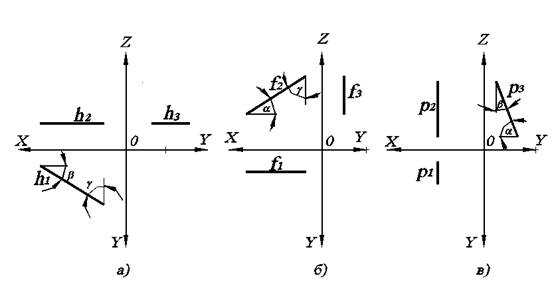
Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная; б) фронтальная; в) профильная.
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
a — угол наклона прямой уровня к П1,
b — угол наклона прямой уровня к П2,
g — угол наклона прямой уровня к П3.
Проецирующие прямые.Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.
Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 2.2.
а)Прямая, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально-проецирующей прямой и обозначается i.
б)Прямая, перпендикулярная фронтальной плоскости проекций П2, называется фронтально-проецирующей прямой и обозначается j.
в)Прямая, перпендикулярная профильной плоскости проекций П3, называется профильно-проецирующей прямой обозначается r.
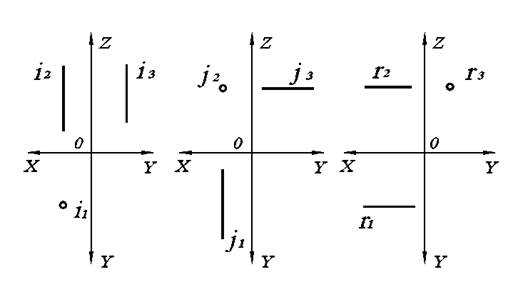
Рис. 2.2. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая; б) фронтально-проецирующая; в) профильно–проецирующая.
У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i2, i3, j1, j3, r1, r2 – это натуральные величины соответствующих прямых i, j, r.
Прямая общего положения.Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.
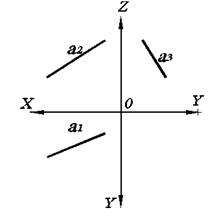
Рис. 2.3. Прямая общего положения на комплексном чертеже.
Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций (рис. 2.3).
Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника.Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.
В соответствии с этим построения необходимо выполнять в следующей последовательности. Из любой точки (например, D1) отрезка С1D1 проведем перпендикуляр к нему (рис. 2.4.).
На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С1 получаем прямоугольный треугольник С1D1D*, в котором С1D* — натуральная величина отрезка СD, a — угол наклона отрезка СD к плоскости П1. Для определения угла наклона к плоскости П2 проведем аналогичные построения на фронтальной проекции.
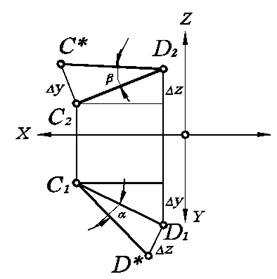
Рис. 2.4. Определение натуральной величины отрезка прямой способом прямоугольного треугольника.
Взаимное положение прямых в пространстве. Конкурирующие точки.Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 2.5 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 2.5 ограничимся двухкартинным комплексным чертежом.
В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 2.5а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 2.5в точки С1 и В2) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С1, получим на каждой из прямых n2 и m2 соответственно две проекции: точки С2 и другой точки D2, а следовательно, на пересечении n1 и m1 лежат две точки С1 и D1, слившиеся в одну.
Точки, лежащие на одном проецирующем луче, называются конкурирующими.. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 2.5в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 2.5в — точки В и Е).
При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П2, будет закрыта от наблюдателя точкой, расположенной дальше от П2, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.
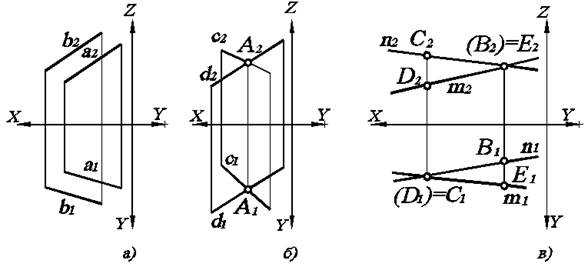
Рис. 2.5. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m
Дата добавления: 2018-01-22; просмотров: 381;
znatock.org
§ 3. Прямые частного положения
Прямые частного положения – это прямые, которые либо параллельны (табл. 3.1), либо перпендикулярны одной из плоскостей проекций (табл. 3.2).
Прямые уровня
Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1).
Таблица 3.1
Прямые уровня
Определение | Наглядное изображение | Комплексный чертеж |
Горизонталью называют всякую линию, параллельную горизонтальной плоскости p1: A2B2 || Оx; A3B3i || y. A1B1 – натуральная величина отрезка, b – угол наклона к p2 |
Фронталью называют линию, параллельную фронтальной плоскости p2: A1B1i || Оx; A2B2 – натуральная величина; А3B3 i || z; – угол наклона к p1
| | |
Профильной линией называют линию, параллельную профильной плоскости p 3; A2B2i || z; A1B1i|| y; A3B3 – натуральная величина отрезка, – угол наклона к p1; – угол наклона к p 2
| |
Проецирующие прямые
Проецирующими прямыми называют прямые, расположенные перпендикулярно к плоскостям проекций p1, p2, p3. Различают три основные проецирующие прямые: горизонтальную, фронтальную и профильную.
Если прямая перпендикулярна какой-либо из плоскостей проекций, то на эту плоскость она проецируется в виде точки. Две другие ее проекции параллельны осям и равны натуральной величине отрезка (табл. 3.2).
Таблица 3.2
Проецирующие прямые
Определение | Наглядное изображение | Комплексный чертеж |
Горизонтально проецирующей прямой называют прямую, перпендикулярную к плоскости p1; A2B2 – натуральная величина AB, в плоскости p1 отрезок АВ проецируется в точку А1 В1 |
Фронтально проецирующей прямой называют прямую, перпендикулярную к плоскости p2; AB || p1 и ABp2, А1В1 – натуральная величина АВ, в плоскости p2 отрезок проецируется в точку А2В2 | ||
Профильно проецирующей прямой называют прямую, перпендикулярную к плоскости p3; AB || p1 и AB || p2, А1В1 и А2В2 – натуральные величины отрезка АВ, А3В3 проецируется на p3 в точку |
При сравнительном анализе изображений прямых частного положения на комплексном чертеже (табл. 3.1 и 3.2) следует:
1. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции обязательно параллельны осям проекций.
2. Проекция прямой уровня, к той плоскости, которой она параллельна, составляет с осями проекций углы, равные углам наклона линии уровня с плоскостями проекций.
3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость является точка, а вторая проекция располагается перпендикулярно осям проекций.
studfiles.net

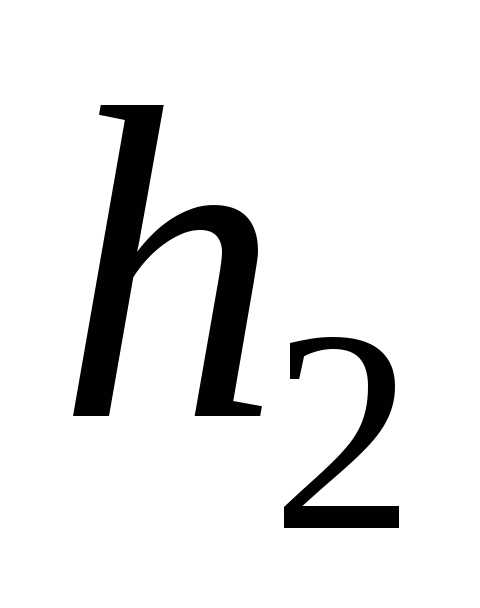 располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиямсвязи).
располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиямсвязи). )
и профильной (
)
и профильной ( )
плоскостям проекций.
)
плоскостям проекций.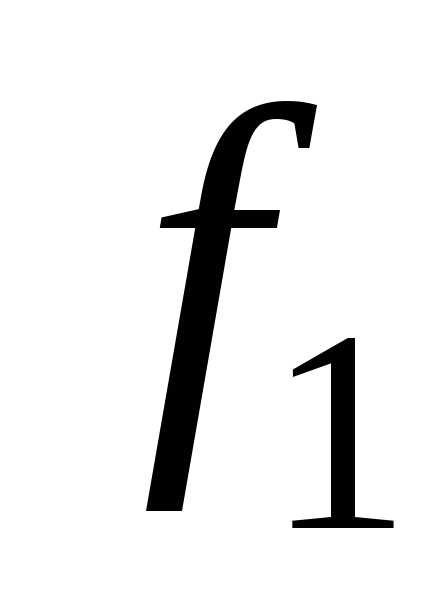 располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиям связи).
располагается параллельно оси0х(или в безосном чертеже перпендикулярно
линиям связи). )
и профильной (
)
и профильной ( )
плоскостям проекций.
)
плоскостям проекций.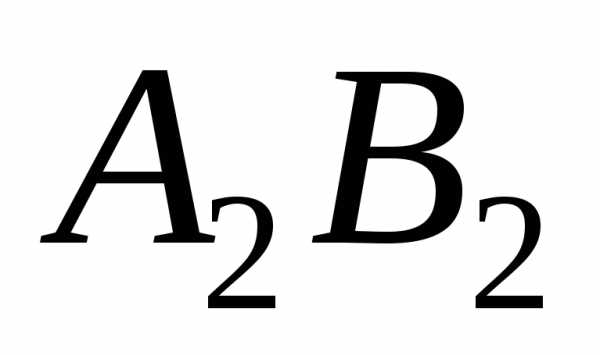 и горизонтальная
и горизонтальная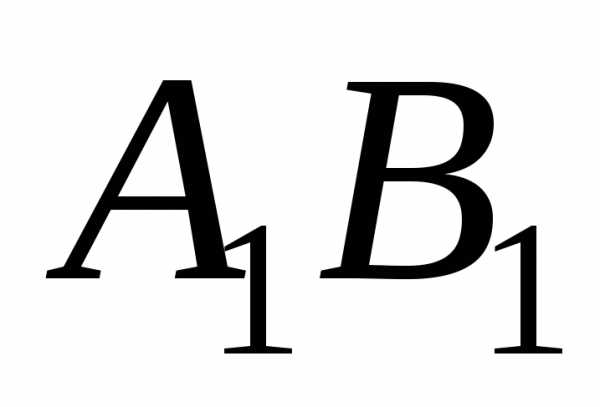 проекции отрезка профильной
прямой располагаются перпендикулярно
осих.
проекции отрезка профильной
прямой располагаются перпендикулярно
осих. )
и горизонтальной (
)
и горизонтальной ( )
плоскостям проекций.
)
плоскостям проекций.