Три признака подобия треугольников – Три признака подобия треугольников

Три признака подобия треугольников

Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).

Доказать, что \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С (рис. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.

Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили \(\Delta\)MBN, который подобен \(\Delta\)ABC. Но \(\Delta\)MBN = \(\Delta\)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).

Если \(\Delta\)MBN \(\sim\) \(\Delta\)AВС, то \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABC. Эта теорема выражает 1-й признак подобия треугольников.

Следствия. 1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Теорема 2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\) и ∠В = ∠В’

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’ (рис. 368).

Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию ^AB/_MB = ^BC/_BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,

т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.

Так как \(\Delta\)MBN \(\sim\) \(\Delta\)А’В’С’, то, следовательно, и \(\Delta\)А’В’С’ \(\sim\) \(\Delta\)ABС.

Эта теорема выражает 2-й признак подобия треугольников.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.

Пусть в треугольниках ABC и А’В’С’ \(\frac{AB}{A’B’} = \frac{BC}{B’C’} = \frac{AC}{A’C’}\) (рис. 369).

Требуется доказать, что \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’

Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, \(\frac{AB}{MB} = \frac{BC}{BN} = \frac{AC}{MN}\).

Докажем, что \(\Delta\)MBN = \(\Delta\)А’В’С’. Для доказательства сравним две пропорции

\(\frac{AB}{MB} = \frac{BC}{NB}\) и \(\frac{AB}{A’B’} = \frac{BC}{B’C’}\).
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.

Сравним ещё две пропорции: \(\frac{AB}{MB} = \frac{AC}{MN}\) и \(\frac{AB}{A’B’} = \frac{AC}{A’C’}\) . В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.

Оказалось, что три стороны \(\Delta\)BMN равны трём сторонам \(\Delta\)А’В’С’, а именно:

MB = А’В’, BN = В’С’ и MN = А’С’.

Следовательно, \(\Delta\)MBN = \(\Delta\)А’В’С’, а \(\Delta\)ABC \(\sim\) \(\Delta\)А’В’С’.

Эта теорема выражает 3-й признак подобия треугольников.

razdupli.ru

Третий признак подобия треугольников | Треугольники

Теорема

(Третий признак подобия треугольников — подобие треугольников по трём сторонам).

Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Дано: ΔABC, ΔA₁B₁C₁,

   

Доказать: ΔABC∼ ΔA₁B₁C₁

Доказательство:

1) Отложим на луче A₁B₁ отрезок A₁B₂, A₁B₂=AB.

2) Через точку B₂ проведём прямую B

2С₂, параллельную прямой B₁C₁.

3) В треугольниках A₁B₂C₂ и A₁B₁C₁:

Поэтому  ΔA₁B₂C₂∼ΔA₁B₁C₁ (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

4) Поскольку A₁B₂=AB, то

   

Так как по условию

   

то A₁C₂=AC и B₂C₂=BC.

5) В треугольниках ABC и A₁B₂C₂:

• A₁B₂=AB (по построению)
• B₂C₂=BC (по доказанному)
• A₁C₂=AC (по доказанному).

Значит, ΔABC=ΔA₁B₂C₂ (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов:

• ∠A=∠A₁
• ∠ABC=∠A₁B₂C₂.

6) В треугольниках ABC и A₁B₁C₁:

• ∠A=∠A₁ (по условию)
• Так как ∠A₁B₂C₂=∠A₁B₁C₁, то и ∠ABC=∠A₁B₁C₁.

Отсюда ΔABC∼ ΔA₁B₁C₁ (по двум углам).

Что и требовалось доказать.

3-й признак подобия треугольников используется реже 1-го.

www.treugolniki.ru

Признаки подобия треугольников

Напомним для начала определение подобных треугольников.

Определение 1

Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны.

Для определения подобия треугольников существуют три признака подобия треугольников. Рассмотрим и докажем их.

Первый признак подобия треугольников

Теорема 1

Теорема 1: Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle A=\angle A_1,\ \angle B=\angle B_1$. (рис. 1).

Рисунок 1. Иллюстрация теоремы 1

Нам нужно доказать, что $\angle C=\angle C_1,$ и что $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$.

По теореме о сумме углов треугольника, имеем:

Далее будем пользоваться следующей теоремой:

Теорема 2

Теорема 0: Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.

По теореме 0, получим

Из этих равенств, получим

Теорема доказана.

Второй признак подобия треугольников

Теорема 3

Теорема 2: Если две стороны одного треугольника пропорциональны соответствующим сторонам второго треугольника и углы между этими сторонами равны, то данные треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle A=\angle A_1$ и$\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$ (рис. 2).

Рисунок 2. Иллюстрация теоремы 2

Используя теорему 1, видим, что для доказательства этой теоремы, достаточно доказать, что $\angle C=\angle C_1$. Построим треугольник $ACB_2$, так, что $\angle CAB_2=\angle A_1$, а $\angle B_2CA=\angle C_1$ (рис. 2).

Рисунок 3. Дополнительное построение

Треугольник $ACB_2$ подобен треугольнику $ABC$ (по теореме 1), следовательно,$\ \frac{AC}{A_1C_1}$ $=\frac{AB_2}{A_1B_1}$. По условию $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}$, следовательно, $AB=AB_2$. Тогда треугольник $ACB_2$ равен треугольнику $ABC$ по двум сторонам и углу между ними. Следовательно, $\angle B_2CA=\angle C$, а так как $\angle B_2CA=\angle C_1,\ то\ \angle C=\angle C_1.$

По первому признаку подобия треугольника получаем доказательство теоремы.

Третий признак подобия треугольников

Теорема 4

Теорема 3: Если три стороны одного треугольника пропорциональны трем соответствующим сторонам второго треугольника, то такие треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}=k$.

Используя теорему 2, видим, что для доказательства этой теоремы, достаточно доказать, что $\angle A=\angle A_1$. Построим треугольник $ACB_2$, так, что $\angle CAB_2=\angle A_1$, а $\angle B_2CA=\angle C_1$ (рис. 3).

Рисунок 4. Дополнительное построение

Треугольник $ACB_2$ подобен треугольнику $ABC$ (по теореме 1), следовательно,$\ \frac{AC}{A_1C_1}$ $=\frac{AB_2}{A_1B_1}=\frac{CB_2}{C_1B_1}$. Принимая во внимание равенства$\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$, получим, что $CB_2=CB,\ AB_2=AB$. Тогда треугольник $ACB_2$ равен треугольнику $ABC$ по трем сторонам. Следовательно, $\angle A=\angle A_1$.

Теорема доказана.

Пример задачи на использование признаков подобия

Пример 1

Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.

Решение.

Пусть даны равнобедренные треугольники $ABC$ и $A_1B_1C_1$ с $\angle A=\angle A_1.$ Так как треугольник $ABC$ равнобедренный, то

\[\angle B=\angle C=\frac{180-\angle A}{2}\]

Так как треугольник $A_1B_1C_1$ равнобедренный, то

\[\angle B_1=\angle C_1=\frac{180-A_1}{2}=\frac{180-\angle A}{2}=\angle B=\angle C\]

То есть $\angle B=\angle B_1,\ \ \angle C=\angle C_1$. По теореме 1, получаем, что треугольники $ABC$ и $A_1B_1C_1$ подобны.

ч. т. д.

spravochnick.ru

Признаки подобия треугольников

Прежде чем разобрать задачи, повторим признаки подобия треугольников и свойства подобных треугольников.

Для доказательства подобия произвольных треугольников в школьном курсе используют три признака.

I. Признак подобия треугольников по двум углам.

 

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

II. Признак подобия треугольников по двум сторонам и углу между ними.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

III. Признак подобия треугольников по трем сторонам.

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Признак подобия прямоугольных треугольников

Для подобия прямоугольных треугольников достаточно, чтобы у них было по одному острому углу.

Из подобия треугольников следует равенство соответствующих углов и пропорциональность сторон:

Периметры подобных треугольников пропорциональны:

   

k — коэффициент подобия.

Все линейные размеры подобных треугольников также пропорциональны, то есть отношение соответствующих биссектрис, высот, медиан также равно k.

Углы между соответствующими линиями подобных треугольников равны.

Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

   

 

 

 

 

www.uznateshe.ru

Третий признак подобия треугольников

Прежде, чем познакомиться с третьим признаком подобия треугольников, вспомним известные нам первый и второй.

Итак, первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Ну а теперь сформулируем третий признак подобия треугольников.

Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство.

.

, , тогда  по 1-му признаку.

.

Получаем, что  , .

Тогда  по 3-му признаку.

Следовательно, .

Так как , то .

Следовательно, .

Что и требовалось доказать.

Давайте найдём среди следующих треугольников подобные.

У каждого из треугольников известны длин трёх его сторон, а тогда воспользуемся только что доказанным третьим признаком подобия треугольников.

Посмотрим внимательно на значения их длин и заметим, что стороны треугольника а пропорциональны сторонам треугольника в, а значит, эти треугольники подобны. При этом коэффициент подобия равен 2.

Задача. Подобны ли треугольники  и , если  см,  см,  см,  см,  см,  см?

Решение.

,

,

.

Значит, .

Следовательно, .

Ответ: .

Задача. Докажите, что прямоугольные треугольники  и  подобны, если стороны  и  треугольника соответственно равны  см и  см, а стороны  и  треугольника соответственно равны  см и  см.

Решение.

,,

 (см).

, ,

 (см).

; ; .

Значит, .

Следовательно,  по 3-му признаку.

Что и требовалось доказать.

Итак, сегодня на уроке мы познакомились с ещё одним признаком подобия треугольников: если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Также мы закрепили материал на практике.

videouroki.net

Сформулируйте 3 признака подобия треугольников

Три стороны, три угла и три бисектриссы.

вроде если все стороны пропорциональны, углы равны, а треть не помню, там какая та крыса чтоль тоже пропорциональна

по стороне и 2-ум углам между ними. по 2-ум углам и стор. между ними и по 3-ём сторонам.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, тогда эти треугольники подобны. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, тогда эти треугольники подобны. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

touch.otvet.mail.ru

Третий признак подобия треугольников. Видеоурок. Геометрия 8 Класс

Треугольники называются подобными, если углы соответственно равны, а сходственные стороны пропорциональны.

Имеем два треугольника ,  (см. Рис. 1).

Сходственные стороны – те стороны, которые лежат против равных углов.

Рис. 1. Подобные треугольники

Определение:

:

Проверять все равенства не нужно, существуют признаки подобия.

Первый признак подобия

Если хотя бы по два соответствующих угла треугольников равны, то эти треугольники подобны.

Второй признак подобия

По углу и пропорциональности прилежащих сторон.

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Дано:

Доказать:

Доказательство

Чтобы доказать третий признак, мы можем использовать второй признак, так как там есть пропорциональность сторон и нам останется доказать равенство угла, например, что . То есть мы докажем, что эти углы равны, сошлемся на второй признак, и третий признак будет доказан.

Вспомогательное построение: (см. Рис. 2).

Построим треугольник : – по первому признаку подобия.

Рис. 2. Доказательство третьего признака

Раз эти треугольники подобны, то можно выписать пропорциональность их сторон, сравнить с данной пропорциональностью и получить важные выводы.

Сравним с пропорциональностью сторон исходных треугольников.

Значит,  и .

Из сравнения двух равенств следует, что треугольник  равен треугольнику  по трем сторонам.

Из равенства треугольников вытекает:

Итак, в двух исходных треугольниках имеем равные углы  и  и прилежащие стороны пропорциональны, значит, эти треугольники подобны по второму признаку подобия треугольников.

Что и требовалось доказать.

Специфика третьего признака подобия треугольников заключается в том, что в нем не фигурируют углы. Есть пропорциональность сходственных сторон. А как найти равные углы?

Перейдем к задачам.

По данным рисунка определите подобие треугольников, отметьте равные углы (см. Рис. 3).

Рис. 3. Условие задачи 1

Решение

Заметим пропорциональность сторон

 – по третьему признаку

Отметим равные углы (см. Рис. 4).

Рис. 4. Подобные углы треугольников

Ответ:  и  подобны.

По данным рисунка определить подобие треугольников (см. Рис. 5).

Решение

Рис. 5. Иллюстрация к задаче 2

Эти треугольники существуют, т. к. их самые большие стороны меньше, чем сумма двух других сторон:

Пропорциональности сторон не наблюдаем.

.

Ответ:  и  не подобны.

Стороны  равны 1; 3; 5. Стороны  равны 2; 6; 10. Определить подобие треугольников.

Решение

 – эти пары отрезков пропорциональны.

Однако треугольники с такими сторонами не существуют.

Ответ:  и  не существуют.

Дано: , ,  (см. Рис. 6).

Найти: ; .

Решение

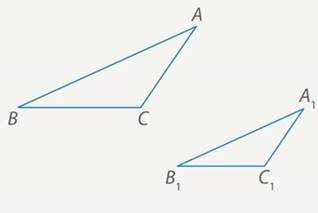
Рис. 6. Иллюстрация к задаче 4

1.                   – по третьему признаку

Стороны одного треугольника выражены через стороны другого треугольника.

Отсюда важное свойство периметров подобных треугольников – их отношение равно коэффициенту подобия.

2.         Чтобы найти площадь, нужно найти высоту, поэтому проведем  – высоту в первом треугольнике: (см. Рис. 7).

Также проведем высоту во втором треугольнике:

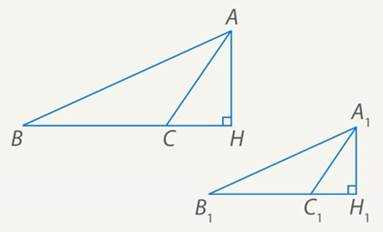
Рис.7. Иллюстрация к задаче 4

Тогда имеем прямоугольные треугольники, которые подобны по первому признаку:

Найдем коэффициент их подобия :

Теперь мы готовы сравнить площади:

Итак, отношение площадей подобных треугольников равно квадрату коэффициенту их подобия.

Ответ: 1. ; 2. .

Дано: ; ; ; ; ; .

По данным рисунка 8 докажите, что .

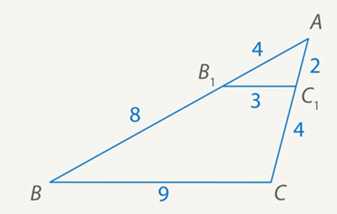
Рис. 8. Условие задачи 5

Доказательство

Есть два треугольника с известными сторонами:  и .

Проверим пропорциональность или непропорциональность этих сторон.

Для подобия нужно, чтобы выполнялось равенство: .

 (по третьему признаку)

Мы видим, что сторона  лежит против угла , стор

interneturok.ru