Решение производные – как найти, вычислить и понять с нуля

примеры решения производных

Производная функции является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.

Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.

Таблица производных и правила дифференцирования

Основные ссылки — таблица производных, правила дифференцирования и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ.

Больше примеров решений →

Производные сложных функций

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание.Найти производную функции

Решение. По правилу дифференцирования сложной функции:

В свою очередь производная также берется по правилу дифференцирования сложной функции:

Ответ.

Больше примеров решений →

Применение дифференциала в приближенных вычислениях

Основные ссылки — теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Геометрический смысл производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Механический смысл производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание.

Точка движется по закону . Чему равна скорость в момент времени ?

Решение. Найдем скорость точки как первую производную от перемещения:

В момент времени скорость равна

Ответ.

Больше примеров решений →

Уравнение касательной, нормали и угол между прямыми

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Записать уравнение касательной к графику функции в точке

Решение. Найдем значение функции в заданной точке:

Найдем производную заданной функции по правилу дифференцирования произведения:

Вычислим её значение в заданной точке

Используя формулу

запишем уравнение касательной:

Ответ. Уравнение касательной:

Больше примеров решений →

Производные высших порядков

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную второго порядка от функции

Решение. Находим первую производную как производную сложной функции:

Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель — — есть сложной функцией:

Ответ.

Больше примеров решений →

Механическое смысл второй производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Уравнение движения материальной точки вдоль оси имеет вид (м). Найти ускорение точки в момент времени c.

Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:

Первая производная

(м/с)

вторая производная

(м/с²)

В момент времени c

(м/с²)

Ответ. (м/с²)

Больше примеров решений →

Дифференциалы высших порядков

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти дифференциал третьего порядка функции

Решение. По формуле

Найдем третью производную заданной функции:

Тогда

Ответ.

Больше примеров решений →

Производная функции, заданной неявно

Основные ссылки — теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Производная функции, заданной параметрически

Основные ссылки — теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Логарифмическое дифференцирование

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Применим логарифмическое дифференцирование:

Тогда, продифференцировав левую и правую часть, будем иметь:

Отсюда получаем, что

Ответ.

Больше примеров решений →

Формулы Маклорена и Тейлора

Основные ссылки — теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Вы поняли, как решать? Нет?

Помощь с решением

www.webmath.ru

Примеры решений производных

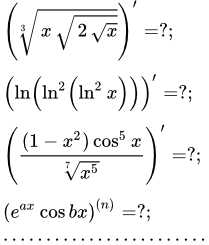
Страница содержит ссылки на 44 примера решений производных.

• Попробуйте найти производные от приведенных ниже функций.
• Нажмите на изображение или стрелку, чтобы попасть на страницу с подробным решением.

Примеры решений производных от явных функций

Найдите производные    следующих функций, зависящих от переменной x:
  Решение > > >
  Решение > > >
  Решение > > >
  > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >
  > > > Здесь , , , – постоянные.
  > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >         > > >

Примеры решений производных высших порядков от явных функций

Найти производные первого и второго порядка следующей функции:
.
Решение > > >

Найти производную третьего порядка:
.
Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Вычислить n-ю производную функции
.
Решение > > >

Найти n-ю производную следующей функции:
,
где и – постоянные.
Решение > > >

Примеры решения производных от функций, заданных параметрическим способом

Найдите производную от функции, заданной параметрическим способом:

Решение > > >

Найдите производную , где и выражены через параметр :

Решение > > >

Найдите производные второго    и третьего    порядка от функции, заданной параметрическим способом:

Решение > > >

Примеры решений производных от неявных функций

Найдите производную первого порядка от функции, заданной неявно уравнением:
.
Решение > > >

Найти производную второго порядка от неявно заданной функции:
.
Решение > > >

Найти производную третьего порядка при от функции, заданной уравнением:
.
Решение > > >

Автор: Олег Одинцов.     Опубликовано: 20-02-2017   Изменено: 10-04-2017

1cov-edu.ru

Как найти производную? Примеры решений

Как найти производную, как взять производную? На данном уроке мы научимся находить производные функций. Но перед изучением данной страницы я настоятельно рекомендую ознакомиться с методическим материалом Горячие формулы школьного курса математики. Справочное пособие можно открыть или закачать на странице Математические формулы и таблицы. Также оттуда нам потребуется Таблица производных, ее лучше распечатать, к ней часто придется обращаться, причем, не только сейчас, но и в оффлайне.

Есть? Приступим. У меня для Вас есть две новости: хорошая и очень хорошая. Хорошая новость состоит в следующем: чтобы научиться находить производные, совсем не обязательно знать и понимать, что такое производная. Более того, определение производной функции, математический, физический, геометрический смысл производной целесообразнее переварить позже, поскольку качественная проработка теории, по моему мнению, требует изучения ряда других тем, а также некоторого практического опыта.

И сейчас наша задача освоить эти самые производные технически. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.

Советую следующий порядок изучения темы: во-первых, эта статья. Затем нужно прочитать важнейший урок Производная сложной функции. Эти два базовых занятия позволят поднять Ваши навыки с полного нуля. Далее можно будет ознакомиться с более сложными производными в статье Сложные производные.

Логарифмическая производная. Если планка окажется слишком высока, то сначала прочитайте вещьПростейшие типовые задачи с производной. Помимо нового материала, на уроке рассмотрены другие, более простые типы производных, и есть прекрасная возможность улучшить свою технику дифференцирования. Кроме того, в контрольных работах почти всегда встречаются задания на нахождение производных функций, которые заданы неявно или параметрически. Такой урок тоже есть:Производные неявных и параметрически заданных функций.

Я попытаюсь в доступной форме, шаг за шагом, научить Вас находить производные функций. Вся информация изложена подробно, простыми словами.

Собственно, сразу рассмотрим пример: Пример 1

Найти производную функции Решение:

Это простейший пример, пожалуйста, найдите его в таблице производных элементарных функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь:

у нас была функция , которая в результате решения превратилась в функцию.

Говоря совсем просто, для того чтобы найти производную

функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным

исключением является экспоненциальная функция , которая

превращается сама в себя. Операция нахождения производной называется дифференцированием.

Обозначения: Производную обозначаютили.

ВНИМАНИЕ, ВАЖНО! Забыть поставить штрих (там, где надо), либо нарисовать лишний штрих (там, где не надо) –ГРУБАЯ ОШИБКА! Функция и её производная – это две разные функции!

Вернемся к нашей таблице производных. Из данной таблицы желательно запомнить наизусть: правила дифференцирования и производные некоторых элементарных функций, особенно:

производную константы:

, где– постоянное число; производную степенной функции:

, в частности:,,.

Зачем запоминать? Данные знания являются элементарными знаниями о производных. И если Вы не сможете ответить преподавателю на вопрос «Чему равна производная числа?», то учеба в ВУЗе может для Вас закончиться (лично знаком с двумя реальными случаями из жизни). Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.

Вреальности простые табличные примеры – редкость, обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.

Вэтой связи переходим к рассмотрению правил дифференцирования:

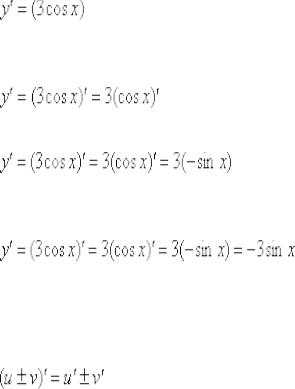
1) Постоянное число можно (и нужно) вынести за знак производной

, где– постоянное число (константа)Пример 2

Найти производную функции

Смотрим в таблицу производных. Производная косинуса там есть, но у нас .

Решаем:

Самое время использовать правило, выносим постоянный множитель за знак производной:

А теперь превращаем наш косинус по таблице:

Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:

Готово.

2) Производная суммы равна сумме производных

Найти производную функции

Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:

Применяем второе правило:

Обратите внимание, что для дифференцирования все корни, степени нужно представить в виде , а если они находятся в знаменателе, то

переместить их вверх. Как это сделать – рассмотрено в моих методических материалах.

Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:

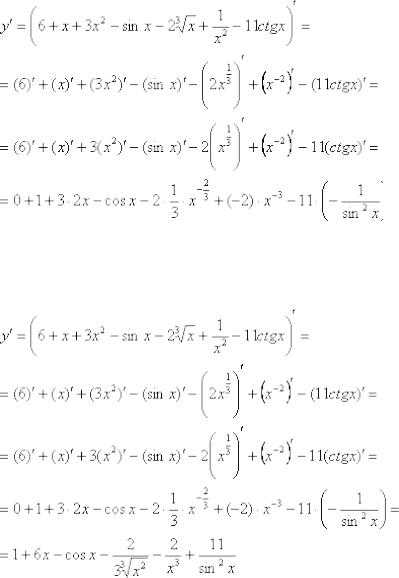
Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).

Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:

Все степени вида желательно снова представить в виде корней,

степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.

Пример 4

Найти производную функции

Попробуйте решить данный пример самостоятельно (ответ в конце урока).

3) Производная произведения функций

Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:

Эта необычное правило (как, собственно, и другие)следует из определения производной. Но с теорией мы пока повременим – сейчас важнее научиться решать:

Пример 5

Найти производную функции

Здесь у нас произведение двух функций, зависящих от . Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:

Сложно? Вовсе нет, вполне доступно даже для чайника.

Пример 6

Найти производную функции

В данной функции содержится сумма и произведение двух функций – квадратного трехчленаи логарифма. Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.

Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:

Теперь для скобки используем два первых правила:

В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:

Готово.

При определенном опыте нахождения производных, простые производные вроде не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу записывается, что.

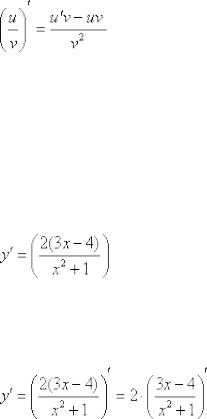
Пример 7

Найти производную функции Это пример для самостоятельного решения (ответ в конце урока)

4) Производная частного функций

В потолке открылся люк, не пугайся, это глюк. А вот это вот суровая действительность:

Пример 8

Найти производную функции

Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:

Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:

Заодно избавляемся от скобок в числителе, которые теперь не нужны. Вообще говоря, постоянные множители при нахождении производной

можно и не выносить, но в этом случае они будут «путаться под ногами», что загромождает и затрудняет решение.

Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:

Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:

Штрихов больше нет, задание выполнено.

На практике обычно (но не всегда) ответ упрощают «школьными» методами:

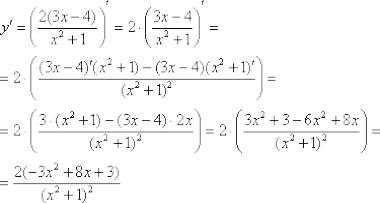
Пример 9

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока). Время от времени встречаются хитрые задачки:

Пример 10

Найти производную функции

Смотрим на данную функцию. Здесь снова дробь. Однако перед тем как использовать правило дифференцирования частного (а его можно использовать), всегда имеет смысл посмотреть, а нельзя ли упростить саму дробь, или вообще избавиться от нее?

Дело в том, что формула достаточно громоздка, и применять ее совсем не хочется.

В данном случае можно почленно поделить числитель на знаменатель. Преобразуем функцию:

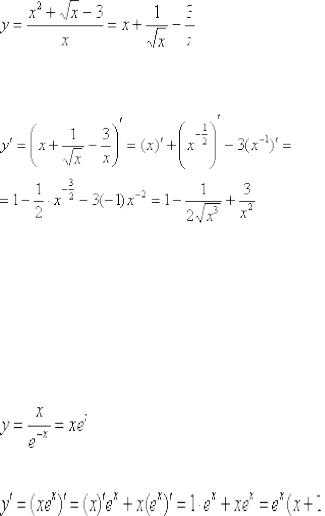
Ну вот, совсем другое дело, теперь дифференцировать просто и приятно:

Готово.

Пример 11

Найти производную функции

Здесь ситуация похожа, превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак:

Произведение все-такидифференцировать проще:

Пример 12

Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).

5) Производная сложной функции

Данное правило также встречается очень часто. Но о нём рассказать можно очень много, поэтому я создал отдельный урок на тему Производная сложной функции.

Желаю успехов!

Ответы:

Пример 4: . В ходе решения

данного примера следует обратить внимание, на тот факт, что и– постоянные числа, не важно чему они равны, важно, что это — константы. Поэтомувыносится за знак производной, а.

Пример 7:

Пример 9:

Пример 12:

studfiles.net

Примеры производных | Математика

Изучить конкретные примеры нахождения производных с подробными пояснениями — лучший способ научиться находить производную самостоятельно.

После разбора производной степени, производной суммы и разности, производной произведения, производной частного и производной сложной функции настал черед рассмотреть примеры производных, в которых используются сразу несколько правил дифференцирования.

1) y=4x²cos(11-x²).

Данная функция представляет собой  произведение функций, где u=4x², v=cos(11-x²). По правилу дифференцирования произведения:

y’=(4x²)’· cos(11-x²)+(cos(11-x²))’·4x²=

первая из функций — степенная, вторая — сложная функция, где внешняя функция f=cos u, внутренняя u=11-x². Применяя соответствующие правила, имеем:

=4·2x·cos(11-x²)+(-sin(11-x²))·(11-x²)’·4x²=8x·cos(11-x²)-sin(11-x²)·(-2x)·4x²=8x·cos(11-x²)+8x³sin(11-x²).

   

Эта функция — частное. u=2sin3x-1, v=√x. По правилу дифференцирования частного:

   

В свою очередь, числитель представляет собой разность двух функций, первая из которых, sin3x — сложная (f=sin u, u=3x, а число выносим за знак производной). Применяем правила для дифференцирования разности и сложной функции, имеем:

   

   

Теперь выражениz в числителе приводим к общему знаменателю 2√x:

   

3) y=(lnx-tg7x)³

Это — сложная функция, внешняя функция f=u³, внутренняя u=lnx-tg7x. По правилу дифференцирования сложной функции: y’=3(lnx-tg7x)²·(lnx-tg7x)’=

в свою очередь, внутренняя функция представляет собой разность двух функций, где вторая — сложная функция (f=tgu, u=7x). Применяя правила для нахождения производной разности и сложной функции, получаем:

   

   

   

   

Это — сложная функция. Внешняя функция f — корень четвертой степени из u, внутренняя u=arctg10x. Преобразуем корень четвертой степени в степень с дробным показателем, затем дифференцируем:

   

   

В свою очередь, arctg10x — также сложная функция. Здесь внешняя функция f=arctgu, внутренняя u=10x:

   

Степень с дробным отрицательным показателем нужно преобразовать:

   

   

Это — пример производной частного:

   

свою очередь, числитель представляет собой производную произведения:

   

Первый множитель, в свою очередь — сложная функция. Внешняя функция — показательная, 4 в степени u, внутренняя — u=cos8x:

   

Внешняя функция f=cos u, внутренняя u=8x:

   

   

   

Это — пример производной, где сначала нужно применить правило дифференцирования суммы:

   

Первое слагаемое — произведение функций, второе — сложная функция (f=lnu, u=cosx), третье слагаемое — также сложная функция (f- е в степени u, u=5x):

   

   

   

   

Эта функция — сложная. Однако здесь можно применить свойства логарифмов, после чего дифференцировать функцию станет гораздо проще:

   

   

   

   

Примеры производных для самопроверки:

   

   

   

   

Показать решение

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

www.matematika.uznateshe.ru

Примеры вычисления производных

Для практического ознакомления с таблицей основных формул дифференцирования рассмотрим примеры.

Пример 1.

Вычислить производные

1)

2)

3)

4)

5)

6)

7)

Решение.

1) По формулам дифференцирования (1), (3), (9) получим

2) Вводим дробные и отрицательные степени и превращаем заданную функцию к виду

Используя формулы (3), (4), (9) находим

3) Данный пример вычисляем по правилу (6)

4) Производную функции ищем по правилу сложной функции (7)

5) Производные от функции

находим по правилу производной от произведения функций, и правилом производной от сложной функции

6) По правилу производной от сложной функции будем иметь

7) Много студентов которые еще толком не знают правил, сначала подносят к квадрату выражение в скобках

а затем проводят дифференцировки. Это неправильно, долго и трудно. Воспользовавшись правилом дифференцирования сложной функции получим

Если Вы будете подносить к квадрату, а затем дифференцировать то получите многочлен, который еще предстоит свести к компактному виду. Результат будет правильный, но зачем идти сложным путем, если за нас уже давно придумали правила дифференцирования, которые упрощают вычисления.

Изучайте их и пользуйтесь на практике.

yukhym.com

Производная функции одной переменной

В этой статье мы будем учиться находить производную от функции одной переменной. Дадим ее определение, вскользь затронем геометрический смысл. Разберемся с вопросом нахождения производной от сложной функции.

Итак, дадим определение производной: пусть в некоторой окрестности точки определена функция . Производной функции в точке называется предел, если он существует,

   

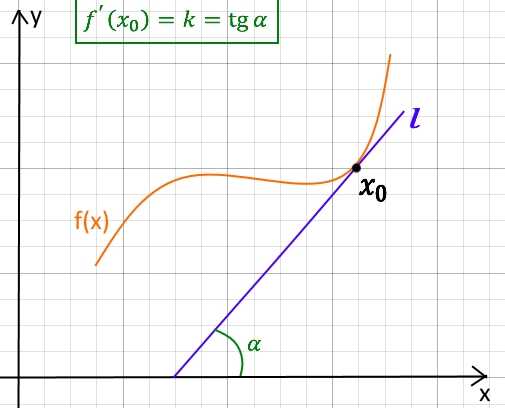
Из школы можно вспомнить формулу для нахождения касательной к функции в точке:  . То есть если говорить о геометрическом смысле производной, то обозначим производную функции в точке как угловой коэффициент или тангенс угла наклона касательной прямой к графику функции в этой точке.

Правила дифференцирования:

1. Производная суммы равна сумме производных, то есть:  
2. Производная произведения:  
3. Вынесение константы за знак производной:  
4. Производная частного:

Прежде чем перейти к задачам, необходимо обзавестись таблицей производных. В идеале вы должны ее знать наизусть, как таблицу умножения 🙂

Таблица производных

[свернуть]

Правилами дифференцирования и таблицей вооружились, двигаемся дальше.

Рассмотрим некоторую функцию . Как видим, функция зависит не просто от переменной , а от другой функции . Будем называть такую функцию сложной. Производная сложной функции вычисляется следующим образом:

Теперь всей необходимой теорией для решения стандартных задач на нахождение производной мы обладаем, а именно: правилами дифференцирования, таблицей производных и формулой производной от сложной функции. Давайте на примерах подробно разберемся с тем, как это работает.

Задачи на применение правила дифференцирования суммы

Пример 1. Найти производную функции

Решение:   Применяем правило дифференцирования суммы функций:

Заглядываем в таблицу производных и ищем там производную от и от

Всё, производная найдена. В ответ запишем

Пример 2. Найти производную функции , где

Решение:   Применяем правило дифференцирования суммы функций:

Открываем таблицу производных и находим производные от и

Производная найдена, в ответе записываем

Пример 3. Найти производную функции

Решение:

[свернуть]

Задачи на применение правила дифференцирования произведения

Пример 4. Найти производную функции

Решение:   Применим правило дифференцирования произведения:

Обращаемся к таблице производных и ищем там производные тангенса и

    или    

Производная найдена.

Пример 5. Найти производную функции

Решение:   Применим правило дифференцирования произведения:

Производная найдена.

Пример 6. Найти производную функции

Решение:

 

Производная найдена.

[свернуть]

Задачи с вынесением константы за знак производной

Это правило дифференцирования самое простое для понимания (редко у кого можно встретить здесь ошибки): мы просто выносим константу за знак производной и находим производную от оставшегося выражения.

Пример 7. Найти производную функции

Решение:   Видим константу , поэтому поступаем в соответствии с нашим правилом:

Всё, задача решена 🙂 Давайте, на всякий случай, рассмотрим еще одну такую задачу.

Пример 8. Найти производную функции

Решение:   Видим дробь. Производную от дроби находить пока не умеем, но может без проблем преобразовать выражение следующим образом:

Теперь константа очевидна, выносим и находим производную:

Производная найдена.

[свернуть]

Задачи на применения правила дифференцирования частного (дроби)

Ничего сложно в дифференцировании дробей нет, но на практике именно здесь чаще всего возникают ошибки, поэтому остановимся на этом моменте подробнее.

Пример 9. Найти производную функции

Решение:  Видим дробь. Мысленно повторяем для себя: «Производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и всё это деленное на квадрат знаменателя«.

Числителем здесь является , а знаменателем — . Тогда, в соответствии с формулой, напишем:

Всё, производная успешно найдена.

Пример 10. Найти производную функции

Решение:  Рассматриваем выражение. Числителем служит , знаменателем — . По формуле получим:

В принципе, на этом этапе можно остановиться, производная найдена. Но, взглянув на числитель, несложно заметить и применить основное тригонометрическое тождество :

.

Вспомнив, что отношение синуса к косинусу есть тангенс, легко проверить получившийся ответ по таблице производных.

Пример 11. Найти производную функции

Решение:   Числитель здесь , знаменатель . По формуле производной для дроби запишем:

Производная найдена, но можно упростить полученное выражение, сделаем это:

Пример 12. Найти производную функции

Решение:   Числитель и знаменатель . Получаем:

Заметим, что здесь необязательно было пользоваться именно формулой для дроби, так как знаменатель представляет собой константу. Эту константу можно было вынести по предыдущему правилу дифференцирования.

[свернуть]

С правилами дифференцирования ознакомились. Переходим к дифференцированию сложной функции. Пока еще нет достаточного опыта, рекомендую на каждом шаге повторять для себя: «Производная сложной функции равна производной внешней функции на производную внутренней функции«.

Пример 13

Найти производную функции .

Решение:   Видим обыкновенный косинус, но воспользоваться таблицей производных сразу не можем, потому что зависит косинус не просто от , а от . Применяем формулу для сложной функции.

Необходимо очень чётко уяснить вопрос с тем, что является в некотором выражении внешней функцией, а что внутренней. Для этого нужно посмотреть на функцию как бы в целом (это может быть нечто очень громоздкое), понять, что это прежде всего: произведение, степень, дробь или что-то другое.

В данной задаче всё просто. Прежде всего наше выражение — это косинус. То есть косинус является внешней функцией. Внутренней функцией будет являться аргумент косинуса . Тогда по формуле запишем:

.

[свернуть]

В 13 и 14 примерах для нахождения производной достаточно было применить формулу для сложной функции всего один раз. Однако на практике чаще всего имеются выражения вида «функция от функции, зависящей от еще одной функции, которая зависит функции и т.д.». В этих случаях принцип нахождения производной не изменяется — мы просто используем формулу несколько раз.

Пример 15

Найти производную функции

Решение:    Имеем натуральный логарифм, который зависит от синуса, который зависит от некоторого выражения. Внешняя функция здесь сам логарифм, то есть , внутренняя — выражение под логарифмом, т.е. .

Производную первого множителя уже можем написать из таблицы производных (сделаем это позже, чтобы не возникло путаницы). Для нахождения производной второго множителя вновь используем формулу, полагая, что внешней функцией является синус, а внутренней — выражение :

Давайте для наглядности покажем на картинке процесс работы с выражением:

Функция слева от стрелки внешняя, справа внутренняя. Количество стрелок равно количеству применений формулы для сложной функции.

[свернуть]

Пример 16

Найти производную функции

Решение:   Нарисуем такую же картинку, как и в предыдущем примере:

Имеем три стрелки, то есть формулу для сложной функции будем последовательно применять именно три раза. На каждом шаге функция слева от стрелки — внешняя, справа — внутренняя.

Ответ получился некрасивым, но это нестрашно, потому что задания придумывал сам 🙂 Здесь все производные мы высчитываем на последнем шаге, чтобы не запутаться. На практике же чаще всего будет удобнее это делать после каждого применения формулы (для внешних функций).

[свернуть]

В первое время будет нелишним рисовать на черновике картинки из примеров 15 и 16 (понятно, применительно к своей задаче). Далее разберем пару примеров на комбинирование правил дифференцирования и формулы дифференцирования сложной функции.

Пример 17

Найти производную функции

Решение:   Видим произведение, поэтому по формуле дифференцирования произведения функций запишем:

Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:

[свернуть]

Пример 18

Найти производную функции

Решение:   Видим дробь, поэтому по формуле дифференцирования дробей запишем:

Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:

Опять получился не очень красивый ответ, но зато правильный 🙂

Здесь стоит заметить, что мы могли избавиться от дроби и перейти к произведению функций с помощью перенесения арксинуса в числитель (арксинус в этом случае получает степень ).

[свернуть]

На этом всё, спасибо за внимание!

higher-math.ru

Примеры решения производных

Пример. Производная суммы функций.

Дано: сумма функций .
Найти:
Вычислить производную суммы функций

Решение:
Исходя из того, что производная алгебраической суммы (разности) функций, имеющих производную, равна такой же сумме (разности) производных этих функций: используя формулы производных (ссылка), вычислим производную, заданной в условии задачи суммы функций:

Ответ: производная суммы функций равна

Пример. Производная произведения функций.

Дано: произведение функций .
Найти:
Вычислить производную произведения функций

Решение:
Исходя из того, что производная двух функций, имеющих производную, вычисляется по формуле: найдем производную, заданного в условии задачи произведения функций:

Ответ: производная произведения функций равна

Пример. Производная отношения функций.

Дано: отношение функций .
Найти:
Вычислить производную отношения функций

Решение:
Исходя из того, что производная отношения двух функций, имеющих производную, вычисляется по формуле: определим производную, заданного в условии задачи отношения функций:

Ответ: производная отношения функций равна

Пример. Производная сложной функций.

Дано: сложная функция .
Найти:
Вычислить производную сложной функции

Решение:
Исходя из того, что функция имеет производную в точке а функция имеет производную в точке причем сложная функция будет иметь производную в точке и в нашем случае получаем следующее а Тогда а значит

Ответ: производная сложной функции равна

Пример. Производная функции заданной параметрически.

Дано: функция заданная параметрически .
Найти:
Вычислить производную функции заданной параметрически.

Решение:
Исходя из того, что производная функции, заданной параметрически, то есть в виде соотношения где изменяется в пределах некоторого множества, определяется по формуле вычислим производную, заданной в задаче функции:

Производная параметрически заданной функции будет тоже функция, заданная параметрически:

Ответ: производная параметрически заданной функции равна

matematika.electrichelp.ru