Сложение и вычитание и умножение векторов – 1. Сложение и вычитание векторов. Умножение вектора на число

Сложение и вычитание векторов

Определение

Сложение векторов иосуществляется поправилу треугольника.

Суммой двух векторов иназывают такой третий вектор, начало которого совпадает с началом, а конец — с концомпри условии, что конец вектораи начало векторасовпадают (рис. 1).

Для сложения векторов применяется также правило параллелограмма.

Определение

Правило параллелограмма — если два неколлинеарных вектора ипривести к общему началу, то векторсовпадает с диагональю параллелограмма, построенного на векторахи(рис. 2). Причем начало векторасовпадает с началом заданных векторов.

Определение

Вектор называетсяпротивоположным вектором к вектору , если онколлинеарен вектору , равен ему по длине, но направлен в противоположную сторону вектору.

Операция сложения векторов обладает следующими свойствами:

1. — коммутативность

2. — ассоциативность

Определение

Разностью векторов иназывается вектортакой, что выполняется условие:(рис. 3).

Умножение вектора на число

Определение

Произведением вектора на число называется вектор, удовлетворяющий условиям:

3. , если ,, если.

Свойства умножения вектора на число:

Здесь и- произвольные векторы,,- произвольные числа.

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет

размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство с введённым на нём положительно определённымскалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.

-мерное евклидово пространство обозначается также часто используется обозначение(если из контекста ясно, что пространство обладает евклидовой структурой).

Для определения евклидова пространства проще всего взять в качестве основного понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на векторах которого задана вещественнозначная функция обладающая следующими тремя свойствами:

Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством^[1].

Пример евклидова пространства — координатное пространство состоящее из всевозможныхn-ок вещественных чисел скалярное произведение в котором определяется формулой

22. Базис и координаты вектора

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

• Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).

• Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,

В конечномерных пространствах обе разновидности базиса совпадают.

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

где — координаты вектора.

23. Скалярное произведение.

операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение

длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

24. Векторное произведение

это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

где

25. Смешанное произведение

Сме́шанное произведе́ние векторов —скалярное произведение вектора навекторное произведение векторов и:

.

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .смешанное произведение трех векторов можно найти через определитель

26. Плоскость в пространстве

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

Некоторые характеристические свойства плоскости

• Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

• Две плоскости являются либо параллельными, либо пересекаются по прямой.

• Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.

• Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.

• Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.

где и— постоянные, причёмиодновременно не равны нулю; в

векторной форме:

где — радиус-вектор точки, векторперпендикулярен к плоскости (нормальный вектор).Направляющие косинусы вектора :

где ,,— отрезки, отсекаемые плоскостью на осяхи.

в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки ,не лежащие на одной прямой:

27. Нормированное уравнение плоскости

нормальное уравнение плоскости вида задает в прямоугольной системе координатOxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .

28. Прямая в пространстве

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

итак, если уравнения двух непараллельных плоскостей — и, то прямая, являющаяся их линией пересечения, задается системой уравнений

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Уравнения (11.11) называют общими уравнениями прямой в пространстве.

29. Уравнение окружности

Уравнение окружности радиуса с центром вначале координат:

30. Эллипс. Каноническое уравнение. Эксцентриситет, фокальный радиус.

Э́ллипс — геометрическое место точек

M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и(называемыхфокусами) постоянна и больше расстояния между фокусами, то есть

причем

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

studfiles.net

2. Линейные операции над векторами

К линейным операциям над векторами относятся следующие операции:

• сложение векторов;

• вычитание векторов;

• умножение вектора на скаляр (действительное число).

2.1 Сложение векторов

Определение 2.1. Суммой двух векторов 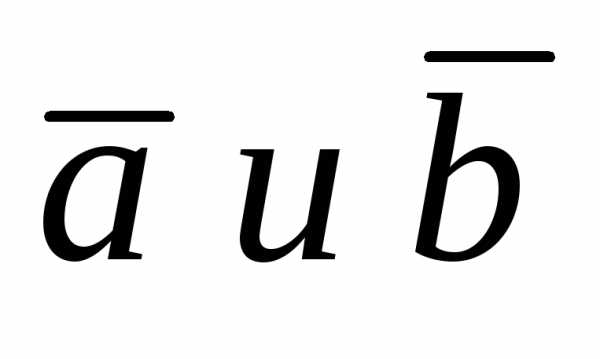называется третий векторимеющий своим началом начало вектора, а концом – конец вектора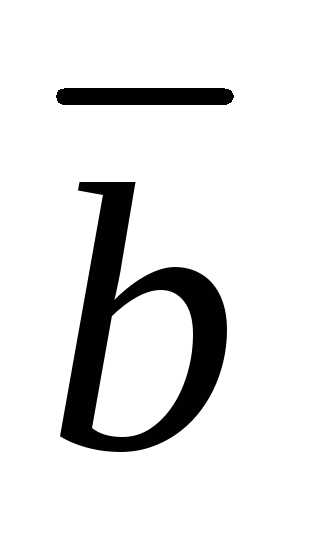при условии, что начало векторасовпадает с концом вектора(вектор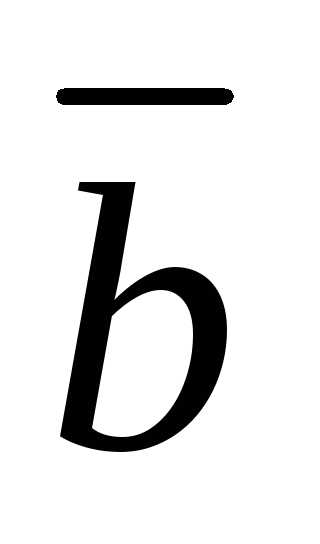приведен к концу вектора)(рис. 2.1).

Это определение сложения двух векторов носит название «правило треугольника.

Это правило сложения векторов можно распространить на любое их количество.

Правило. Чтобы сложить любое количество векторов, следует расположить их так, чтобы конец каждого предыдущего вектора был началом следующего и построить вектор началом в начале первого и концом в конце последнего вектора(рис. 2.2).

Наряду с правилом треугольника сложения векторов существует «правило параллелограмма»

Определение 2.1^*. Суммой векторов и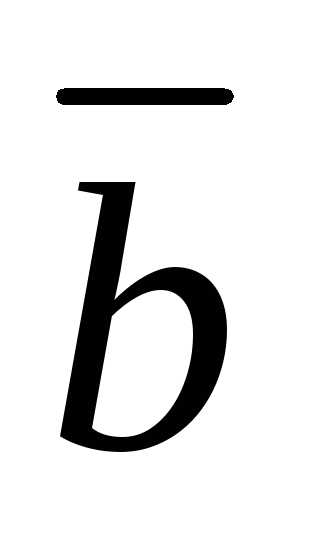является вектор– вектор-диагональ параллелограмма, построенного на векторахи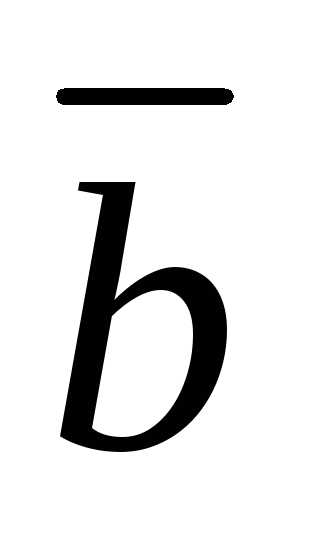, причем векторыи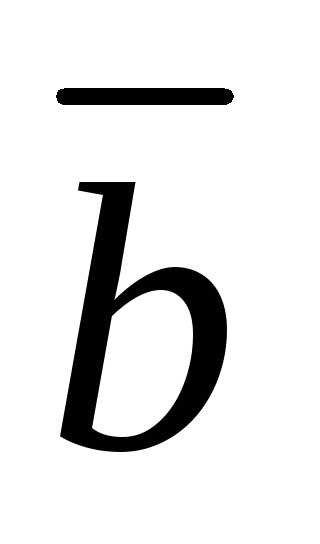приведены к одному началу(рис. 2.3).

На рис 2.3 этой диагональю является диагональ .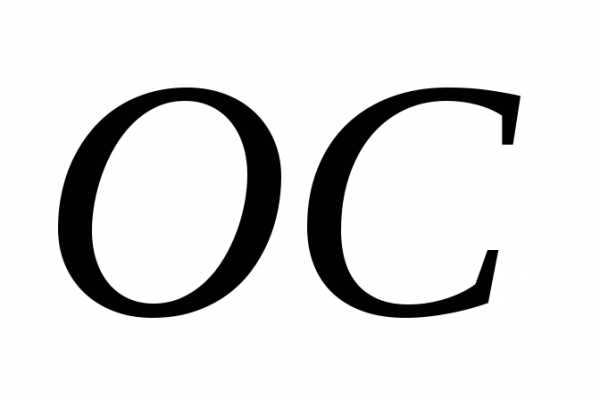

По правилу параллелограмма определяется равнодействующая двух сил. Для нахождения равнодействующей сил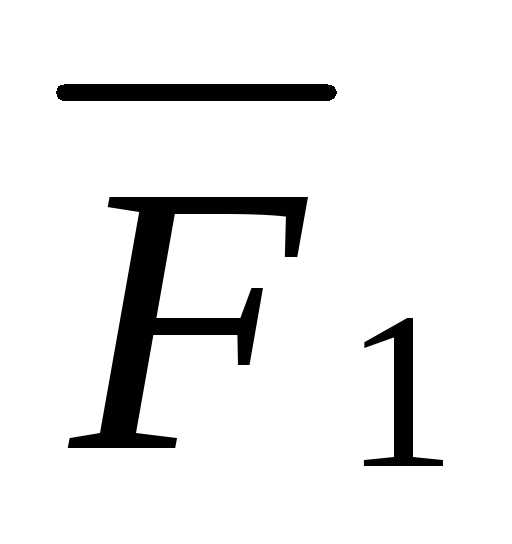и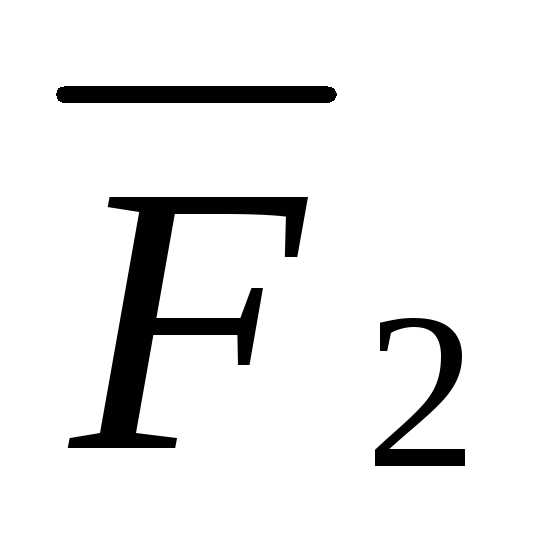,, приводим эти силы к точкеи строим на них параллелограмм. Вектор-диагональпараллелограмма и является равнодействующих этих сил (рис. 2.4).

Свойства сложения векторов

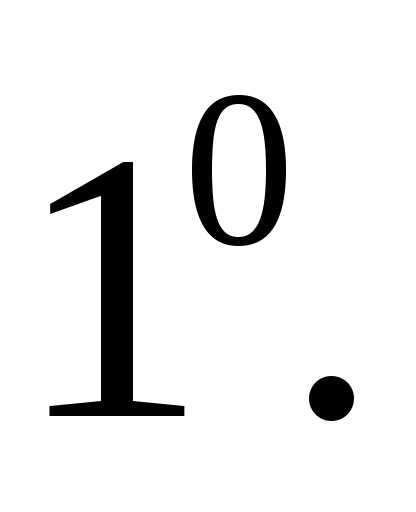–коммутативный (переместительный) закон.

Рис. 2.3 иллюстрирует справедливость свойства. В самом деле:

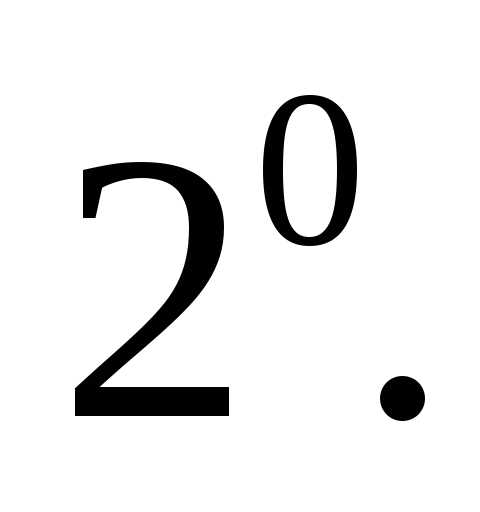‑ассоциативный (сочетательный) закон.

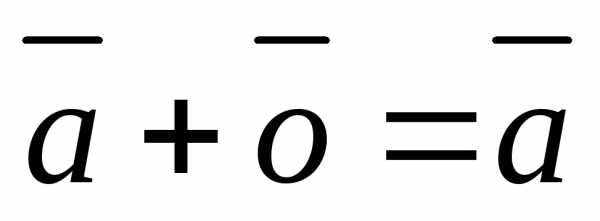для любого вектора .

Для любого вектора : .

2.2 Вычитание векторов

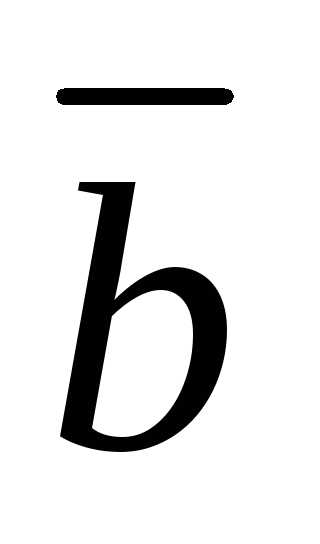Определение 2.2. Разностью двух векторов иназывается третий вектор, такой, что.

Покажем, как реализуется на практике сформулированное определение понятия разности.

Задача 2.1. Даны два вектора:

Найти: разность векторов и.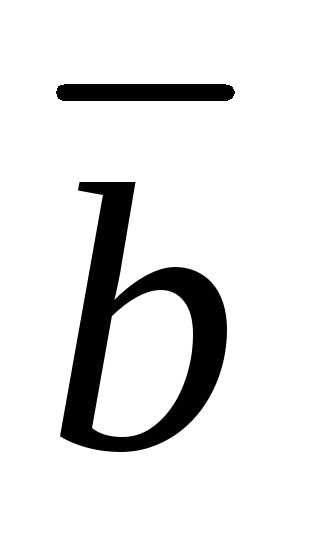

Решение.Приведем варианта два решения.

1⁰. Из определения следует: чтобы построить разность двух векторов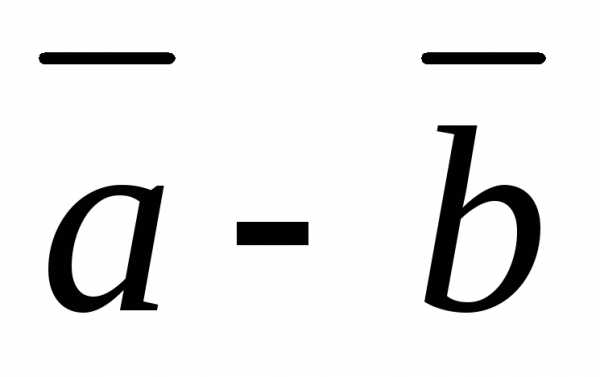эти векторы надо привести к одному началу, а затем построить вектор с началом в конце вектора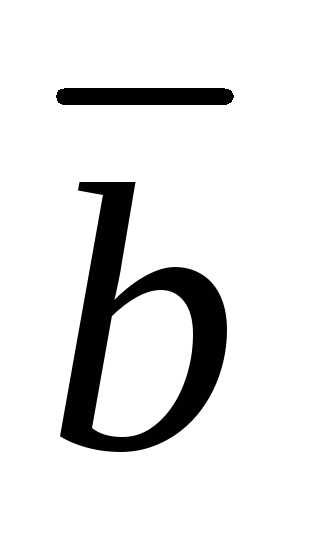и концом в конце вектора(рис. 2.5). Суммой векторови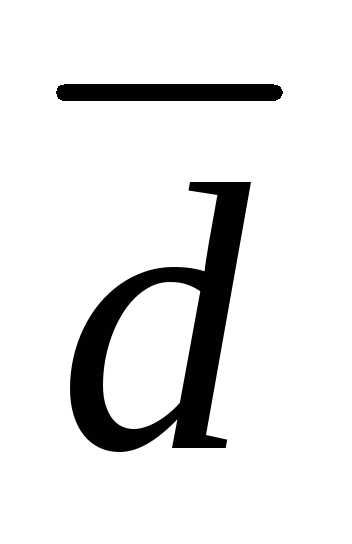является вектор .

Обратимся к рис. 2.3. В параллелограмме OACB диагональOC является суммой векторови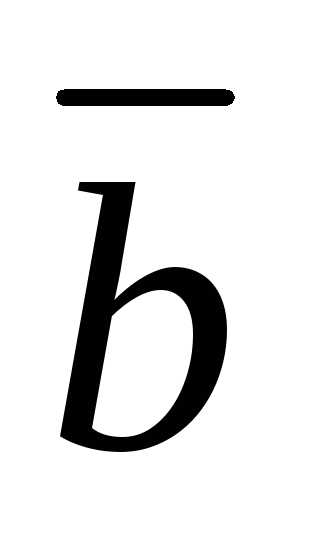, а диагональBA – разностью этих векторов.

2⁰. Преобразуем равенство 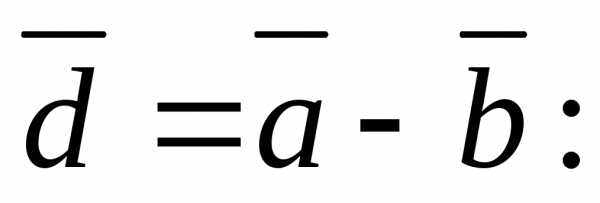. Следовательно, вектор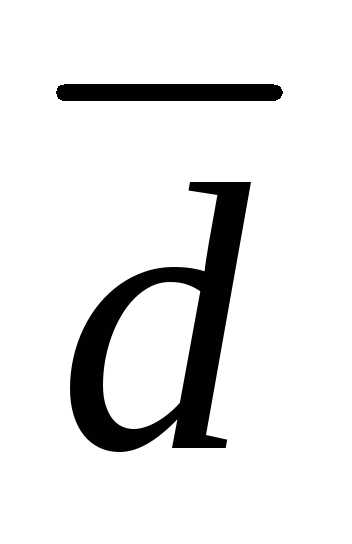является суммой вектораи вектора, противоположного вектору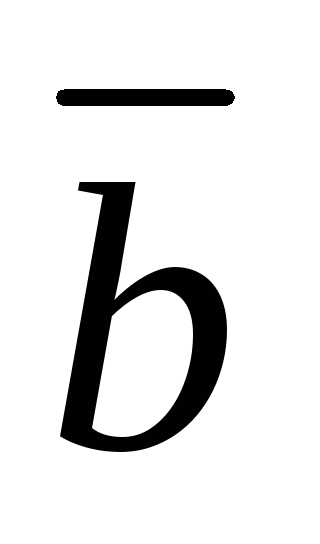. Отсюда следует построение искомой разности векторов (рис. 2.6).

2.3. Умножение вектора на скаляр

Определение 2.3. Произведением вектора на скалярназывается вектор , удовлетворяющий двум условиям:

Свойства умножения вектора на скаляр

.;

.;

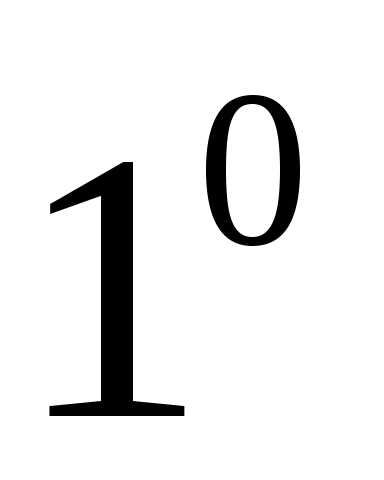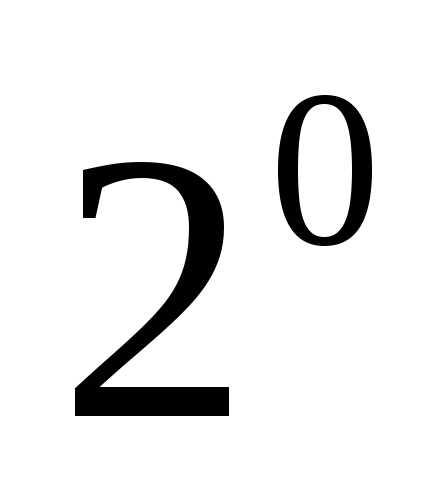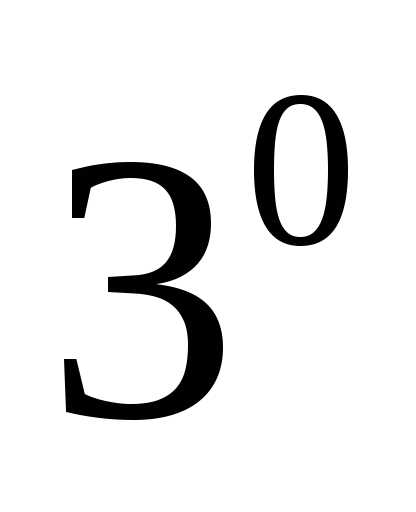. ассоциативный (сочетательный) закон по отношению к скалярным множителям;

. – дистрибутивный (распределительный) закон по отношению к векторному множителю;

. – дистрибутивный (распределительный) закон по отношению к числовому множителю.

Замечание. Свойства сложения векторов и умножения вектора на число свидетельствуют о следующем: векторные одночлены и многочлены можно преобразовывать относительно этих операций по правилам преобразования алгебраических одночленов и многочленов.

В заключение рассмотрим пример использования изученных свойств на практике.

Задача 2.2.Даны два вектора и: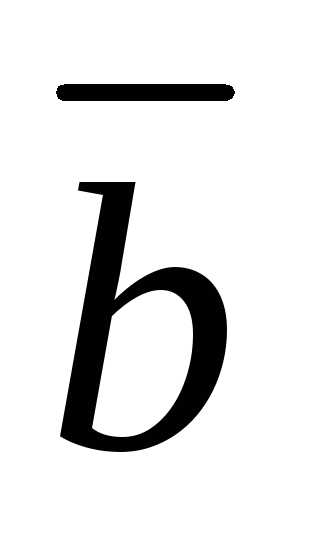

Найти: вектор .

Решение.Преобразуем выражение вектора, используя свойства сложения векторов и умножения вектора на скаляр:

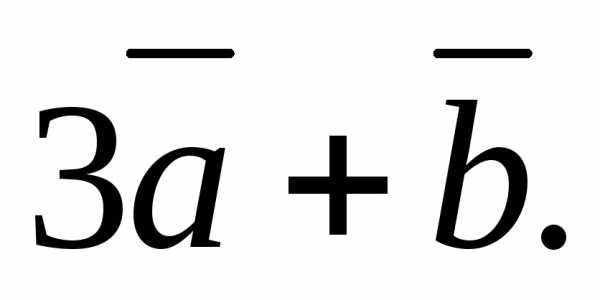
Полученную сумму построим по правилу треугольника (рис. 2.8).

studfiles.net

Операции с векторами, сложение векторов, умножение вектора на действительное число.

Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .

Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.

Теперь рассмотрим с A = (x₁, y₁) и C = (x₂, y₂). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x₂ — x₁, y₂ — y₁) и радиус вектор есть .

Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 — x₁, y₂ — y₁ >.

Компонентная форма с A = (x₁, y₁) и C = (x₂, y₂) есть
= 2 — x₁, y₂ — y₁ >.

Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).

Решение Мы имеем
= = .

Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.

Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v₂ >, мы имеем
|v|² = v²₁ + v²₂          Используя теорему Пифагора
|v| = √v²₁ + v²₂.

Длина, или величина ветктора v = 1, v₂ > находится как |v| = √v²₁ + v²₂.

Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.

Пусть u = 1, u₂ > и v = 1, v₂ >. Tогда
1, u₂ > = 1, v₂ >          только если u₁ = v₁ and u₂ = v₂.

Операции с векторами

Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное. Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.

Для действительного числа k и вектора v = 1, v₂ >, скалярное произведение k и v есть
kv = k.1, v₂ > = 1, kv₂ >.
Вектор kv есть скалярным кратным вектора v.

Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.

Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .

Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u₂ > и v = 1, v₂ >. Тогда
u + v = 1 + v₁, u₂ + v₂ >

Например, если v = и w = , тогда
v + w = =

Если u = 1, u₂ > и v = 1, v₂ >, тогда
u + v = 1 + v₁, u₂ + v₂ >.

Перед тем, как мы определим вычитание векторов нам нужно дать определение — v. Противоположный вектору v = 1, v₂ >, изображенному внизу, есть
— v = (- 1).v = (- 1)1, v₂ > = 1, — v₂ >

Вычитание векторов, такое как u — v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u — v как u + (- v). Если u = 1, u₂ > и v = 1, v₂ >, тогда
u — v = u + (- v) = 1, u₂ > + 1, — v₂ > = 1 + (- v₁), u₂ + (- v₂) > = 1 — v₁, u₂ — v₂ >

Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма , как мы это делали для сложения векторов.

www.math10.com

Сложение и вычитание векторов. Умножение вектора на число

Отметим, что сложение векторов производится аналогично планиметрии, только все действия выполняются в пространстве.

Итак, пусть заданы два произвольных вектора в пространстве (рис. 1):

Рис. 1. Произвольные векторы в пространстве

Определим, что же называется суммой двух этих векторов.

Точно так же, как в планиметрии, из любой удобной точки, назовем ее точкой А, можно единственным образом отложить вектор, равный вектору . Напомним, что заданные векторы, как и любые другие, свободны, важно лишь направление и длина, сам вектор можно параллельно переносить в любое место как на плоскости, так и в пространстве. Так, мы получили вектор  – в результате действия вектора  точка А переместилась в точку В. Теперь из точки В откладываем единственно возможным образом вектор , получаем вектор  – так, в результате действия вектора  точка В переместилась в точку С. В результате точка А переместилась в точку С, получен вектор , который и называется суммой векторов  и  (рис. 2).

Рис. 2. Сумма двух векторов в пространстве

Так, получено правило треугольника для сложения векторов в пространстве.

Правило треугольника

Из любой точки пространства (точка А) откладываем первый вектор, из конца первого вектора (точка В) откладываем второй вектор и получаем точку С. Вектор, соединяющий начало первого вектора (точка А) и конец второго (точка С), и будет результирующим.

Отметим, что результат сложения векторов не зависит от выбора начальной точки, существует соответствующая теорема, которая это доказывает на основании того, что из точки можно отложить вектор, равный заданному, единственным образом.

Определение

Разностью двух векторов называется такой третий вектор, который, будучи сложенным со вторым вектором, даст первый вектор.

Введем разность векторов  и , для этого сложим вектор  с противоположным вектором :

Итак, из произвольной точки А откладываем вектор , получаем точку В. Чтобы получить вектор  мы строим вектор, равный вектору  по длине, но противонаправленный. Полученный вектор откладываем из точки В – получаем точку D. Вектор  и будет искомым вектором разности.

Проиллюстрируем (рис. 3):

Рис. 3. Вычитание двух векторов в пространстве

Построим на заданных векторах  и  параллелограмм (рис. 4):

Рис. 4. Параллелограмм на двух заданных векторах

Т. к. вектор ; аналогично .

По правилу треугольника:

Так, одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов.

Рассмотрим разность векторов. По правилу треугольника:

.

Так, вторая диагональ параллелограмма, построенного на двух векторах, соответствует разности этих векторов.

Для сложения и вычитания нескольких векторов применяется правило многоугольника. Пусть заданы векторы  и :

Рис. 5. Три вектора в пространстве

Необходимо построить вектор .

Видим, что перед некоторыми векторами стоят численные множители. Напомним, что при умножении вектора на число получаем сонаправленный вектор, длина которого – это длина исходного вектора, умноженная на заданное число. Получим векторы  и . Вектор  сонаправлен с вектором , длина его в три раза больше. Вектор  противонаправлен вектору , длина его в два раза больше. Проиллюстрируем (рис. 6):

Рис. 6. Умножение вектора на число

Приступаем к сложению. Из произвольной точки А откладываем полученный вектор  – получаем точку В. Из точки В откладываем вектор  – получаем точку С. Из точки С откладываем вектор  – получаем точку D. Согласно правилу многоугольника, вектор  соответствует искомому вектору :

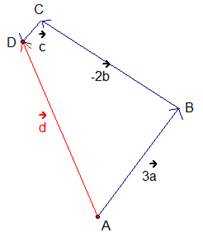
Рис. 7. Сложение векторов по правилу многоугольника

Задача 1:

Задан тетраэдр ABCD (рисунок 8). Доказать:

 

Рис. 8. Тетраэдр, задача 1

Решение:

По правилу треугольника:

Аналогично:

, ч. т. д.

По правилу треугольника:

Аналогично: , ч. т. д.

Задача 2

Упростить выражение:

Рассмотрим отдельно сумму двух векторов: , ее значение очевидно:

Проиллюстрируем (рис. 9):

Рис. 9. Сумма двух векторов

Теперь сократим противоположные векторы:

Можно было сразу заметить:

.

В результате упрощения получено:

.

Итак, мы ввели операции сложения и вычитания векторов, умножения вектора на число в стереометрии, отметили, что операции аналогичны таким же для планиметрии. Кроме того, решили несколько задач, базирующихся на описанных операциях.

 

Список литературы

1. Геометрия. 10–11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил.
2. Геометрия. 10–11 класс: учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Геометрия. 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Ru.onlinemschool.com (Иточник).
2. Emomi.com (Источник).
3. Cleverstudents.ru (Источник).

 

Домашнее задание

Задача 1: задан параллелепипед (рисунок 10). Доказать:

1.

2.

3.

Рис. 10. Параллелепипед

Задача 2: упростить выражение:

Задача 3: построить вектор , если векторы  и  заданы на рисунке 11:

Рис. 11. Векторы, задача 3

interneturok.ru

12.Линейные операции над векторами. Сложение, вычитание и умножение вектора на число.

Сложение векторов

В алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака:

с_x = a_x + b_x ; с_y = a_y + b_y ; с_z = a_z + b_z .

Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или материальной точке).

Вычитание векторов

Вычитание векторов с = a – b можно представить как 2.narod.ru/info/vectors.htm»сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак:

с_x = a_x – b_x ; с_y = a_y – b_y ; с_z = a_z – b_z .

Умножение вектора на число

При умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число:

b_x = k · a_x ; b_y = k · a_y ; b_z = k · a_z .

В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи.

Операция умножения на число является коммутативной  a · k = k · a  (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда 2.narod.ru/info/vectors.htm»коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет 2.narod.ru/info/vectors.htm»нулевой вектор, говорить о направлении которого некорректно.

Операция умножения на число является дистрибутивной  k · (a + b) = k · a + k · b  (произведение суммы векторов на число равно сумме произведений слагаемых на это же число).

Скалярное произведение векторов

Результатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними.

Вычисление скалярного произведения

В алгебраической форме скалярное произведение  d = a · b  вычисляется как

d = a_x · b_x + a_y · b_y + a_z · b_z .

Свойства скалярного произведения

Коммутативность:  a · b = b · a .

Дистрибутивность:  a · (b + c) = a · b + a · c .

Сочетательность (линейность) относительно скалярного множителя:  k · (a · b) = (k · a) · b = a · (k · b) .

Скалярный квадрат вектора равен квадрату его 2.narod.ru/info/vectors.htm»модуля:  a · a = |a|²  (норма вектора).

Векторное произведение

.Вычисление векторного произведения

В алгебраической форме векторное произведение  c = [a × b]  в правой системе координат вычисляется как

с_x = a_y · b_z – a_z · b_y ; с_y = a_z · b_x – a_x · b_z ; с_z = a_x · b_y – a_y · b_x .

В левой системе координат знаки слагаемых меняются на противоположные.

Свойства векторного произведения

Антикоммутативность:  [a × b] = –[b × a] .

Дистрибутивность:  [a × (b + c)] = [a × b] + [a × c] .

Сочетательность относительно скалярного множителя:  k · [a × b] = [(k · a) × b] = [a × (k · b)] .

Смешанное произведение:  a · [b × c] = [a × b] · c .

Векторный квадрат вектора всегда является 2.narod.ru/info/vectors.htm»нулевым вектором:  [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора).

studfiles.net

Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение (произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости. Взаимное расположение векторов. Разложение вектора по координатным векторам.

dpva.ru

Сложение и вычитание векторов [wiki.eduVdom.com]

Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).

Сложение двух векторов

Рис.1

Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника).

Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ {правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$

Действительно, каждый из векторов $\overrightarrow{a} + \overrightarrow{b} \,и\, = \overrightarrow{b} + \overrightarrow{a}$ равен одному и тому же вектору $\overrightarrow{OB}$ .

---

---

Пример 1. В треугольнике ABC АВ = 3, ВС = 4, ∠ В = 90°. Найти: $а)\,\ \overrightarrow{|АВ|} + \overrightarrow{|ВС|};\,\,\ б)\,\ |\overrightarrow{АВ} + \overrightarrow{ВС}|$ .

Решение

а) Имеем: $|\overrightarrow{АВ}| = АВ,\,\,\ |\overrightarrow{ВС}| = ВС$ и, значит, $|\overrightarrow{АВ}| + |\overrightarrow{BC}| = 7$ .

б) Так как $\overrightarrow{AB} + \overrightarrow{ВС} = \overrightarrow{АС} \,\,,\,\, то\,\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = |\overrightarrow{АС}| = АС$ .

Теперь, применяя теорему Пифагора, находим $$ AC = \sqrt{AB^2 + BC^2} = \sqrt{9 + 16} = 5 \\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5. $$

Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.

Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).

Сложение трех векторов

Рис.2

Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2 $$ \overrightarrow{ОА} = \overrightarrow{a}\,; \overrightarrow{АВ} = b\,; \overrightarrow{ОВ} = \overrightarrow{a} + \overrightarrow{b}\,; \overrightarrow{BC} = \overrightarrow{c} \\ и \\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} $$ Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор $\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ . Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством. Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .

Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}\,,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .

Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).

Вычитание векторов

Рис.3

Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О. Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .

---

Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} — \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} — \overrightarrow{АС}|$ .

Решение а) Так как $\overrightarrow{ВА} — \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} — \overrightarrow{ВС}| = а$ .

б) Так как $\overrightarrow{АВ} — \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} — \overrightarrow{АС}| = а$ .

Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda < 0$ . Так, например, $2\overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $\overrightarrow{a}$ , а длину, вдвое большую, чем вектор $\overrightarrow{a}$ (рис.4).

Умножение вектора на число

Рис.4

В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4): $$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$ Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .

---

Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .

Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .

Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что $$ \overrightarrow{a} = |\overrightarrow{a}|\,\ \overrightarrow{a_0} $$ , т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.

Таким образом, получаем следующую теорему.

---

Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.

Видео-решение.

---

---

www.wiki.eduvdom.com

No related posts.