| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
как перевести широту и долготу в минуты секунды и градусы
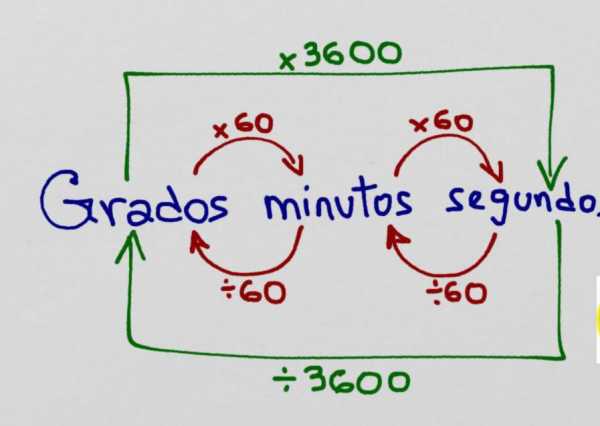
Всё очень просто: 1 градус делится на 60 долей, которые называют «минутами» . А каждая минута в свою очередь содержит 60 «секунд» . Как видим, здесь полная аналогия с теми минутами и секундами, которые для нас всегда были больше связаны с измерением времени, чем углов и координат. Таким удобным единообразием размерности мы обязаны жителям Вавилона, от которых в наследство современной цивилизации достались все эти часы, минуты и секунды. Вавилоняне использовали шестидесятеричную систему исчисления. Конечно, кроме минут и секунд есть и меньшие доли градуса. К сожалению, здесь древняя простота заканчивается и начинается современная бюрократия. Логично было бы и секунды делить на 60 долей или хотя бы на привычные миллисекунды, микросекунды и т. д. Но и в системе СИ, и в родных ГОСТах делать этого не рекомендуется, поэтому доли градуса, меньшие угловой секунды, следует пересчитывать в радианах. К счастью, измерение столь малых углов может понадобиться только людям достаточно подготовленным. А нам с вами могут встретиться более простые задачи. Итак, чтобы величину угла, указанную в формате (градусы минуты секунды) перевести в десятичные доли градуса, следует к количеству целых градусов прибавить количество минут, разделённое на 60 и кол-во секунд, разделённое на 3600. Например, географические координаты одного замечательного места в г. Краснодаре — 45° 2′ 32″ северной широты и 38° 58′ 50″ восточной долготы. Если пересчитать это в обычные градусы, то получится 45° + 2/60 + 32/3600 = 45.0421° северной широты и 38 + 58/60 + 50/3600 = 38.9806 восточной долготы. Это несложно проделать в калькуляторе, но можно воспользоваться и интернет-ресурсами. В интернете вам предложат лёгким движением мышки перевести секунды в градусы, радианы, обороты, да хоть в мили, если такое желание возникнет! Вот несколько ссылок на он-лайн конверторы угловых координат: <a rel=»nofollow» href=»http://convertr.ru/angle/» target=»_blank»>http://convertr.ru/angle/</a> <a rel=»nofollow» href=»http://www.unitconversion.org/unit_converter/angle.html» target=»_blank»>http://www.unitconversion.org/unit_converter/angle.html</a> <a rel=»nofollow» href=»http://www.1728.com/angles.htm» target=»_blank»>http://www.1728.com/angles.htm</a> <a rel=»nofollow» href=»http://www.fcc.gov/mb/audio/bickel/DDDMMSS-decimal.html» target=»_blank»>http://www.fcc.gov/mb/audio/bickel/DDDMMSS-decimal.html</a> <a rel=»nofollow» href=»/» title=»40536924:##:scol/ccangle.htm» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> <a rel=»nofollow» href=»http://convert-to.com/120/angle-units.html» target=»_blank»>http://convert-to.com/120/angle-units.html</a> <a rel=»nofollow» href=»http://www.engineeringtoolbox.com/angle-converter-d_1095.html» target=»_blank»>http://www.engineeringtoolbox.com/angle-converter-d_1095.html</a>
56 градусов 19 минут 52,302 секунды 46 градусов 32 минуты 44,9196 секунды
Как градусы перевести в минуты, секунды и радианы?
Образование 25 мая 2018Любые тела, форма которых является круглой, например сфера или окружность, нуждаются в специальных единицах измерения, отличающихся от таковых для линейных объектов. Этими единицами измерения стали градусы и радианы. При этом часто возникает вопрос о том, как градусы перевести в минуты, секунды и в радиальную систему измерения.
Единицы измерения: градусы
Приблизительно за тысячу лет до нашей эры древние вавилоняне применяли систему измерения небесных тел, по которой вся небесная сфера разделялась на 360 равных частей, что записывалось как 360 °. Одну трехсот шестидесятую часть они называли градусом.
Поскольку система исчисления древних вавилонян являлась шестидесятеричной, они разделяли каждый градус на 60 равных частей, и одна такая часть получила название минуты и обозначалась 1′. В свою очередь каждая минута делилась еще на 60 частей, 1/60 минуты называлась секундой и обозначалась 1».
Наша система исчисления, в отличие от системы древних вавилонян, является десятеричной, однако в области измерения круглых и сферических форм по-прежнему используются градусы, минуты и секунды в их первоначальном понимании. Например, прямым углом является угол в 90°, один градус содержит 60 минут, а одна минута — 60 секунд. Эту информацию рекомендуется запомнить, поскольку она помогает понять, как градусы перевести в минуты.
Единицы измерения: радианы
Наряду с градусами часто используются другие единицы измерения — радианы (от лат. radii — радиус). Радиан является более подходящей единицей измерения круглых тел, поскольку он непосредственно связан с их геометрией. Так, один радиан представляет собой угол, который опирается на длину дуги окружности, равную ее радиусу. Поскольку длина окружности вычисляется по формуле L = 2piR, где pi — число пи, равное 3,14, то полная окружность составляет 2pi радиан.
Измерение углов в радианах очень удобно в тригонометрии, где вычисления и преобразования тригонометрических функций выполняются именно в этой системе исчисления. Например, sin(pi/2) = 1.
Как градусы перевести в минуты, секунды и радианы
Как сделать все правильно? Чтобы выполнить процедуру перевода градусов в минуты и секунды, нужно вспомнить, что в минутах он равен 60, а в секундах 60 x 60 = 3600 или 1° = 60′ и 1′ = 60».
Приведем пример: есть угол a = 12°. Как градусы перевести в минуты для него? Для этого составим пропорцию, из которой получим: a = 60′ x 12º/1º = 720′. Теперь рассмотрим более сложный случай: есть угол a = 32º 45′ 23». Для перевода этого угла в минуты необходимо прибегнуть к сложению в минутах каждого его разряда. В итоге получаем: a = 32 x 60 + 45 + 23/60 = 1965,383′. В секундах этот угол будет равен: a = 32 x 60 x 60 + 45 x 60 + 23 = 117923».

Чтобы перевести угол a из примера выше в радианы, нужно вспомнить, что 360° = 2pi. Теперь нужно указанный угол привести к градусам, получаем: a = 32 + 45/60 + 23/3600 = 32,75639°. Полученный в градусах угол через пропорцию переводим в радианы: a = 2pi x 32.75639°/360° = 0,5717 радиан.
Источник: fb.rumonateka.com
