Учебно-методический материал по алгебре (10 класс) по теме: Графики,содержащие знак модуля.Построение графиков,содержащих знак модуля.
Исследовательская работа
«Построение графиков
функций, аналитическое выражение которых содержит знак абсолютной величины»
2008
Оглавление.
I. Введение——————————————————————————1
II. Основная часть.——————————————————————-1-13
1. Историческая справка——————————————————- -3-4
2. Геометрическая интерпретация понятия |а|—————————- -4-5
3. График функции у=f |(х)|——————————————————5-8
4. График функции у = | f (х)| —————————————————8-10
5. График функции у=|f |(х)| | — —- ——————————————10-13
III. Заключение.————————————————————————-13
IV. Список литературы —————————————————————14
I. Введение.
Построение графиков функций одна их интереснейших тем в школьной математике. Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано , то вы сразу видите параболу; если , вы видите параболу, опущенную на четыре единицы; если же , то вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Хотя уравнения с модулями мы начали изучать уже с 6-го – 7-го класса, где мы проходили самые азы уравнений с модулями, я выбрала именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах построения графиков, содержащих знак абсолютной величины.
Цель работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования: линейные функции, аналитическое выражение которых содержит знак абсолютной величины.
Методы исследования: построение графиков функций.
II. Основная часть.
1. Историческая справка.
В первой половине ХVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты тоски кривой от ее абсциссы. А английский ученый Исаак Ньютон (1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:
Из определения следует, что для любого действительного числа a,
2. Геометрическая интерпретация понятия модуля |а|
Каждому действительному числу можно поставить в соответствие точку числовой прямой, это точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует её расстояние от начало отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Длина отрезка всегда рассматривается как величина неотрицательная. Геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа.
-а 0 а
3. График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
Рис.1
Рис.2.
1. Построить график функции у= |х|
- Если х≥0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
- Если х
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, я сделала вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину? Для этого я рассмотрела несколько функций, и сделала для себя вывод.
2. Например: у=х2 — |х| -3
а) Строю у=х2 -х -3 для х>0.
Квадратичная функция, графиком является парабола, ветви которой направлены вверх, т.к. а = , а > 0
- х0 = —
у0 =-4
(2; -4) – координаты вершины параболы.
- х=0, у= -3
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
- у =0, х2 -х -3 = 0
х2 -4х -12 = 0 Имеем, х1= — 2; х2 = 6.
(-2; 0) и (6; 0) – координаты точки пересечения графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
Вывод: Для построения графика функции у=f |(х)|
- Достаточно построить график функции у=f(х) для х>0;
- Строить для х
4. График функции у = | f (х)|
По определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у=f(х), если f(х) ≥0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то | f (х)| = f(х), значит в этой части график функции у = | f (х)| совпадает с графиком самой функции у=f(х). Если же f(х) f (х)| = — f(х),т.е. точка (х; | f (х)| ) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика.
1. Построить график функции у= | х2 – х – 6 |.
а) Построить график функции у= х2 – х – 6 . Квадратичная функция, графиком является парабола, ветви направлены вверх, т.к. а = 1, а >1.
х0 = —
у0 = — (1/2; — 6,25) координаты вершины
х=0; у = -6 (0; -6) координаты точки пересечения с осью ОУ.
у= 0, х2 – х – 6=0
х1 = -2; х2 = 3. (-2;0) и (3;0) –координаты точек пересечения с осью ОХ
б) Часть графика, расположенного в нижней полуплоскости, отобразить симметрично оси ОХ. (Рис.5)
Вывод: Для построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
(Рис.6, 7.)
5. График функции у=|f |(х)| |
Применяя, определение абсолютной величины и исследуя, графиков функции
у = | 2 · |х | — 3|
у = | х2 – 5 · |х| |
у = | |х3 | — 2 |, я нашла алгоритм построения графиков.
Для того чтобы построить график функции у=|f |(х)| | надо:
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
1. у = | 2 · |х | — 3|
1) Строю у = 2х-3, для х>0. (1; -1) (; 0)
2) Строю прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ. Рис.8
2. у = | х2 – 5 · |х| |
а) Строю график функции у = х2 – 5 х для х>0.
Квадратичная функция, графиком является парабола, ветви направлены, т.к. а=1, а>0
х0 = -;
у0 = 6,25 -12,5 = -6,25 (2,5; -6,25) – координаты вершины
х=0; у=0; (0; 0) – координаты точки пересечения с осью ОУ
у=0; х2 – 5 х =0 (0; 0) и ( 5; 0) – координаты точек пересечения с осью ОХ.
х1 =0; х2=5
(Рис.9)
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
3. у =| |х|3 | — 2 |
а) Строю у=х3 -2 для х > 0.
х1= 0; у1= -2
у2 = 0; х3 -2 =0
х2 =
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ. (Рис.10)
III. Заключение.
При выполнении исследовательской работы я делала такие выводы:
— сформировала алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f(х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
— приобрела опыт построения графиков таких функций, как:
у=f |(х)|; у = | f (х)|; у=|f |(х)| |;
— научилась работать с дополнительной литературой и материалами, производить отбор
научных сведений;
— приобрела опыт выполнения графических работ на компьютере.
Список литературы:
- И. М.Гельфанд, Е.Г. Глаголева. Функции и графики. Издательство «Наука»
- Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука»
- М.К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука»
- Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику.
Москва, «Просвещение».
у
0
х
0
у
х
х
у
х
у
Рис 3.
0
6
-6
-3
х
у
Рис.4
0
6
-6
-2
3
х
у
Рис.5
у
х
Рис.6
у
х
Рис.7
0
у
х
-3/2
3/2
-3
3
Рис.8
1
-1
-6
-6
0
5
5
Рис.9
-2
0
1
2
2
-2
у
х
Рис.10
nsportal.ru
Графики уравнений, содержащих знак модуля
Разделы: Математика
Цель:
- закрепить методы построения графика линейной функции,
- закрепить умение учащихся задавать уравнением функцию, заданную при помощи графика,
- познакомить учащихся с тем, каким образом влияет знак модуля на отображение графика линейной функции
Оборудование: презентация (приложение 1)
Ход урока №1
При решении многих математических задач необходимо быстро и точно строить графики любых функций, изучаемых в школьном курсе алгебры. Т.к. на уроке предстоит много построений, начинаем, вспоминая, как строить график линейной функции y = kx + b на основе анализа углового коэффициента и коэффициента смещения (слайд 2)
Сопоставляем уравнения и графики (слайд 3):
Построим в тетрадях в одной системе координат графики функций (y = —x; y = —x -4; y = -1/3 x – 2; y = 2x + 5; y = x + 1), проверяя себя при помощи слайда 4
Вспомним определение модуля числа x (слайд 5)
Рассматриваем, как можно построить график функции y = |x| на основании определения модуля, отбрасывая части прямых, не лежащих в полуплоскостях x < 0 и x> 0 (слайд 6)
Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)
Сравнивая графики и уравнения функций (слайд 8-9),
делаем вывод о том, как можно построить график функции y = |x + a| — b
смещением графика функции y = |x| (слайд 10-11)Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| — 2, y = |x+2| — 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12
Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:
При построении графиков очень важно научить ребят анализировать область определения и множество значений функции и “переносить” указанные множества на координатную плоскость.
Заполняем таблицу (слайд 12):
D(y) E (y) y = |x| y = |x – 3| y = |x – 3| +2 y = — |x| y = |x + 2| -5 y = — |x +2| -5
И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)
Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):
Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):
Анализируя графики и уравнения (слайд 18), ученики делают вывод о том, как влияет знак минуса перед модульными скобками на график. И самостоятельно задают уравнение по графикам, представленным на слайде 19.
Ход урока № 2
Устно проговариваем уравнения функций по графикам (слайд 20):
Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:
Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:
y = |0,5
y = 3 при -1 < x< 1;
y = -|x + 3| + 6 при -4 < x < -2;
y = -|x — 3| + 6 при 2 < x < 4;
y = |x + 3| + 4 при -4 < x < -2;
y = |x — 3| + 4 при 2 < x ? 4;
y = -|0,5x – 1,5| + 7 при -5 < x < -1;
y = -|0,5x + 1,5| + 7 при 1 < x < 5.
Проверяют себя по слайду 29:
Домашнее задание: придумать картину, состоящую из отрезков прямых, и описать ее при помощи уравнений функций.
Ход урока № 3
Построим графики функций y = |3x| — 3 и y = |3x – 3|. Как в каждом случае связаны y(x) и y(-x)?
Наличие условия y(x) = y(-x) означает симметрию относительно …?
Приведите примеры уравнений функции, графики которых будут симметричны относительно оси ординат
Если в модульные скобки заключается переменная y, то мы получаем условие |y| = |-y|. Какую симметрию задает это условие?
На слайде 34 последовательно рассматриваем цепочку построения графиков:
y = 3x – 3, |y| = 3x – 3, |y| = |3x| — 3, |y| = |3x – 3| путем преобразований симметрии.
Выводим и запоминаем три правила:
Распределите, к какому типу из трех (y = f(|x|,
|y| =
|y| = 2 – x, y = |3x — 4|, |x| + |y| = 2, |y| = 3x – 4, y = |3|x| — 4|, y = |3x| — 4, |y| = |3|x| — 4|, |y| = |3x – 4|.
Проверяем себя (слайд 35)
Строим последовательную цепочку графиков (тонкими линиями в тетрадях):
1) y = 3x – 4, y = |3x – 4|, y = |3|x| - 4|, |y| = |3|x| — 4|
2) y = 3x – 4, y = 3|x| — 4, y = |3|x| — 4|
Рассматриваем способ построения графика соответствия |x| + |y| = 2.
Самостоятельно строим график |x| — |y| = 2 и проверяем себя по слайду 39.
Домашнее задание: придумать пять уравнений соответствий с модулем, в которых встречаются все случаи, рассмотренные на уроке, и построить графики.
17.03.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»
Разделы: Математика
“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”
Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.
Ход урока
I. Вводное слово учителя
Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х2 математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.
Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.
Модуль и квадратичная функция
Построение графиков функций:
- Y = АХ2 + ВX + C,
- Y = АХ2 + ВX + C ,
- Y = АХ2 + ВХ + С
II. Устная работа
1) Дать определение модуля числа Х
2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).
3) Найти на рисунке график функции Y = –Х2 + 4Х – 3.
4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?
5) Вспомнить, как построить график функции Y = Х
По определению модуля
График функции Y = Х симметричен относительно оси У.
III. Построение графиков функций:
Y = АХ2 + ВX + C,
Y = АХ2 + ВX + C,
Y = АХ2 + ВХ + С
Работа проводится в группах, т.к. графики в К–1 в) и К–3 в) одинаковы, их необходимо сравнить и сделать вывод (всего 3 группы). Каждой группе выдается карточка, в ней 3 задания. Учащиеся должны построить графики квадратичной функции, содержащей модуль, используя определение модуля и сделать вывод: как построить график данной функции, используя график квадратичной функции и симметрию относительно осей координат.
Работа в группах.
Задание: построить график функции, используя:
а) определение модуля;
б) график функции Y = АХ2 + ВХ + С;
в) симметрию относительно осей координат.
а) Y = Х2 – 4 Х + 3
б) Y = Х2 – 4 Х + 3
в) Y = Х2 – 4 Х + 3
а) Y = Х2 + 2 Х – 3
б) Y = Х2 + 2 Х – 3
в) Y = Х2 + 2 Х – 3
а) Y = –Х2 + 4 Х – 3
б) Y = –Х2 + 4 Х – 3
в) Y = –Х2 + 4 Х – 3
IV. Учащиеся делают вывод о расположении графиков указанных функций
Вопрос: а) Как построить график функции Y = f (X)?
(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х<
0.
2 способ. Построить график функции Y = f (X) и
отобразить правую часть графика симметрично
относительно оси Y).
б) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).
в) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)
г) Почему графики функций Y = –Х2 + 4X – 3 и Y = Х2 – 4X + 3 одинаковы?
(Так как А = А , –А = А)
V.
У рассмотренных функций под знаком модуля была независимая переменная. Теперь рассмотрим функции, где под знаком модуля стоит либо сама функция, либо и функция, и независимая переменная одновременно, т.е. зависимости вида
Y = АХ2 + ВX+ C и Y = АХ2 + ВX + C
Приведем конкретные примеры.
а) Y = Х2 – 4X+ 3
По определению
Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х2 – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.
б) Y = Х2 – 4X+ 3
Сначала строим график функции Y = Х2 – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х2 – 4X+ 3 , т.е. график функции Y = Х2 – 4X+ 3 отображаем относительно оси Х.
VI. Творческое задание
Дана функция Y = Х2 + 2X– 3
Выполнить всевозможные преобразования данной квадратичной функции с модулем.
10.03.2005
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Как построить график модуля 🚩 график функции модуль 🚩 Математика
Автор КакПросто!
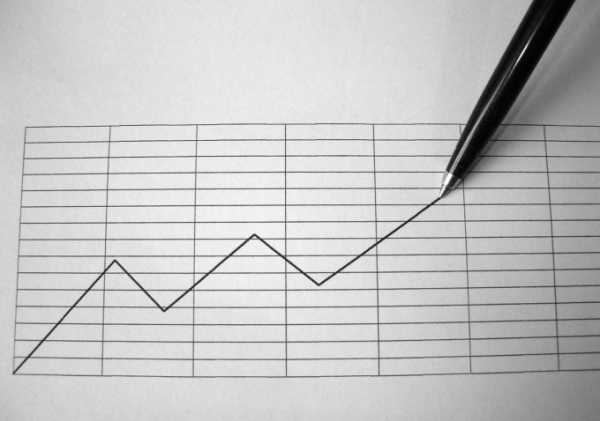
С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. Также в математике модуль разности двух величин равен расстоянию между ними.
Статьи по теме:
Инструкция
Координатной плоскостью в математике называют плоскость на которой задана декартова система координат. Декартова система координат обладает тем свойством, что разбивает координатную плоскость на четыре четверти. Первая четверть ограничена положительными направлениями осей абсцисс и ординат, остальные четверти нумеруются по порядку, против часовой стрелки. При построении графиков функций, в которых присутствует модуль наиболее интересны третья и четвертая четверти, то есть там, где функция принимает отрицательные значения.Рассмотрим функцию f(x) = |x|. Для начала построим график этой функции без знака модуля, то есть график функции g(x) = x. Этот график является прямой, проходящей через начало координат и угол между этой прямой и положительным направлением оси абсцисс составляет 45 градусов.
Так как модуль величина неотрицательная, то ту часть графика, которая находится ниже оси абсцисс необходимо зеркально отобразить относительно нее. Для функции g(x) = x получим, что график после такого отображения станет похож на букву V. Этот новый график и будет являться графической интерпретацией функции f(x) = |x|.
Видео по теме
Обратите внимание
График модуля функции никогда не будет находится в 3 и 4 четверти, так как модуль не может принимать отрицательных значений.
Полезный совет
Если в функции присутствуют несколько модулей, то их нужно раскрывать последовательно, а затем накладывать друг на друга. Результат и будет искомым графиком.
Источники:
- как построить график функции с модулями
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
График модуля — Как построить график функции y=lxl (модуль «х»)??? — 22 ответа
График функции модуль х
В разделе Домашние задания на вопрос Как построить график функции y=lxl (модуль «х»)??? заданный автором DArk_mUnn лучший ответ это 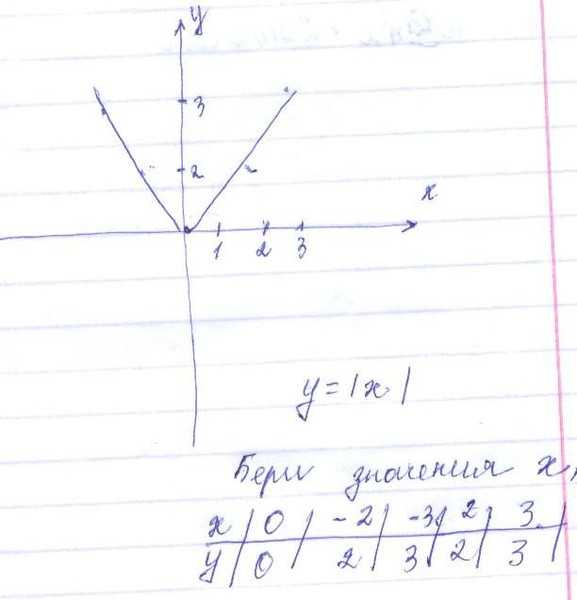
Привет! Вот подборка тем с ответами на Ваш вопрос: Как построить график функции y=lxl (модуль «х»)???
Ответ от шеврон[гуру]
прямая выходящая из начала координат и идет в первую четверть с такими координатами как (1;1), (2;2)(3;3)(4;4)
Ответ от Пользователь удален[гуру]
строишь у=х, потом левую его часть отображаешь вверх. получается галочка с вершиной в 0
Ответ от Особь[гуру]
Если вся функция с модулем, то все отрицательное на графике зеркально отражаешь вверх относительно осиХ (оси абсцисс).
Ответ от ростепель[гуру]
1. Берешь линейку
2. берешь карандаш
3. рисуешь оси координат x и y
4. рисуешь внизу (слева, справа, на черновике, где понравится) таблицу из двух колонок.
5. В шапке пишешь x и y соответственно в левой и правой колонке.
6. Далее в левую колонку выставляешь знчения х: -2, -1, 0, 1,2,3…
7. В правой выставляешь подсчитанный результат. (если х = -2, то |x| = 2, т. к. y = x, следовательно у = 2)
8. Вписываем результат и действуем аналогично с другими числами
9. Рисуем на графике, пользуясь подсчитанными координатами из таблицы.
10. Любуемся и несем сдавать работу
11. получаем отличную оценку)
Удачи!
Ответ от АДЕЛИНА ЮСУПОВА[активный]
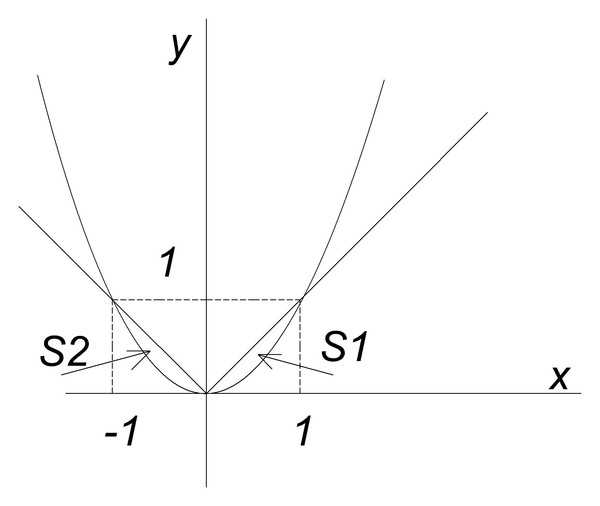
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Ответить на вопрос:
22oa.ru
