Тема: Дроби. Математика
Тема урока: «Дроби»
Тип урока: урок изучения нового материала.
Вид урока: с применением ИКТ
Цель и задачи урока:
Образовательная:
ввести новое понятие «доля числа»,
учить определять долю числа,
записывать дроби,
познакомить с терминами «дробь», «числитель», «знаменатель». (ПК6)
Воспитательная
воспитывать интерес к учебе, к предмету;
воспитывать самостоятельность;
формировать коммуникативные навыки (взаимоотношения между учениками и учителем). (К3)
Развивающая
развивать логическое мышление,
математическую речь,
развивать внимание, память ;
развивать личностные качеств учащихся эмоционально-волевой сферы: навыки самоконтроля, усидчивость и выдержку, умение выражать свои чувства. (К1)
Оборудование урока: ИКТ, учебник, рабочая тетрадь, слайды, индивидуальные карточки, модель круга, арбуз, яблоко, мультимедийная презентация.
Х о д у р о к а
1. Организационный момент. Проверка готовности к уроку.
-Добрый день, уважаемые гости и ребята!-Говорят если день начинать с улыбки, то можно надеяться, что он пройдёт удачно. Давайте сегодняшний урок проведём с улыбкой.
-Я, рада, что у вас хорошее настроение, ведь улыбка — залог успеха в любой работе. Пусть на уроке вам помогут ваша сообразительность, смекалка и те знания, которые вы уже приобрели.
— Откройте тетради и запишите число и классная работа.
2. Проверка домашнего задания. Повторение пройденного материала.
—Какое задание было задано? Стр. 139 № 623
-Справились с домашним заданием?
-Проверяем домашнее задание. Что нужно было сделать?
3. Работа над новым материалом.
1) Разгадайте ребус и узнаете с чем мы сейчас познакомимся.
-Тема сегодняшнего урока-«Дроби»
2) Сценка «Буратино на уроке у Мальвины»
– А сейчас Буратино мы займемся математикой.
– Вот вам яблоко (дает).
Представьте, что к вам подошел Некто и просит поделиться яблоком. Сколько достанется каждому?
– Нисколько! Я не дам Некто яблока, хоть он со мной дерись!
– Буратино, подумайте внимательно. Вам не надо отдавать яблоко, вам надо его поделить. (Буратино думает.)
– Никак не делится. Вот если бы у меня было 2 яблока, то может быть и можно было бы поделить, и то вряд ли, а одно, ну ни как не делится.
– Нет в арифметике такого действия, чтобы одно яблоко на двоих делить.
– Буратино, у вас нет никаких способностей к арифметике. Придётся Вас отправить в 4 «б» класс. У них как раз это изучают.
-Что, ребята, поможем Буратино?
3) Объяснение нового материала.
Нам часто в жизни приходится делить целое на части. Например, торт, пирог, арбуз режут на равные куски, их называют доли.
А помните известный мультик «Апельсин», как животные делили апельсин.
-Как в песенке называлась каждая часть апельсина?
Давайте вспомним что такое доля?
Доля – это каждая из равных частей одного целого
У вас на партах лежит модель арбуза – круг.
На сколько частей его разделим? (на 6)
Каким образом? (Путём сгибания сначала пополам, потом ещё на 3 части)
Заштрихуйте 1/6 долю.
Сколько долей осталось? (5)
Какую часть составят 5 таких долей?
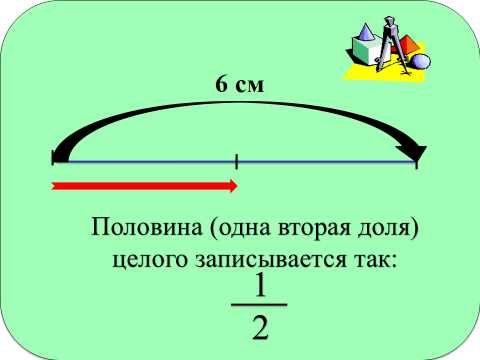
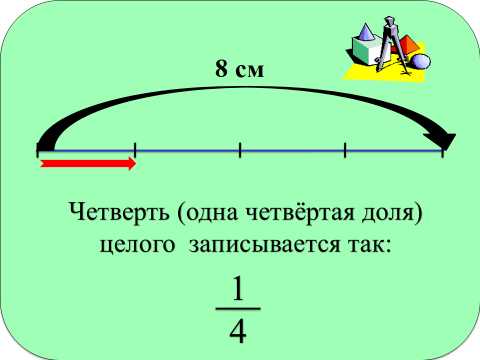
А как записать доли?
Доли мы запишем с помощью дробей. (5/6)
Дробь – это одна или несколько равных долей, записанных с помощью двух натуральных чисел, разделенных чертой
Делается запись на доске, а дети записывают в тетрадь.
Черта дроби означает действие деления. Соответственно числа, записанные с этим знаком, называются дробными.
Под чертой пишут число, которое показывает, на сколько равных частей разделили предмет или фигуру. Это число называют знаменателем.
А число над чертой, показывает сколько таких частей взяли. Это число называют числителем.
4)Исторический экскурс
1) 2)
3) 5)
— Долгое время дроби считались трудным разделом математики. У немцев сложилась поговорка «попасть в дроби» — т.е. в трудное положение, откуда нет выхода. Как вы понимаете смысл этого фразеологизма? (оказаться в трудном положении)
5) Работа с учебником
Стр. 141 № 626
– Прочитаем задание.
Физкультминутка с проверкой восприятия нового материала.
Упражнение для снятия зрительного напряжения.
— Охотник отправился в лес, дойдя до места, он внимательно огляделся по сторонам и увидел зайца.(Учащиеся с помощью движений и жестов изображают то, что произносит учитель)
— Охотник прицелился, а заяц попытался скрыться от настигающей его, выпущенной из ружья дроби. Проследите глазами путь, который проделал заяц.
— А теперь сильно-сильно зажмурьте глаза и представьте, что произошло дальше.
— Откройте глаза.
— Человек, пришедший в лес, оказался не обычным охотником, а фотоохотником. Результатом его охоты стала фотография зайца.
Вдобавок ко всему, он оказался творческим человеком. Полученную фотографию, он разрезал на части и сделал пазлы для своего ребёнка.
Он передал и вам фотографию.
— Посмотрите внимательно, как охотник разрезал фотографию.
-Давайте её соберём.
-Возьмём 2 части, 3 части, 4 части. Кто назовёт дробь?
4. Закрепление. Самостоятельная работа.
1) Задание №1.
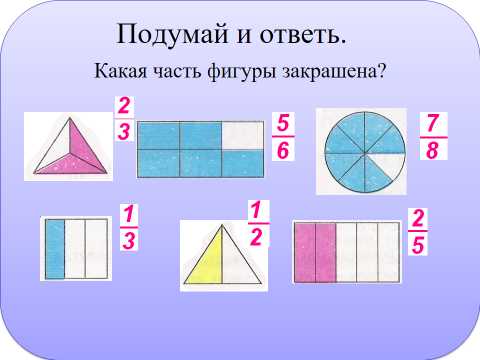
— Я уверена, что вы не «попадёте в дроби», исследуя фигуры на слайде.
Какая часть фигуры закрашена? Запишите соответствующую дробь.
2) Задание № 2.
— А теперь проверим вашу сообразительность. Сыр нужно разделить на 8 частей, сделав только 3 разреза. Попробуйте решить ее, можете посовещаться с соседом. Подготовьтесь для объяснения.
После выступления детей с вариантами решения, проверка по слайду.
— Какая часть сыра осталась на блюде? (половина, ½, 4/8)
3) 4)
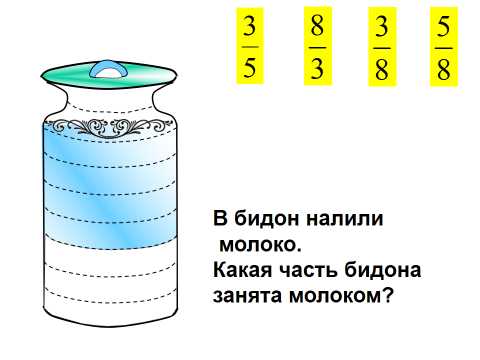
5) 6)
5. Подведение итогов урока. Оценивание.
-Сегодня мы сделали большое дело, открыли новую тему — дверь в один из самых сложных разделов математики. А это могло получиться только у очень дружных ребят.
Доля — это каждая из равных частей одного целого.
Дробь — одну или несколько равных долей целого.
Знаменатель — число, которое показывает, на сколько равных частей разделили предмет или фигуру.
Числитель –число, которое показывает сколько таких частей взяли.
6. Домашнее задание.
Окончен урок, и выполнен план
Спасибо, ребята, огромное вам.
За то, что упорно и дружно трудились
И знания точно уж вам пригодились.
videouroki.net
Повторение по теме: Дроби
ДРОБИ
1
2
- Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел
ЧТО ТАКОЕ ДРОБЬ
ВИДЫ ДРОБЕЙ.
ОБЫКНОВЕННЫЕ,
ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ
СМЕШАННЫЕ
СОСТАВНЫЕ
ДЕСЯТИЧНЫЕ
ОБЫКНОВЕННАЯ ДРОБЬ.
- Обыкновенная (или простая) дробь — запись рационального числа. Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.
ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ.
СМЕШАННАЯ ДРОБЬ.
- Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
СОСТАВНАЯ ДРОБЬ.
- Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт
12
2
14
26
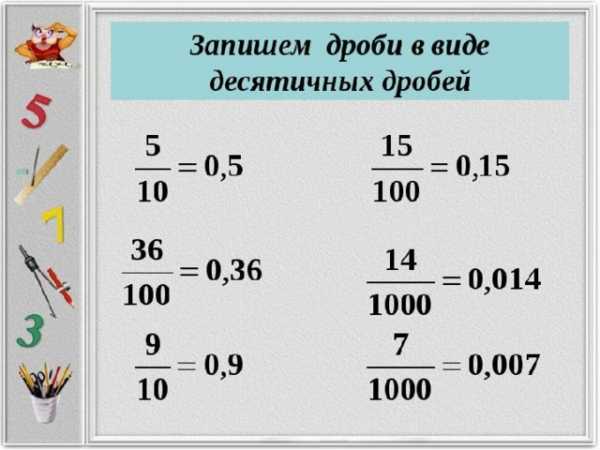
ДЕСЯТИЧНАЯ ДРОБЬ.
- Десятичная дробь — это любая числовая дробь, в знаменателе которой стоит степень десятки.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИИ
- Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ.
- Правило. Чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.
- СПАСИБО ЗА ВНИМАНИЕ
videouroki.net
Урок математики 4 класс на тему «Дроби»
Седовская общеобразовательная школа
Математика
4 класс
Тема урока:
«Ознакомление с дробями»
Подготовила учитель начальных классов
Чекунаева Е.Г.
Тема. Ознакомление с дробями.
Цель: довести до сознания детей как образовываются дроби; показать запись дроби и ознакомить с терминами числитель и знаменатель; развивать логическое мышление, математическую речь, познавательную активность; воспитывать стремление достигать поставленную цель, чувство ответственности, уверенности в себе, умение работать в коллективе.
Тип урока: урок совершенствования знаний и умений
Оборудование: Наглядный материал, карточки, интерактивная доска,
презентация.
Ход урока
І Организационный момент
Создание ситуации успеха.
Девиз урока:
Думать – коллективно
Решать – оперативно
Отвечать – доказательно
Работать – старательно
И это для всех обязательно.
Перед тем, как приступить к работе вспомним, какие правила мы должны соблюдать на уроке? (Учитель выслушивает ответы детей)
ПРАВИЛА:
Слушать.
Слышать друг друга.
Дополнять.
Исправлять, помогать.
ІІ Актуализация опорных знаний
-Вычислив значения выражений и расположив их в порядке возрастания, вы узнаете тему урока:
1. «Мозговой штурм» Устный счет
Р 6300 : 100 : 7 x 9 = 81
О 12000 : 4000 х 7 х 10 = 210
Б 720 : 90 x 10 x 8 = 640
И 90 x 30 : 100 x 1000= 27000
Д 16 x 100 : 10:40 = 4
2. Работа в тетрадях
-Записать число, классная работа, тема урока.
3. Минутка каллиграфии
-Напишите ту цифру, которая у вас меньше всего получается.
4 Технология «Микрофон»
У немцев сохранилась пословица: Попасть в дроби, то есть попасть в трудное положение. Я думаю, что сегодня мы выдержим все испытания и преодолеем все трудности.
О какой дроби пойдет речь? (охотничья дробь, барабанная дробь и обыкновенная дробь)
Какие цели и задачи стоят сегодня перед нами? (Наша задача выяснить- смогут ли дроби поставить нас в затруднительное положение или нет?
ІІІ Изучение нового материала
1.Практическая работа. Работа в парах
— У вас на столах фигуры. Возьмите прямоугольник. Разделите его на 2 части, не пользуясь линейкой и карандашом. (Ученики находят выход: разделить перегибанием.)
— На сколько частей разделили прямоугольник? (На 2 части)
— Заштрихуйте 1 часть.
— Сколько частей не раскрашено?
— Возьмите круг. Разделите его на 4 части, не пользуясь линейкой и карандашом. (Ученики действуют так же).
— Сколько получилось частей? (4 части)
— Закрасьте 1 часть. Какая это часть круга? (четвертая)
— Сколько частей не раскрашено? (3 части)
Дополнительно: Самая известная из долей – это, конечно. Половина. Слова с приставкой “пол” можно услышать часто: полчаса, полкилометра. Разделить целое на две равные части – половина. Долю называют “половина”. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на три части — “треть”. Долю называют “треть”. Если целое разделить на 4 равные части, то получится или по-другому говорят “четверть”. Скажите, когда мы говорим четверть? (Учебная четверть, четверть часа)
2. Объяснение материала учителем.
а)Нахождение долей
(арбуз разделили на 6 долей, 1 доля-…)
б)Вывод: в математике существуют числа, выражающие части единиц счета (измерения). Они называются – дроби.
(Число под чертой показывает на сколько равных частей разделен отрезок.
Число над чертой показывает, сколько таких частей взяли.
3. Игра «Числитель-знаменатель»
Чтобы запомнить, что такое числитель и знаменатель и не путать их поиграем в игру. Если я называю числитель, поднимаем руки вверх — показываем, что он записывается сверху. Если я называю знаменатель, показываем, что он пишется внизу. Если показываю черту дроби, складываем руки горизонтально
4.Игра «Доли»
Найти дробь и щелкнуть по ней мышкой, записать в тетрадь.
-Мы делили апельсин…
5. Работа в группах.
-Какая часть фигуры закрашена ?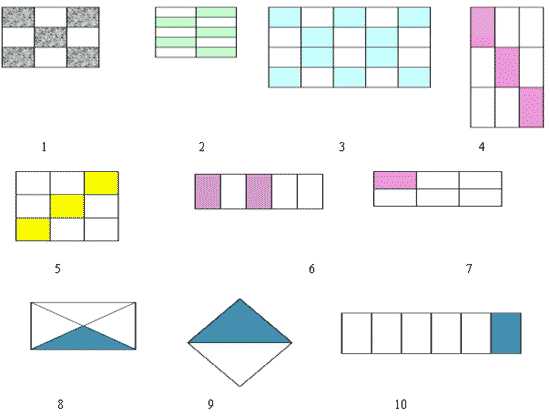
Записать.
6.Решить задачи (устно)
ІV Развитие математических умений учащихся
1.Комментированное решение задачи №662
2.Решение логической задачи
-Как разрезать головку сыра на 8 равных долей, сделав только 3 разреза?
V Рефлексия
Оцените свою работу на уроке. Если вам понравилось, то улыбнитесь, если было трудно и вы что-то не поняли, задайте вопрос.
Каждый из обучающихся произносит продолжение одной из фраз:
На уроке я узнал…
Мне было легко…
Я пока затрудняюсь…
Я узнал новое…
Я понял, мне необходимо поработать над темой.
VІ Домашнее задание
Решить задачи № 664, 665 на стр. 102, выучить правило стр. 101
VІ І Итог урока
— Что мы называем дробью?
— Как записывается дробь?
— Что обозначает дробная черта?
— Как называются числа дроби? Что показывает числитель? Знаменатель дроби?
Спасибо за внимание!
infourok.ru
Основные свойства дробей, с примерами
Если числитель дроби меньше знаменателя, то такая дробь называется правильной, а если числитель больше знаменателя, то неправильной. В неправильной дроби можно выделить целую часть.
Свойства дробей
Сложение и вычитание дробей. Чтобы сложить (вычесть) две дроби с одинаковыми знаменателями нужно сложить (вычесть) их числители:
Чтобы сложить (вычесть) две дроби с разными знаменателями нужно привести их общему знаменателю, а потом сложить числители (вычесть из первого числителя второй):
Умножение и деление дробей. Чтобы умножить две обыкновенные дроби нужно умножить их числители и знаменатели:
Чтобы умножить дробь на число нужно умножить числитель дроби на это число:
Чтобы разделить одну дробь на другую нужно первую дробь умножить на дробь, обратную ко второй:
Сравнение дробей. Чтобы сравнить две дроби, нужно привести их одному знаменателю и сравнить числители. У какой дроби числитель больше та дробь и больше.
Основное свойство дроби. Числитель и знаменатель дроби можно умножать и делить на одно и то же число, при этом величина дроби не изменится:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Этапы урока | Деятельность учителя | Деятельность учащихся | Универсальные учебные действия |
1.Этап мотивации (самоопределения) к учебной деятельности | Здравствуйте, ребята! Сегодня на уроке у нас гости, поэтому наша задача показать какие вы активные, смышленые и сообразительные! Урок мы начнем со слов индийского математика XII века Бхаскары «Искра знаний возгорится в том, кто достигнет понимания собственными силами». СЛАЙД 1
| Приготовили все необходимое к уроку (учебник, дневник, тетрадь, канц.принадл.). Заняли свои места. | Личностные: самоопределение. Коммуникативные: планирование учебного сотрудничества с учителем и сверстникам. |
2.Этап актуализации и пробного учебного действия. | Ребята, я хочу, чтобы вы мне помогли решить задачу: СЛАЙД 2 У Светы было 4 целых яблока, 6 половинок, 8 четвертинок. Сколько яблок у Светы было? Каким числом можно записать целое яблоко? Каким числом можно записать половинку, четвертинку? Каким одним словом можно назвать эти числа? | 1 ½, ¼ Дроби | Познавательные: самостоятельное выделение и формулирование познавательной цели. Регулятивные: целеполагание Логические: формулирование проблемы. |
3.Этап постановки темы урока и учебной цели. | Вам приходилось слышать это слово не один раз и с разными значениями: охотничья дробь, барабанная дробь, обыкновенная дробь. -Как вы думаете, о какой дроби сегодня пойдет речь? Сформулируем тему нашего урока. СЛАЙД 3 ТЕМА Продолжите предложение Сегодня на уроке я хочу научиться… Я хочу повторить… СЛАЙД 4 ПРЕДЛОЖЕНИЯ
| Отвечают: «Обыкновенная дробь» Предложили и согласовали тему урока «Понятие дроби. Обыкновенная дробь» Заканчивают предложения, тем самым формулируют цель, объединив все, получаем «Повторить понятие обыкновенной дроби, запись, чтение и умение изображать на рисунке» | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; Познавательные: самостоятельное выделение и формулирование познавательной цели. Логические: – формулирование проблемы. |
4.Этап открытия «новых» знаний | ПУСТОЙ СЛАЙД 5 У вас на парте лежат полоски: мы с вами проведем небольшой опыт
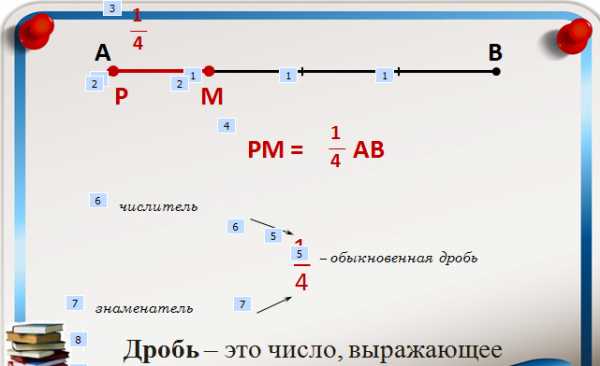
При помощи нашей полоски мы попробуем ответить на вопросы: -Что такое дробь? Как называется черта, которую вы провели? -Что находится над дробной чертой под дробной чертой? -Что показывает числитель, знаменатель? — На какие вопросы отвечает числитель? знаменатель? Вывод: Дробь – это число, выражающее части единицы счета или измерения. СЛАЙД 6 СЛАЙД 7 | дробь Числитель — сколько? Знаменатель — Какая? Каких? Запись дроби Заполняют пропуски | Познавательные: построение логических цепей, анализ, умение структурировать знания Предметные: формирование навыков построения математических моделей и решения практических задач |
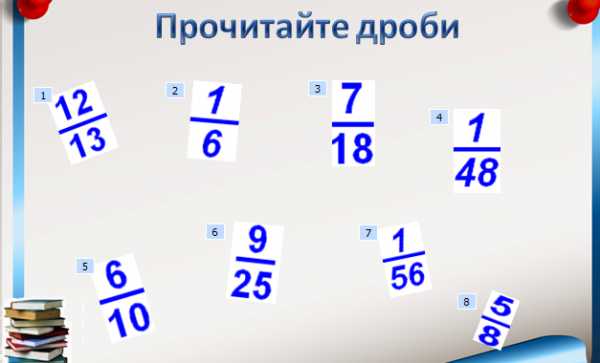
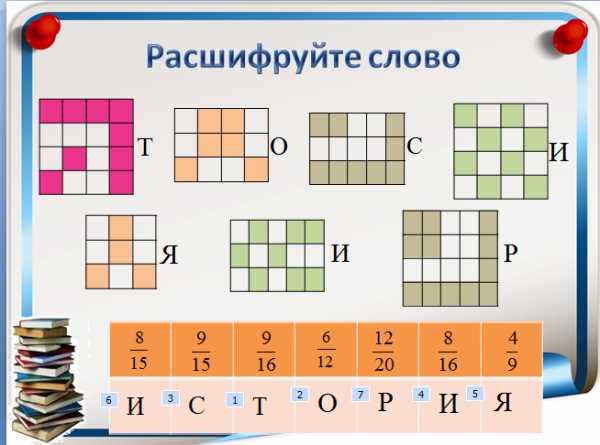
5. Этап первичного закрепления | Прочитайте дроби. СЛАЙД 8 Задания для индивидуального выполнения. На слайде написаны выражения, самостоятельно запишите в тетради дроби. СЛАЙД 9 Расшифруйте слово. На слайде представлены фигуры, определить, какая часть закрашена и заполнить таблицу. СЛАЙД 10 Как вы думаете, почему я зашифровала это слово? Т.к. каждое математическое понятие имеют свою историю возникновения. Историческая справка (с.123). СЛАЙД 11 ФИЗКУЛЬМИНУТКА
СЛАЙД 12 | Читают вслух дроби, называют числитель и знаменатель. Записывают дроби. Меняются тетрадями, проверяют. Разгадывают слово «история». Предлагают свои ответы. Поднимают круг или квадрат. Встают/ не встают. | Регулятивные: уметь планировать и осуществлять деятельность, контроль, оценка, выделение и осознание того, что усвоено, что ещё подлежит усвоению Предметные: развитие представлений о дроби, умение применять изученный материал |
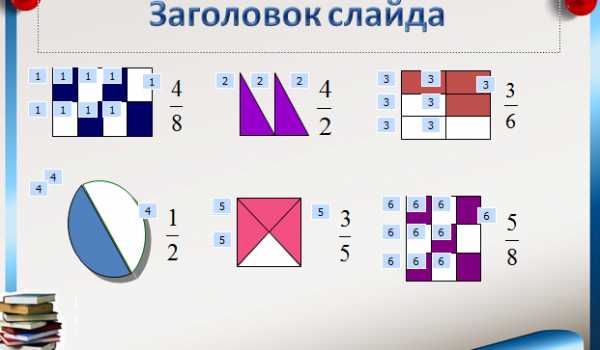
| СЛАЙД 13 СЛАЙД 14 Самостоятельная работа СЛАЙД 15 (ответы) СЛАЙД 16 СЛАЙД 17-22 | Отвечают. Решают с.р. Самопроверка Записывают дз. Дополняют пословицы | Регулятивные: выделение и осознание того, что усвоено, что ещё подлежит усвоению Познавательные: анализ, синтез, обобщение, аналогия, сравнение, классификация и построение логической цепи рассуждений Предметные: формирование навыков построения математических моделей и решения практических задач |
7. Рефлексия учебной деятельности, подведение итогов урока. | Закончите предложения СЛАЙД 23 | Заканчивают предложения. |
videouroki.net
история дробей. История возникновения обыкновенных дробей
Одним из самых сложных разделов математики по сей день считаются дроби. История дробей насчитывает не одно тысячелетие. Умение делить целое на части возникло на территории древнего Египта и Вавилона. С годами усложнялись операции, проделываемые с дробями, менялась форма их записи. У каждого государства древнего мира были свои особенности во «взаимоотношениях» с этим разделом математики.
Что такое дробь?
Когда возникла необходимость делить целое на части без лишних усилий, тогда и появились дроби. История дробей неразрывна связана с решением утилитарных задач. Сам термин «дробь» имеет арабские корни и происходит от слова, обозначающего «ломать, разделять». С древних времен в этом смысле мало что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.
Сегодня различают два способа их записи. Обыкновенные и десятичные дроби возникли в разное время: первые являются более древними.
Пришли из глубины веков
Впервые оперировать дробями начали на территории Египта и Вавилона. Подход математиков двух государств имел значительные отличия. Однако начало и там и там было положено одинаково. Первой дробью стала половина или 1/2. Дальше возникла четверть, треть и так далее. Согласно данным археологических раскопок, история возникновения дробей насчитывает около 5 тысяч лет. Впервые доли числа встречаются в египетских папирусах и на вавилонских глиняных табличках.
Древний Египет
Виды обыкновенных дробей сегодня включают в себя и так называемые египетские. Они представляют собой сумму нескольких слагаемых вида 1/n. Числитель — всегда единица, а знаменатель — натуральное число. Появились такие дроби, как ни трудно догадаться, в древнем Египте. При расчетах все доли старались записывать в виде таких сумм (например, 1/2 + 1/4 + 1/8). Отдельными обозначениями обладали только дроби 2/3 и 3/4, остальные разбивались на слагаемые. Существовали специальные таблицы, в которых доли числа представлялись в виде суммы.
Наиболее древнее из известных упоминаний такой системы встречается в Математическом папирусе Ринда, датируемом началом второго тысячелетия до нашей эры. Он включает таблицу дробей и математические задачи с решениями и ответами, представленными в виде сумм дробей. Египтяне умели складывать, делить и умножать доли числа. Дроби в долине Нила записывались с помощью иероглифов.
Представление доли числа в виде суммы слагаемых вида 1/n, характерное для древнего Египта, использовалось математиками не только этой страны. Вплоть до Средних веков египетские дроби применялись на территории Греции и других государств.
Развитие математики в Вавилоне
Иначе выглядела математика в Вавилонском царстве. История возникновения дробей здесь напрямую связана с особенностями системы счисления, доставшейся древнему государству в наследство от предшественника, шумеро-аккадской цивилизации. Расчетная техника в Вавилоне была удобнее и совершеннее, чем в Египте. Математика в этой стране решала гораздо больший круг задач.
Судить о достижениях вавилонян сегодня можно по сохранившимся глиняным табличкам, заполненным клинописью. Благодаря особенностям материала они дошли до нас в большом количестве. По мнению некоторых ученых, математики в Вавилоне раньше Пифагора открыли известную теорему, что, несомненно, свидетельствует о развитии науки в этом древнем государстве.
Дроби: история дробей в Вавилоне
Система счисления в Вавилоне была шестидесятеричной. Каждый новый разряд отличался от предыдущего на 60. Такая система сохранилась в современном мире для обозначения времени и величин углов. Дроби также были шестидесятеричными. Для записи использовали специальные значки. Как и в Египте, примеры с дробями содержали отдельные символы для обозначения 1/2, 1/3 и 2/3.
Вавилонская система не исчезла вместе с государством. Дробями, написанными в 60-тиричной системе, пользовались античные и арабские астрономы и математики.
Древняя Греция
История обыкновенных дробей мало чем обогатилась в древней Греции. Жители Эллады считали, что математика должна оперировать лишь целыми числами. Поэтому выражения с дробями на страницах древнегреческих трактатов практически не встречались. Однако определенный вклад в этот раздел математики внесли пифагорейцы. Они понимали дроби как отношения или пропорции, а единицу считали также неделимой. Пифагор с учениками построил общую теорию дробей, научился проводить все четыре арифметические операции, а также сравнение дробей путем приведения их к общему знаменателю.
Священная римская империя
Римская система дробей была связана с мерой веса, называемой «асс». Она делилась на 12 долей. 1/12 асса называлась унцией. Для обозначения дробей существовало 18 названий. Приведем некоторые из них:
семис — половина асса;
секстанте — шестая доля асса;
семиунция — пол-унции или 1/24 асса.
Неудобство такой системы заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100. Римские математики преодолели трудность с помощью использования процентов.
Написание обыкновенных дробей
В Античности дроби уже писали знакомым нам образом: одно число над другим. Однако было одно существенное отличие. Числитель располагался под знаменателем. Впервые так писать дроби начали в древней Индии. Современный нам способ стали использовать арабы. Но никто из названных народов не применял горизонтальную черту для разделения числителя и знаменателя. Впервые она появляется в трудах Леонардо Пизанского, более известного как Фибоначчи, в 1202 году.
Китай
Если история возникновения обыкновенных дробей началась в Египте, то десятичные впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.
В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже.
Аль-Каши из Самарканда
Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.
Десятичные дроби в Европе
Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Франсуа Виет. Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта.
Однако это были лишь частные случаи научного использования. Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.
Точка, точка, запятая
Стевин также не пользовался запятой. Он отделял две части дроби при помощи нуля, обведенного в круг.
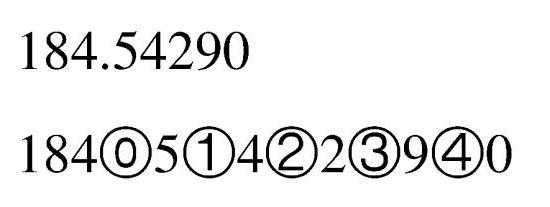Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом.Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1616-1617 гг. Запятой пользовался и немецкий ученый Иоганн Кеплер.
Дроби на Руси
На русской земле первым математиком, изложившим деление целого на части, стал новгородский монах Кирик. В 1136 году он написал труд, в котором изложил метод «счисления лет». Кирик занимался вопросами хронологии и календаря. В своем труде он привел в том числе и деление часа на части: пятые, двадцать пятые и так далее доли.
Деление целого на части применялось при расчете размера налога в XV-XVII веках. Использовались операции сложения, вычитания, деления и умножения с дробными частями.
Само слово «дробь» появилось на Руси в VIII веке. Оно произошло от глагола «дробить, разделять на части». Для названия дробей наши предки использовали специальные слова. Например, 1/2 обозначалась как половина или полтина, 1/4 — четь, 1/8 — полчеть, 1/16 — полполчеть и так далее.
Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения.
Сегодня по-прежнему в числе самых сложных разделов математики называются дроби. История дробей также не была простой. Разные народы иногда независимо друг от друга, а иногда заимствуя опыт предшественников, пришли к необходимости введения, освоения и применения долей числа. Всегда учение о дробях вырастало из практических наблюдений и благодаря насущным проблемам. Необходимо было делить хлеб, размечать равные участки земли, высчитывать налоги, измерять время и так далее. Особенности применения дробей и математических операций с ними зависели от системы счисления в государстве и от общего уровня развития математики. Так или иначе, преодолев не одну тысячу лет, раздел алгебры, посвященный долям чисел, сформировался, развился и с успехом используется сегодня для самых разных нужд как практического характера, так и теоретического.
fb.ru
Обыкновенные дроби
Основные понятия и определения, которые понадобятся при изучении раздела «обыкновенные дроби», вы также сможете найти здесь: делители и кратные, обыкновенные (простые) дроби, сложение и вычитание обыкновенных дробей, умножение и деление обыкновенных дробей. Знания, полученные из интерактивных уроков, можно развить и закрепить при помощи тренажёров, количество заданий в которых не ограничено. Большое количество разнообразных тестов и задач, анимированные герои и занимательная форма подачи материала способствуют качественному усвоению знаний. |
|||
|
Демонстрационный урок «Делители и кратные» |
Демонстрационная самостоятельная работа |
||
В серии «Обыкновенные дроби» представлены следующие темы:
Первая часть каждого из уроков представляет собой объяснение нового материала с использованием различных примеров и игровых ситуаций.
Целью второй части урока является проверка того, насколько хорошо усвоена новая тема.
Для всех уроков, кроме уроков по решению задач, существуют специальные тренажеры. В них примеры генерируются «на лету», поэтому количество заданий неограниченно. При решении заданий тренажера производится не только проверка: «Правильно»/«Неправильно», но и анализируются ошибки, сделанные ребенком. При завершении работы с тренажером на экране появляется текст, помогающий понять свои слабые места и исправить сделанные ошибки.
Демонстрационный ролик
О наших уроках
Наши уроки серии «Обыкновенные дроби» — простой и увлекательный способ усвоения темы «Простые дроби» по математике (4 класс, 5 класс, 6 класс). Игровая форма подачи материала и красочные герои понравятся ребёнку и превратят уроки по Обыкновенным дробям в увлекательную игру!
Предлагаемые уроки и тренажёры включают весь материал школьной программы по обыкновенным дробям. Перечень уроков с рассмотренными темами:
Урок 1. Делители и кратные. Разложение на простые множители
- Делители и кратные
- Простые и составные числа
- Разложение на простые множители
Урок 2. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное
- Наибольший общий делитель (НОД)
- Взаимно простые числа
- Наибольшее общее кратное (НОК)
Урок 3. Основное свойство дробей и правило сокращения дробей
- Обыкновенные дроби
- Основное свойство дробей
- Сокращение дробей
Урок 4. Приведение дробей к общему знаменателю. Сравнение дробей
- Приведение дробей к общему знаменателю
- Сравнение дробей
Урок 5. Сложение и вычитание дробей с разными знаменателями
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание дробей с разными знаменателями
Урок 6. Смешанные числа. Сложение и вычитание смешанных чисел
- Смешанные числа
- Сложение и вычитание смешанных чисел
Урок 7. Умножение и деление обыкновенных дробей
- Умножение дробей на число
- Умножение дроби на дробь
- Деление дроби на число
- Деление дробей на дробь
Урок 8. Задачи. Нахождение долей
Урок посвящён объяснению решения задач на нахождение долей.
Урок 9. Задачи. Нахождение дроби от числа
Урок посвящён объяснению решения задач на нахождение дроби от числа.
Урок 10. Задачи. Нахождение числа по его дроби
Урок посвящён объяснению решения задач на нахождение числа по его дроби.
Планируется выпуск уроков по темам:
- Перевод обыкновенных дробей в десятичные
- Перевод десятичных дробей в обыкновенные
После изучения нового материала по Обыкновенным дробям необходимо закрепить полученные знания на практике. Поэтому мы предлагаем специальные тренажёры, которые предусмотрены для всех уроков. Перечень тренажёров к урокам:
- Тренажёр 1. Делители и кратные. Разложение на простые множители
- Тренажёр 2. Наибольший общий делитель. Взаимно простые числа
- Тренажёр 3. Основное свойство дробей и правило сокращения дробей
- Тренажёр 4. Приведение дробей к общему знаменателю. Сравнение дробей
- Тренажёр 5. Сложение и вычитание дробей с разными знаменателям
- Тренажёр 6. Смешанные числа. Сложение и вычитание смешанных чисел
- Тренажёр 7. Умножение и деление обыкновенных дробей
Количество заданий в тренажёрах неограниченно. При решении заданий анализируются ошибки, сделанные ребёнком. Сочетание обучающих уроков и тренажёров к урокам способствуют качественному усвоению знаний. Наши тренажёры — отличный тест, который поможет ребёнку закрепить тему «Обыкновенные дроби».
На нашем сайте Вы можете скачать уроки «Обыкновенные дроби» (демо-версии), а также купить полную серию уроков. Наши интерактивные уроки — лёгкий и быстрый способ понять тему по обыкновенным дробям.
Учителям на заметку
Интересные игры на уроках математики по теме «Обыкновенные дроби»
Во всех представленных играх ученики делятся на 3 команды (Например, по рядам).
Разминка перед играми
Учитель выдаёт на каждую команду коробку, в которой находятся два кружка синего и жёлтого цвета. Синий круг разделён на 12 равных частей, а жёлтый – на 6 равных частей. По розданному материалу учитель задаёт несколько вопросов:
- На сколько частей разделёны синий и жёлтый кружки?
- Соберите из частей кружки одинакового цвета.
- Какую часть синего кружка составляют 1/6 доли? Определить, какую часть жёлтого кружка составляют его 4/8 доли.
- Найдите 1/4 часть синего кружка и 2/3 части жёлтого кружка и сравните полученные доли. (результат ученики записывают в тетради, а учитель на доске).
- Что вы можете сказать о числах 2/3, 1/4, 2/6 и 3/12?
Игра «Солнышко»
На лучах солнышка записываются дроби, которые нужно складывать, вычитать, перемножать или делить с числом, записанным на солнышке. Команды учеников по очереди решают данные примеры и говорят ответ учителю. Правильный ответ приносит команде очко. Солнышко можно представить в таком виде:
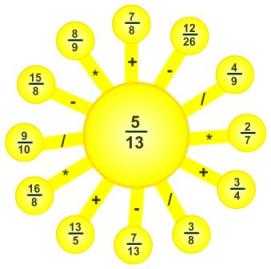
Игра «Отгадай число»
Учитель загадывает любое дробное число. Команды учеников по очереди задают вопросы учителю, чтобы отгадать, какое число он задумал. Учитель может отвечать только: «Да», «Нет», «Не могу ответить».
Ученики задают вопросы следующего характера:
- Это обыкновенная дробь?
- В этом числе есть цифра ___?
- Числитель этой дроби делится на ___?
- Можно ли сократить эту дробь?
Игра «Самый быстрый»
Учитель озвучивает ученикам одно задание. Отвечает тот ученик, который первым поднимет руку. Если его ответ правильный, то ученик приносит своей команде очко.
Примеры заданий:
- Задание 1: Сравните дроби
- Задание 2: Назовите дроби в порядке возрастания
- Задание 3: Выделите целую часть из неправильных дробей
- Задание 4: Представить дробные числа в виде неправильных дробей
- Задание 5: Решите уравнения с дробями
Игра «Цветик-семицветик»
На каждом лепестке цветика-семицветика написано по одному вопросу. Представитель команды выбирает один лепесточек и отвечает на вопрос, написанный на нём. Если ответ ученика правильный, то ученик приносит очко своей команде. Каждая команда учеников должна ответить на 3 вопроса.
Примеры вопросов на лепесточках:
- Что показывают знаменатель и числитель дроби?
- Какая дробь называется правильной?
- Какая дробь равна единице?
- Какая дробь больше единицы?
- Как выделить целую часть из неправильных дробей?
- Какая их двух дробей с равными знаменателями меньше?
- Какая дробь называется неправильной?
- Какое из двух чисел с одинаковыми знаменателями больше?
- Как перевести десятичную дробь в обыкновенную?
- Как из одной дроби вычесть другую, если знаменатели одинаковые?
- Как сложить дроби с одинаковыми знаменателями?
- Дроби какого вида называются основными, единичными дробями?
Игра «Счетовод»
Ученики выбирают дома по 5-6 примеров по теме «Обыкновенные дроби» для устного счёта. Каждая команда выдвигает ученика, который будет защищать честь своей команды (назовем его счетовод). Ученики из других команд задают подобранные дома примеры счетоводу до тех пор, пока он не ошибется. После него выступает счетовод из другой команды. Побеждает команда, в которой счетовод решил наибольшее количество примеров правильно.
Игра «Дробная схватка»
На листочках записаны дроби 1/1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, 4/4, 1/5, 2/5, 3/5, 4/5, 5/5, 1/6, 2/6, 3/6, 4/6, 5/6, 6/6, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 8/8, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 9/9, 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 10/10, 1/12, 2/12, 3/12, 4/12, 5/12, 6/12, 7/12, 8/12, 9/12, 10/12, 11/12, 12/12.
Учитель перемешивает листочки и кладет их в две стопки так, чтобы сторона с дробями была снизу. Ученики по очереди открывают верхние листочки и сравнивают выпавшие дроби. Ученик, на чьем листочке дробь оказалась большей, забирает обе карточки. Если выпали равные дроби, начинается «дробная схватка»: каждый ученик выкладывает в ряд три листочка лицевой стороной вниз, а четвертый листочек – лицевой стороной вверх. Тот ученик, на чьем листочке выпадает большая дробь, забирает все восемь листочков и листочки, с которых началась схватка. Когда игра закончилась,ученики подсчитывают количество выигранных листочков. Побеждает тот ученик, у которого листочков оказалось больше.
Интересные задачи по дробям
Задача 1. Длина прямоугольника 4/5 дм, его ширина составляет 2/3 его длины. Найдите площадь данного прямоугольника.
Задача 2. Сколько километров проедет велосипедист за 1 5/12 ч, если его скорость составит 9 3/5 км/ч?
Задача 3. За 1 ч автоматическая линия производит 11/25 ц пластмассы. Сколько пластмассы линия производит за 3/4 ч?
Задача 4. В бидоне 3/2 л молока. Сколько молока в 5 таких бидонах?
Задача 5. Дети убрали 3/4 площади квартиры, что составляет 30 квадратных метров. Необходимо найти площадь всей квартиры.
Задача 6. Взрослый билет на электричку стоит 104 рубля. Школьный билет составляет 1/4 стоимости взрослого билета. Найдите стоимость школьного билета.
Задача 7. Храбрый рыцарь боится заболеть, поэтому всегда возит с собой 56 бутылочек с лекарством от ангины. Как-то раз его конь споткнулся, и 3/4 всех бутылочек пролилось. Сколько осталось полных бутылочек?
Задача 8. Сыну 8 лет, его возраст составляет 2/9 возраста отца. А возраст отца составляет 6/10 возраста дедушки. Сколько лет дедушке?
Задача 9. Двое учеников играли в шашки 3 часа. Сколько времени играл каждый ученик?
Задача 10. В клетке сидели 3 цыпленка, 3 мальчика попросили дать им по 1 цыпленку. Их желание было исполнено и каждому из них досталось по 1 цыпленку, а в клетке остался 1 цыпленок. Как такое могло произойти?
Задача 11. Весёлый клоун, чтобы рассмешить детей придумал, что рост у него 9/5000 км, а вес 2/25 т. Дети рассмеялась — они поняли, что весельчак подобрал не те единицы массы и длины. Каков на самом деле рост весельчака в см и каков его вес в кг? (Ответ: 180 см, 80 кг)
Задача 12. Весёлый клоун предложил кому-нибудь из детей сыграть с ним в следующую игру. Клоун называет дробь. Ребёнок называет меньшую дробь. Затем весельчак придумывает еще меньшую дробь, ребенок – еще меньшую и так далее. Побеждает тот, кто назовет дробь, меньше которой дробей уже нет. Как можно победить в такой игре и возможно ли это вообще?
yroki.com