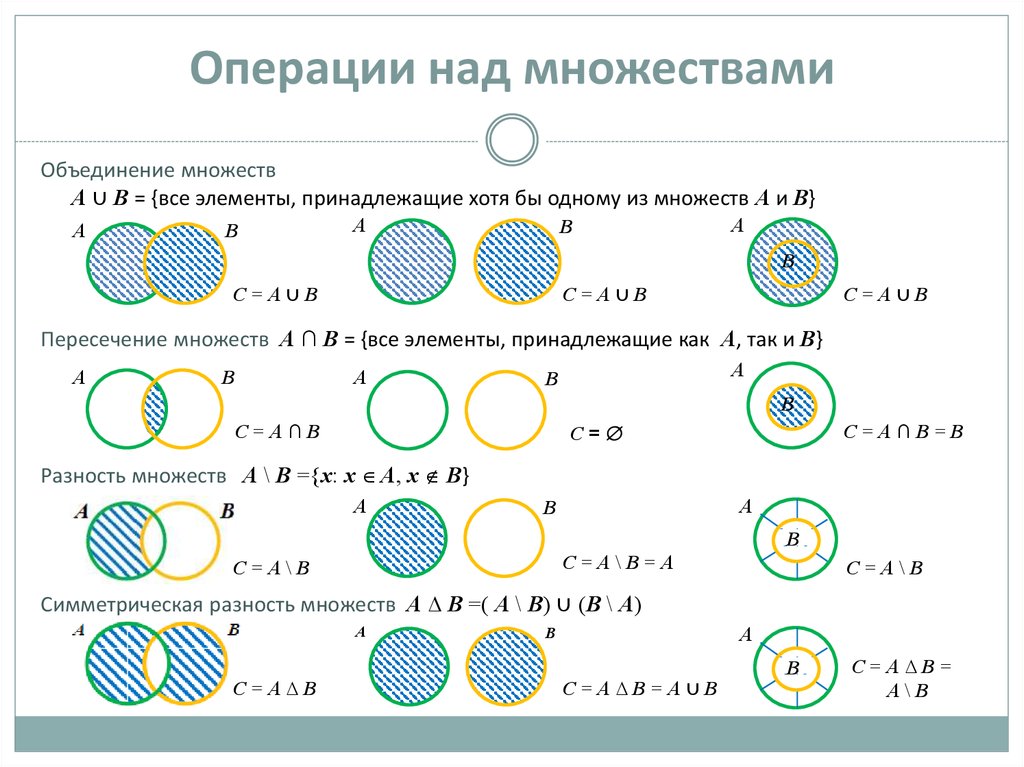
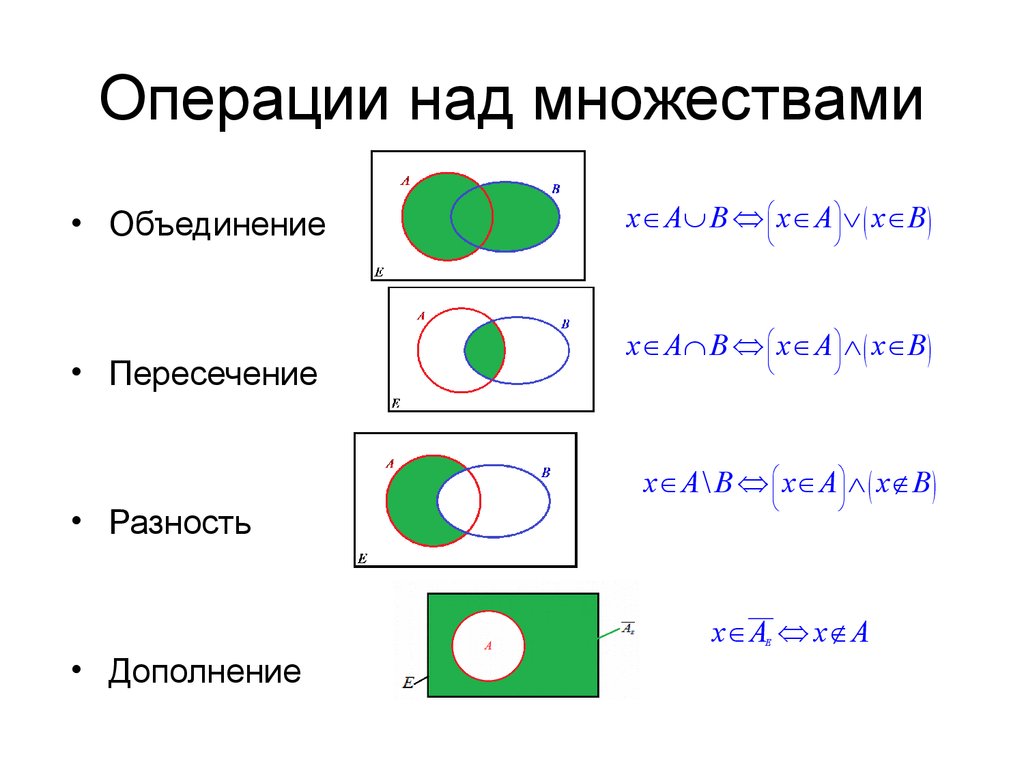
Подборка по базе: КЛАССИЧЕСКИЕ ОПЕРАЦИИ БАНКОВ И ПРЕДПРИЯТИЙ С ВЕКСЕЛЯМИ.doc, Расчетно кассовые операции.docx, ПРАКТИЧЕСКАЯ РАБОТА № 2 Арифметические операции в сист. счислени, Банковские операции.Косырев.docx, Доходность финансовой операции.pptx, Реабилитация больных после операции на кишечнике по поводу добро, Тема 1.2.5. Логистические операции.pptx, Лекция 2.48 Монтаж зубчатых передач. Подготовительные операции п, Карточки множества..docx, 7 дарис после операции.docx МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ Государственное бюджетное профессиональное образовательное учреждение Московской области «Красногорский колледж» Специальность 09.02.03 «ПРОГРАММИРОВАНИЕ В КОМПЬЮТЕРНЫХ СИСТЕМАХ» РЕФЕРАТ По на тему: «Множества. Операции над множествами» Студент, группа 36.1Пд-15К _______________________ / Кузнецов Г.М./ ( подпись) (ФИО) « ___ » ____________ 2018 г. Преподаватель ________________________/ Ускова С.В./ ( подпись) (ФИО) « ___ » ____________ 2018 г. г. Красногорск, 2018 год Включение и равенство множеств Диаграммы Эйлера-Венна Операции над множествами а) Объединение множеств б) Пересечение множеств в) Разность множеств Дополнение множества Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством. Примеры множеств:
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое».  И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами, а элементы множества ? малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А. Например, пусть N–множество натуральных чисел. Тогда 5N , но N, N. Если А — множество корней уравнения х2-5х+6=0, то 3 А, а 4А. В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения: N- множество всех натуральных чисел; Z- множество всех целых чисел; Q- множество всех рациональных чисел; R- множество всех действительных чисел. Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел. Способы задания множества
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d ,обозначают с помощью фигурных скобок: А={a; b; c; …;d} . 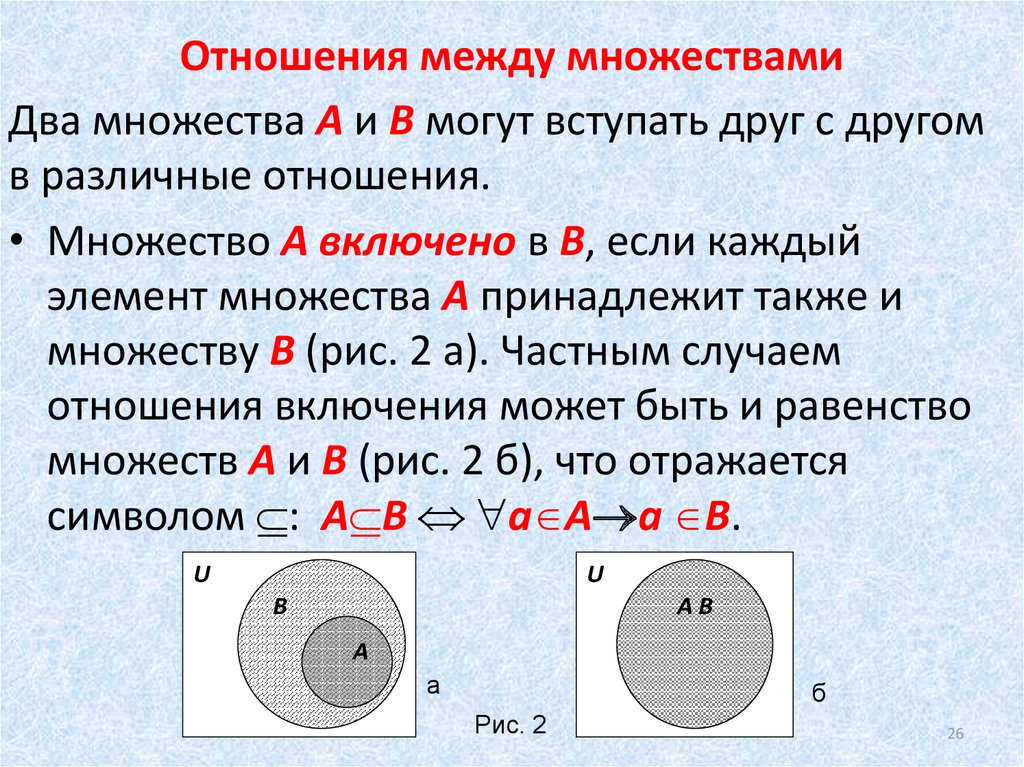 Множество корней уравнения х2Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2-5х+6=0}. Решив уравнение х2-5х+6=0, мы можем записать множество А первым способом: А={2; 3}. Другой пример: Х={х | -1 ? х Z}, т.е. Х есть множество целых чисел х, таких, что –1 ? х Рассмотрим и такой пример: F={f | ?fґ(x)?? 1 , 1 Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А — пустое (не содержит ни одного элемента) и пишут: А= Ш. Например, А={х | хІ+9=0, хR} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т. Включение и равенство множеств Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Если Х У, но Х? У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U . Диаграммы Эйлера-Венна С помощью такой диаграммы становиться наглядным, например, такое утверждение: Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому А С. Операции над множествами Объединение множеств Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В. Символическая запись этого определения: А В={х | хА или хВ}. Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз). Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна: На диаграмме объединение множеств А и В выделено штриховкой. Если множество А определяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х), то А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств. Примеры объединений двух множеств: 1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}. 2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] . 3) Пусть А= {х | х=8k, k Z}, B={x | x=8n-4, n Z}. Тогда A B ={x | 4m, mZ}. Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество А Объединением системы множеств {Аα} называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются. Таким образом, элемент х тогда и только тогда, когда найдется такой индекс α 0 М, что х A α0 . В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись Если M=N, то имеем объединение последовательности множеств . Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда = [0;2). Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1 A2 = A2 А1, и ассоциативна, т.е. (А1 A2) А3 = А1 (A2 А3). Пересечение множеств Пересечением А ? В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В. Символическая запись этого определения: А ? В={х | х А и х В}. Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна: А ? В На диаграмме пересечение множеств А и В выделено штриховкой. Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ? В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х). Примеры пересечений двух множеств:
Операцию пересечения можно определить и для произвольной системы множеств {Аα}, где α М. Пересечением системы множеств {Аα}, называется множество , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α М, т.е. = {x | x Аα для каждого α М}. В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись . Если M=N, то имеем пересечение последовательности множеств . В рассмотренном выше примере системы множеств Аα =[0; α], αМ =(1; 2) получим:=[0;1]. Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т. Разность множеств Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е. На диаграмме разность А\В выделена штриховкой. Примеры разностей множеств:
На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА: |
Тогда А ? В= [-1/4; 3/2].
е. А1?A2 = A2 ?А1 и (А1?A2)?А3= А1?(A2 ? А3).
Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.ТЕМА №1. Множества и операции над ними — Студопедия
Поделись
§1. Основные понятия о множествах.
1.1. Основные определения.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству.
Примеры:
1. Множество студентов данной учебной группы.
2. Множество планет солнечной системы.
3. Множество букв русского алфавита.
4. Множество натуральных чисел.
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.
Остановимся на символике, обычно использующейся при обращении с множествами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C,…,X,Y,…,A1,B1,…
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c,…,x,y,…,a1,b1,…
В математике особую роль играют множества, элементами которых являются числа.
Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
N – множество всех натуральных чисел;
Zc (или Z+ или C+) – множество всех целых неотрицательных чисел;
Z (или C) – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R+ — множество всех действительных положительных чисел.
По числу элементов, входящих в множество, множества делятся на три класса:
1 – конечные, 2 – бесконечные, 3 – пустые.
1. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ.
Пример 1.
Множество гласных букв в слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т.е. элементы множества при перечислении не повторяются.
2. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ.
Пример 2.
Множество натуральных чисел бесконечно.
Пример 3.
Множество точек отрезка [0;1] бесконечно.
3. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком Æ.
Пример 4.
Множество действительных корней уравнения x2 +1=0.
Пример 5.
Множество людей, проживающих на Солнце.
В математике часто приходится определять принадлежность данного элемента конкретному множеству.
Пример 6.
Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически принадлежность множеству записывается с помощью знака Î. В данном случае символическая запись будет такой: 5 Î N. Читается: “5 принадлежит множеству натуральных чисел”.
Число 5,2 не принадлежит множеству натуральных чисел, т.к. не является натуральным числом.
Символически отношение “не принадлежит” записывается с помощью знака (реже Ï). Таким образом, здесь имеем: 5,2 Ï N
Читается: “5,2 не принадлежит множеству натуральных чисел”.
Операции над множествами: формулы, свойства, примеры и упражнения
В этой статье
Что такое операции над множествами?
Набор операций и диаграммы Венна
4 Набор операций
Свойства операций над множествами
Дополнительные термины для теории множеств и операций с множествами
Практика работы с наборами
Что такое набор операций?
Операции над множествами описывают отношения между двумя или более множествами. В математике множество — это просто набор объектов.
Эти объекты (более часто называемые элементами) могут принимать множество форм, такие как:
Числа
Буквы
Переменные
Наиболее распространенные операции над множествами:
Набор операций и диаграмм Венна
Мы часто представляем операции над множествами с помощью диаграмм Венна.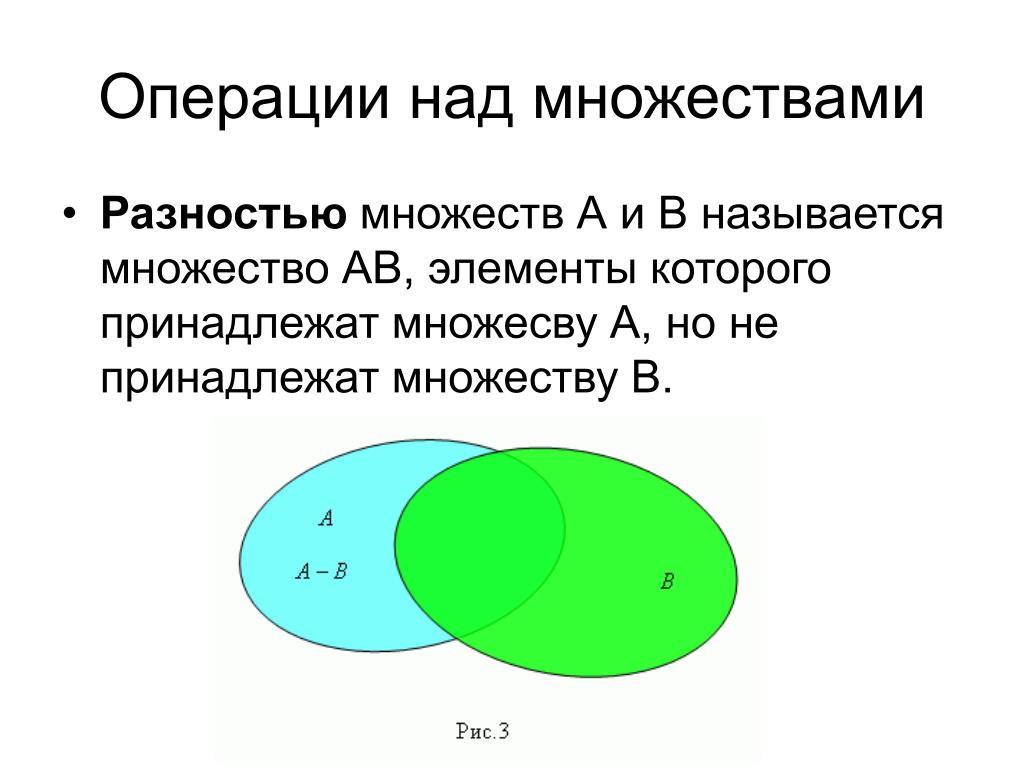
На диаграмме Венна каждый набор представляет кружок. Связь между наборами визуально передается степенью, в которой каждый круг перекрывается другим. Перекрывающиеся разделы представляют элементы, которые существуют в обоих наборах.
4 Набор операций
Используя диаграммы Венна, давайте рассмотрим каждую из основных операций над множествами.
1. Союз (А∪В)
Объединение двух наборов, A и B, представляет собой набор различных элементов, которые находятся в наборе A, наборе B или в обоих наборах A и B.
На диаграмме Венна объединение множества A и множества B представлено областью, отличной от множества A, плюс область, отличная от множества B, плюс перекрывающаяся часть, принадлежащая обоим множествам.
Пример :Если A = {1, 2, 3, 4, 5} и B = {3, 4, 5, 6}, объединение множества A и множества B, A∪B = {1 , 2, 3, 4, 5, 6}.
2. Перекресток (A∩B)
Пересечение двух множеств, А и В, — это множество элементов, которые входят в ОБА Множества А и В.
На диаграмме Венна пересечение — это часть, в которой два множества перекрываются.
Если A = {2, 4, 6, 8, 10} и B = {3, 6, 9, 12, 15}, пересечение множества A и множества B, A ∩ B = {6}.
3. Разница (А-Б)
Разность двух наборов, A-B, представляет собой набор элементов, уникальных для набора A. Другими словами, разность включает в себя элементы, которые есть только в наборе A и не входят в набор B. 9в Ас).
Дополнением к набору, Set A, являются элементы данного универсального набора, Set U, которые не входят в Set A. Универсальный набор — это набор, содержащий все заданные объекты.
Свойства операций над множествами
Точно так же, как основные математические операции (+, -,÷,×) имеют определенные свойства, операции над множествами также имеют определенные свойства. Вот некоторые из них.
1. Коммунативное право
Закон перестановочности для множеств аналогичен переместительному свойству основных математических операций, таких как сложение и умножение.
Точно так же, как 3+4 равно 4+3, объединение (или пересечение) множества A и множества B равно объединению (или пересечению) множества B и множества A.
2. Ассоциативный закон
Ассоциативный закон для множеств подобен ассоциативному свойству для основных математических операций. Как и 3+(4+5) = (3+4)+5, ассоциативный закон для операций над множествами гласит, что при нахождении объединения или пересечения трех множеств группировка (или ассоциация) между множествами не влияет на результат. .
The union between Sets A, B, and C is не зависит от группировки (или ассоциации) наборов.
3. Распределительный закон
Закон дистрибутивности для объединений гласит, что объединение множества A и пересечения множеств B и C равно пересечению объединения множеств A и B и объединения множеств A и C.
Закон распределения для пересечений гласит что пересечение между множеством A и объединением множеств B и C равно объединению между пересечением множеств A и B и пересечением множеств A и C.
Это похоже на распределительный закон для умножения, который гласит , например, что 2(3+4) = (2×3)+(2×4).
Закон Де Моргана состоит из двух частей. Первая утверждает, что дополнение объединения двух множеств, A и B, равно пересечению дополнения A и дополнения B. Вторая часть утверждает, что дополнение пересечения двух множеств, A и B , равно объединению дополнения A и дополнения B 9cAc∪Bc
5. Идемпотентное свойство
Свойство идемпотента утверждает, что объединение множества с самим собой просто равно множеству. Точно так же пересечение между набором и самим собой равно набору.
Additional Terms for Set Theory and Set Operations
Вот некоторые другие ключевые термины, с которыми вы можете столкнуться при изучении теории множеств и операций над множествами:
Пустой набор — Пустой набор — это набор, не содержащий элементов.
Одиночка — Одиночка (или набор единиц измерения) содержит только один элемент.
Конечное множество — Конечное множество — это множество, состоящее из счетного числа элементов.
Бесконечный набор — Бесконечное множество — это множество с неограниченным количеством элементов.
Общие элементы — Общие элементы — это элементы, общие для обоих наборов. Это элементы на пересечении множеств.
Подмножества — Набор A является подмножеством другого набора B, если все элементы в A также находятся в B.
Непересекающиеся множества — Два множества A и B называются непересекающимися, если они не имеют общих элементов.
Симметричная разность — Симметричная разность двух множеств, A и B, представляет собой множество всех элементов в A или B, но не на пересечении A и B.
Практический набор операций
Проверьте свое понимание операций над множествами с помощью этих пяти упражнений. Вы можете проверить свои ответы в конце.
Упражнение 1
Найдите объединение множества A и множества B, A ∪ B.
A = {синий, фиолетовый, оранжевый, желтый, серый}
B= {синий, зеленый, розовый, черный}
Упражнение 2
Найдите пересечение множества A и множества B, A ∩ B.
А = {25, 30, 35, 40}
В= {23, 24, 25, 26, 27, 28, 29, 30}
Упражнение 3
Найдите разницу наборов А и Б, А-Б.
А = {-1, 0, 3, 5}
В= {1, 2, 3, 4, 7, 12}
Упражнение 4 9cAc.
U = {Skittles, Kit Kat, Snickers, Starbursts, Smarties, Warheads, Reese’s}
A = {Кит Кэт, Сникерс, Риз}
Упражнение 5
Сопоставьте каждое свойство набора с соответствующим уравнением.
Ассоциативный закон пересечений ____
Коммутативное право союзов ____
Распределительный закон пересечения ____
Закон союзов Де Моргана ____ 9cAc = {Кегли, Старбёрстс, Смартиз, Боеголовки}
С, Д, Ф, Соль, Дж
Узнайте об отмеченных наградами курсах Outlier For-Credit - логика
- мягкий вопрос
- теория множеств
Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.
Ознакомьтесь с этими связанными курсами:
Введение в статистику
Изучите курс
Введение в статистику
Как данные описывают наш мир.
Изучить курс
Введение в микроэкономику
Изучить курс
Введение в микроэкономику
Почему маленькие решения имеют большое влияние.
Изучить курс
Введение в макроэкономику
Изучить курс
Введение в макроэкономику
Как деньги движут нашим миром.
Изучить курс
Введение в психологию
Изучить курс
Введение в психологию
Наука о разуме.
Изучить курс
логика — Какова интуиция, почему вся математика может быть разработана с использованием теории множеств?
$\begingroup$
Я узнал, что формальный язык чистой теории множеств позволяет формализовать все математические понятия и аргументы. В языке есть только один нелогический символ (!) «принадлежит отношению», это очень меня удивляет, есть ли какая-то интуиция, почему это так? Я имею в виду, что удивительно, что в математике есть такой простой «кирпичик».
Обратите внимание, что я спрашиваю почему (например, почему это интуитивно), а не как [я знаю как]
$\endgroup$
12
$\begingroup$
В большинстве областей математики вы можете описать интересующие вас объекты как упорядоченные $n$-кортежи, где первый элемент кортежа будет набором, а остальные элементы будут операциями, отношениями и т. д. Например, группа определяется как пара $(G,*)$, где $*$ — операция, удовлетворяющая некоторым аксиомам. Или $(X,d)$ называется метрическим пространством, если $d: X\times X \rightarrow \mathbb{R}_{\leq 0}$ удовлетворяет симметрии, равенству треугольников и разделимости точек. Этот список можно продолжить, но поскольку я могу определить большинство объектов в математике таким образом, это означает, что можно говорить о большей части математики, просто имея возможность выполнять основные операции над множествами (объединение, пересечение, декартово произведение, степенное множество.
.. ) и имеют основные числовые наборы ($\mathbb{N}$,$\mathbb{Z}$,$\mathbb{Q}$,$\mathbb{R}$,$\mathbb{C}$). Но все числовые множества можно определить с помощью основных операций над множествами, начиная с $\mathbb{N}$. Определение числовых множеств от «более простых» было проектом, выполненным задолго до введения аксиоматической теории множеств. У нас то что в начале 19Гамильтон формализует комплексные числа, начиная с вещественных. Во второй половине 19 века вы видите различные попытки формализовать множество действительных чисел. Двумя наиболее известными конструкциями являются классы эквивалентности последовательностей Коши рациональных чисел, которые были сделаны Кантором, а вторая — это множество разрезов Дедекинда. Если вы наблюдаете за этими конструкциями, вы заметите, что используете простые операции теории множеств для их определения. Построение рациональных чисел из целых чисел является случаем более общего понятия поля частных области целостности, которое само по себе является частным случаем локализации.