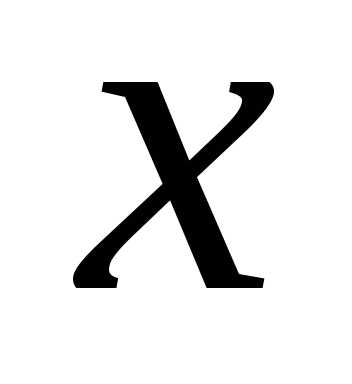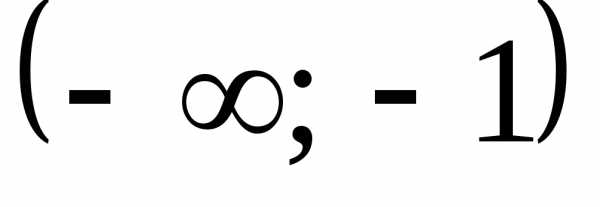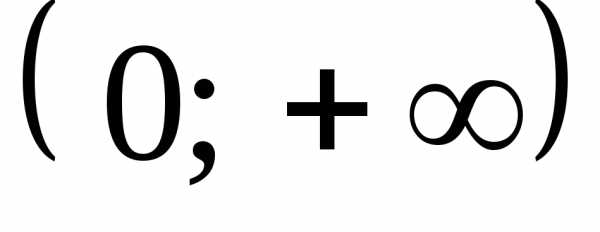Интервалы возрастания/убывания
возрастает на всей области определения
8. Наибольшее/наименьшее значение функции
— не существует.
График функции
(рис 11).
7. Свойства функции и её график
Рассмотрим окружность с центром, расположенным в начале координат, и радиусом, равным единице (это так называемая тригонометрическая окружность).
Для любогодействительного числа можно провести радиус ON этой окружности, образующий с осью угол, радианная мера которого равна числу (положительным считается направление поворота против хода часовой стрелки). (рис 5)
О. Число, равное ординате конца единичного радиуса, задающего угол , называется синусом
Т.к. каждому значению величины угла на тригонометрической окружности соответствует единственная точка , такая, что радиус ON образует угол с осью , то данное определение задает функцию .
Свойства:
1. Область определения функции: .
Т.к. для любого значения угла однозначно определена точка, являющаяся концом соответствующего радиуса, то область определения функции : .
2. Множество значений функции:
Теорема.
Множеством значений функции является промежуток
Доказательство:
Действительно, ордината всякой точки, являющейся концом радиуса тригонометрической окружности, может принимать лишь значения из отрезка .
С другой стороны, для значения ординаты из этого отрезка можно указать хотя бы одну точку на окружности, имеющую эту ординату.
Следовательно, это значение будет синусом угла, образованного положительным направлением оси и радиусом, соединяющим центр окружности и построенную точку.
3. Периодичность:
Наименьший положительный период функции равен
Доказательство:
Т.к. центральный угол, соответствующий полной окружности, равен , то точки, соответствующие углам изображаются на тригонометрической окружности одной и той же точкой, следовательно, синусы этих углов равны.
Это означает, что число является периодом рассматриваемой функции.
Докажем, что — наименьший положительный период.
Рассмотрим значение функции , равное 1. Оно достигается только при . Значит, никакое число, меньшее , не может быть периодом. Значит, что — действительно наименьший положительный период функции .
Чётность/нечётность
Рассмотрим точки
Точки пересечения графика с осями координат.
График пересекает ось в точках с абсциссами, определяемыми уравнением , т.е. , график пересекает ось в точке с ординатой, определяемой равенством , т.е. таким образом, , ,
6. Промежутки знакопостоянства функции:
Т.к. ординаты точек, лежащих в верхней полуплоскости, положительны, то значения синуса положительны для углов, расположенных в первой и второй координатных четвертях, и отрицательны — для углов, расположенных в третьей и четвертой координатных четвертях.
Т.о., при ; при ;
Интервалы возрастания/убывания
Теорема.
Функция не является монотонной на всей области определения, она возрастает на и убывает на .
Доказательство:
Докажем, например, возрастание функции на . В силу периодичности функции, достаточно рассмотреть отрезок .
Для этого рассмотрим 2 различных значения , такие, что .
Рассмотрим разность значений синусов этих углов: .
Заметим, что правая часть полученного равенства отрицательна. Действительно, т.к. числа расположены на отрезке и , то , поэтому ; аналогично , поэтому . Тем самым доказано, что из неравенства следует неравенство , т.е. функция возрастает на , а значит, возрастает на каждом из промежутков вида .
Докажем убывание функции на . В силу периодичности функции, достаточно рассмотреть отрезок .
Для этого рассмотрим 2 различных значения , такие, что .
Рассмотрим разность значений синусов этих углов:
.
Заметим, что правая часть полученного равенства положительна. Действительно, т.к. числа расположены на отрезке и , то , поэтому ; аналогично , значит . Т.о. , т.е. функция убываетна , а значит, убывает на каждом из промежутков вида .
Рекомендуемые страницы:
lektsia.com
Промежутки возрастания и убывания функции. Максимум и минимум функции.
Определение возрастающей функции.
Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
К примеру, из свойств основных элементарных функций мы знаем, что y = sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале мы можем утверждать о возрастании на отрезке .
Точку называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют
Точку называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .
Под окрестностью точки понимают интервал , где — достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Достаточные признаки возрастания и убывания функции.
На основании достточных признаков находятся промежутки возрастания и убывания функции.
— если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
— если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
— найти область определения функции;
— найти производную функции
— решить неравенства f’(x)>0 и f’(x)<0 на области определения;
— к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Достаточные признаки экстремума функции.
Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда
• если при и при , то — точка максимума;
• если при и при , то — точка минимума.
Другими словами:
• если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то — точка максимума;
• если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то — точка минимума.
Первообразная. Неопределённый интеграл. Таблица интегралов.
Первообразная. Функция F(х) называется первообразной для функции f (х) на промежутке X, если для любого х из Х выполняется равенство F'(x)=f(x)
ТАБЛИЦА ПЕРВООБРАЗНЫХ

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом . Как следует из изложенного выше, если F(x) — некоторая первообразная функции f(x), то , где C — произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx — подынтегральным выражением.
Свойства неопределённого интеграла, непосредственно следующие из определения:
1) .
2) (или ).
ТАБЛИЦА ИНТЕГРАЛОВ
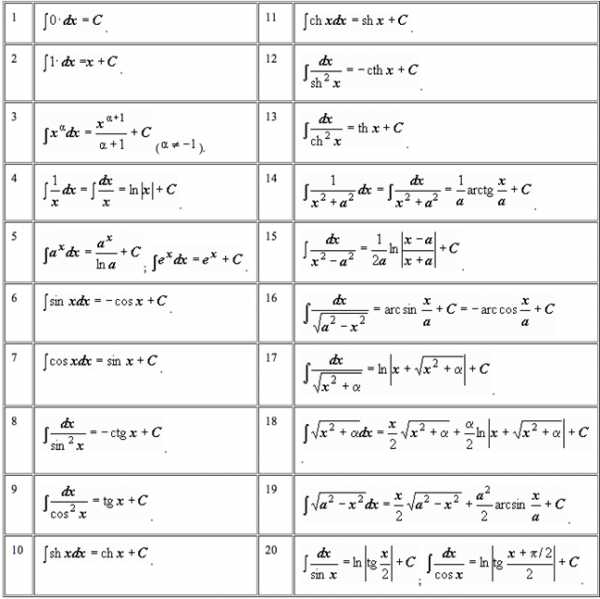
cyberpedia.su
Интервалы возрастания и убывания функции. Исследование на экстремум с помощью первого достаточного условия существования экстремума
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ
АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика СП. КОРОЛЕВА
Кафедра высшей математики
Расчетно-графическая работа
Полное исследование функции
Выполнил: Пугачев Сергей гр. 313
Сдано, дата:
г. Самара
Задание:
1. Указать область определения функции.1
2. Определить чётность-нечетность функции. Указать на особенность графика функции (есть ли симметрия). Найти точки пересечения графика с осями координат.2
3. Найти точки разрыва функции. Указать род точек разрыва. Найти пределы функции при x→+∞, x→-∞.3
4. Найти интервалы возрастания и убывания функции. Исследовать функцию на экстремум с помощью первого достаточного условия.4
5. Найти интервалы выпуклости и вогнутости графика функции, точки перегиба.6
6. Исследовать функцию на экстремум с помощью второго достаточного условия.7
7. Записать уравнения асимптот графика функции.8
8. Построить график функции.9
Область определения функции
Функция
. x≠-1. Таким образом, D(y):x (-∞;-1)∩(-1;+∞).
Чётность-нечетность функции. Особенности графика функции
f(-x) = ≠f(x) => f(x) – функция общего вида.
Найдем пересечение графика с осью ox:
y=0; 4x=0; x= ; x=0.
Найдем пересечение с осью oy:
y=0; y=0.
3. Точки разрыва функции. Род точек разрыва. Пределы функции при x→+∞, x→-∞
Односторонние пределы не являются конечными, следовательно, x=-1 — точка разрыва второго рода.
Схематично построим график функции в окрестности точки x=-1 и при x→+∞, x→-∞.
Интервалы возрастания и убывания функции. Исследование на экстремум с помощью первого достаточного условия существования экстремума
Для полного исследования функции найдем первую и вторую производные:
Исследуемая функция: . Производные:
y´= ;
y´´= .
Таким образом , y´= , y´´= .
Найдем критические точки. По определению:
| Критической точкой функции y=f(x) называется внутренняя точка области определения, в которой производная f´(x) равна нулю или не существует. |
В нашем случае производная не существует в точке x=-1. Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.
Приравняем производную к нулю: y´=
Отсюда 4-4x=0; 1-x=0; x=1. Таким образом: x=1 — критическая точка, x= -1 — точка разрыва функции.
| ДОСТАТОЧНОЕ УСЛОВИЕ ВОЗРАСТАНИЯ, УБЫВАНИЯ ФУНКЦИИ: Если на интервале производная f´(x) положительна, то функция y=f(x) возрастает, если отрицательна, то убывает. |
Знак производной может измениться только в критических точках или в точках разрыва функции.
Покажем знаки производной на числовой оси:
Функция возрастает на интервале: (-1;1].
Функция убывает на интервале: (-∞;-1), (1;+∞).
| ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА: Пусть функция y=f(x) непрерывна в точке x1 и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку x1 слева направо производная f´(x) меняет знак: 1) с + на -, то в точке x1 максимум; 2)с – на +, то в точке x1 минимум. Если производная не меняет знак, то экстремума в этой критической точке нет. |
В нашем случае: ymax = f(1)=
ymin — не существует.
5. Интервалы выпуклости и вогнутости графика функции, точки перегиба
Первая производная функции f´(x) позволяет найти интервалы возрастания и убывания функции y=f(x), а также точки экстремума. Для нахождения интервалов выпуклости и вогнутости графика функции, а также точки перегиба, нужно определить знаки второй производной f´´(x).
| ДОСТАТОЧНОЕ УСЛОВИЕ ВЫПУКЛОСТИ И ВОГНУТОСТИ ГРАФИКА ФУНКЦИИ: Если на интервале вторая производная f´´(x) положительна, то график функции y=f(x) на этом интервале вогнутый. Если на интервале вторая производная f´´(x) отрицательна, то график функции y=f(x) на этом интервале выпуклый. Если вторая производная f´´(x) при переходе через точку c меняет знак, то эта точка является точкой перегиба. При этом в точке с функция должна быть непрерывна. Точка разрыва функции не считается точкой перегиба. |
| Запомнить это правило можно с помощью рисунка. На шарике показан знак второй производной. Условимся считать, что если график выпуклый, то шарик не устойчив на кривой и на нем должен стоять знак минус. Если график вогнутый, то шарик устойчив на кривой и на нем должен стоять знак плюя. Таким образом, условно установим связь между выпуклостью-вогнутостью и знаком второй производной. |
Для исследуемой функции y´´= .
Знак производной может измениться в точке, где она равна нулю или в точке, где она не существует. В нашем случае уравнение = 0 имеет один корень x=2, следовательно, в точке x=2y´´= 0. Существует y´´ в точке x=-1.
График функции выпуклый на интервале (-∞;-1)∩(-1;+∞). Точка x=-1 на графике функции y=f(x) является точкой разрыва, поэтому не считается точкой перегиба.
megaobuchalka.ru
2.4.2. Возрастание и убывание функции на интервале
Функция 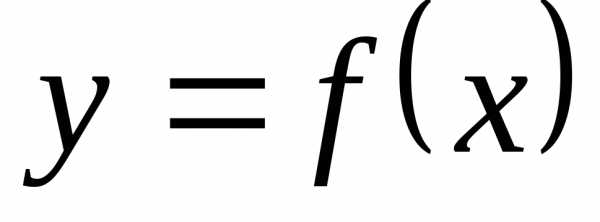 называется возрастающей на интервале
называется возрастающей на интервале  ,
если большему значению аргумента из
этого интервала соответствует большее
значение функции, т.е. при
,
если большему значению аргумента из
этого интервала соответствует большее
значение функции, т.е. при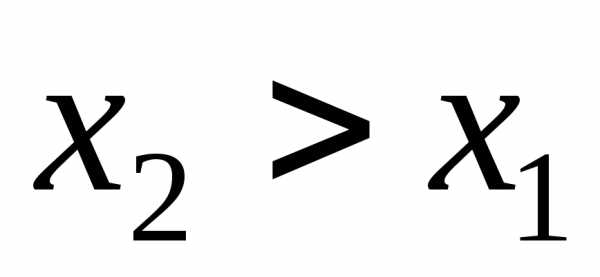 ,
где
,
где 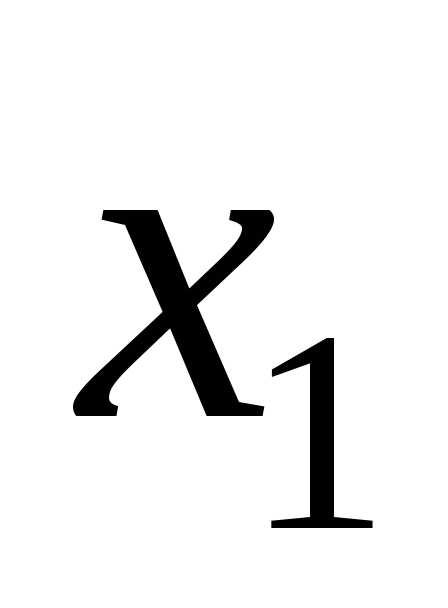 и
и  – любые две точки из интервала
– любые две точки из интервала 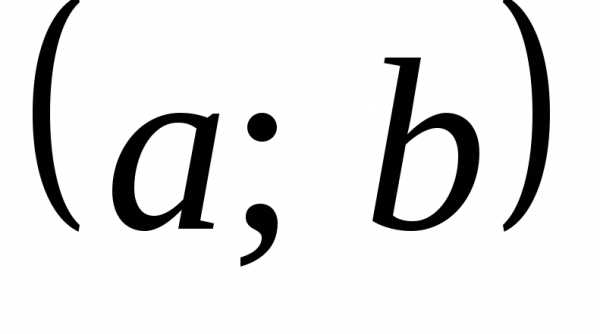 верно неравенство
.
верно неравенство
.
Если
большему
значению аргумента из этого интервала
соответствует меньшее значение функции,
т.е. при 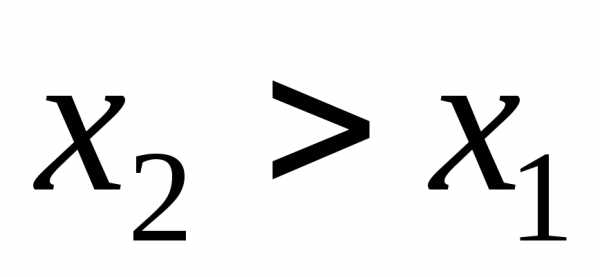 верно неравенство
,то функция
верно неравенство
,то функция 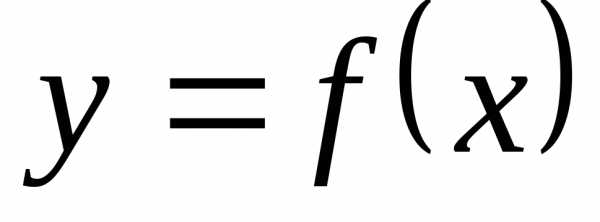 называется убывающей на интервале
называется убывающей на интервале 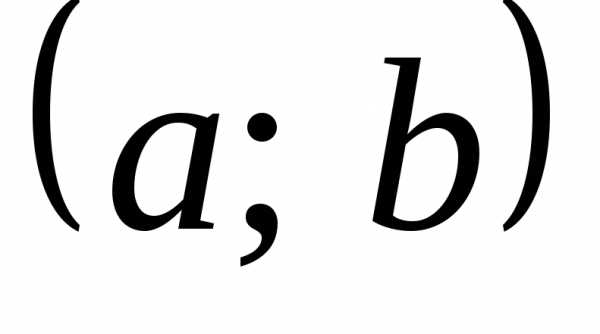 .
.
Возрастание
и убывание функции на интервале тесно
связано со знаком производной 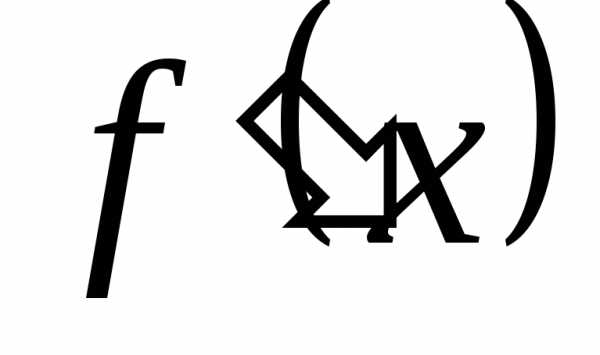 функции
функции 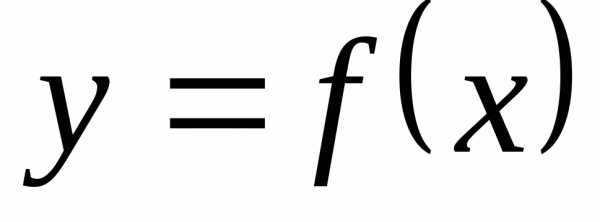 в точках
этого интервала.
в точках
этого интервала.
Необходимые условия возрастания и убывания функции:
Если
дифференцируемая функция 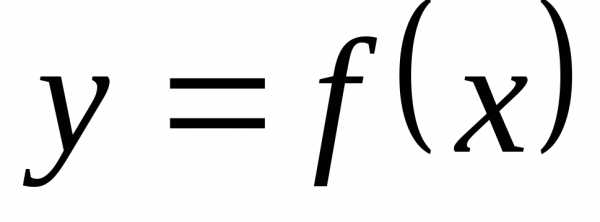 на интервале
на интервале  возрастает (убывает), то её производная
на этом интервале неотрицательная
(неположительная), т.е.
возрастает (убывает), то её производная
на этом интервале неотрицательная
(неположительная), т.е. (
( ).
).
Достаточные условия возрастания и убывания функции:
Если
непрерывная на отрезке 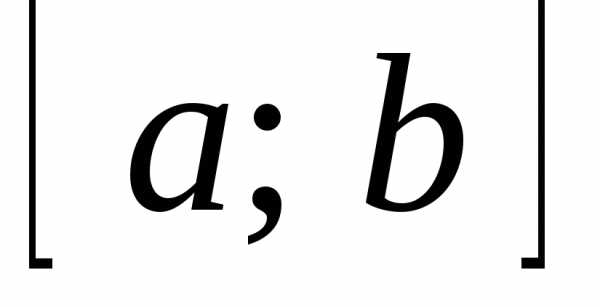 функция
функция 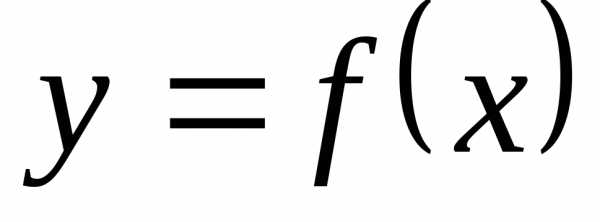 в каждой точке отрезка имеет положительную
(отрицательную) производную, то она
возрастает (убывает) на этом отрезке.
в каждой точке отрезка имеет положительную
(отрицательную) производную, то она
возрастает (убывает) на этом отрезке.
Интервалы, в которых функция является только возрастающей или только убывающей, называются интервалами монотонности.
Эти интервалы ограничены критическими точками І рода – значениями аргумента, в которых производная функции равна нулю или не существует.
Для
нахождения интервалов монотонности,
необходимо нанести на числовую ось
граничные точки области определения и
все критические точки функции. Числовая
ось при этом разбивается на некоторое
число интервалов, на каждом из которых
производная не меняет знак. Для того
чтобы узнать возрастает или убывает
функция на данном интервале, достаточно
выяснить какой знак имеет производная
в произвольной точке этого интервала.
Если в этой точке  ,
то функция возрастает на данном интервале,
если
,
то функция возрастает на данном интервале,
если 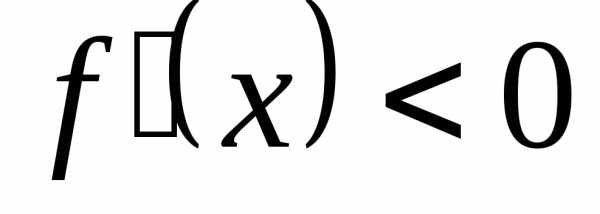 – то функция
убывает на данном интервале.
– то функция
убывает на данном интервале.
2.4.3. Экстремумы функции
Точка 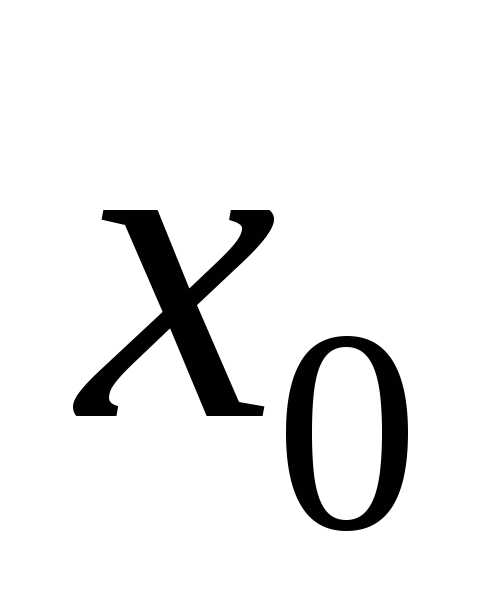 называется точкой
максимума функции
называется точкой
максимума функции 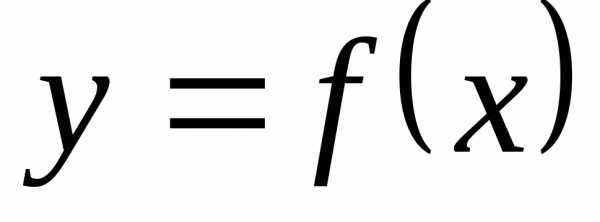 ,
если существует такая окрестность точки
,
если существует такая окрестность точки 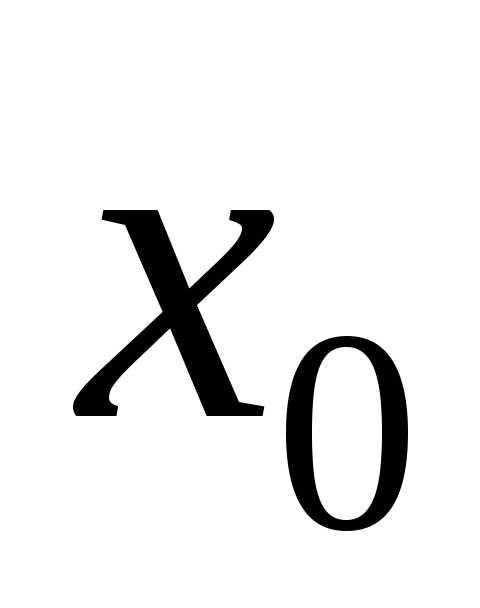 ,
что для всех точек
,
что для всех точек 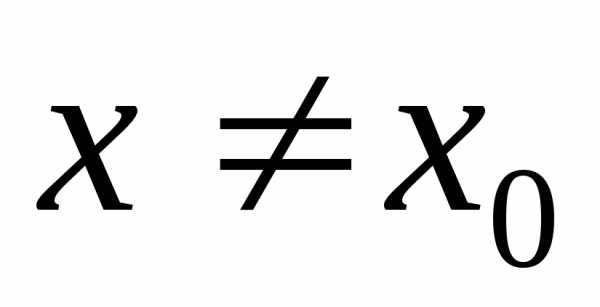 этой окрестности выполняется неравенство.
этой окрестности выполняется неравенство.
Значение
функции в точке максимума  называетсямаксимумом функции.
называетсямаксимумом функции.
Точка 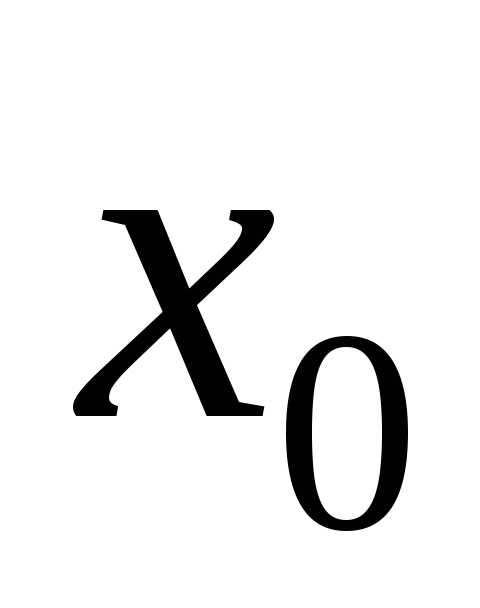 называется точкой
минимума функции
называется точкой
минимума функции 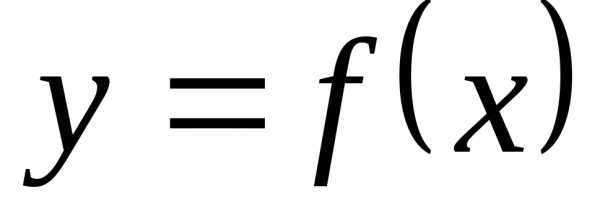 ,если
существует такая окрестность точки
,если
существует такая окрестность точки 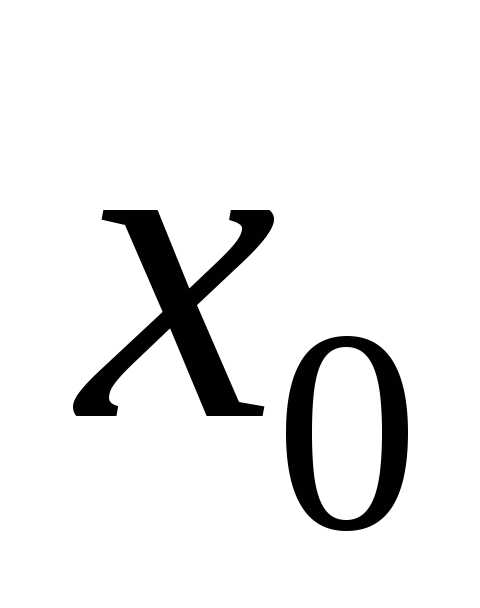 ,
что для всех точек
,
что для всех точек  этой окрестности выполняется неравенство.
этой окрестности выполняется неравенство.
Значение
функции в точке минимума 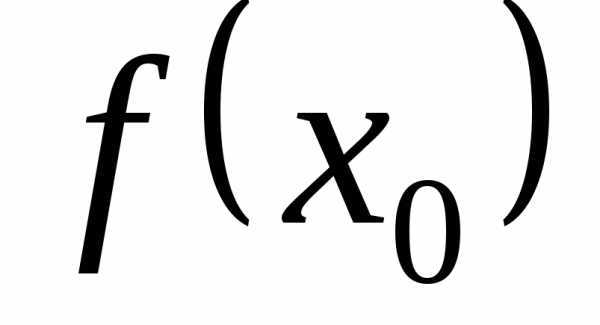 называетсяминимумом функции.
называетсяминимумом функции.
Максимум и минимум объединяются под общим названием экстремум функции, а точки максимума и минимума называются точками экстремума.
Функция 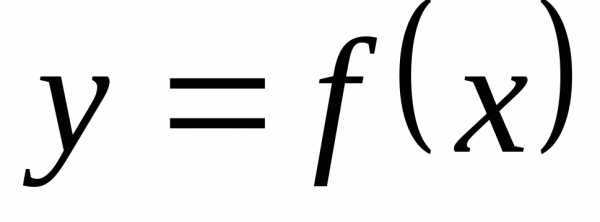 на всей области определенияможет
иметь несколько точек экстремума. Это
означает, что понятие максимума и
минимума функции носят локальный
характер. Это наибольшее и наименьшее
значение функции только в окрестности
рассматриваемой точки, а не во всей
области её определения.
на всей области определенияможет
иметь несколько точек экстремума. Это
означает, что понятие максимума и
минимума функции носят локальный
характер. Это наибольшее и наименьшее
значение функции только в окрестности
рассматриваемой точки, а не во всей
области её определения.
Необходимое условие существования экстремума функции:
Если
непрерывная функция  в точке
в точке 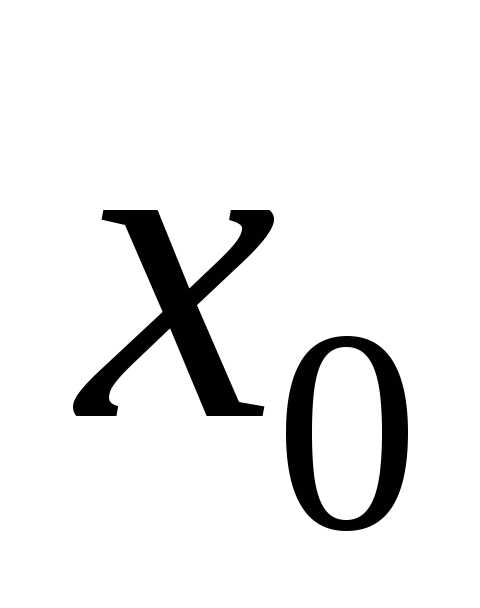 имеет экстремум, то её производная
имеет экстремум, то её производная 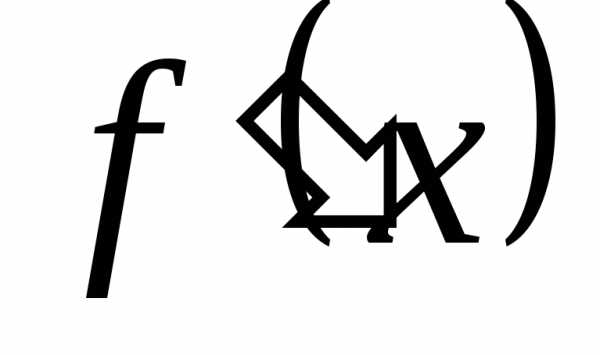 в этой точке равна нулю или не существует,
т.е.
точка
экстремума является критической точкой
І рода.
в этой точке равна нулю или не существует,
т.е.
точка
экстремума является критической точкой
І рода.
Замечание: Не во всякой критической точке функция имеет экстремум.
Так,
например, для функции  (график функции показан на рис. 5)
производная
(график функции показан на рис. 5)
производная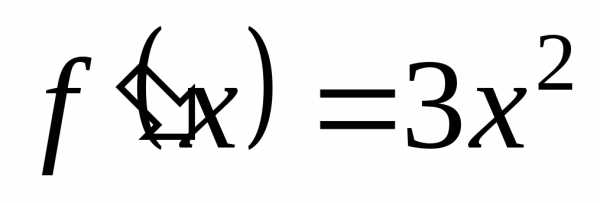 .
Производная существует при любом
значении аргумента и равна нулю при
.
Производная существует при любом
значении аргумента и равна нулю при 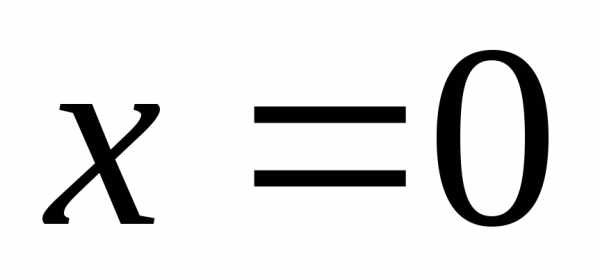 ,
т.е. функция имеет одну критическую
точку І рода:
,
т.е. функция имеет одну критическую
точку І рода:  .Однако в данной
критической точке экстремума нет.
.Однако в данной
критической точке экстремума нет.
SHAPE \* MERGEFORMAT
Чтобы проверить, имеет ли функция в критической точке экстремум, необходимо дополнительное исследование. Для этого используют достаточные условия существования экстремума.
Первое достаточное условие существования экстремума.
Если
непрерывная функция  имеет
производную во всех точках интервала,
содержащего критическую точку
имеет
производную во всех точках интервала,
содержащего критическую точку 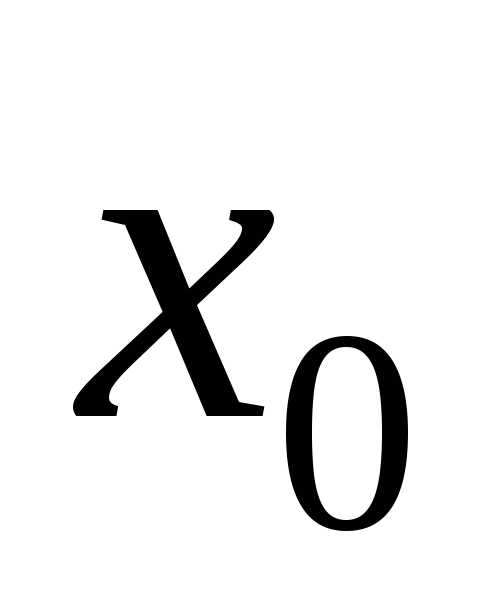 ,
(за исключением, может быть, самой этой
точки) и производная
,
(за исключением, может быть, самой этой
точки) и производная 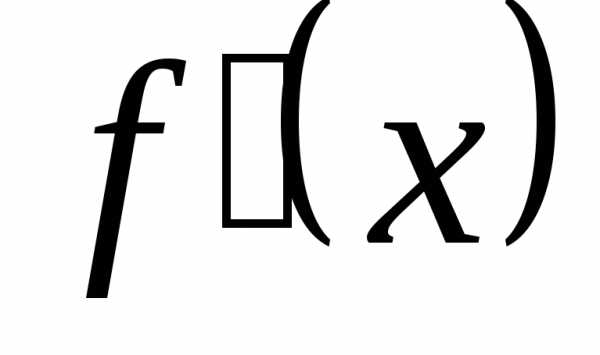 при переходе через точку
при переходе через точку 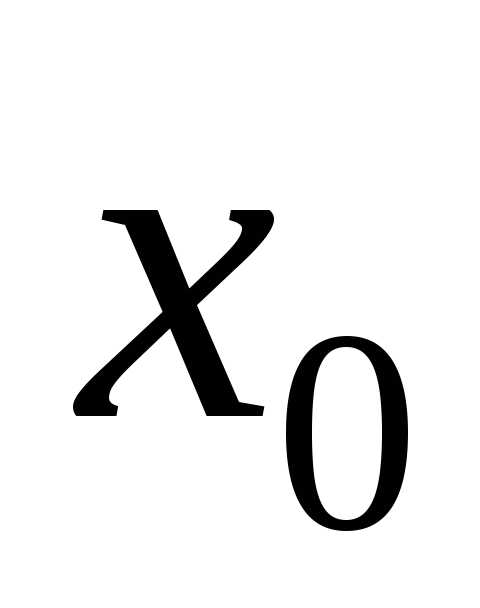 слева
направо меняет
знак с плюса на минус,
то функция в этой точке имеет максимум,
а если меняет
знак с минуса на плюс – минимум.
слева
направо меняет
знак с плюса на минус,
то функция в этой точке имеет максимум,
а если меняет
знак с минуса на плюс – минимум.
Второе достаточное условие существования экстремума.
Если
в точке 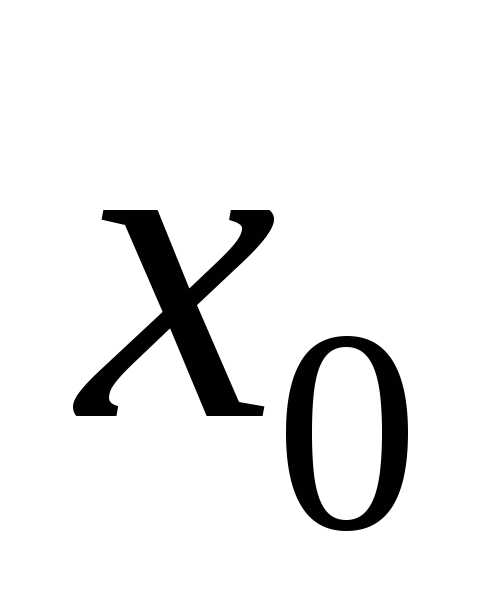 первая производная равна нулю
,
а вторая производная существует и не
равна нулю
,
то при функция в этой точке имеет максимум, а
при функция имеет минимум.
первая производная равна нулю
,
а вторая производная существует и не
равна нулю
,
то при функция в этой точке имеет максимум, а
при функция имеет минимум.
Замечание:
В тех случаях, когда в критической точке  вторая производная
вторая производная 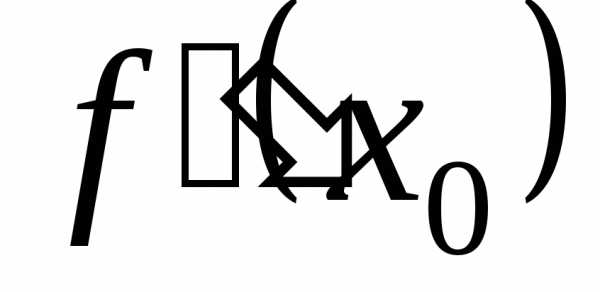 равна нулю или не существует, то второй
достаточный признак существования
экстремума неприменим.
равна нулю или не существует, то второй
достаточный признак существования
экстремума неприменим.
Схема исследования функции на монотонность и экстремум
Найти область определения функции
 .
.Найти первую производную .
Найти критические точки І рода.
Разбить область определения функции
 критическими точками на интервалы.
критическими точками на интервалы.Определить знак производной
 на полученных интервалах (методом
подстановки значений аргумента или
методом интервалов).
на полученных интервалах (методом
подстановки значений аргумента или
методом интервалов).Сделать вывод об интервалах монотонности.
Определить, используя первый достаточный признак экстремума, какие из критических точек являются точками экстремума.
Вычислить значение функции в полученных точках экстремума.
Результаты оформить в виде таблицы.
Пример 18.
Найти интервалы монотонности и точки экстремума функции .
Решение.
Функция определена на всей числовой оси. Область определения функции имеет вид: .
Найдем первую производную функции:
.
Найдем критические точки первого рода:
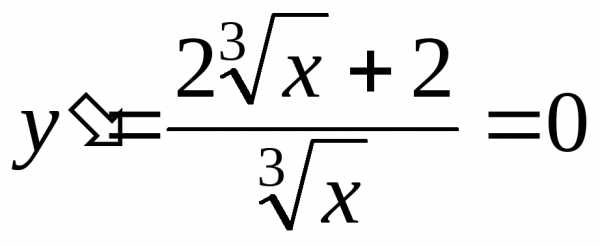 .
.
Дробь равна нулю, если числитель равен нулю и знаменатель не равен нулю:
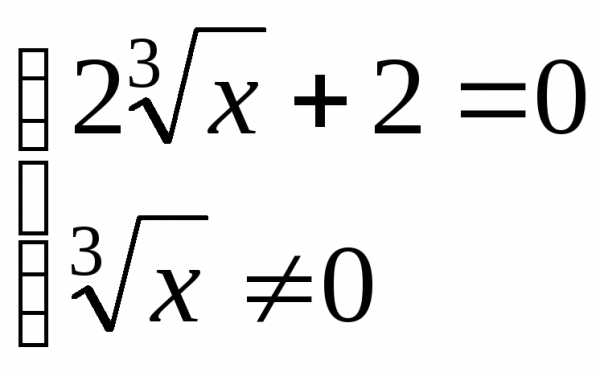 ;
;  ;
;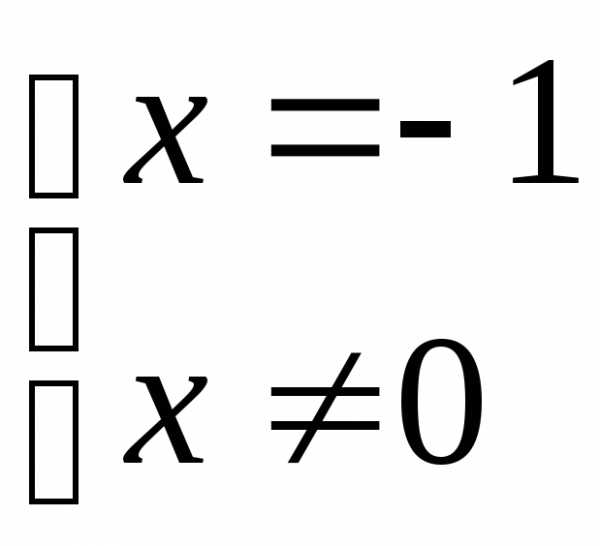 .
.
Следовательно,
точки 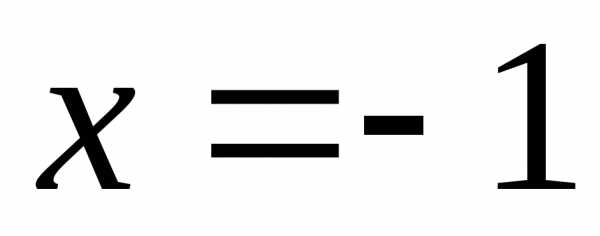 и
и 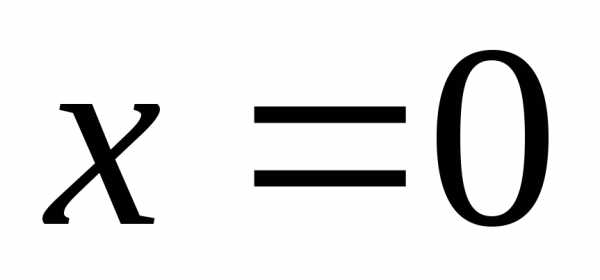 – критические точки І рода.
– критические точки І рода.
Разбиваем всю числовую ось на интервалы и определяем знак производной на каждом интервале.
|
| – 1 |
| 0 |
|
| + | 0 | – | не сущ. | + |
| ↗ | 1 | ↘ | 0 | ↗ |
max min
Так как на интервалах производная положительная значит, на этих интервалах функция возрастает.
Так как на интервале производная отрицательная значит, на этом интервале функция убывает.
Так
как при переходе через критическую
точку 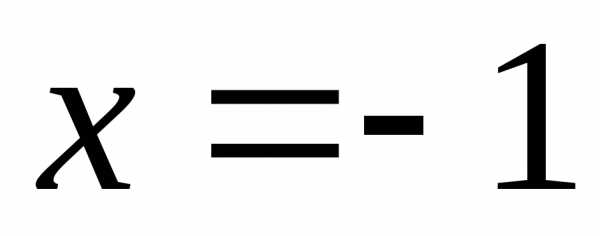 производная меняет знак с «+» на «–»,
то в этой точке функция имеет максимум.
производная меняет знак с «+» на «–»,
то в этой точке функция имеет максимум.
Так
как при переходе через критическую
точку 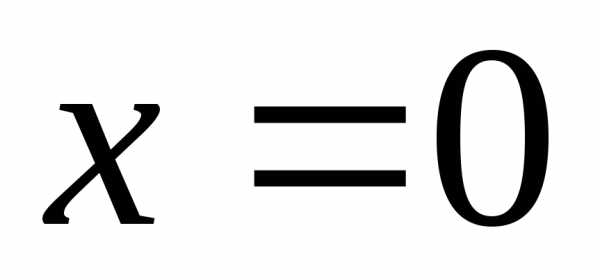 производная меняет знак с «–» на «+»,
то в этой точке – минимум функции.
производная меняет знак с «–» на «+»,
то в этой точке – минимум функции.
Определим значения функции в критических точках.
;
.
Приближенный вид графика функции показан на рис 6.
studfiles.net
Найдите промежутки возрастания и убывания функций (через…
Решается с помощью приравнивания производной к нулю и нахождения корня
1)
нет корней, это обозначает, что на все отрезке функция либо убывает, либо возрастает.
смотрит на знак старшей степени функции положительный, значит функция возростающая.
— промежуток возрастания
2)
отмечаем точки на интервале и расставляем знаки начиная с плюса, т.к. у производной у «x»-а старшей степени положительный знак
_+_(-1)_-_(2)_+_
Интервалы с плюсами — возрастание
интевал с минусом — убывание
— промежутки возрастания
— промежуток убывания
3)
косинус не может быть меньше -1 и больше 1.
значит функция либо возрастает, либо убывает на всем промежутке
лучше её для этого построить и посмотреть. но и по положительному знаку «x»-а видно, что она возрастающая.
— промежуток возрастания
Оцени ответ
shkolniku.com

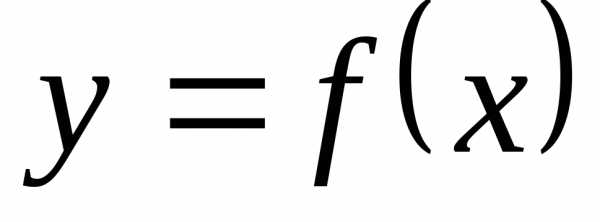 .
.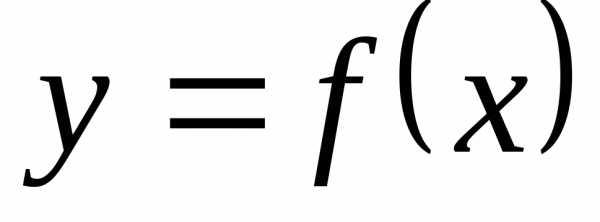 критическими точками на интервалы.
критическими точками на интервалы. на полученных интервалах (методом
подстановки значений аргумента или
методом интервалов).
на полученных интервалах (методом
подстановки значений аргумента или
методом интервалов).