1.11. Поняття про ірраціональні числа. Дійсні числа
Арифметичним
квадратним коренем з
невід’ємного числа а називають невід’ємне число, квадрат
якого дорівнює а.
Арифметичний квадратний корінь із числа а позначають 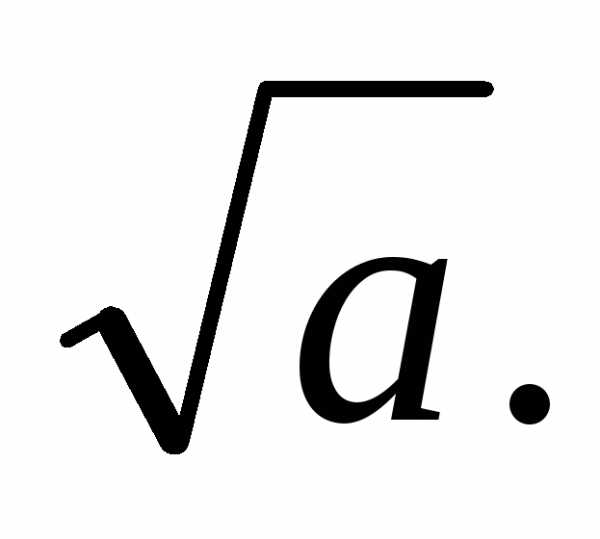
Теорема. Серед
раціональних чисел немає такого, яке
дорівнювало б значенню 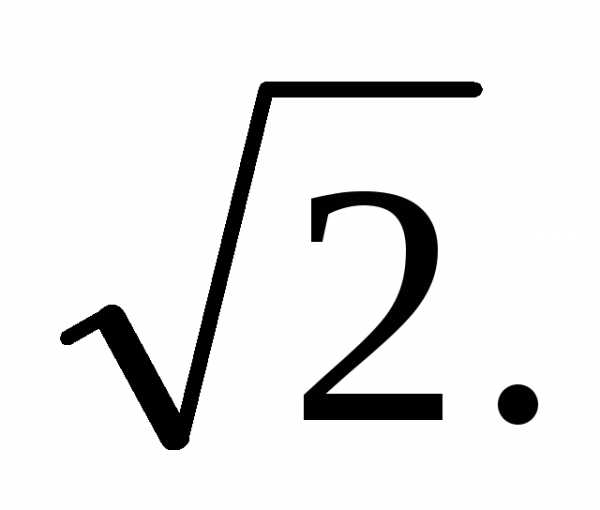
Припустимо
протилежне. Нехай існує таке раціональне
число, квадрат якого дорівнює 2. Це число
можна подати у вигляді нескорочуваного
дробу 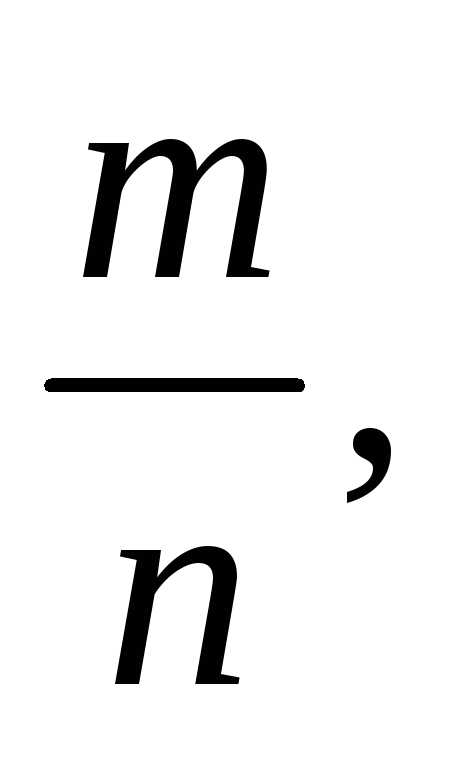 де
де 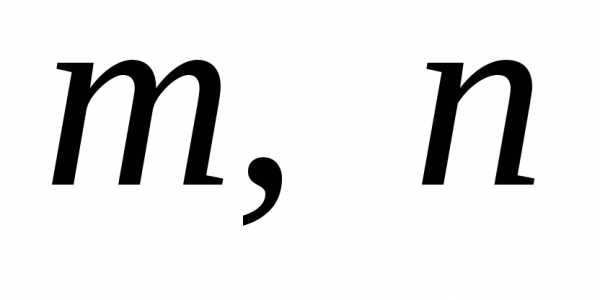 — натуральні числа. Тоді Оскільки число
— натуральні числа. Тоді Оскільки число 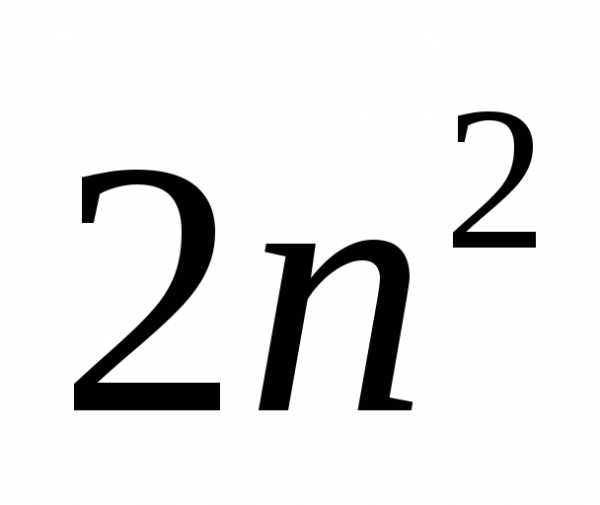 — парне, то й число
— парне, то й число 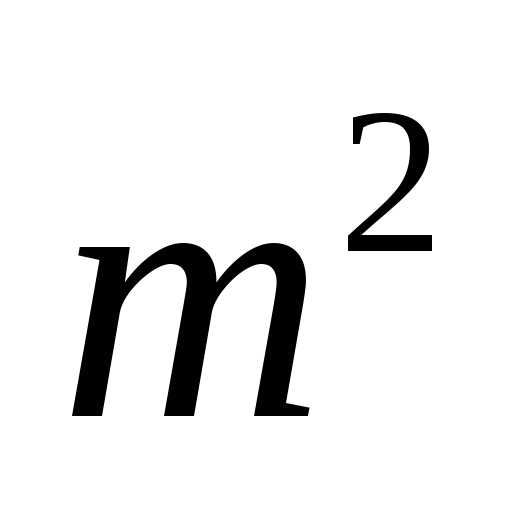
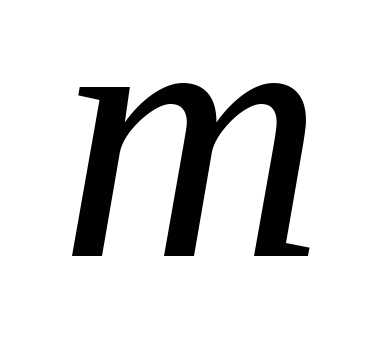 — також парне (адже квадрат непарного
числа є непарне число), тобто
— також парне (адже квадрат непарного
числа є непарне число), тобто 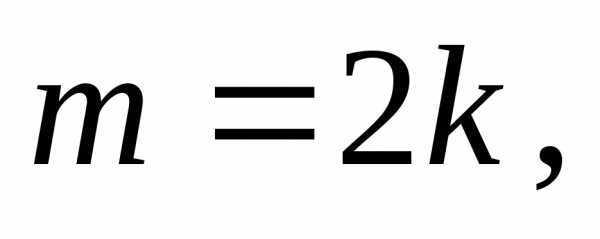 де
де  — натуральне число. Підставивши цей
вираз у рівність
— натуральне число. Підставивши цей
вираз у рівність 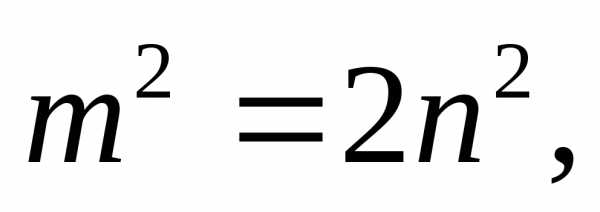 дістанемо
дістанемо 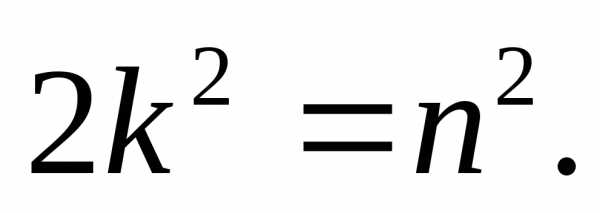 Оскільки
Оскільки  — парне число, то
— парне число, то 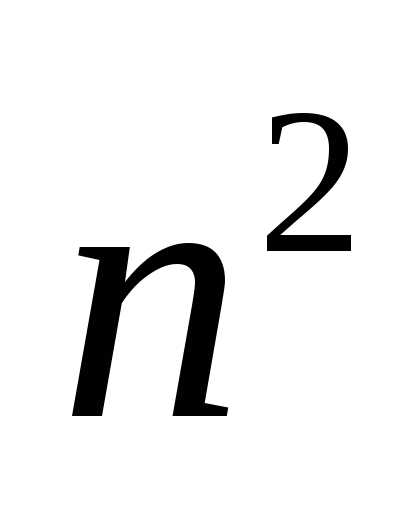 — також парне, тому і
— також парне, тому і 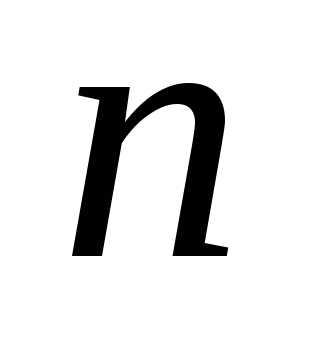 — парне число. Отже,
— парне число. Отже, 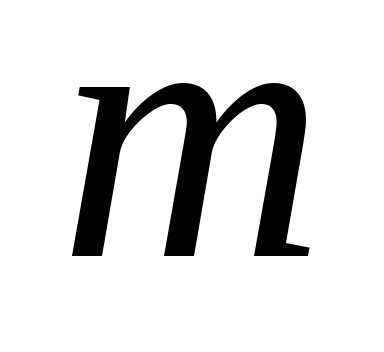 і
і 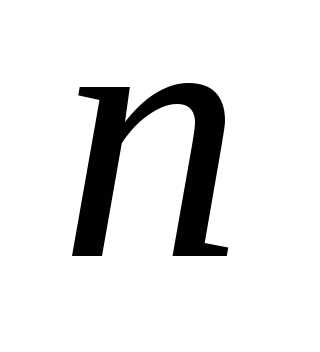 — парні числа, а це суперечить припущенню,
що дріб
— парні числа, а це суперечить припущенню,
що дріб  нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,
нескоротний. Звідси випливає, що не
існує раціонального числа, квадрат
якого дорівнює 2. Таким чином,  не є раціональним числом.
не є раціональним числом. Це число
називають ірраціональним. Ірраціональними числами є 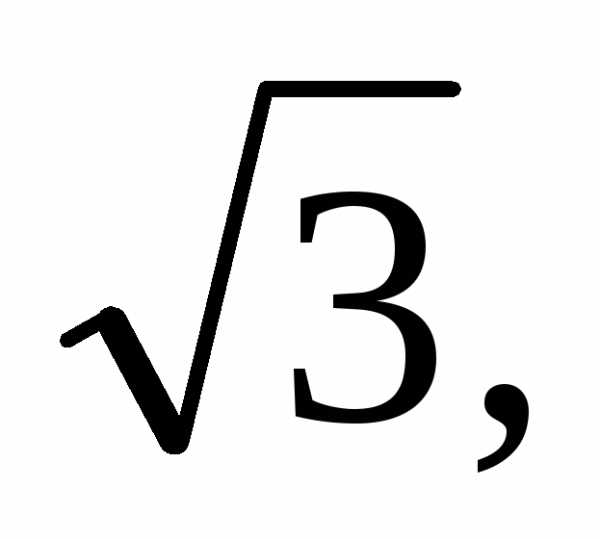


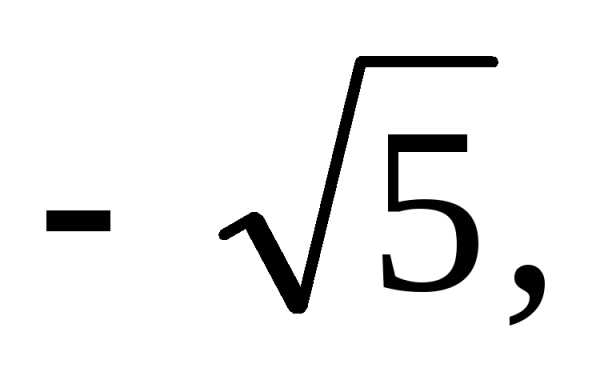

 і т. ін.
і т. ін.
Зауважимо,
що до ірраціональних чисел належить
число 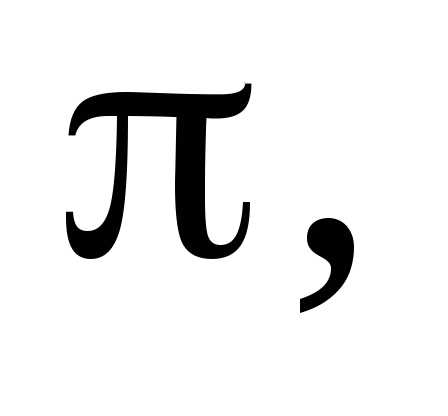 яке виражає відношення довжини кола до
його діаметра.
яке виражає відношення довжини кола до
його діаметра.
У теоремі 1.10 доведено, що кожне раціональне число є нескінченним періодичним десятковим дробом. Було зазначено також, що будь-який періодичний десятковий дріб є поданням деякого раціонального числа.
Крім
періодичних нескінченних десяткових
дробів, існують неперіодичні
дроби: такий, наприклад, дріб в якого після першої двійки одна одиниця,
після другої — дві одиниці і т. д. Кожний
неперіодичний нескінченний десятковий
дріб де 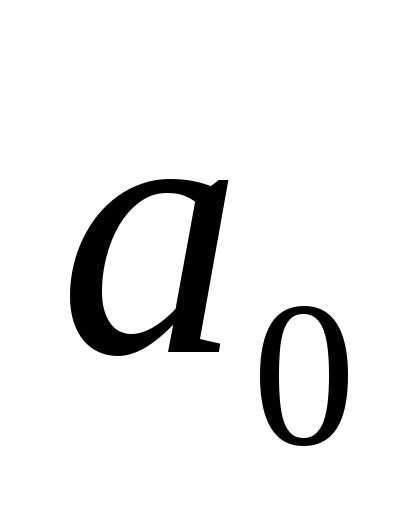 — ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.
— ціла частина числа х; —
десяткові знаки, є поданням деякого
нового (не раціонального) числа, що
називається ірраціональним. Множину
всіх таких чисел називають множиною
ірраціональних чисел.
Множиною дійсних чисел називають множину всіх раціональних і всіх ірраціональних чисел. Таким чином, з’ясовується, що будь-яке дійсне число подається нескінченним десятковим дробом. Множина всіх дійсних чисел позначається R.
Дійсні
числа впорядковано за величиною, тобто
для будь-яких двох дійсних чисел 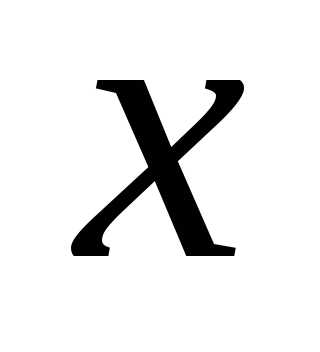 і
і 
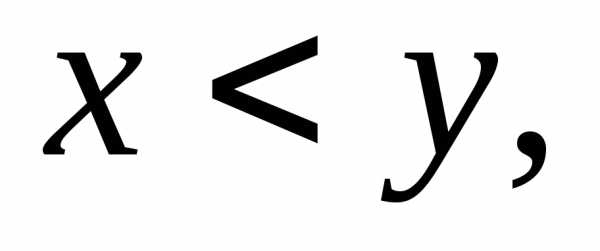

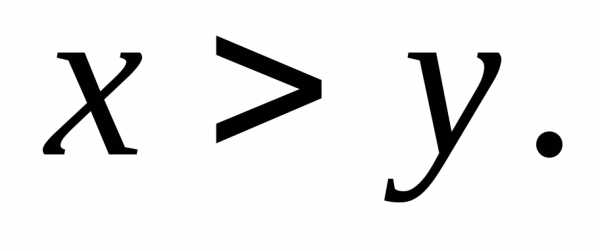 Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів.
Сенс нерівності між дійсними числами
визначається правилом порівняння
нескінченних десяткових дробів. Для
дійсного числа наближення з точністю до 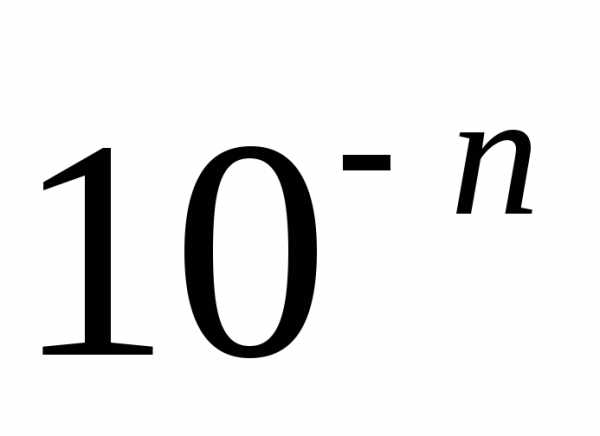 з недостачею
з недостачею 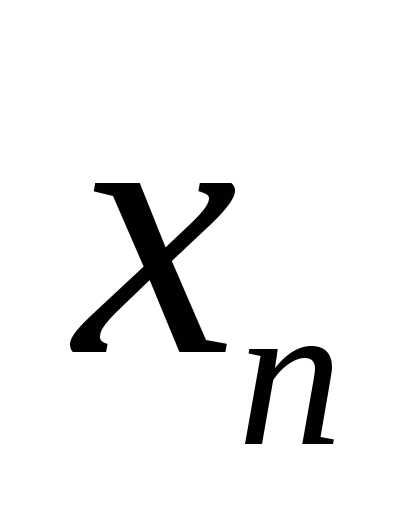 і з надлишком
і з надлишком 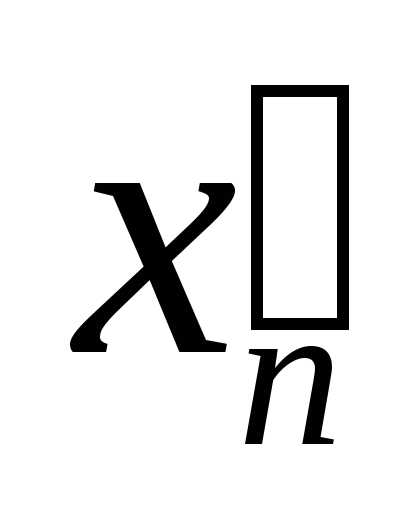 визначаються так:
визначаються так:
Очевидно, що
Додавання
до десяткового дробу числа 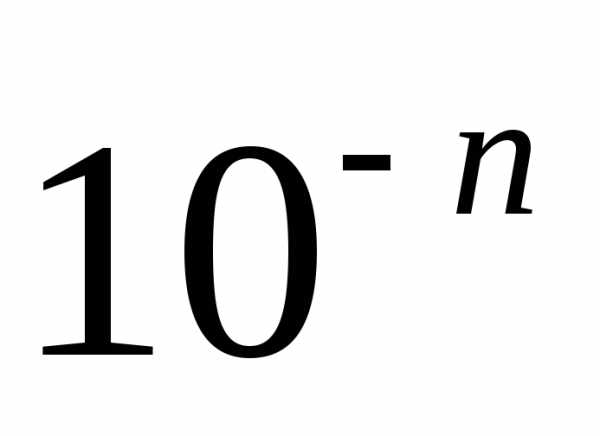 рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень
рівносильне збільшенню
останньої цифри дробу на одиницю.
Зауважимо, що кожне з десяткових наближень 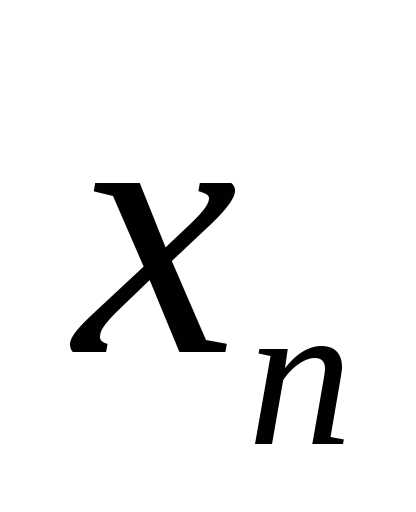
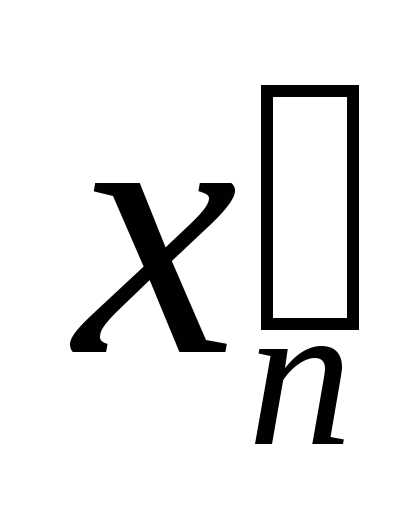 дійсного числа
дійсного числа 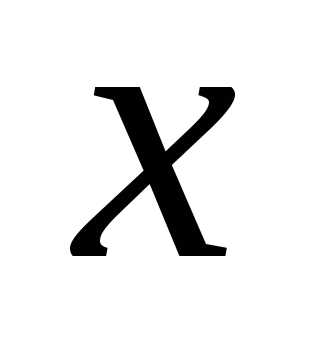 є раціональним числом.
є раціональним числом.Приклад. Випишемо перші п’ять наближень (з недостачею та надлишком) для числа
Для дійсних чисел можна визначити арифметичні операції додавання і множення. Віднімання визначається як дія, обернена до додавання, а ділення — як дія, обернена до множення. Основні властивості арифметичних дій із цілими числами справеджуються і для дійсних чисел.
Визначимо
суму і добуток двох дійсних чисел 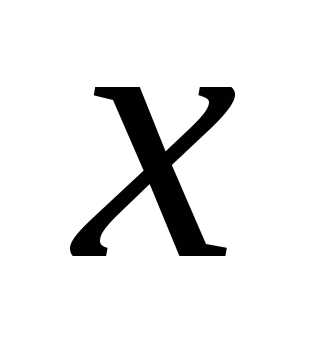 і
і  Для їхніх наближень з недостачею та
надлишком із точністю до
Для їхніх наближень з недостачею та
надлишком із точністю до 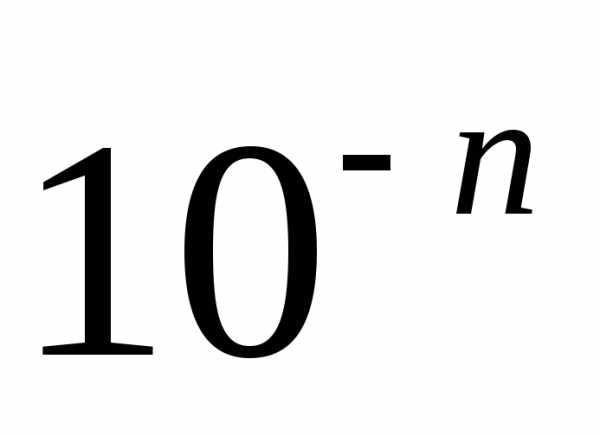 справджуються такі нерівності
справджуються такі нерівності
Сумою
дійсних чисел 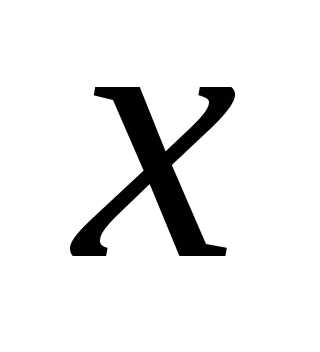 і
і  називають таке дійсне число
називають таке дійсне число 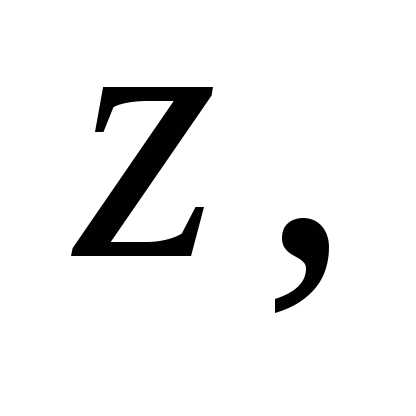 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному 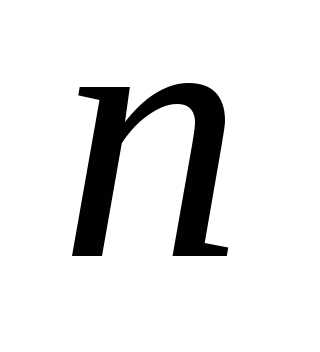 задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине.
Добутком
невід’ємних дійсних чисел 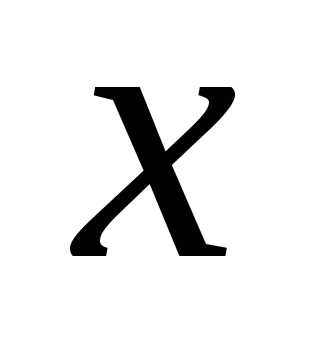 і
і  називають таке дійсне число
називають таке дійсне число 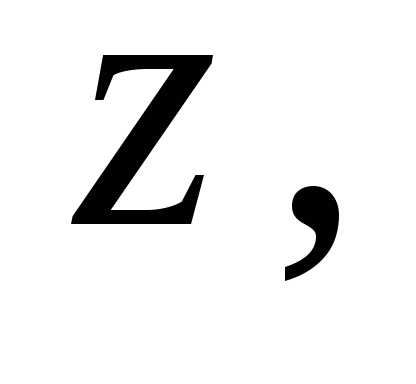 яке при будь-якому цілому невід’ємному
яке при будь-якому цілому невід’ємному 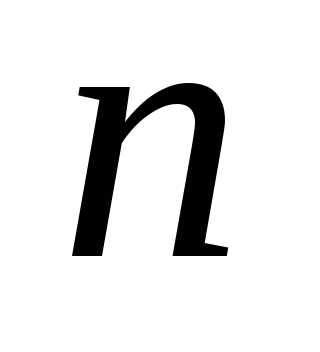 задовольняє нерівності Можна довести, що таке число існує і
єдине.
задовольняє нерівності Можна довести, що таке число існує і
єдине.
Дійсні числа можна зображати точками координатної осі.
Множину всіх дійсних чисел називають числовою віссю; вона зображається всією координатною прямою, її позначають (читається: «проміжок від мінус нескінченності до плюс нескінченності»).
Множина
всіх чисел, що задовольняють подвійну
нерівність називають числовим
проміжком (або проміжком)
і позначають  (читається: «проміжок від
(читається: «проміжок від  до
до  ».
».
Множину
всіх чисел, що задовольняють нерівності і позначають відповідно 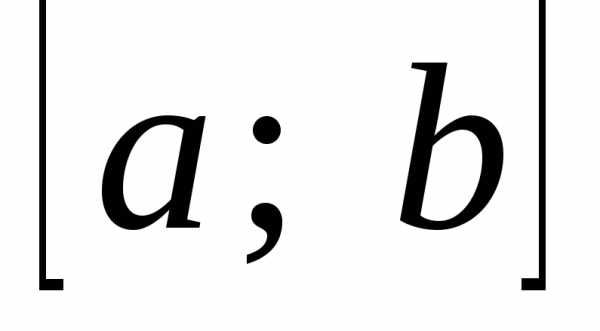 (читається: «проміжок від
(читається: «проміжок від  до
до 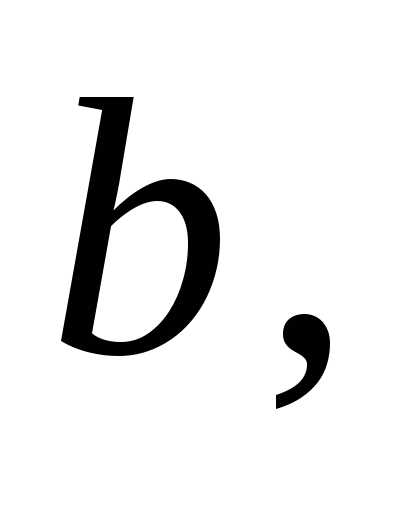 включаючи
включаючи  та
та 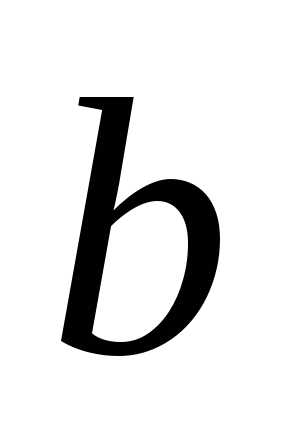 »),
[a; b)
і (a; b].
»),
[a; b)
і (a; b].
Проміжок 
 — відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.
— відрізком або сегментом,
а проміжки [a; b)
і (a; b]
— напівінтервалами.studfiles.net
ірраціональне число
Ірраціональне число — це дійсне число. яке не є раціональним. тобто не може бути представлено у вигляді дробу m n >>. де m — ціле число. n — натуральне число. Ірраціональне число може бути представлено у вигляді нескінченної неперіодичної десяткового дробу.
Безліч ірраціональних чисел зазвичай позначається великою латинською літерою I> в напівжирному зображенні без заливки. Таким чином: I = R ∖ Q = \ mathbb \ backslash \ mathbb>. тобто безліч ірраціональних чисел є різниця множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків. несумірних з відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа 2 >>.
античність
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені [джерело не вказано 571 день].
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок [джерело не вказано 571 день].
Немає точних даних про те, ірраціональність якого числа було доведено Гіппаса. Згідно з легендою він знайшов його вивчаючи довжини сторін пентаграми. Тому розумно припустити, що це було золотий перетин [джерело не вказано 542 дня].
Грецькі математики назвали це відношення несумірних величин алогос (невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Феодор Киренский довів ірраціональність коренів натуральних чисел до 17 (виключаючи, природно, точні квадрати — 1, 4, 9 та 16), але зупинився на цьому, тому що имевшаяся в його інструментарії алгебра не дозволяла довести ірраціональність квадратного кореня з 17. З приводу того , яким могло бути це доказ, істориками математики було висловлено кілька різних припущень. Згідно найбільш правдоподібного [2] припущенням Жана ІТАР [fr]. воно було засноване на теоремі про те, що непарне квадратне число ділиться на вісім із залишком один [3].
Пізніше Евдокс Кнідський (410 або 408 р. До н.е.. — 355 або 347 р. До н.е..) Розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Оскільки жодне кількісне значення не пов’язана із величиною, Евдокс зміг охопити і співмірні, і несумірні величини при визначенні дробу як відносини двох величин, і пропорції як рівності двох дробів. Прибравши з рівнянь кількісні значення (числа), він уникнув пастки, що складається в необхідності назвати ірраціональну величину числом. Теорія Евдокса дозволила грецьким математикам зробити неймовірний прогрес в геометрії, надавши їм необхідне логічне обгрунтування для роботи з непомірними величинами. «Книга 10 Елементів» Евкліда присвячена класифікації ірраціональних величин.
Середньовіччя
Середні століття ознаменувалися прийняттям таких понять як нуль, негативні числа, цілі і дробові числа, спершу індійськими, потім китайськими математиками. Пізніше приєдналися арабські математики, які першими стали вважати негативні числа алгебраїчними об’єктами (поряд і на рівних правах з позитивними числами), що дозволило розвинути дисципліну, нині звану алгеброю.
Раціональної [величиною] є, наприклад, 10, 12, 3%, 6% і так далі, оскільки ці величини вимовлені і виражені кількісно. Що не раціонально, то ірраціонально, і неможливо вимовити або надати відповідну величину кількісно. Наприклад, квадратний корінь чисел таких так 10, 15, 20 — не є квадратами.
На противагу концепції Евкліда, що величини суть в першу чергу відрізки прямих, Аль Махане вважав цілі числа і дроби раціональними величинами, а квадратні і кубічні корені — ірраціональними. Він також ввів арифметичний підхід до безлічі ірраціональних чисел, оскільки саме він показав ірраціональність наступних величин:
результат складання ірраціональної величини і раціональної, результат віднімання раціональної величини з ірраціональної, результат віднімання ірраціональної величини з раціональної.
Єгипетський математик Абу Каміл (бл. 850 р. Н.е.. — бл. 930 р. Н.е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного і результатів інших математичних перетворень над ірраціональними і раціональними числами. Ал Хазін (900 р. Н.е.. — 971 р. Н.е..) Подає таке визначення раціональної та ірраціональної величини:
Нехай одинична величина міститься в даній величині один або кілька разів, тоді ця [дана] величина відповідає цілому числу … Кожна величина, яка становить половину, або третину, або чверть одиничної величини, або, порівняно з одиничною величиною становить три п’ятих від неї, це раціональна величина. І в цілому, будь-яка величина, яка відноситься до одиничної як одне число до іншого, є раціональною. Якщо ж величина не може бути представлена як кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів.
Багато з цих ідей були пізніше перейняті європейськими математиками після перекладу на латину арабських текстів в XII столітті. Аль Хассар, арабська математик з Магрибу, який спеціалізувався на ісламських законах про спадщину, в XII столітті ввів сучасну символьну математичну нотацію для дробів, розділивши чисельник і знаменник горизонтальною лінією. Та ж нотація з’явилася потім в роботах Фібоначчі в XIII столітті. Протягом XIV-XVI ст. Мадхава з Сангамаграми і представники Керальской школи астрономії та математики досліджували нескінченні ряди, що сходяться до деяких ірраціональним числам, наприклад, до π, а також показали ірраціональність деяких тригонометричних функцій. Джестадева привів ці результати в книзі «Йуктібхаза».
Новий час
Ланцюгові дроби. тісно пов’язані з ірраціональними числами (ланцюговий дріб, що представляє дане число, нескінченна тоді і тільки тоді, коли число є ірраціональним), були вперше досліджені Катальді в 1613 році, потім знову привернули до себе увагу в роботах Ейлера, а на початку XIX століття — в роботах Лагранжа. Діріхле також вніс значний вклад в розвиток теорії ланцюгових дробів. У 1761 року Ламберт з помощю ланцюгових дробів показав, що π не є раціональним числом, а також що e x> і tg x x> ірраціональні при будь-якому ненулевом раціональному x. Хоча доказ Ламберта можна назвати незавершеним, прийнято вважати його досить суворим, особливо з огляду на час його написання. Лежандр в 1794 році, після введення функції Бесселя — Кліффорда, показав, що π 2> ірраціонально, звідки ірраціональність π слід тривіально (раціональне число в квадраті дало б раціональне).
Існування трансцендентних чисел було доведено Ліувілль в 1844-1851 роках. Пізніше Георг Кантор (1873) показав їх існування, використовуючи інший метод, і обгрунтував, що будь-який інтервал речового ряду містить нескінченно багато трансцендентних чисел. Шарль Ерміта довів в 1873 році, що e трансцендентно, а Фердинанд Ліндеман в 1882 році, грунтуючись на цьому результаті, показав трансцендентність π. Доказ Ліндеманна було потім спрощено Вейерштрассом в 1885 році, ще більш спрощено Давидом Гільбертом в 1893 році і, нарешті, доведено до майже елементарного Адольфом Гурвіцем і Паулем Горданом.
Схожі статті
jak.magey.com.ua
ірраціональні числа
Визначення ірраціонального числа
Ірраціональними називають такі числа, які в десяткового запису є нескінченні неперіодичні десяткові дроби.

Так, наприклад, числа, отримані шляхом вилучення квадратного кореня з натуральних чисел, є ірраціональними і не є квадратами натуральних чисел. Але не всі ірраціональні числа отримують шляхом вилучення квадратних коренів, адже отримане шляхом розподілу, число «пі», також є ірраціональним, і його ви навряд чи отримаєте, намагаючись витягти квадратний корінь з натурального числа.
Властивості ірраціональних чисел
Числа, не є ірраціональними
Іноді досить складно відповісти на питання, чи є число ірраціональним, особливо у випадках, коли число має вигляд десяткового дробу або у вигляді числового виразу, кореня або логарифма.
Тому не зайвим буде знати, які числа не належать до ірраціональним. Якщо слідувати визначення ірраціональних чисел, то нам вже відомо, що раціональні числа не можуть бути ірраціональними.
Ірраціональними числами не є:
• По-перше, всі натуральні числа;
• По-друге, цілі числа;
• По-третє, звичайні дроби;
• По-четверте, різні змішані числа;
• По-п’яте, це нескінченні періодичні десяткові дроби.
Крім усього перерахованого, ірраціональним числом не може бути будь-яка комбінація раціональних чисел, яка виконується знаками арифметичних операцій, як +, -, •. так як при цьому підсумком двох раціональних чисел буде також раціональне число.
А тепер подивимося, які ж з чисел є ірраціональними:
Цікаві факти

А чи відомо вам про існування фан-клубу, де шанувальники цього загадкового математичного феномена шукають все нові відомості про Пі, намагаючись розгадати його таємницю. Членом цього клубу може сталь будь-яка людина, яка знає напам’ять певну кількість чисел Пі після коми;
А чи знаєте ви, що в Німеччині під охороною ЮНЕСКО знаходиться палац Кастадель Монте, завдяки пропорціям якого можна обчислити Пі. Цілий палац присвятив цьому числу король Фрідріх II.
Виявляється, число Пі намагалися використовувати при будівництві Вавилонської вежі. Але на превеликий жаль, це призвело до краху проекту, так як на той момент було недостатньо вивчено точне обчислення значення Пі.
Співачка Кейт Буш у своєму новому диску записала пісню під назвою «Пі», в якій прозвучало сто двадцять чотири числа з знаменитого числового ряду 3, 141 ….
Схожі статті
jak.magey.com.ua
Ірраціональні числа вікі
Ірраціональне число — це дійсне число. яке не є раціональним. тобто не може бути представлено у вигляді дробу m n >>. де m — ціле число. n — натуральне число. Ірраціональне число може бути представлено у вигляді нескінченної неперіодичної десяткового дробу.
Безліч ірраціональних чисел зазвичай позначається великою латинською літерою I> в напівжирному зображенні без заливки. Таким чином: I = R # X2216; Q = \ mathbb \ backslash \ mathbb>. тобто безліч ірраціональних чисел є різниця множин речових і раціональних чисел.
Про існування ірраціональних чисел, точніше відрізків. несумірних з відрізком одиничної довжини, знали вже стародавні математики: їм була відома, наприклад, несумісність діагоналі і сторони квадрата, що рівносильно ірраціональності числа 2 >>.
Властивості [| ]
Приклади [| ]
Приклади докази ірраціональності [| ]
Зведено передбачуване рівність в квадрат:
У канонічний розклад лівій частині рівності число 2 входить в парному ступеня, а в розкладання 2n 2 — в непарній. Тому рівність m 2 = 2n 2 неможливо. Значить, вихідне припущення було невірним, і 2 >> — ірраціональне число.
Двійковий логарифм числа 3 [| ]
log 2 # X2061; 3 = m n # X21D2; m = n log 2 # X2061; 3 # X21D2; 2 m = 2 n log 2 # X2061; 3 = (2 log 2 # X2061; 3) n = 3 n 3 => \ Rightarrow m = n \ log _3 \ Rightarrow 2 ^ = 2 ^ 3> = \ left (2 ^ 3> \ right) ^ = 3 ^>
Але 2 m> парно, а права частина отриманого рівності непарна. Отримуємо протиріччя.
Історія [| ]
Античність [| ]
Концепція ірраціональних чисел була неявним чином сприйнята індійськими математиками в VII столітті до нашої ери, коли Манава (бл. 750 р. До н.е.. — бл. 690 р. До н.е..) З’ясував, що квадратний корінь деяких натуральних чисел, таких як 2 і 61, не можуть бути явно виражені [джерело не вказано 672 дня].
Перший доказ існування ірраціональних чисел зазвичай приписується Гіппаса з Метапонта (бл. 500 рр. До н. Е.), Піфагорійці. За часів піфагорійців вважалося, що існує єдина одиниця довжини, досить мала і неподільна, яка ціле число раз входить в будь-який відрізок [джерело не вказано 672 дня].
Немає точних даних про те, ірраціональність якого числа було доведено Гіппаса. Згідно з легендою він знайшов його вивчаючи довжини сторін пентаграми. Тому розумно припустити, що це було золотий перетин [джерело не вказано 643 дня].
Грецькі математики назвали це відношення несумірних величин алогос (невимовним), проте згідно з легендами не віддати Гіппаса належної поваги. Існує легенда, що Гиппас зробив відкриття, перебуваючи в морському поході, і був викинутий за борт іншими піфагорійцями «за створення елементи всесвіту, який заперечує доктрину, що все суті у всесвіті можуть бути зведені до цілих чисел і їх відносин». Відкриття Гіппаса поставило перед піфагорейської математикою серйозну проблему, зруйнувавши яке лежало в основі всієї теорії припущення, що числа і геометричні об’єкти єдині і нероздільні.
Феодор Киренский довів ірраціональність коренів натуральних чисел до 17 (виключаючи, природно, точні квадрати — 1, 4, 9 та 16), але зупинився на цьому, тому що имевшаяся в його інструментарії алгебра не дозволяла довести ірраціональність квадратного кореня з 17. З приводу того , яким могло бути це доказ, істориками математики було висловлено кілька різних припущень. Згідно найбільш правдоподібного [2] припущенням Жана ІТАР [fr]. воно було засноване на теоремі про те, що непарне квадратне число ділиться на вісім із залишком один [3].
Пізніше Евдокс Кнідський (410 або 408 р. До н.е.. — 355 або 347 р. До н.е..) Розвинув теорію пропорцій, яка брала до уваги як раціональні, так і ірраціональні відносини. Це послужило підставою для розуміння фундаментальної суті ірраціональних чисел. Величина стала вважатися не числом, але позначенням сутностей, таких як відрізки прямих, кути, площі, обсяги, проміжки часу — сутностей, які можуть змінюватися безперервно (в сучасному розумінні цього слова). Величини були протиставлені числах, які можуть змінюватися лише «стрибками» від одного числа до сусіднього, наприклад, з 4 на 5. Числа складаються з найменшою неподільною величини, в той час як величини можна зменшувати нескінченно.
Оскільки жодне кількісне значення не пов’язана із величиною, Евдокс зміг охопити і співмірні, і несумірні величини при визначенні дробу як відносини двох величин, і пропорції як рівності двох дробів. Прибравши з рівнянь кількісні значення (числа), він уникнув пастки, що складається в необхідності назвати ірраціональну величину числом. Теорія Евдокса дозволила грецьким математикам зробити неймовірний прогрес в геометрії, надавши їм необхідне логічне обгрунтування для роботи з непомірними величинами. «Книга 10 Елементів» Евкліда присвячена класифікації ірраціональних величин.
Середні століття [| ]
Середні століття ознаменувалися прийняттям таких понять як нуль, негативні числа, цілі і дробові числа, спершу індійськими, потім китайськими математиками. Пізніше приєдналися арабські математики, які першими стали вважати негативні числа алгебраїчними об’єктами (поряд і на рівних правах з позитивними числами), що дозволило розвинути дисципліну, нині звану алгеброю.
Раціональної [величиною] є, наприклад, 10, 12, 3%, 6% і так далі, оскільки ці величини вимовлені і виражені кількісно. Що не раціонально, то ірраціонально, і неможливо вимовити або надати відповідну величину кількісно. Наприклад, квадратний корінь чисел таких так 10, 15, 20 — не є квадратами.
На противагу концепції Евкліда, що величини суть в першу чергу відрізки прямих, Аль Махане вважав цілі числа і дроби раціональними величинами, а квадратні і кубічні корені — ірраціональними. Він також ввів арифметичний підхід до безлічі ірраціональних чисел, оскільки саме він показав ірраціональність наступних величин:
результат складання ірраціональної величини і раціональної, результат віднімання раціональної величини з ірраціональної, результат віднімання ірраціональної величини з раціональної.
Єгипетський математик Абу Каміл (бл. 850 р. Н.е.. — бл. 930 р. Н.е..) Був першим, хто визнав прийнятним визнати ірраціональні числа рішенням квадратних рівнянь або коефіцієнтами в рівняннях — в основному, у вигляді квадратних або кубічних коренів, а також коренів четвертого ступеня. У X столітті іракський математик Аль Хашимі вивів загальні докази (а не наочні геометричні демонстрації) ірраціональності твори, приватного і результатів інших математичних перетворень над ірраціональними і раціональними числами. Ал Хазін (900 р. Н.е.. — 971 р. Н.е..) Подає таке визначення раціональної та ірраціональної величини:
Нехай одинична величина міститься в даній величині один або кілька разів, тоді ця [дана] величина відповідає цілому числу … Кожна величина, яка становить половину, або третину, або чверть одиничної величини, або, порівняно з одиничною величиною становить три п’ятих від неї, це раціональна величина. І в цілому, будь-яка величина, яка відноситься до одиничної як одне число до іншого, є раціональною. Якщо ж величина не може бути представлена як кілька або частина (l / n), або кілька частин (m / n) одиничної довжини, вона ірраціональна, тобто невимовна інакше як за допомогою коренів.
Багато з цих ідей були пізніше перейняті європейськими математиками після перекладу на латину арабських текстів в XII столітті. Аль Хассар, арабська математик з Магрибу, який спеціалізувався на ісламських законах про спадщину, в XII столітті ввів сучасну символьну математичну нотацію для дробів, розділивши чисельник і знаменник горизонтальною лінією. Та ж нотація з’явилася потім в роботах Фібоначчі в XIII столітті. Протягом XIV-XVI ст. Мадхава з Сангамаграми і представники Керальской школи астрономії та математики досліджували нескінченні ряди, що сходяться до деяких ірраціональним числам, наприклад, до π, а також показали ірраціональність деяких тригонометричних функцій. Джестадева привів ці результати в книзі «Йуктібхаза».
Новий час [| ]
Ланцюгові дроби. тісно пов’язані з ірраціональними числами (ланцюговий дріб, що представляє дане число, нескінченна тоді і тільки тоді, коли число є ірраціональним), були вперше досліджені Катальді в 1613 році, потім знову привернули до себе увагу в роботах Ейлера, а на початку XIX століття — в роботах Лагранжа. Діріхле також вніс значний вклад в розвиток теорії ланцюгових дробів. У 1761 року Ламберт з помощю ланцюгових дробів показав, що # X03C0; не є раціональним числом, а також що e x> і tg # X2061; x x> ірраціональні при будь-якому ненулевом раціональному x. Хоча доказ Ламберта можна назвати незавершеним, прийнято вважати його досить суворим, особливо з огляду на час його написання. Лежандр в 1794 році, після введення функції Бесселя — Кліффорда. показав, що # X03C0; 2> ірраціонально, звідки ірраціональність # X03C0; слід тривіально (раціональне число в квадраті дало б раціональне).
Існування трансцендентних чисел було доведено Ліувілль в 1844-1851 роках. Пізніше Георг Кантор (1873) показав їх існування, використовуючи інший метод, і обгрунтував, що будь-який інтервал речового ряду містить нескінченно багато трансцендентних чисел. Шарль Ерміта довів в 1873 році, що e трансцендентно, а Фердинанд Ліндеман в 1882 році, грунтуючись на цьому результаті, показав трансцендентність # X03C0; . Доказ Ліндеманна було потім спрощено Вейерштрассом в 1885 році, ще більш спрощено Давидом Гільбертом в 1893 році і, нарешті, доведено до майже елементарного Адольфом Гурвіцем і Паулем Горданом.
Див. Також [| ]
Примітки [| ]
Схожі статті
jak.magey.com.ua
Що таке ірраціональні числа.
Ірраціональні числа відносяться до речових, але не є раціональними, тобто їх точне значення невідоме. Але якщо мається опис способу, яким було отримано ірраціональне число, то воно вважається відомим. Іншими словами, його значення можна обчислити з необхідною точністю.

Відповідно до понять геометрії, якщо в двох відрізках міститься якась кількість однакових значень, то вони сумірні. Наприклад, різні сторони прямокутника сумірні. Але от сторона квадрата і його діагональ не є сумірними. Вони не мають спільної міри, в якій їх можна було б висловити. Ірраціональні числа відносяться до неявно вираженим. Вони несумірні з раціональними числа мі.К раціональним ставляться цілі, дробові, а також кінцеві і періодичні десяткові числа . Вони є сумірними одиниці. Нескінченні десяткові неперіодичні дроби називають ірраціональними, з одиницею вони несумірні. Але може бути вказаний спосіб отримання такого числа , тоді вона вважається заданим точно. За допомогою такого способу можна знайти будь-яку кількість знаків після коми у ірраціонального числа , це називається обчислити число з певною точністю, яка якраз і задається кількістю необхідних до обчислення знаков.Свойства ірраціональних чисел в чому схожі з властивостями раціональних . Наприклад, порівнюються вони однаково, над ними можливо виробляти ті ж самі арифметичні дії, вони можуть бути позитивними чи негативними. Множення ірраціонального числа на нуль, точно так само як і раціонального, дає ноль.Еслі операція проводиться над двома числа ми, одне з яких раціональне, а інше ірраціональне, то прийнято по можливості не використовувати наближене значення, а брати точним чином заданий число (наприклад, у вигляді недесяткових дроби) Вважається, що першим концепцію ірраціональних чисел відкрив Гіппас Метапонтський, що жив приблизно в VI в. до н.е. Він був послідовником піфагорейської школи. Своє відкриття Гиппас скоїв під час морського походу, перебуваючи на кораблі. Згідно з легендою, коли він розповів іншим піфагорійцям про ірраціональні числа х, надавши доказ їхнього існування, ті вислухали його і визнали його викладки правильними. Проте, відкриття Гиппаса настільки шокувало їх, що він був викинутий за борт за те, що створив щось, що спростовує центральну пифагорейскую доктрину про те, що все у всесвіті може бути зведене до цілим числа м і їх відносинам.
tips-ua.com
Ірраціональні числа — Gpedia, Your Encyclopedia
Математична константа пі (π) є ірраціональним числом. Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом.
Число 2{\displaystyle \scriptstyle {\sqrt {2}}} є ірраціональним числом.Ірраціональні числа (позначення для множини — I{\displaystyle \mathbb {I} }) — це всі дійсні числа, що не є раціональними: I=R∖Q{\displaystyle \mathbb {I} =\mathbb {R} \setminus \mathbb {Q} }, — тобто не можуть бути записані як відношення цілих чисел zn{\displaystyle {\frac {z}{n}}} (z∈Z{\displaystyle z\in \mathbb {Z} }, n∈N{\displaystyle n\in \mathbb {N} }), а лише нескінченними неперіодичними десятковими дробами.
Уперше І. ч. постали в геометрії під час вивчення довжин відрізків піфагорцями, які, як стверджує легенда[джерело?], виявили неспівмірність з одиничною деяких геометричних величин. Оскільки це суперечило їхній філософії (цілком побудованій на натуральних числах), відкриття якнайсуворіше були приховували, навіть покаравши на смерть одного зі своїх братів — Гіппаса Метапонтського, який (за різними джерелами) чи-то першим знайшов, чи-то розголосив цей факт.
Відмінності записування дійсних чисел
Десятковий дріб будь-якого раціонального числа має періодично повторювану частину (зокрема це можуть бути нулі, як у скінченних дробів і цілих чисел), н-д:
- 13=.3¯{\displaystyle {\frac {1}{3}}={}.{\overline {3}}},[1] що означає «нуль цілих і три в періоді» (довжина періоду — один), тобто 3{\displaystyle 3} повторюється нескінчену кількість разів;
- 227=3.142857¯{\displaystyle {\frac {22}{7}}=3.{\overline {142857}}}, що означає «три цілих і сто сорок дві тисячі вісімсот п’ятдесят сім у періоді» (довжина періоду — шість), тобто 142857{\displaystyle 142857} повторюється нескінчену кількість разів;
- 265132=2.0075¯{\displaystyle {\frac {265}{132}}=2.00{\overline {75}}}, що означає «дві цілих, нуль сотих і сімдесят п’ять у періоді» (довжина періоду — два), тобто 75{\displaystyle 75} повторюється нескінчену кількість разів;
- 52=2.5≡2.50¯{\displaystyle {\frac {5}{2}}=2.5\equiv 2.5{\overline {0}}}, скінченний дріб «дві цілих, п’ять десятих»,[2] тобто 0{\displaystyle 0} повторюється нескінчену кількість разів;
- 31=3.≡2.9¯{\displaystyle {\frac {3}{1}}=3.{}\equiv 2.{\overline {9}}}, ціле число «три еквівалентне двом цілим і дев’ять у періоді»,[3] тобто 9{\displaystyle 9} повторюється нескінчену кількість разів.
Періодичність дробу можна вважати критерієм приналежності числа до множини раціональних чисел.
Розкладання І. ч. у десятковий дріб не позначається такою періодичністю. Наприклад, відомо, що число пі — ірраціональне та навіть трансцендентне, тому, хоча в його десятковому записі окремі цифри та їх комбінації повторюються, не існує групи цифр, яка б нескінченно повторювалася, утворюючи період.
Інший спосіб записування додатних дійсних чисел: за допомогою ланцюгових дробів. Відмінність полягає в тому, що ланцюгові дроби раціональних чисел скінченні, а І. ч. — нескінченні, хоча для квадратичних ірраціональностей ланцюговий дріб періодичний.
Приклади
Квадратні корені
Квадратний корінь з двох — це перше число, ірраціональність якого було доведено. Іншим відомим ірраціональним числом є золотий перетин. Квадратні корені усіх натуральних чисел, які не є квадратними числами, є ірраціональними.
Приклади
- 355113=3+17+116,{\displaystyle {\frac {355}{113}}=3+{\cfrac {1}{7+{\cfrac {1}{16}}}},} — скінченний;
- 2=1+12+12+12+…=[1;2,2,2…]=[1;(2)]{\displaystyle {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ldots }}}}}}=[1;2,2,2\ldots ]=[1;(2)]} — з періодом довжини один;
- 3=1+11+12+11+12+…=[1;1,2,1,2…]=[1;(1,2)]{\displaystyle {\sqrt {3}}=1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+\ldots }}}}}}}}=[1;1,2,1,2\ldots ]=[1;(1,2)]} — з періодом довжини два;
- π=3+17+115+11+1292+…=[3;7,15,1,292,1,1,1,2,…]{\displaystyle \pi =3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+\ldots }}}}}}}}=[3;7,15,1,292,1,1,1,2,\ldots ]} (A001203 в енциклопедії цілих послідовностей) — неперіодичний.
Філософське значення
Про існування неспівмірних відрізків знали вже древні математики: їм була відома, наприклад, неспівмірність діагоналі та сторони квадрата, що рівносильно ірраціональності числа 2{\displaystyle {\sqrt {2}}} (перше знайдене І. ч.).
Піфагорове твердження, що всі речі є числа, відображало метафізичні уявлення стародавніх греків про Всесвіт як місце гармонії, яку власне можна описати відношеннями натуральних чисел. Так поєднання двох звуків, відношення частот яких є раціональним числом, дає приємне для вуха звучання.
З’ясування того, що 2≈1,4142135{\displaystyle {\sqrt {2}}\approx 1{,}4142135} не є раціональним числом, призвело до глибокої кризи давньогрецької математики, яка полягала в усвідомлені факту існування математичних величин, які не можливо відобразити числами, а лише через геометричні побудови. Як наслідок — давньогрецька математика відмовилася від алгебраїчного підходу, на користь геометричного.
Властивості
Топологічні властивості R∖Q{\displaystyle \mathbb {R} \setminus \mathbb {Q} }
Примітки
- ↑ Тут використано англійську систему записування дробів без нулів. У пострадянських країнах для розділення цілої частини від дробної використовують кому замість крапки, а для позначення повторюваної частини — дужки замість верхньої риски.
- ↑ Десяткові дроби є нескінченними за побудовою, тому зрозуміло, що після певного десяткового знака можуть стояти самі нулі (a0,a1…an000…{\displaystyle a_{0},a_{1}…a_{n}000…}), відкиданням яких отримують скінченні дроби.
- ↑ Можемо записати як нескінченний періодичний дріб, оскільки з означення маємо, що 2+910+9100+…=3{\displaystyle 2+{\frac {9}{10}}+{\frac {9}{100}}+…=3}.
- Докладніше: 0,(9)
Література
1.Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (вид. Dover reprint of 1978). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 507446.
www.gpedia.com
