Иррациональное неравенство – Иррациональные неравенства. Теория и примеры.

Иррациональные неравенства. Часть 2

13 июня 2013

В этом видеоуроке мы продолжаем разбирать иррациональные неравенства вида . Благодаря прошлому уроку мы знаем, что нельзя просто взять и возвести его обе стороны в квадрат, потому что мы рискуем потерять большой кусок решения. Поэтому предлагаю еще раз записать общую формулу, по которой решаются все подобные задачи:

Erroneous nesting of equation structures

\begin{align}& \left\{ \begin{align}& g\ge 0 \\& f\rangle {{g}^{2}} \\\end{align} \right. \\& \left\{ \begin{align}& g\langle 0 \\& f\ge 0 \\\end{align} \right. \\\end{align}

Вот такая совокупность из двух выражений. Теперь с помощью этой формулы попробуем посчитать:

x+−x2+8x−12−−−−−−−−−−−√⟩4×2+8x−12−−−−−−−−−−√⟩4−x

\begin{align}& x+\sqrt{-{{x}^{2}}+8x-12}\rangle 4 \\& \sqrt{{{x}^{2}}+8x-12}\rangle 4-x \\\end{align}

Предлагаю сначала рассмотреть первую иррациональную конструкцию, когда правая часть больше или равна нулю:

{4−x≥0−x2+8x−12⟩(4−x)2

\left\{ \begin{align}& 4-x\ge 0 \\& -{{x}^{2}}+8x-12\rangle {{(4-x)}^{2}} \\\end{align} \right.

Первое решается просто:

\[\begin{array}{·{35}{l}}

4\text{ }-\text{ }\text{ }\ge \text{ }0 \\-\text{ }\ge \text{ }-4 \\\text{ }\le \text{ }4 \\\end{array}\]

Со вторым все чуть сложнее:

−x2+8x−12>16−2×2+16x−28>0|:2(−2)x2−8x+14<0

\begin{align}& -{{x}^{2}}+8x-12>16 \\& -2{{x}^{2}}+16x-28>0|:2(-2) \\& {{x}^{2}}-8x+14<0 \\\end{align}

Теперь найдем иксы:

D = 64 − 4 ⋅ 14 = 64 − 56 = 8D−−√=8√=4⋅2−−−√=22√

\begin{align}& D\text{ }=\text{ }64\text{ }-\text{ }4\text{ }\cdot \text{ }14\text{ }=\text{ }64\text{ }-\text{ }56\text{ }=\text{ }8 \\& \sqrt{D}=\sqrt{8}=\sqrt{4\cdot 2}=2\sqrt{2} \\\end{align}

Давайте найдем иксы:

x1=8+22√2=4+2√x2=4−2√

\begin{align}& {{x}_{1}}=\frac{8+2\sqrt{2}}{2}=4+\sqrt{2} \\& {{x}_{2}}=4-\sqrt{2} \\\end{align}

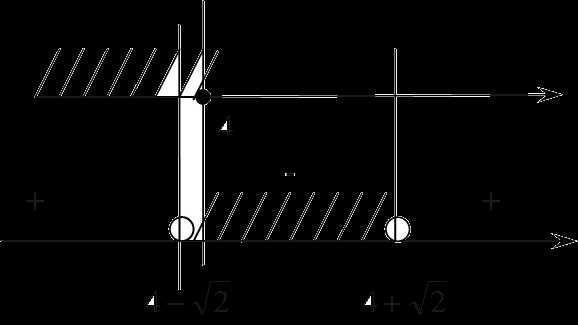
Мы получили два числа, отмечаем их на прямой. Поскольку неравенство строгое, точки выколотые:

[Подпись к рисунку]

Смотрим знаки. Для этого подставим любое число, больше наших корней. Справа стоит «плюс», далее везде «плюс» и «минус» меняются, поскольку нигде нет корней четной кратности. Поскольку нам нужно найти «меньше», поэтому нас интересует интервал «минус». Осталось пересечь его решением второго неравенства. Для этого отметим наше множество на параллельных прямых:

Пересекаем и видим, что единственное, что нас устраивает — это

x∈(4−2√;4]

x\in (4-\sqrt{2};4]

Переходим ко второй части нашей совокупности. Теперь мы будем требовать, чтобы правая была меньше нуля, а подкоренное выражение больше или равно нулю, т. е.:

{4−x⟨0−x2+8x−12≥0

\left\{ \begin{align}& 4-x\langle 0 \\& -{{x}^{2}}+8x-12\ge 0 \\\end{align} \right.

Вот наша вторая система. Решаем ее.
Первое неравенство иррациональной системы решается очень легко:

\[\begin{array}{·{35}{l}}

4\text{ }-\text{ }\text{ }<\text{ }0 \\-\text{ }<\text{ }-4 \\\text{ }>\text{ }4 \\\end{array}\]

Посчитаем второе:

−x2+8x−12≥0|:(−1)x2−8x+12≤0

\begin{align}& -{{x}^{2}}+8x-12\ge 0|:(-1) \\& {{x}^{2}}-8x+12\le 0 \\\end{align}

Решаем это уравнение нашей иррациональной конструкции, используя формулыВиета:

(x−6)(x−2)≤0x1=6×2=2

\begin{align}& (x-6)(x-2)\le 0 \\& {{x}^{1}}=6 \\& {{x}^{2}}=2 \\\end{align}

Отмечаем эти числа на прямой:

[Подпись к рисунку]

Берем 1 млрд. и подставляем в нашу конструкцию, чтобы определить знаки. Первый из них будет «плюс», далее они меняются, потому что корней четно кратности нет. Нас интересует то, что меньше 0, т. е. там, где стоит «минус».
Теперь предлагаю пересечь решение нашего неравенства с результатами второго, начертив параллельные прямые:

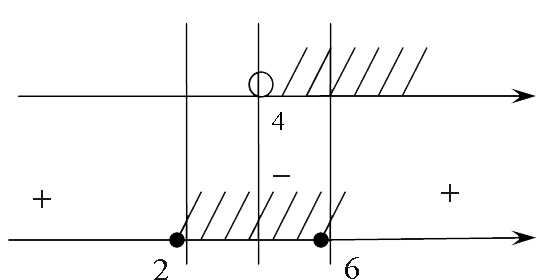[Подпись к рисунку]

Единственный отрезок, заштрихованный на обеих прямых — это от четырех до шести до 6. Вот мы и получили ответ ко второй системе из нашей иррациональной совокупности:

∈(4; 6]

\text{ }\in \left( 4;\text{ }6 \right]

И вот мы уже очень близки к ответу. Осталось объединить интервалы, которые мы нашли. Отметим найденные точки на прямой:

[Подпись к рисунку]

От нас требуется объединить эти отрезки. Получаем:

Обратите внимание, мы именно объединили эти отрезки, а не пересекли, потому что в случае пересечения у нас бы получилось пустое множество, а не интервал.

Это ответ. Задача решена.

Ключевые моменты

В предыдущем уроке (см. урок «Иррациональные неравенства. Часть 1» мы рассмотрели самый простой тип иррациональных неравенств — когда корень меньше функции. Но и там на выходе получилась система, которую надо аккуратно решать.

Сегодня мы рассмотрели более жесткий тип иррациональных неравенств, когда корень больше функции. При решении таких неравенств возникает уже две системы, решения которых надо объединить (не пересечь, а именно объединить!), чтобы получился окончательный ответ.

Поскольку на иррациональных неравенствах такого вида регулярно «обламываются» даже весьма подготовленные ученики (каюсь — сам завалил контрольную в 10-м классе), предлагаю вашему вниманию сразу два видеоурока, в которых разобран буквально каждый шаг решения. Чтобы при одном виде таких неравенств в вашей голове проскакивала мысль: «Нельзя возводить в квадрат! Тут что-то еще!»

Вот первый урок:

Смотрите также:

1. Нестандартные иррациональные неравенства
2. Иррациональные неравенства. Часть 1
3. Тест по теории вероятностей (1 вариант)
4. Правила вычисления производных
5. Тест: простейшие показательные уравнения (1 вариант)
6. Как решать простейшие логарифмические уравнения

www.berdov.com

Иррациональные неравенства

Стандартное иррациональное неравенство (\(\lor\) — один из знаков \(\geqslant,>,\leqslant,<\)):

 

\[{\Large{I. \ \sqrt{f(x)}\lor a}},\quad a\ -\ \text{число.}\] Для того, чтобы решить данное неравенство, нужно посмотреть на знак числа \(a\), на знак неравенства, а также помнить, что \(\sqrt{f(x)}\) всегда неотрицателен и \(f(x)\geqslant 0\). Если обе части неравенства неотрицательны, то можно возводить их в квадрат.

 

Например:

 

1) \(\sqrt{f(x)}\geqslant 5\). Корень из числа будет \(\geqslant 5\) тогда и только тогда, когда само число \(\geqslant 25\). В этом случае ОДЗ (\(f(x)\geqslant 0\)) учитывается автоматически, следовательно, данное неравенство равносильно неравенству
\(f(x)\geqslant 25\).

 

2) \(\sqrt{f(x)}>-2\). Т.к. по определению квадратного корня \(\sqrt{f(x)}\geqslant 0\) всегда, то данное неравенство выполняется при всех \(x\), при которых выполнено ОДЗ. Значит, решением данного неравенства является только ОДЗ: \(f(x)\geqslant 0\).

 

3) \(\sqrt{f(x)}<-2\). Т.к. по определению квадратного корня \(\sqrt{f(x)}\geqslant 0\) всегда, то данное неравенство не выполняется ни при каких \(x\). Следовательно, решением неравенства является пустое множество: \(x\in \varnothing\).

\[{\Large{II. \ \sqrt{f(x)}\lor g(x)}}\] В данном неравенстве справа стоит уже функция \(g(x)\), которая может быть как отрицательной, так и неотрицательной. Таким образом, в данном неравенстве необходимо рассматривать отдельно эти два случая, а также не забыть про ОДЗ.

 

Например:

 

1) \(\sqrt{f(x)}\leqslant g(x)\). При условии \(f(x)\geqslant 0\) : если \(g(x)\geqslant 0\), то можно возвести в квадрат; если \(g(x)<0\), то в силу определения квадратного корня данное неравенство никогда не может быть выполнено.
Таким образом, данное неравенство равносильно совокупности: \[\left[ \begin{gathered} \begin{aligned} & \begin{cases} g\geqslant 0\\ 0\leqslant f\leqslant g^2\end{cases}\\ & \begin{cases} g<0\\ x\in \varnothing \end{cases} \end{aligned} \end{gathered} \right. \Leftrightarrow \begin{cases} g\geqslant 0\\ 0\leqslant f\leqslant g^2\end{cases}\]

2) \(\sqrt{f(x)}> g(x)\). При условии \(f(x)\geqslant 0\) : если \(g(x)\geqslant 0\), то можно возвести в квадрат; если \(g(x)<0\), то в силу определения квадратного корня данное неравенство всегда выполняется.
Таким образом, данное неравенство равносильно совокупности: \[\left[ \begin{gathered} \begin{aligned} & \begin{cases} g\geqslant 0\\ f> g^2\\f\geqslant 0\end{cases}\\ & \begin{cases} g<0\\ f\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} \begin{aligned} & \begin{cases} g\geqslant 0\\ f> g^2\end{cases}\\ & \begin{cases} g<0\\ f\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right.\]

shkolkovo.net

Разработка занятия по математике на тему «Иррациональные неравенства» (11 класс)

Тема занятия: Иррациональные неравенства

(изучение нового материала)

Цели педагога: создать условия учащимся

• для формирования представлений об основном методе решения иррациональных неравенств – методе возведения обеих частей в одну и ту же степень и сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем; о доказательстве неравенства методом от противного;

• овладения умением использовать для доказательства неравенства методы: с помощью определения, от противного.

Цели ученика: изучить тему «Иррациональные неравенства» и получить последовательную систему математических знаний, необходимую для изучения школьных естественнонаучных дисциплин на профильном уровне. Для этого необходимо:

• иметь представление об основном методе решения иррациональных неравенств – методе возведения обеих частей в одну и ту же степень и сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем; о доказательстве неравенства методом от противного;

• овладение умением использования метода решения иррациональных неравенств – метода возведения обеих частей в одну и ту же степень.

Планируемые результаты изучения темы:

Личностные: проявлять познавательный интерес к изучению предмета.

Предметные: уметь использовать метод возведения обеих частей неравенства в одну и ту же степень.

Метапредметные результаты изучения темы (универсальные учебные действия): регулятивные: учитывать правило в планировании и контроле способа решения; познавательные: строить речевое высказывание в устной и письменной форме; свободная работа с текстом научного стиля; коммуникативные: договариваться и приходить к общему решению совместной деятельности, в том числе в ситуации столкновения интересов.

Сценарий занятия

Этап урока

Действия учителя

Действия ученика

1. Организационный момент.

Сообщить тему занятия, сформулировать цели занятия.

Тему записывают в тетрадь

2. Изучение нового материала (лекция).

Определение иррационального неравенства, метод решения.

Определение. Под иррациональным неравенством понимается неравенство, в котором неизвестные величины (или некоторые функции неизвестных величин) находятся под знаком радикала.

Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем.

Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, т.е. найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или её частях. При решении иррационального неравенства приходится, как правило, возводить обе части неравенства в натуральную степень. При этом необходимо следить за тем, чтобы при преобразовании неравенств каждый раз получалось неравенство, равносильное исходному на ОДЗ.

При решении иррациональных неравенств следует помнить, что при возведении обеих частей неравенства в нечётную степень всегда получается неравенство, равносильное исходному неравенству. Если же обе части неравенства возводить в чётную степень, то будет получаться неравенство, равносильное исходному и имеющее тот же знак лишь в случае, если обе части исходного неравенства неотрицательны.

Рассмотрим равносильность простейших иррациональных неравенств.

Иррациональные неравенства, содержащие корни в нечётной степени.

Пусть неравенство содержит корни в нечётной степени:

1. Неравенство вида , nN, равносильно неравенству .

2. Неравенство вида , nN, равносильно неравенству .

3. Неравенство вида , nN, равносильно неравенству .

4. Неравенство вида > , nN, равносильно неравенству .

Эти неравенства после возведения в нужную степень становятся рациональными и решаются методом интервалов.

Иррациональные неравенства, содержащие корни в чётной степени.

Рассмотрим решения неравенств, содержащих корни в чётной степени. Эти неравенства решаются более сложно, чем предыдущие.

1. Неравенство вида < , nN, равносильно системе

2. Неравенство вида , nN, равносильно системе

3. Неравенство вида > , nN, равносильно совокупности двух систем неравенств:

Конспектируют теоретический материал в тетрадь

3. Первичное закрепление

Примеры решения неравенств, содержащих корни в нечётной степени.

Рассмотрим примеры.

Пример 1 (записывает на доске с комментариями).

Решить неравенство .

Решение. Возведём обе части неравенства в третью степень, получим линейное неравенство Решая его получим

Ответ.

Пример 2 (контроль правильности решения и записи). Решить неравенство

Решение. Данное неравенство определено для всех х. Возведём обе его части в третью степень. Исходное неравенство тогда равносильно неравенству

Решая последнее неравенство, получим

Ответ.

Примеры решения неравенств, содержащих корни в чётной степени. Рассмотрим примеры решения некоторых конкретных иррациональных неравенств такого вида.

Пример 3 (записывает на доске с комментариями).

Решить неравенство .

Решение.

Согласно пункту 2, это иррациональное неравенство равносильно системе или или

Из первых двух неравенств найдём, что .

Решая квадратное уравнение получим корни x₁=-1, x₂=5. Поскольку ветви параболы левой части уравнения направлены вверх, то решением неравенства будет множество.

Найдём пересечение полученных множеств, получим ;).

Ответ.;).

Пример 4 (контроль правильности решения и записи)

Решить неравенство

Решение. Найдём ОДЗ данного неравенства. Это множество тех х, когда
Поскольку корнями левой части являются точки х₁ = 1 и х₂ = 5 и графиком левой части неравенства является парабола, ветви которой направлены вниз, то решением будет отрезок .

На ОДЗ исходное неравенство равносильно совокупности двух систем

Когда правая часть исходного неравенства неотрицательна, мы возводим в квадрат обе части, а когда правая часть отрицательна, то это неравенство верно для любого х из ОДЗ.

Решим сначала вторую систему этой совокупности. Имеем

Решением этой системы будет множество.

Решим первую систему совокупности. Имеем

Левая часть первого неравенства этой системы имеет корни х₁=3 и х₂=23/5, поэтому его решением будет множество . В пересечении с решением второго неравенства, мы получим промежуток .

Объединяя решения совокупности систем, получим .

Ответ..

Решение иррациональных неравенств более сложного вида.

Рассмотрим решение неравенств более сложного вида.

Пример 5. (контроль правильности решения и записи)

Решить неравенство

Решение. Найдём ОДЗ данного неравенства или Тогда ОДЗ будет множество

Решим сначала уравнение Корнями первого сомножителя являются точки х₁ = -1, х₂ = 3, а корнем второго – точка х₃ = 1. Значения х₂ = 3 и х₃ = 1, входящие в ОДЗ неравенства, обязательно должны войти в ответ.

Решим строгое неравенство . Поскольку второй сомножитель всегда неотрицателен, то неравенство будет выполняться, если . Решая его, получим Возьмём пересечение этого множества и ОДЗ, получим решение строгого неравенства на ОДЗ:

Поскольку точки х₂ = 3 и х₃ = 1 входят в ОДЗ неравенства, то мы их включим в ответ:

Ответ.

Пример 6 (записывает на доске с комментариями)

Решить неравенство

Решение. Найдём ОДЗ данного неравенства из решения системы

Решая её получим множество .

Поскольку на ОДЗ обе части исходного неравенства неотрицательны, поэтому, возведя левую и правую части этого неравенства в квадрат и приведя подобные члены, получим равносильное неравенство

Поскольку при или правая часть неравенства отрицательна, а левая часть неотрицательна, то неравенство справедливо при всех x.

Если , то для всех обе части неравенства (1) неотрицательны. Возведя обе части этого неравенства в квадрат и приведя подобные члены, получим неравенство

Решением этого неравенства будет множество В пересечении с отрезком [5/2; 5], мы получим промежуток (3; 5].

Объединяя множества решений, соответствующие двум рассмотренным случаям, получаем решение исходного неравенства (3; +∞).

Ответ. (3; +∞).

Пример 7. (записывает на доске с комментариями)

Решить неравенство

Решение. Областью допустимых значений данного неравенства будет множество
[-1; +∞). На этом множестве неравенство равносильно совокупности двух систем

Решим первую систему совокупности. Рассмотрим решение второго неравенства этой системы

или или или

Поскольку пересечение множеств решений первого и второго неравенств этой системы пусто, то у этой системы решений нет.

Решим вторую систему. Решением первого и второго неравенства этой системы будет множество

Решим последнее неравенство второй системы. Для этого приведём его к виду

Поскольку каждое слагаемое правой части этого неравенства больше соответствующего слагаемого левой части, то оно справедливо для всех х из ОДЗ. Поэтому решением второй системы будет множество [-1;+∞).

Ответ. [-1; +∞).

Записывают в тетрадь

На доске и в тетради

Записывают в тетрадь

На доске и в тетради

На доске и в тетради

Записывают в тетрадь

Записывают в тетрадь

4. Итог урока. Рефлексия

• Что нового узнали на уроке?

• Чему научились?

• Оцените свою работу на уроке.

Отвечают на вопросы

Список литературы

[1] Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. М.: Наука, 1987.

[2] Мельников И.И., Сергеев И.Н. Как решать задачи по математике на вступительных экзаменах. М.:МГУ, 1994.

[3] Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Математика. М.: Русское слово, 2001.

[4] Михайлова Ж.Н. Алгоритмы – ключ к решению задач по алгебре. 10 – 11 классы. М.: Просвещение, 2009.

infourok.ru

Решение иррациональных уравнений. Решение иррациональных неравенств.

Урок по теме: «Решение иррациональных уравнений. Решение иррациональных уравнений с помощью возведения обеих частей уравнения в n-ю степень». УМК Мордковича (профильный уровень), 11 класс.

Учитель первой квалификационный категории: Максименко Светлана Александровна, МАОУ «Лицей № 28 имнеи Н.А.Рябова» г.Тамбова.

Тип урока: обобщение и систематизация знаний.

Цели: вспомнить основные методы решения иррациональных уравнений; подготовка к ЕГЭ, воспитать трудолюбие.

Определение. Уравнение с одной переменной  называют иррациональным, если хотя бы одна из функций  или  содержит переменную под знаком радикала.

При решении иррациональных уравнений необходимо установить область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими.

1. Метод подбора

Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число  входит в множество значений, то уравнение  имеет единственное решение.”

Для реализации метода, основанного на этом утверждении требуется:

1) Выделить функцию, которая фигурирует в уравнении.

2) Записать область определения данной функции.

3) Доказать ее монотонность в области определения.

4) Угадать корень уравнения.

5) Обосновать, что других корней нет.

6) Записать ответ.

Пример 1. .

Наличие радикалов четной степени говорит о том, что подкоренные выражения должны быть неотрицательными. Поэтому сначала найдем область допустимых значение переменной .

Очевидно, что левая часть уравнения не существует ни при одном значении неизвестного . Таким образом, вопрос о решении уравнения снимается – ведь нельзя же осуществить операцию сложения в левой части уравнения, так как не существует сама сумма. Каков же вывод? Уравнение не может иметь решений, так как левая часть не существует ни при одном значении неизвестного .

Пример 2. 

Рассмотрим функцию .

Найдем область определения данной функции:

Данная функция является монотонно возрастающей.

Для  эта функция будет принимать наименьшее значение при , а далее только возрастать.. Число 5 принадлежит области значения, следовательно, согласно утверждению .

Проверкой убеждаемся, что это действительный корень уравнения..

2. Метод возведения обеих частей уравнений в одну и ту же степень.

Теорема.

Если возвести обе части уравнения  (1) в натуральную степень , то уравнение  (2) является следствием уравнения (1).

Доказательство. Если выполняется числовое равенство , то по свойствам степени выполняется равенство , т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).

Если , то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.

Если , равенство  справедливо, если выполняется хотя бы одно из равенств и . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения  приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование . В этом случае уравнение  равносильно системе . В системе отсутствует требование , обеспечивающее существование корня степени , т.к. оно было бы излишним в связи с равенством .

Пример 1.

,

,

.

Ответ:

Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида  При этом полезно учитывать область допустимых значений исходного уравнения.

Пример 2. 

Ответ: 

3. Решение уравнений с использованием замены переменной.

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

Пример1. 

Пусть  тогда исходное уравнение примет вид:

, корни которого  и  Решая уравнение , получаем  и 

Ответ: 

В следующих примерах используется более сложная замена переменной.

Пример 2

Перенесем в левую часть все члены уравнения и произведем дополнительные преобразования: .

Замена  приводит уравнение к виду  корнями которого являются  и 

Осталось решить совокупность двух уравнений:

Ответ: 

4. Метод разложения на множители выражений, входящих в уравнение.

Теорема.

Уравнение , определенное на всей числовой оси, равносильно совокупности уравнений 

Пример1.

При  уравнение принимает вид: которое равносильно совокупности двух уравнений: 

Ответ: 

Иррациональные неравенства. Решение иррациональных неравенств.

УОСЗ

Цели: вспомнить основные методы решения иррациональных неравенств; подготовка к ЕГЭ, воспитать активность.

Теория:

A1. Неравенство

равносильно совокупности систем

Замечание. Из утверждения A1 следует что неравенство

при b ≥ 0 равносильно неравенству f(x) > [b]²ⁿ, а при b < 0, равносильно неравенствуf(x) ≥ 0.

A2. Неравенство

равносильно следующей системе неравенств

Замечание.. Из утверждения A2 следует, что если правая часть неравенства есть числоb (g(x) = b), то A3. Неравенство

равносильно системе неравенств

A4. Неравенство

равносильно системе неравенств

A5. Неравенство

равносильно следующей совокупности систем

A6. Неравенство

равносильно совокупности

где D(g) означает область определения функции g.

A7. Неравенство

равносильно совокупности

A8. Неравенства

   и   f(x) < [g(x)]²ⁿ⁺¹

равносильны.

A9. Неравенства

   и   f(x) > [g(x)]²ⁿ⁺¹

равносильны.

Замечание. Если m нечетное число, то

f(x) < g(x)      [f(x)]^m < [g(x)]^m,

f(x) > g(x)      [f(x)]^m > [g(x)]^m,

т.е. при возведении в нечетную степень знак неравенства не изменяется.

Расмотрим несколько примеров.

Пример 1. Решить неравенства

Подведение итогов. Выставление отметок.

Домашнее задание: № 30.8 а)б), 30.9 а), 30.14 а), 30.16 а), 30.20 а), 30.34 а)б)

Литература:

1. http://diffur.kemsu.ru/1/teori/ir-yr.htm

2. http://ege-ok.ru/2012/02/20/reshenie-irratsionalnyih-uravneniy-2

3. http://yukhym.com/ru/matematika/irratsionalnye-uravneniya-na-primerakh.html

infourok.ru

Иррациональные уравнения и неравенства

Иррациональные уравнения

Рассмотрим теперь понятие рационального неравенства.

Определение 1

Уравнение, в котором неизвестная величина находится под радикалами или в дробных степенях будем называть иррациональным.

Здесь надо всегда помнить о том, что не под любым корнем может быть отрицательное число. В связи с этим здесь будет появляться понятие области определения уравнения (ООУ). Оно заключается в том, что под корнями с четными степенями не может быть отрицательных величин.

Решение классических иррациональных уравнений заключается в следующем: Вначале мы находим ООУ, с помощью простейших преобразований приводим уравнение к виду $\sqrt[n]{P(x)}=\sqrt[n]{Q(x)}$. Возводим в $n$-ю степень и находим корни получившегося уравнения. Выкидываем корни, не попадающие в ООУ.

Пример решения иррационального уравнения

Пример 1

Решить

$\sqrt[5]{x^2-4x+4}-\sqrt[5]{x-2}=2$

Решение.

Применяя формулу квадрата суммы, получим:

$\sqrt[5]{(x-2)^2}-\sqrt[5]{x-2}-2=0$

Так как степень корня нечетна, то нам здесь не требуется нахождения ООУ.

Сделаем замену $\sqrt[5]{x-2}=t$, получим

$t^2-t+2=0$

Это уравнение имеет своими корнями числа $-1$ и $-2$.

Получим два уравнения:

$\sqrt[5]{x-2}=-1$ и $\sqrt[5]{x-2}=-2$

$x-2=-1$ и $x-2=-32$

$x=1$ и $x=-30$

Ответ: $1$ и $-30$.

Иррациональные неравенства

Рассмотрим теперь понятие иррационального неравенства.

Определение 2

Неравенство, которое имеет вид $\sqrt[n]{P(x)}>(≥)\sqrt[n]{Q(x)}$ будем называть иррациональным неравенством.

Чаще всего неравенства решаются методом промежутков (интервалов). В основе этого метода лежит следующее рассуждение.

Пусть нам дана функция $f(x)=\frac{(x-n)(x-m)}{(x-l)(x-k)}$, причем $n

$x∈(-∞,n)$: Используя неравенство (1) будем получать:

$(x-n)

Четыре минуса, в общем, нам дадут плюсовое значение, то есть $f(x)>0$.

$x∈(n,m)$:

Используя неравенство (1) будем получать:

$(x-n)>0,(x-m)

Три минуса, в общем, нам дадут минусовое значение, то есть $f(x)

$x∈(m,l)$:

Используя неравенство (1) будем получать:

$(x-n)>0,(x-m)>0,(x-l)0$.

$x∈(l,k)$:

Используя неравенство (1) будем получать:

$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)

Один минус дает нам минусовое значение, то есть $f(x)

$x∈(k,+∞)$:

Используя неравенство (1) будем получать:

$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)>0$.

Все плюсы нам дадут плюсовое значение, то есть $f(x)>0$

Это рассуждение можно иллюстрировать на числовой прямой (рис. 1).

Эта иллюстрация называется кривой знаков и используется для решения рациональных и других неравенств $q(x)>(≥)0$ методом промежутков.

Замечание 1

На самом деле знаки на такой кривой не всегда чередуются. К примеру такое может быть при наличии в уравнение квадратного множителя.

Суммируя, получим:

Метод промежутков (интервалов)

1. Вначале необходимо найти все корни уравнения $q(x)=0$ и значения, в которых область определения имеет разрыв.
2. И всех полученных в пункте $1$ числовых значений составляем кривую знаков для данного уравнения.
3. Записываем ответ из кривой знаков, с учетом знака неравенства.

Пример решения иррационального неравенства методом промежутков

Пример 2

Решить

$\sqrt[4]{z-1}≤\sqrt[8]{z+5}$

Решение.

Найдем ООУ:

$z-1 ≥0$ и $z+5 ≥0$

$z ≥1$ и $z ≥-5$

ООУ: $[1,∞)$.

Решим для начала следующее уравнение и найдем точки разрыва ее области определения:

$\sqrt[4]{z-1}-\sqrt[8]{z+5}=0$

$\sqrt[4]{z-1}=\sqrt[8]{z+5}$

$z^2-2z+1=z+5$

$z^2-3z-4=0$

Корни: $z=-1$ и $z=4$

Изобразим все полученные точки и ООУ на числовой прямой и построим кривую знаков:

Так как у нас знак неравенства «меньше или равно», то нам нужно выбрать промежуток со знаком минус.

Ответ: $[1,4]$.

spravochnick.ru

Иррациональные неравенства — PDF

Транскрипт

1 Содержание И. В. Яковлев Материалы по математике MathUs.ru Иррациональные неравенства Учёт ОДЗ Равносильные преобразования Двукратное возведение в квадрат Дробно-иррациональные неравенства Замена переменной Умножение на сопряжённое Задачи Как и в случае уравнений, мы называем неравенство иррациональным, если оно содержит переменную под знаком корня. Данная статья посвящена методам решения иррациональных неравенств. Учёт ОДЗ Напомним, что область допустимых значений ОДЗ неравенства есть множество значений переменной, при которых обе части данного неравенства имеют смысл. Задача. Решить неравенство x x >. Решение. Квадратный корень может принимать только неотрицательные значения, поэтому данное неравенство выполнено всегда, когда квадратный корень определён. Иными словами, множеством решений данного неравенства служит его ОДЗ: Ответ: ;. x x 0 x. Поиск ОДЗ неравенства далеко не всегда является целесообразным занятием; однако в отдельных ситуациях предварительное нахождение ОДЗ даёт ключ к решению задачи. Задача. Решить неравенство x x + x > x 7. Решение. По виду неравенства ясно, что никакие стандартные методы тут работать не будут. Давайте найдём ОДЗ: { { x x 0, x, x =. x 0 x Вот ситуация и прояснилась: ОДЗ состоит из одного-единственного числа. Поэтому достаточно подставить x = в неравенство и проверить, выполняется ли оно. Подставляем и убеждаемся, что x = решение. Ответ:.

2 Равносильные преобразования Приступаем к рассмотрению стандартных видов иррациональных неравенств. В каждом из случаев нет нужды предварительно искать ОДЗ; самое эффективное решение обеспечивается соответствующими равносильными преобразованиями. Неравенства вида A < B Рассмотрим неравенство A < B, где A и B некоторые выражения, содержащие переменную. В силу монотонного возрастания функции x должно быть выполнено неравенство A < B; но надо не забыть «подпереть нулём» это неравенство снизу: 0 A < B. Таким образом, имеет место эквивалентность: A < B 0 A < B { A < B, A 0. Обратите внимание, что нет необходимости ради поиска ОДЗ решать неравенство B 0. Выражение B автоматически получается неотрицательным ведь в силу системы величина B больше неотрицательной величины A. Ясно, что эквивалентность сохраняется при замене знака < на. Задача. Решить неравенство x + 4 < x + 8x. Решение. В силу неравенство равносильно системе { x + 4 < x + 8x, x { x + 6x 7 > 0, x. Первое неравенство системы имеет решения x < 7 или x >. Отсюда легко получаем ответ. Ответ: ; +. Теперь, кстати, представьте себе, что вы решили предварительно поискать ОДЗ, занявшись решением неравенства x + 8x 0. Представили? ;- Задача 4. МГУ, геологич. ф-т, 006 Решить неравенство x x x x. Решение. Неравенство равносильно системе x x x { x, x 4x + x 0, x x x 0 6x 0 { xx x 0, xx 6 0 x 0, x, 0 x 6 x = 0, x 6. Ответ: {0} ; 6.

3 Перейдём к рассмотрению неравенства Неравенства вида A B 0 A B 0. Ввиду неотрицательности корня возможны два случая: B = 0, и при этом A определено; A 0, и при этом B > 0. Таким образом, имеет место эквивалентность: { B = 0, A B 0 A определено, { A 0, B > 0. Задача. МГУ, ВМК, 978 Решить неравенство x x x 0. Решение. В силу неравенство равносильно совокупности x x = 0, { x 0, x x > 0. Уравнение совокупности имеет корни и. Множество решений квадратного неравенства: x < или x >, поэтому множество решений системы есть x >. Объединяя множество {, } корней уравнения c множеством решений системы, получаем ответ. Ответ: { } ; +. Переходим к неравенствам, для решения которых требуется возведение обеих частей в квадрат. Сделаем предварительно два замечания.. При возведении в квадрат иррациональных уравнений можно в принципе обойтись без равносильных переходов, так как лишние корни можно отсеять непосредственной поочерёдной проверкой конечного набора корней уравнения-следствия это бывает сложно технически, но теоретически всегда возможно. Однако в результате возведения в квадрат неравенства может появиться бесконечное множество лишних решений, и все их проверить уже не представляется возможным. Поэтому использование равносильных переходов при решении иррациональных неравенств становится жизненной необходимостью.. Неравенство можно возводить в квадрат лишь в том случае, когда обе его части неотрицательны: a < b a < b при a, b 0. В противном случае верное неравенство может превратиться в неверное: < 9 < 4, или, наоборот, неверное неравенство может превратиться в верное: < 4 < 9. Мы берём именно случай нестрогого неравенства, так как он чаще встречается в экзаменационной практике; разобравшись в нём, вы без труда напишете правильную эквивалентность для строгого неравенства.

4 Неравенства вида A < B Рассмотрим в качестве примера неравенство x < x. Если x 0, то неравенство решений не имеет, поскольку арифметический квадратный корень не может быть меньше неположительного числа. Если x > 0, то обе части неравенства неотрицательны, и мы имеем право возвести неравенство в квадрат: x < x, не забыв при этом, что подкоренное выражение должно быть неотрицательным: x 0. Таким образом, имеем равносильный переход: x < x x > 0, x < x, x 0. Решая полученную систему, находим: x ;. После этого примера хорошо понятно, что в общем случае имеет место следующая эквивалентность: B > 0, A < B A < B, A 0. Если же неравенство нестрогое, то величина B может быть нулём: A B B 0, A B, A 0. 4 Задача 6. МГУ, физический ф-т, 00 Решить неравенство x x + 0 < 0 x. Решение. Согласно неравенство равносильно системе 0 x > 0, x x + 0 < 0 x, x x Из полученной системы легко находим x < 0. Ответ: ; 0. x < 0, x + 0 x > 0, x + x 0 Задача 7. МГУ, мехмат, 00 Решить неравенство x7 x x x 4 x. 4 x < 0, x < 0, x > + 0, x.

5 Решение. Сразу же отметим, что имеет место разложение на множители x x + 4 = x x + x 4 = x x x. Согласно 4 неравенство равносильно системе x 0, x 7 x x x 4 x6, x 7 x x x 4 0 x 0, x 0, x x 6 + 4x 0, x x 4 x x 4 x x x x 4x + 8 x x x 0, 7 x x 4 x x x 0 7 x 0, x x 4 x x 0, 7 x x 4 x x 0 7 мы разложили на множители разности квадратов и кубов, после чего, воспользовавшись условием x 0, удалили все заведомо положительные сомножители. Чтобы решить второе неравенство системы, нам нужно сравнить числа 4 и 7 понятно, что оба они больше. Для этого сравним с нулём разность их кубов: 7 4 = = = = 4 7 = 7 = 44 4 > 0, поэтому 4 > 7. Теперь, решая второе неравенство методом интервалов, получим x = 0, < x < 7, x 4 6 отрицательные значения x отброшены в силу первого неравенства. Для решения третьего неравенства системы нужно сравнить числа 4 и 7. Сравниваем с нулём разность их четвёртых степеней: 7 = 4 = = 4 = = = поэтому 4 > 7. Теперь решаем третье неравенство : = > 0, 0 0 x <, 7 < x 4. 7

6 Решением исходного неравенства служит пересечение «рамочек» множеств 6 и 7. Остаётся только сравнить числа 4 и 4. Для этого сравниваем с нулём разность их -х степеней: Следовательно, 4 4 = < 4, и окончательно имеем: = = < 0. Ответ: {0} 4; 4. x = 0, 4 4 x. Неравенства вида A > B Теперь в качестве примера рассмотрим неравенство x > x. Пусть сначала x < 0. Поскольку в левой части стоит неотрицательное выражение x, множеством решений неравенства в этом случае является ОДЗ: x 0. Пусть теперь x 0. Поскольку обе части неравенства неотрицательны, имеем право возвести неравенство в квадрат: x > x. Таким образом, имеем эквивалентность: { { x < 0, x <, x > x x 0, { x 0, x > x x, { x, x x < 0. Решением первой системы служит множество x <. Решением второй системы служит множество x <. Объединяя эти множества, получаем ответ: x <. Ясно теперь, что в общем случае имеет место эквивалентность: { B < 0, A > B A 0, { B 0, A > B. 8 Аналогично в случае нестрого неравенства имеем: { B 0, A B A 0, { B > 0, A B. 9 6

7 Задача 8. МФТИ, 998 Решить неравенство x 8x > x Решение. В соответствии с совокупностью 8 рассмотрим два случая. Пусть сначала x < 0, то есть. 0 x >. При ограничении исходное неравенство 0 равносильно неравенству x 8x 0, решения которого x, x. Пересекая множества и, получаем первую часть множества решений неравенства 0: x. Пусть теперь x 0, то есть x. 4 При ограничении 4 неравенство 0 равносильно неравенству x x 8x > x 68x 8 > 0, решения которого x < x = 4 0, x > x = Ясно, что x < 0 <, x > > ; пересекая множества 4 и, получим вторую часть множества решений неравенства 0: x < 4 0 Остаётся объединить «рамочки» множества и 6. Ответ: ; +. ; Задача 9. МФТИ, 006 Решить неравенство 6x x. 7 Решение. При ограничении неравенство 7 равносильно неравенству x 0 8 6x x Пересечение 8 и 9 даёт часть решений неравенства 7: 9 4 x

8 Теперь рассмотрим случай x > 0. При ограничении неравенство 7 равносильно неравенству 6x x 6x + 6 x 6. Очевидно, что значения 0 < x 6 удовлетворяют неравенству. Остаётся рассмотреть ограничение при котором неравенство равносильно неравенству x > 6, 4 6x + 6 x 6 xx x 6 0 xx + x 4 0. Решения полученного неравенства, удовлетворяющие условию 4, суть значения 6 < x 4. Множество решений исходного неравенства 7 является объединением всех «рамочек», то есть множеств 0, и. Ответ: 9 4 ; 4. Двукратное возведение в квадрат Если неравенство содержит сумму или разность двух радикалов, то, возможно, придётся возводить в квадрат два раза. Задача 0. МГУ, геологич. ф-т, 999 Решить неравенство 0x x 4 x x + 4 x x + 0. Решение. Здесь полезно начать с нахождения ОДЗ: 4 x 6, 0x x 4 0, x 6, x x + 4 0, x 7, x x x, x 6 4 x, x = 6. Перепишем исходное неравенство, разложив каждый из квадратных трёхчленов на множители: 6 xx 4 6 x7 x 6 x x 6 каждый из сомножителей неотрицателен в ОДЗ. Легко видеть, что x = 6 является решением неравенства 6; остаётся рассмотреть данное неравенство на множестве E = 4;. Делим обе части неравенства 6 на выражение 6 x, которое положительно на множестве E, и приходим к равносильному на E неравенству x 4 7 x x x 4 + x 7 x. 8

9 Обе части последнего неравенства положительны на множестве E; возводя в квадрат, получим равносильное на E неравенство + x 4 x 7 x 9x x 0 6 x. Поскольку 6 x > 0 на множестве E, снова возводим в квадрат: 49x x 0 6 x x 48x Полученное неравенство равносильно на множестве E неравенству 6. Но ввиду отрицательности дискриминанта это квадратное неравенство не имеет решений. Следовательно, не имеет решений на множестве E и неравенство 6. Таким образом, x = 6 единственное решение нашего неравенства. Ответ: 6. 4 Дробно-иррациональные неравенства Как вы знаете, метод интервалов применяется для решения рациональных или, как ещё говорят, дробно-рациональных неравенств; в таких неравенствах фигурируют только дроби, у которых числитель и знаменатель многочлены. Если же в числителе или знаменателе появляется переменная под знаком корня, то мы будем говорить о дробно-иррациональных неравенствах. Мы позволим себе не вдаваться в более подробное обсуждение этой терминологии; на рассматриваемых ниже примерах станет ясно, о неравенствах какого типа идёт речь и какой они обладают спецификой. Задача. МГУ, ф-т гос. управления, 00 Решить неравенство x < x 0x + 6. Решение. Сразу сделаем замену t = x : < t t +. 7 Теперь замечаем, что выражение t + положительно при всех t, и поэтому можно умножить на него обе части неравенства 7; получим равносильное неравенство t + < t, которое решается уже известным вам способом. Легко находим t >, откуда x >. Ответ: ; +. Задача. МГУ, биологич. ф-т, 00 Решить неравенство 6 x. 8 x Решение. ОДЗ неравенства есть множество 4; ; 4. Пусть сначала x E = 4;. Тогда x > 0; умножая неравенство на x, получим равносильное на множестве E неравенство 6 x x 6 x x x 6x

10 Решения полученного квадратного неравенства суть x и x + ; пересекая это с множеством E и учитывая, что + > + 6 >, получаем часть решений исходного неравенства: 4 x. 9 Пусть теперь x E = ; 4. Тогда x < 0 и неравенство 8 выполнено, поскольку его левая часть неположительна. Значит, любой x E служит решением нашего неравенства. Объединяя множества 9 и E, получаем ответ. Ответ: 4; ; 4. Задача. МФТИ, 997 Решить неравенство 6 x + x x 4 x 0 <. Решение. Перенося влево и приводя к общему знаменателю, получим равносильное неравенство 6 x + x x 4 < 0. 0 x 0 ОДЗ этого неравенства есть множество ; 4 6; 0 0; +. Пусть сначала x E = ; 4 6; 0. Тогда x 0 < 0, в силу чего неравенство 0 равносильно на множестве E неравенству 6 x + x x 4 > 0 x x 4 > x 6. Любой x < 8, входящий в E, является решением неравенства. Если же x 8; 0, то неравенство равносильно неравенству x x 4 > x 6 x 6x + 80 < 0, решения которого образуют множество 0 ; 4, содержащее в себе рассматриваемое множество 8; 0. Следовательно, любой x 8; 0 также является решением неравенства, и, значит, множество E часть множества решений нашего неравенства. Пусть теперь x E = 0; +. Тогда x 0 > 0, и неравенство равносильно на множестве E неравенству 6 x + x x 4 < 0 x x 4 < x 6. Ввиду того, что x 6 > 0 на множестве E, полученное неравенство в свою очередь равносильно неравенству x x 6 < x 6 x 6x + 80 > 0, решения которого, принадлежащие E, суть x > 4. Ответ: ; 4 6; 0 4; +. Задача 4. «Физтех», 0 Решить неравенство x + x x

11 Решение. Знаменатель, равный 9 + x, обращается в нуль при x = и отрицателен при всех x. Следовательно, на множестве x наше неравенство равносильно неравенству x + x x + 0 x x + 0 x. Полученное неравенство не представляет трудностей, и вы легко доведёте дело до конца самостоятельно. Ответ: 4 ; ; +. Замена переменной В некоторых задачах бывает полезно сделать замену переменной, обозначив новой буквой имеющийся корень из некоторого выражения. Задача. МГУ, геологич. ф-т, 997 Решить неравенство x 0 x < 0. Решение. Обозначим x = t; тогда x = t. Наше неравенство принимает вид: t 0 t < 0 t + 0t 00 t 0 > 0 t 0t + 0 t 0 Решаем полученное неравенство методом интервалов и делаем обратную замену: > 0. 0 < t < 0, t > 0 0 < x < 0, x > 0 0 x < 00, x > 400. Ответ: 0; ; +. Задача 6. «Покори Воробьёвы горы!», 006 Решите неравенство x + > x. Решение. Вы уже знаете, как решать подобные неравенства, но в данном случае можно поступить и по-другому. Обозначим t = x + ; тогда x = t, и наше неравенство принимает вид t > t t t < 0 После обратной замены с учётом условия < 0 имеем: < t < +. < x + < + 0 x + < + = + x < 7 +. Ответ: ; 7+.

12 Задача 7. «Покори Воробьёвы горы!», 04, 0 Найдите сумму целых чисел, являющихся решениями неравенства x x x + x 6x +. Решение. Обозначим u = x, v = x 6x +. Наше неравенство запишется в виде u v v u u vu + v + 0. Учитывая, что величина u + v + положительна при всех допустимых значениях x, имеем u v x x x + { x x x +, x x + 0 { x 6x + 0, x x + 0. Система равносильна исходному неравенству. Решения первого неравенства системы образуют множество ; 6, которое содержит лишь два целых числа и. Непосредственной проверкой убеждаемся, что x = не удовлетворяет второму неравенству, а x = удовлетворяет ему. Значит, исходное неравенство имеет единственное целое решение x =. Это и есть ответ. Ответ:. 6 Умножение на сопряжённое В некоторых ситуациях полезно бывает умножить и разделить на выражение, сопряжённое данному. Задача 8. «Физтех», 06, 9 Решите неравенство x x + + x +. Решение. Имеем: x x + + x x x + + x x x + + x + x x x x x + + x + 0 x + + x + x x ОДЗ нашего неравенства есть множество x > 0. На этом множестве полученное неравенство равносильно неравенству x + x 0 x 0 x. В пересечении с ОДЗ имеем 0 < x. Ответ: 0;. Задача 9. МГУ, ВМК, 006 Решить неравенство 0 x 7x 44 > x. 0.

13 Решение. Сразу делаем замену t = x: 0 t 4t 44 > t. Найдём ОДЗ данного неравенства: t 4t t 44 t { t 0, 0 4t 44 t t 0, t 6, t 0 t 6. Умножим и разделим подкоренное выражение в на сопряжённое t+ 4t 44 которое положительно при всех t 6: t t 4t 44 t + 4t 44 4t 44 = t + = t 4t 44 4t 44 t + 4t 44 = t t + 4t 44. В результате придём к равносильному неравенству 0 t t + 4t 44 > t. 4 Все значения t 6; являются решениями неравенства 4, поскольку его правая часть отрицательна при данных t, а левая положительна. Значение t =, как легко видеть, не является решением 4. Пусть теперь t >. В этом случае неравенство 4 равносильно неравенству 0t t + 4t 44 > t 0 t + 4t 44 > t + 4t 44 < 0 t + 4t 44 < 00 { 00 t > 0, 4t 44 < 00 t 4t 44 < 00 t { t < 00, t < 00, t t < 0 6, 4t > 0 t > + 0 t < Итак, имеем множество решений неравенства : 6 t <, < t < 0 6. Остаётся сделать обратную замену x = t/ и получить множество решений исходного неравенства: Ответ: ; 4 4; 0 6. x < 4, 4 < x < 0 6.

14 7 Задачи Во всех задачах требуется решить неравенство. Учёт ОДЗ. а x + x ; б + x x + x > x 7. а ; ; + ; б. МГУ, геологич. ф-т, 994 4x x 0. ;. «Покори Воробьёвы горы!», 0, 9 x + x 4x + + x + x.,, 4. «Покори Воробьёвы горы!», 0, 0 x 006 x 0 + > x МГУ, ВМК, 006 x x + x 4x x x 09. ; 0 {} 4; + Равносильные преобразования 6. а x < x x ; б x 4 x + x МГУ, геологич. ф-т, 006 x x 6x x. ; + 0 {0} ; а ; 4 ; ; б 8. «Ломоносов», 0, x x 4x x. ; {} 9. МГУ, ИСАА, 004 x x < 0. ; 0. МГУ, биологич. ф-т, 006 x + x + x 4 0. { } ; + 4

15 . МГУ, геологич. ф-т, 988 x + 8x + x { 4} ; +. МГУ, экономич. ф-т, 986 x + x 8x 6x + 0. ; 4 { }. МГУ, физический ф-т, 996 x x 0 + x x > 0. ; 0 ; 4. МГУ, биологич. ф-т, 00 x + x 84 x 7 0. { } 7; +. МГУ, ВШБ, 00 x + x x + 0. ; {} 6. МГУ, географич. ф-т, 004 x6 64 x 0. {, } ; + 7. МГУ, ИСАА, 00 x x x x ; {, } ; + 8. МГУ, мехмат, x x x x x. x + 4 ; {} 9. МГУ, биологич. ф-т, 00 x < x. ; 0. МГУ, ф-т психологии, 00 x + > x. ; +

16 . МГУ, геологич. ф-т, 99 0x + x. + ; +. МГУ, физический ф-т, 979 x + x < x. ;. МГУ, МШЭ, 00 x + x x >. ; 4. МГУ, геологич. ф-т, 984 x 8x + 6 < x 4. 8; 0. МГУ, экономич. ф-т, 98 x + x 6 > x. ; 7 ; + 6. МГУ, экономич. ф-т, 00 4x x x. ; 7. МГУ, геологич. ф-т, x + x > x 4. ; 4 8. МГУ, биологич. ф-т, 980 x + 6x > 8 x. ; 9. МГУ, геологич. ф-т, 00 x x + 6 x. 4 ; 4 0. МГУ, физический ф-т, 00 x x + 6 < 6 x. ; 0. МФТИ, 998 x 7x 4 > x 4. ; ; +. МГУ, экономич. ф-т, 98 4x < x + 9x + 0. ; 4 ; 4. МГУ, МШЭ, 007 x x + x. {} ; + 4. МГУ, геологич. ф-т, x x +. { } 0; 6

17 . «Физтех», 0, 0 x 6 x x 6. {4} ; + 6. МГУ, физический ф-т, 006 x x + x 4 x. 4 9; ; 9 4 {} 7. МГУ, экономич. ф-т, 007 Для каждого значения x, удовлетворяющего условию x x 4 = 0, найдите все числа y, для которых выполнено неравенство 7 y 0y + 4 4x + 7. Если x = 7, то y = ; если x = 7, то таких y не существует 8. МГУ, биологич. ф-т, 00 x 7 4x x. 4 ; 7 4 ; + 9. МГУ, мехмат, 00 x x > x x + 4. ; МГУ, ИСАА, x x x + > 9 x. ; 0 9 ; 7 4. МГУ, мехмат, 00 4×7 0x 4x x x. {0} 4 ; 4. «Физтех», 00 x + x > x. ; 7

18 4. МФТИ, 008 x x x. ; ; 0 ; МФТИ, x x x. 4 ; 8 8 ; + 4. МГУ, мехмат, 99 4x + 4x 4x + + x 0. 4 ; ; 46. МФТИ, x < 4 x. 4 ; 47. МФТИ, 006 x x ; «Физтех», 007 x x 4x x 6 x 4x x МГУ, ИСАА, 00 x x x x x. ; {} 0. МГУ, ф-т психологии, 99 x x >. 0; 6. МГУ, ф-т фунд. мед., 00 x 4 + x x ;. МФТИ, 00 x + 4x + < + x x +. ; ; 7 8 8

19 . МГУ, экономич. ф-т, 998 x + x + x x + <. ; ; МГУ, геологич. ф-т, 999 4x x x 7x + x x МГУ, геологич. ф-т, 00 6x x 8 7 x 8x x., 7 Дробно-иррациональные неравенства 6. МГУ, ф-т психологии, 999 x 7x 4 <. 4 7 ; МГУ, ф-т гос. управления, 00 < x 4 x 8x + 7. ; + 8. МГУ, ВМК, 98 9x 4 x x +. ; ; 9. МГУ, физический ф-т, 00 > x x. ; + ; 60. МГУ, физический ф-т, 00 x x <. ; ; 6. МГУ, биологич. ф-т, 00 x 4 x. ; ; 8+ 0 ; + 9

20 6. МГУ, физический ф-т, x x x <. ; 0 ; + 6. МГУ, ИСАА, 99 x x + 8 x. ; 64. МГУ, ф-т психологии, 98 x x x <. ; ; + 6. МГУ, ф-т психологии, 998 4x + 7 x + 6 x + x ; 7+ 7 ; МГУ, геологич. ф-т, 00 x 6x 7 x 7 x +. ; { } 7; МФТИ, 997 6x + 4x x 6 x >. ; ; 7 ; МГУ, мехмат, 990 x + x x. ; 0; 69. МГУ, ДВИ, 0 x + x + >. ; ; + 0

21 70. «Физтех», 0 x x x + 6. ; ; + 7. МФТИ, 999 x x + 60x x 6 x 0. 0; 4 {} 6; 7. МФТИ, 006 4x x + 8 x + 4x ; 4 ; + 7. МФТИ, 007 4x + 4x + 4x + 4x 0. 4 ; 74. «Ломоносов», 00 x 4 x x + 6 x 4. 6; + Замена переменной 7. МГУ, геологич. ф-т, > x 60 x 0; ; МГУ, геологич. ф-т, 99 x + 4 x. {0} 6; МГУ, физический ф-т, 000 x + x > x. ; + 4

22 78. МФТИ, 00 x x 7 x. 9 ; 4 9 ; МГУ, химический ф-т, 979 x + > x +. ; 80. «Покори Воробьёвы горы!», 006 x + > x. ; + 8. МГУ, ф-т психологии, 997 x + > x. 89 ; МГУ, ф-т почвоведения, 98 4x 8 x. ; 8. МГУ, ф-т почвоведения, 996 x +. { } ; МГУ, биологич. ф-т, 99 x > 7x x. ; 8 8. МГУ, химический ф-т, x x x 0; ; ; 86. МГУ, ФНМ, 000 x + < + x +. ; 0; +

23 87. МГУ, экономич. ф-т, 998 x x < x x 0. 7; «Покори Воробьёвы горы!», 04, 0 Найдите сумму целых чисел, являющихся решениями неравенства 6x x x + x 9x «Покори Воробьёвы горы!», 04, 0 Решите неравенство x x 4. + x x 0; 8; МГУ, мехмат, 00 x x x + x + x 0. {0} ; + ; + 9. «Покори Воробьёвы горы!», 00, 0 Один из корней квадратного уравнения px + qx + = 0 p < 0 равен 00. Решите неравенство x + q x + p > 0. x > 00 Умножение на сопряжённое 9. «Физтех», 06, 9 Решите неравенство x x + x. ;

24 9. «Ломоносов», 0, 0 Решите неравенство x x 6 x x + 6 < 8 x + 7 x 8. ; 7 8; МГУ, мехмат, 00 x x x x x + 4. x + 4 x + x x + 9. МГУ, ВМК, 006 x 48x 44 > x. ; 6 6; «Покори Воробьёвы горы!», 0, 0 4x x > x + x x +. 6; 7 4

docplayer.ru

Иррациональные неравенства | Cubens

Понятие иррационального неравенства

Определение: Иррациональное неравенство — неравенство, содержащее переменную под знаком корня -ой степени.

Решению иррациональных уравнений

Метод интервалов для решению иррациональных неравенств

1. Найти ОДЗ неравенства.
2. Найти нули функции
3. Отменить нули функции на ОДЗ и найти знак функции на каждом из промежутков, на которые разбивается ОДЗ .

Пример 1:

Розвяжіть уравнения:

Решение: Заданное неравенство равносильно неравенству

Обозначим

ОДЗ: , т. е.

Нули: подносим в квадрат левую и правую часть

— корень, — посторонний корень.

Ответ:

Равносильные преобразования

1. При поднесении обеих частей неравенства до нечетного степень (с сохранением знака неравенства) получаем неравенство, равносильное данному.

Пример 2:

Розвяжіть уравнения:

Решение: ОДЗ:

Заданное неравенство равносильно неравенствам:

Ответ:

2. Если обе части неравенства невідємні, то при подъеме обеих частей неравенства к парному степени (с сохранением знаком неравенства) получаем неравенство, равносильное данному.

Пример 3 :

Розвяжіть уравнения:

Решение: ОДЗ:

Обе части заданного неравенства невідємні, следовательно, она равносильно неравенствам:

Учитывая ОДЗ, получаем .

Ответ:

3. Если на ОДЗ заданного неравенства какая-то часть неравенства может приобретать как положительные, так и неотъемлемых значений, то, прежде чем подносить обе части неравенства до парного степеня, эти случаи стоит рассмотреть отдельно.

Пример 4 :

Розвяжіть уравнения:

Решение: Заданное неравенство равносильно совокупности систем:

или

Тогда или

Розвязавши неравенство имеем

Учитывая неравенство , получаем решение первой системы . Решение второй системы: Обєднуючи эти развязки, получаем ответ.

Ответ:

cubens.com

No related posts.