Построение графиков функций — урок. Алгебра, 10 класс.
построить график функции y=x2+1×2−1.
Решение 1. Введём обозначение: f(x)=x2+1×2−1. Найдём область определения функции. Она задаётся условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).
2. Исследуем функцию на чётность:
f(−x)=−x2+1−x2−1=x2+1×2−1=f(x).
Значит, заданная функция чётна, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.
3. Найдём асимптоты. Вертикальной асимптотой является прямая \(x=1\), поскольку при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):
limx→∞x2+1×2−1=limx→∞x2x2+1x2x2x2−1×2=limx→∞1+1×21−1×2=1.
Значит, \(y=1\) — горизонтальная асимптота графика функции.
4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y′=x2+1×2−1′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′x2−12=2x⋅(x2−1)−(x2+1)⋅2xx2−12==−4xx2−12.
Производная существует всюду в области определения функции, значит, критических точек у функции нет.
Стационарные точки найдём из соотношения y′=0. Получаем: \(-4x=0\) — откуда находим, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Значит, \(x=0\) — точка максимума функции, причём ymax=f(0)=02+102−1=−1.
При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=1\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;1) функция убывает, на промежутке (1;+∞) функция также убывает.
5. Составим таблицу значений функции f(x)=x2+1×2−1 при x≥0:
\(x\) | \(0\) | \(0.5\) | \(2\) | \(3\) | \(4\) |
\(y\) | \(-1\) | −53 | 53 | 54 | 1715 |
6. Отметим найденные точки на координатной плоскости, учтя при этом, что \((0;-1)\) — точка максимума, что \(y=1\) — горизонтальная асимптота, что \(x=1\) — вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график.
www.yaklass.ru
10 класс. Алгебра. Производная. Применение производной к исследованию функции. — Исследование функции и построение графика
Комментарии преподавателя
Построение графика произвольной функции может быть как отдельной задачей, так и вспомогательной — например, при решении уравнений графическим способом, или при решении задач с параметрами.
Алгоритм исследования функции и построения ее графика таков:
1. Находим область определения (D(f)) функции .
2. Если область определения функции симметрична относительно нуля (то есть для любого значения из D(f) значение также принадлежит области определения, то проверяем функцию на четность.
Если , то функция четная. (Примером четной функции является функция )
Для нас важно, что график четной функции симметричен относительно оси OY.
Если , то функция нечетная. (Примером нечетной функции является функция )
График
Если функция является четной или нечетной, то мы можем построить часть ее графика для , а затем соответствующим образом отразить ее.
3. Н
www.kursoteka.ru
Уроки 9-10. Исследование функций (факультативное занятие) | Поурочные планы по алгебре и начала анализа 10 класс
Уроки 9-10. Исследование функций (факультативное занятие)
09.07.2015 5982 0Цель: отработать схему исследования функции, построения графика функции.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определения возрастающей функции и минимума функции.
2. Найдите промежутки возрастания и убывания, точки экстремума и экстремумы функции y = x2 — 3|x|, ее наименьшее и наибольшее значения на отрезке [-1; 4]. Постройте график функции.
Вариант 2
1. Дайте определения убывающей функции и максимума функции.
2. Найдите промежутки возрастания и убывания, точки экстремума и экстремумы функции y = 2|х| — х2, ее наименьшее и наибольшее значения на отрезке [-2; 3]. Постройте график функции.
III. Изучение нового материала
Построение графиков функций
В младших классах, пожалуй, единственным методом построения графиков функций был способ построения «по точкам». В случае хорошо изученных функций (линейной, квадратичной, дробно-линейной, степенной и т. д.) такой способ дает хорошие результаты. В случае незнакомой функции при использовании этого способа можно просмотреть какие-то принципиальные особенности поведения функции. Например, в физике очень распространены резонансные явления. Суть их состоит в том, что при плавном изменении какой-то физической величины вдруг возникает очень резкое ее увеличение или уменьшение.
Таким образом, для грамотного и обоснованного построения графика функции предварительно необходимо эту функцию исследовать. На примере покажем, какие этапы необходимо пройти при исследовании функции и построении ее графика.
Пример 1
Исследуем функцию и построим ее график.
1. Найдем область определения функции. Так как знаменатель х2 + 1 дроби не обращается в нуль, то D(y) — вся числовая прямая.
2. Определим особенности функции. Очевидно, что данная функция четная. Действительно, Поэтому исследуем и построим график функции при х ≥ 0. Затем эту часть графика отразим влево относительно оси ординат.
3. Найдем точки пересечения графика функции с осями координат. Чтобы найти точку пересечения с осью ординат, положим х = 0 и получим у = -1. Точка пересечения с осью ординат (0; -1). Чтобы найти точку пересечения с осью абсцисс, положим у = 0 и получим уравнение или 0 = x2 — 1, откуда х = 1. Точка пересечения с осью абсцисс (1; 0).
4. Выясним промежутки знакопостоянства функции, т. е. на каких промежутках функция принимает положительные значения, а на каких — отрицательные. Для нахождения промежутка отрицательности функции решим неравенство или x2 — 1 < 0, откуда 0 ≤ х < 1. Для нахождения промежутка положительности функции решим неравенство или х2 — 1 > 0, откуда х > 1.
5. Определим монотонность функции. Пусть х2 и х1 — две точки из промежутка [0; ∞), причем х2 > x1. Запишем функцию в виде Найдем разность В этой дроби знаменатель всегда положительный. В числителе множитель x2 – x1 > 0 (так как x2 > x1),x2 + x1 > 0 (так как x1,2 > 0). Потому числитель дроби также положительный. Следовательно, дробь положительна, так как у(х2) — y(x1) > 0 или y(x2) > y(x1). Поэтому функция у(х) возрастает на промежутке [0; ∞). Учитывая четность функции y(x), на промежутке (-∞; 0] она убывает.
6. Найдем экстремумы функции. Так как только в точке х = 0 убывание функции сменяется возрастанием, то точка минимума xmin = 0 и минимум функции ymin = -1.
7. Выясним поведение функции при больших значениях х. Данная функция имеет вид: При неограниченном возрастании х знаменатель дроби х2 + 1 также неограниченно возрастает. Поэтому значения дроби приближаются к нулю, оставаясь положительными. Следовательно, значения функции у(х) неограниченно приближаются к 1, оставаясь меньше 1. Поэтому прямая у = 1 является горизонтальной асимптотой функции y(x).
8. Наименьшее значение функции yнаим = -1 достигается при х = 0, наибольшего значения нет.
9. Функция ограничена.
10. Функция непрерывная.
11. Выпуклость графика функции установить трудно (она меняется).
Исследованные свойства функции позволяют построить ее график. Сделаем сначала такое построение для промежутка х ∈ [0; ∞).
Построим точки пересечения с осями координат (0; -1), (1; 0). Учтем, что на промежутке [0; 1) значения у < 0, на промежутке (1; ∞) значения у > 0. Значения функции возрастают от y = -1 и стремятся к значению у = 1 при больших х. Проводим непрерывную кривую.
Учитывая четность данной функции y(x) отражаем кривую, построенную при х ≥ 0, влево симметрично относительно оси ординат. Получаем график функции y(x).
Схема исследования функции
На рассмотренном примере были фактически отработаны все этапы такого исследования. Они сводятся к следующему:
1. Найти области определения и значений функции y(x).
2. Выяснить особенности функции, облегчающие ее исследование и построение графика: а) четность или нечетность; б) периодичность.
3. Вычислить координаты точек пересечения графика функции с осями координат.
4. Найти промежутки знакопостоянства функции.
5. Определить промежутки возрастания и промежутки убывания функции.
6. Найти точки экстремума, определить вид экстремума (максимум или минимум), вычислить экстремум функции.
7. Исследовать поведение функции в окрестности точек разрыва (как правило, возникают вертикальные асимптоты) и при больших по модулю значениях аргумента (могут возникать горизонтальные или наклонные асимптоты).
8. Найти наименьшее и наибольшее значения функции.
Заметим, что этот план носит ориентировочный характер. Практически любой пункт плана может вызвать технические трудности, например даже в пункте 1 при нахождении области определения и значений данной функции f(х). Предположим, что функция f(х) рациональная, т. е. имеет вид: (где h(x), g(x) – некоторые многочлены). Тогда область определения функции f(х) задается условием g(x) ≠ 0. Поэтому необходимо найти корни многочлена g(x). Если этот многочлен имеет степень выше второй и иррациональные корни, то такая задача практически нерешаема. Нахождение области значений функции f(х) является еще более тяжелой задачей. Для этого необходимо найти промежутки монотонности функции f(х), ее экстремумы, исследовать поведение функцииf(х) при больших значениях |х|. Эти процедуры можно выполнить только с помощью теории предела функции, которая изучается в школе в очень урезанном объеме (см. главу 5).
Остановимся на понятии асимптот графика функции f(x). Асимптоты разделяются на два вида — вертикальные и наклонные (в частности, горизонтальные). Строгое определение асимптот может быть дано только с помощью теории предела функции. Поэтому ограничимся только понятием асимптот.
Вертикальная прямая х = а называется вертикальной асимптотой функции f(х), если при приближении значений х к величине а значения функции f(x) неограниченно возрастают или убывают, т. е. при х → а f(х) → ±∞.
Пример 2
Рассмотрим функцию и построим ее график.
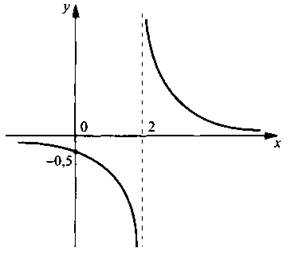
Г рафик данной функции получается из графика функции у = 1/x его смещением на 2 единицы вправо. Видно, что при х → 2 (при этом х < 2) знаменатель х — 2 отрицательный и х — 2 → 0. Поэтому значения функции неограниченно убывают, т. е. у → -∞. При х → 2 (при этом х > 2) знаменатель х — 2 положительный и х — 2 → 0. Поэтому значения функции неограниченно возрастают, т. е. у → ∞. Следовательно, вертикальная прямая х = 2 является вертикальной асимптотой данной функции .
Из примера видно, что часто в случае рациональных функций вертикальными асимптотами являются те значения х, при которых знаменатель дроби обращается в нуль. Однако не всегда в случае рациональных функций возникают вертикальные асимптоты (даже если знаменатель дроби обращается в нуль).
Пример 3
Построим график функции
Разложим числитель данной дроби на множители и сократим ее. Получаем: (при этом х ≠ 2). Видно, что при х → 2 значения функции у → 3. Поэтому данная функция вертикальной асимптоты не имеет. Существует только значение х = 2, при котором функция не определена.
Обратимся теперь к понятию наклонной асимптоты. Прямая у = kx + b называется наклонной асимптотой функции f(х), если при неограниченном возрастании или убывании х значения функции f(х) стремятся к значениям линейной функции y(x), т. е. при х → ±∞f(х) → у(х).
Пример 4
Построим график функции
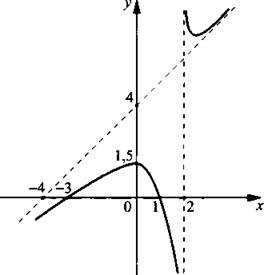
Найдем точки пересечения графика функции с осями координат. При x = 0 находим: — точка пересечения с осью ординат. При у = 0 получаем уравнение или 0 = х2 + 2х — 3, корни которого x1 = -3 и x2 = 1 — точки пересечения с осью абсцисс.
Очевидно, что прямая х = 2 — вертикальная асимптота. При х → 2 числитель дроби х + 2х – 3 → 22 + 2 · 2 — 3 = 5. При х < 2 знаменатель дроби х — 2 отрицательный и х — 2 → 0. Поэтому значения функции у → -∞. При х > 2 знаменатель дроби х — 2 положительный и х — 2 → 0. Поэтому значения функции у → ∞.
Разделим числитель дроби х2 + 2х — 3 на ее знаменатель х — 2 столбиком и выделим целую часть. Тогда функция у(х) имеет вид Очевидно, при x → ∞ дробь и значения функции y(х) стремятся к значениям линейной функции у = х + 4. Поэтому линейная функция у = х + 4 является наклонной асимптотой для данной функцииy(x).
Учитывая точки пересечения графика функции с осями координат, наличие вертикальной и наклонной асимптот, строим график данной функции. Очевидно, что график функции не пересекает асимптоты. На графике видно, что функция имеет максимум и минимум (найти их координаты можно только с помощью производной).
Частным случаем наклонной асимптоты является горизонтальная асимптота (при k = 0). Горизонтальная прямая у = b называется горизонтальной асимптотой функции f(х), если при неограниченном возрастании или убывании х значения функции f(x) стремятся к величине b, т. е. при х → ±∞ f(x) → b.
Пример 5
Построим график функции
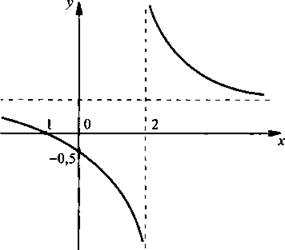
Найдем точки пересечения графика функции с осями координат. При х = 0 находим: у = -0,5 — точка пересечения с осью ординат. При у = 0 получаем уравнение или 0 = x + 1, корень которого х = -1 — точка пересечения с осью абсцисс.
Очевидно, что прямая x = 2 — вертикальная асимптота. При х → 2 числитель дроби x + 1 → 3. При x < 2 знаменатель дроби x — 2 отрицательный и x — 2 → 0. Поэтому значения функции у → -∞. При x > 2 знаменатель дроби x — 2 положительный и x — 2 → 0. Поэтому значения функции у → ∞.
Разделим числитель дроби x + 1 на ее знаменатель x — 2 столбиком и выделим целую часть. Тогда функция y(x) имеет вид:
Очевидно, при х → ∞ дробь и значения функции у(х) стремятся к 1. Поэтому прямая у = 1 является горизонтальной асимптотой для графика данной функции
Учитывая проведенное исследование данной функции, строим ее график. Очевидно, что такой график получается смещением графика функции у = 3/x на 2 единицы вправо и на 1 единицу вверх.
Чтение графиков функций
Практически во всех исследованиях результаты представляются в виде графиков. Поэтому необходимо уметь их читать, т. е. понимать и представлять свойства функций, которые им соответствуют.
Пример 6
На рис. а представлена зависимость х(t) для точки, двигающейся из пункта А в пункт В (где х — координата точки, начало отсчета совмещено с пунктом А).
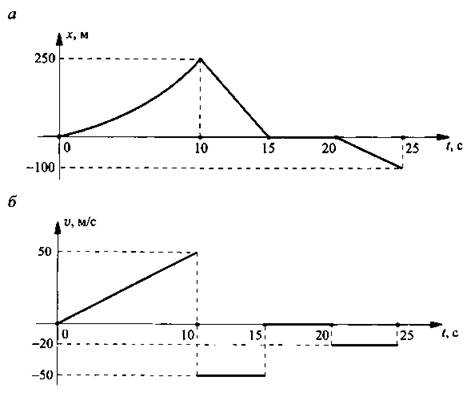
Опишем происходящее движение, которое дополнительно будем иллюстрировать графиками б: зависимостью скорости от времени v(t) и в: зависимостью ускорения от времени a(t). При этом координата (перемещение) х измеряется в м, скорость v — в м/с, ускорение a — в м/с2, время t – в с.
На промежутке 0 ÷ 10 с перемещение х меняется по квадратичному закону, т. е. движение является равноускоренным. Поэтому скорость v меняется по линейному закону и ускорение а постоянно. При этом точка движется по направлению от А к В, так как перемещение х имеет положительный знак.
При t = 10 с точка изменяет направление движения на противоположное и начинает двигаться к пункту А. При этом координата х меняется по линейному закону, т. е. движение является равномерным со скоростью v = -50 м/с. Отрицательный знак скорости при t = 10 ÷ 15 с указывает на движение в направлении к пункту А. Очевидно, что ускорение a = 0.
В течение времени t = 15 ÷ 20 с координата х не меняется и х = 0. Это означает, что точка находится в состоянии покоя в пункте А. Разумеется скорость v = 0 и ускорение a = 0.
На промежутке t = 20 ÷ 25 с координата х меняется по линейному закону, т. е. движение является равномерным со скоростью v = -20 м/с. Отрицательные знаки перемещения х и скорости v указывают на удаление точки от пунктов А и В. Разумеется, ускорение a = 0.
IV. Контрольные вопросы
1. Приведите схему исследования функции.
2. Дайте определение вертикальной асимптоты графика функции.
3. Приведите определение наклонной асимптоты графика функции.
4. Дайте определение горизонтальной асимптоты графика.
V. Творческое задание
Проведите исследование функции и постройте ее график:
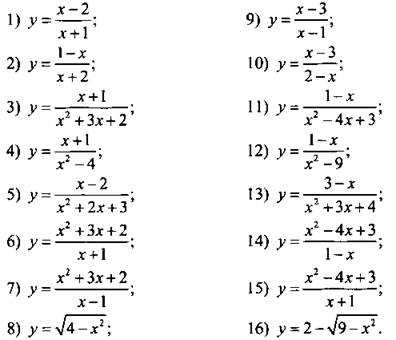
VI. Подведение итогов уроков
tak-to-ent.net
План-конспект урока (алгебра, 10 класс) по теме: Урок на тему: «Схема исследования функции».
Урок на тему: Схема исследования функции (1 курс, 2 ч)
Цели: повторить схему исследования функции для построения ее графика и рассмотреть исследование функции с помощью производной; упражнять учащихся в исследовании функции с помощью производной и построении графиков функций; развивать навыки исследования функций и построения графиков; закрепить знания нахождения промежутков возрастания и убывания функции, экстремумов функции с помощью производной
Ход урока:
1. Повторение пройденного материала
- Повторить схему исследования функции.
- Исследовать функции на возрастание (убывание) и на экстремум удобно проводить с помпощью производной.
2. Изучение нового материала
- Разобрать по учебнику пример 1. Пояснить осоставление таблицы и построения графика на рис 111.
- Исследовать функцию и построить ее график: у= х4/4-х3/3- х2.
Р е ш е н и е.
1) Область определения — D(y)=R
2) функция не является ни четной, ни нечетной, ни периодической;
3) найдем точки пересечения графика с осью ОХ (т. е. нули функции): х4/4-х3/3- х2=0,
3х4-4х3-12х2=0, х2(3х2-4х-12)=0; х1=0; х2≈ -1,4; х3≈2,8.
Пересечение с осью ОУ: х=0,у=0.
Возьмем также две дополнительные точки: у(1)= — 13/12; у(3)=9/4;
4) находим производную: у’ = х3-х2-2х=х(х2-х-2)=х(х+1)(х-2).
у’=0, х(х+1)(х-2) =0, х=0, х= -1, х=2;
5) найденные критические точки разбивают числовую прямую на четыре промежутка:
(-∞;-1), (-1;0), (0;2), (2;+∞).
Составим таблицу:
х | (-∞;-1) | -1 | (-1;0) | 0 | (0;2) | 2 | (2;+∞) |
f ‘(x) | — | 0 | + | 0 | — | 0 | + |
f(x) | -5/12 | 0 | -8/3 | ||||
убывает | min | возрастает | max | yбывает | min | возрастает |
6) Строим график.
3. Закрепление изученного материала
1. (Устно). Определите по следующим данным характер монотонности функции и указанных промежутках и вид экстремума:
а)
х | (-∞;-1) | -1 | (-1;0) | 0 | (0;+∞) |
f ‘(x) f(x) | — | 0 -4 | + | 0 4,5 | — |
б)
х | (-10;2) | 2 | (2;7) | 7 | (7;10) |
f ‘(x) f(x) | + | 0 5 | — | 0 -3 | — |
в)
х | (-4;0) | 0 | (0;3) | 3 | (3;7) | 7 | (7;+∞) |
f ‘(x) f(x) | + | 0 -3 | — | 0 -4 | + | 0 6 | — |
2. Внесите необходимые данные, при которых в указанных точках функция имела бы заданные виды экстремумов:
х | (-7;-2) | -2 | (-2;3,5) | 3,5 | (3,5;+∞) |
f ‘(x) f(x) | 0 max | 0 min |
3. Назовите промежутки возрастания (убывания) и вид каждого из экстермумов функции. Изобразите эскиз графика функции, если, исследуя ее с помощью производной, получили данные:
х | (-∞;-5) | -5 | (-5;0) | 0 | (0;3) | 3 | (3;7) |
f ‘(x) f(x) | + | 0 3 | — | 0 0 | _ | 0 -2 | + |
4. Постройте эскиз графика функции у=ах2, если: а)а>0; б)a
5. Найдите экстремум квадратичной функции у=ах2+bx+c (a≠0), если а)а>0; б)a
6. Изобразите эскиз графика функции у=ах2+bx+c (a≠0), если в левой полуокрестности точки х0 (х0- абсцисса вершины параболы) у’>0, а в правой полуокрестности х0 у’ 0.
7. Определите (с использованием производной) вершину параболы и изобразите эскиз графика функций: а)у=х2-3х+2; б)у= -х2-4х+5; в) у=3х2-х-1; г)у= 2х2+5х-3.
4. Самостоятельная работа (СО)
Карточка — задания №1
Вариант 1. Исследуйте функцию у=х2 +2х-8 с помощью производной и постройте ее график.
П л а н р е ш е н и я:
1)Установите область определения функции.
2) Найдите производную функции.
3) Определите критические точки функции.
4) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
5) Запишите промежутки возрастания и убывания функции.
6) Найдите точку экстремума функции и значение функции в ней.
7) Постройте график функции.
Карточка- задания№2
Вариант 2. Исследуйте функцию у=х3/9 +х2 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Найдите производную функции.
3) Определите критические точки функции.
4) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
5) Запишите промежутки возрастания и убывания функции.
6) Найдите точку экстремума функции и значение функции в них.
7) Постройте график функции.
Карточка — задания №3
Карточка- задания№2
Вариант 3. Исследуйте функцию у=х2-х3/6 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Определите критические точки функции.
3) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
4) Запишите промежутки возрастания и убывания функции.
5) Найдите точку экстремума функции и значение функции в них.
6) Постройте график функции.
Карточка — задания №4
Вариант 4. Исследуйте функцию у=х4/4-х2 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Определите критические точки функции.
3)Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
4) Запишите промежутки возрастания и убывания функции.
5) Найдите точку экстремума функции и значение функции в них.
6) Постройте график функции.
5. Математический диктант:
Вариант 1. Изобразите схематично график непрерывной функции y=f(x), обладающей следующими свойствами:
х | (-∞;-2) | -2 | (-2;1) | 1 | (1;+∞) |
f(x) | 4 max | -3 min |
Вариант 2. Изобразите схематично график непрерывной функции y=f(x), обладающей следующими свойствами:
х | (-∞;-3) | -3 | (-3;2) | 2 | (2;+∞) |
f(x) | 6 max | 1 min |
6. Итог урока.
nsportal.ru
Урок алгебры по теме «Применение производной к исследованию функции и построение ее графика». 10-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательные:
- систематизировать пройденный материал по производным и функциям;
- научить учащихся исследовать функцию с помощью производной и строить её график;
- развивать вычислительные навыки.
Развивающие:
- умение применять полученные знания при изучении нового материала;
- развитие элементов творческой деятельности;
- развитие целеустремлённости в достижении поставленной цели.
Воспитательные:
- воспитывать самостоятельность и ответственное отношение к своему делу;
- воспитывать умение выстраивать отношения в диалоге с товарищами и учителем, чувства взаимопомощи;
- воспитание интереса к математике.
Оборудование:
- Справочный материал для библиотеки;
- Карточки для индивидуальной работы;
- Карточки для групп при составлении плана;
- Бейджики с указанием специалистов на данный урок(научный сотрудник, старший научный сотрудник, профессор, академик, журналист)
- Компьютер, интерактивная доска
Тип урока: Открытие новых знаний(изучение нового).
Форма работы: групповая, одноуровневая.
Форма занятия: Урок-игра “Научно-исследовательская лаборатория” (ролевая) с применением элементов проектно-исследовательской технологии.
Средства обучения: наглядность, ИКТ, сигнальные карточки трех цветов(синий, зеленый, красный)
Форма контроля: листы доверия, листы самооценки.
Поощрение учащихся: Вручение медалей - “Нобелевская премия” за открытие и сладкие призы.
План урока.
1.Организационный момент.
2.Актуализация опорных знаний.
а) письменная работа индивидуальная б) устная работа
3.Постановка проблемы.
4.Постановка цели урока исходя из проблемы.
5.Мотивация к достижению цели.(примеры из жизни)
6.Опорные знания для достижения цели.
7.Выявление темы урока учащимися.
8.Запись в тетрадях темы и цели урока.
9. Работа с карточками, составление плана исследования функции. Работа с учебником. Работа с библиотекой (справочным материалом).
10.Решение проблемы по плану исследования.
11.Достижение цели.
12.Вручение “нобелевской премии” учащимся, достигнувших цели.
13.Рефлексия.
14.Задание на дом.
15.Самооценка
16.Итог урока.
Ход урока
Девиз к уроку: “Решай ,ищи, твори и мысли”
1. Организационный момент.
Перед уроком оформляется библиотека, где собран необходимый материал для изучения темы. Класс разбивается на 4 лаборатории, где назначаются старший научный сотрудник и сотрудники; профессора и академик. Выбирается журналист (может и учитель быть), который в ходе работы групп интересуется решениями и проявляет любознательность.
Перед учащимися ставится задача, которую они должны решить в ходе урока, определить цель урока, сформулировать тему , достичь цели, подвести итог своей деятельности и сделать соответствующие выводы.
2. Актуализация опорных знаний.
а) письменная работа индивидуальная дифференцированная (слайд 2)
Научным сотрудникам задания:
Найти область определения.
Определить четность или нечётность.
Найти точки пересечения графика функции с осями координат.
Профессорам и академикам
Найти критические точки.
Найти промежутки возрастания и убывания.
Найти точки экстремума и экстремум функции
б) устная работа . Назвать графики известных функций. (слайд 3)
- у = -2х+5
- у = х2 + 4х — 3
- у = х2+1
- у = х2
- у = 0,5х
- у = 8
- у =
- у = х2— 2
- х = 3
- у = 3х — х3
- у = х4 -2х2 -3
3. Постановка проблемы. (слайд3)
Не умею и не знаю графики многих функций.
Выдвигаем цель: Научиться строить график незнакомой функции (слайд 4)
4. Мотивация к достижению цели.(примеры из жизни) (слайд 5,6,7,8)
Для чего нужно научиться строить график? Где пригодятся эти знания?
Функции в жизни.
(слайд 5) Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций? – от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.
Итак, чем больше гостей, тем на большее количество порций мы должны разделить торт.
Здесь наглядно можно представить прямую пропорциональную зависимость.
(слайд 6) — Во втором случае, чем больше гостей, тем меньше вес порции.
Здесь наглядно можно представить обратную пропорциональную зависимость.
(Слайд 7)Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, Интернета. Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая является графиком показательной функции.
(Слайд 8) В жизни часто приходится встречаться с такими фактами, когда скорость изменения какой-нибудь величины пропорциональна самой величине. Так по закону показательной функции можно рассмотреть размножение ланцетника. А так же размножение всего живого на земле, если бы для этого имелись бы благоприятные условия. Доказательство тому – распространение в Австралии кроликов, которых там раньше не было. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.
6. Опорные знания для достижения цели.
Вопрос учителя: Какие свойства необходимы знать для построения графика функции? (ответы учащихся, перечисляют)
Учитель: Найти ответы для нахождения критических точек, промежутков возрастания, убывания поможет… (учащиеся должны ответить что — производная)
7. Выявление темы урока учащимися. (слайд 9)
Учащиеся объединяют цель (в начале) урока и понятие производной, и формулируют тему урока.
Тема: “Применение производной к исследованию функции и построение её графика”.
8. Запись в тетрадях темы и цели урока.(слайд 9)
9. Составление плана исследования функции.
Из набора слов по карточкам составляем план в алгоритмическом порядке. Выслушиваем учащихся, корректируем. Записываем в тетрадь.
(слайд 10) План исследования.
- Найти область определения.
- Область значений (если возможно найти)
- Исследовать на чётность и нечётность, периодичность (для тригонометрических) функцию.
- Найти точки пересечения графика с осями координат (с осью Ох и осью Оу)
- Найти критические точки.
- Найти промежутки монотонности (возрастания и убывания).
- Найти точки экстремума и экстремум функции(хmax, xmin, ymax, ymin)
- Построить график.
- Если необходимо вычислить дополнительные точки.
10. Решение проблемы по плану исследования. (слайд 11)
Исследовать и построить график.
у= 3х — х3 (для научных сотрудников)
у = х4 -2х2 -3 (для профессоров)
11. Достижение цели. Работают в группах и обсуждают до первого победителя, кто построит правильно график. Проверка. (Слайд12)
Журналисты (в лице учащихся со слабыми знаниями) ходят по группам, интересуются, задают вопросы, делают записи в своих тетрадях. Получают знания с интересом.
Во время работы учащиеся обращаются к справочному материалу (библиотека), где найдут и теоретический материал по пройденным темам и образцы.
Учитель выступает в роли старшего товарища, наблюдает за ходом работы учащихся.
12. Вручение медали “Нобелевская премия” учащимся ,достигнувших цели,
и сладкий приз (слайд 13)
13. Рефлексия. Используем сигнальные карточки при ответе на вопросы.(слайд 13) .
- Чему научился на уроке.
- Смог ли понять новый материал.
- Самооценка своей деятельности.
1) Усвоил хорошо.
2) Усвоил, но есть проблемы.
3) Усвоил плохо.
14. Задание на дом. Индивидуально-дифференцированая работа. (слайд 13)
Стр. 147 – 148 всем.
№296 (в) – научным сотрудникам
№297(а) – академикам и профессорам
15. Самооценка
Заполняют листы самооценки и сдают учителю.
16. Окончание урока. Итог.
4.05.2014
xn--i1abbnckbmcl9fb.xn--p1ai
Исследование функции и построение ее графика
1) Найдем область определения функции. Функция представляет собой рациональную дробь, поэтому нужно исключить значения обнуляющие знаменатель.
таким образом, область определения функции:
2) Точки пересечения графика функции с осями координат:
с осью ;
с осью .
Таким образом, функция проходит через начало координат — точку .
3) Функция не периодическая. Исследуем функции на четность:
Ни одно из равенств или не выполняется, поэтому функция не является ни четной, ни нечетной. График функции не будет иметь никакой симметрии.
4) Найдем асимптоты графика функции.
В точке функция разрывная. Определим, как ведет себя точка в окрестности этой точки
Таким образом, — уравнение вертикальной асимптоты.
Найдем наклонные асимптоты , где
Получаем уравнение наклонной асимптоты .
5) Найдем экстремум функции и интервалы возрастания и убывания. Для этого вычислим первую производную, используя правило дифференцирования частного:
Найдем критические точки: при
не существует при , но эта точка не принадлежит области определения. Находим знак производной в каждом из интервалов и результаты занесем в таблицу
То есть точка — точка максимума.
6) Найдем точки перегиба, интервалы выпуклости и вогнутости. Для этого находим вторую производную
Найдем критические точки: при не существует при , но эта точка не принадлежит области определения. Находим знак второй производной в каждом из интервалов и результат занесем в таблицу:
Значение функции в точке перегиба . Точка — точка перегиба.
7) Используя полученные данные, строим пунктиром асимптоты и жирным график функции.
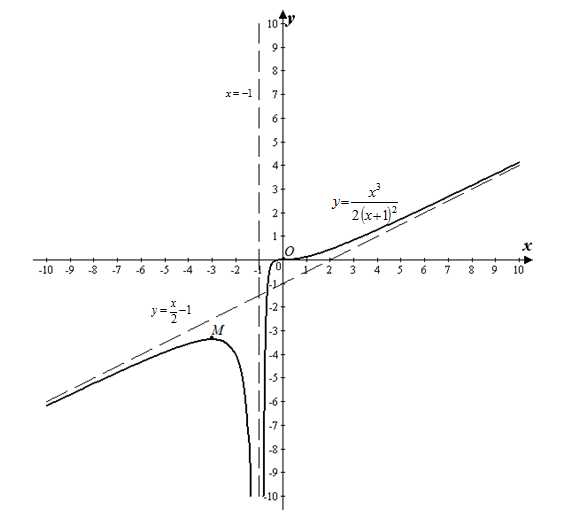
ru.solverbook.com
| 1. |
Вертикальная асимптота
Сложность: лёгкое |
1 |
| 2. |
Горизонтальная асимптота
Сложность: лёгкое |
1 |
| 3. |
Выпуклости графика функции
Сложность: лёгкое |
2 |
| 4. |
Построение графика дробной функции
Сложность: среднее |
8 |
| 5. |
Точки перегиба функции
Сложность: среднее |
2 |
| 6. |
Доказательство выпуклости функции
Сложность: среднее |
4 |
| 7. |
Исследование и построение графика сложной функции, содержащей квадратный корень
Сложность: сложное |
6 |
| 8. |
Уравнение с параметром
Сложность: сложное |
4 |
| 9. |
Определение количества корней
Сложность: сложное |
3 |
www.yaklass.ru
