Исследование функции на экстремум
Пример 1. Исследовать на max и min
 2.
2.
1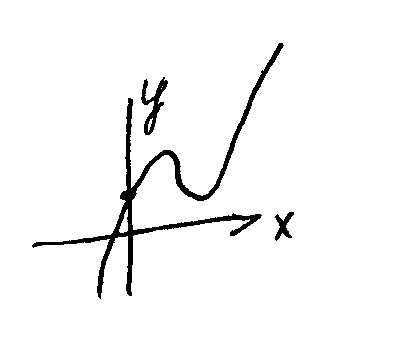 )2)
)2)
с помощью второй производной.
Пусть
при 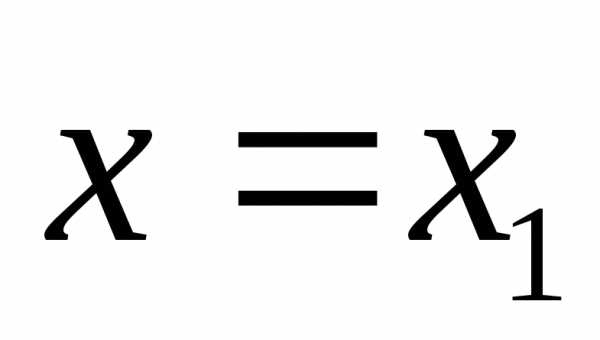 производная от
производная от 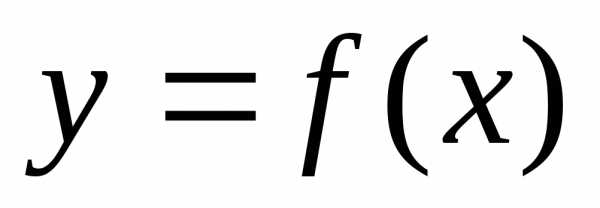 обращается в нуль, т.е.
обращается в нуль, т.е.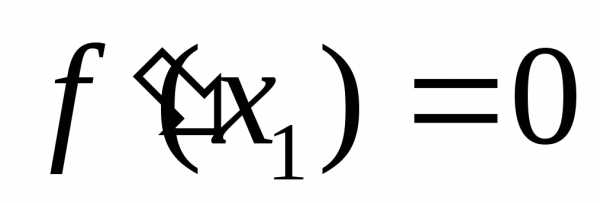 .
Пусть, кроме того,
.
Пусть, кроме того,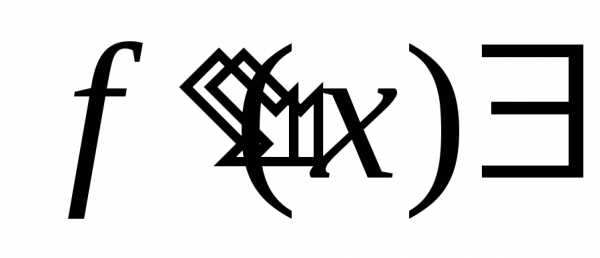 и непрерывна в окрестности
и непрерывна в окрестности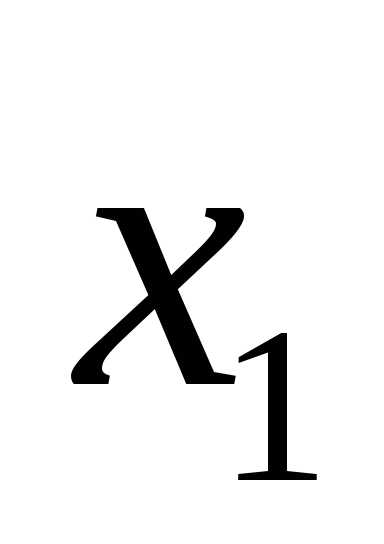 .
Тогда справедлива
.
Тогда справедлива
Теорема.
Пусть 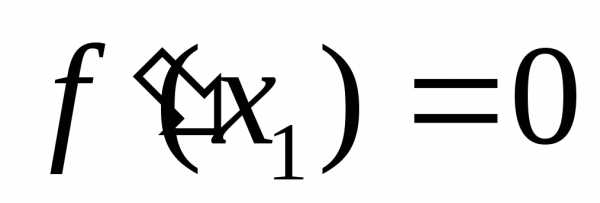
Доказательство.
Пусть 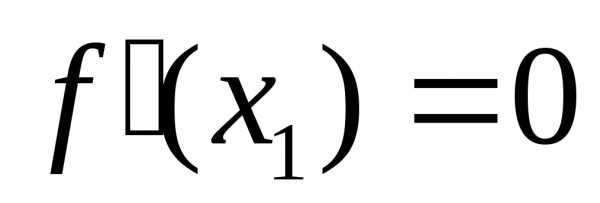 и.
Т.к.
и.
Т.к.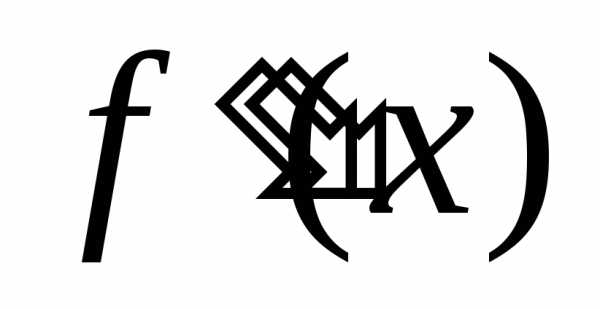 непрерывна, то
непрерывна, то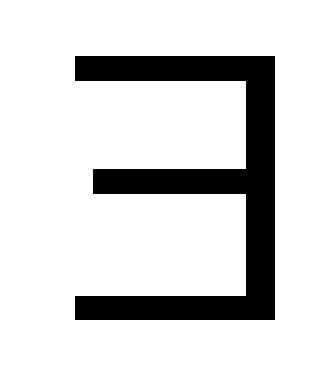 малый отрезок, содержащий
малый отрезок, содержащий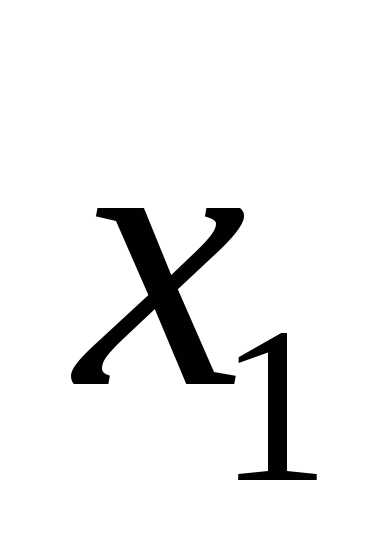 ,
во всех точках которого.
,
во всех точках которого.
Т.к.
убывает на выбранном отрезке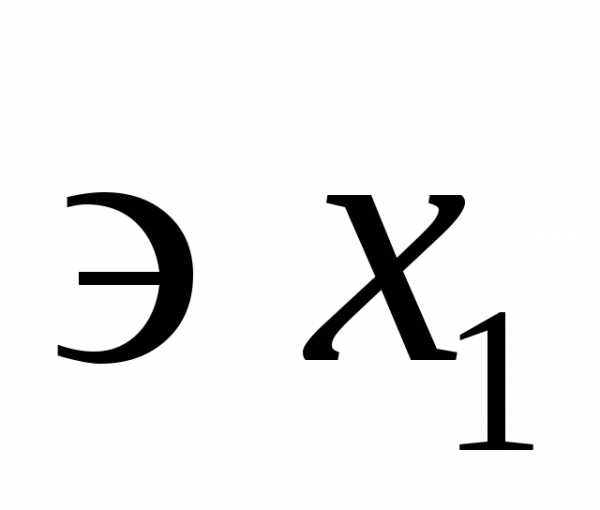 .
Но,
при
.
Но,
при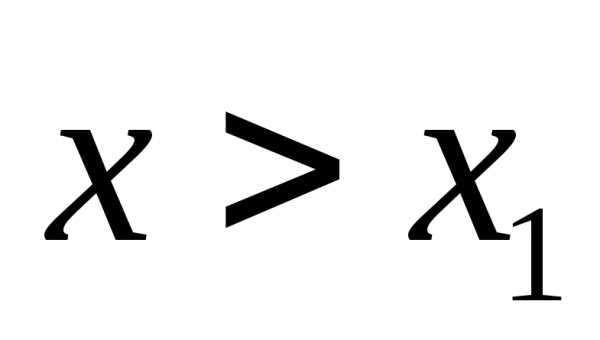 и
и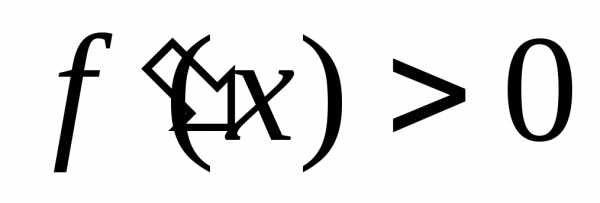 при
при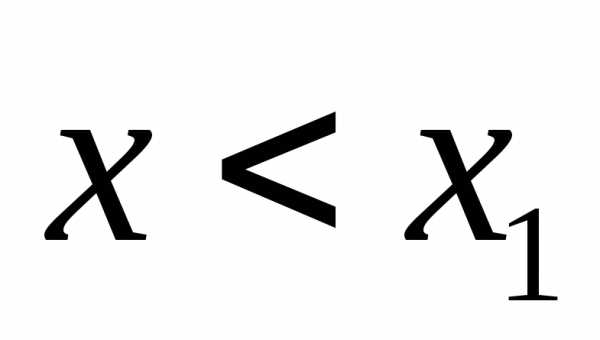 .
Т.е. при переходе через
.
Т.е. при переходе через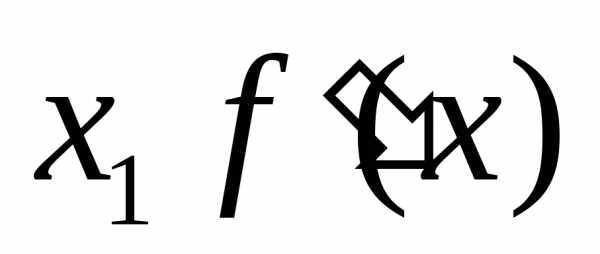 меняет знак с “+” на “-“, а это значит,
что
меняет знак с “+” на “-“, а это значит,
что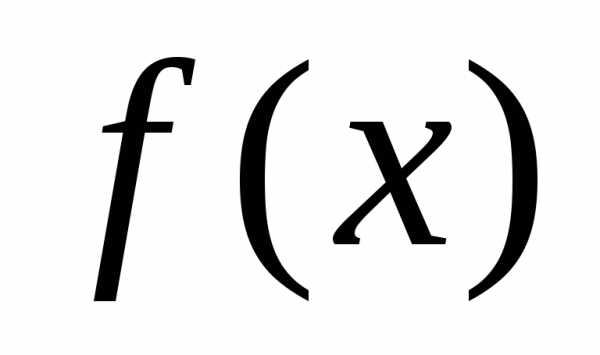
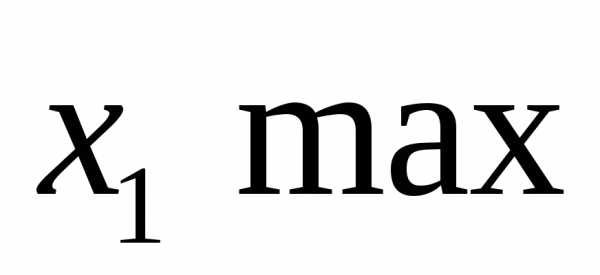 .
. Пусть
теперь
в
окрестности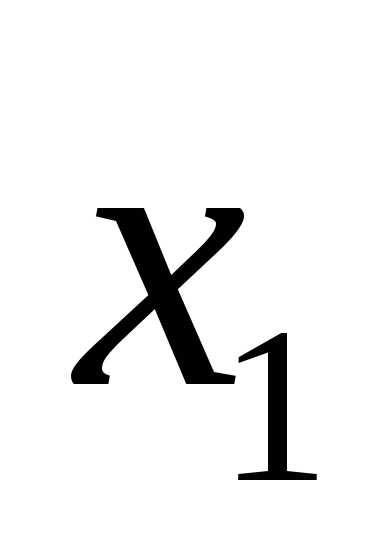 .
Т.к.при
.
Т.к.при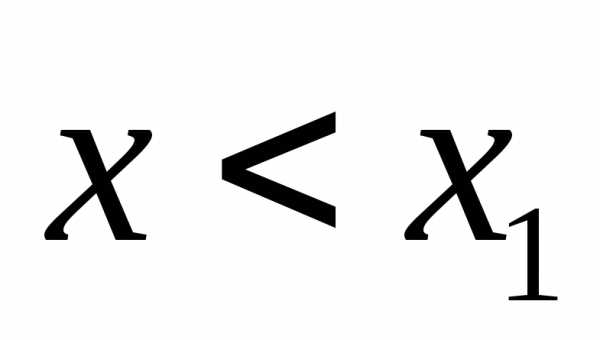 и
и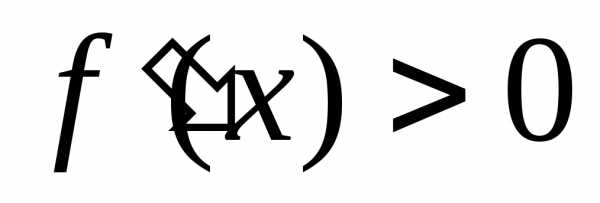 при
при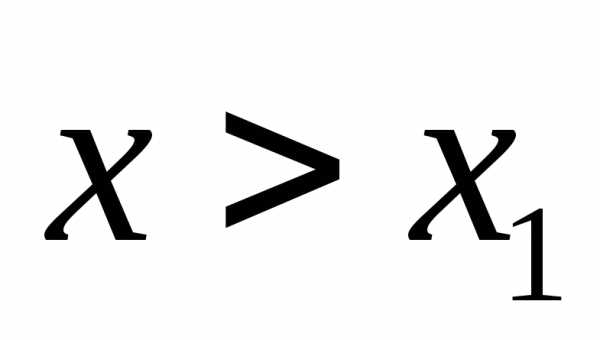 .
Т.о., при переходе через
.
Т.о., при переходе через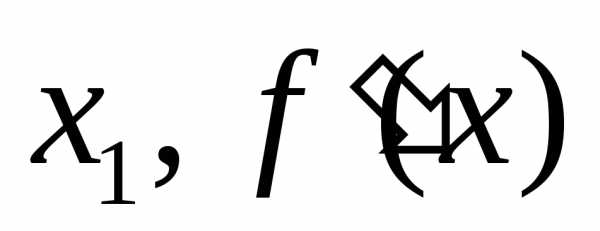 изменяет знак с “-” на “+“, т.о. мы имеем
в.
изменяет знак с “-” на “+“, т.о. мы имеем
в.
Если
в 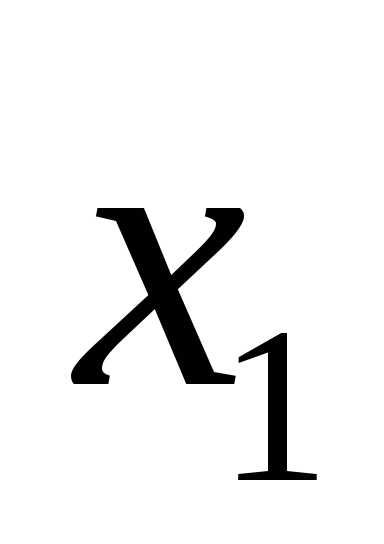 ,
то в этой точке может бытьmax,
min,
или не быть ни того ни другого. В этом
случае исследование
функции надо вести первым способом
(т.е. исследовать знак первой производной).
,
то в этой точке может бытьmax,
min,
или не быть ни того ни другого. В этом
случае исследование
функции надо вести первым способом
(т.е. исследовать знак первой производной).
Схема исследования.


Крит. точка
0
<0, “ – “
max
0
>0, “+”
min
0
0
неизвестно
П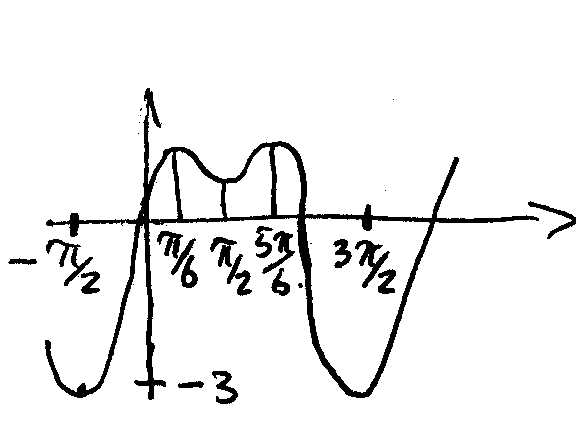 ример:
ример:
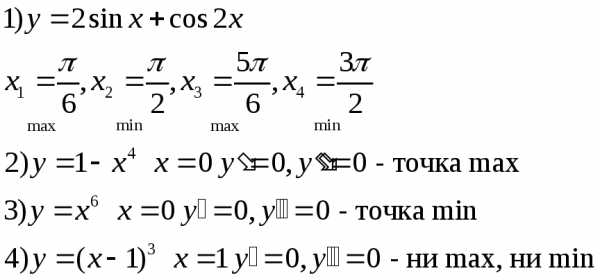
Наибольшее и наименьшее значения функции на отрезке.
Пусть 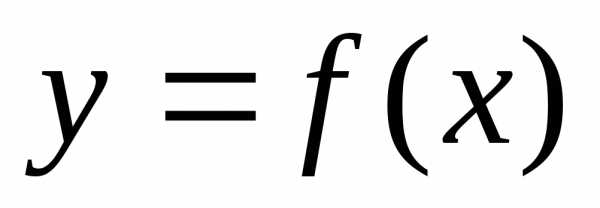 непрерывна на [a, b].
Тогда она достигает на нём своего
наибольшего и наименьшего значений.
непрерывна на [a, b].
Тогда она достигает на нём своего
наибольшего и наименьшего значений.
Предположим,
что 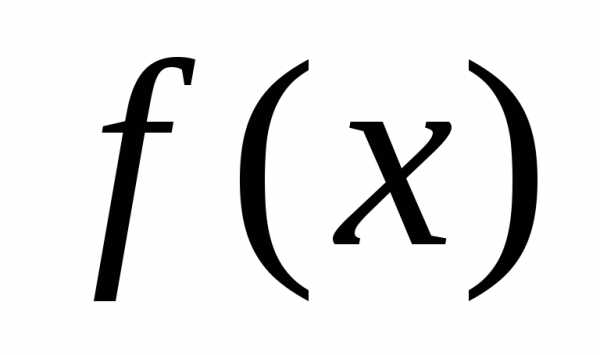 имеет на [a, b]
конечное число критических точек. Если
,
где-
точкаmax
(одного из), точнее – наибольший max.
Однако может случиться, что sup
достигается на одном из концов отрезка.
имеет на [a, b]
конечное число критических точек. Если
,
где-
точкаmax
(одного из), точнее – наибольший max.
Однако может случиться, что sup
достигается на одном из концов отрезка.
Итак, достигаетsup либо в одной из точек max, либо на концах отрезка.
То
же самое можно сказать и о наименьшем
значении 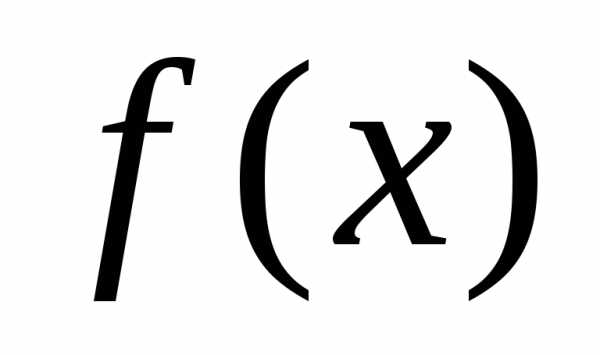 :
оно достигается либо на конце (концах)
отрезка, либо во внутренней точке,
является точкойmin.
:
оно достигается либо на конце (концах)
отрезка, либо во внутренней точке,
является точкойmin.
Итак, если требуется найти наибольшее (наименьшее) значение непрерывной , то необходимо:
Найти все max (min)
 на отрезке [a, b]
на отрезке [a, b]Вычислить значения
 при
приИз всех полученных выше значений выбрать наибольшее (наименьшее).
Пример.
.
Найтиsupr
и inf
на 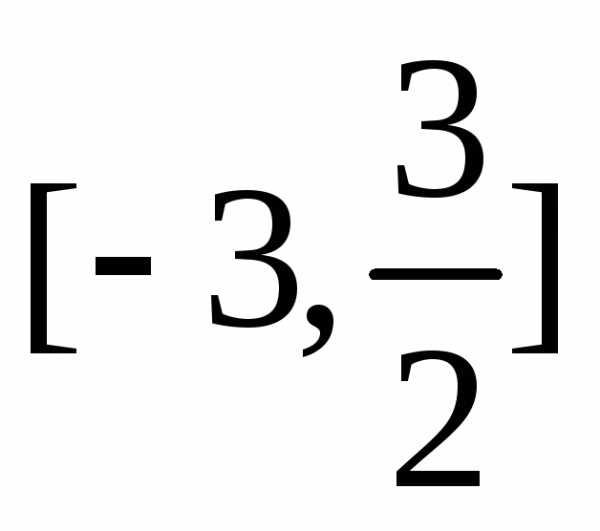
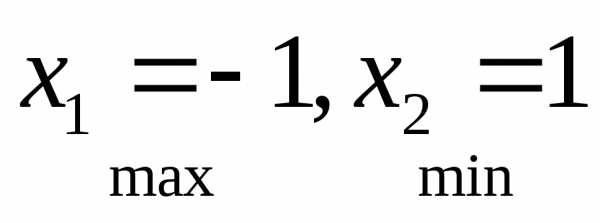
Формула Тейлора
Предположим,
что 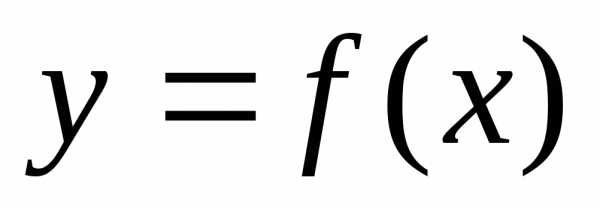 имеет все произвольные доn+1 –го порядка включительно в окрестности
имеет все произвольные доn+1 –го порядка включительно в окрестности 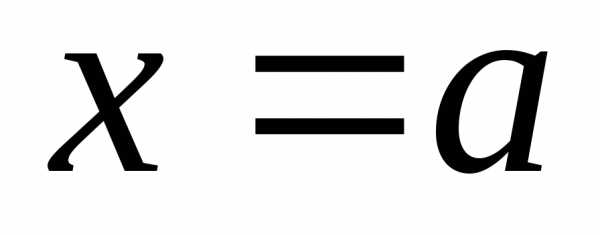 .
Найдём многочлен
.
Найдём многочлен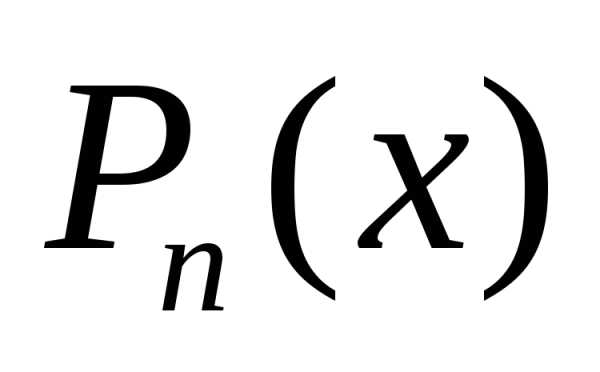
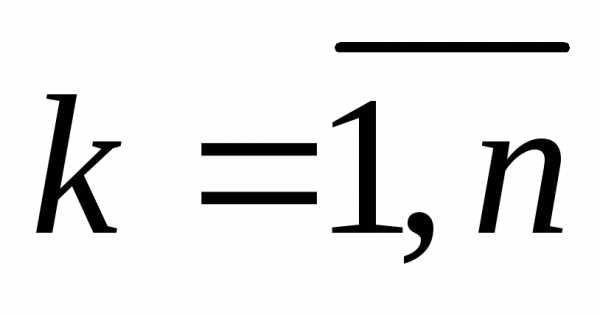 :
Итак
:
Итак(1)
Естественно предположить,
то 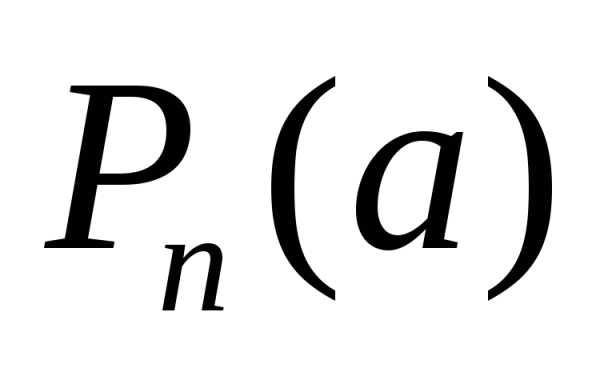 «близок» к
«близок» к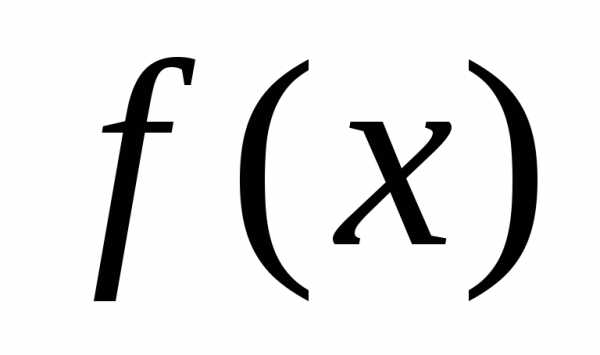 в некотором смысле.
в некотором смысле.
Будем искать 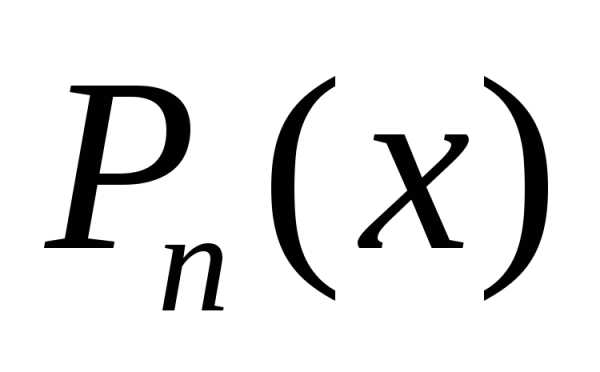 в форме многочлена по степеням
в форме многочлена по степеням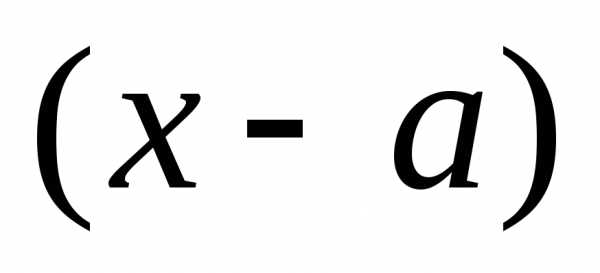 с неопределёнными коэффициентами:
с неопределёнными коэффициентами:
(2)
 будем
искать из условия (1). Предварительно
найдём производные от
будем
искать из условия (1). Предварительно
найдём производные от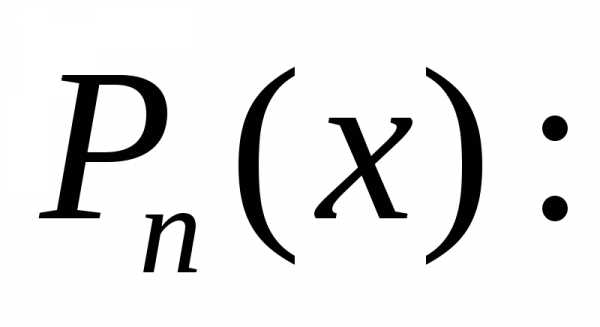
(3)
Подставляя
теперь вместо 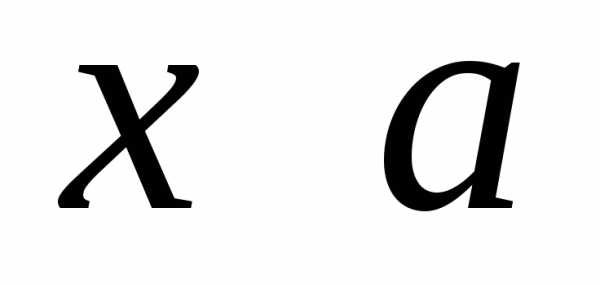
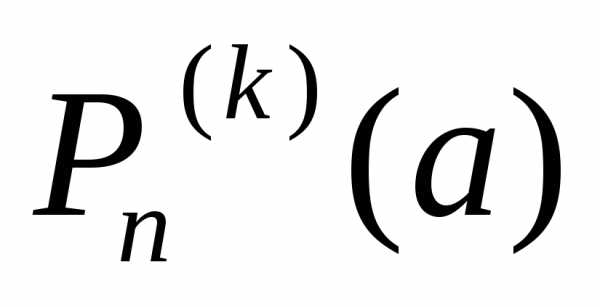 на
на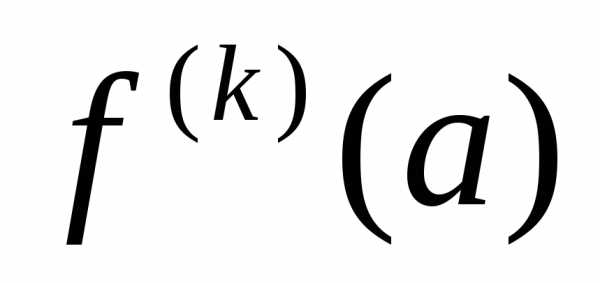 ,
согласно (1), получим:
,
согласно (1), получим: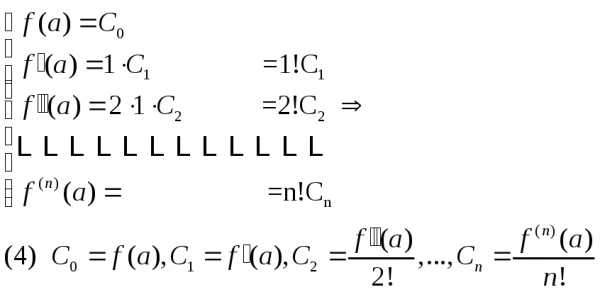
Подставляя
теперь вместо  вполучим
вполучим
(5)
Обозначим
теперь через 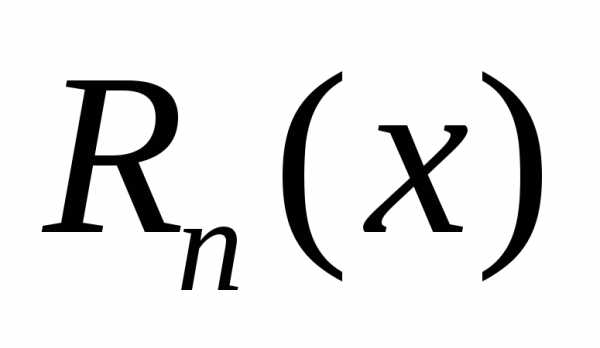 разность между
разность между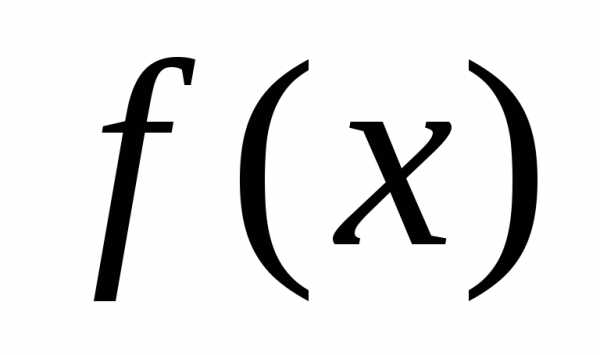 :
:
и тогда или в развёрнутом виде
(6)
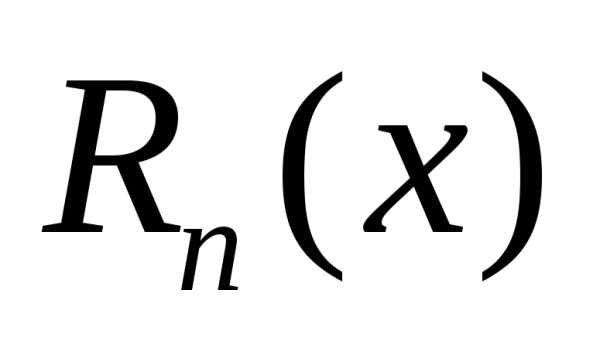 называют
остаточным членом. Для тех значений
называют
остаточным членом. Для тех значений 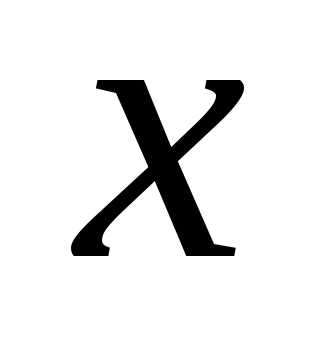
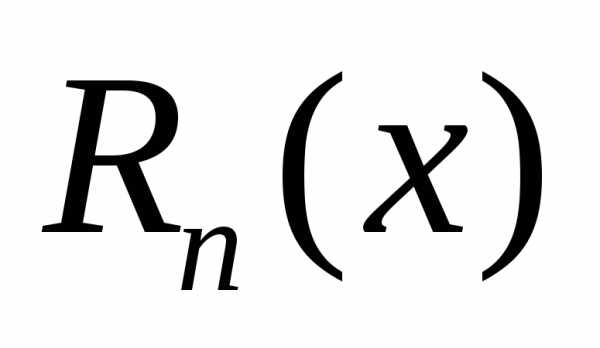 мал,
мал,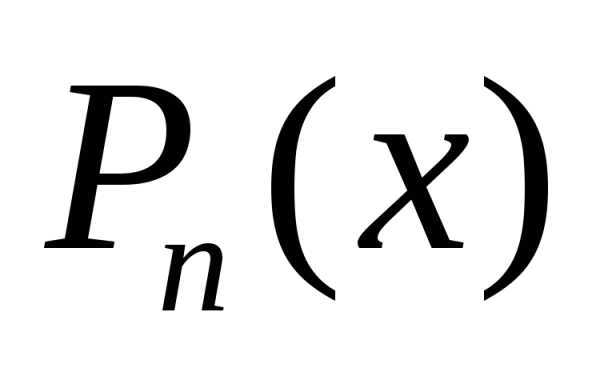 даёт приближённое представление
даёт приближённое представление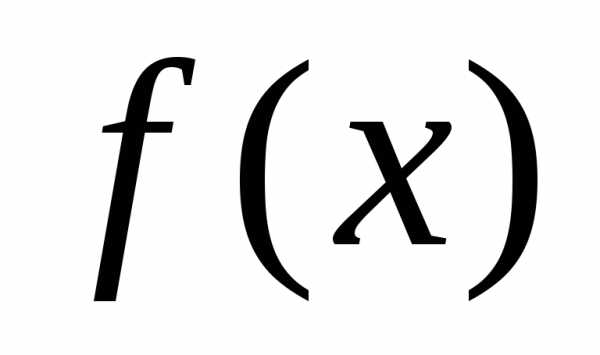 .
. Т.о.
(6) даёт возможность заменить 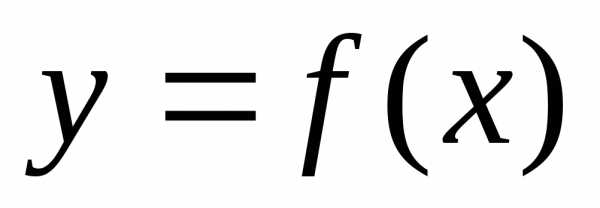 многочленом
многочленом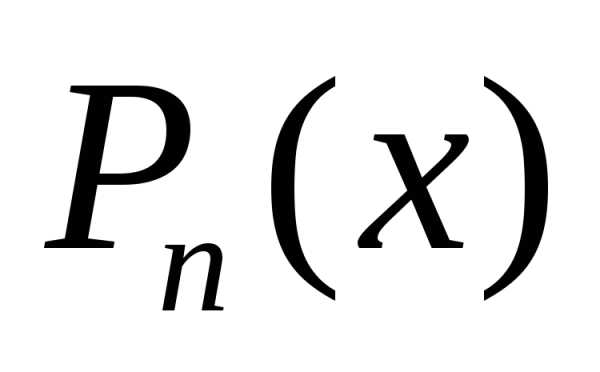 с точностью, определяемой
с точностью, определяемой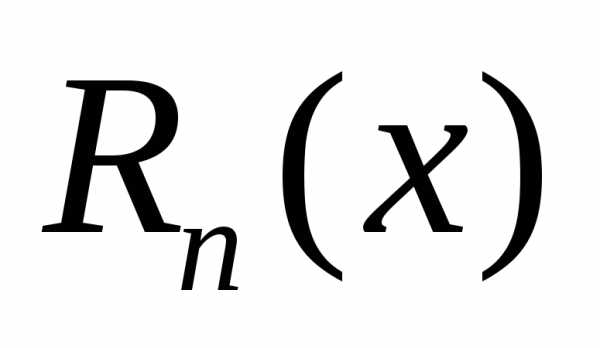 .
.
Следующая
задача – оценить 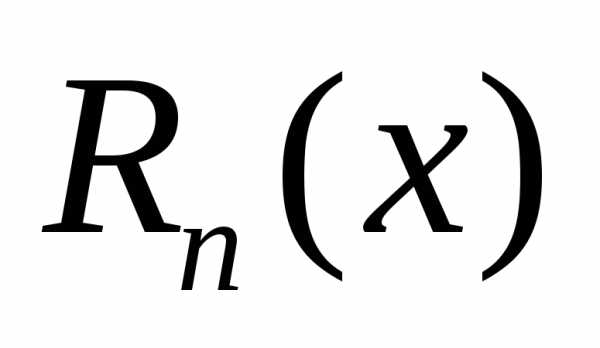 при различных
при различных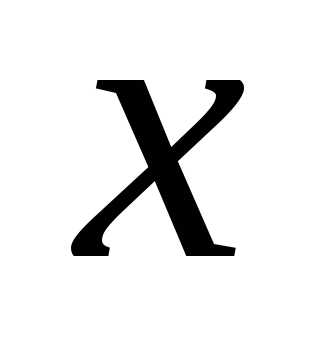 .
Запишем
.
Запишем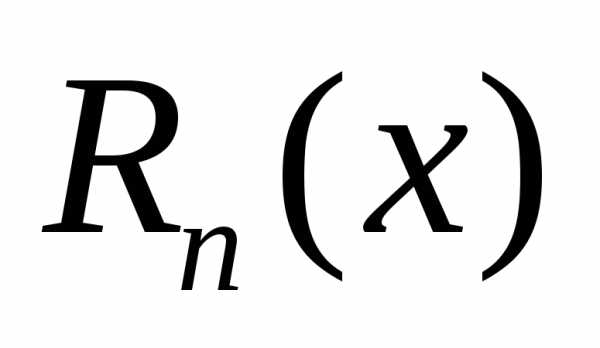 в форме
в форме
,
где 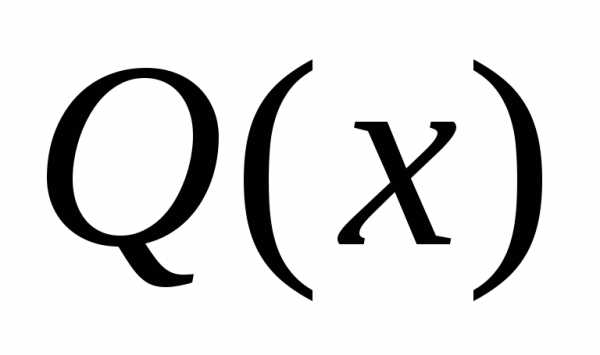 —
некоторая функция, которую нужно
определить. При фиксированных
—
некоторая функция, которую нужно
определить. При фиксированных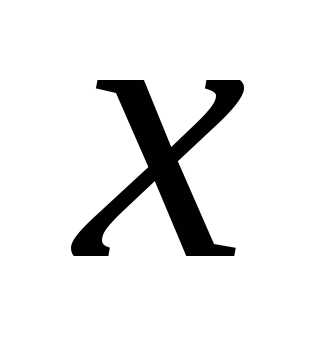 и
и
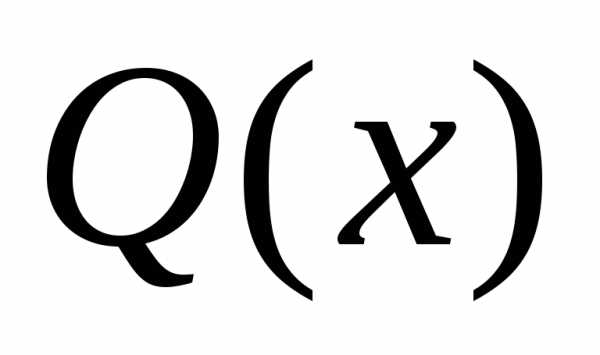 имеет определённое значение
имеет определённое значение .
.
Рассмотрим далее вспомогательную функцию от
Далее
найдём 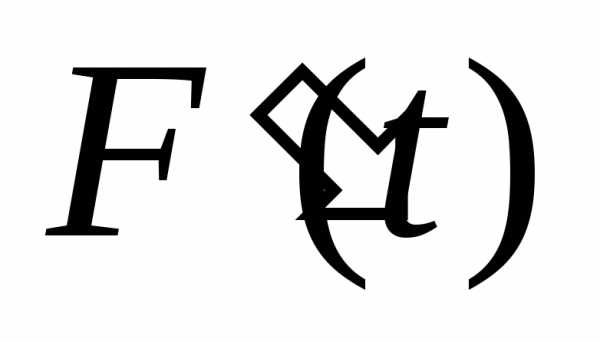
После сокращения получим
(*)
Итак, 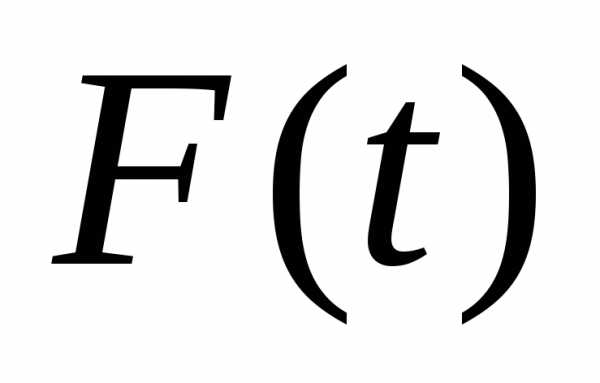 имеет производную для,
причём
имеет производную для,
причём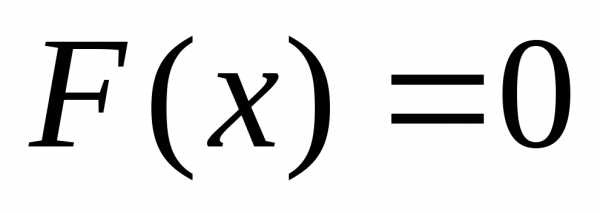 и
и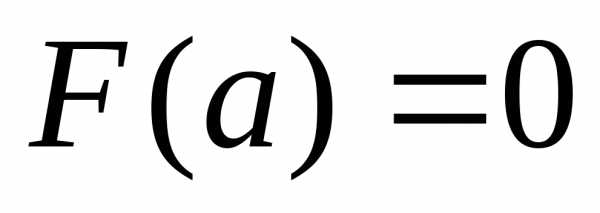
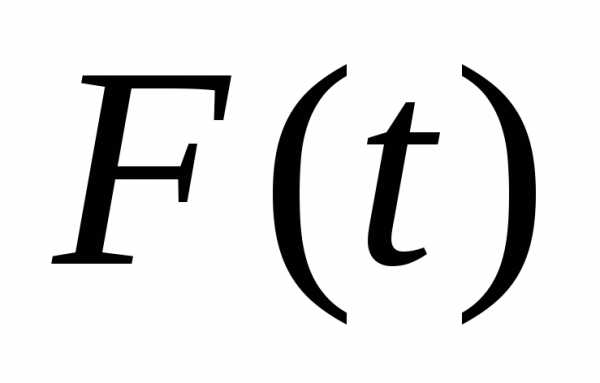 применима т. Ролля:,
в которой.
Отсюда и из (*) следует, что
применима т. Ролля:,
в которой.
Отсюда и из (*) следует, чтоили
и тогда
остаточный
член в форме Лагранжа. Т.к.  заключено между
заключено между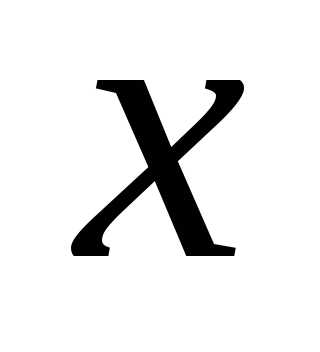 и
и ,
то его можно представить в виде,
где,
и тогда
,
то его можно представить в виде,
где,
и тогда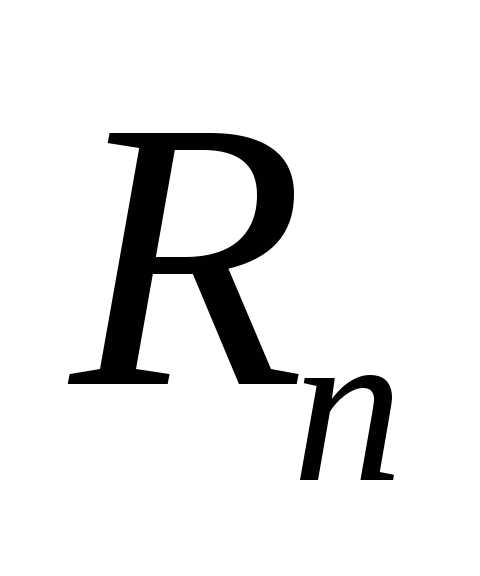 можно записать в виде:
можно записать в виде:
Формула
называется
формулой Тейлора для 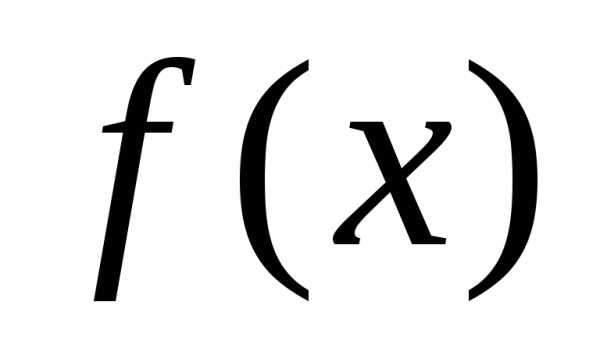 .
.
Если
в формуле Тейлора положить 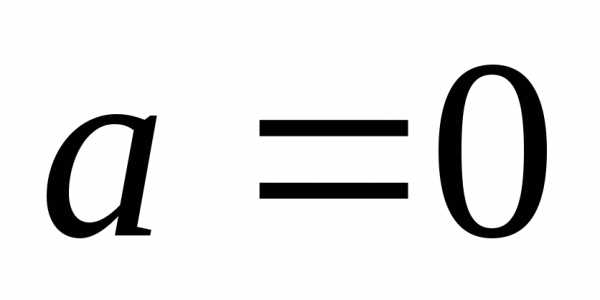
(**) .
Этот частный случай формулы Тейлора называют формулой Маклорена.
studfiles.net
Примеры исследования на экстремум — МегаЛекции
Исследование функции нескольких переменных на экстремум
Определение экстремума
Набору значений двух переменных и соответствует точка на плоскости, набору значений трех переменных – точка в пространстве. По аналогии набор значений нескольких переменных будем называть точкой М, набор значений будем называть точкой .
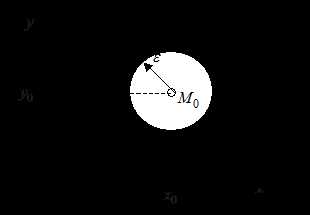 Нарисуем на плоскости круг с центром в точке и радиусом . Для всех точек этого круга расстояние до не превосходит :
Нарисуем на плоскости круг с центром в точке и радиусом . Для всех точек этого круга расстояние до не превосходит :
.
Будем называть такой круг -окрестностью точки . Аналогично, для произвольного числа переменных -окрестностью точки называется множество точек , для которых выполняется условие:
.
Используя введенные понятия, дадим определение экстремума функции нескольких переменных. Функция имеет в точке максимум(минимум, если существует такая -окрестность точки , для всех точек которой выполняется условие: .
Если составить приращение , то в точке минимума приращение всегда положительно ( ), в точке максимума – отрицательно ( ).
Необходимые и достаточные условия экстремума
Рассмотрим функцию двух переменных . Пусть в точке у нее имеется экстремум. Зафиксируем значение одной из переменных, например, возьмем , тогда функция является функцией одной переменной, и для нее в точке экстремума должно выполняться условие: производная равна 0 или не существует. Во втором случае функция имеет так называемый «острый» экстремум. Такие функции достаточно редки, поэтому в дальнейшем будем рассматривать только функции с «гладкими» экстремумами, когда производная равна 0: . Аналогично можно показать, что и . Продолжая рассуждения для функции произвольного числа переменных, можно показать, что необходимым условием существования экстремума функции нескольких переменных является равенство 0 всех частных производных функции:
Точки, которые являются решением этой системы, называются стационарными. Чтобы узнать, будут ли они точками экстремума, и, если да, то какого, нужно проверить выполнение достаточных условий экстремума.
Для функции нескольких переменных, также, как и для функции одной переменной можно написать формулу Тейлора в следующем виде:
При малых дифференциалах независимых переменных (меньше 1), основной вклад в приращение дают дифференциалы малых порядков — первого, второго и т.д. Чем больше порядок, тем меньше величина слагаемого . Поскольку в точке экстремума все частные производные первого порядка обращаются в 0, то и величина приращения определяется величиной второго дифференциала: .
Из этого обстоятельства следуют достаточные условия существования экстремума.
Если в стационарной точке второй дифференциал функции при любых значениях дифференциалов независимых переменных положителен, то в этой точке имеется минимум, если второй дифференциал при любых значениях дифференциалов независимых переменных отрицателен, то в этой точке имеется максимум.
Примеры исследования на экстремум
Пример 1. Исследовать на экстремум функцию .
Необходимые условия: .
Найдем вторые производные: . Составим дифференциал второго порядка и преобразуем его, выделив полный квадрат:
.
Из последней формулы видно, что знак второго дифференциала в стационарной точке при любых и положителен, следовательно, в ней имеется минимум и .
Пример 2. Исследовать на экстремум функцию .
Необходимые условия: .
Найдем вторые производные: . Составим дифференциал второго порядка и преобразуем его:
.
Исследуем знак второго дифференциала в зависимости от соотношения между и :
Знак второго дифференциала зависит от значений независимых дифференциалов, значит, в исследуемой точке экстремума нет.
Пример 3. Исследовать на экстремум функцию
.
Необходимые условия: .
Вторые производные: .
. Видно, что знак второго дифференциала всегда положителен, значит, в исследуемой точке у функции имеется минимум и .
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Исследование функции на экстремум

35
Рис. 26. Приближенное решение системы уравнений, если прямая не пересекается с окружностью
Приближенное решение систем уравнений
(функция Minerr)
Для приближенного решения систем уравнений используется вычислительный блок Given-minerr.Обращение к нему аналогично обращению к блокуGiven-find.
Если решение системы уравнений существует x+y=2 (рис. 26), функцияminerr дает тот же ответ, что и функцияfind.
Если решение системы уравнений не существует, функцияminerr возвращает минимум невязки решения. В случаеx+y=10 функцияminerr возвращает значение координатыx, при котором расстояние между кривыми минимально.
Функцию minerr удобно использовать для поиска экстремума негладких функций с переломами на графике.
Отметим четыре пути поиска экстремума.
1)Для непрерывной функции используем равенство нулю производной от заданной функции. В этой процедуре используют функцию root.
2)Для функции с переломами используем функцию minerr. Для этого по графику выбираем число заведомо большее (или меньшее) экстремального значения функции и записываем его в качестве ограничения в блокеgivenminerr. Функцияminerr возвращает значение аргумента, при котором расхождение между заданным числом и значением функции минимально . Возвращаемый результат зависит от выбора начального приближения.
3)Для непрерывных функций удобно использовать функции maximize иminimize (они вводятся аналогично применению функцииfind. Ключевое словоgiven обычно можно опустить. Оно необходимо лишь в случае наличия ограничений.
4)Для ступенчатых функций целесообразно использовать функцию Fmax, реализующую простой метод перебора значений функции (функция Fmax
описана в электронной книге в разделе Изгиб Расчет на изгиб консольной балки). Другого средства определения максимума ступенчатой функции в Mathcad нет.
СОВЕТ
При анализе конкретного уравнения желательно внимательно изучить поверхностный график функции, на котором хорошо видны области нахождения экстремумов.
studfiles.net
Схема исследования функции на экстремум — КиберПедия
1. Найти производную .
2. Найти критические точки, т.е. точки, в которых или производная не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.
4. Найти экстремальные значения функции.
Пример. Исследовать на экстремум функцию .
Решение:
1) ;
2) , , ;
3) применяя метод интервалов, находим, что на и на , а неравенство выполняется на .
Следовательно, в точке имеется максимум, а в точке – минимум;
4) находим , .
Исследование функции с помощью
второй производной
Будем рассматривать дважды дифференцируемую функцию, т.е. функцию , которая имеет производные и .
Второе достаточное условие экстремума. Если в точке первая производная равна нулю: , а вторая положительна: , то есть точка минимума функции ; если же , , то – точка максимума.
Доказательство. Пусть , . Тогда, так как , первая производная возрастает в окрестности точки . Значит, слева от она отрицательна: , а справа – положительна: . Итак, при переходе через производная меняет знак с минуса на плюс. Следовательно, в этой точке минимум. Аналогично рассматривается случай , .
Пример. . .
Имеем:
,
, ; .
Следовательно, в точке имеется минимум.
Функция и ее график характеризуются также направлением выпуклости и наличием асимптот. Говорят, что на данном интервале выпуклость графика направлена вверх (вниз), если все его точки находятся ниже (соответственно выше) любой касательной на этом интервале.
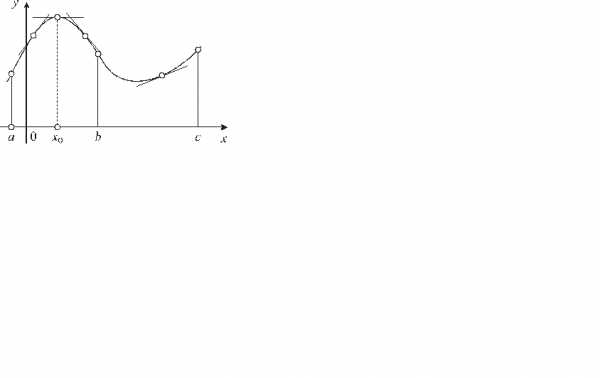
На рис. 2 показан график функции, у которого на интервале выпуклость направлена вверх, а на интервале – вниз.
Точка, в которой меняется направление выпуклости, называется точкой перегиба.
 |
| Рис. 2 |
Можно доказать, что если на данном интервале , то выпуклость графика направлена вниз, если же , то выпуклость направлена вверх.
Если – точка перегиба, то .
Асимптоты
Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от переменной точки М графика до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат.
Различают вертикальные и наклонные асимптоты. Прямая называется вертикальной асимптотой, если или . Вертикальные асимптоты сопутствуют обычно точкам разрыва второго рода.
Из школьного курса известно, в частности, что ось Oy (т.е. прямая ) есть вертикальная асимптота графика функции .
Прямая есть наклонная асимптота графика функции при , если
,
где при .
Коэффициенты k и b в уравнении наклонной асимптоты находят по формулам:
,
.
Пример. Найти наклонную асимптоту графика функции .
Решение.
1) ;
2)
.
Уравнение асимптоты: .
Заметим, что наличие у функции наклонной асимптоты означает, что при больших значениях аргумента функция мало отличается от линейной функции.
Общая схема исследования функций
и построения их графиков
Для исследования функции и построения графика следует найти:
1) область определения функции;
2) точки разрыва функции;
3) интервалы возрастания и убывания функции;
4) максимумы и минимумы;
5) направление выпуклости графика функции, точки перегиба;
6) асимптоты.
Кроме того, учитываются четность (или нечетность) функции, периодичность, точки пересечения графика с осями координат.
На основании проведенного исследования строится график функции, при этом полезно намечать элементы графика параллельно с исследованием.
Пример 1. Исследовать функцию и построить ее график.
1. Область определения – вся числовая прямая за исключением точки , т.е. множество
.
2. – точка разрыва 2-го рода, так как
, .
3. Вычислим производную:
.
Определим области возрастания и убывания функции:
при имеем – функция возрастает;
при и имеем – функция убывает;
при имеем – функция возрастает.
4. Из равенства находим критические точки , . В точке производная меняет знак с плюса на минус при ; при ). Следовательно, в точке имеется максимум:
.
В точке производная меняет знак с минуса на плюс ( при , при ). Следовательно, в точке имеется максимум:
.
5. Вычислим вторую производную:
Определим направление выпуклости:
при имеем – выпуклость направлена вверх,
при имеем – выпуклость направлена вниз.
Точек перегиба нет.
Определим асимптоты графика.
Очевидно, – вертикальная асимптота.
Определим наклонную асимптоту.
,
.
Итак, – наклонная асимптота.
График исследуемой функции изображен на рис. 3.
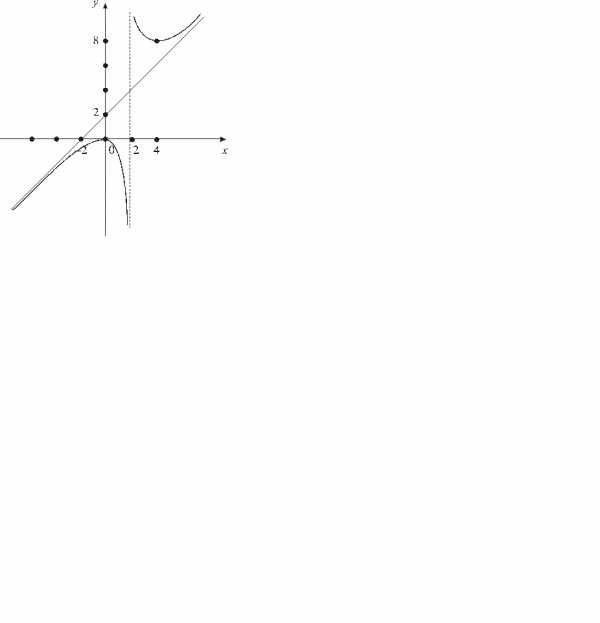 |
| Рис. 3 |
Пример 2. В теории вероятностей и в статистике весьма важную роль играет функция
– дифференциальная функция нормального распределения. Исследуем эту функцию методами дифференциального исчисления по приведенной выше схеме и построим ее график. Заметим, что этот график называют нормальной кривой (кривой Гаусса).
Решение. 1. Область определения функции – вся ось Ox.
2. Функция непрерывна на всей оси Ox.
3. Вычислим первую производную:
.
Легко видеть, что при , при . Следовательно, на интервале функция возрастает, а на интервале – убывает.
4. Приравнивая производную к нулю, находим критическую точку . В точке производная меняет знак с плюса на минус, следовательно, в ней имеется максимум:
.
5. Вычисляем вторую производную:
Легко видеть, что вторая производная равна нулю, когда
, т.е. при и .
Имеем
выпуклость направлена вниз
выпуклость направлена вверх
выпуклость направлена вниз.
При переходе через точки , вторая производная меняет знак. Значение функции в обеих этих точках одно и то же:
.
Таким образом, точками перегиба графика являются точки
и .
6. Вертикальных асимптот, очевидно, нет. Предел функции при равен нулю: .
Следовательно, ось Ox есть горизонтальная асимптота графика (очевидно, , и наклонных асимптот нет).
При построении графика учтем дополнительно, что при всех значениях аргумента , т.е. кривая расположена выше оси Ox, а также тот факт, что кривая симметрична относительно прямой (так как разность содержится в аналитическом выражении функции в квадрате).
Возьмем для определенности , .

Рис. 4
cyberpedia.su
Исследование функции на экстремум — КиберПедия
Функция называется возрастающей (убывающей)в некотором интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, то есть при выполняется неравенство < >
Для исследования функций применяются следующие признаки:
1. Если дифференцируемая функция на отрезке возрастает (убывает), то ее производная на этом отрезке неотрицательна (неположительна), то есть
2. Если непрерывная на отрезке и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.
Функция называется неубывающей (невозрастающей) в некотором интервале, если для любых из этого интервала .
Интервалы, в которых функция не убывает или не возрастает, называются интервалами монотонности функции. Характер монотонности функции может изменяться только в тех точках ее области определения, в которых меняется знак первой производной. Точки, в которых первая производная функции обращается в ноль или терпит разрыв, называются критическими или стационарными.
Точка называется точкой локального максимума (минимума) функции , если существует такая окрестность этой точки, что для всех точек из этой окрестности выполняется неравенство > < . Точки максимума и минимума называются точками экстремума функции, а максимумы и минимумы функции – ее экстремальными значениями.
Для исследования функций на экстремум применяются следующие теоремы.
Теорема.Если функция имеет в точке экстремум, то либо , либо не существует.
Для отыскания экстремумов функции находят все критические точки, а затем исследуют каждую из них по отдельности, чтобы выяснить будет ли в этой точке максимум или минимум, или же в ней нет экстремума.
Теорема. Пусть функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала (кроме, возможно, самой точки ). Если при положительна, а при отрицательна, то при функция , имеет максимум. Если же при отрицательна, а при положительна, то при данная функция имеет минимум.
На отрезке функция может достигать наименьшего и наибольшего значения либо в критических точках функции, лежащих в интервале ( ), либо на концах отрезка .
Пример. Найти наименьшее и наибольшее значения функции
на отрезке .
Решение. Производная данной функции . Тогда приравнивая производную функции к нулю, получаем уравнение , решая которое, находим критические точки и .
Точка не принадлежит исследуемому интервалу, поэтому ее исключаем из рассмотрения.
Вычисляем значение функции в критической точке и на концах отрезка:
,
,
Сравнивая полученные числа, получаем, что наименьшее значение на отрезке функция принимает в точке , а наибольшее значение − в точке .
Итак, на отрезке , .
Ответ: , .
Кривая, заданная функцией , называется выпуклой в интервале , если все точки кривой лежат не выше любой ее касательной в этом интервале, и вогнутой в интервале , если все ее точки лежат не ниже любой ее касательной в этом интервале.
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.
Для нахождения интервалов выпуклости и вогнутости графика функции и точек перегиба пременяются следующие теоремы.
Теорема.Если во всех точках интервала вторая производная функции отрицательна (положительна), то есть , то кривая в этом интервале выпукла ( вогнута).
Прямая называется асимптотой данной кривой , если расстояние от точки кривой до прямой при удалении точки в бесконечность стремится к нулю.
Если существуют числа ( ), при которых , то есть функция имеет бесконечные разрывы, то прямые называютсявертикальными асимптомами кривой .
Наклонная асимптома задается уравнением , гдe, , , если оба предела существуют и конечны. При получается частный случай наклонной асимптоты – горизонтальная.
Алгоритм полного исследования функции и построения графика:
1. Найти область определения функции.
2. Исследовать функцию на четность – нечетность.
3. Найти точки разрыва функции, и вертикальные асимптомы (если они существуют).
4. Найти точки пересечения графика функции с осями координат.
5. Найти наклонные асимптомы графика функции.
6. Найти экстремумы и интервалы монотонности функции.
7. Найти интервалы выпуклости и вогнутости, точки перегиба.
8. При необходимости выполнить дополнительные вычисления.
9. Построить график функции.
Пример. Провести полное исследование функции и построить ее график.
Решение. 1. Функция не определена в тех точках, в которых знаменатель равен 0, то есть при . Область определения ; ; .
2. Функция является четной, если и нечетной, если , при условии, что область определения функции симметрична относительно начала координат.
.
Данная функция не является ни четной, ни нечетной.
3. Точка является точкой разрыва функции. Так как левосторонний предел функции при и правосторонний предел функции при бесконечны, то есть и , то прямая (ось ) является вертикальной асимптотой.
4. Чтобы найти точки пересечения с осью приравниваем функцию к нулю и решаем полученное уравнение:
.
График функции пересекает ось в точке . Для нахождения точки пересечения графика функции с осью необходимо вычислить значение функции при . Так как исследуемая функция не определена при , то нет точек пересечения с осью .
5. График функции имеет наклонную асимптому , если существуют пределы для и . Вычислим их для данной функции:
,
.
Следовательно, уравнение наклонной асимптоты
6. Находим производную функции:
при и не существует в точке Эти точки разбивают всю область определения функции на интервалы , . Внутри каждого из полученных интервалов производная сохраняет знак, а именно: на интервалах и на интервале . Это означает, что функция возрастает на интервале убывает на интервале и возрастает на интервале . В точке функция не определена, она не является точкой экстремума, а точка является точкой минимума функции.
7. Находим вторую производную:
Вторая производная не равна 0 ни при каких значениях , поэтому график функции не имеет точек перегиба. Точка , в которой не определена исследуемая функция, разбивает ее область определения на интервалы и . на обоих интервалах, поэтому кривая вогнута на всей области определения.
8. Для более точного построения графика функции вычислим ее значения в нескольких точках:
9. По результатам исследования строим график функции.
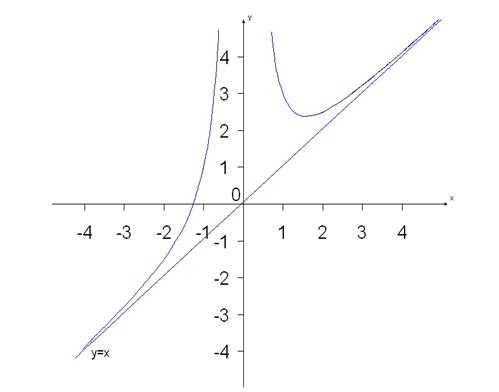
cyberpedia.su
5.8. Экстремум функции многих переменных
Рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условий, которые позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли точки точками минимума, максимума или седловыми точками.
Определение. Экстремумом функции двух переменных называется её максимальное или минимальное значение на заданном множестве изменения переменных.
Экстремумы и методы их нахождения имеют широкое применение в экономических исследованиях, при выборе наилучших вариантов инвестиций, производственных программ, вложения денег в покупки и т. п.
Определение. Значение функции F(M) в точке М0 называется Максимумом (минимумом), если оно является набольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках:
.
|
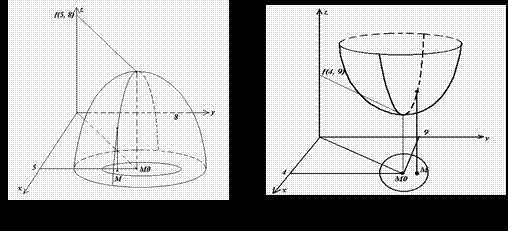
Пример 53. На рис. 37 представлен график функции двух переменных, точка М0(5, 8), в которой достигается максимум функции, окрестность точки М0(5, 8), максимальное значение функции F(X, Y), равное F(5, 8); на рис. 38 – график функции точка М0(4, 9), в которой достигается минимум функции, окрестность точки М0(4, 9), минимальное значение функции F(4, 9).
Из определения экстремума функции видно, что понятие экстремума является локальным. Другими словами, можно сказать, что приведенное определение экстремума является определением локального экстремума, функция может иметь несколько локальных максимумов или минимумов. Ясно, что при нахождении лучшего решения следует ориентироваться на наибольший из локальных максимумов, если ищется наибольшее значение функции, и на наименьший из локальных минимумов, если ищется наименьшее значение функции.
Определение. Наибольшая величина из локальных максимумов называется Глобальным максимумом, наименьший из локальных минимумов – Глобальным минимумом.
Задача нахождения локальных экстремумов, а тем более глобальных, для функции нескольких переменных является достаточно трудной, в общем случае для произвольного числа переменных практически неразрешимой. Для выпуклых функций разработаны специальные методы нахождения экстремумов.
Замечание. Любой локальный экстремум выпуклой функции является глобальным.
Определение. Функция многих переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которых все ее частные производные первого порядка равны нулю или не существуют. Такие точки называются Критическими.
Замечание. Это необходимые условия экстремума, но недостаточные, они могут выполняться и в точках, где нет экстремума.
Это определение дает схему нахождения экстремальных точек. Составляется система уравнений относительно переменных Х и У:
Решение системы представляет собой пары (х0, у0), (х1, у1) и т. д., которые называются точками «подозрительными» на экстремум, т. е., если функция имеет экстремумы, то они могут достигаться только в этих точках. Для определения, достигается ли в каждой из найденных точек максимальное (минимальное) значение или в рассматриваемой точке нет экстремума, требуется проведение дополнительных исследований.
Пример 54. Найти экстремум функции Z = X2 + (Y – 1)2.
Найдя частные производные и приравняв их к нулю, получаем систему уравнений:
Решение этой системы очевидно: Х = 0, у = 1. Поскольку Z 0 при всех Х, у, то ясно, что найденная точка (0, 1) есть точка минимума.
Пример 55. Определить, имеет ли функция Z = X3 + Y3 экстремумы.
Решение. Найдем частные производные и приравняем их к нулю:
Точка (0, 0) является «подозрительной». Однако экстремума функция в этой точке не имеет, так как в любой окрестности этой точки она принимает значения разных знаков, а в самой точке (0, 0) значение функции равно нулю.
Рассмотрим Достаточные условия экстремума для функции двух переменных.
Пусть функция z = f(x, y) непрерывна со своими частными производными первого и второго порядка в некоторой окрестности точки М(х0, у0). Пусть в этой точке выполнены необходимые условия экстремума:
В этой точке пусть вычислены частные производные второго порядка.
Введем обозначения:
Тогда Достаточные условия максимума и минимума имеют вид:
1) если D>0, то в точке М функция F(X, Y) имеет экстремум, а именно, Максимум при A<0 и Минимум при A>0;
2) если D<0, то в точке М функция F(X, Y) экстремума не имеет;
3) если D = 0, то требуются дополнительные исследования.
Пример 56. Исследовать на экстремум функцию: Z = F(X, Y) = X3 + Y3 – 3Xy.
Решение. Составим систему уравнений:
Её решением являются пары (0, 0) и (1, 1), т. е. на экстремум надо проверить точки М0(0, 0) и М1(1, 1). Частные производные второго порядка имеют вид:
Вычислим D в точках М0 и М1 : < 0, значит экстремума в этой точке нет; > 0, при этом А = 6 > 0 и, следовательно, в точке М1 – минимум.
Пример 57. Исследовать на экстремум функцию
Решение. Ищем критические точки:
Находим М0(1, 0) и М1(-1, 0). Эти точки принадлежат области определения исследуемой функции: - < X < +, 0 Y < + (которая представляет половину плоскости ХОу, лежащую выше оси Ох, включая и ось Ох), но они расположены не внутри этой области, а на её границе У = 0. Поэтому точки М0 и М1 Не являются критическими. Частные производные по Х и по У существуют во всей области определения функции U. Поэтому данная функция, как не имеющая критических точек, не имеет экстремума.
Пример 58. Исследовать на экстремум функцию
Решение. Ищем критические точки:
Решая систему, найдем единственную критическую точку функции М(1; 1).
Далее, чтобы установить, будет ли экстремум в точке М, вычисляем
Здесь оказалось, что D = 0. Чтобы установить, имеет ли экстремум функция V В критической точке М, исследуем знак её приращения
вблизи точки М.
Пусть М1 лежит на биссектрисе У = х. Тогда Если М1 будет ниже М, т. е. если УМ1 < 1, то < 0, а если М1 будет выше М, т. е. если УМ1 > 1, то> 0. Здесь оказалось, что вблизи точки М разность Не сохраняет знака, вследствие чего в точке М нет экстремума.
Замечание. Для функций с числом переменных больше двух достаточные условия экстремума имеют сложный вид и требуют глубоких знаний по математическому анализу
Пример 59. Исследовать на экстремум функцию
Решение. Ищем критические точки:
Эти частные производные не обращаются в нуль ни при каких значениях X, Y, Z; они не существуют (обращаются в бесконечность) в точке М(0, 0, 0). Эта точка лежит внутри области определения функции W, которая представляет совокупность всех точек (X, Y, Z) пространства. Поэтому М(0, 0, 0) критическая точка.
Исследуя знак разности Вблизи точки М, убеждаемся, что при любых отличных от нуля значениях Х, Y, Z она сохраняет положительный знак. Поэтому М есть точка минимума,
Вопросы к главе 5
1. Дайте определение функции многих переменных.
2. Приведите примеры функций многих переменных, используемых в экономике.
3. Что называется графиком функции двух переменных? Приведите примеры.
4. Сформулируйте определение множества (линии) уровня функции двух переменных. Может ли множество уровня функции двух переменных не быть линией?
5. Опишите взаимосвязь между градиентом функции двух переменных и ее линией уровня.
6. Перечислите основные свойства градиента функции.
7. Дайте определение возрастающей (убывающей) функции многих переменных.
8. В каком случае функция является вогнутой?
9. Всегда ли локальный экстремум выпуклой функции является глобальным?
10. Дайте определение экстремума функции двух переменных.
11. Сформулируйте достаточные условия максимума и минимума функции двух переменных.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Исследование функции на экстремумы
Значение называется максимумом функции , если существует окрестность точки такая, что для всех точек из этой окрестности выполняется неравенство , .
Другими словами, значение функции в точке максимума больше всех соседних значений функции.
Значение называется минимумом функции , если существует окрестность точки такая, что для всех точек из этой окрестности выполняется неравенство , .
Другими словами, значение функции в точке минимума меньше всех соседних значений функции.
Максимум и минимум функции называются также одним словом – экстремум функции.
Экстремумы могут быть “гладкими”, как на рисунках внизу.
Касательные, проведенные к графику функции в точках экстремума, параллельны оси OX. Пусть a – угол между касательной и положительным направлением оси OX, тогда и , а так как , то производная в точках “гладкого” экстремума равна 0. Точки, в которых производная равна 0, называются стационарными. Однако не в каждой стационарной точке имеется экстремум функции. На рисунке представлен график функции , ее производная при равна 0, но из рисунка видно, что никакого экстремума при у функции нет. Из рисунков 1 и 2 видно, что вблизи экстремума производная функции должна менять знак: вблизи максимума с “+” на “–”, а вблизи минимума с “–”на “+”.
Экстремумы функции могут быть “острыми”, как на рисунках 3 и 4. Касательные к графику функции, проведенные при , образуют прямой угол с OX ( ), следовательно, значение в точках острого экстремума не существует (не определено), а т.к. , то не существует и производная. Как и в предыдущем случае, можно заметить, что не для всех значений переменной, для которых производная не существует, будет существовать экстремум функции.
Рассмотрим график функции ; её производная при не существует, но и сама функция в этой точке не определена, поэтому определение экстремума для этой точки не применимо (нет значения, которое можно сравнивать с другими).
Итак, чтобы исследовать функцию на экстремум, нужно найти производную. Затем найти критические точки: те значения переменной, при которых производная равна 0 или не существует. Из критических точек выбрать те, где сама функция непрерывна (определена). Для таких точек проверить смену знака производной вблизи критических точек: если производная при увеличении аргумента меняет знак с “+” на “–”, значит, в данной точке максимум, при смене знака с “–”на “+” в точке имеется минимум; если смены знака не происходит, экстремума нет.
Для тех точек, где производная равна 0, проверку на экстремум можно выполнить и по-другому. На рис. 1 видно, что в районе максимума функция вначале возрастает, затем убывает, т.е. первая производная меняет знак с “+” на “–”, другими словами, убывает. Следовательно, вторая производная (производная от ) отрицательна (см. п. 1.1.). Аналогично, из рис. 2 видно, что в районе минимума функция вначале убывает, затем возрастает, т.е. первая производная меняет знак с “–”на “+”, возрастает и, следовательно, (производная от ) положительна.
Следовательно, если в критической точке первая производная равна 0, а вторая отрицательна, то в ней имеется максимум; если же в критической точке первая производная равна 0, а вторая положительна, то в ней имеется минимум.
Похожие статьи:
poznayka.org

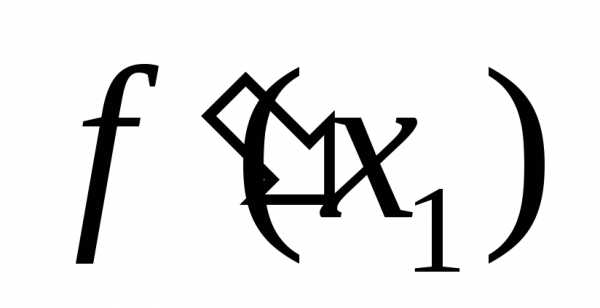
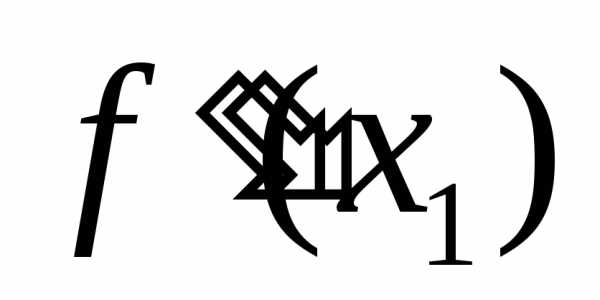
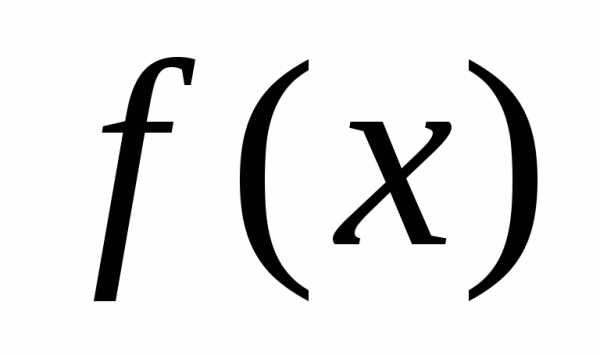 на отрезке [a, b]
на отрезке [a, b]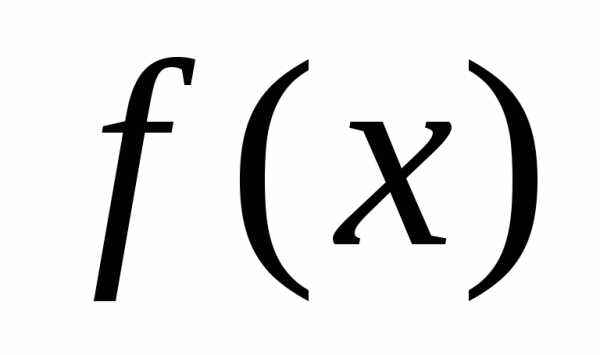 при
при