Исследовать функцию на непрерывность, определить характер разрыва. Контрольные онлайн
Исследовать функцию на непрерывность, определить характер разрыва.
Пример 1.
Функция не определена в точках , уже нарушено первое условие непрерывности, следовательно, в этих точках функция испытывает разрыв.
Для выяснения характера разрыва нужно вычислить односторонние пределы в точках .
.
.
Так как левый предел в точке равен бесконечности, то в ней разрыв II рода.
;
.
Так как правый предел в точке равен бесконечности, то в ней разрыв II рода.Пример 2 Функция определена на всей числовой прямой, но при этом она не является непрерывной, так как , , , т.е. правый и левый пределы в нуле не равны между собой и не равны значению функции в нуле, нарушены 2 и 3 условия непрерывности. Так как правый и левый пределы в нуле существуют и конечны, то это разрыв I рода.Пример 3 Функция неопределена в нуле, следовательно , – точка разрыва.
Так как и , то это устранимый разрыв, функцию можно в нуле доопределить “по непрерывности”, положив равной единице.
Пример 4 Функция является элементарной, поэтому она непрерывна в области её определения. В область определения не входят точки , , , следовательно, они являются точками разрыва данной функции.
Определим тип точек разрыва.
1) .
;
.
Так как , то точка является точкой
разрыва второго рода функции .
2) .
;
.
Односторонние пределы функции в точке равны, но функция при не определена, следовательно, является устранимой точкой разрыва первого рода.
3) .
Так как заданная функция является четной функцией, то, очевидно, что
, и является точкой разрыва второго рода функции .
Для построения эскиза графика функции исследуем поведение функции при
и . Так как функция четная, то
.
Построим эскиз графика функции .
точки разрыва — 30 Мая 2013 — Примеры решений задач
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
1) Функция f (x) имеет точку разрыва первого рода при x=a, если в этой точке
- Существуют левосторонний предел и правосторонний предел ;
- Эти односторонние пределы конечны.
- Если односторонние пределы конечны и равны, то x=a называется точкой устранимого разрыва первого рода
2) Функция f (x) имеет точку разрыва второго рода при x=a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Калькулятор для исследования точек разрыва функции.
Калькулятор находит левый и правый пределы функции в точке разрыва, а также строит схематический чертеж в точке разрыва.
Пример 1. Исследовать функцию на непрерывность, определить точки разрыва, выполнить схематический чертеж функции в точке разрыва
Решение. Не трудно заметить, что исследовать на непрерывность необходимо точку x = -1 (знаменатель обращается в ноль).
Вставляем в калькулятор функцию в виде x^2/((x+1)^3), точка разрыва x = -1.
Получаем, что левый и правый пределы в точке x = -1 бесконечны, отсюда делаем вывод, что точка x = -1 является точкой разрыва второго рода.
Для того чтобы найти точки разрыва можно воспользоваться калькулятором область определения функции.
www.reshim.su
Непрерывность функции в точке и на промежутке. С примерами
На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на то что записываются как и .
Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.
Графически функция непрерывна в точке , если её график не «разрывается» в этой точке. График такой непрерывной функции — показан на рисунке ниже.
Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:
А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому стремится икс, прибавляется или вычитается всего лишь нуль? Могут. Когда и почему — это объяснено на уроке о точках разрыва функции и их видах.
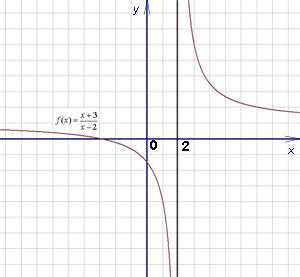
Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 — на рисунке ниже.
Пример 1. Функция f(x) определена следующим образом:
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0, x = 1, x = 3?
Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.
Точка x = 0. Найдём левосторонний предел в этой точке:
.
Найдём правосторонний предел:
.
Предел функции и значение функции в точке x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
.
Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0.
Точка x = 1. Найдём левосторонний предел в этой точке:
.
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
.
Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1.
Точка x = 3. Найдём левосторонний предел в этой точке:
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
.
Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3.
Основной вывод: данная функция является непрерывной в каждой граничной точке.
Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение
Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .
Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m, то есть l = f(m), m≥0.
Непрерывность функции на промежутке
Пусть функция y = f(x) определена в интервале ]a, b[ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a, b[. Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b[, ]a, + ∞[, ]- ∞, + ∞[. Пусть теперь функция y = f(x) определена на отрезке [a, b]. Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a, оставаясь на отрезке [a, b], мы можем приближаться только справа, а к точке b — только слева. Функция называется непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b.
Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a, b], функция непрерывна на отрезке [0, b], функция непрерывна на любом отрезке, не содержащем точку a = 2.
Пример 4. Исследовать функцию на непрерывность.
Решение. Проверяем первое условие. Функция не определена в точках — 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах
.Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Найдём правосторонний предел при :
.
Очевидно, что значение в точке x = 2 должно быть равно ax:
Ответ: функция непрерывна на всей области определения при a = 1,5.
К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t, выраженная законом s = f(t), даёт пример непрерывной функции f(t). Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t).
В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.
1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.
2. Функция f(x), непрерывная на интервале [a
3. Если функция непрерывна на интервале, то на этом интервале она достигает своего наибольшего и своего наименьшего значения: если m — наименьшее, а M — наибольшее значение функции на интервале [a, b], то найдутся на этом отрезке такие точки и , что и . Теорема, в которой изложено это свойство, называется второй теоремой Вейерштрасса.
Пример 7. Используя первое из приведённых выше свойств непрерывных функций, доказать, что уравнение имеет по меньшей мере один вещественный корень в интервале [1; 2].
Решение.
Пусть .Вычислим значения функции при x = 1 и x = 2.
.
.
Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.
Следовательно, в интервале [1; 2] существует такое число a, при котором f(a) = 0. То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.
Установление непрерывности функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.
Весь раздел «Исследование функций»
function-x.ru
Проверить непрерывность функции | UpByte.Net
Функция \(y=f\left(x \right)\), определенная на интервале \(\left(a,b \right)\) называется непрерывной в точке \(x_{0}\in \left(a,b \right)\), если предел функции равен ее значению при предельном значении аргумента, т.е. \[\lim_{x\rightarrow x_{0}}f\left(x \right)=f\left(x_{0} \right).\] Если \(x_{0}\in \left(a,b \right)\) и \(x\in \left(a,b \right)\), то разность \(\bigtriangleup x=x-x_{0}\) называется приращением аргумента в точке \(x_{0}\). Разность \(\bigtriangleup y=f\left(x \right)-f\left(x_{0} \right)\), или \(\bigtriangleup y=f\left(x_{0}+\bigtriangleup x \right)-f\left(x_{0} \right)\) называется приращением функции в этой же точке \(x_{0}\).Рассмотрим функцию \(y=f\left(x \right)\), определенную на интервале \(\left(a,b \right)\), кроме, может быть, точки \(x_{0}\in \left(a,b \right)\). Значение аргумента \(x_{0}\) называется точкой разрыва данной функции, если при \(x=x_{0}\) функция определена, но не является непрерывной, или не определена при этом значении \(x\).
С помощью нашего решебника вы можете проверить является ли функция непрерывной, найти разрывы функции. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку «Решить».
Определить, является ли функция непрерывной
Is f(x)=x sin(x^2) continuous over the reals?
is sin(x-1.1)/(x-1.1)+heaviside(x) continuousОпределить непрерывность в указанной точке
is tan(x) continuous at pi?
is 1/(x^2-1)+UnitStep[x-2]+UnitStep[x-9] continuous at x=9Определить разрывы функции
discontinuities (x^3+8)/(x^3+3x^2-4x-12)
discontinuities of sec(x)tan(x)
upbyte.net
Точки разрыва функции, с примерами
ОПРЕДЕЛЕНИЕ Если в точке функция не является непрерывной, то эта точка называется точкой разрыва функции.Классификация точек разрыва функции
Точка называется точкой устранимого разрыва функции , если в этой точке односторонние пределы конечны и равны между собой, но не равны значению функции в этой точке; или функция в точке не определена (рис. 1).
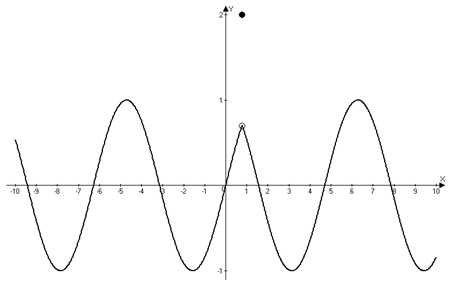
Рис. 1
Точка называется точкой разрыва первого рода функции , если в этой точке односторонние пределы конечны и не равны между собой (рис. 2).
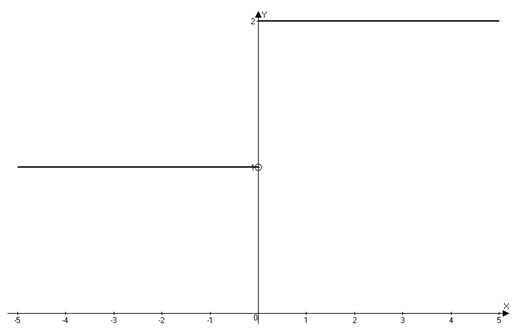
Рис. 2
Модуль разности значений односторонних пределов называется скачком функции.
Пример. На рисунке 2 скачок функции равен
Точка называется точкой разрыва второго рода функции , если в этой точке, по крайней мере, один из односторонних пределов равен бесконечности или не существует (рис. 3).
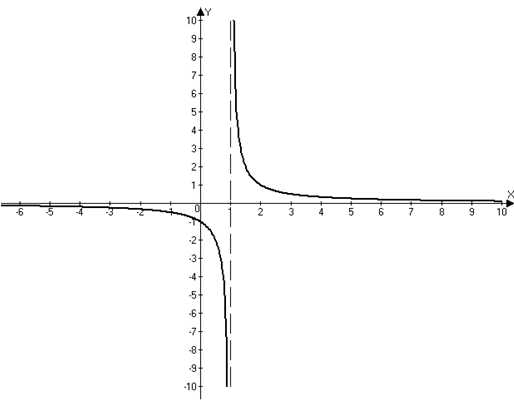
Рис. 3
Примеры решения задач
ПРИМЕР| Задание | Исследовать функцию на непрерывность и классифицировать точки разрыва.
|
| Решение | Функция является непрерывной как отношение двух непрерывных функций (многочленов), разрыв может быть лишь в точках, в которых знаменатель обращается в нуль, то есть
Итак, если разрыв есть, то он может быть лишь в точках . Исследуем функцию на непрерывность в этих точках. Для этого найдем односторонние пределы:
аналогично
Поскольку односторонние пределы бесконечны, то в точке функция имеет разрыв второго рода. Аналогично для второй точки :
то есть и точка – точка разрыва другого роду. |
| Ответ | Функция терпит разрыв второго рода в точках |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
функции исследовать на непрерывность, построить эскиз графиков — 15 Июля 2014 — Примеры решений задач
Ключевые слова: исследовать функцию на непрерывность, определение непрерывности, точки разрыва первого и второго рода, односторонние пределы, значение функции в точке, предел функции в точке.
Определение: функция непрерывна в точке x=a, если предел функции в данной точке равен значению функции в этой точке:
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке x=a, то есть должно существовать значение f(a).
2) Должен существовать общий предел функции
. — это подразумевает существование и равенство односторонних пределов.
3) Предел функции в данной точке должен быть равен значению функции в этой точке:
Пример 1. Функции исследовать на непрерывность. Построить эскиз графика функции.
Решение.
1) y(0)=0-1= -1 — функция определена, условие выполняется;
2) Односторонние пределы
— конечны и различны, следовательно функция имеет в точке x=0 разрыв первого рода со скачком.
Исследуем функцию на непрерывность в точке x=2:
1) y(2)=4— функция определена, условие выполняется;
2) Односторонние пределы
— конечны и равны, следовательно функция имеет в точке x=2 общий предел
— условие выполняется.
3) предел функции в точке x=2
равен значению данной функции в данной точке, условие выполняется,
следовательно функция в точке x=2 непрерывна.
Строим эскиз графика
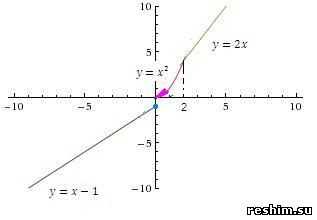
www.reshim.su
Исследование функции на непрерывность — Мегаобучалка
Для исследования функции на непрерывность необходимо:
1. Найти область определения функции;
2. Рассмотреть односторонние пределы в точках, где функция не существует; если функция кусочная, то рассмотреть односторонние пределы в точках «склейки»;
3. Исследовать функцию на бесконечности;
4. Построить эскиз графика функции.
Для классификации точек разрыва функции можно пользоваться таблицей, приведенной ниже.
Пусть – заданная функция, – исследуемая точка, – соответственно левый и правый пределы функции.
Рассмотрим примеры.
Пример 1. Задана функция .
Областью определения функции является множество . Действительно, функция не существует в единственной точке , следовательно, эта точка и будет точкой разрыва. Именно в ней мы должны найти односторонние пределы (левосторонний и правосторонний).
· Если отыскивается предел функции в точке при условии, что и , то этот предел, если он существует, называется левосторонним пределом функции и обозначается .
· Если отыскивается предел функции в точке при условии, что и , то этот предел, если он существует, называется правосторонним пределом функции и обозначается .
Найдем односторонние пределы в точке .
· Если левосторонний предел и правосторонний предел функции в точке существуют, но не равны между собой, то есть то точка называется точкой разрыва первого рода.
Согласно теории, точка является точкой разрыва первого рода, то есть в ней функция претерпевает скачок.
Далее исследуем поведение функции на бесконечности, для этого найдем пределы при
Следовательно, – прямая, которая является для функции горизонтальной асимптотой.
Сделаем эскиз графика.
Пример 2. Задана функция .
Областью определения функции является множество . Действительно, функция не существует в единственной точке , следовательно, эта точка и будет точкой разрыва. Определим с помощью односторонних пределов тип разрыва в этой точке.
· — это неопределенность, которую можно раскрыть, разложив на множители числитель и знаменатель.
· Если в точке функция имеет левосторонний и правосторонний пределы, и эти пределы равны между собой, но их значения не совпадают со значением функции в этой точке, то эта точка называется точкой устранимого разрыва:
Делаем вывод, что точка будет точкой устранимого разрыва.
Графиком функции является прямая с выколотой точкой при .
Построим график функции, для этого подберем кроме точки (3,1) еще одну произвольную. Пусть это будет (0,–2).
Сделаем эскиз графика функции.
Устранимый разрыв можно ликвидировать, если доопределить функцию в точке разрыва, задав:
Пример 3. Функция имеет две точки разрыва: и . Найдем односторонние пределы в этих точках.
Рассмотрим Разложив знаменатель на множители и сократив, получим следующее: – это гипербола, с точками разрыва и .
Тогда
Делаем вывод, что точка является точкой устранимого разрыва.
· Если в точке не существует левосторонний или правосторонний предел функции (или оба одновременно), то эта точка называется точкой разрыва второго рода (бесконечный разрыв).
Найдем предел функции на бесконечности:
Следовательно, прямая y= 0 будет горизонтальной асимптотой для заданной функции.
Построим график функции:
Рассмотрим примеры кусочных функций.
Пример 4.
Функции являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в , . Исследуем поведение функции в окрестности этих точек:
При функция определена и равна нулю, а функция в эту точку не заходит по условию.
· Функция называется непрерывной в , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть
Следовательно, точка x= 0 является точкой непрерывности функции.
Делаем вывод, что точка x= 2 является точкой разрыва первого рода и непрерывна слева (по условию).
Строим график склеенной функции:
Пример 5.
Элементарные непрерывные функции и не определены в точке , а функции и «склеены» в точке , которая, быть может, также является точкой разрыва. Исследуем поведение функции в этих точках.
Точка является точкой устранимого разрыва.
При функция принимает значение, равное 2. Следовательно, точка является точкой непрерывности.
Строим график заданной функции:
Пример 6.
Функция задана несколькими аналитическими выражениями, поэтому точки разрыва могут быть как в точках склейки , , так и в точках , , , где знаменатели дробей обращаются в нуль.
Сделаем некоторые упрощения: Далее будем рассматривать функцию с точками разрыва , .
Исследуем все точки:
Точка – точка разрыва второго рода.
Точка – точка разрыва первого рода, функция непрерывна справа (по условию).
Точка – точка разрыва первого рода, функция непрерывна справа (по условию).
Точка является точкой устранимого разрыва.
Точка является точкой разрыва второго рода.
Исследуем поведение функции при , а функции при .
Сделаем эскиз графика функции:

megaobuchalka.ru
