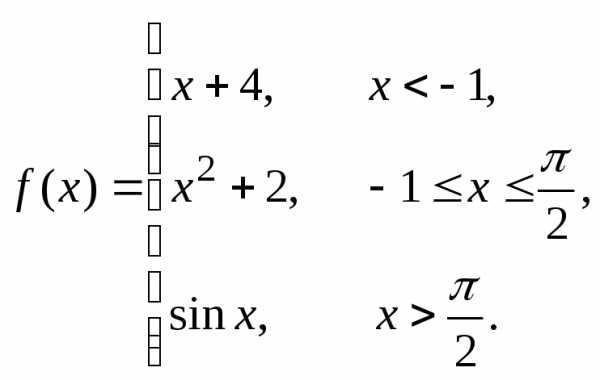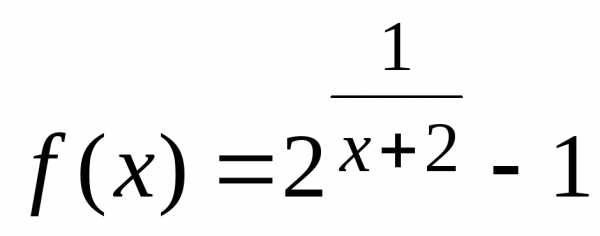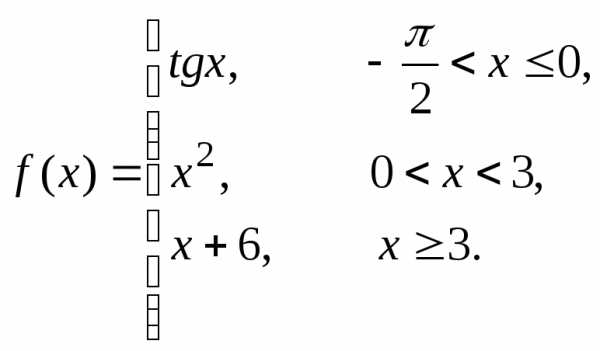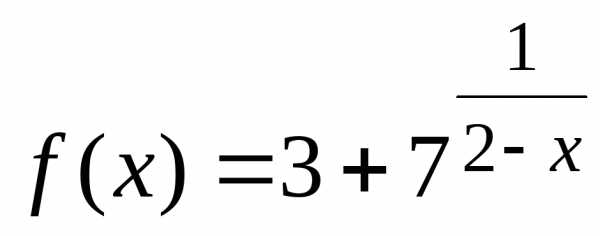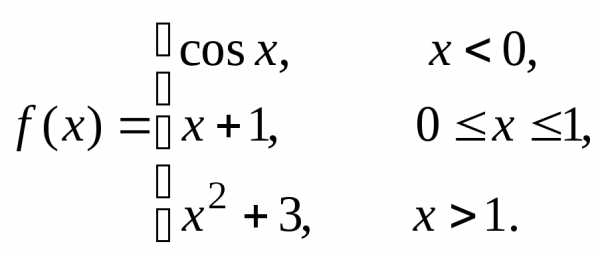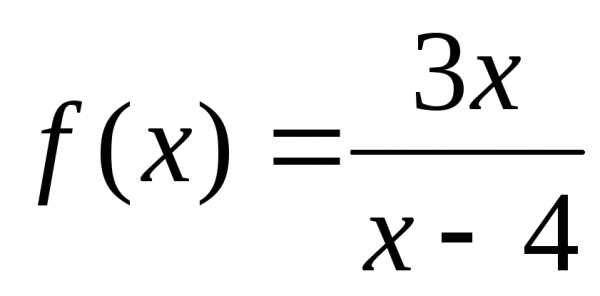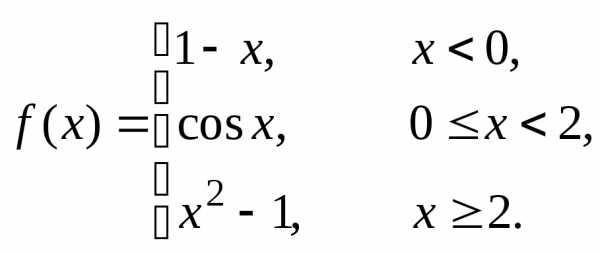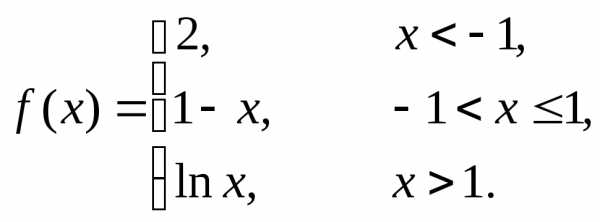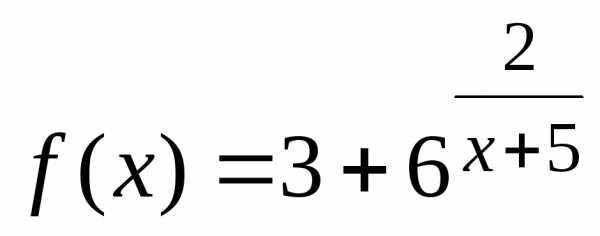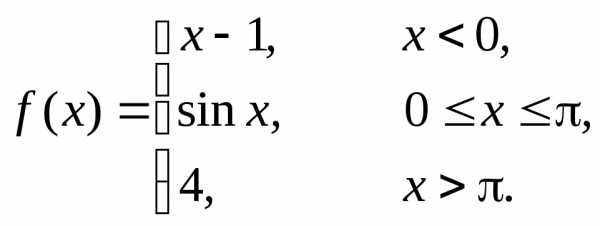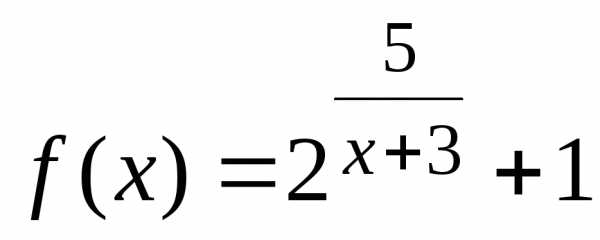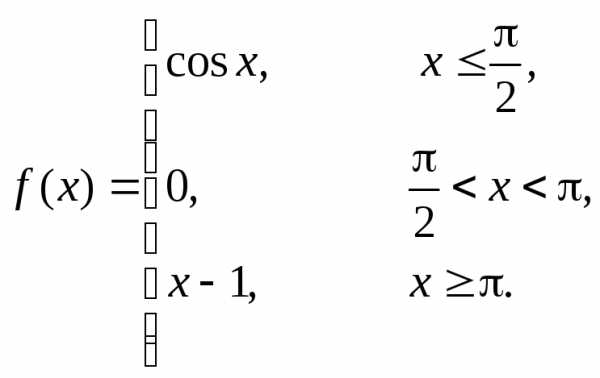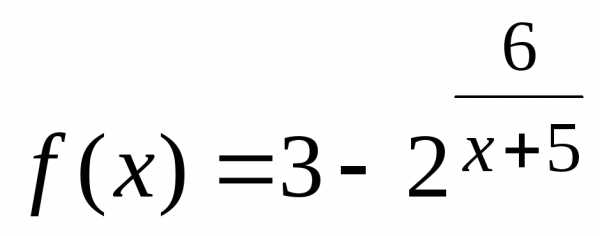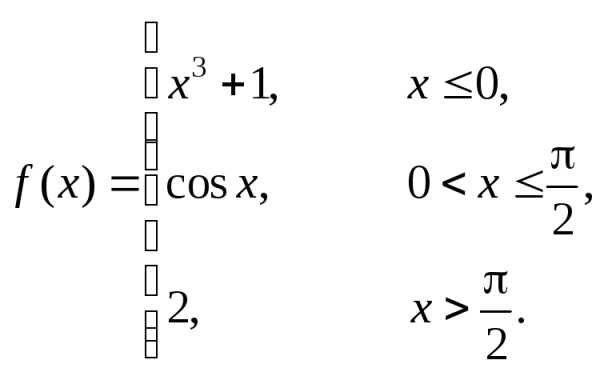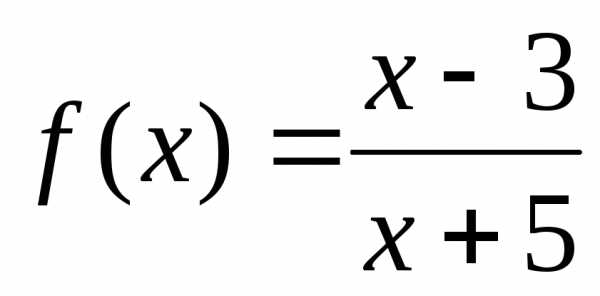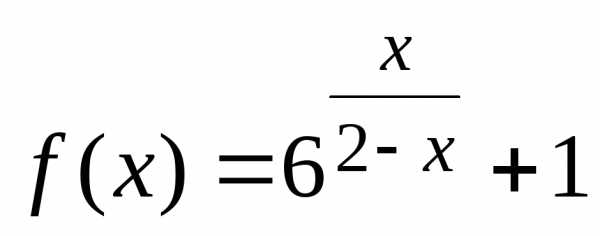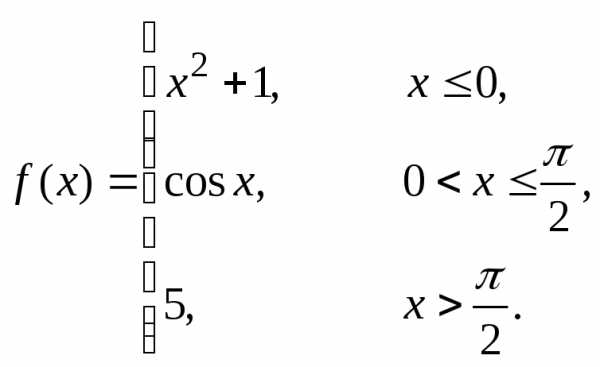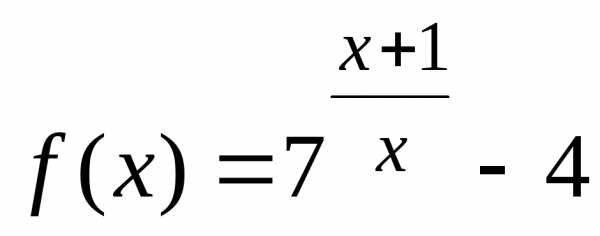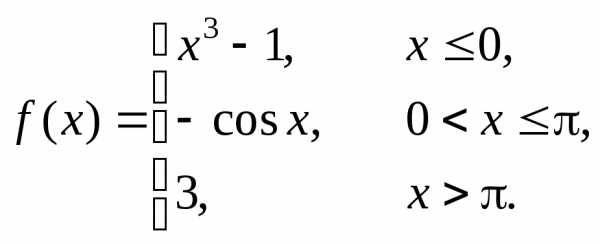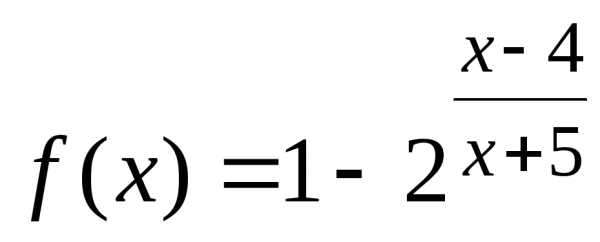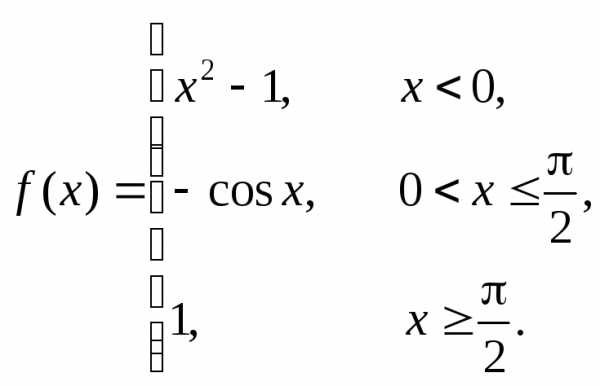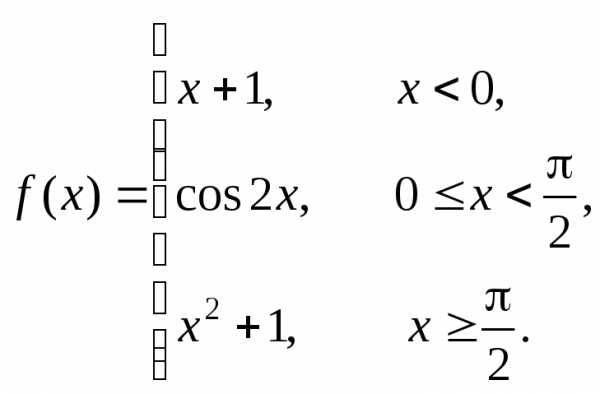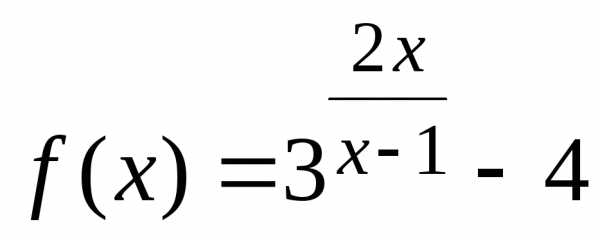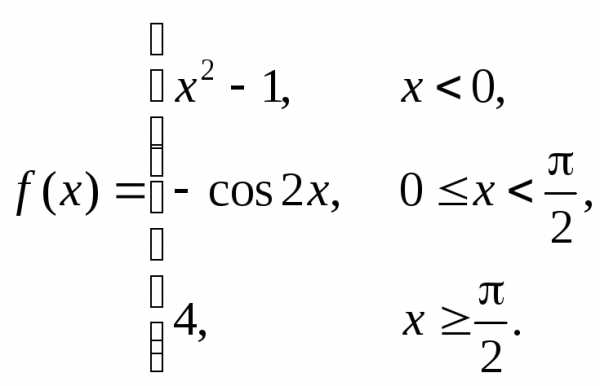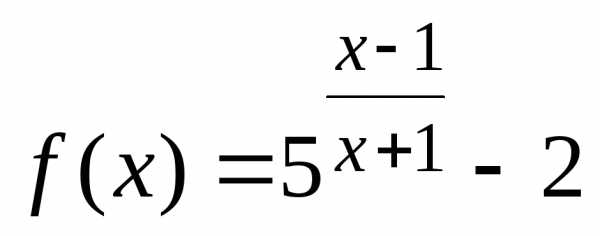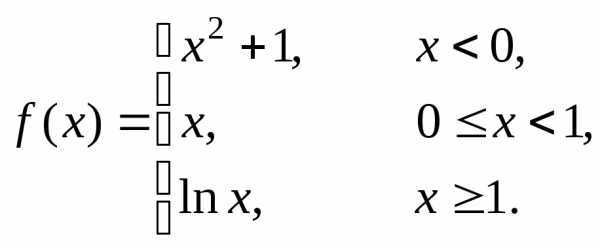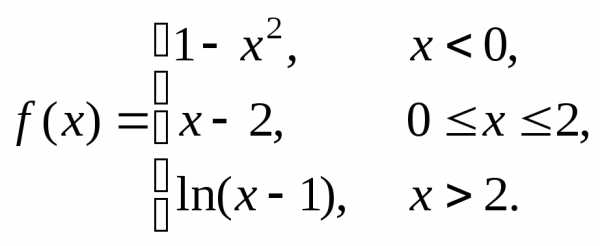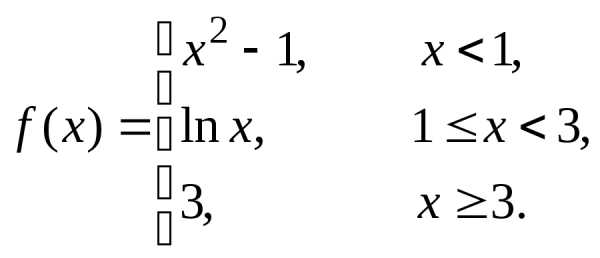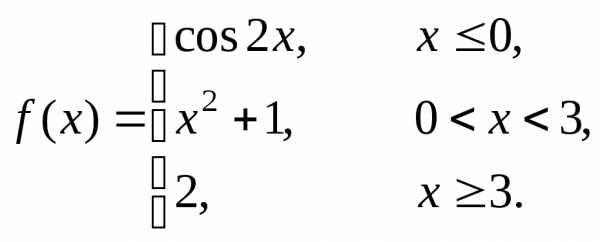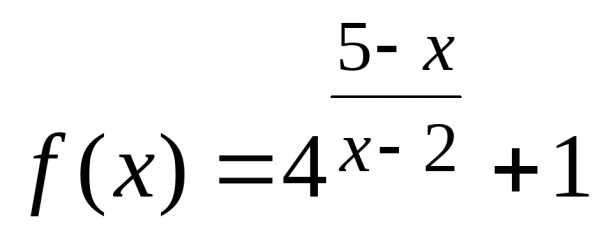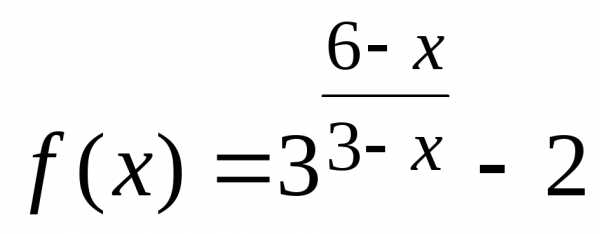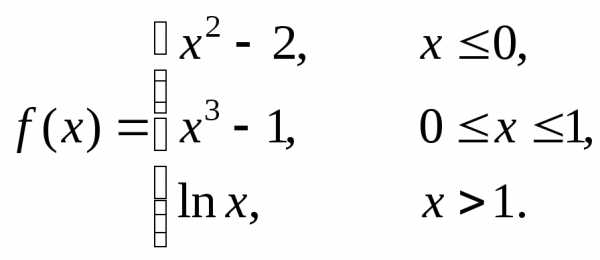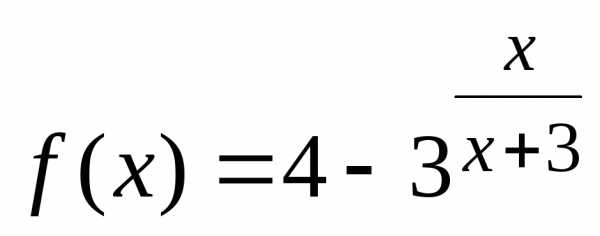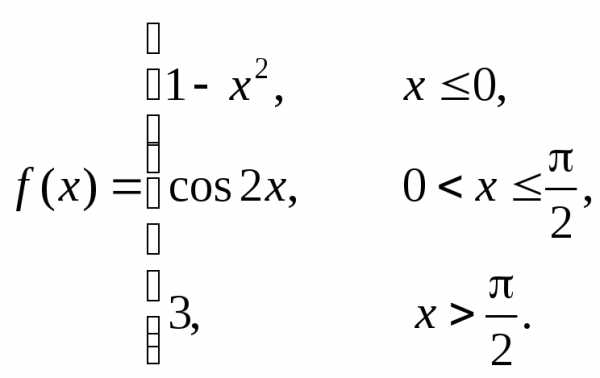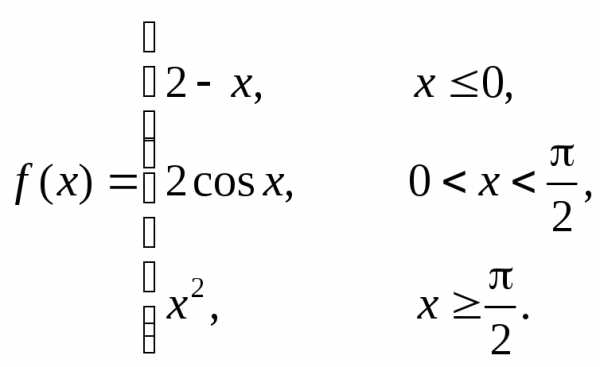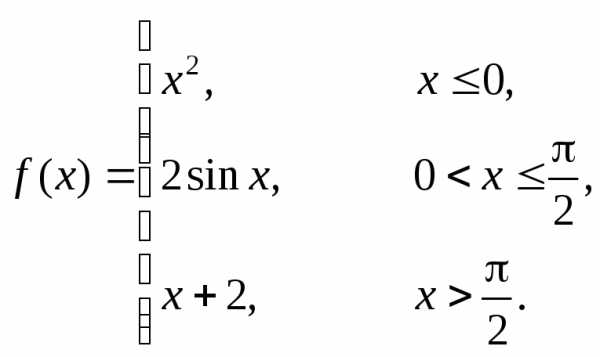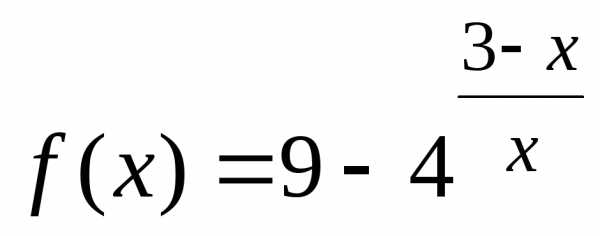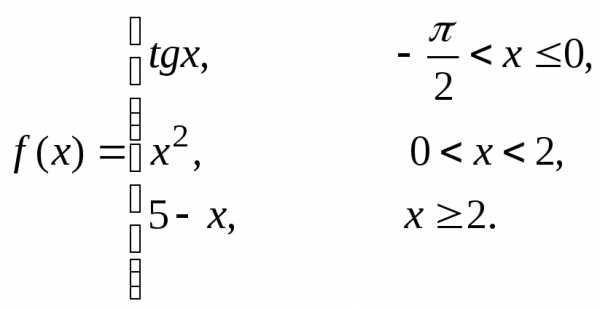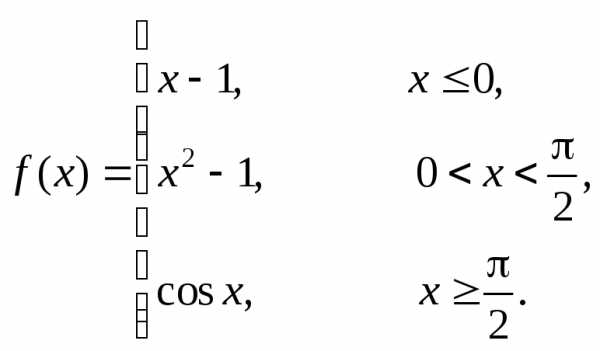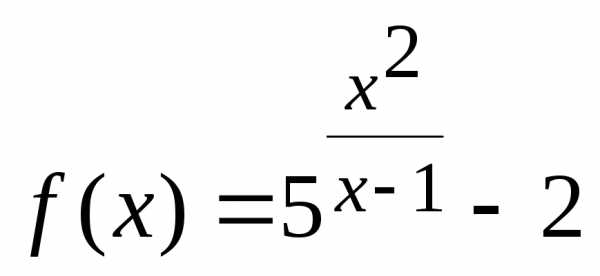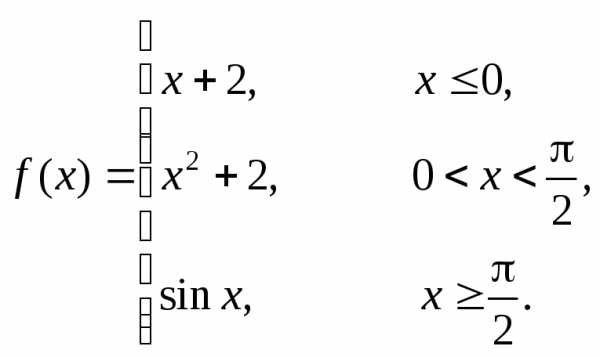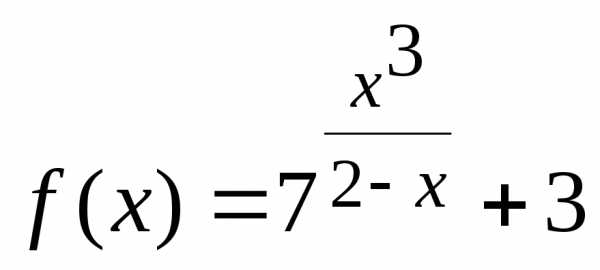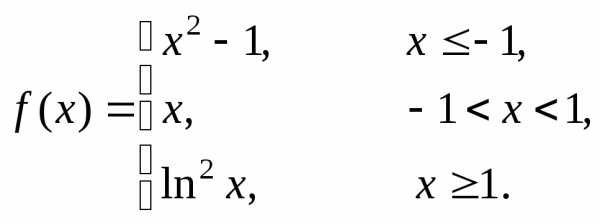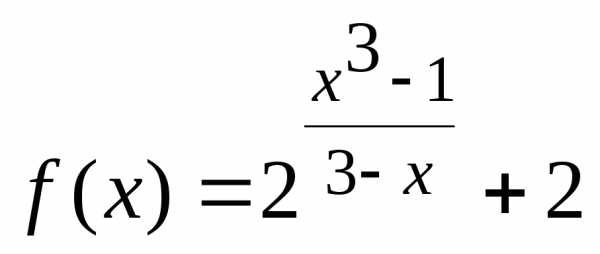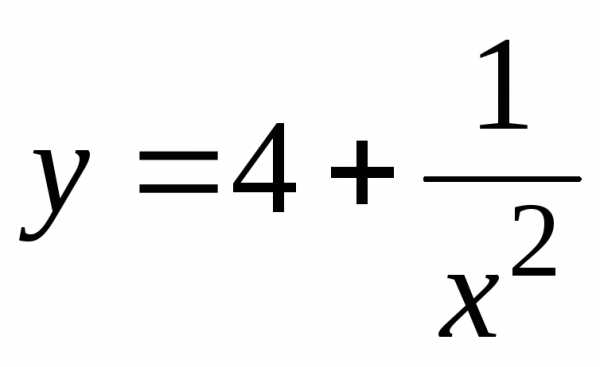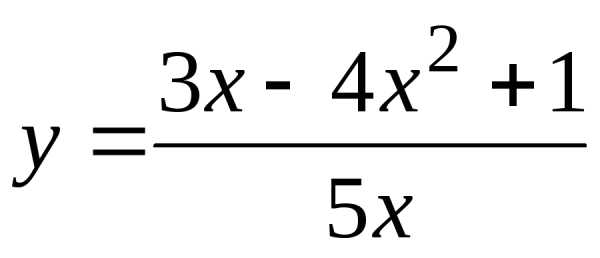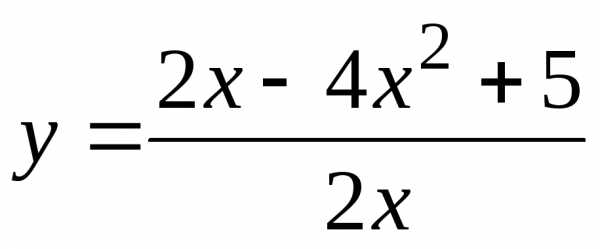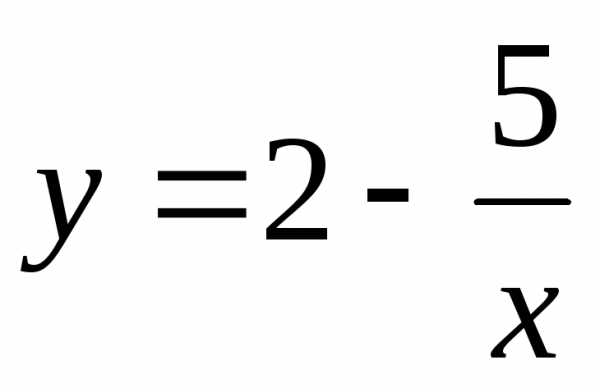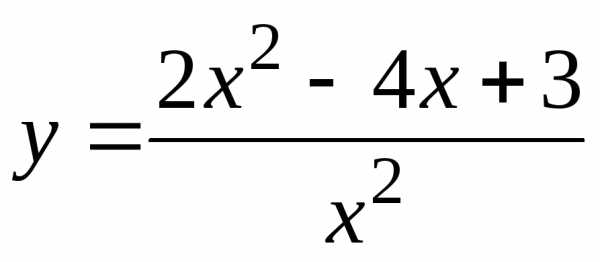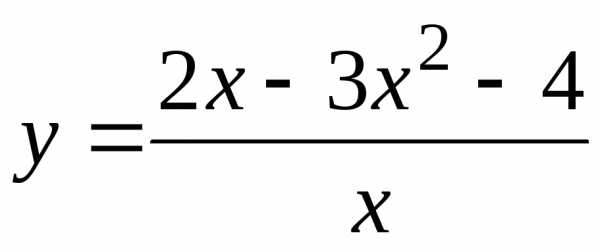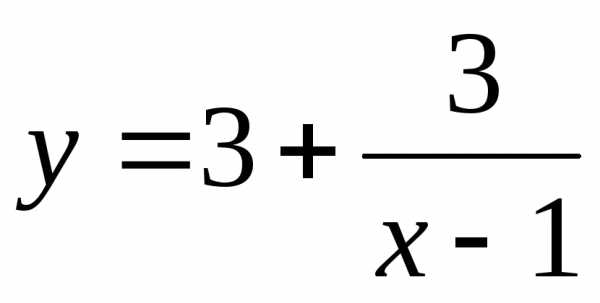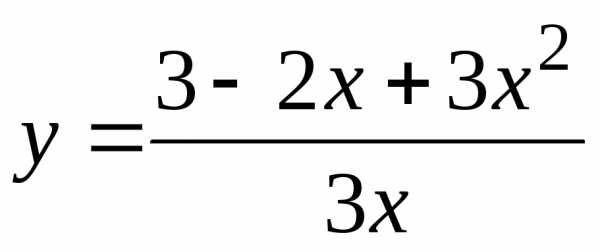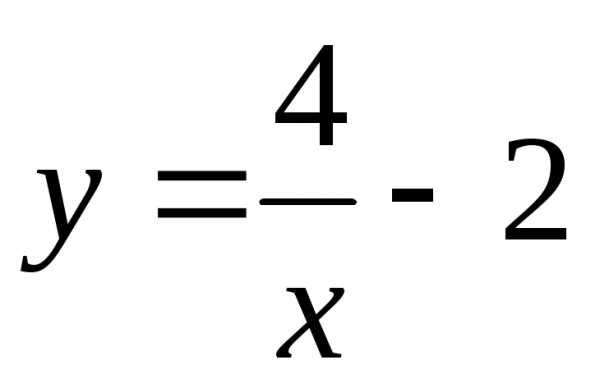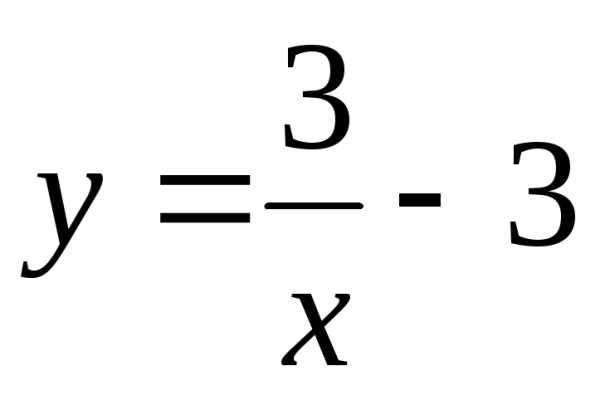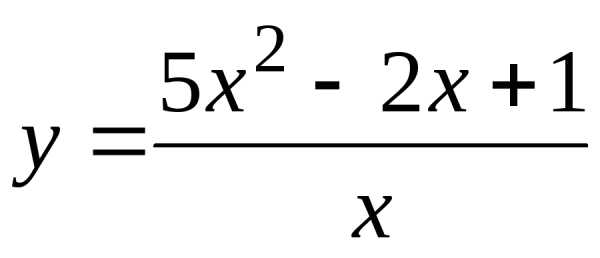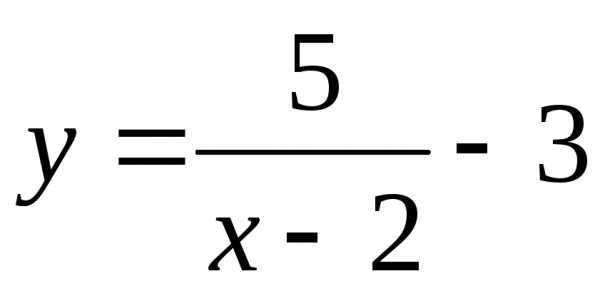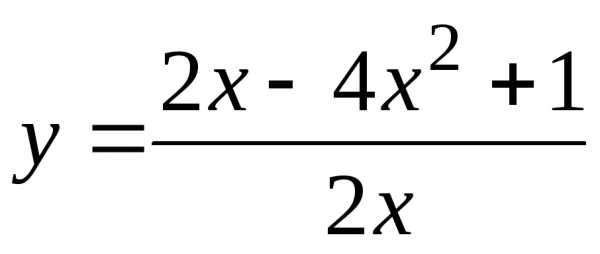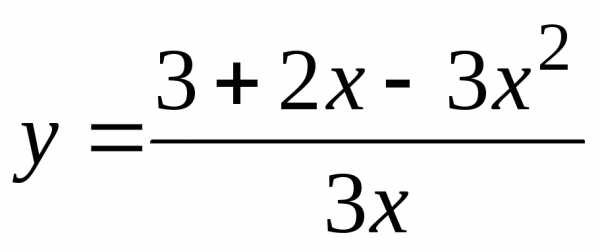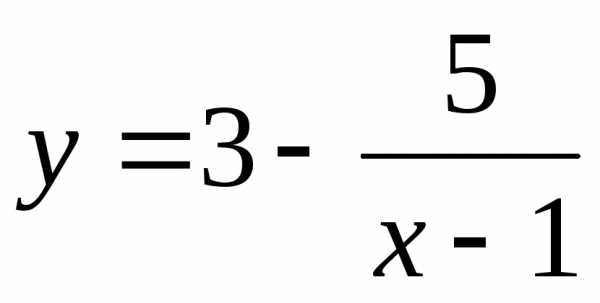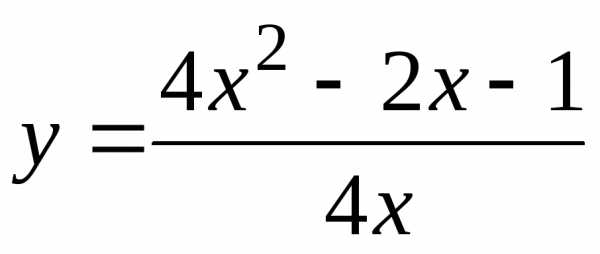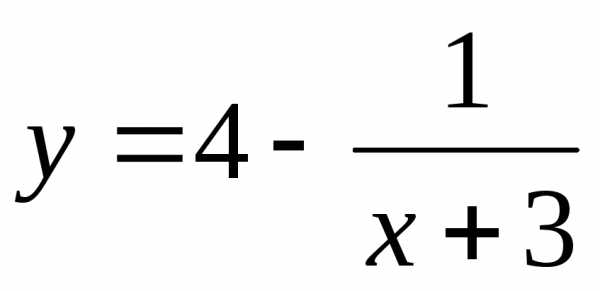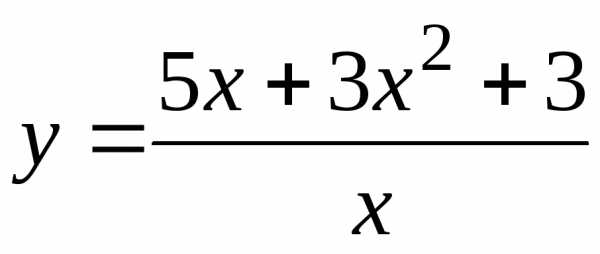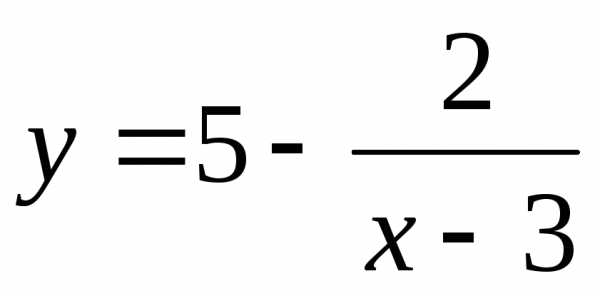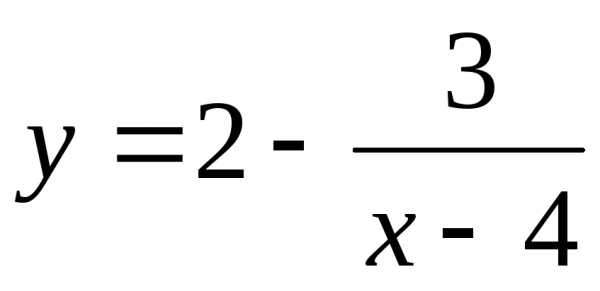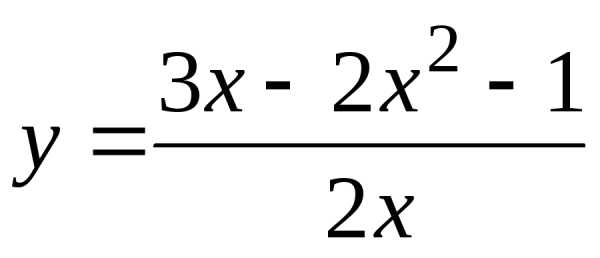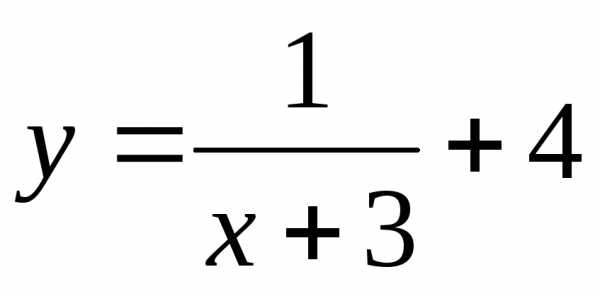§ 5. Непрерывность функций
Непрерывность и построение графиков кусочно-заданных функций – сложная тема. Учиться строить графики лучше непосредственно на практическом занятии. Здесь в основном показано исследование на непрерывность.
Известно, что элементарная функция (см. с. 16) непрерывна во всех точках, в которых определена. Поэтому нарушение непрерывности у элементарных функций возможно только в точках двух типов:
а) в точках, где функция «переопределяется»;
б) в точках, где функция не существует.
Соответственно только такие точки и проверяются при исследовании на непрерывность, что показано в примерах.
Для неэлементарных функций исследование сложнее. Например, функция (целая часть числа) определена на всей числовой оси, но терпит разрыв при каждом целом
Перед изучением материала следует повторить по лекции или учебнику, какими (какого рода) бывают точки разрыва.
Исследование кусочно-заданных функций на непрерывность
Функция задана кусочно, если она на разных участках области определения задаётся разными формулами.
Основная идея при исследовании таких функций – выяснить, задана ли функция в тех точках, в которых переопределяется, и как. Затем проверяется, совпадают ли значения функции слева и справа от таких точек.
Пример 1. Покажем, что функция 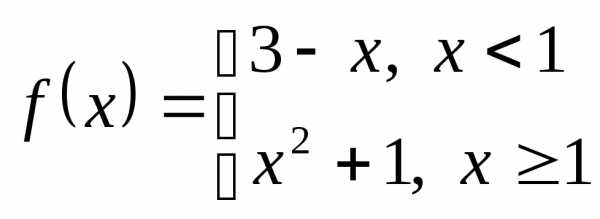 непрерывна.
непрерывна.
Функция
элементарна и потому непрерывна в тех
точках, в которых определена. Но, очевидно,
она определена во всех точках.
Следовательно, во всех точках она и
непрерывна, в том числе при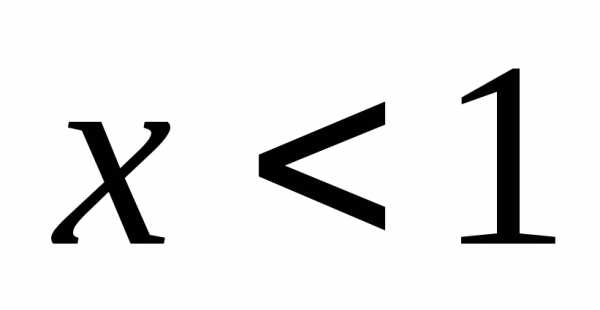 ,
как требует условие.
,
как требует условие.
То же справедливо
для функции
,
и при она непрерывна.
она непрерывна.
В таких случаях
непрерывность может нарушаться только
там, где функция переопределяется. В
нашем примере это точка 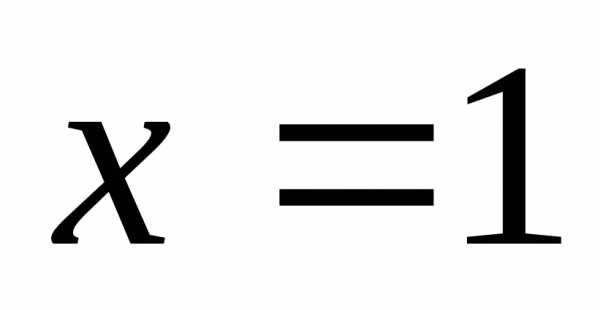 .
Проверим её, для чего найдём пределы
слева и справа:
.
Проверим её, для чего найдём пределы
слева и справа:
а) ;
б) .
Пределы слева и справа совпадают. Остаётся узнать:
а) определена ли
функция в самой точке 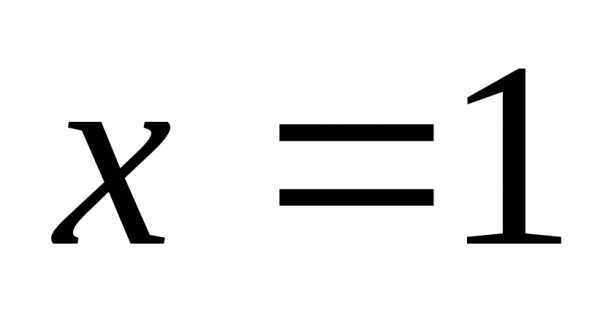 ;
;
б) если да, то
совпадает ли 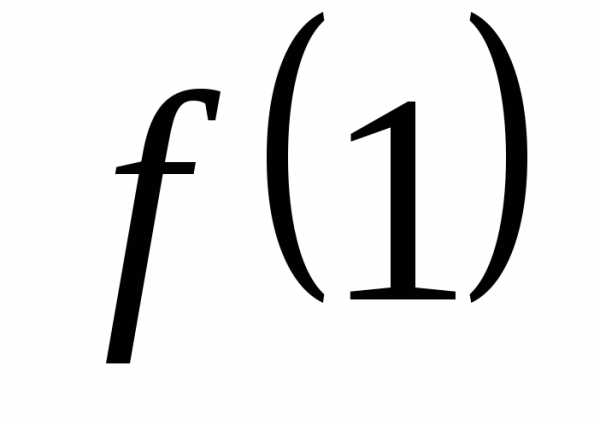 со значениями пределов слева и справа.
со значениями пределов слева и справа.
По условию, если 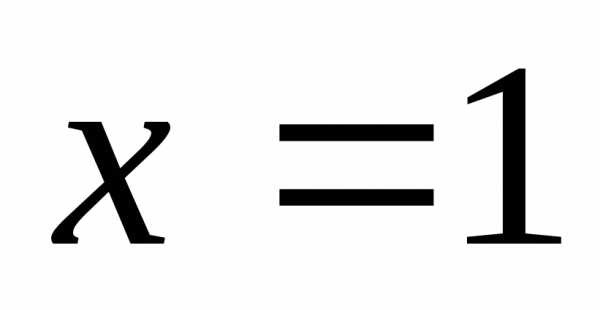 ,
то.
Поэтому.
,
то.
Поэтому.
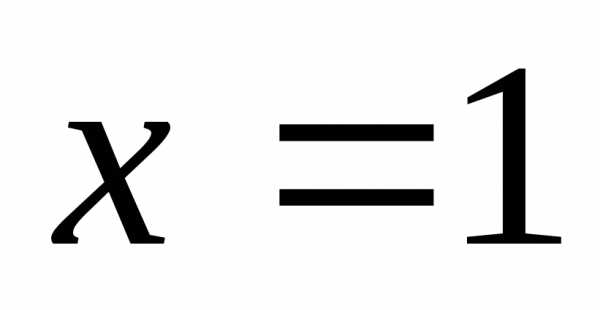 функция
непрерывна.
Итак, функция непрерывна на всей оси,
включая точку
функция
непрерывна.
Итак, функция непрерывна на всей оси,
включая точку 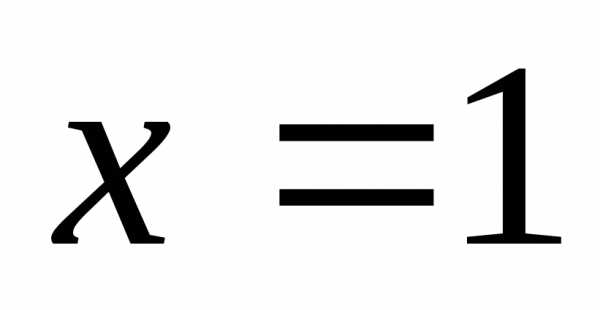 .
.Замечания к решению
а) При вычислениях
не играло роли, подставляем мы в конкретную формулу число  или
или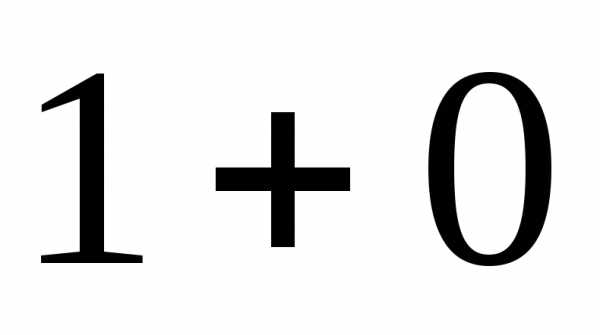 .
Обычно это важно, когда получается
деление на бесконечно малую величину,
поскольку влияет на знак бесконечности.
Здесь же
.
Обычно это важно, когда получается
деление на бесконечно малую величину,
поскольку влияет на знак бесконечности.
Здесь же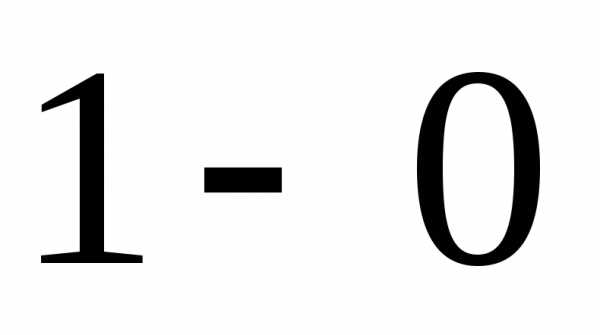 и
и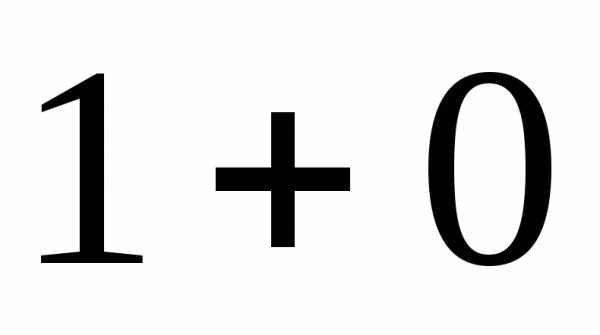 отвечают только завыбор
функции;
отвечают только завыбор
функции;
б) как правило,
обозначения 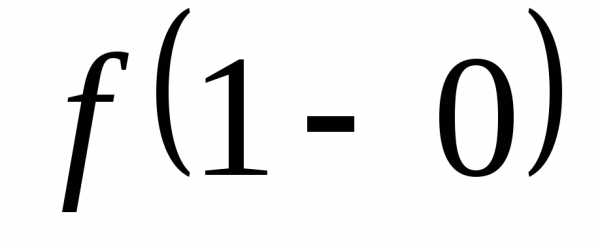
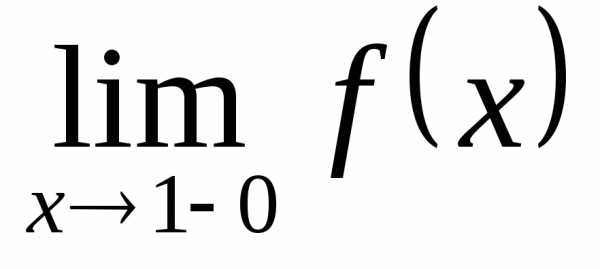 равноправны, то же касается обозначений
равноправны, то же касается обозначений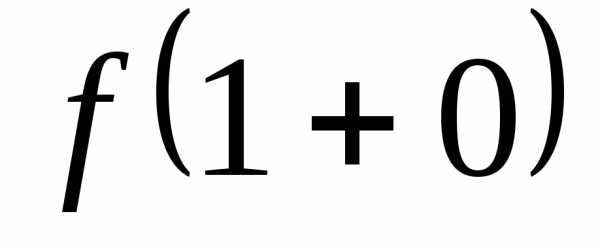 и
и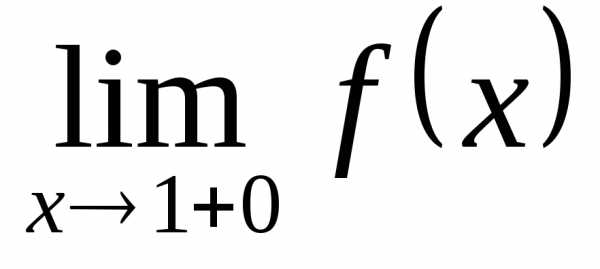 (и справедливо для любой точки, а не
только для
(и справедливо для любой точки, а не
только для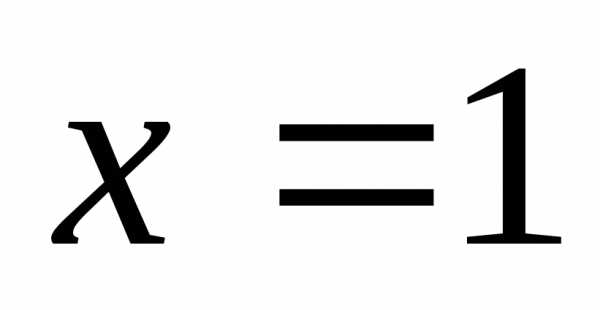 ).
Дальше для краткости применяются
обозначения вида
).
Дальше для краткости применяются
обозначения вида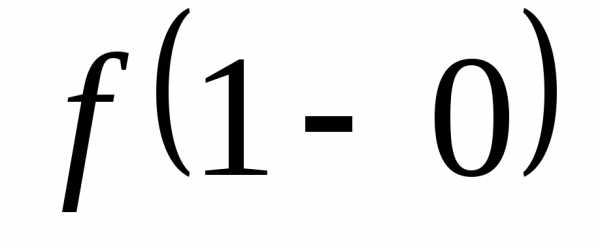 ;
;в) когда пределы слева и справа равны, для проверки на непрерывность фактически остаётся посмотреть, будет ли одно из неравенств нестрогим. В примере таковым оказалось 2-е неравенство.
Пример 2. Исследуем на непрерывность функцию 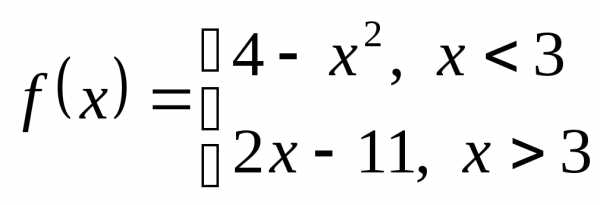 .
.
По тем же причинам,
что в примере 1, непрерывность может
нарушаться только в точке 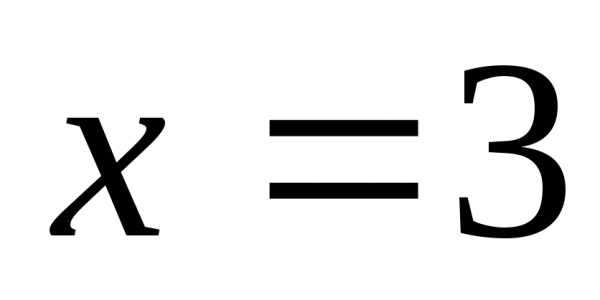
а) ;
б) .
Пределы слева и
справа равны, но в самой точке 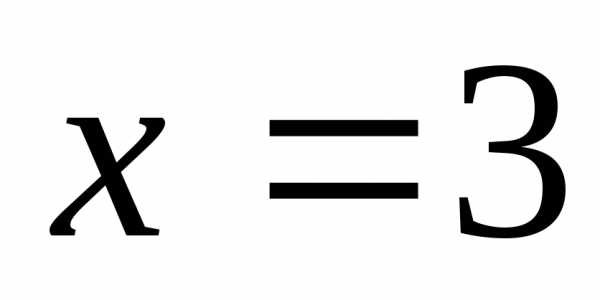 функция не определена (неравенства
строгие). Это означает, что
функция не определена (неравенства
строгие). Это означает, что – точкаустранимого
разрыва.
– точкаустранимого
разрыва.
«Устранимый
разрыв» означает, что достаточно или
сделать любое из неравенств нестрогим,
или придумать для отдельной точки 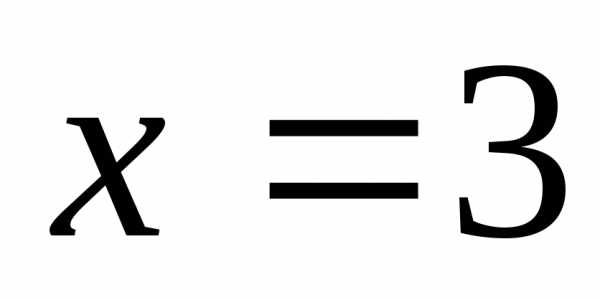 функцию, значение которой при
функцию, значение которой при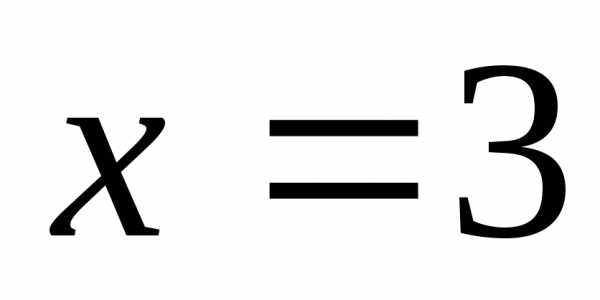 равно –5, или просто указать, что
равно –5, или просто указать, что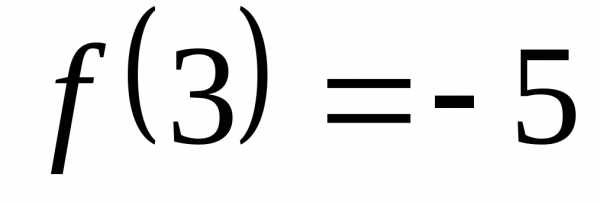 ,
чтобы вся функция
,
чтобы вся функция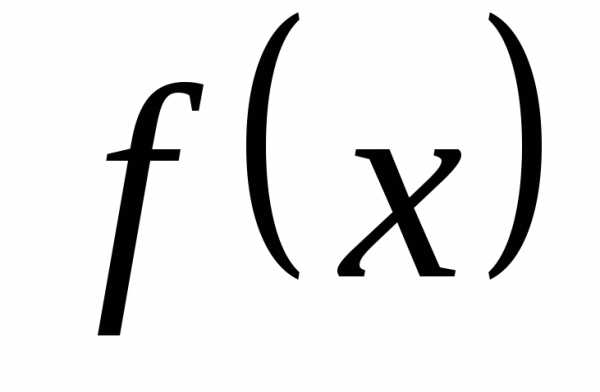 стала непрерывной.
стала непрерывной.
 – точка устранимого разрыва.
– точка устранимого разрыва.Замечание 1. В литературе устранимый разрыв обычно считается частным случаем разрыва 1-го рода, однако студентами чаще понимается как отдельный тип разрыва. Во избежание разночтений будем придерживаться 1-й точки зрения, а «неустранимый» разрыв 1-го рода оговаривать особо.
Пример 3. Проверим, непрерывна ли функция 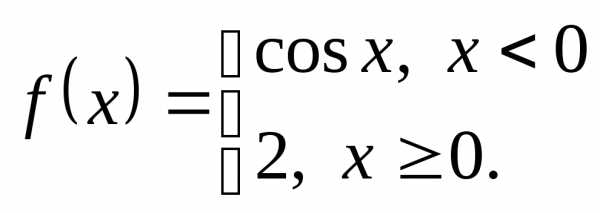
В точке 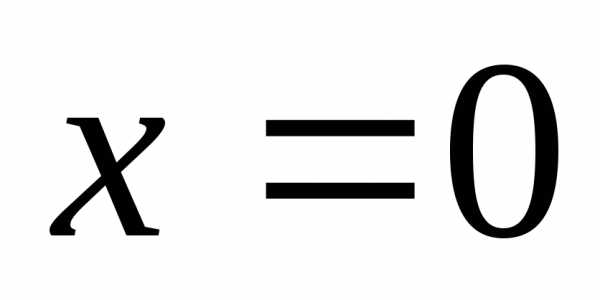
а) ;
б) .
Пределы слева и
справа различны: 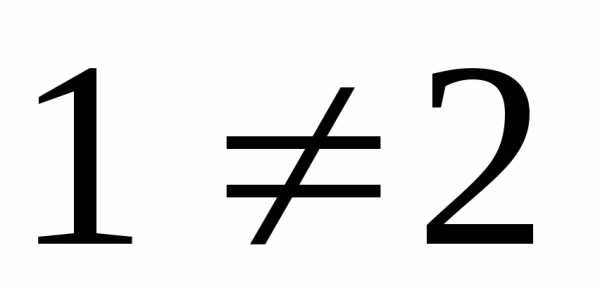 .
Независимо от того, определена ли функция
при
.
Независимо от того, определена ли функция
при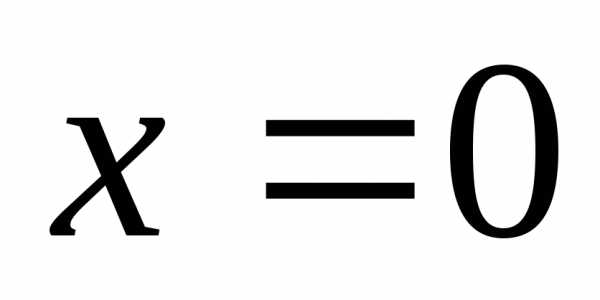 (да) и если да, то чему равна (равна 2),
точка
(да) и если да, то чему равна (равна 2),
точка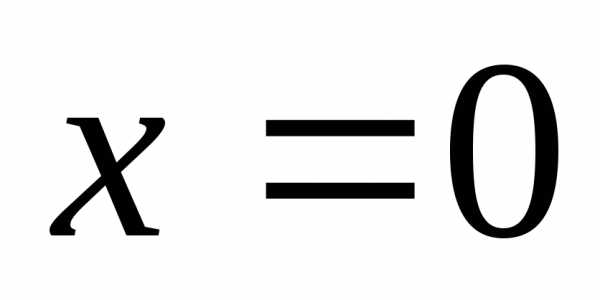
В точке 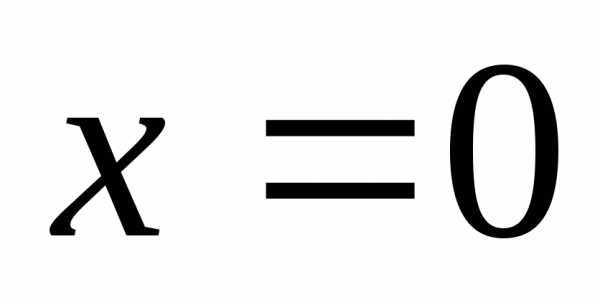 происходитконечный
скачок (от
1 к 2).
происходитконечный
скачок (от
1 к 2).
Ответ: точка 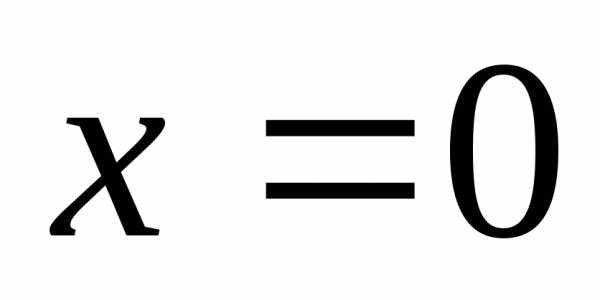 – точка неустранимого разрыва 1-го рода.
– точка неустранимого разрыва 1-го рода.
Замечание 2. Вместо  и
и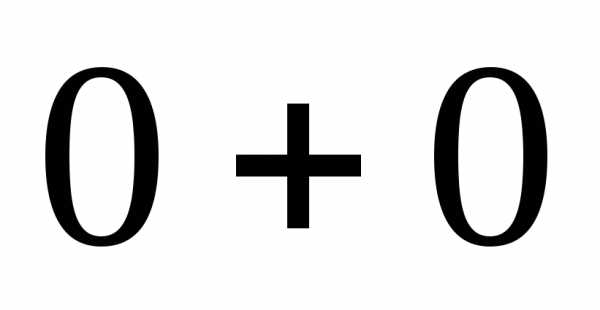 обычно пишут
обычно пишут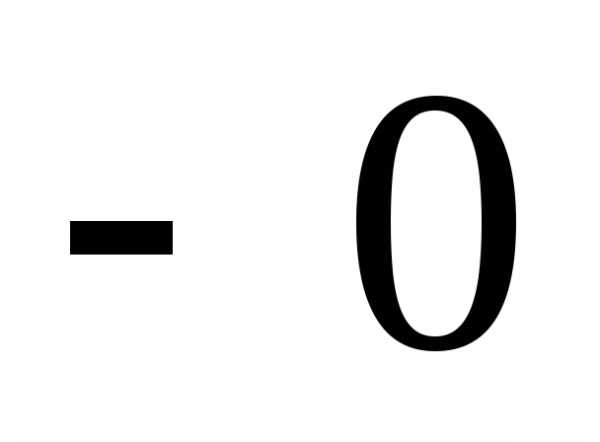 и
и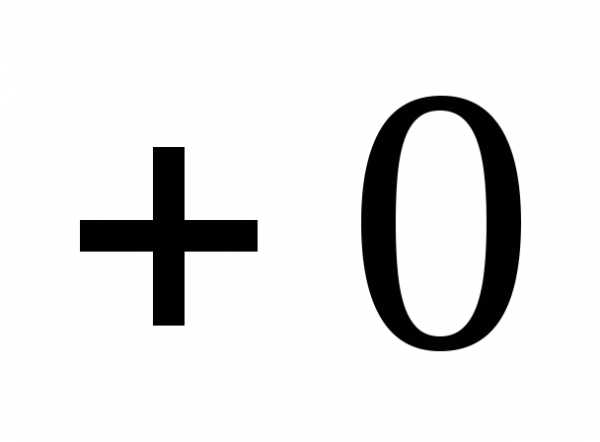 соответственно.
соответственно.
Возможен вопрос: чем отличаются функции
 и
и 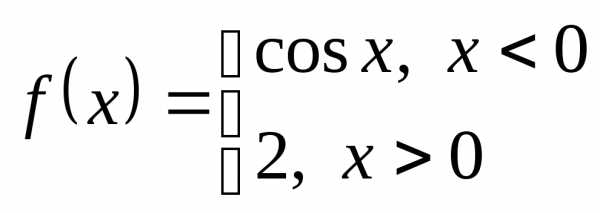
а также их графики? Правильный ответ:
а) 2-я функция не
определена в точке 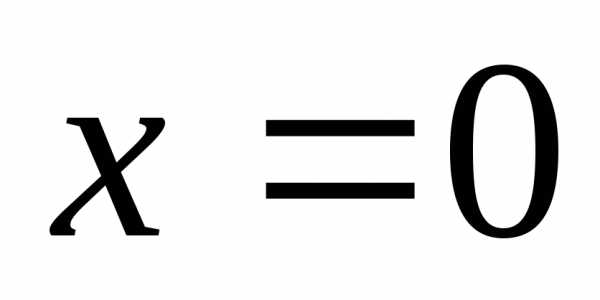 ;
;
б) на графике 1-й
функции точка 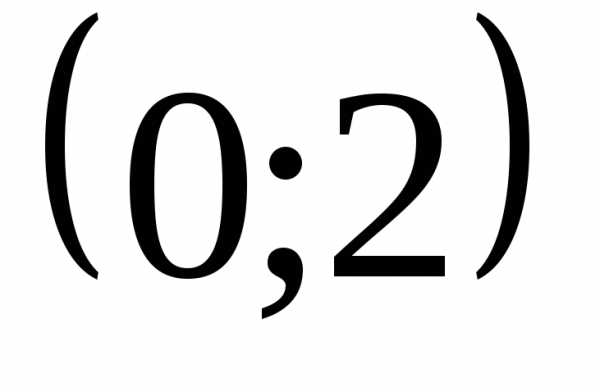 «закрашена», на графике 2-й – нет
(«выколотая точка»).
«закрашена», на графике 2-й – нет
(«выколотая точка»).
Точка 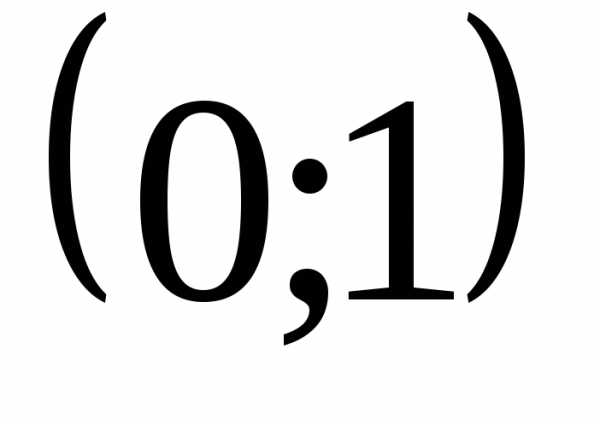 ,
где обрывается график,
не закрашена на обоих графиках.
,
где обрывается график,
не закрашена на обоих графиках.
Сложнее исследовать функции, по-разному определённые на трёх участках.
Пример 4. Непрерывна ли функция 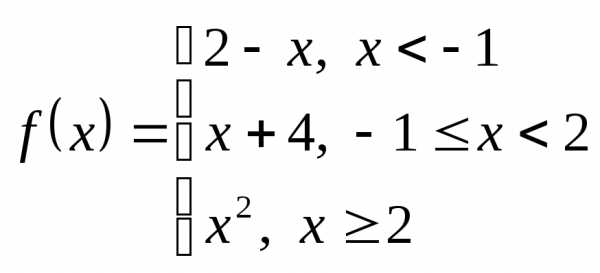 ?
?
Так же, как в
примерах 1 – 3, каждая из функций  ,
,
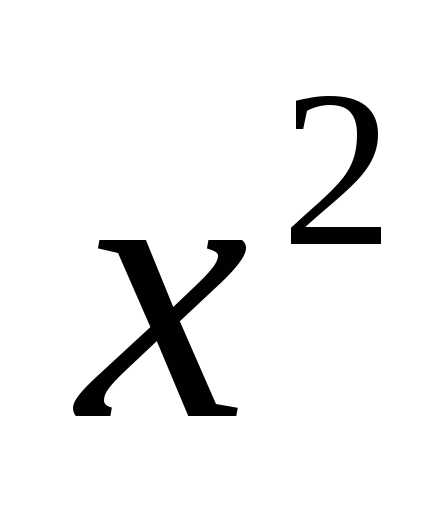 непрерывна на всей числовой оси, в том
числе – на участке, на котором задана.
Разрыв возможен только в точке
непрерывна на всей числовой оси, в том
числе – на участке, на котором задана.
Разрыв возможен только в точке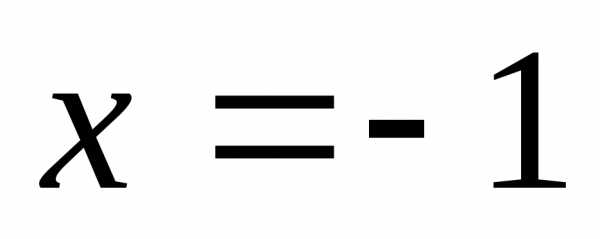 или (и) в точке
или (и) в точке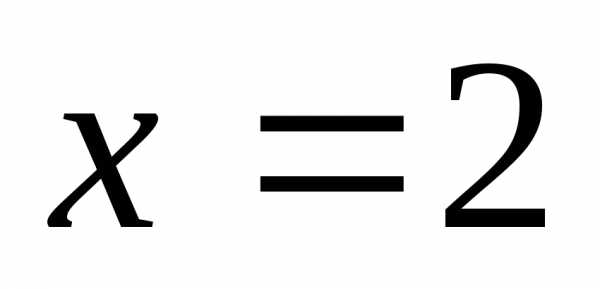 ,
где функция переопределяется.
,
где функция переопределяется.Задача распадается на 2 подзадачи: исследовать на непрерывность функции
и 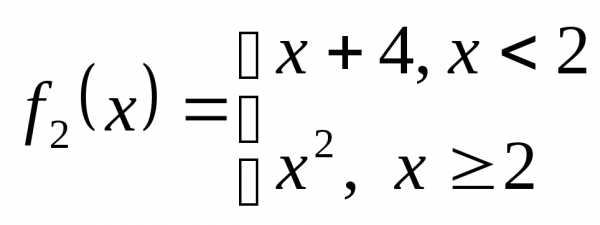 ,
,
причём точка 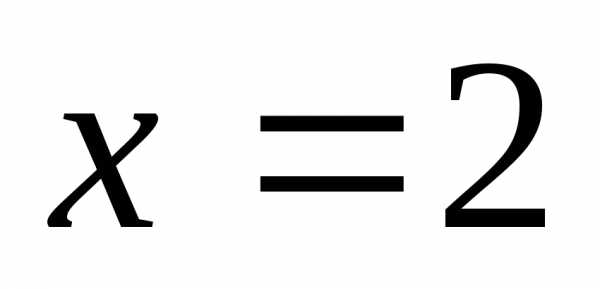 не представляет интереса для функции
не представляет интереса для функции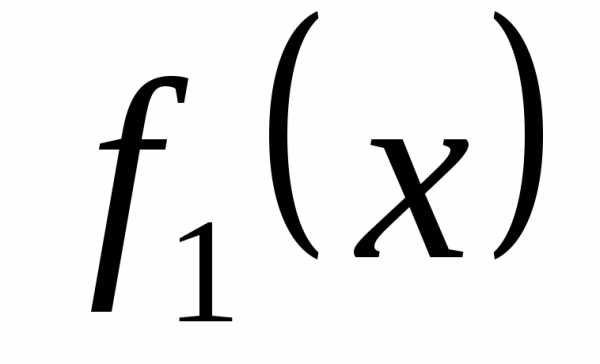 ,
а точка
,
а точка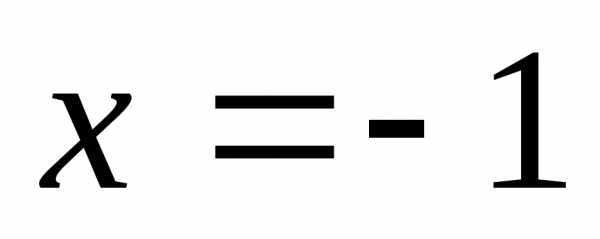 – для функции
– для функции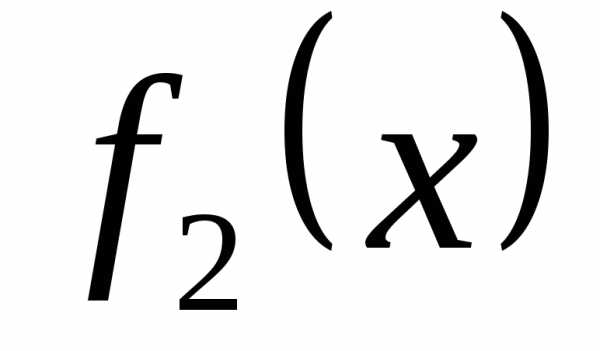 .
.
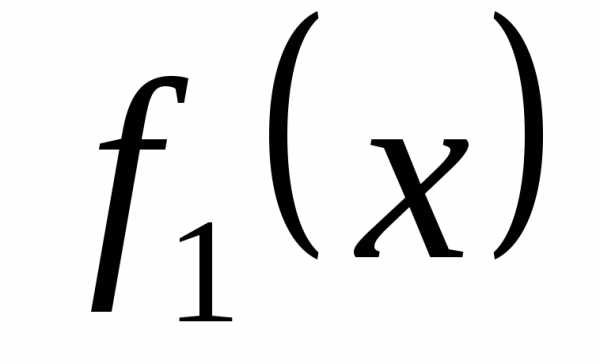 (индекс не пишем):
(индекс не пишем):а) ;
б) .
Пределы совпадают.
По условию,
(если пределы слева и справа равны, то
фактически функция непрерывна, когда
одно и из неравенств нестрогое). Итак,
в точке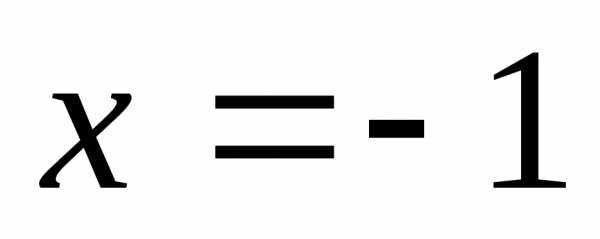 функция непрерывна.
функция непрерывна.
2-й
шаг. Проверяем
точку 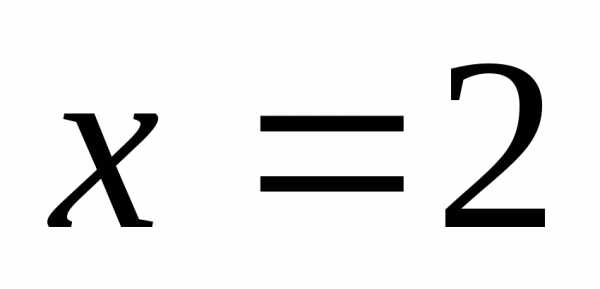 и функцию
и функцию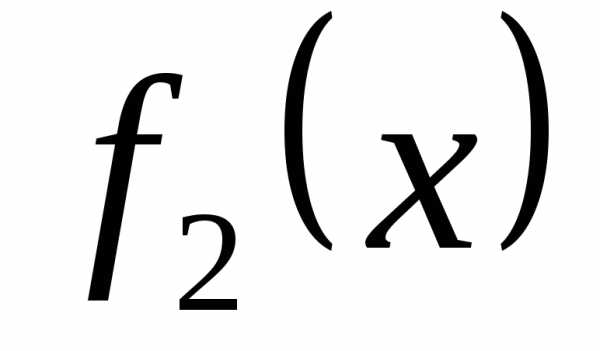 :
:
а) ;
б) .
Поскольку 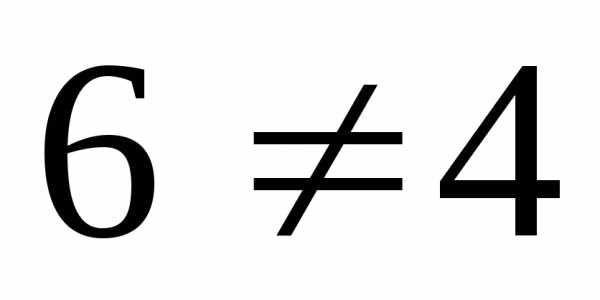 ,
точка
,
точка – точка разрыва 1-го рода, и значение
– точка разрыва 1-го рода, и значение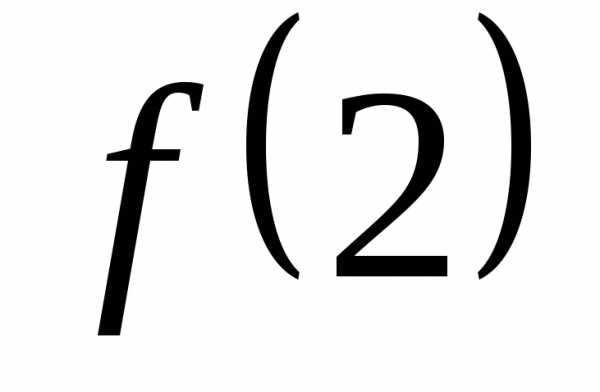
Ответ: функция непрерывна во всех точках, кроме
точки 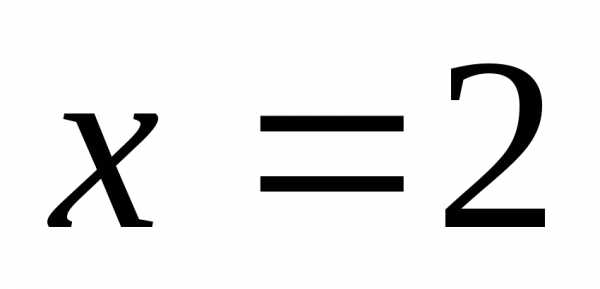 ,
где имеет место неустранимый разрыв
1-го рода – скачок от 6 к 4.
,
где имеет место неустранимый разрыв
1-го рода – скачок от 6 к 4.
Пример 5. Найти точки разрыва функции 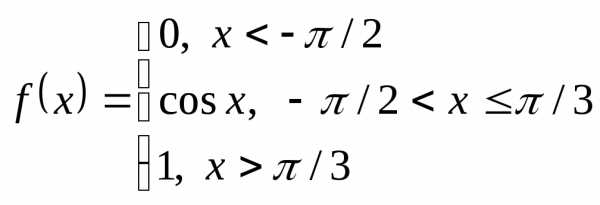 .
.
Действуем по той же схеме, что в примере 4.
1-й шаг. Проверяем точку :
а) 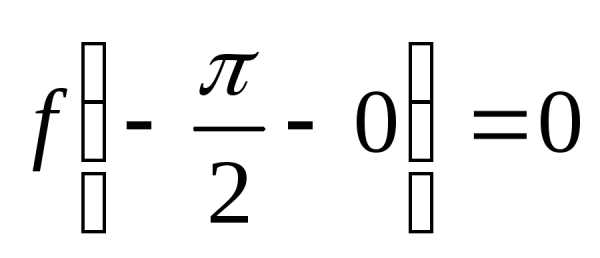 ,
поскольку слева от
,
поскольку слева от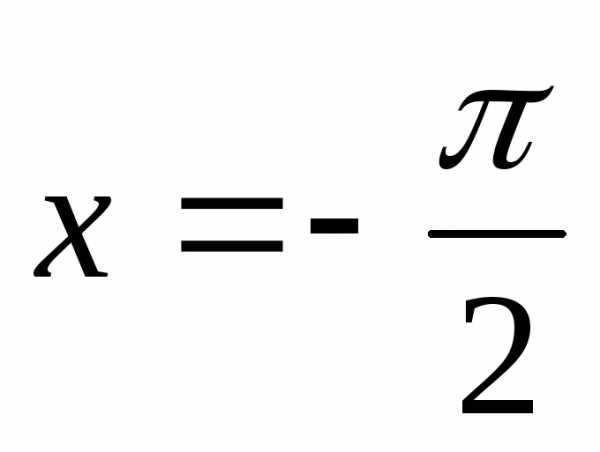 функция постоянна и равна 0;
функция постоянна и равна 0;
б)
( – чётная функция).
– чётная функция).
Пределы совпадают,
но при 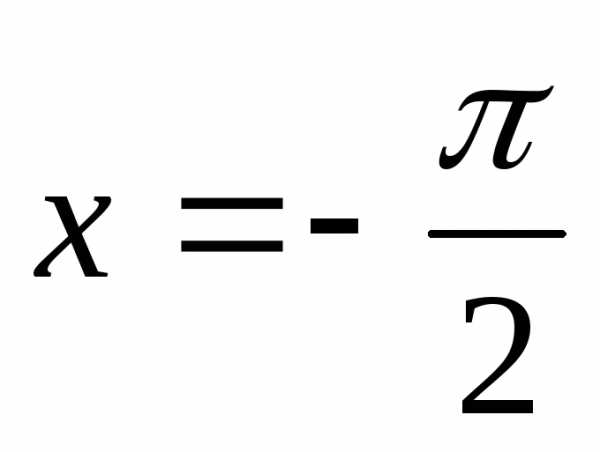 функция по условию не определена, и
получается, что
функция по условию не определена, и
получается, что – точка устранимого разрыва.
– точка устранимого разрыва.
2-й
шаг. Проверяем
точку 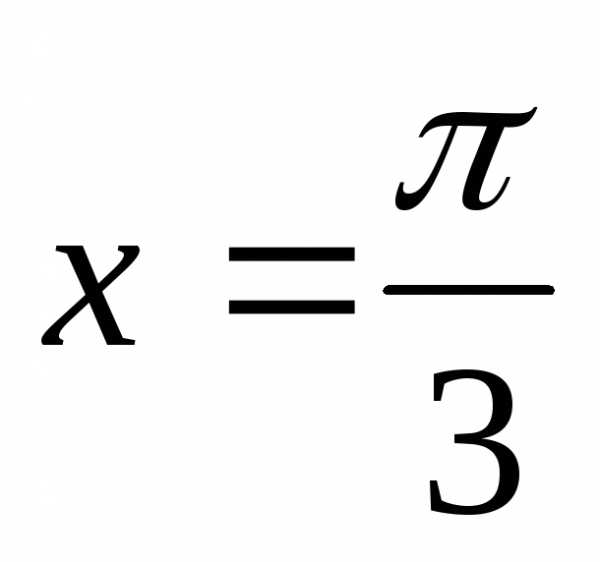 :
:
а) ;
б) – значение функции не зависит от переменной.
Пределы различны: 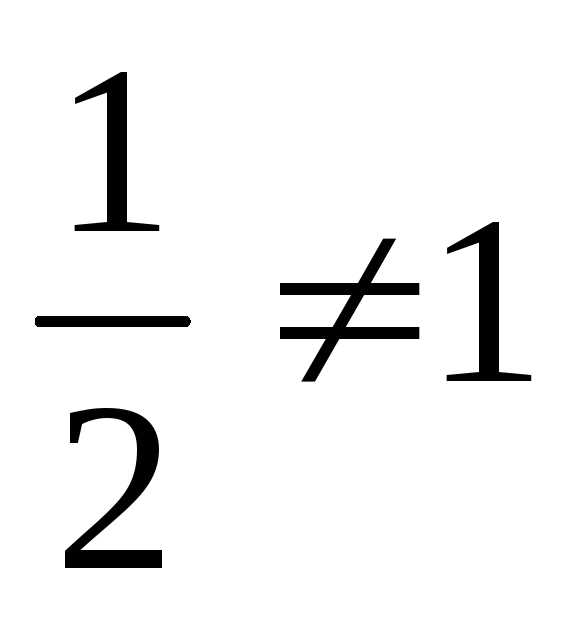 ,
точка
,
точка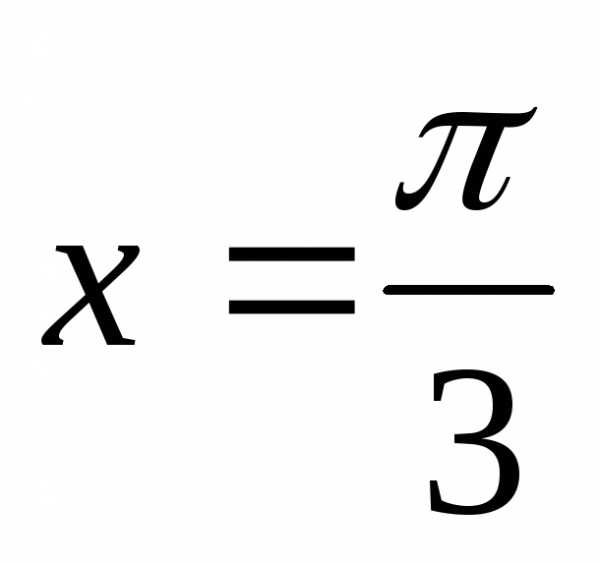 – точка неустранимого разрыва 1-го рода.
– точка неустранимого разрыва 1-го рода.
Ответ: 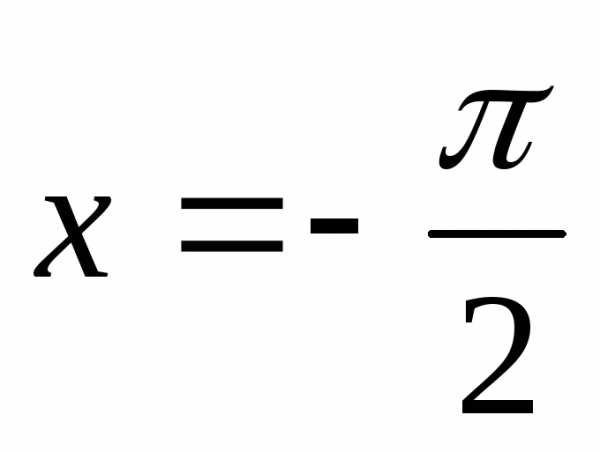 – точка устранимого разрыва,
– точка устранимого разрыва,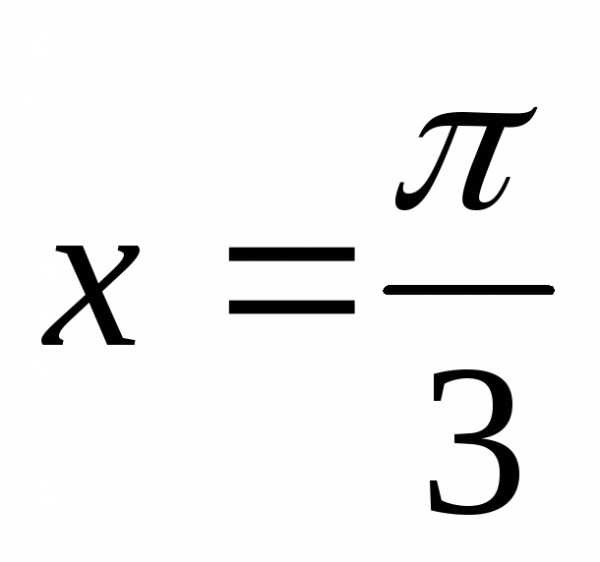 – точка неустранимого разрыва 1-го рода,
в остальных точках функция непрерывна.
– точка неустранимого разрыва 1-го рода,
в остальных точках функция непрерывна.
Пример 6. Непрерывна ли функция ?
Функция 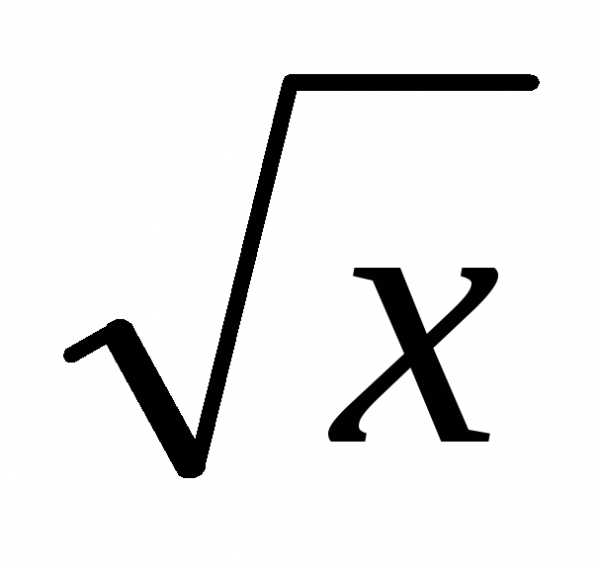 определена при
определена при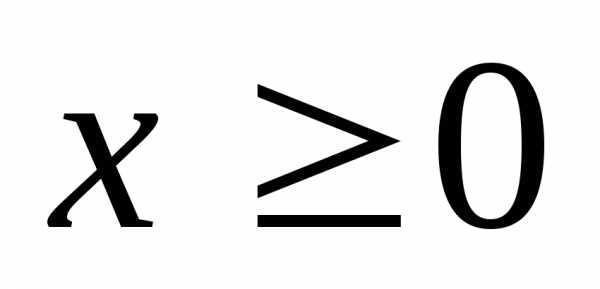 ,
поэтому условие
,
поэтому условие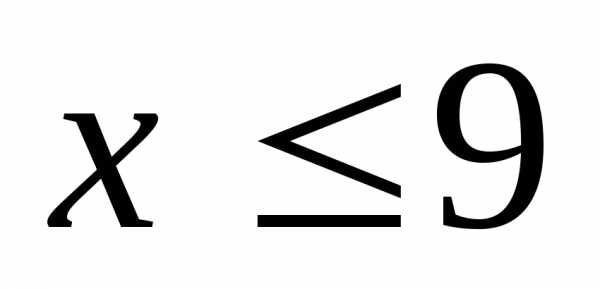 превращается в условие.
превращается в условие.
С другой стороны,
функция 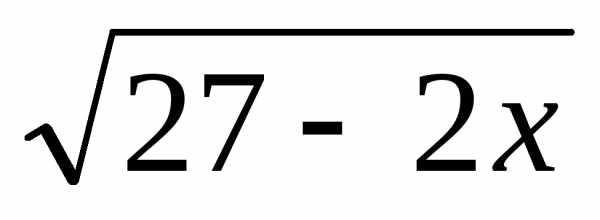 определена при,
т.е. при
определена при,
т.е. при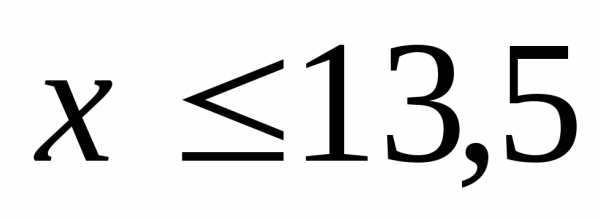 .
Значит, условие
.
Значит, условие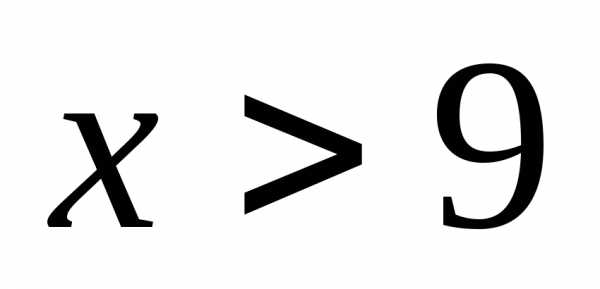 превращается в условие.
превращается в условие.
Получается, что
должно выполняться условие
,
и область определения всей функции –
отрезок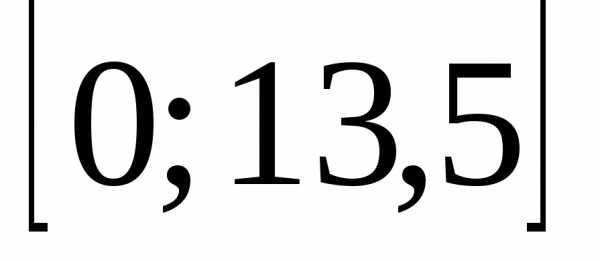 .
.
Сами по себе
функции 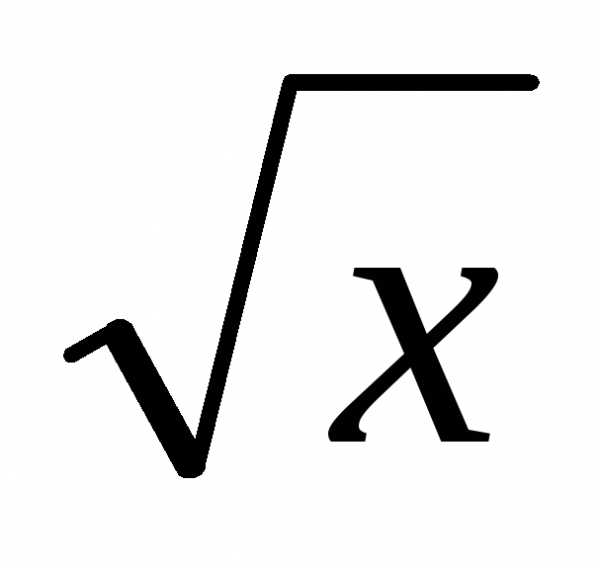 и
и элементарны и потому непрерывны во всех
точках, в которых определены – в
частности, и при.
элементарны и потому непрерывны во всех
точках, в которых определены – в
частности, и при.
Остаётся проверить,
что происходит в точке  :
:
а) ;
б) .
Поскольку 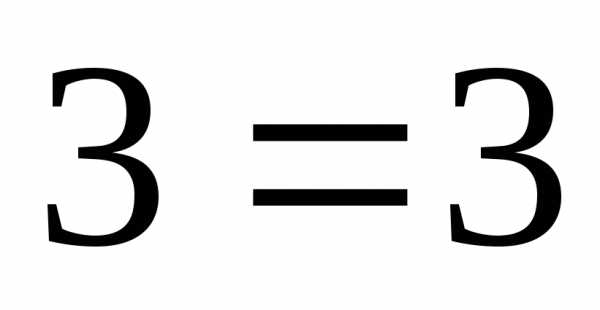 ,
смотрим, определена ли функция в точке
,
смотрим, определена ли функция в точке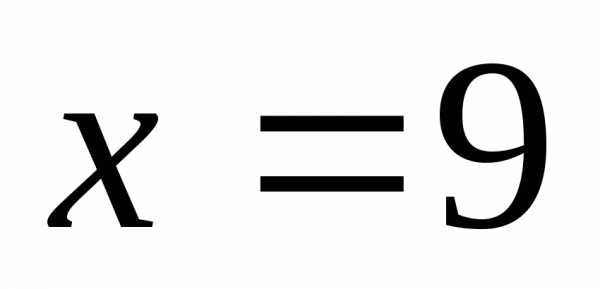 .
Да, 1-е неравенство – нестрогое относительно
.
Да, 1-е неравенство – нестрогое относительно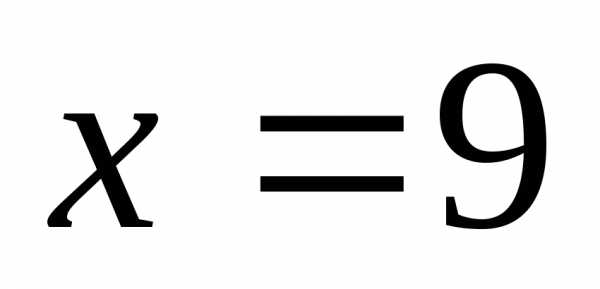 ,
и этого достаточно.
,
и этого достаточно.
Ответ: функция определена на отрезке 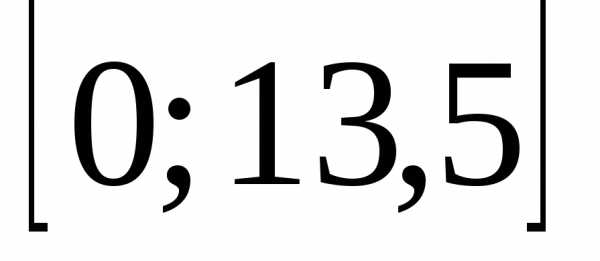 и непрерывна на нём.
и непрерывна на нём.
Более сложные случаи, когда одна из составляющих функций неэлементарна или не определена в какой-либо точке своего отрезка, выходят за рамки пособия.
НФ1. Постройте графики функций. Обратите внимание, определена ли функция в той точке, в которой переопределяется, и если да – каково значение функции (слово «если» в определении функции для краткости пропущено):
1) а) 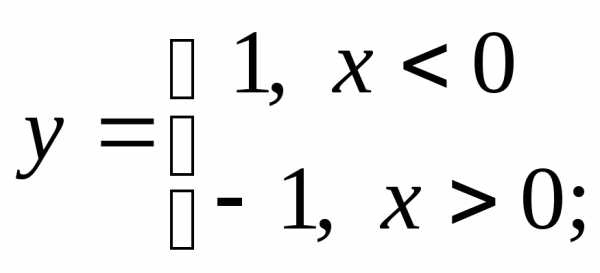 б)
б) в)
в)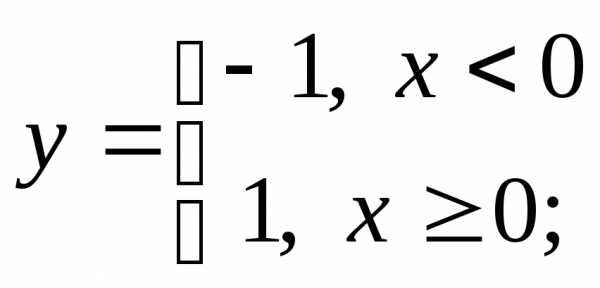 г)
г)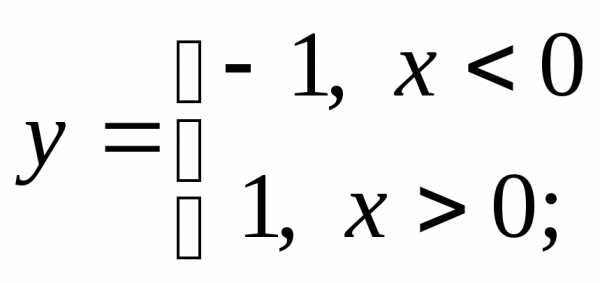
2) а) 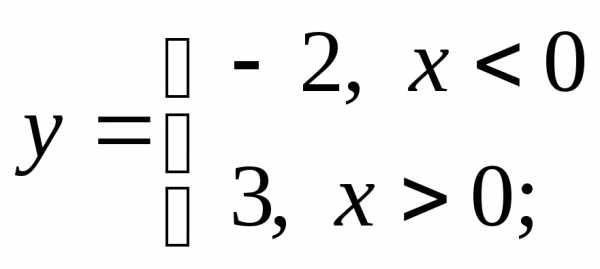 б)
б)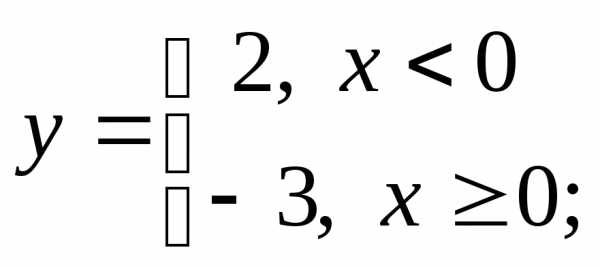 в)
в)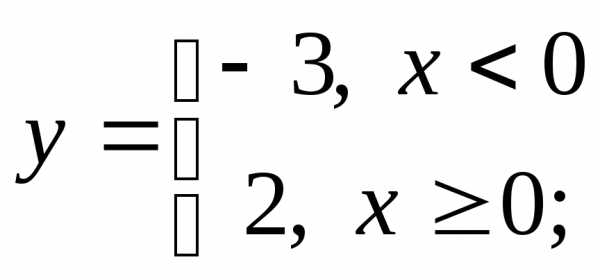 г)
г)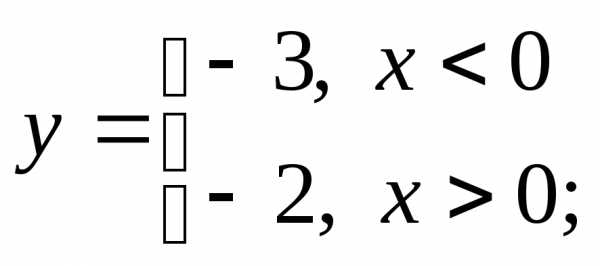
3) а) 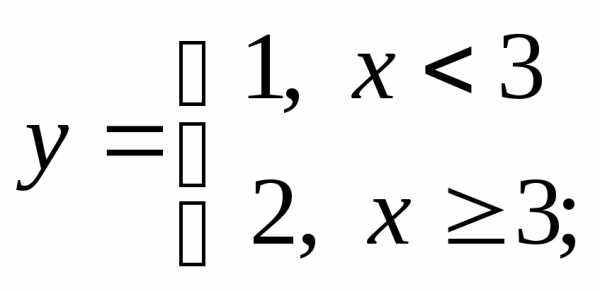 б)
б)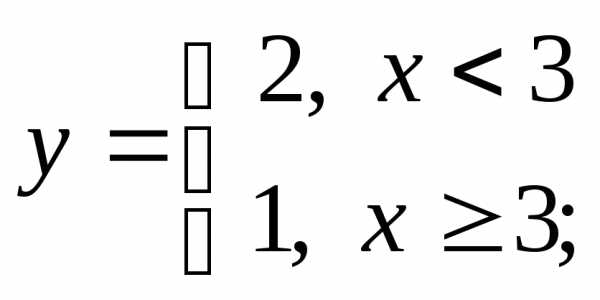 в)
в)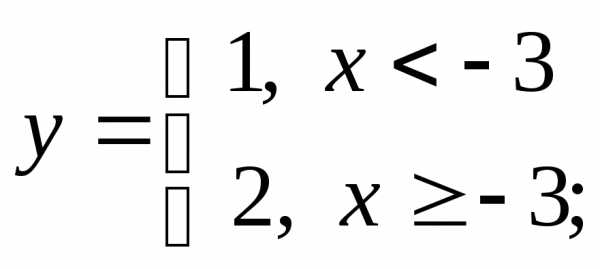 г)
г)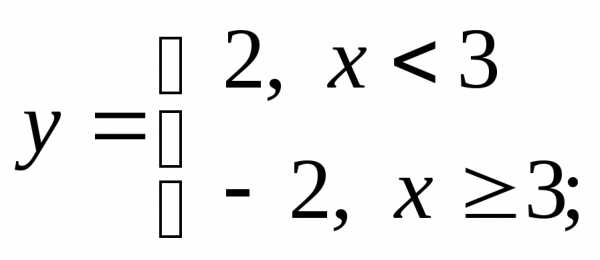
4) а) 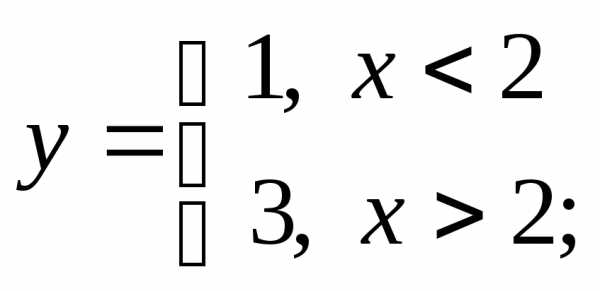 б)
б)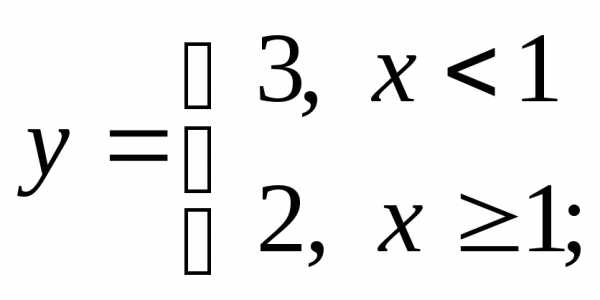 в)
в)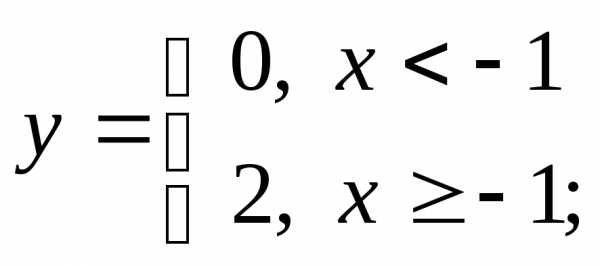 г)
г)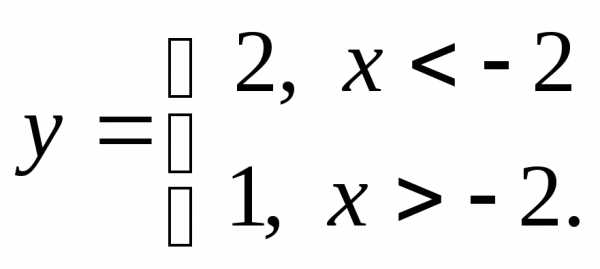
Пример 7. Пусть 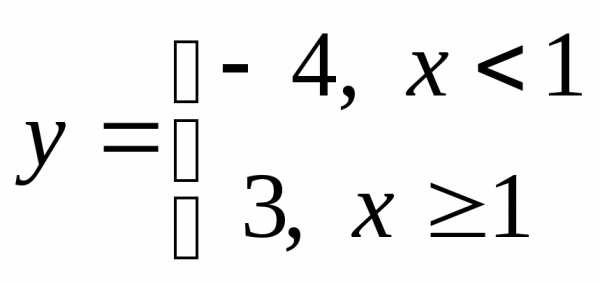 .
Тогда на участке
.
Тогда на участке строим горизонтальную прямую
строим горизонтальную прямую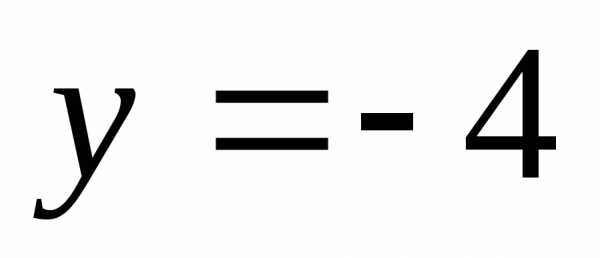 ,
а на участке
,
а на участке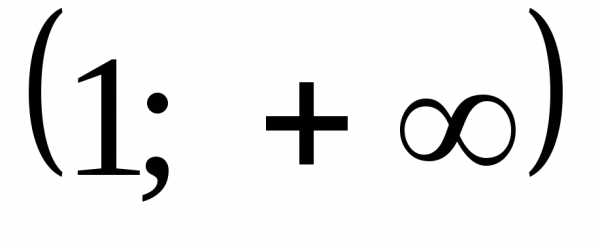 строим горизонтальную прямую
строим горизонтальную прямую .
При этом точка с координатами
.
При этом точка с координатами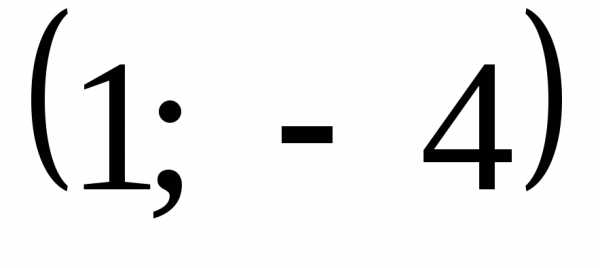 «выколота», а точка
«выколота», а точка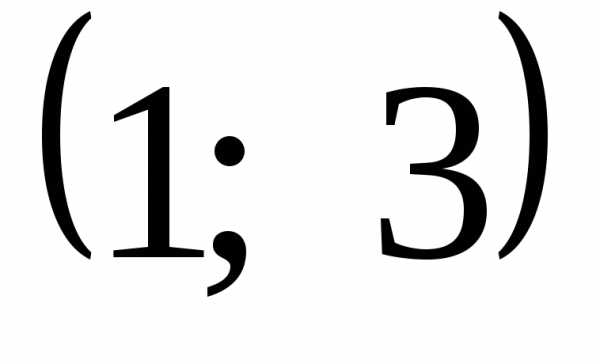 «закрашена». В точке
«закрашена». В точке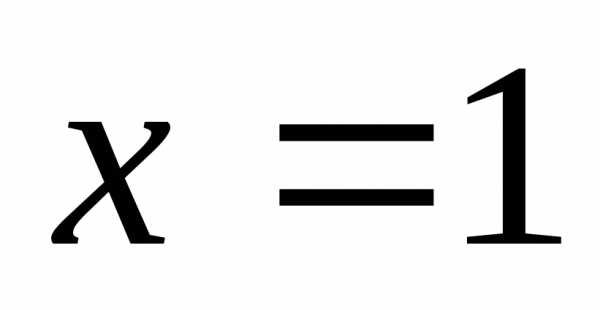 получается разрыв 1-го рода («скачок»),
и
получается разрыв 1-го рода («скачок»),
и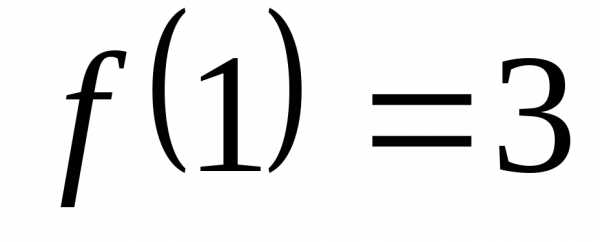 .
.
НФ2. Исследуйте на непрерывность функции, по-разному определённые на 3-х интервалах. Постройте графики:
1) а) 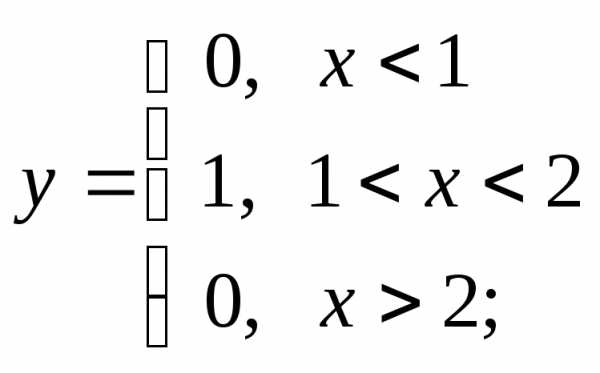 б)
б)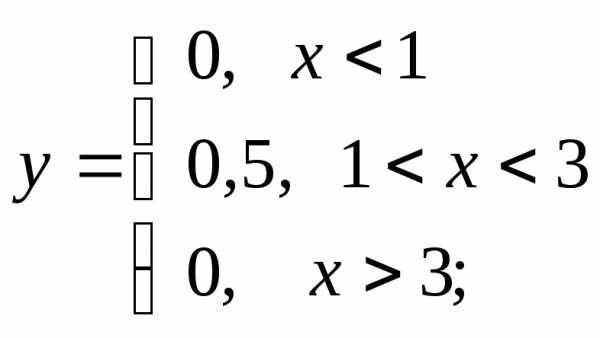 в)
в)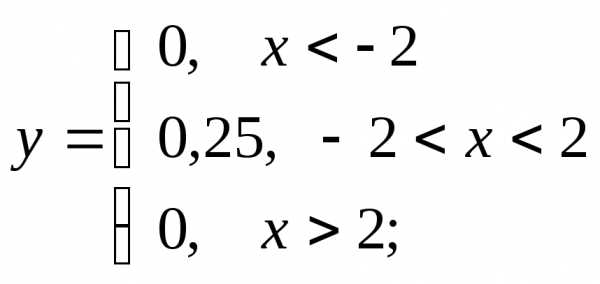
г) 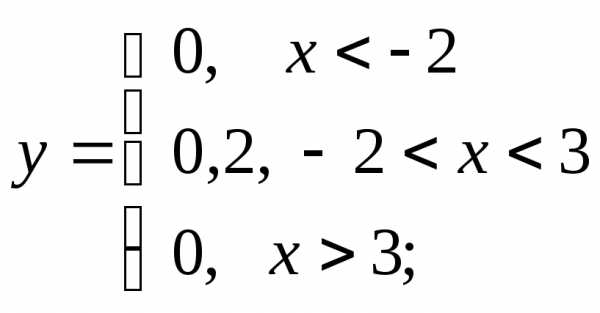 д)
д)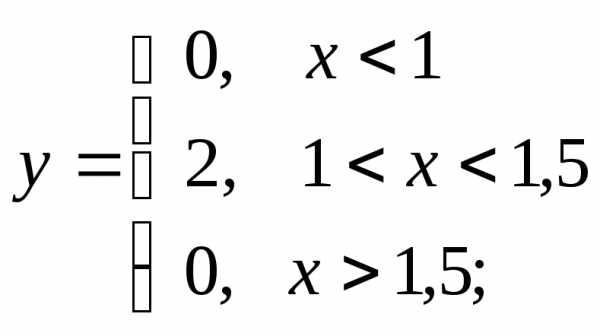 е)
е)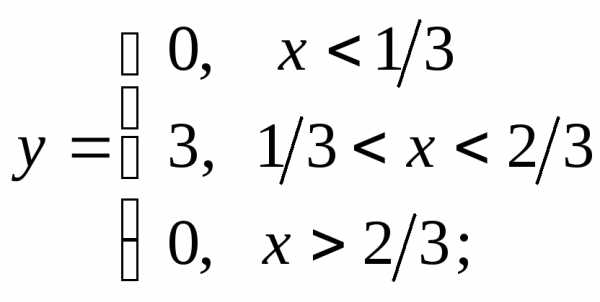
2) а)  б)
б)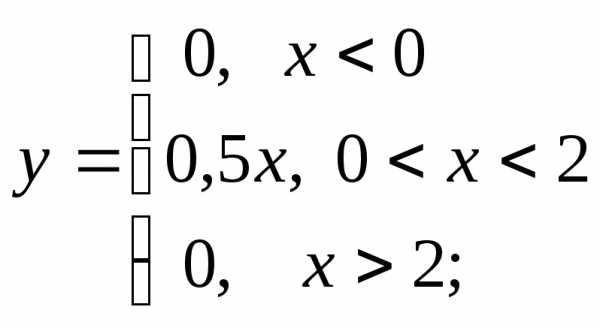 в)
в)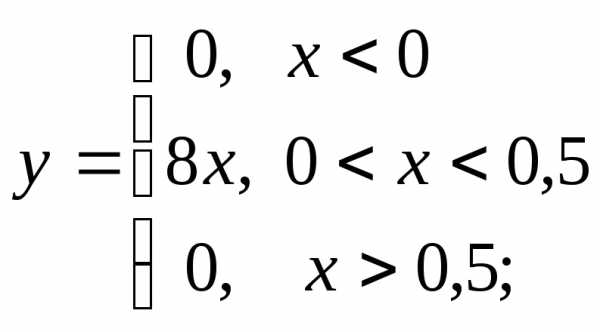
г) 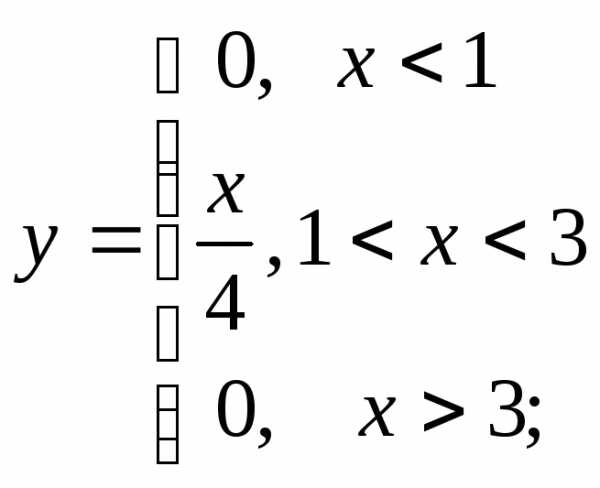 д)
д)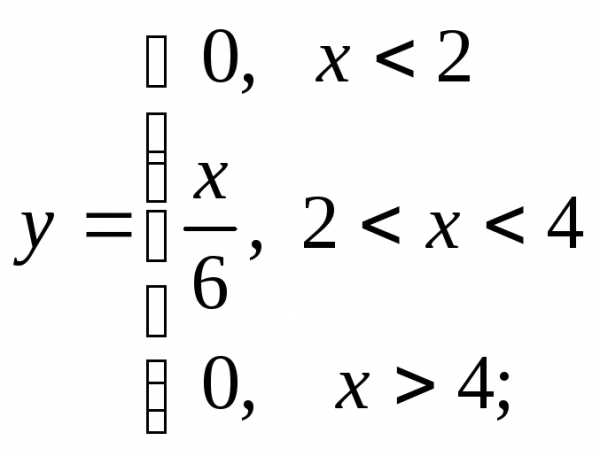 е)
е)
3) а) 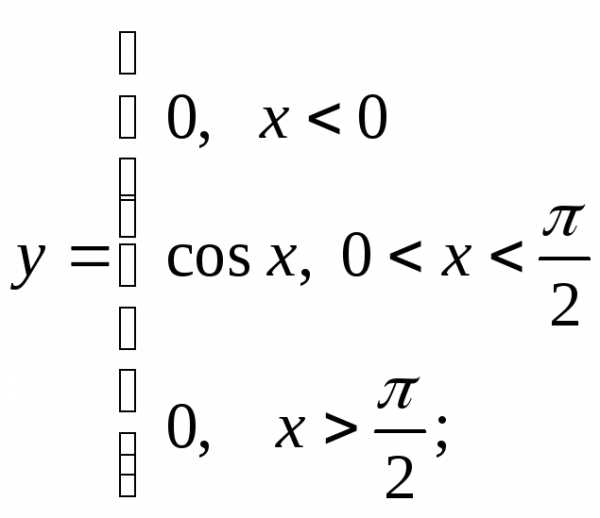 б)
б)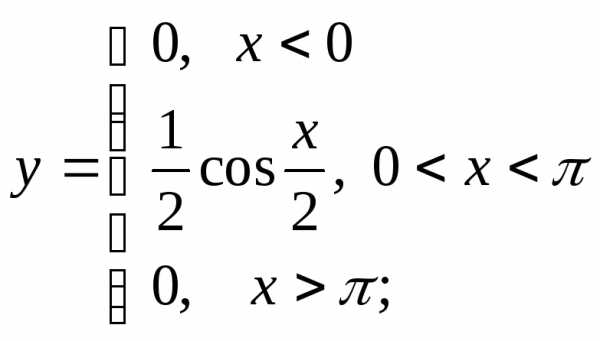 в)
в)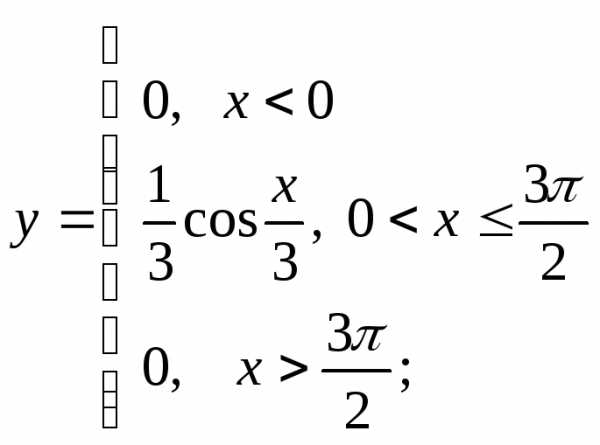
г)  д)
д)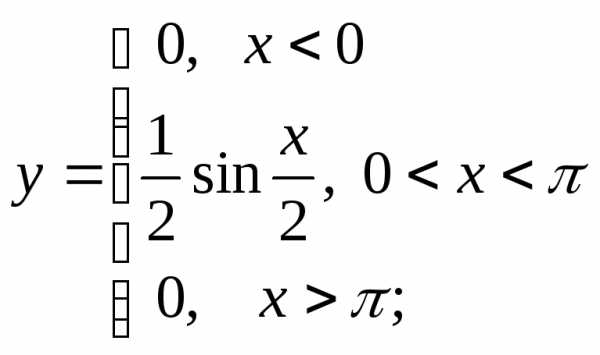 е)
е)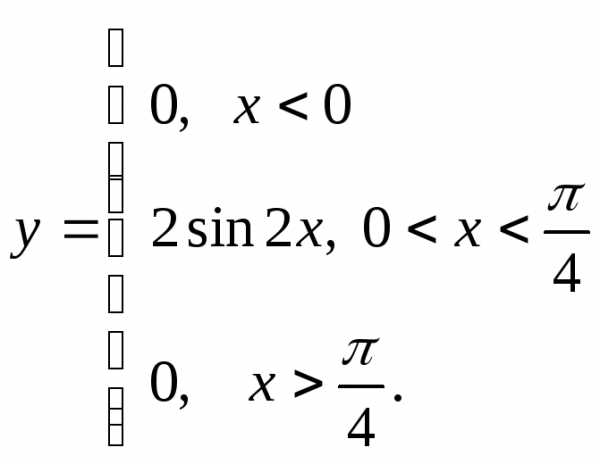
Пример 8. Пусть 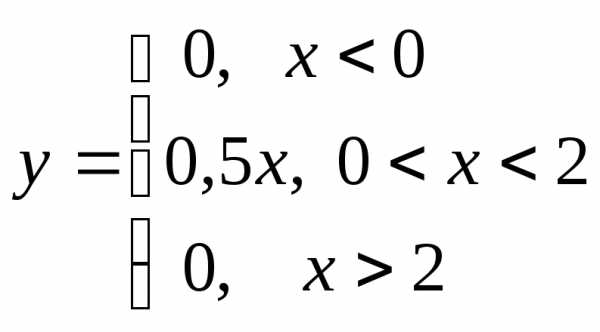 .
На участке
.
На участке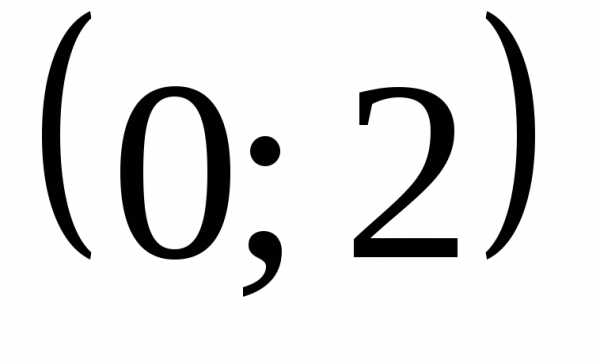 строим прямую
строим прямую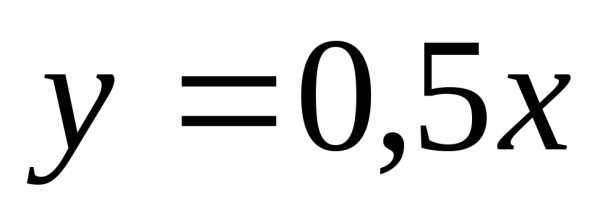 ,
для чего находими.
Соединяем точки
,
для чего находими.
Соединяем точки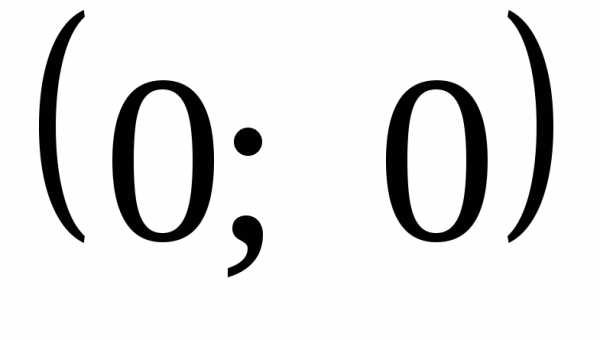 и
и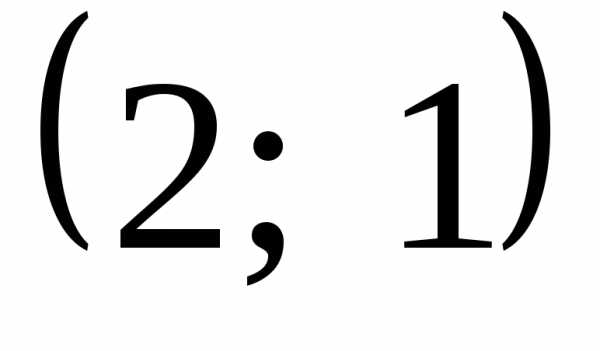 отрезком. Сами точки не включаем,
поскольку при
отрезком. Сами точки не включаем,
поскольку при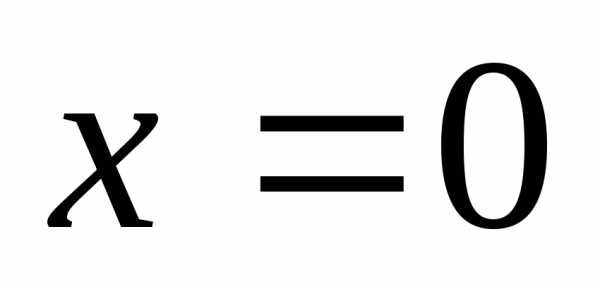 и
и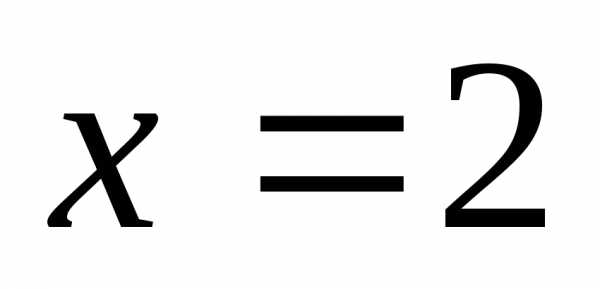 функция по условию не определена.
функция по условию не определена.
На участке  и
и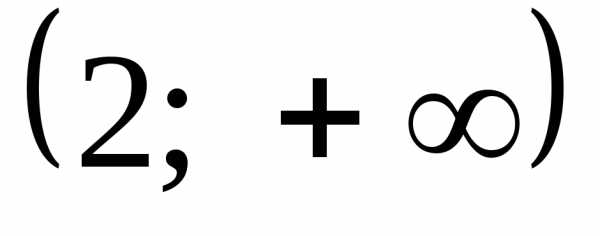 обводим осьOX
(на ней
обводим осьOX
(на ней  ),
однако точки
),
однако точки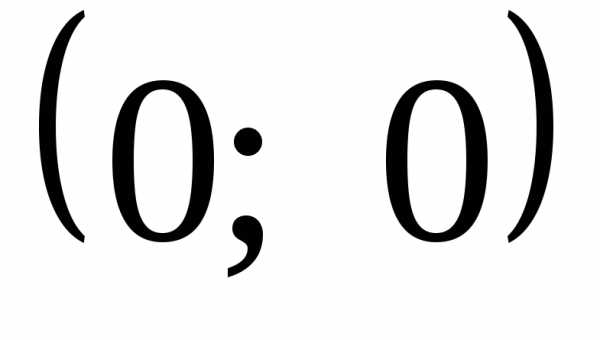 и
и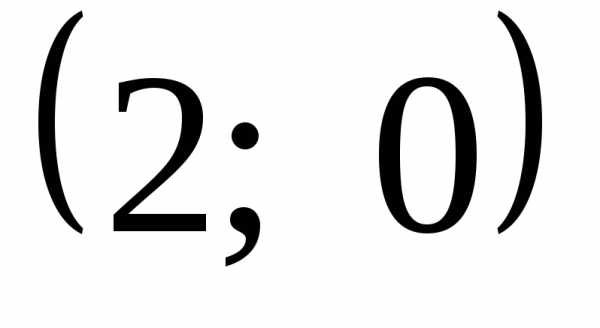 «выколоты». В точке
«выколоты». В точке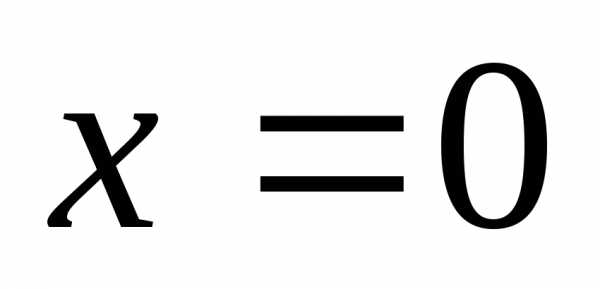 получаем устранимый разрыв, а в точке
получаем устранимый разрыв, а в точке – разрыв 1-го рода («скачок»).
– разрыв 1-го рода («скачок»).
НФ3. Постройте графики функций и убедитесь в их непрерывности:
1) а) 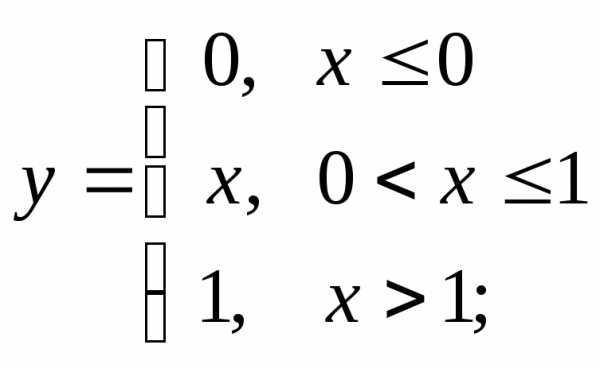 б)
б)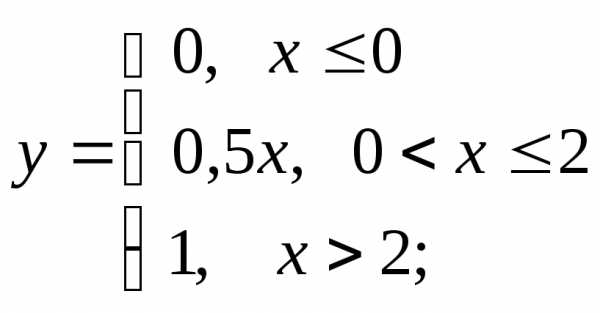 в)
в)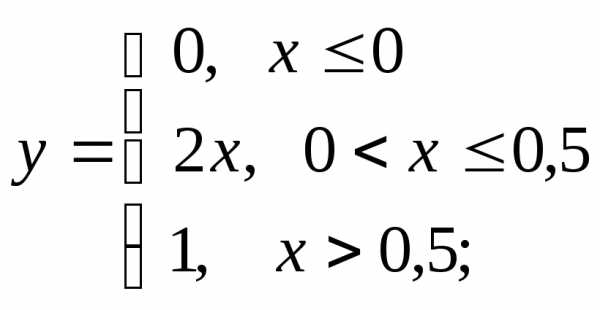
г) 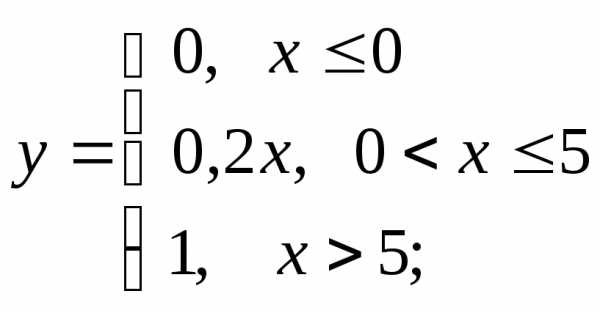 д)
д)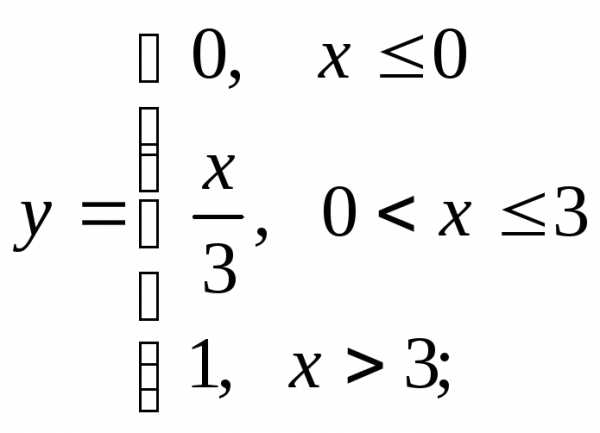 е)
е)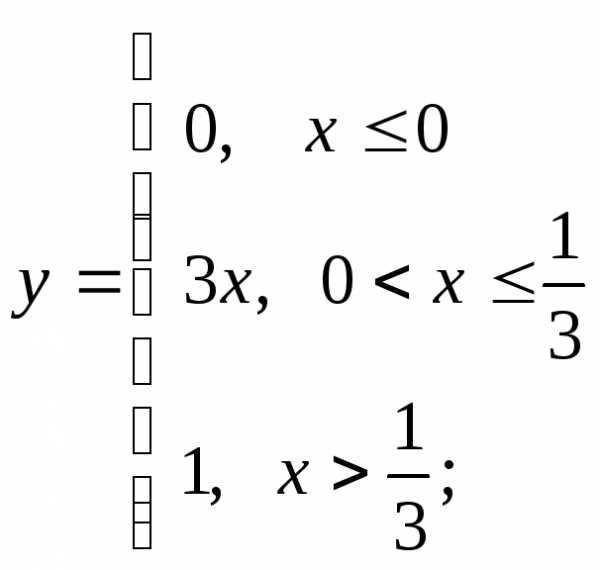
2) а) 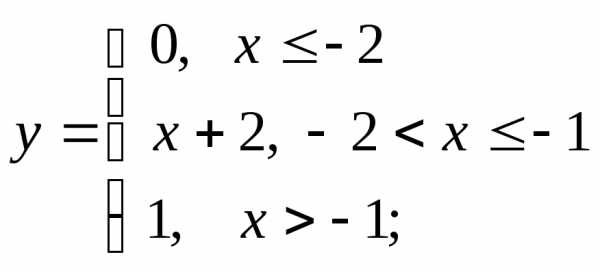 б)в)
б)в)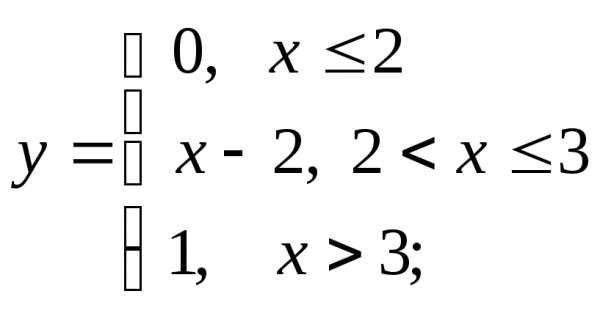
г) 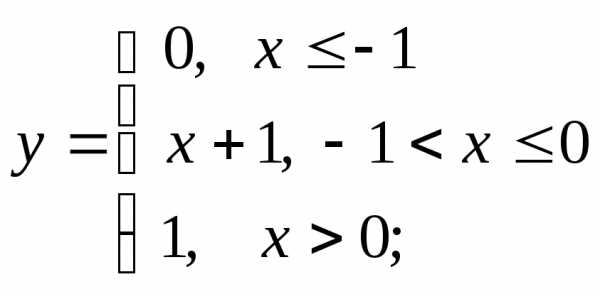 д)
д)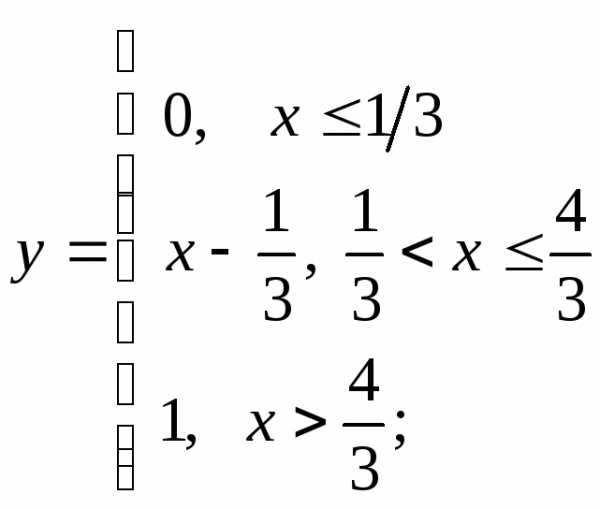 е)
е)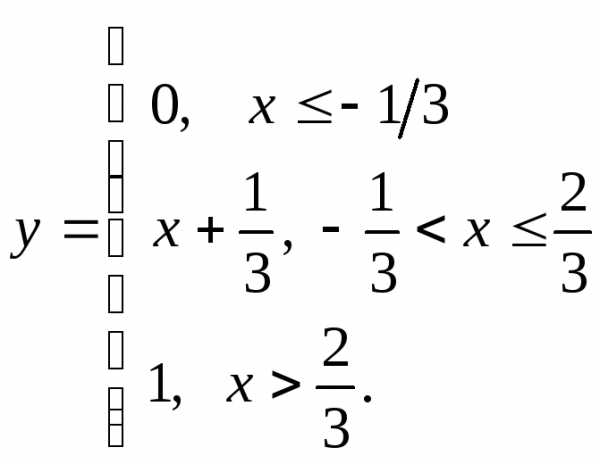
НФ4. Убедитесь в непрерывности функций и постройте их графики:
1) а) 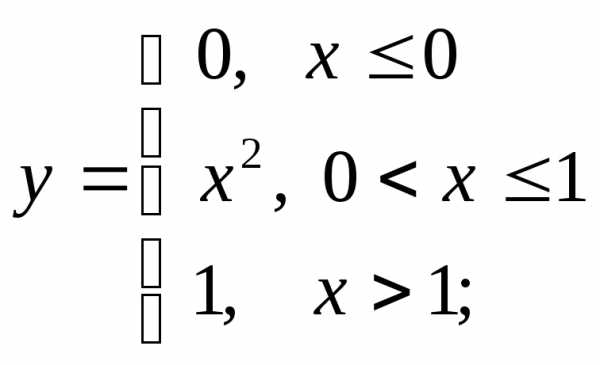 б)
б)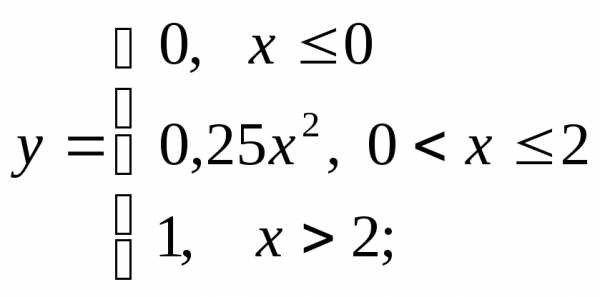 в)
в)
2 а)
б) в)
в)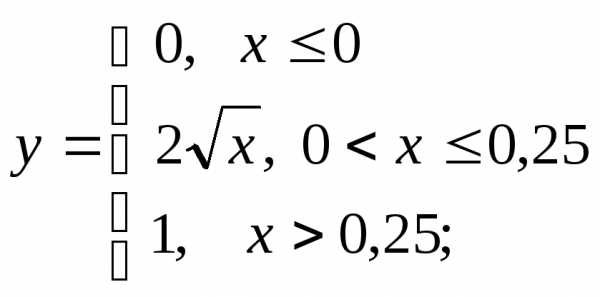
3) а) 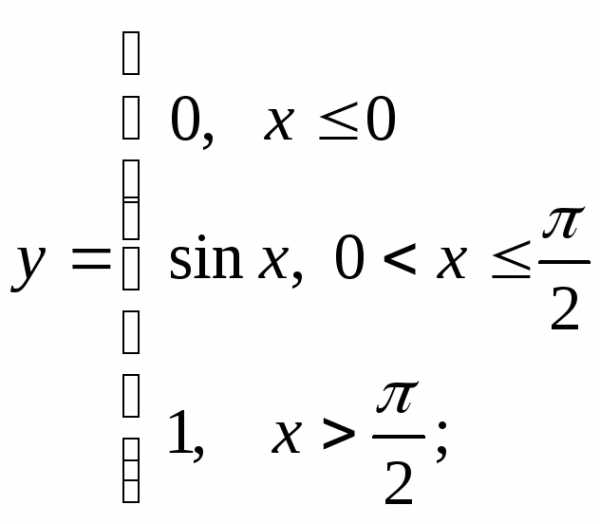 б)
б) в)
в)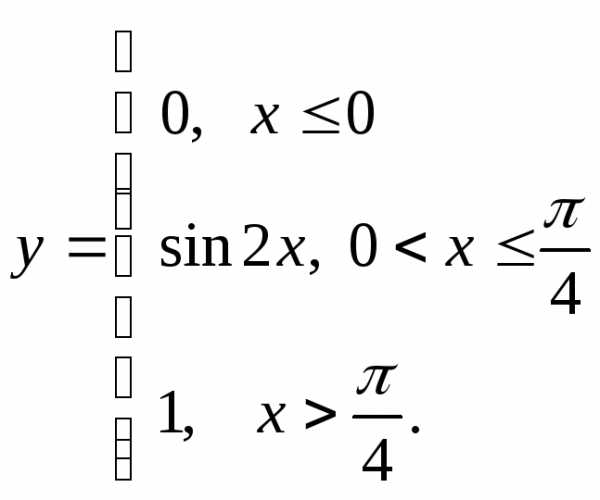
НФ5. Постройте графики функций. Обратите внимание на непрерывность:
1) а) 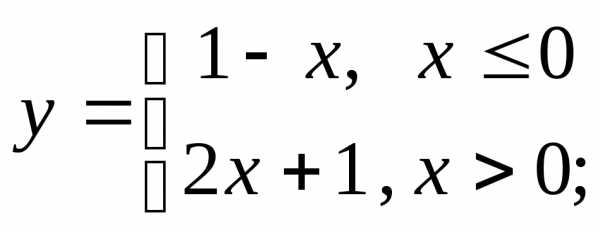 б)
б)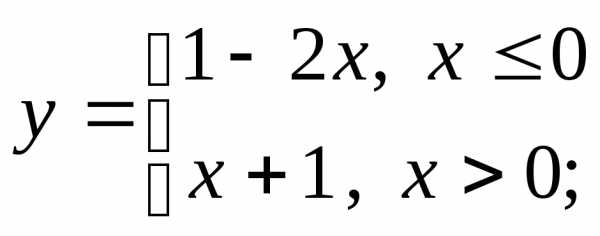 в)
в)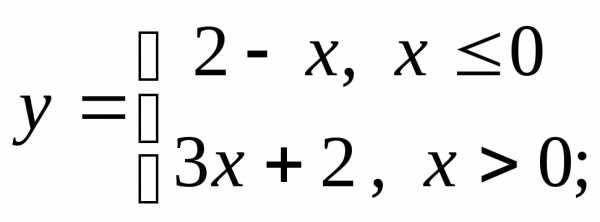
г) 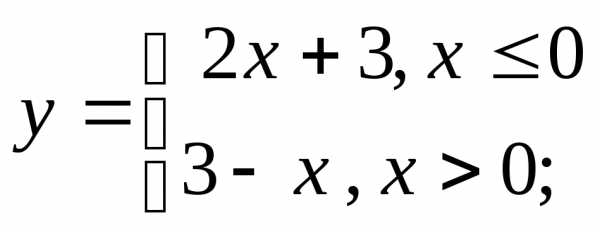 д)
д)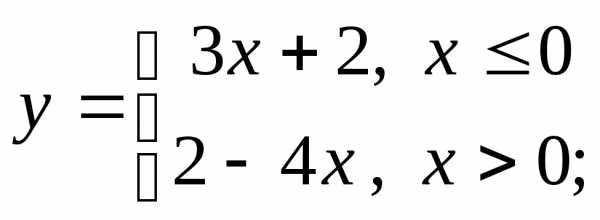 е)
е)
2) а)  б)
б)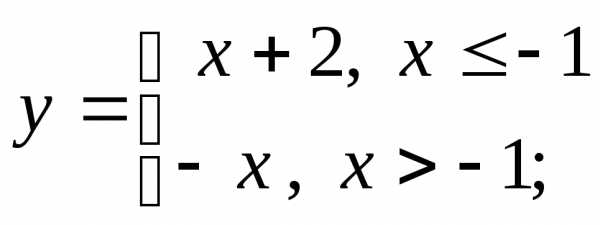 в)
в)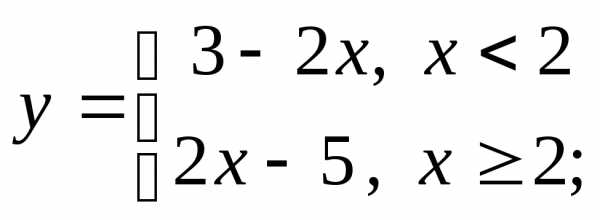
г)
д)е)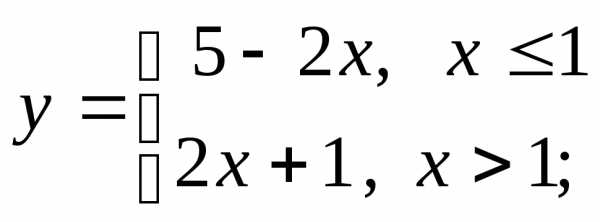
3) а) 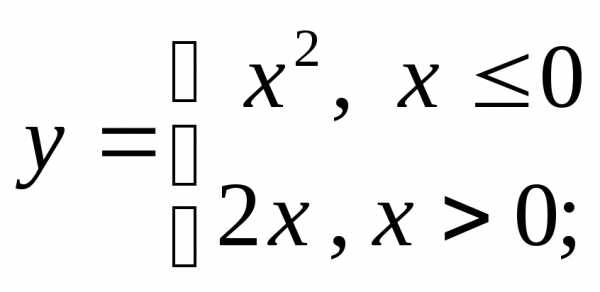 б)
б)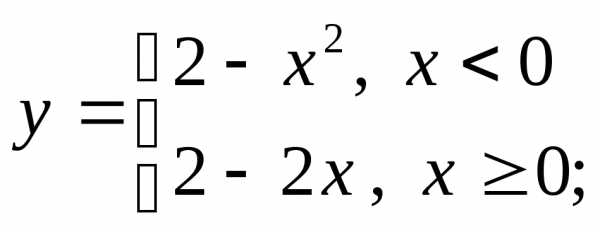 в)
в)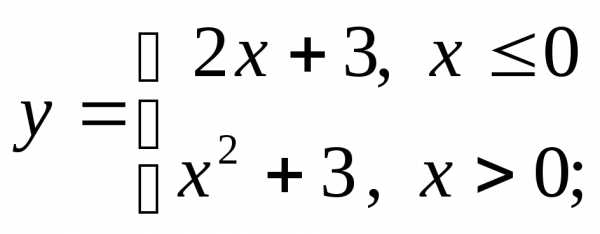
г) 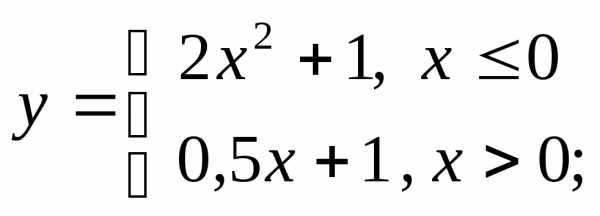 д)
д)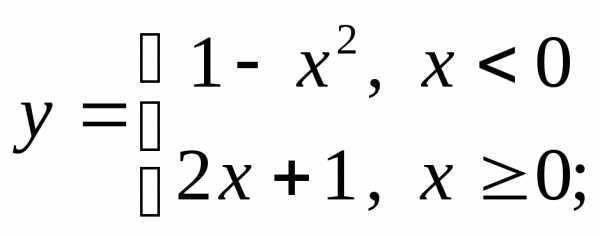 е)
е)
4) а) 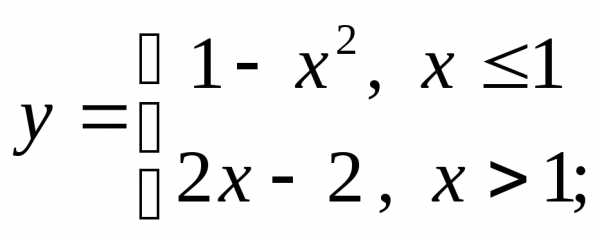 б)в)
б)в)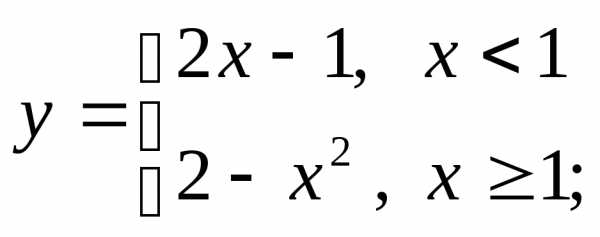
г) 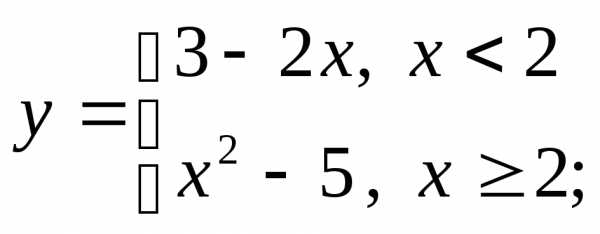 д)
д)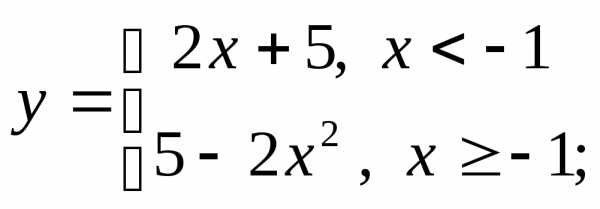 е)
е)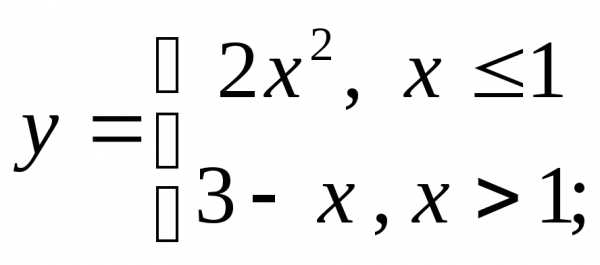
5) а) 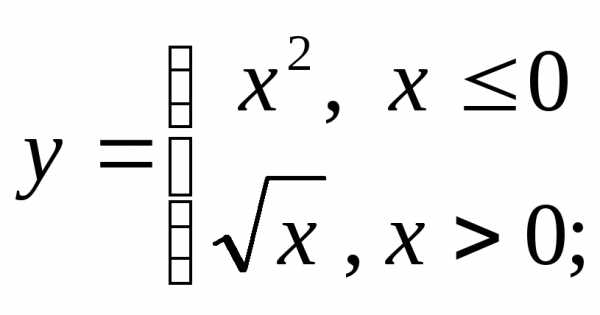 б)
б)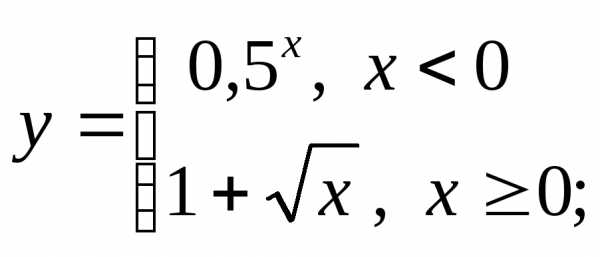 в)
в)
г) 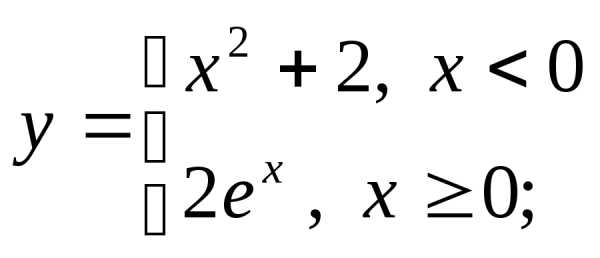 д)
д)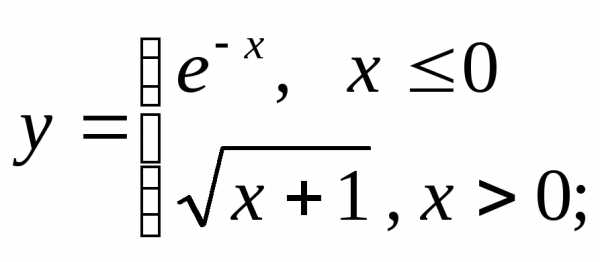 е)
е)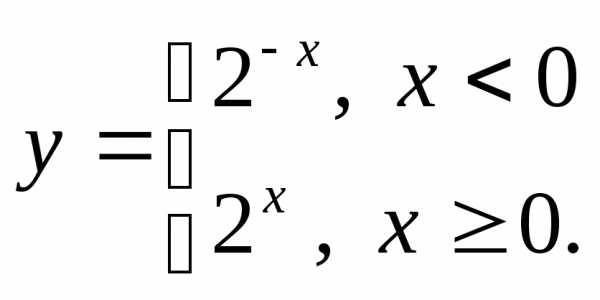
НФ6. Постройте графики разрывных функций. Обратите внимание на значение функции в той точке, где функция переопределяется (и существует ли оно):
1) а)  б)
б)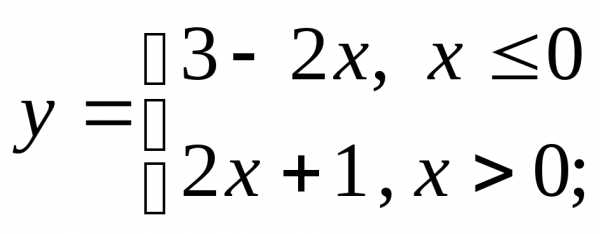 в)
в)
г) 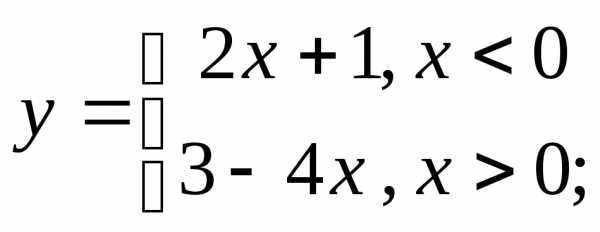 д)
д)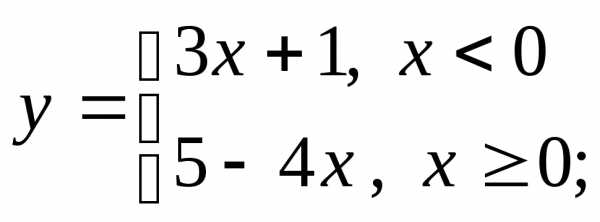 е)
е)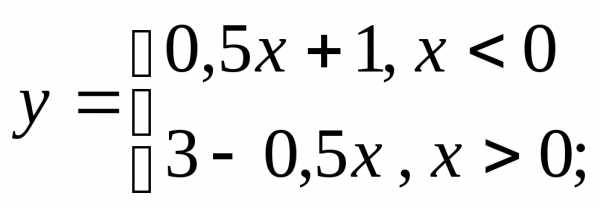
2) а) 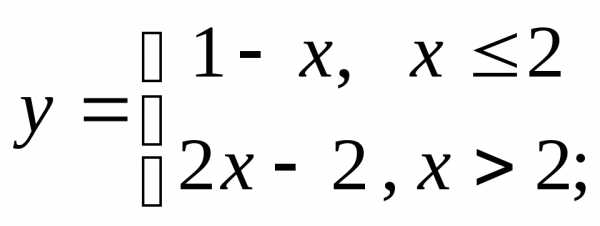 б)
б)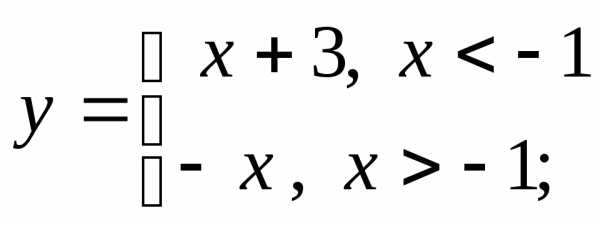 в)
в)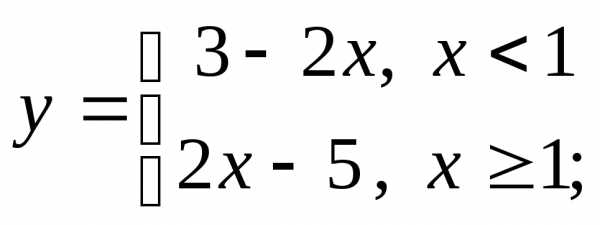
г) 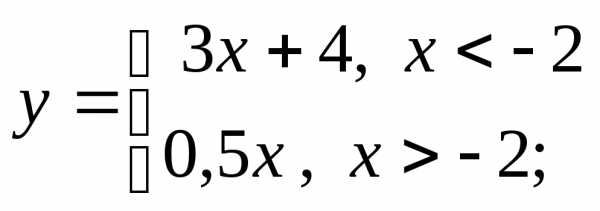 д)
д)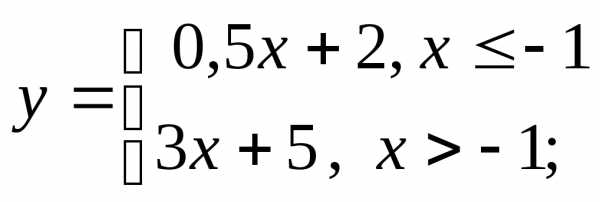 е)
е)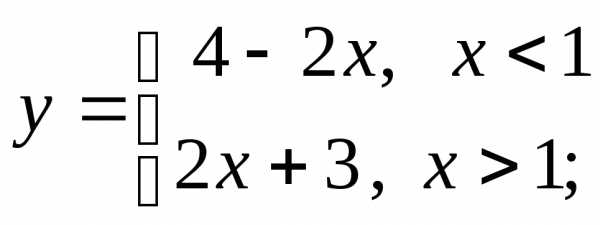
3) а)  б)
б)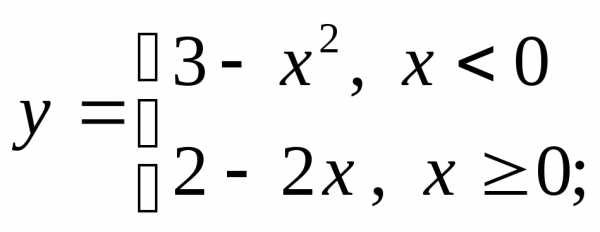 в)
в)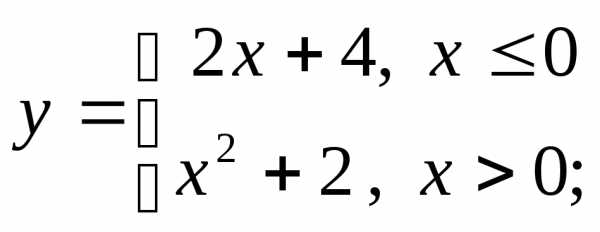
г) 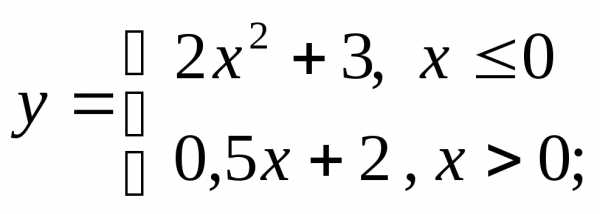 д)
д)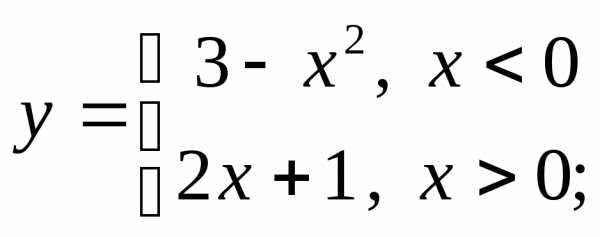 е)
е)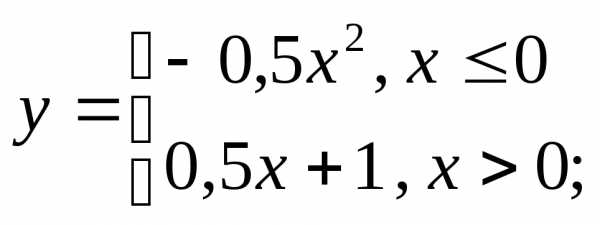
4) а) 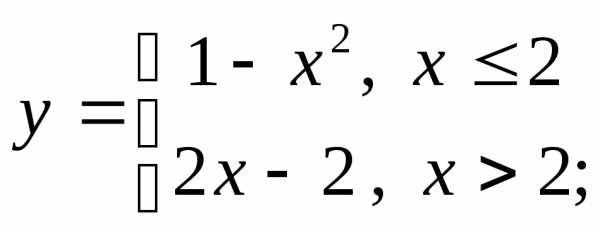 б)
б)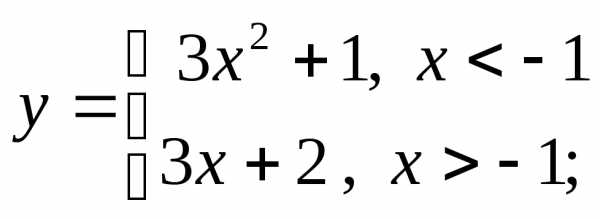 в)
в)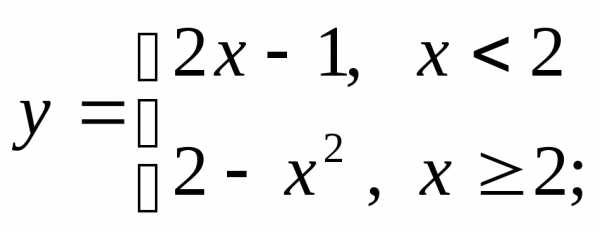
г) 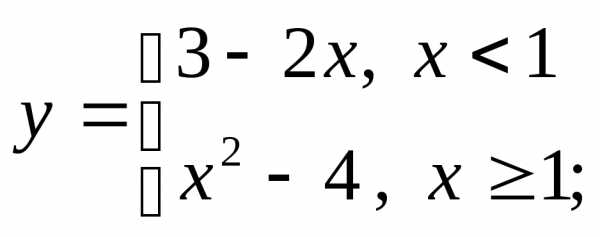 д)
д) е)
е)
5) а) 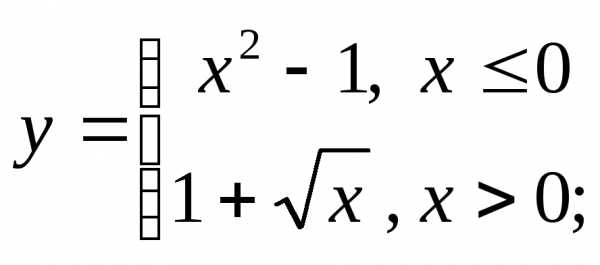 б)
б)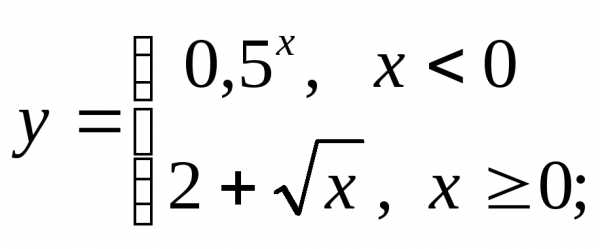 в)
в)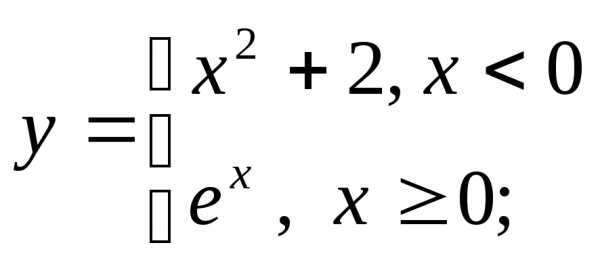
г) 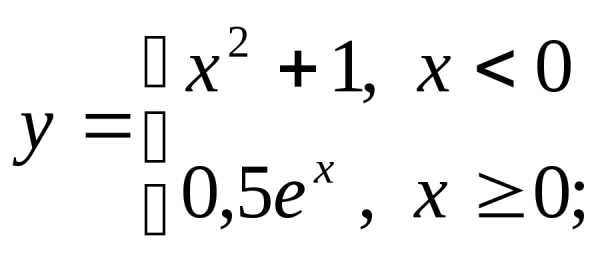 д)
д)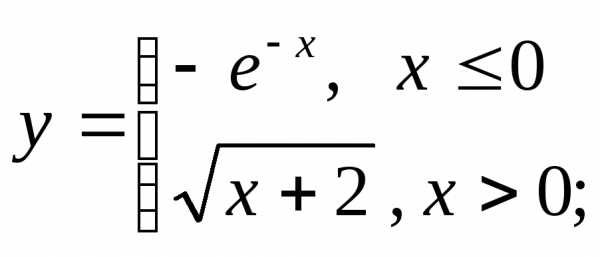 е)
е)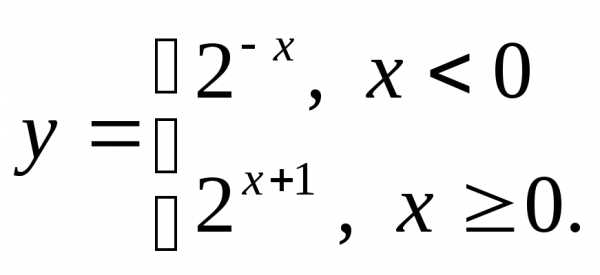
НФ7. То же задание, что и в НФ6:
1) а) 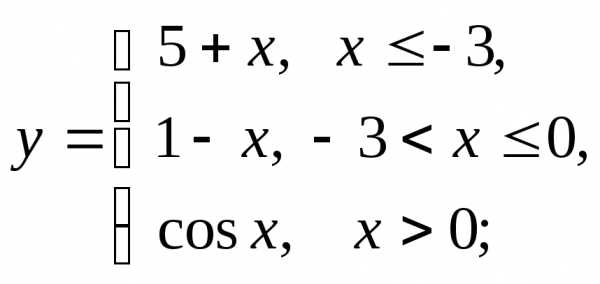 б)
б)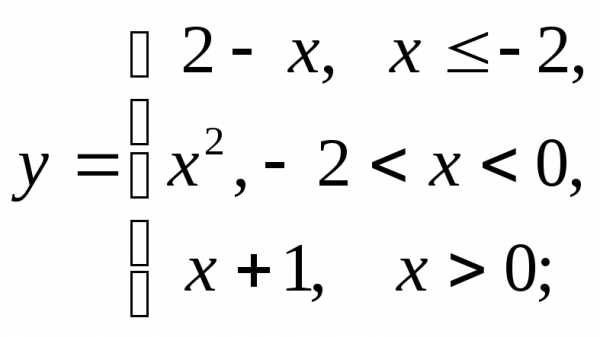 в)
в)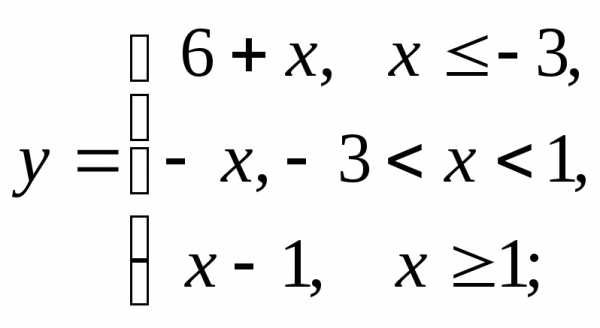
г) 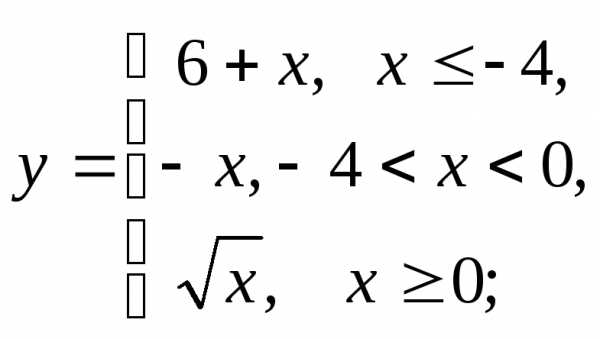 д)
д)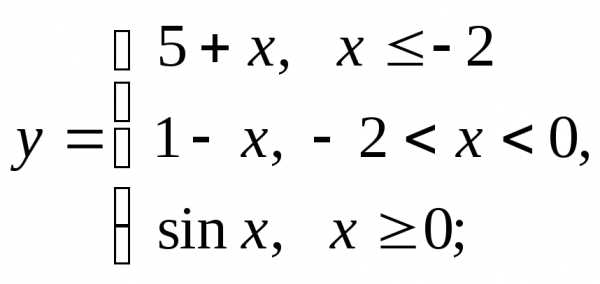 е)
е)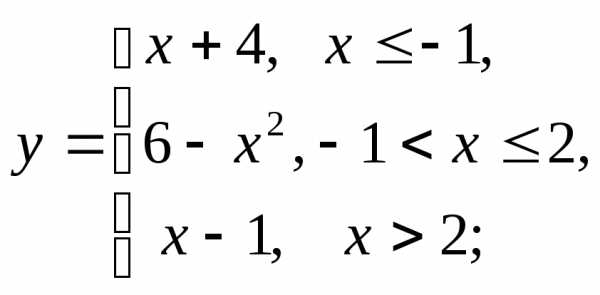
2) а) 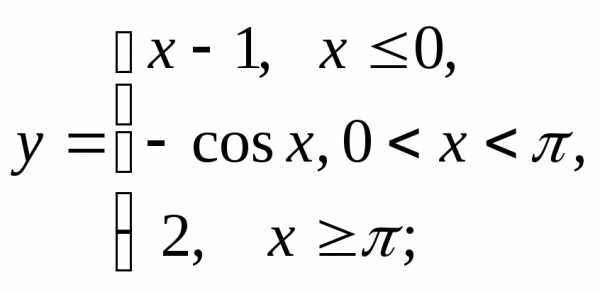 б)
б)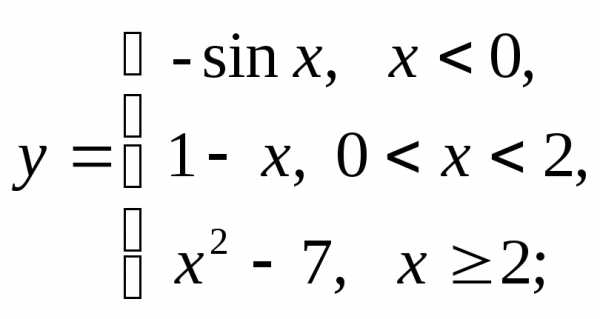 в)
в)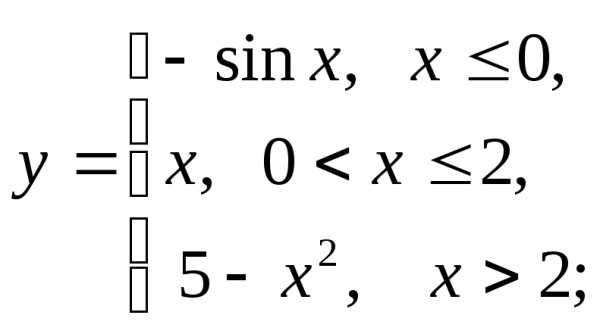
г)  д)
д)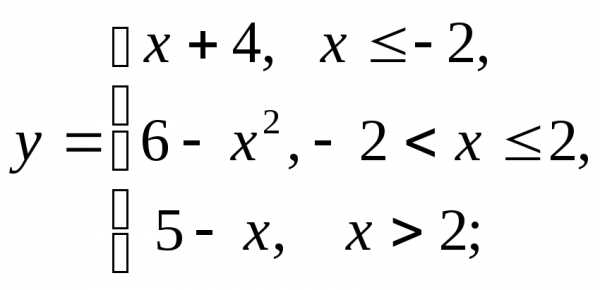 е)
е)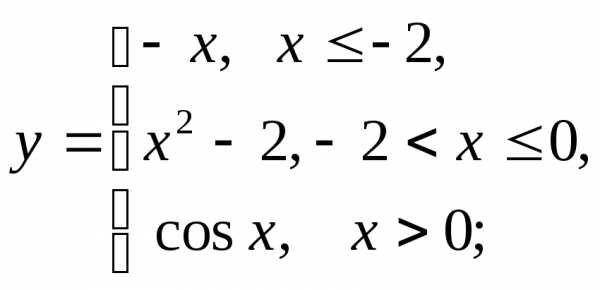
3) а) 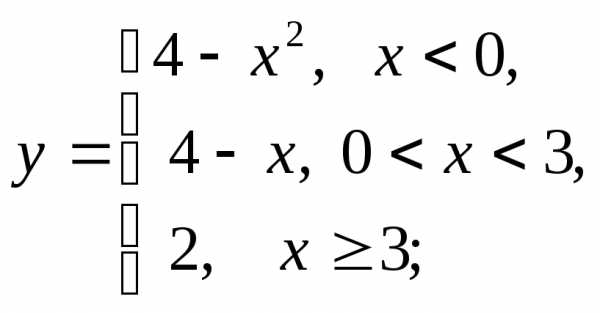 б)
б) в)
в)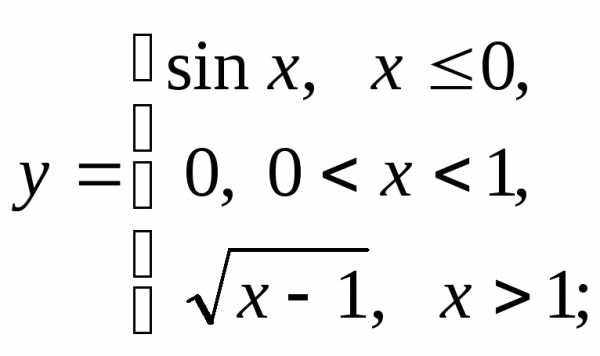
г) 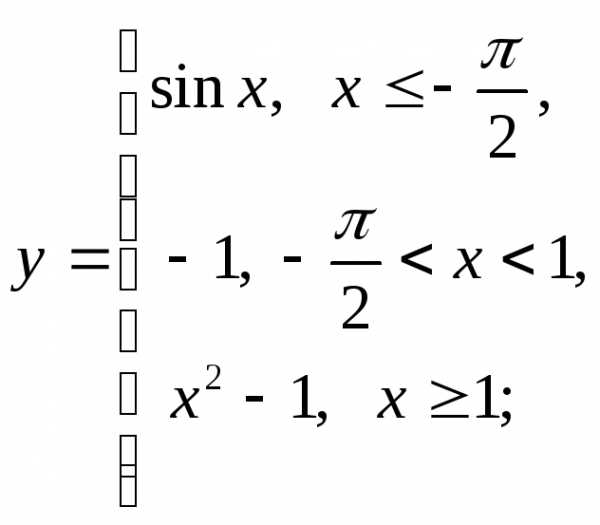 д)
д)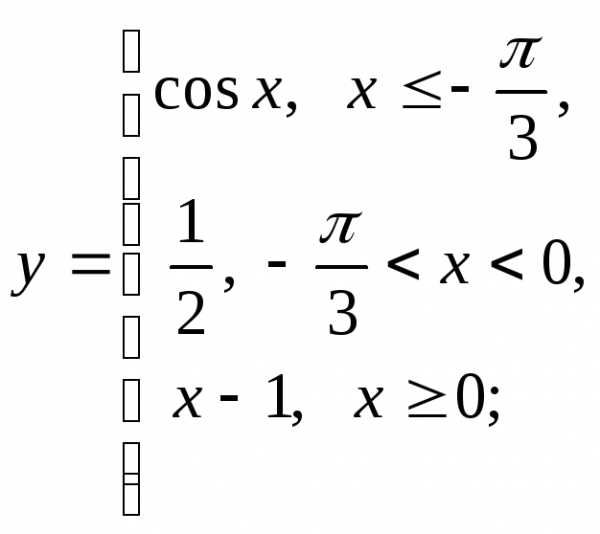 е)
е)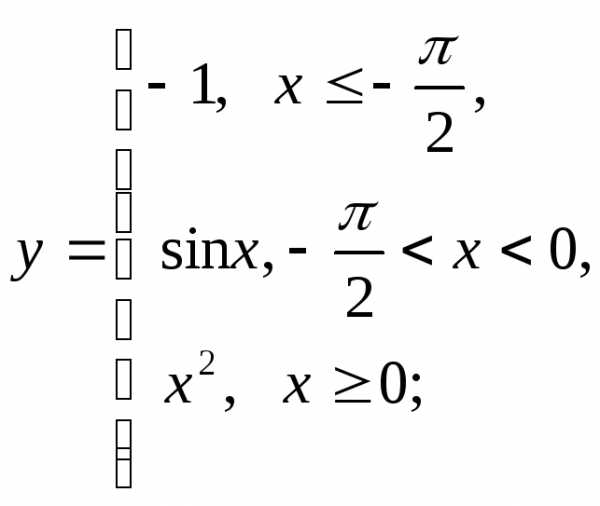
4) а) 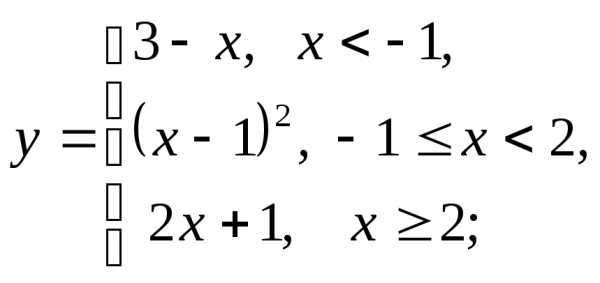 б)
б)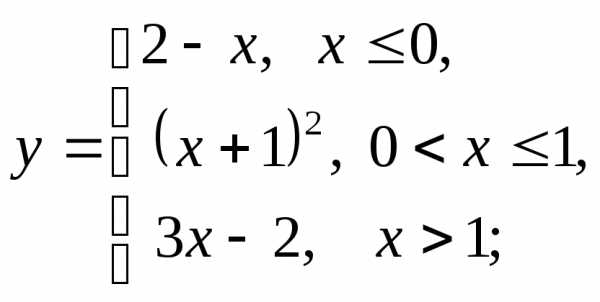 в)
в)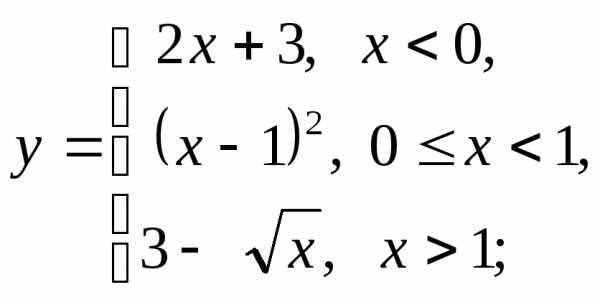
г) 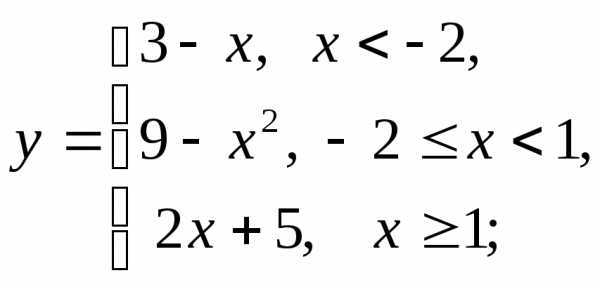 д)
д)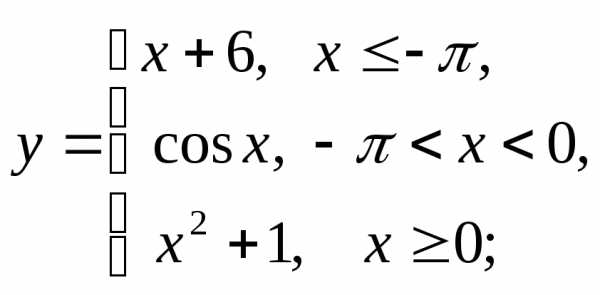 е)
е)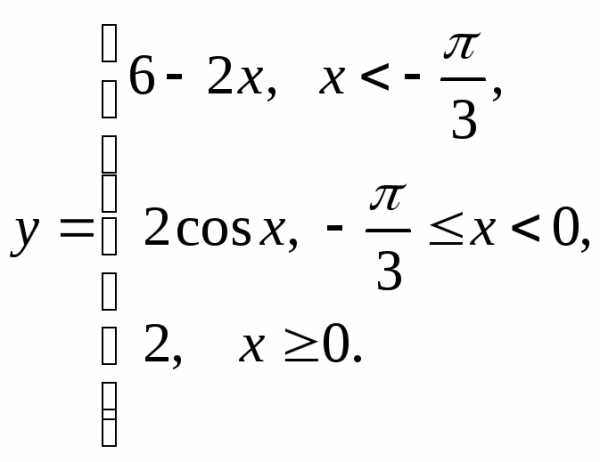
studfiles.net
Непрерывность функций
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Непрерывность функций одной переменной»
студентами бухгалтерского факультета заочной формы получения
образования (НИСПО)
Горки, 2013
Непрерывность функций одной переменной
Односторонние пределы
Пусть
функция 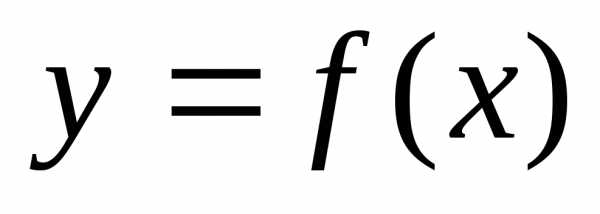 определена на множестве
определена на множестве 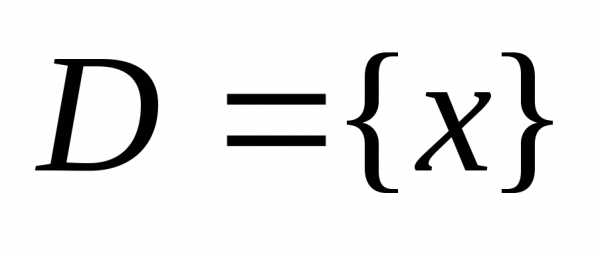 .
Введём понятие односторонних пределов
функции при
.
Введём понятие односторонних пределов
функции при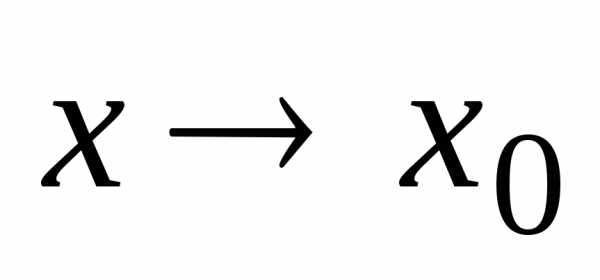 .
Будем рассматривать такие значениях,
что
.
Будем рассматривать такие значениях,
что 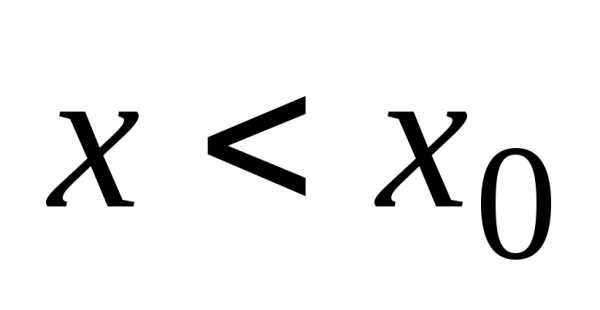 . Это означает, что
. Это означает, что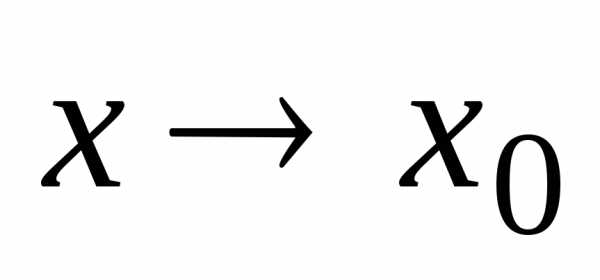 ,
оставаясь всё время слева от
,
оставаясь всё время слева от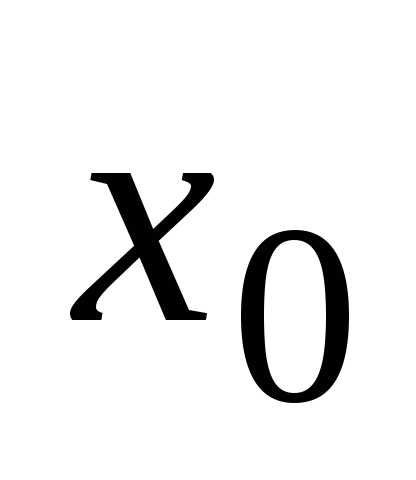 .
Если при этом существует предел функции
.
Если при этом существует предел функции 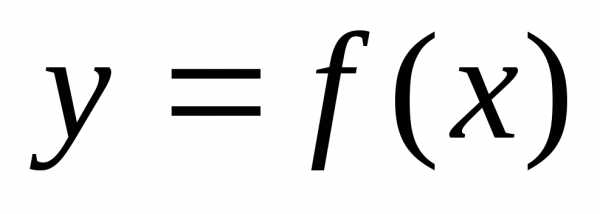 при
при  то он называетсялевым
пределом этой функции в точке
то он называетсялевым
пределом этой функции в точке 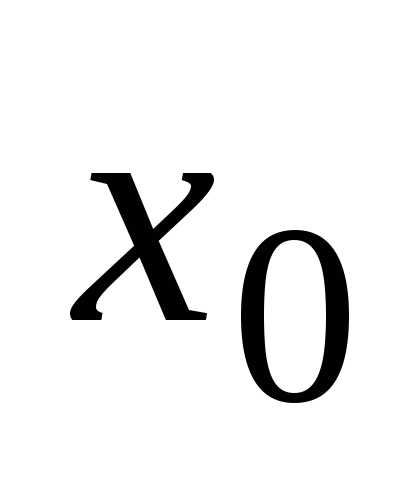 ( или при
( или при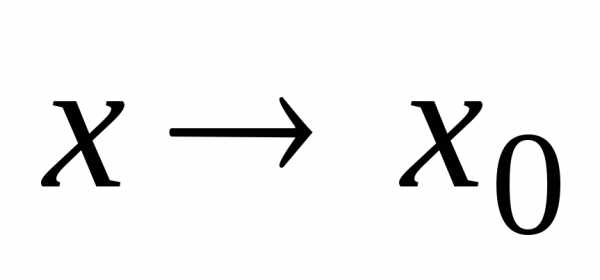 )
и обозначается
)
и обозначается
.
Пусть
теперь 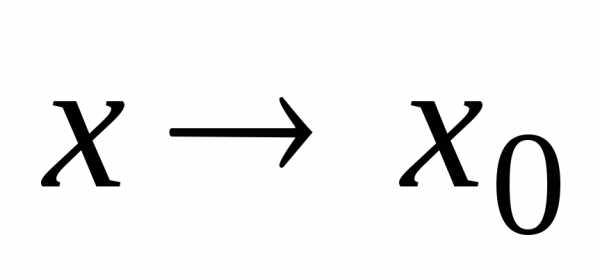 ,
оставаясь всё время справа от
,
оставаясь всё время справа от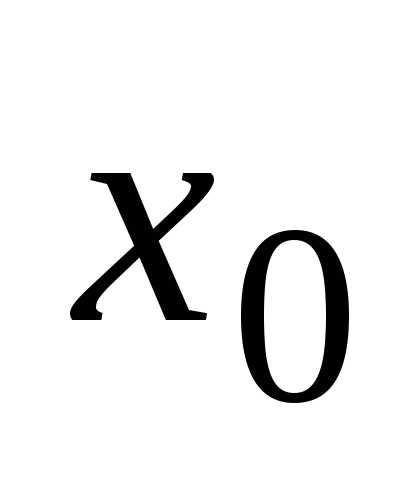 ,
т.е. оставаясь больше
,
т.е. оставаясь больше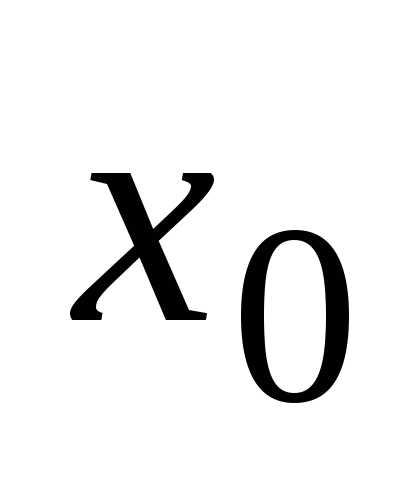 .
Если при этом существует предел функции
.
Если при этом существует предел функции 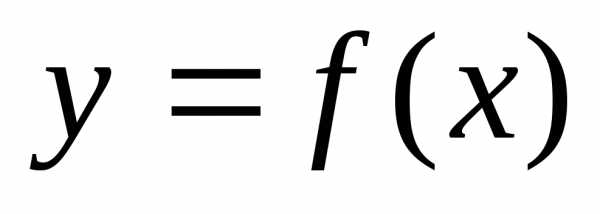 ,
то он называется правым
пределом этой функции в точке
,
то он называется правым
пределом этой функции в точке 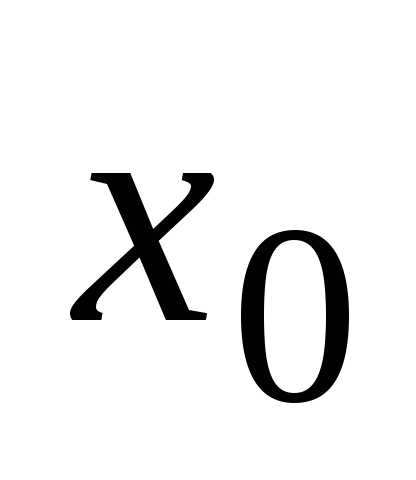 и обозначается
и обозначается
.
Левый и правый пределы называются односторонними пределами функции в точке.
Если существуют односторонние пределы функции в точке и они равны между собой, то функция имеет тот же предел в этой точке:
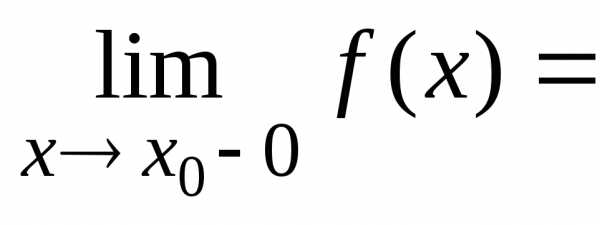
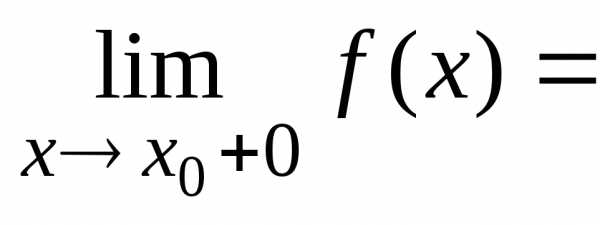
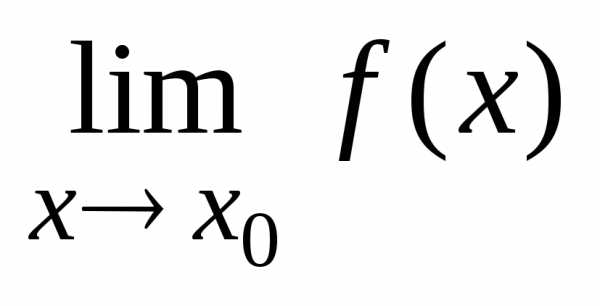 .
.
Если односторонние пределы функции в точке существуют, но не равны между собой, то предел функции в этой точке не существует.
Непрерывность функции в точке
Пусть
функция 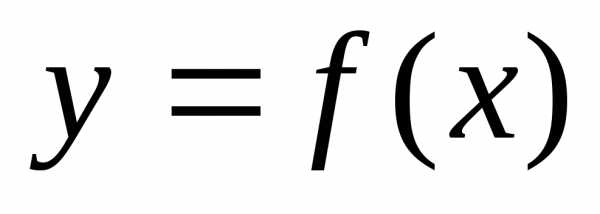 определена
на некотором множестве D.
Пусть независимая переменная х переходит от одного своего (начального)
значения
определена
на некотором множестве D.
Пусть независимая переменная х переходит от одного своего (начального)
значения 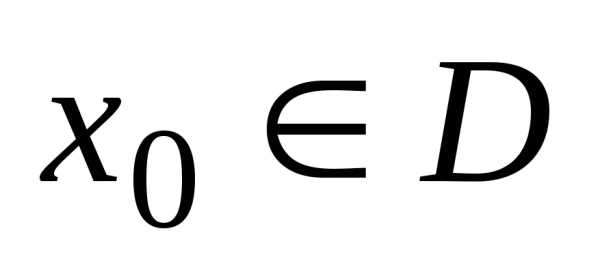 к другому (конечному) значению
к другому (конечному) значению . Разность
конечного и начального значений
называется приращением величины х и обозначается
.
Приращение может быть как положительным,
так и отрицательным. В первом случае
величинах при переходе от
. Разность
конечного и начального значений
называется приращением величины х и обозначается
.
Приращение может быть как положительным,
так и отрицательным. В первом случае
величинах при переходе от 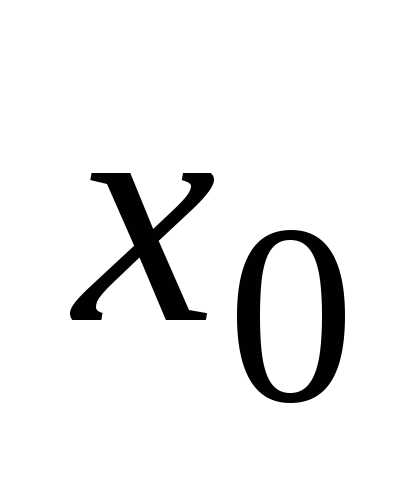 кх увеличивается, а во втором случае —
уменьшается.
кх увеличивается, а во втором случае —
уменьшается.
Если
независимая переменная х получает некоторое приращение
,
то функция  получает приращение
.
Так как,
то.
получает приращение
.
Так как,
то.
Приращением
функции 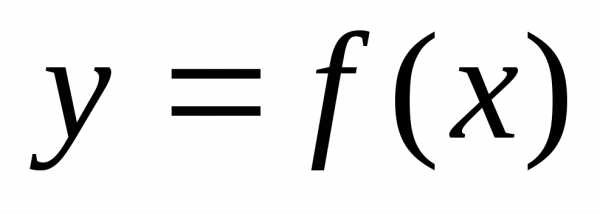 в
точке
в
точке 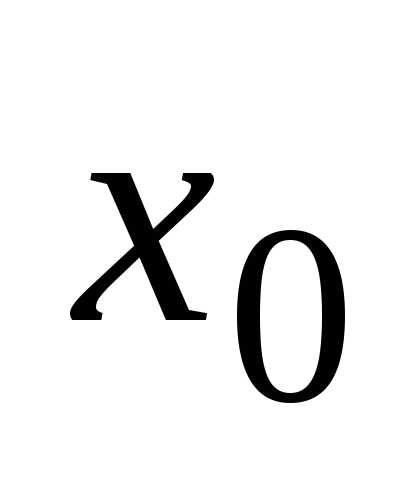 называется разность,
где
называется разность,
где – приращение независимой переменной.
– приращение независимой переменной.
Можно дать несколько определений непрерывности функции в точке.
Функция
 называется непрерывной в
точке
называется непрерывной в
точке  ,
если она определена в окрестности точки
,
если она определена в окрестности точки и
и т.е.
т.е. при
при .
Это означает, что функция непрерывна
в токе
.
Это означает, что функция непрерывна
в токе ,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.Функция
 называется непрерывной в
точке
называется непрерывной в
точке  ,
если предел функции при
,
если предел функции при равен значению функции в этой точке:.
равен значению функции в этой точке:.
Функция
 называется непрерывной
в точке
называется непрерывной
в точке  ,
если существуют левый и правый пределы
этой функции при
,
если существуют левый и правый пределы
этой функции при и если эти пределы равны между собой
и равны значению функции в этой точке:
и если эти пределы равны между собой
и равны значению функции в этой точке:
.
Функция
называется непрерывной
в интервале,
если она непрерывна в каждой точке этого
интервала. Геометрически непрерывность
функции 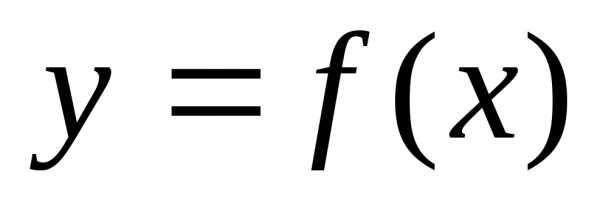 в замкнутом интервале означает, что
график функции представляет собой
сплошную линию без разрывов.
в замкнутом интервале означает, что
график функции представляет собой
сплошную линию без разрывов.
Непрерывные на отрезке функции обладают важными свойствами, которые выражаются следующими утверждениями.
 Если
функция
Если
функция 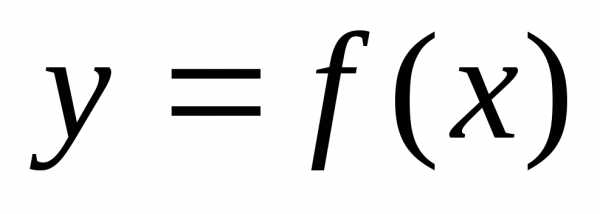 непрерывна
на отрезке [a, b],
то она ограничена на этом отрезке.
непрерывна
на отрезке [a, b],
то она ограничена на этом отрезке.
 Если
функция
Если
функция 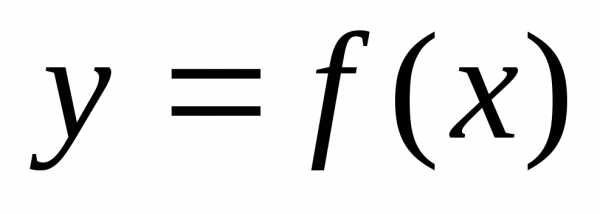 непрерывна
на отрезке [a, b],
то она достигает на этом отрезке своего
наименьшего и наибольшего значений.
непрерывна
на отрезке [a, b],
то она достигает на этом отрезке своего
наименьшего и наибольшего значений.
 Если
функция
Если
функция 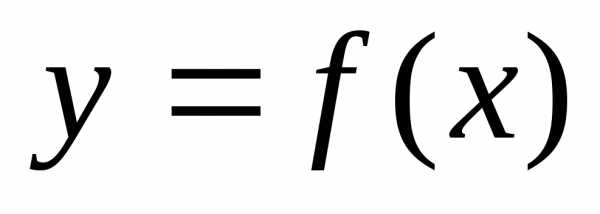 непрерывна
на отрезке [a,b]
и
,
то каким бы ни было числоС,
заключённое между числами А и В,
найдётся точка
непрерывна
на отрезке [a,b]
и
,
то каким бы ни было числоС,
заключённое между числами А и В,
найдётся точка 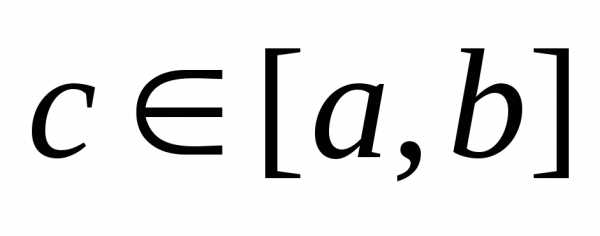 ,
что
,
что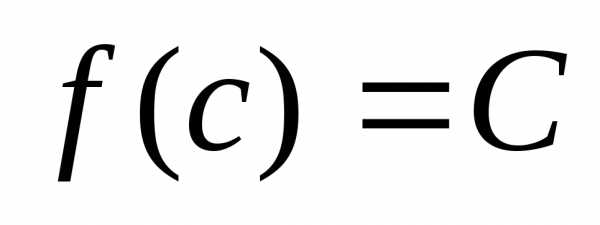 .
.
Из
этого утверждения следует, что если
функция 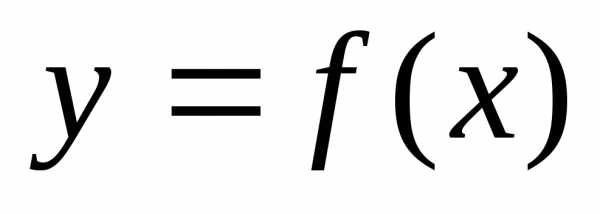 непрерывна на [a, b]
и на концах этого отрезка принимает
значения разных знаков, то на этом
отрезке существует хотя бы одна точка c,
в которой функция обращается в нуль.
непрерывна на [a, b]
и на концах этого отрезка принимает
значения разных знаков, то на этом
отрезке существует хотя бы одна точка c,
в которой функция обращается в нуль.
Справедливо следующее утверждение: если над непрерывными функциями производить арифметические действия, то в результате получается непрерывная функция.
Пример 1. Исследовать на непрерывность функцию
в
точке 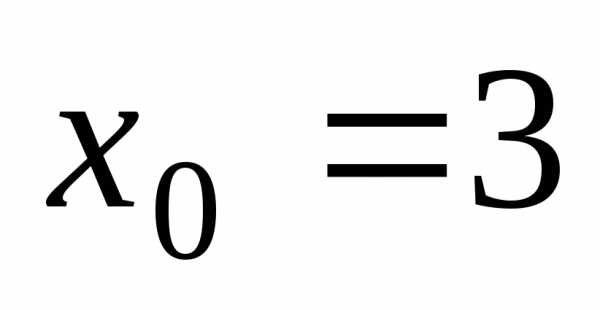 .
.
Решение.
Значение функции при 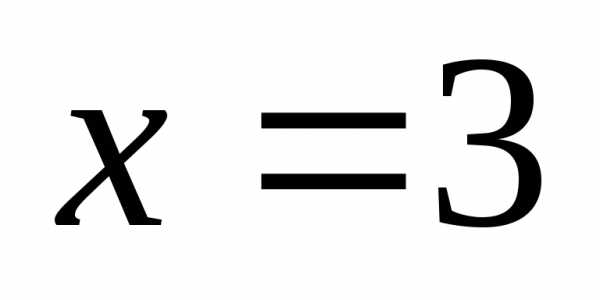 есть.
Вычислим односторонние пределы функции
в точке
есть.
Вычислим односторонние пределы функции
в точке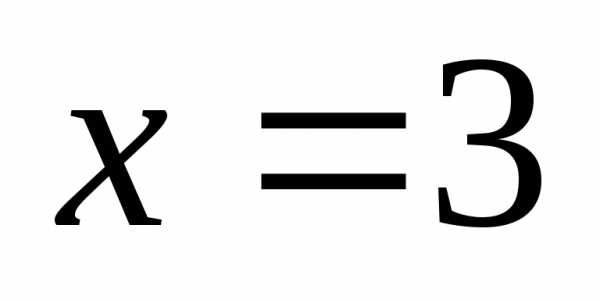 :
:
,
.
Так
как односторонние пределы при 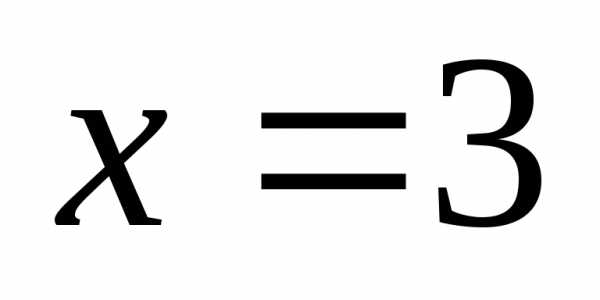 равны между собой и равны значению
функции в этой точке, то данная функция
непрерывна в точке
равны между собой и равны значению
функции в этой точке, то данная функция
непрерывна в точке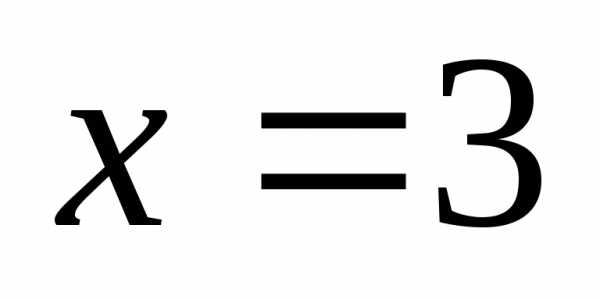 .
.
3. Непрерывность элементарных функций
Рассмотрим
функцию  .
Эта постоянная функция непрерывна в
любой точке
.
Эта постоянная функция непрерывна в
любой точке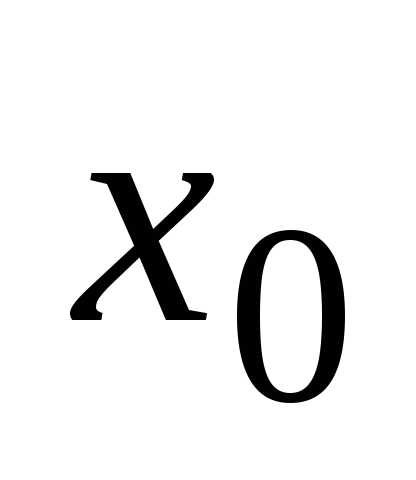 ,
так как.
,
так как.
Функция 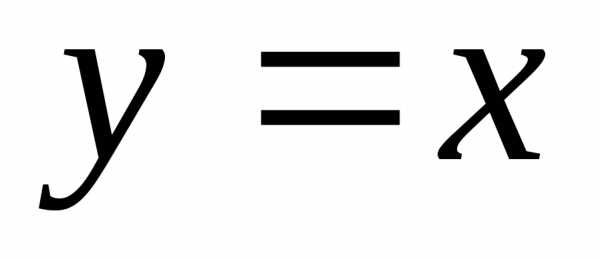 также непрерывна в каждой точке
также непрерывна в каждой точке  ,
так как
,
так как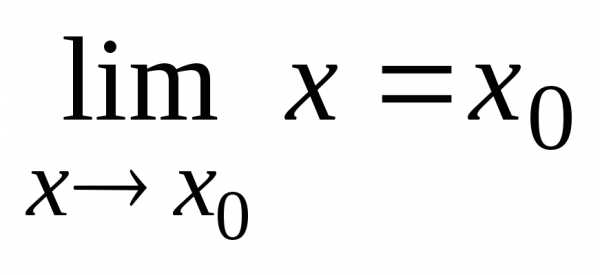 .
Так как,
то на основании приведённого утверждения
об арифметических операциях над
непрерывными функциями
.
Так как,
то на основании приведённого утверждения
об арифметических операциях над
непрерывными функциями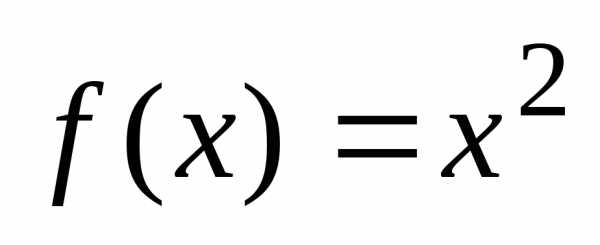 будет непрерывной. Непрерывными будут
такжен функции.
будет непрерывной. Непрерывными будут
такжен функции.
Аналогично можно показать непрерывность остальных элементарных функций.
Таким образом, любая элементарная функция непрерывна в своей области определения, т.е. область определения элементарной функции совпадает с областью её непрерывности.
Непрерывность сложной и обратной функций
Пусть
функция 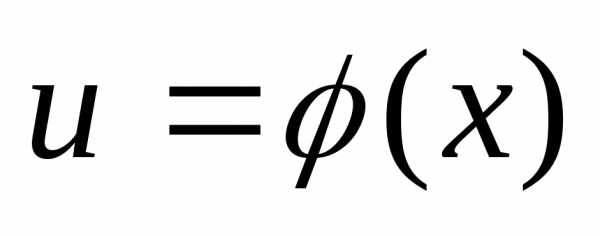 непрерывна в точке
непрерывна в точке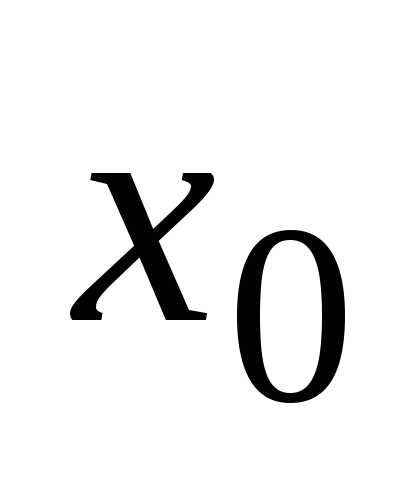 ,
а функция
,
а функция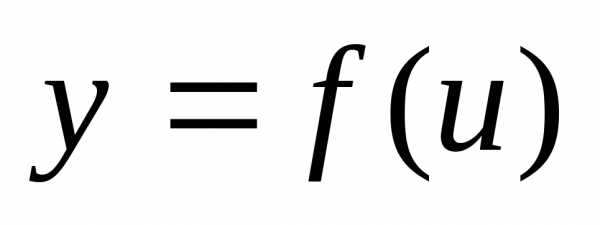 непрерывна в точке.
Тогда сложная функциянепрерывна в точке
непрерывна в точке.
Тогда сложная функциянепрерывна в точке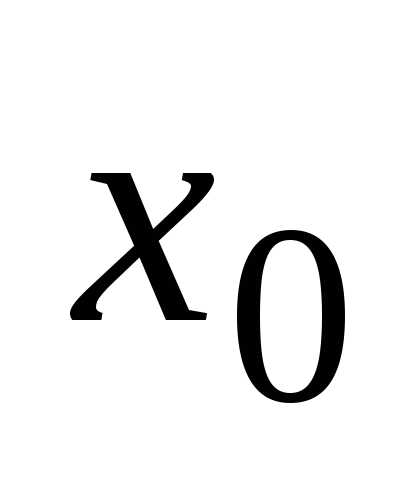 .
Это означает, что если сложная функция
составлена из непрерывных функций, то
она также будет непрерывной, т.е.непрерывная
функция от непрерывной функции есть
функция непрерывная.
Это определение распространяется на
конечное число непрерывных функций.
.
Это означает, что если сложная функция
составлена из непрерывных функций, то
она также будет непрерывной, т.е.непрерывная
функция от непрерывной функции есть
функция непрерывная.
Это определение распространяется на
конечное число непрерывных функций.
Из этого определения следует, что под знаком непрерывной функции можно переходить к пределу:
.
Это означает, что если функция непрерывна, то знак предела и знак функции можно поменять местами.
Пусть
функция 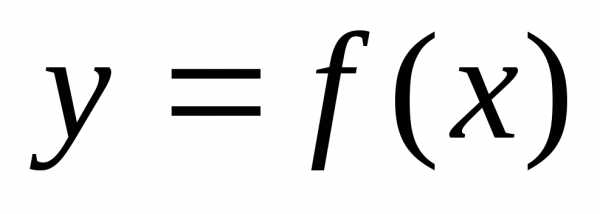 определена, строго монотонна и непрерывна
на отрезке [a, b].
Тогда обратная ей функция
определена, строго монотонна и непрерывна
на отрезке [a, b].
Тогда обратная ей функция 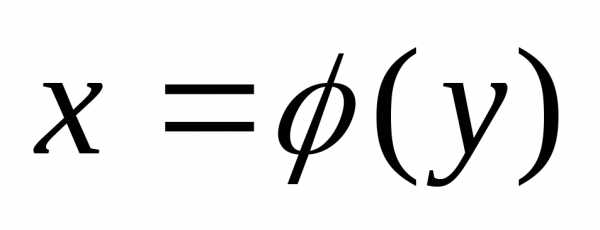 определена, строго монотонна и непрерывна
на отрезке [A, B],
где
.
определена, строго монотонна и непрерывна
на отрезке [A, B],
где
.
Точки разрыва и их классификация
Как
уже известно, что если функция 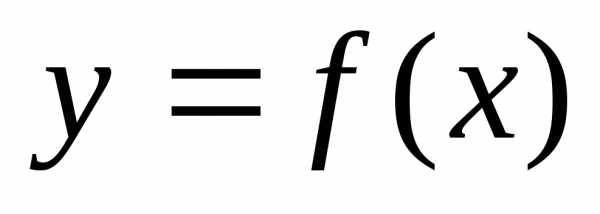 определена на множестве D и в точке
определена на множестве D и в точке 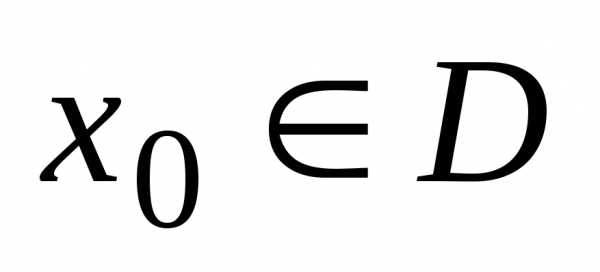 выполняется условие,
то функция непрерывна в этой точке. Если
же это условие непрерывности не
выполняется, то в точкех0 функция имеет разрыв.
выполняется условие,
то функция непрерывна в этой точке. Если
же это условие непрерывности не
выполняется, то в точкех0 функция имеет разрыв.
Точка 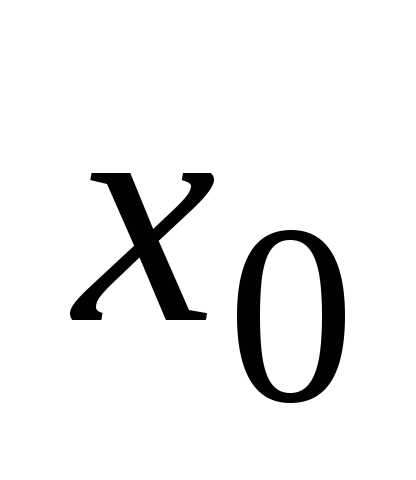 называетсяточкой
разрыва первого рода функции
называетсяточкой
разрыва первого рода функции  ,
если в этой точке функция имеет конечные
односторонние пределы, не равные друг
другу, т.е.
.
При этом величина
,
если в этой точке функция имеет конечные
односторонние пределы, не равные друг
другу, т.е.
.
При этом величина
называется скачком функции  в точке
в точке 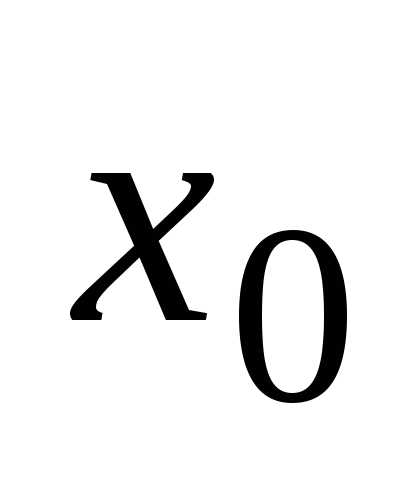 .
.
Точка  называетсяточкой
устранимого разрыва функции
называетсяточкой
устранимого разрыва функции 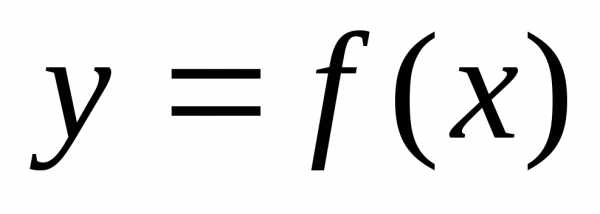 ,
если односторонние пределы функции в
этой точке равны друг другу и не равны
значению функции в этой точке, т.е.
В
этом случае для устранения разрыва в
точке
,
если односторонние пределы функции в
этой точке равны друг другу и не равны
значению функции в этой точке, т.е.
В
этом случае для устранения разрыва в
точке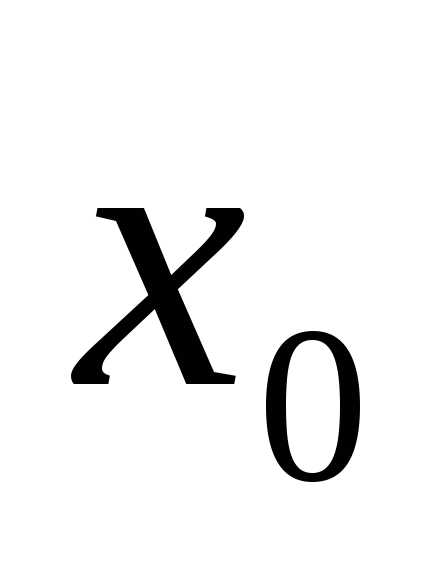 нужно положить
нужно положить
Точка х0 называется точкой
разрыва второго рода функции 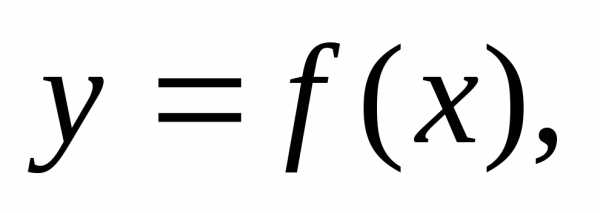 если
хотя бы один из односторонних пределов
если
хотя бы один из односторонних пределов 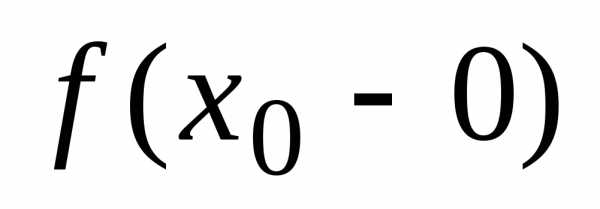 или
или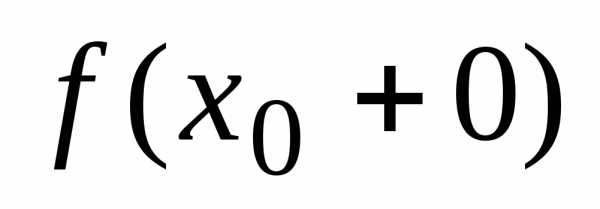 в этой точке либо не существует, либо
равен бесконечности.
в этой точке либо не существует, либо
равен бесконечности.
Пример 2. Исследовать на непрерывность функцию
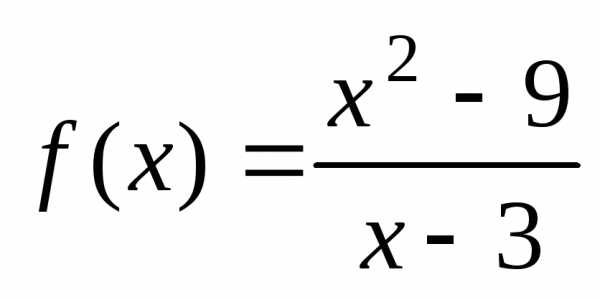 .
.
Решение.
Функция определена и непрерывна на всей
числовой прямой, за исключением точки  .
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции в точке
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции в точке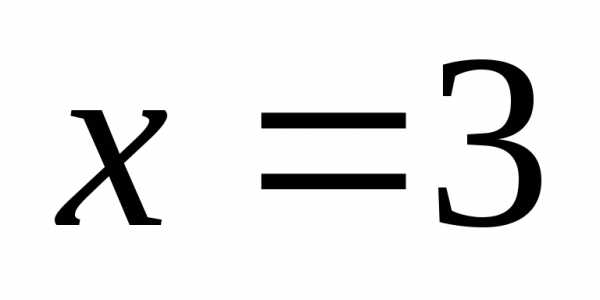 :
:
,
.
Так
как в точке  односторонние пределы равны между
собой, а функция в этой точке не определена,
то точка
односторонние пределы равны между
собой, а функция в этой точке не определена,
то точка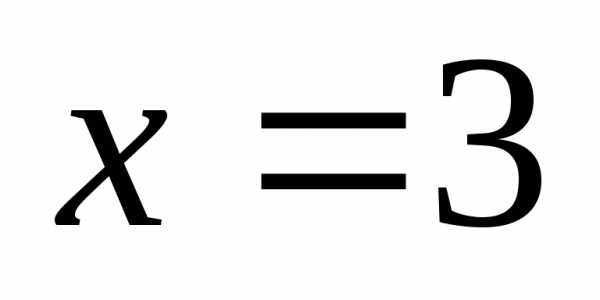 является точкой устранимого разрыва.
Чтобы устранить разрыв в этой точке,
необходимо доопределить функцию, положив
является точкой устранимого разрыва.
Чтобы устранить разрыв в этой точке,
необходимо доопределить функцию, положив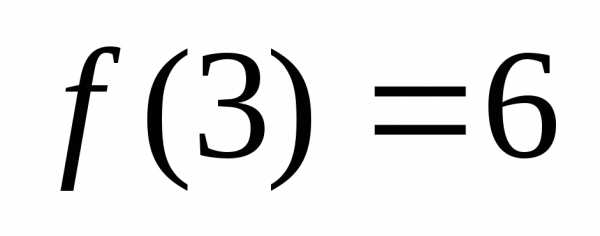 .
.
Пример 3. Исследовать на непрерывность функцию
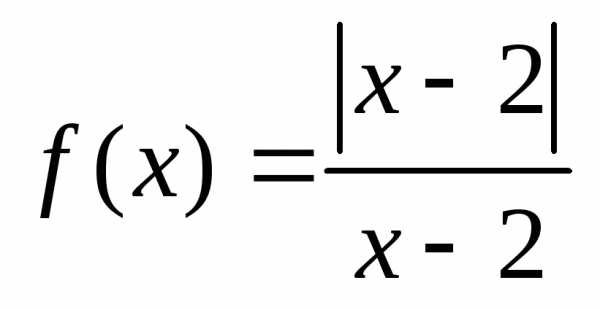 .
.
Решение.
Функция определена и непрерывна на всём
множестве действительных чисел, кроме  .
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции при
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции при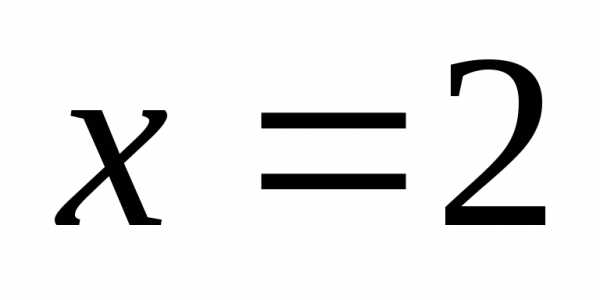 :
:
,
.
Так
как данная функция в точке 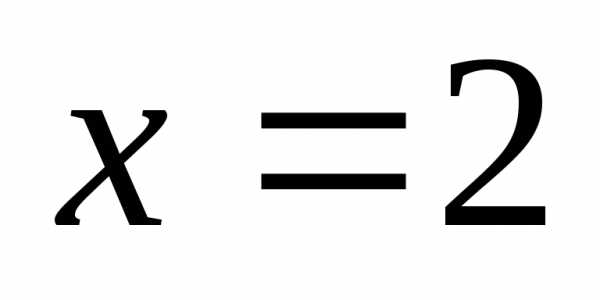 имеет конечные односторонние пределы,
не равные друг другу, то эта точка
является точкой разрыва первого рода.
Скачок функции в точке
имеет конечные односторонние пределы,
не равные друг другу, то эта точка
является точкой разрыва первого рода.
Скачок функции в точке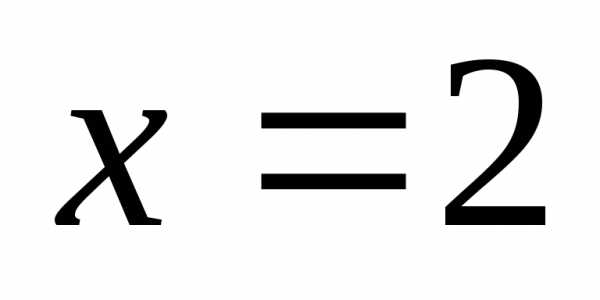 равен.
равен.
Вопросы для самоконтроля знаний
Что называется приращением аргумента и приращением функции?
Что называется левосторонним (левым) пределом функции?
Что называется правосторонним (правым) пределом функции?
Какая функция называется непрерывной в точке, в интервале?
Какая точка называется точкой разрыва функции?
Какая точка называется точкой разрыва первого рода?
Какая точка называется точкой разрыва второго рода?
Какая точка называется точкой устранимого разрыва?
Задания для самостоятельной работы
Исследовать функции на непрерывность:
 ;
2)
;
2)  ;
3)
;
3) ;
;
в
точке 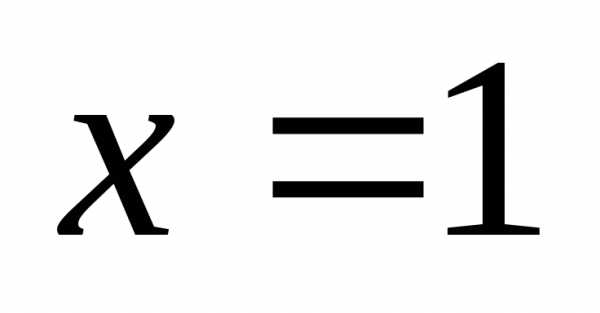 .
.
10
studfiles.net
Исследование функции на непрерывность — Мегаобучалка
Пусть функция определена на интервале , содержащем точку , за исключением, быть может, самой точки .
Точка , в которой не выполняется хотя бы одно из условий непрерывности функции, называется точкой разрыва функции. Точки разрыва бывают двух типов.
Точка называется точкой разрыва I-го рода, если функция не определена в ней, но существуют конечные односторонние пределы . При этом, если , то точка – точка устранимого разрыва. Если односторонние пределы не равны между собой, то есть , то – точка разрыва I-го рода типа «конечного скачка». Число называется скачком функции в точке .
Точка называется точкой разрыва II-го рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.
Схема исследования функции на непрерывность:
1) Найти область определения функции, точки разрыва.
2) Определить тип точек разрыва.
3) Определить характер разрыва в точках разрыва I-го рода.
4) Найти вертикальные асимптоты , если –точка разрыва II-го рода.
5) Найти, если есть, горизонтальные асимптоты графика функции где .
6) Построить эскиз графика функции хотя бы в окрестности точек разрыва, если затруднительно построить его в целом.
Пример12. Исследовать на непрерывность функции
а) ; б) и построить эскизы их графиков.
Решение.
а) Так как
то
Функция определена на всей числовой оси. Подозрительной на разрыв точкой является точка . Найдем односторонние пределы функции в этой точке: , следовательно, функция непрерывна как при , так и при всех других значениях . Вертикальных асимптот нет, так как нет точек разрыва II-го рода. Горизонтальных асимптот нет тоже, поскольку . График функции изображен на рис.1.
Рис.1.
б) 1. Область определения функции D: , – точка разрыва, так как не определена.
2. Найдем пределы слева и справа, чтобы определить тип точки разрыва:
Итак, , значит, – точка разрыва II -го рода.
3. – скачок функции.
4. – вертикальная асимптота графика функции, так как .
5. , следовательно, – горизонтальная асимптота.
Эскиз графика функции имеет вид:
Рис.2.
Вопросы к теории:
1. Действительные числа. Свойства действительных чисел.
2. Функция. Примеры функций.
3. Понятие предела функции в точке. Геометрический смысл предела функции.
4. Теорема об ограниченности функции, имеющей предел.
5. Теорема о переходе к пределу в неравенствах
6. Теорема о пределе промежуточной функции.
7. Теорема об арифметических операциях над пределами.
8. Понятие сложной функции. Теорема о замене переменной для пределов функции.
9. Предел функции в бесконечности. Неопределенности.
10. Понятие числовой последовательности и ее предела.
11. Теореме о пределе монотонной ограниченной последовательности. Число е. Натуральные логарифмы.
12. Теорема Больцано — Вейерштрасса.
13. Непрерывность функции в точке. Теорема о непрерывности суммы, произведения, частного непрерывных функций.
14. Непрерывность основных элементарных функций. Гиперболические функции, их графики.
15. Теорема о непрерывности сложной функции.
16. Обратная функция, теорема о существовании непрерывной обратной функции.
17. Первый замечательный предел.
18. Бесконечно малые функции и их основные свойства.
19. Второй замечательный предел.
20. Теорема о связи между функцией, ее пределом и бесконечно малой.
21. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими функциями.
22. Сравнение бесконечно малых функций.
23. Условие эквивалентности бесконечно малых функций.
24. Таблица эквивалентностей.
25. Теорема об эквивалентных бесконечно малых, применяемая при вычислении пределов.
26. Классификация разрывов функции. Схема исследования функций на непрерывность.
Упражнения:
1. Доказать эквивалентность неравенств: .
2. Доказать, что для любых и имеют место неравенства: .
3. Доказать, что если , то .
4. Доказать, что отбрасывание или замена конечного числа членов последовательности не влияют на сходимость последовательности, причем в случае сходящейся последовательности не влияют на величину предела.
5. Пусть , а не существует, . Что можно сказать о в каждом из этих случаев?
6. Пусть имеет предел в точке , а функция не имеет предела в этой точке. Будут ли существовать пределы: , . Рассмотреть пример
7. При каких значениях функция будет не ограничена при ?
8. Функцию , имеющую предел при , представить в виде суммы постоянной величины и некоторой функции, бесконечно малой при .
9. Доказать, что если – непрерывная функция, то функция также непрерывная. Верно ли обратное утверждение?
10. Исследовать непрерывность функции Дирихле.
megaobuchalka.ru
1.2. Непрерывность и точки разрыва функции
Функция 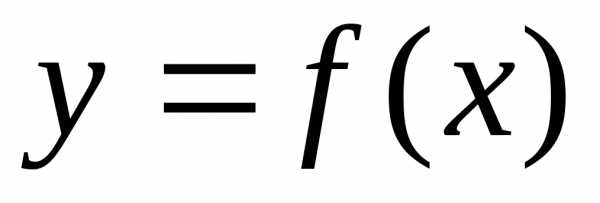 называетсянепрерывной в точке
называетсянепрерывной в точке 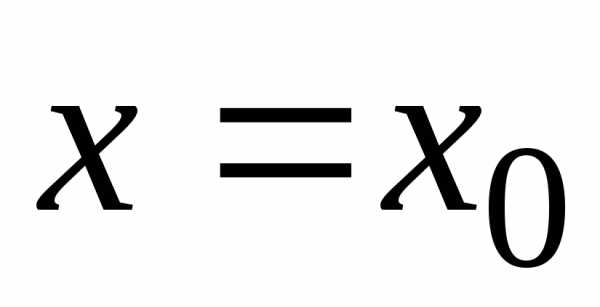 если:
если:
1) 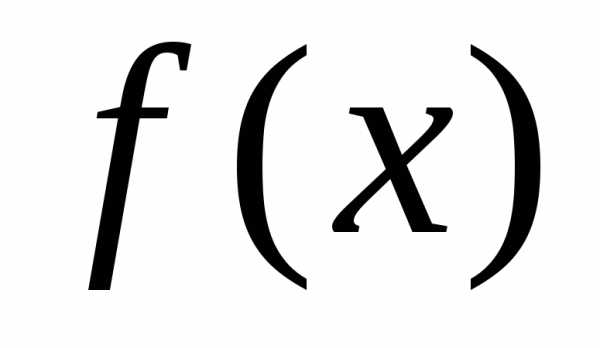 определена в точке
определена в точке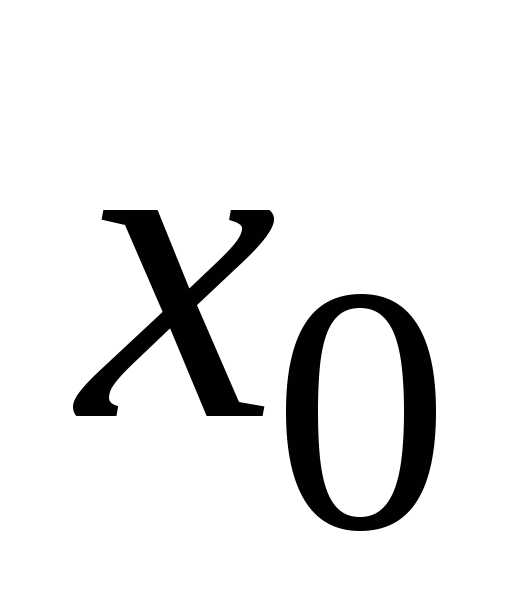 и её окрестности;
и её окрестности;
2)
существует конечный предел функции 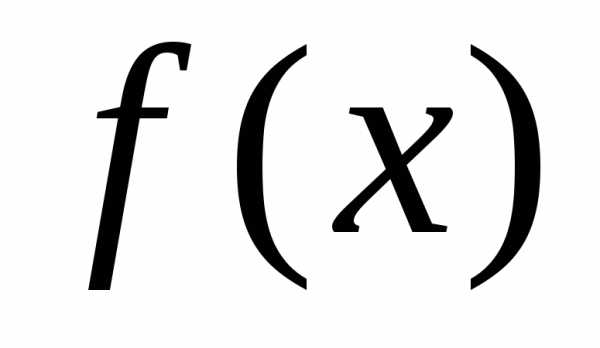 в точке
в точке ;
;
3)
этот предел равен значению функции в
точке 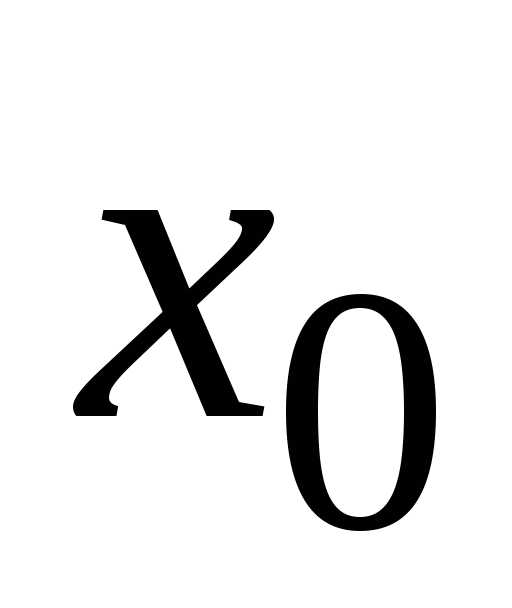 ,
т.е.
,
т.е.
Функция,
непрерывна в каждой точке некоторой
области, называется непрерывной
в этой области. Точка 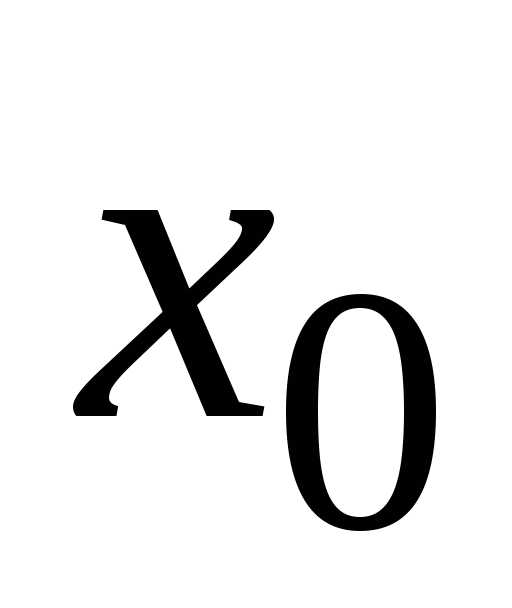 ,
в которой нарушено хотя бы одно из трех
условий непрерывности функции, называетсяточкой разрыва
функции.
,
в которой нарушено хотя бы одно из трех
условий непрерывности функции, называетсяточкой разрыва
функции.
Точка 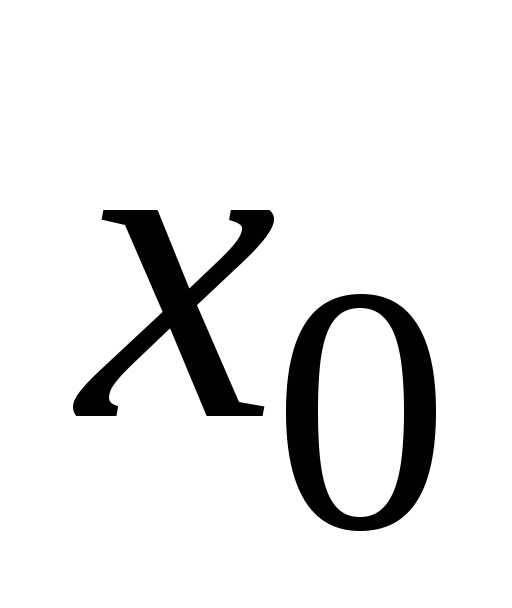 называется точкой разрывапервого
рода, если
функция
называется точкой разрывапервого
рода, если
функция  имеет в этой точке конечный правый и
левый предел, т.е.
имеет в этой точке конечный правый и
левый предел, т.е.
Если
хотя бы одна из этих пределов не
существует или равен бесконечности, то
точка 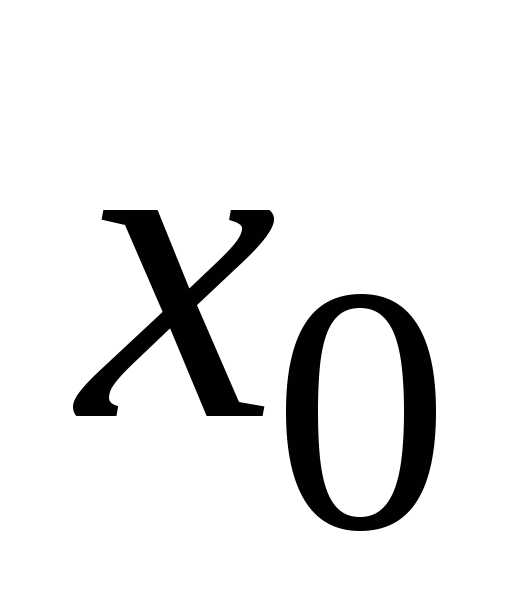 называют точкой разрывавторого
рода.
называют точкой разрывавторого
рода.
Пример. Исследовать функцию
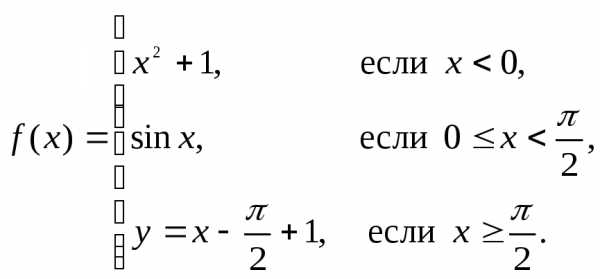
на непрерывность, построить её график.
Решение.
Функция 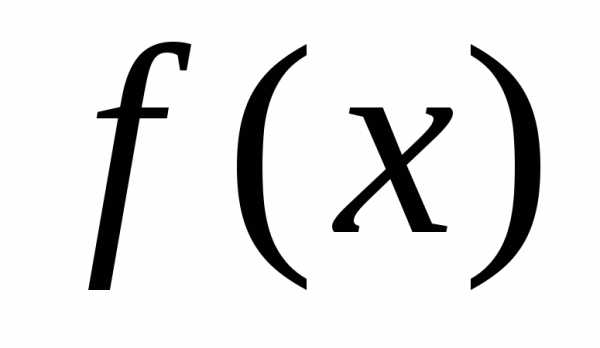 определена и непрерывна на интервалет.к. на этих интервалах она задана
непрерывными элементарными функциями.
Следовательно, разрыв возможен только
в точках
определена и непрерывна на интервалет.к. на этих интервалах она задана
непрерывными элементарными функциями.
Следовательно, разрыв возможен только
в точках
Для
точки 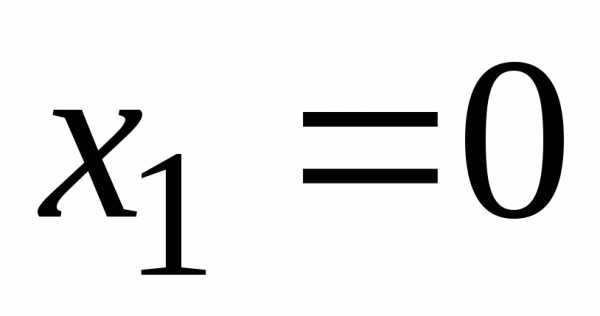 имеем
имеем
,
,
.
т.к.
и оба они конечны, то функцияf(x) в точке 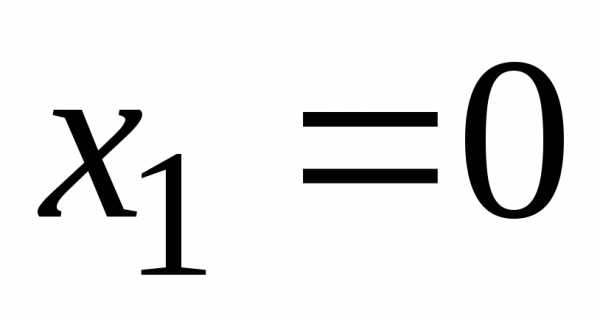 имеет разрыв первого рода.
имеет разрыв первого рода.
Для
точки 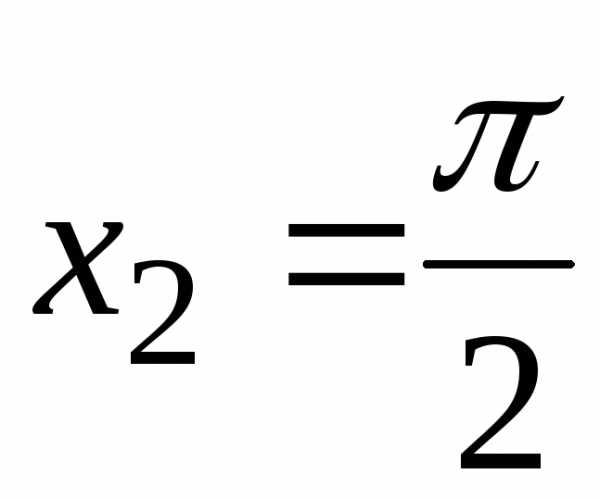 имеем
имеем
,
,
т.е.
и в точке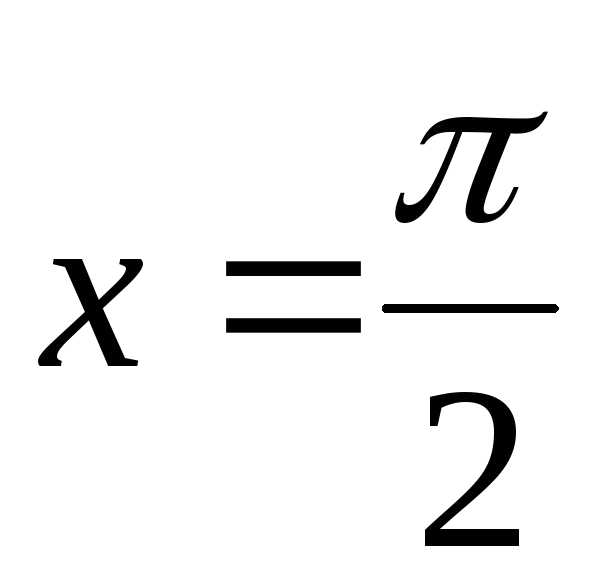 функция непрерывна.
функция непрерывна.
Пример.
Найдите точку разрыва функции  .
.
Решение.
Единственной точкой разрыва данной
функции является точка 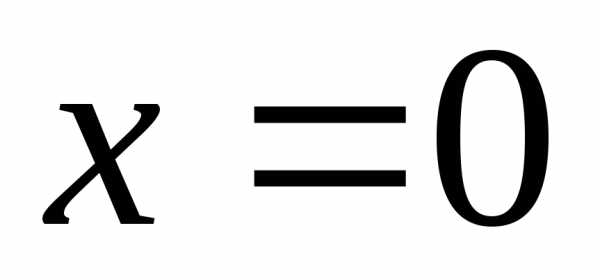 т.к. функция в этой точке не определена.
Найдем односторонние пределы в окрестности
точки
т.к. функция в этой точке не определена.
Найдем односторонние пределы в окрестности
точки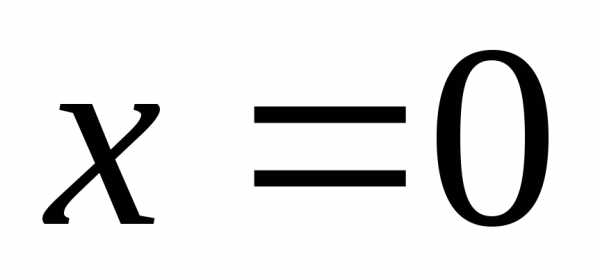 :
:
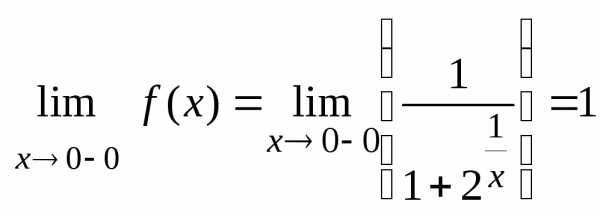 ,
т.к.
,
т.к.
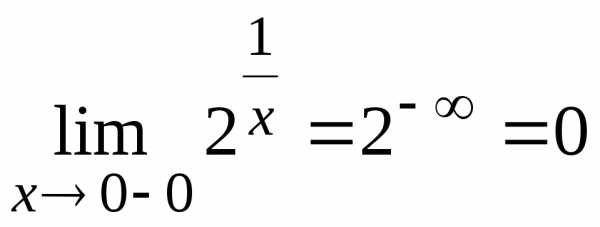 ,
,
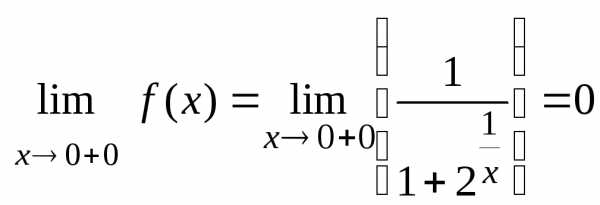 ,
т.к.
,
т.к.
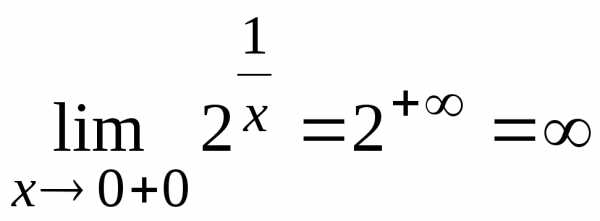 .
.
Т.к.
то в точке имеем
разрыв первого рода.
имеем
разрыв первого рода.
Вычислим 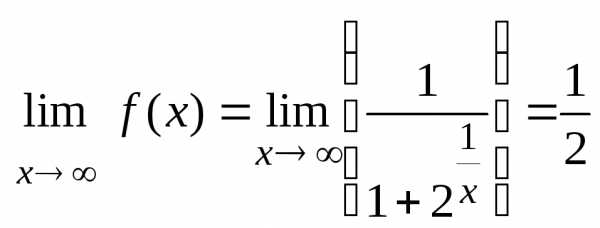 ,
т.к.
,
т.к.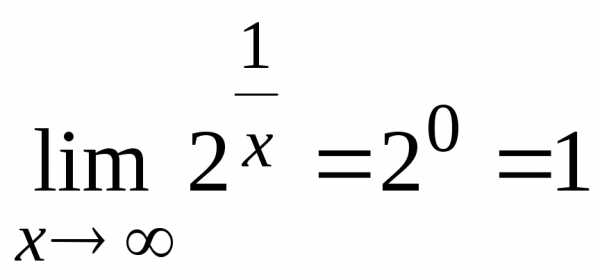 ,
,
т.е. 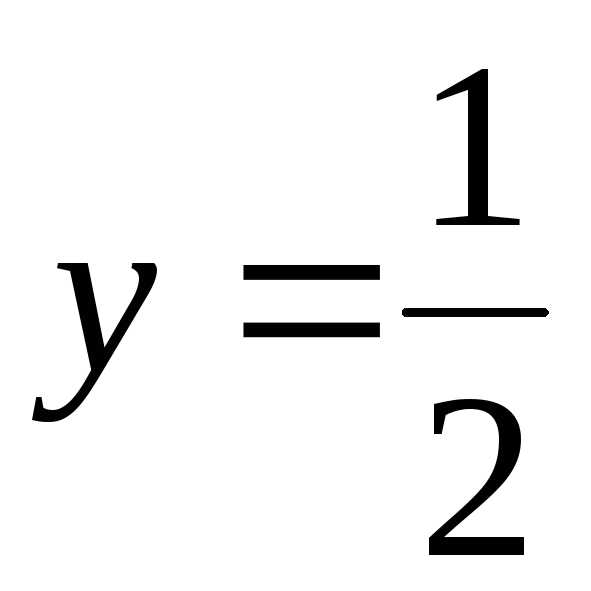 горизонтальная асимптота графика данной
функции.
горизонтальная асимптота графика данной
функции.
Задание 5.
Исследовать данные функции на непрерывность и построить их графики
№ зад. № вар. | 1 | 2 |
1 |
| |
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
| |
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
1.3. Асимптоты графика функции
Прямая
L
называется асимптотой данной кривой 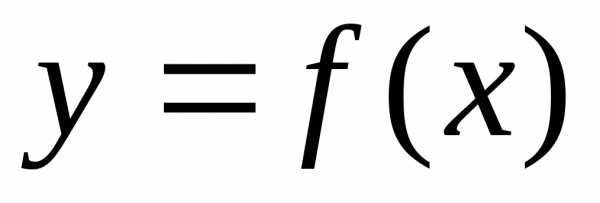 ,
если расстояние от точки М кривой до
прямойL
при удаление точки М в бесконечность
стремится к нулю.
,
если расстояние от точки М кривой до
прямойL
при удаление точки М в бесконечность
стремится к нулю.
Если
существует числа 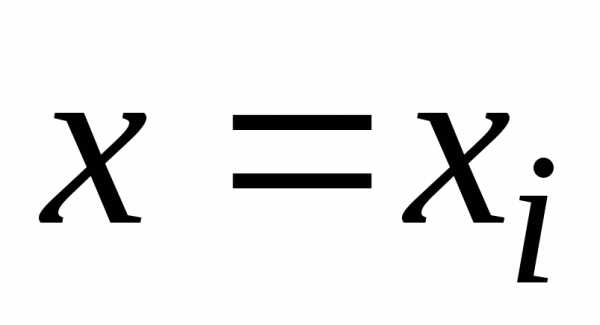
 при которой,
т.е. функция имеет бесконечный разрыв,
то прямые
при которой,
т.е. функция имеет бесконечный разрыв,
то прямые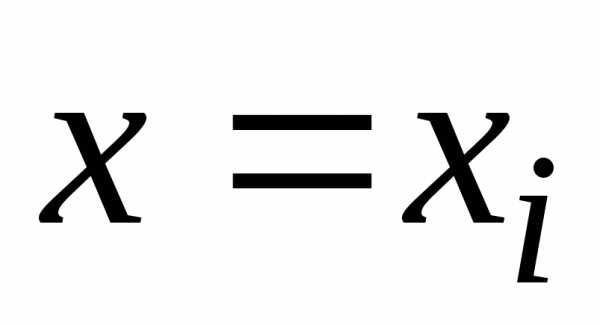 называютсявертикальными асимптотами кривой
называютсявертикальными асимптотами кривой 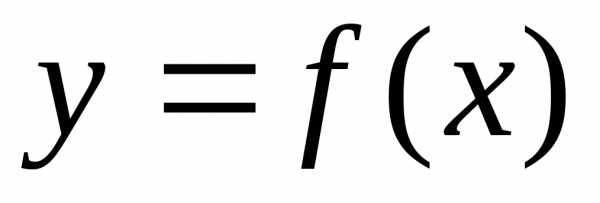 .
.
Если существуют пределы
то
прямая
являетсянаклонной асимптотой кривой 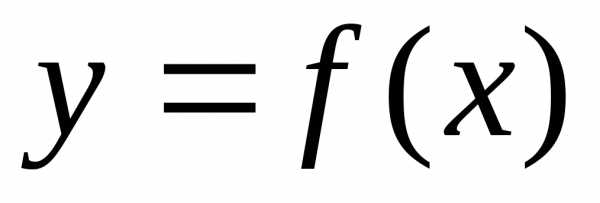 (приk=0
— горизонтальной).
(приk=0
— горизонтальной).
Пример. Найти асимптоты графика функции 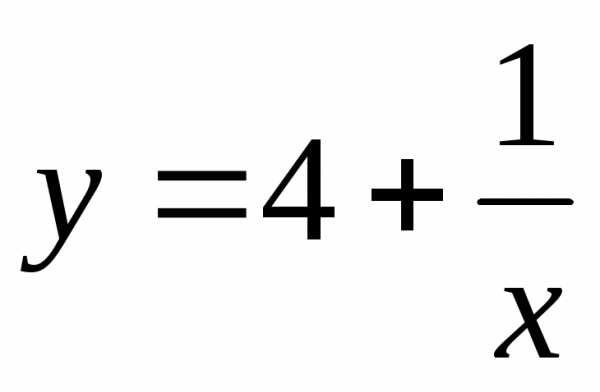 .
.
Решение. Функция терпит разрыв в точке . Находим левый и правый пределы в этой точке
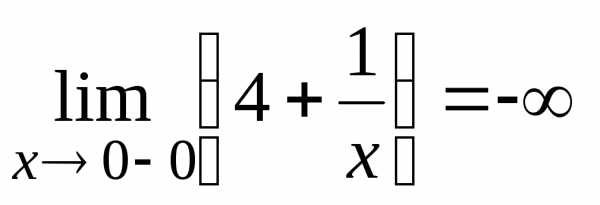 ,
,
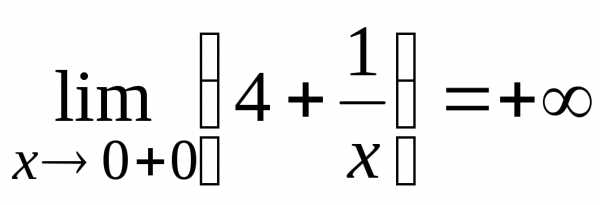 .
.
Таким
образом 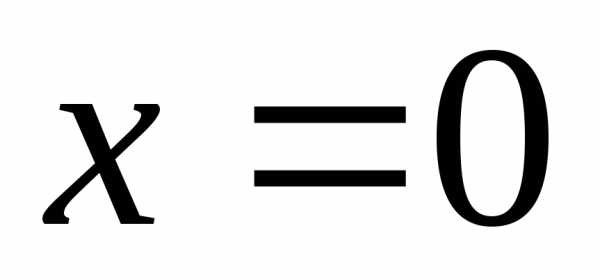 — вертикальная асимптота графика функции.
— вертикальная асимптота графика функции.
Находим
 ,
поэтому у=4
— горизонтальная асимптота.
,
поэтому у=4
— горизонтальная асимптота.
Пример.
Найти асимптоты графика функции 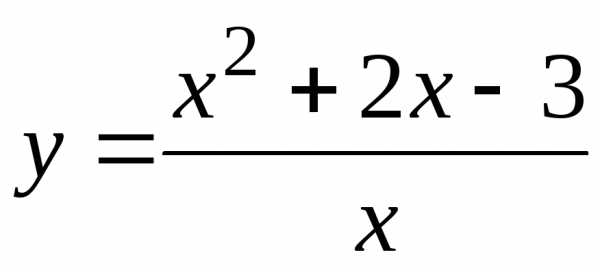 .
.
Решение.
Данная функция терпит разрыв в точке 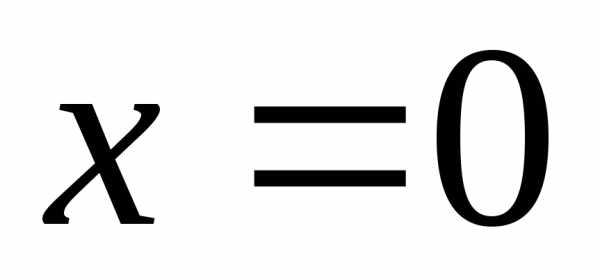 .
Находим
.
Находим
,
.
Поэтому
прямая 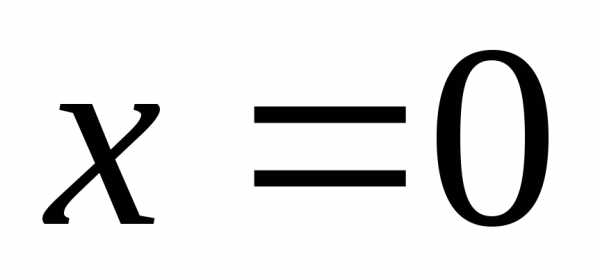 является вертикальной асимптотой
графика функции.
является вертикальной асимптотой
графика функции.
Находим горизонтальные асимптоты.
,
,
следовательно,
прямая 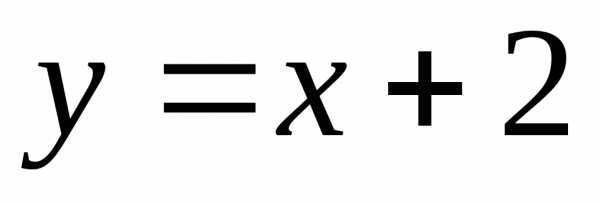 является наклонной асимптотой графика
данной функции.
является наклонной асимптотой графика
данной функции.
Задание 6.
Найти асимптоты графика функции
№ зад. № вар. | 1 | 2 |
1 |
| |
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
studfiles.net
4. Непрерывность функций. Точки разрыва и их классификация
4.1. Основные теоретические сведения
Определение. Функция у = f(x) называется непрерывной в точке х0, если эта функция определена в какой-нибудь окрестности точки х0 и если
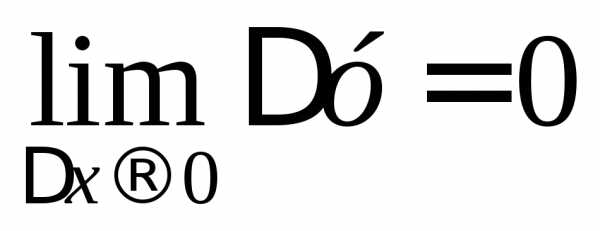
то есть бесконечно малому приращению аргумента в окрестности точки х0 соответствует бесконечно малое приращение функции.
Определение. Функция у=f(x) непрерывна в точке х0, если она определена в некоторой окрестности этой точки и если предел функции при стремлении независимой переменной х к х0 существует и равен значению функции при х=х0, то есть
Определение. Пусть х → х0, оставаясь все время слева от х0. Если при этом условии f(x) стремится к пределу, то он называется левым пределом функции f(x) в точке х0, то есть
Аналогично определяется и правый предел
Определение. Функция непрерывна в точке х0 если:
функция определена в точке х0;
существуют левый и правый пределы функции f(x) при х → х0;
все три числа (х0), f(x0 –0), f(x0 +0) совпадают, то есть
Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой его точке.
Теорема. Если две функции f(x) и g(x) определены в одном и том же
интервале и обе непрерывны в точке х0, то в той же точке будут непрерывны и функции
Теорема. Сложная функция, состоящая из конечного числа непрерывных функций, является непрерывной.
Все основные элементарные функции непрерывны в своей области определения.
Определение. Если в какой-либо точке х0 функция не является непрерывной, то точка х0 называется точкой разрыва функции, а сама функция – разрывной в этой точке.
Определение. Если в точке х0 существует конечный lim f(x) = А
(левосторонний и правосторонний пределы существуют, конечны и равны между собой), но он не совпадает со значением функции в точке, или же функция в точке не определена, то точка х0 называется точкой устранимого разрыва. Принятое изображение точки устранимого разрыва представлено на рис. 1.
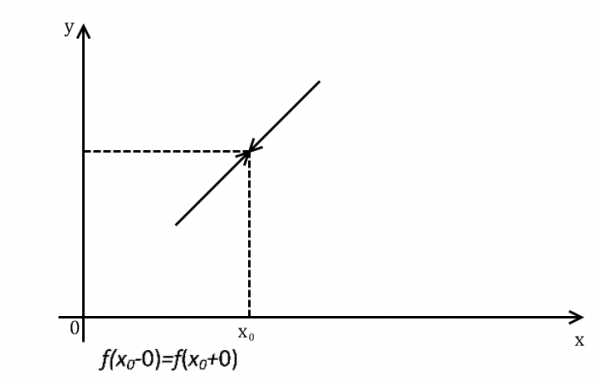
Рис. 1
Определение. Точкой разрыва первого рода или точкой конечного разрыва называется такая точка х0, в которой функция имеет левый и правый конечные пределы, но они не равны между собой.
На рис. 2 приведено графическое представление разрыва функции первого рода в точке х0
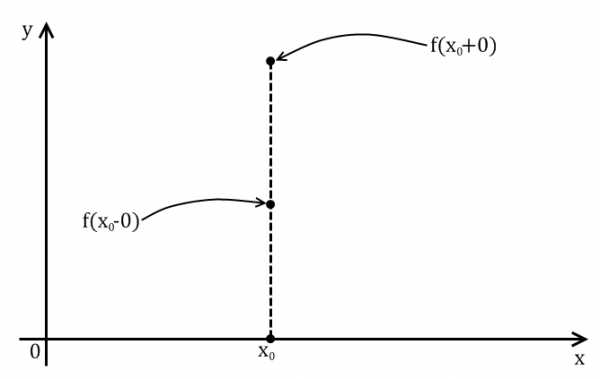
Рис.2
Определение. Если хотя бы один из пределов f(x0 – 0) или f(x0 + 0) не существует или бесконечен, то точка х0 называется точкой разрыва, второго рода.
Графические представления разрывов функций второго рода в точке х0 приведены на рис. 3 (а, б, в).
Приведенные выше определения непрерывности функции f(x) в точке х0
представлены на рис. 4, где отмечено, что основной посылкой при определении непрерывности функции (необходимым условием) в точке х0 является то, что f(x) определена в точке и ее окрестности.Рис.3
Пример Исследовать на непрерывность, определить характер точек разрыва,изобразить в окрестности точек разрыва функцию
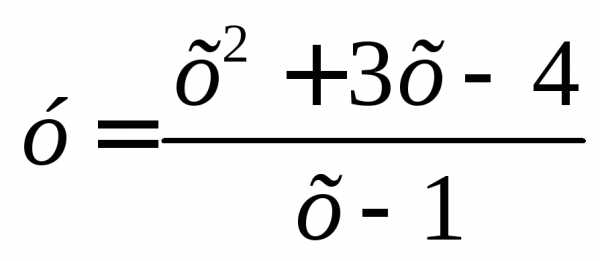
Решение.
Это рациональная функция Она определена и непрерывна при всех значениях х, кроме х = 1, так как при х = 1 знаменатель обращается, в нуль. В точке х = 1 функция терпит разрыв. Вычислим предел этой функции при
х → 1, имеем
Конечный предел функции при х→ 1 существует, а функция в точке
х = 1 не определена; значит точка х = 1 является точкой устранимого разрыва.
Если доопределить функцию, то есть положить f (1) = 5, то функция
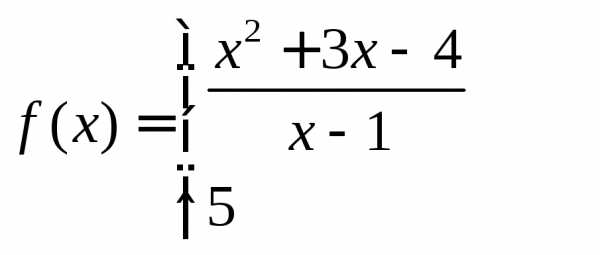
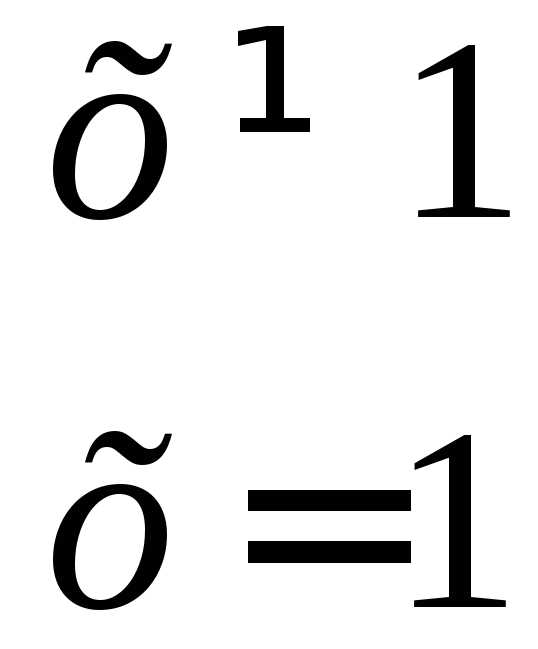 будет непрерывной.
будет непрерывной.
Рис. 4
Поведение функции в окрестности точки х = 1 изображено на рис. 4.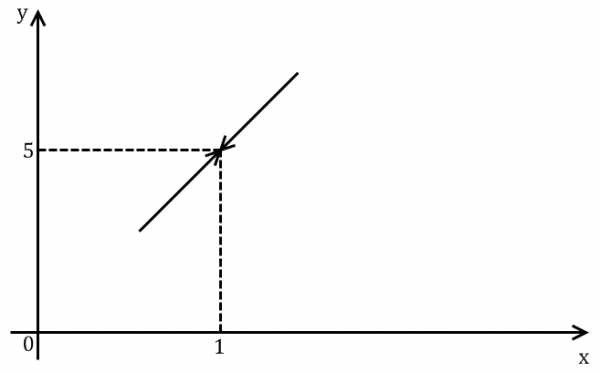
Замечание. Данная функция
неопределенная при х = 1, совпадает с непрерывной функцией
во всех точках кроме х =1
Пример.
Исследовать на непрерывность функцию и определить характер ее точек разрыва
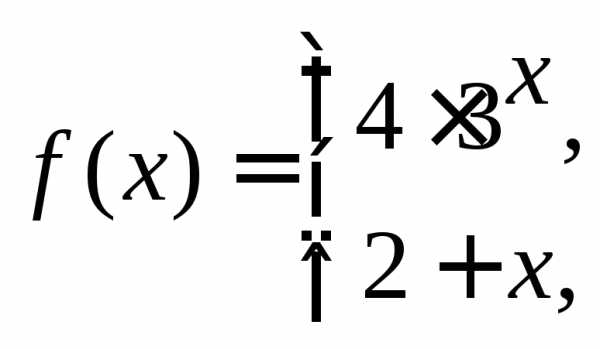
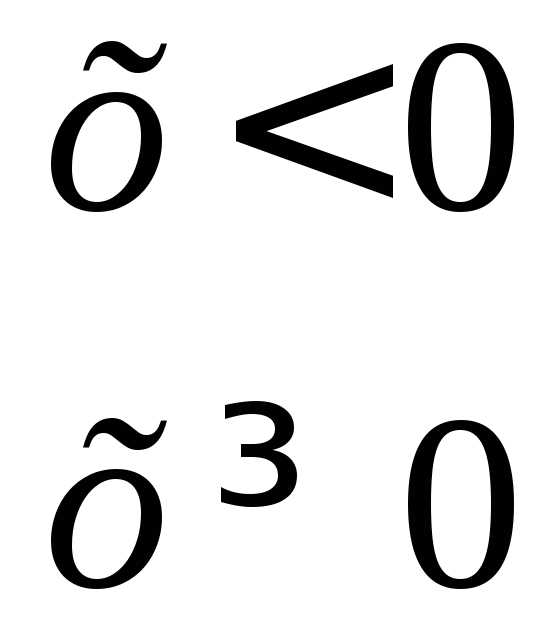
Решение.
Область определения функции – вся числовая ось. На интервалах(–, 0), (0,+) функция непрерывна. Разрыв возможен только в точке х = 0, в которой изменяется аналитическое задание функции.
Найдем односторонние пределы функции:
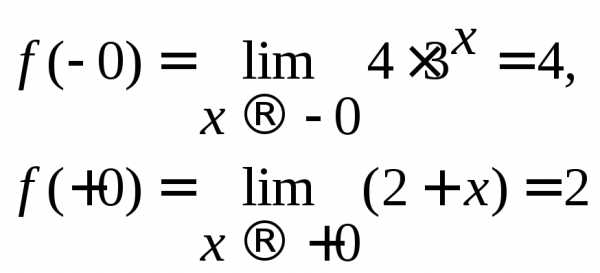
Левый и правый пределы хотя и конечны, но не равны между собой. Поэтому в точке х = 0 функция имеет разрыв первого рода. Скачок функции в точке разрыва равен
Поведение функции в окрестности точки х = 0 изображено на рис. 5.

Рис. 5
Пример Исследовать функцию f(x) на непрерывность, определить характер ее точек разрыва, изобразить ее поведение в окрестности точек разрыва.

Решение.
Функция определена и непрерывна на всей числовой оси, кроме точек х, = –2 и х2 = 2, причем
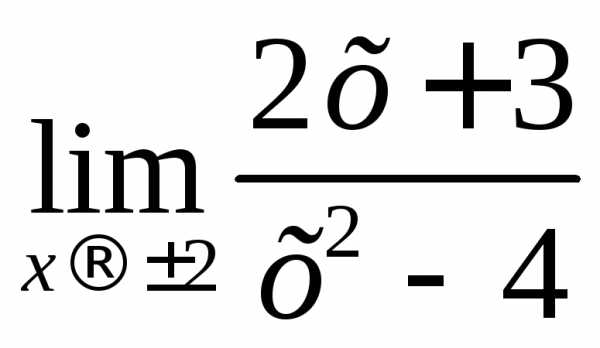
не существует.
Вычисляем односторонние пределы в точке х, = –2.
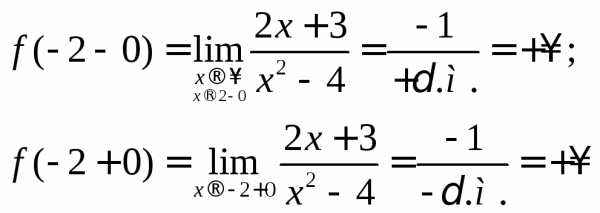
Итак, в точке х = –2 функция терпит разрыв второго рода. Исследуем характер разрыва функции в точке х2 =2. Имеем

В точке х2 =2 функция также терпит разрыв второго рода.
Поведение функции в окрестности точек хх= –2 и х2 = 2 изображено на рис. 6.
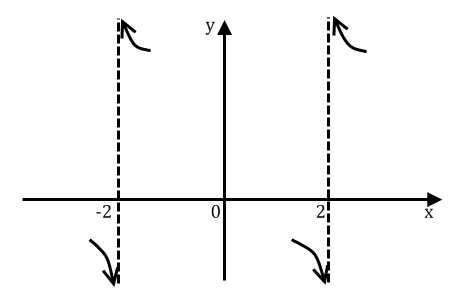
Рис. 6
Пример.
Исследовать функцию f(x) = ex+i на непрерывность, определить характер точек разрыва, изобразить поведение функции в окрестности точек разрыва.
Решение.
Функция 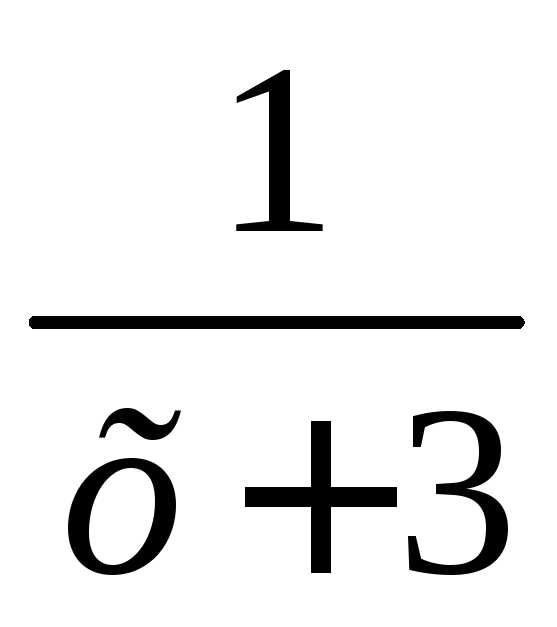 неопределена прих = –3, поэтому
функция
неопределена прих = –3, поэтому
функция 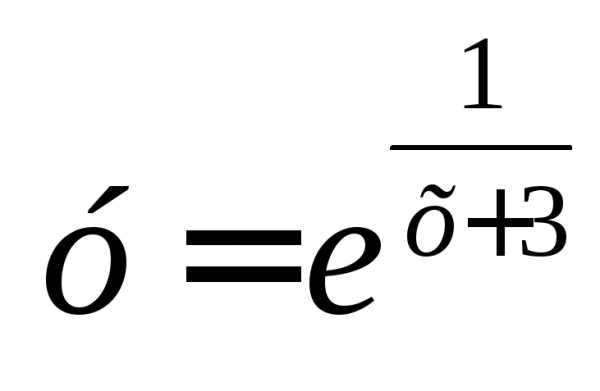 непрерывна при всех
непрерывна при всех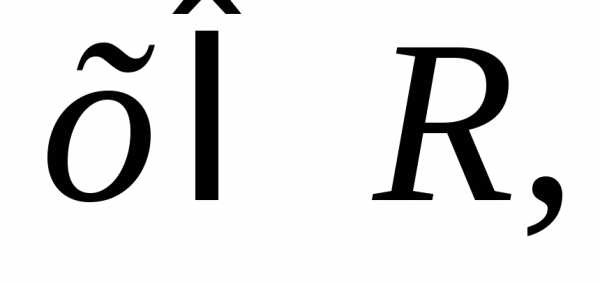 кромех =
–3. Определим
характер разрыва функции. Имеем
кромех =
–3. Определим
характер разрыва функции. Имеем
то есть один из пределов равен бесконечности, а значит функция терпит разрыв
второго рода.
Поведение функции f(x) = ex+3 в окрестности точки разрыва х = –3 изображено на рис. 7
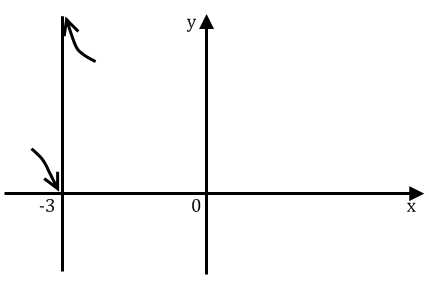
Рис. 7
4.2. Упражнения для самостоятельной работы студентов
1. Исследовать функции на непрерывность, определить характер их точек разрыва, изобразить графически поведение функций в окрестности
2. Исследовать функции на непрерывность, определить характер их точек разрыва, изобразить графически поведение функций в окрестности точек разрыва
studfiles.net
Равномерная непрерывность — ПриМат
Пусть функция определена на . Тогда называется равномерно непрерывной, если такие, что , , выполняется неравенство .
Очевидно, что равномерно непрерывная в своей области определения функция непрерывна в ней. Но обратное не всегда верно.
Рассмотрим некоторые примеры.
Спойлер
Показать, что равномерная функция на не является равномерно непрерывной.
, что , что .
, .
Это значит, что может быть меньше заданного положительного числа, но какое бы мы не взяли положительное , мы можем приближать к так близко, что , однако . Следовательно, функция является непрерывной, но не равномерно непрерывной на .Исследовать на равномерную непрерывность функцию на отрезке .
.
.
Зафиксируем произвольное и положим .
Тогда , .
Следовательно, функция на равномерно непрерывна.
- Доказать, что функция равномерно непрерывна на .
По теореме Лагранжа и
Если для выбрать любое , , то при выполняется , иначе говоря, является равномерно непрерывной на .
[свернуть]
- Б.П.Демидович «Сборник задач и упражнений по математическому анализу», 13 изд-е, Москва, изд-во ЧеРо, 1997г., стр.92
- Г.М.Вартанян «Математический анализ», Одесса, 2009г., стр.30
- Л.Д.Кудрявцев «Курс математического анализа», том 1, Москва, «Высшая школа», 1981г., стр.228
Поделиться ссылкой:
Похожее
ib.mazurok.com

 называется непрерывной в
точке
называется непрерывной в
точке 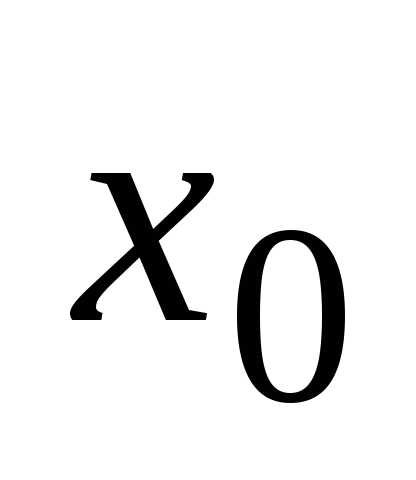 ,
если она определена в окрестности точки
,
если она определена в окрестности точки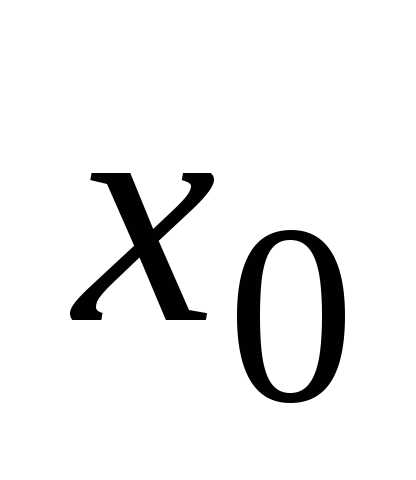 и
и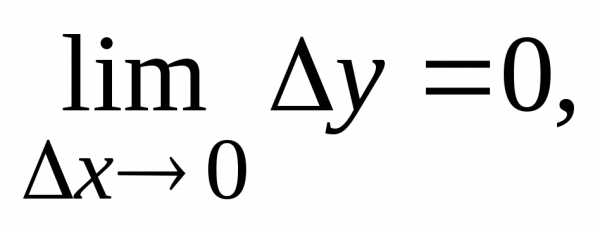 т.е.
т.е. при
при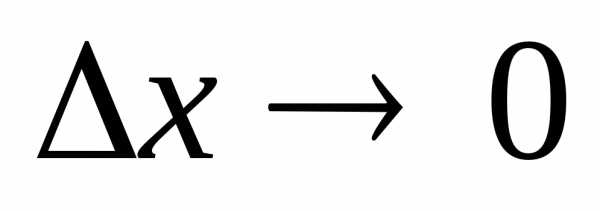 .
Это означает, что функция непрерывна
в токе
.
Это означает, что функция непрерывна
в токе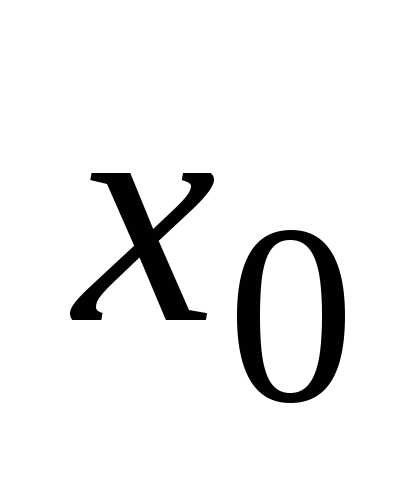 ,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.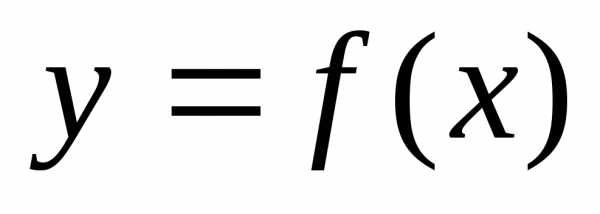 называется непрерывной в
точке
называется непрерывной в
точке 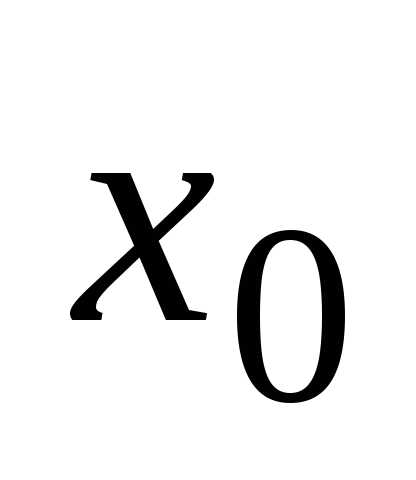 ,
если предел функции при
,
если предел функции при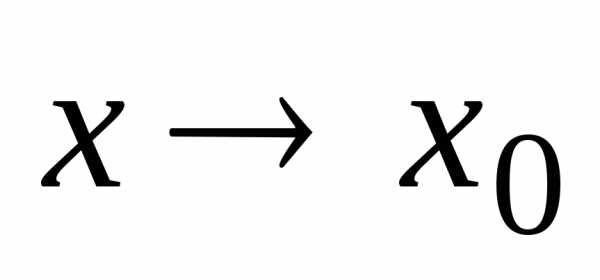 равен значению функции в этой точке:.
равен значению функции в этой точке:. называется непрерывной
в точке
называется непрерывной
в точке 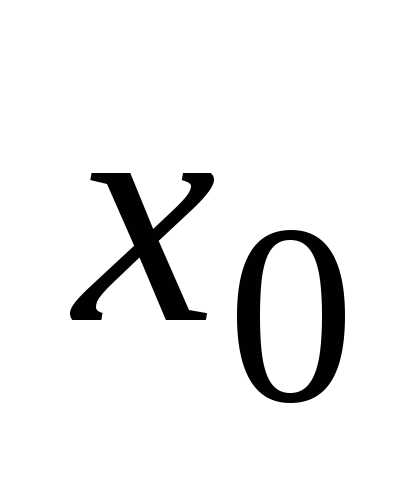 ,
если существуют левый и правый пределы
этой функции при
,
если существуют левый и правый пределы
этой функции при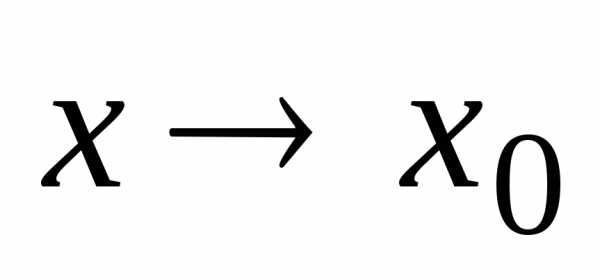 и если эти пределы равны между собой
и равны значению функции в этой точке:
и если эти пределы равны между собой
и равны значению функции в этой точке: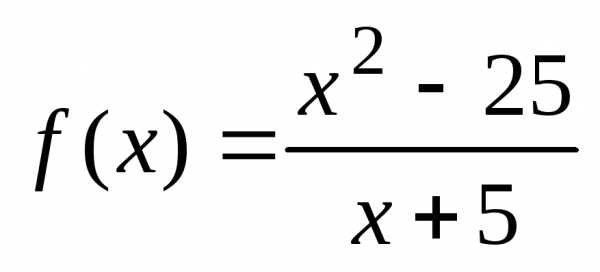 ;
2)
;
2) 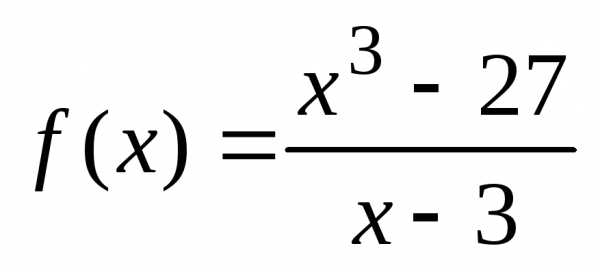 ;
3)
;
3)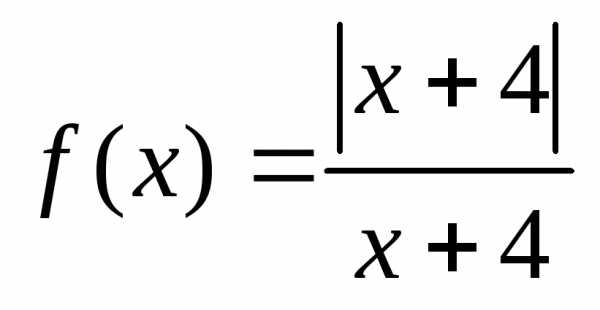 ;
;