Абсолютно и условно сходящиеся ряды
Доказательство.
\(\circ\) Докажем, что сходится ряд
$$
\sum_{s=1}^{\infty}|a_{j_{s}}b_{j_{s}}|,\label{ref15}
$$
Пусть \(\tilde{\tau}_{m}\) — \(m\)- я частичная сумма ряда \eqref{ref15}, \(A\) и \(B\) — суммы рядов \(\displaystyle\sum_{n=1}^{\infty}|a_{n}|\) и \(\displaystyle\sum_{n=1}^{\infty}|b_{n}|\) соответственно. Тогда
$$
\tilde{\tau}_{m} = \sum_{s=1}^{m}|a_{j_{s}}b_{j_{s}}| \leq \sum_{s=1}^{m}|a_{j_{s}}| \sum_{s=1}^{m}|b_{j_{s}}| \leq AB\nonumber
$$
то есть частичные суммы ряда \eqref{ref15} ограничены сверху и по критерию сходимости ряда с неотрицательными членами ряд \eqref{ref15} сходится.
Докажем, что
$$
\tau = S\sigma,\label{ref16}
$$
где \(\tau\), \(S\), и \(\sigma\) — суммы рядов \eqref{ref14}, \eqref{ref1} и \eqref{ref13} соответственно. Заметим, что все члены ряда \eqref{ref14} содержатся в следующей таблице:
Занумеруем элементы этой таблицы, присваивая им номера, указанные в таблице (такой метод перечисления называют “методом квадратов”). В этом случае получается ряд
$$
a_{1}b_{1} + (a_{2}b_{1} + a_{2}b_{2} + a_{1}b_{2}) + (a_{3}b_{1} + a_{3}b_{2} + a_{3}b_{3} + a_{2}b_{3} + a_{1}b_{3}) +\\
+ (a_{4}b_{1} + a_{4}b_{2} + a_{4}b_{3} + a_{4}b_{4} + a_{3}b_{4} + a_{2}b_{4} + a_{1}b_{4}) + \ldots,\label{ref17}
$$
образованный из всевозможных попарных произведений членов рядов \eqref{ref1} и (13), то есть ряд вида \eqref{ref14}.
По доказанному выше всякий ряд вида \eqref{ref14} и, в частности, ряд \eqref{ref17}, абсолютно сходится и, значит, сходится (свойство 1), а сумма ряда \eqref{ref14} не зависит от порядка расположения его членов (свойство 4). Поэтому ряд \eqref{ref17} сходится, а его сумма равна \(\tau\).
Пусть \(S_{n}\), \(\sigma_{n}\), \(\tau_{n}\) — \(n\)-е частичные суммы рядов \eqref{ref1}, \eqref{ref13} и \eqref{ref17} соответственно; тогда \(\displaystyle\tau_{n^{2}} = S_{n}\sigma_{n}\). Так как \(S_{n} \rightarrow S\) и \(\sigma_{n} \rightarrow \sigma\) при \(n \rightarrow \infty\), то \(\tau_{n^{2}} \rightarrow S_{\sigma}\) при \(n \rightarrow \infty\). С другой стороны, \(\{\displaystyle\tau_{n^{2}}\}\) — подпоследовательность сходящейся к числу \(\tau\) последовательности \(\{\tau_{n}\}\), и поэтому \(\tau_{n^{2}} \rightarrow \tau\) при \(n \rightarrow \infty\). Отсюда следует, что \(\tau = S_{\sigma}\). Равенство \eqref{ref16} доказано. \(\bullet\)
univerlib.com
Исследование сходимости знакочередующихся рядов. Исследование числовых рядов на абсолютную и условную сходимость — КиберПедия
Цель: Формирование навыков исследования сходимости знакочередующихся рядов; исследования числовых рядов на абсолютную и условную сходимость
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Числовой ряд
(23.1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд (23.1) называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. Этот ряд является частным случаем знакопеременного ряда.
Признак сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося ряда (23.1) монотонно убывают по абсолютной величине и общий член стремиться к нулю при , то ряд (23.1) сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд (23.1) называется абсолютно сходящимся, если сходится ряд
, (23.2)
составленный из абсолютных величин его членов, то есть всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд (23.1) сходится, а составленный из абсолютных величин его членов ряд (23.2) расходится, то данный ряд (23.1) называется условно (неабсолютно) сходящимся. Заметим, что из расходимость ряда (23.2) в общем случае не следует расходимость ряда (23.1).
Для установления абсолютной сходимости знакопеременного (и знакочередующегося) ряда используются те же признаки, что и для сходимости ряда с положительными членами.
Для решения вопроса об абсолютной или условной сходимости знакочередующегося ряда необходимо рассмотреть ряд, составленный из абсолютных величин членов знакочередующегося ряда.
Если при исследовании этого ряда с помощью одного из признаков сходимости (признака Даламбера, признака сравнения рядов) ряд окажется сходящимся, то данный знакочередующийся ряд сходится абсолютно; если же ряд окажется расходящимся, то знакочередующийся ряд сходится условно.
Примеры
Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
1) ;
2) ;
3) ;
4) .
Решение: 1) Члены данного ряда по абсолютной величине монотонно убывают: и . Следовательно, согласно признаку Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд , составленный из абсолютных величин членов данного ряда, который, как, известно, расходится. Поэтому данный ряд сходится условно.
2) Члены данного ряда по абсолютной величине монотонно убывают , но . Ряд расходится, так как признак Лейбница не выполняется.
3) Используя признак Лейбница, получим ; , то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: . Это геометрический ряд вида , который сходится. Поэтому данный ряд сходится абсолютно.
4) Используя признак Лейбница, имеем ; , то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного рада: , или . Это обобщенный гармонический ряд, который расходится, так как . Следовательно, данный ряд сходится условно.
Задания для практической работы
1. Используя признак Лейбница, исследуйте сходимость знакочередующегося ряда:
1) ; 2) ;
3) ; 4) .
2. Исследуйте на сходимость (абсолютную или условную) знакочередующиеся ряды:
1) ; 2) ;
3) ; 4) ;
5) .
Контрольные вопросы:
1. Какой ряд называется знакопеременным?
2. Какой ряд называется знакочередующимся?
3. Сформулируйте признак Лейбница для знакочередующихся рядов.
4. Какой ряд называется абсолютно сходящимся, условно сходящимся?
5. Какие признаки используются для установления абсолютной сходимости знакопеременного ряда?
Рекомендуемая литература: 1.2[с. 405-430], 2.2[с. 66-113].
Практическая работа №24
cyberpedia.su
5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
Рассмотрим важный
класс рядов, называемых знакочередующимися.
Такими рядами называется ряд вида:
,
где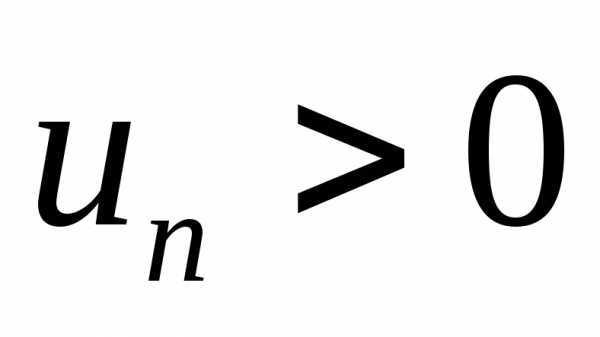
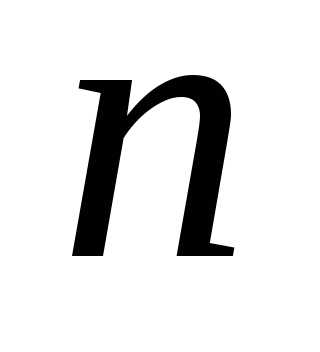 .
Для знакочередующихся рядов имеет место
достаточный признак сходимости (Признак
Лейбница).
.
Для знакочередующихся рядов имеет место
достаточный признак сходимости (Признак
Лейбница).Теорема Лейбница. Знакочередующийся ряд сходится, если:
последовательность абсолютных величин членов ряда монотонно убывает, т.е.
общий член ряда стремится к нулю
 .
При этом сумма
.
При этом сумма ряда
удовлетворяет неравенствам
ряда
удовлетворяет неравенствам .
.
Доказательство:
Рассмотрим сначала
частичную сумму четного числа 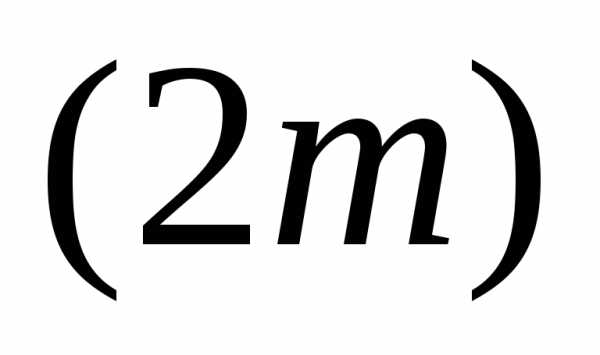
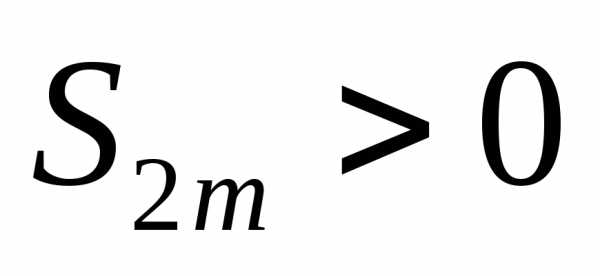 и
возрастает с возрастанием номера
и
возрастает с возрастанием номера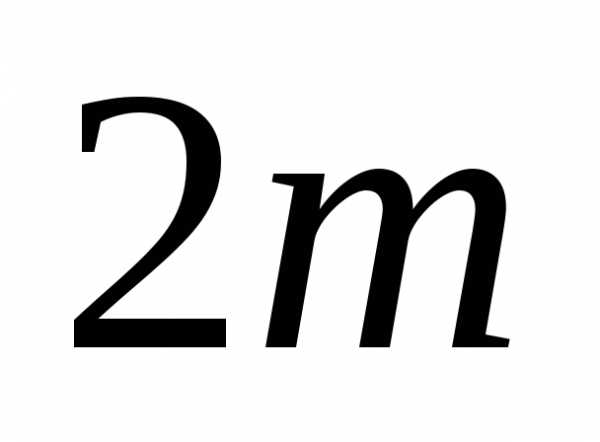 .
. С другой стороны 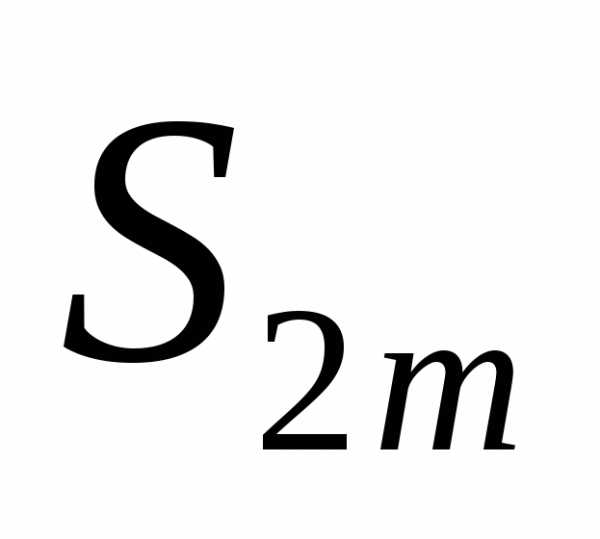 ,
можно переписать так:.
Легко увидеть, что
,
можно переписать так:.
Легко увидеть, что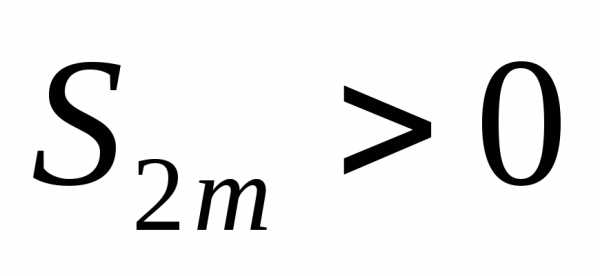 . Таким образом, последовательностьвозрастает и ограничена сверху.
Следовательно, она имеет предел
. Таким образом, последовательностьвозрастает и ограничена сверху.
Следовательно, она имеет предел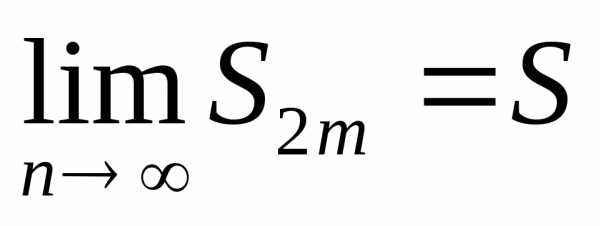 ,
причем
,
причем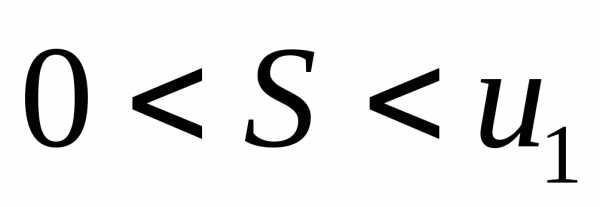 .
.
Рассмотрим теперь
частичные суммы нечетного числа 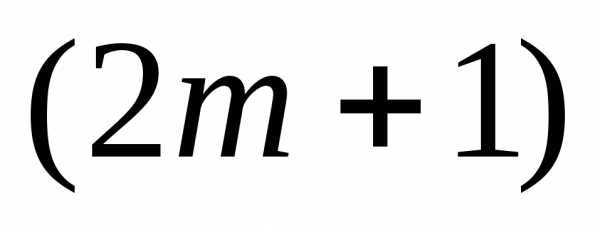
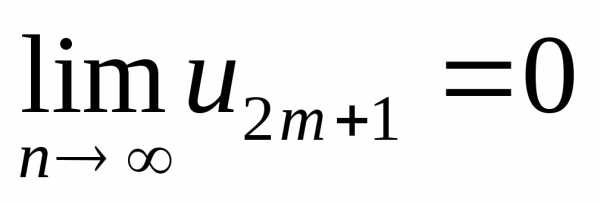 в
силу второго условия теоремы. Итак,
в
силу второго условия теоремы. Итак,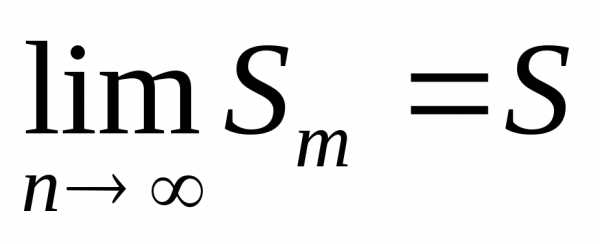 как при четном
как при четном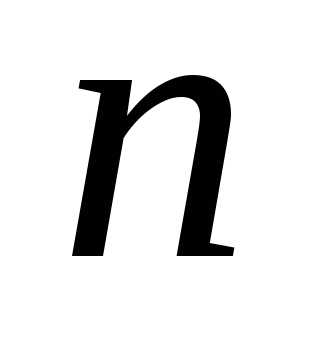 ,
так и при нечетном
,
так и при нечетном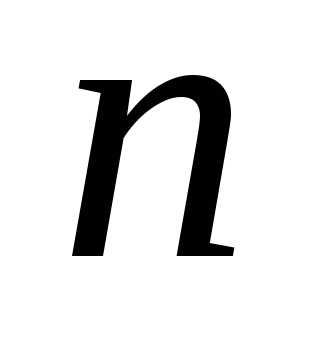 .
Следовательно, наш ряд сходится, причем
.
Следовательно, наш ряд сходится, причем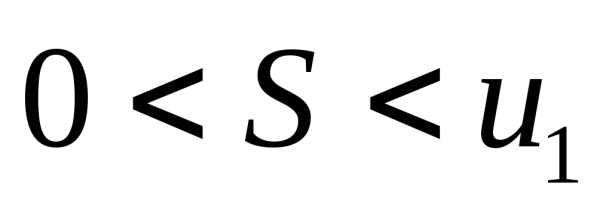 .
.Замечания.
Исследование знакочередующихся рядов вида (с отрицательным первым членом) сводится путем умножения всех его членов на (-1) к исследованию ряда с + первым членом.
Соотношение
позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму
 данного ряда его частичной суммой
данного ряда его частичной суммой .
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е.
.
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е. поэтому
ошибка меньше модуля первого из
отброшенных членов.
поэтому
ошибка меньше модуля первого из
отброшенных членов.
Пример.
Вычислить сумму
ряда 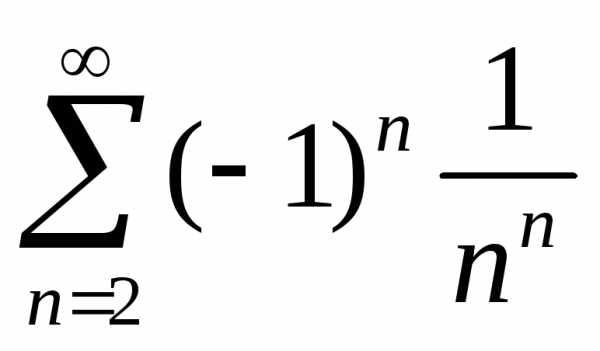 .
Данный ряд лейбницевского вида. Он
сходится. Можно записать.
Взяв 5 членов, т.е. заменив
.
Данный ряд лейбницевского вида. Он
сходится. Можно записать.
Взяв 5 членов, т.е. заменив насделаем ошибку, меньшую чем
насделаем ошибку, меньшую чем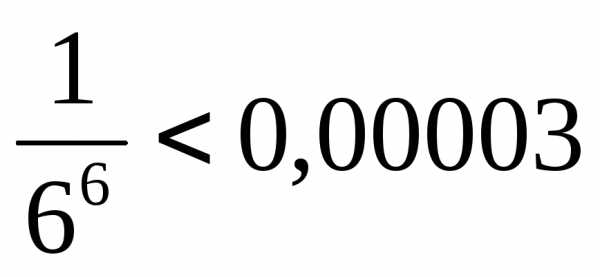
Общий достаточный признак сходимости знакопеременных рядов
Знакочередующийся
ряд является частным случаем
знакопеременного ряда. Числовой ряд 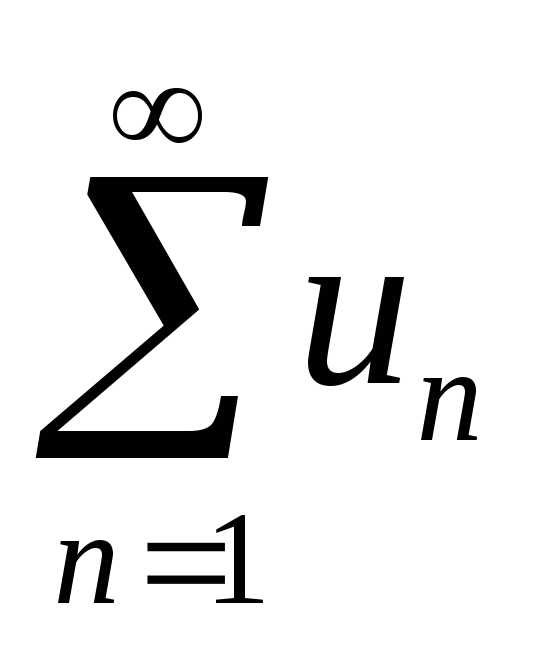 ,
содержащий бесконечное множество
положительных и бесконечных множеств
отрицательных членов, называетсязнакопеременным. Для
знакопеременных рядов имеет место
следующий общий достаточный признак
сходимости.
,
содержащий бесконечное множество
положительных и бесконечных множеств
отрицательных членов, называетсязнакопеременным. Для
знакопеременных рядов имеет место
следующий общий достаточный признак
сходимости.
Теорема. Пусть дан знакопеременный ряд . Если сходится ряд, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
Доказательство:
Рассмотри
вспомогательный ряд, составленный из
членов рядов  и
и .
.
.
Очевидно, что
для
всех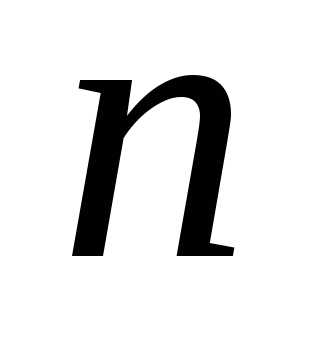
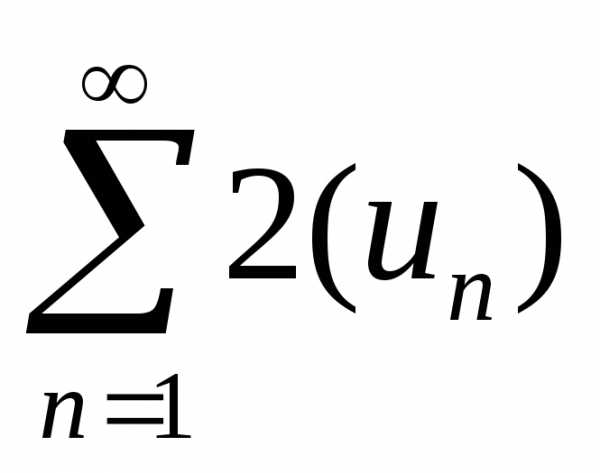 сходится в силу условий теоремы исвойства 1 числовых рядов. Следовательно, на
основании признака сравнения сходится
и ряд
сходится в силу условий теоремы исвойства 1 числовых рядов. Следовательно, на
основании признака сравнения сходится
и ряд 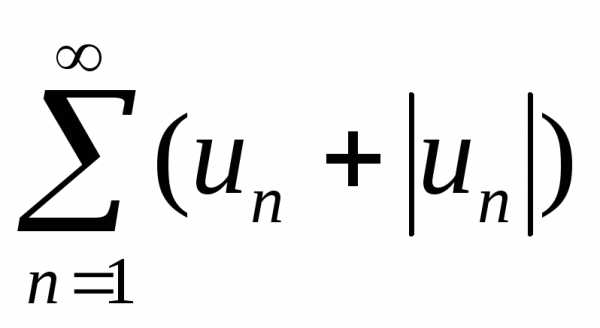 .
Поскольку данный знакопеременный ряд
представляет собой разность двух
сходящихся рядов,
то на основаниисвойства
2 числовых
рядов ряд
.
Поскольку данный знакопеременный ряд
представляет собой разность двух
сходящихся рядов,
то на основаниисвойства
2 числовых
рядов ряд 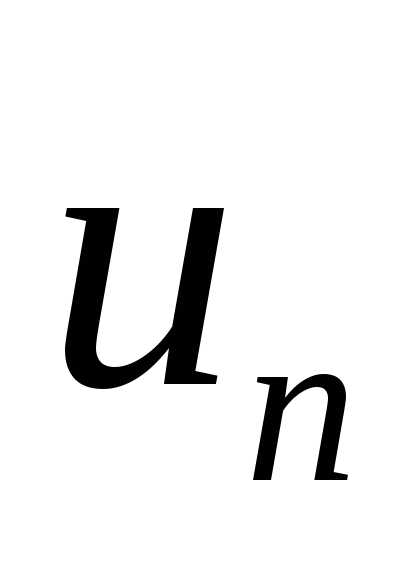 сходится.
сходится. Отметим, что
обратное утверждение несправедливо:
если сходится ряд 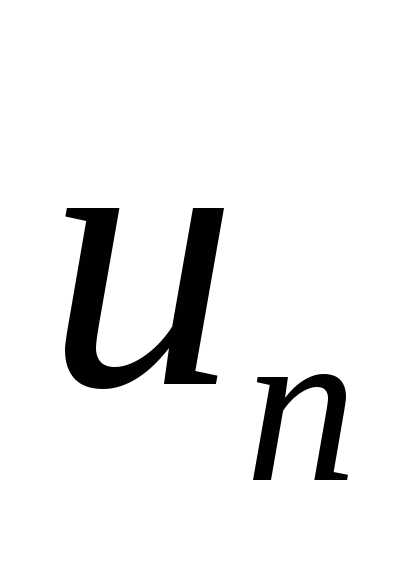 ,
то это не означает, что сходится ряд
,
то это не означает, что сходится ряд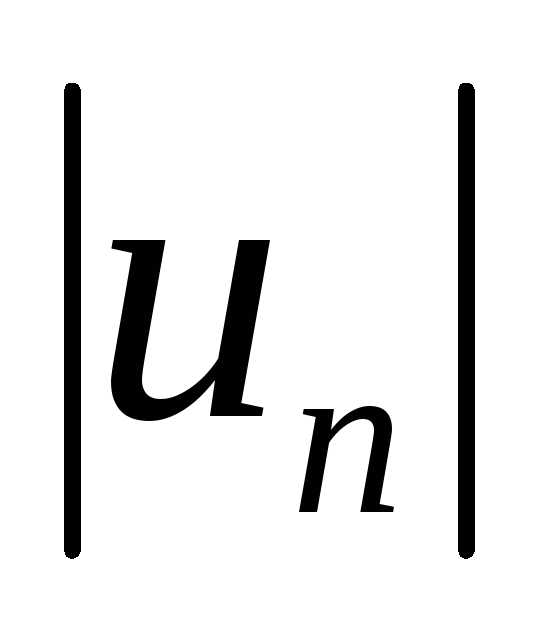 .
.
Исследовать
сходимость ряда 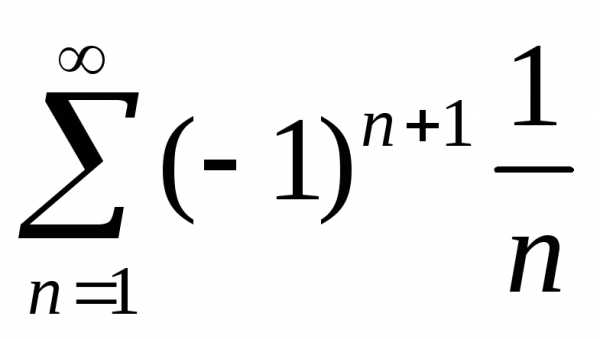 .
Для этого ряда выполнены условия признака
Лейбница. Следовательно, ряд сходится.
Однако ряд, составленный из модулей
членов этого ряда, т.е.
.
Для этого ряда выполнены условия признака
Лейбница. Следовательно, ряд сходится.
Однако ряд, составленный из модулей
членов этого ряда, т.е.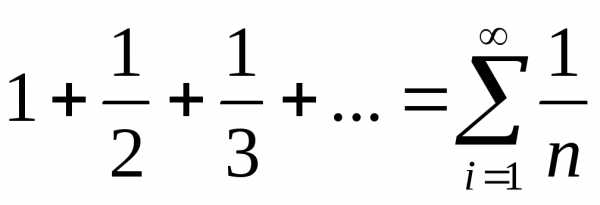 расходится (гармонический ряд).
расходится (гармонический ряд).
5.8. Абсолютная и условная сходимость числовых рядов
Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называют условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Т.е. абсолютно сходящиеся ряды суммируются, вычитаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов, такие свойства, вообще говоря, не имеют места.
studfiles.net
Признак Лейбница. Абсолютная и условная сходимость ряда
Теорема (признак Лейбница). Знакочередующийся ряд сходится, если:
1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. .
2) общий член ряда стремится к нулю: . При этом сумма S ряда удовлетворяет неравенствам
Пусть дан знакопеременный ряд , где – произвольные числа (действительные или комплексные). Если ряд , составленный из абсолютных величин его членов, сходится, то данный ряд также сходится. В этом случае знакопеременный ряд называется абсолютно сходящимся. Следовательно, если же знакопеременный ряд сходится, а ряд расходится, то данный ряд называется условно сходящимся.
Пример 1.Исследовать на сходимость ряд Решение. 1. Исследуем на сходимость ряд из абсолютных величин членов данного ряда: = .Сравним этот ряд с рядом . Так как < , то > для всех n.Ряд расходится, так как расходится ряд (как ряд Дирихле при p= <1). Значит, по 1-му признаку сравнения расходится и ряд .
Итак, исходный ряд не является абсолютно сходящимся.
2. Выясним, сходится ли данный знакочередующийся ряд, применяя признак Лейбница.
· Проверим, выполняется ли неравенство > для абсолютных
величин членов данного ряда:
= > .
Данное неравенство эквивалентно неравенству < , которое верно для любого n=1,2….Значит для все номеров n = 1,2…
· Найдём предел общего члена ряда: = = 0.
Таким образом, для данного знакочередующегося ряда выполнены оба условия, содержащиеся в признаке Лейбница, откуда следует, что исходный ряд сходится, однако он не является абсолютно сходящимся, поэтому данный ряд сходится условно. Ответ: ряд сходится условно.
Задание 6. Исследовать на абсолютную и условную сходимость ряды:
Функциональные ряды
Понятие функционального ряда
Ряд, членами которого являются функции от x, называется функциональным:
Придавая определенное значение , получим числовой ряд
который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимостифункционального ряда. Совокупность числовых значений аргумента x, при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой функцией от : . Определяется она в области сходимости равенством , где частичная сумма ряда.
Степенные ряды
Степенным рядом называется ряд вида:
.
Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.
Число R называется радиусом сходимости степенного ряда, если при ряд сходится и притом абсолютно, а при ряд расходится. Радиус сходимости найдем, используя признак Даламбера:
т.е. если степенной ряд сходится при любых , удовлетворяющих данному условию и расходится при . Отсюда следует, что если существует предел ,то радиус сходимости ряда равен этому пределу и степенной ряд сходится при , т.е. в промежутке , который называется промежутком (интервалом) сходимости.
Если , то степенной ряд сходится в единственной точке . На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.
Сходимость степенного ряда при и исследуется с помощью какого-либо из признаков сходимости.
Пример 2. Найти область сходимости ряда. Решение. Найдём радиус сходимости ряда:
Следовательно, ряд сходится при , т.е. при . При имеем ряд , который сходится по признаку Лейбница.
При имеем расходящийся ряд: . Ответ: областью сходимости исходного ряда является промежуток Задание 7. Найти область сходимости степенного ряда:
Ответы:
Задание 1. 1) , 2) , 3) , 4), 5) , 6) , 7) ,
8) , 9) , 10) .
Задание 2. 1) да, 2) да, 3) да, 4) нет, 5) нет, 6) да, 7) да, 8) нет, 9) нет, 10) да.
Задание 3. 1)сходится , 2) расходится, 3) расходится, 4) расходится, 5) сходится, 6) сходится, 7) расходится, 8) расходится, 9) сходится, 10) сходится.
Задание 4. 1) расходится, 2) сходится, 3) сходится, 4) сходится, 5) сходится, 6) сходится, 7) сходится, 8) расходится, 9) сходится, 10) расходится.
Задание 5. 1) расходится, 2) сходится, 3) сходится, 4) расходится, 5)
сходится, 6) расходится, 7) сходится, 8) расходится, 9) расходится, 10)
расходится.
Задание 6. 1) абсолютно сходится, 2) условно сходится, 3) условно сходится, 4) условно сходится, 5) абсолютно сходится, 6) абсолютно сходится, 7) абсолютно сходится, 8) абсолютно сходится, 9) условно сходится, 10) условно сходится.
Задание 7. 1) (-2;2], 2) , 3) , 4) (-4;4), 5) [-3;1), 6) [-1;5], 7) (-6;2), 8) (-2;1), 9) , 10) (0;4).
infopedia.su
Знакопеременные ряды. Абсолютная и условная сходимость
Если не все члены ряда имеют одинаковые знаки, то ряд называется знакопеременным. В случае конечного числа членов, имеющих один знак, при исследовании сходимости эти члены можно отбросить и рассматривать остающийся знакопостоянный ряд. Исследование же рядов с бесконечным количеством положительных и отрицательных членов имеет некоторые принципиальные отличия от исследования знакопостоянных рядов.
Одним из важных достаточных признаков сходимости знакопеременного ряда является следующая теорема:
Ряд с членами произвольных знаков
= (3.6)
сходится, если сходится ряд
= , (3.7)
составленный из абсолютных величин членов ряда (3.6).
В этом случае ряд (3.6) называется абсолютно сходящимся. Исследование сходимости абсолютно сходящегося знакопеременного ряда сводится к исследованию сходимости соответствующего ряда с положительными членами.
Пример. Исследовать сходимость ряда ., где – любое число.
◄ Рассмотрим ряд, составленный из абсолютных величин исходного ряда: . Так как члены полученного положительного ряда не больше соответственных членов сходящегося ряда Дирихле , исходный тоже сходится (абсолютно). ►
Возможны случаи, когда ряд (3.6) сходится, а ряд (3.7) расходится. Тогда ряд называют неабсолютно, или условно сходящимся.
Таким образом, из расходимости ряда расходимость знакопеременного ряда , вообще говоря, не следует. Однако, если, применяя к ряду признак Даламбера (или признак Коши), получаем предел (или ), то в этом случае оба ряда – и – расходятся.
Пример. Исследовать на сходимость ряд .
◄ Рассмотрим ряд из абсолютных величин членов данного ряда: . Для исследования сходимости последнего ряда с положительными членами применим признак Даламбера:
.
Отсюда
,
т. е. ряд с положительными членами расходится и, следовательно, исходный ряд не является абсолютно сходящимся. Кроме того, из следует, что для всех номеров, начиная с некоторого и, следовательно, . Так как необходимое условие сходимости не выполняется, исходный ряд расходится. ►
Если ряд абсолютно сходится, то ряд, полученный из него любой перестановкой членов, также сходится и имеет ту же сумму, что и исходный (переместительное свойство абсолютно сходящихся рядов).
Неабсолютно (условно) сходящиеся ряды переместительным свойством не обладают. Более того, можно так переставить члены неабсолютно сходящегося ряда, чтобы преобразованный ряд имел сумму, равную любому наперед заданному числу, или стал расходящимся (теорема Римана).
Пример. Рассмотрим ряд
.
Позже будет показано, что этот ряд является условно сходящимся. Обозначим его сумму через (показано, что ). Умножим этот ряд на множитель и запишем полученный ряд под исходным следующим образом:
Так как последний ряд получен умножением сходящегося ряда на постоянное число, то он также будет сходящимся и его сумма будет равна . Сложив теперь оба ряда почленно, соединяя вместе члены, стоящие друг под другом, получим
.
Полученный при сложении двух сходящихся рядов будет также сходящимся, а его сумма равна . Но этот ряд можно, очевидно, получить из исходного путем перестановки его членов. Таким образом, от перестановки сумма ряда умножилась на .
Знакопеременный ряд можно представить состоящим из двух рядов: ряда, составленного только из его положительных членов, и ряда, составленного только из его отрицательных членов. В случае абсолютно сходящегося ряда оба этих знакопостоянных ряда сходятся и его сумма равна разности сумм двух рядов с положительными членами. Для условно сходящегося ряда оба ряда расходящиеся, т. е. его нельзя рассматривать как разность двух сходящихся рядов, один из которых состоит из положительных членов данного ряда, а другой – из абсолютных величин его отрицательных членов.
infopedia.su
Глава 94. Ряды с членами произвольного знака. Абсолютная и условная сходимость
Рассмотрим распространенный тип числового ряда, так называемые знакочередующиеся ряды, элементы которых имеют чередующиеся знаки. Полагая первый член положительным, знакопеременный ряд можно записать в виде
(9.4.1) |
Где .
Для знакопеременных рядов имеет место достаточный признак сходимости.
Теорема (признак Лейбница)
Если члены знакочередующегося ряда (9.4.1), будучи взяты по модулю, образуют Не возрастающую бесконечно малую последовательность, т. е. и , то этот ряд Сходится.
Приведем Примеры знакочередующихся рядов.
Пример
Исследовать сходимость ряда .
Решение
Этот ряд сходится по признаку Лейбница, так как его члены убывают по абсолютной величине и при .
Пример
Исследовать сходимость ряда .
Решение
Нетрудно убедиться, что данный ряд удовлетворяет условиям Теоремы 1 и потому сходится.
Пример
Исследовать сходимость ряда .
Решение
Так как члены знакочередующегося ряда убывают по абсолютной величине и предел общего члена ряда , то по признаку Лейбница ряд сходится.
Замечание
В теореме Лейбница существенно не только условие , но и условие . Так, например, для ряда второе условие нарушено и, хотя , ряд расходится. Это видно, если данный ряд представить в виде , т. е. удвоенного гармонического ряда.
Определение
Под Знакопеременным рядом будем понимать ряд, в котором любой его член может быть как Положительным, так и Отрицательным.
Рассмотрим случай ряда с членами, имеющими произвольные знаки:
(9.4.2) |
Одновременно рассмотрим ряд
(9.4.3) |
Где – члены ряда (9.4.2).
Теорема (достаточный признак сходимости знакопеременного ряда)
Из Сходимости ряда (9.4.3) следует Сходимость ряда (9.4.2).
Определение
Ряд называется Абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение
Ряд называется Условно сходящимся, Если сам ряд сходится, а ряд, составленный абсолютных величин его членов, расходится.
Приведем Примеры Абсолютной и условной сходимости числовых рядов.
Пример
Ряд сходится по признаку Лейбница, однако гармонический ряд расходится, следовательно, сходимость условного ряда является условной.
Пример
, . При этот ряд Сходится абсолютно (как обобщенный гармонический ряд). При данный ряд Сходится условно.
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся ряды – в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, ряд . Переставим члены местами и сгруппируем их следующим образом: . Перепишем ряд в виде: , т. е. от перестановки членов ряда сумма его уменьшилась в два раза.
Можно показать (Теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
В заключение приведем без доказательства один важный признак сходимости числового ряда.
Теорема (признак Дирихле –Абеля)
Пусть дан ряд
. | (9.4.4) |
Если последовательность частичных сумм ряда Ограничена и последовательность является Не возрастающей и бесконечно малой, то ряд (9.4.4) Сходится.
Заметим, что признак Лейбница является частным случаем этой теоремы при .
Пример
Применим сформулированный выше признак Дирихле–Абеля к установлению сходимости ряда
, . | (9.4.5) |
Решение
Положим , . Вычислим частичные суммы ряда . Для этого умножим и поделим каждое слагаемое этой суммы на постоянную величину :
Таким образом, частичные суммы ряда ограничены, а последовательность является не возрастающей и бесконечно малой; условия Дирихле–Абеля выполняются, т. е. ряд (9.4.5) Сходится.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Интегральный признак сходимости. Сходимость ряда
Теорема. Пусть — непрерывная, неотрицательная, монотонно убывающая функция, определенная при . Тогда ряд и интеграл либо оба сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех выполняются неравенства . Интегрируя, получаем . Тогда , или . Поэтому если сходится, то . Тогда и , ряд сходится.
Пусть теперь наоборот, известно, что ряд сходится. Тогда . Взяв произвольное выберем так, чтобы . Тогда . Значит, сходится.
Абсолютная сходимость. Свойства абсолютно сходящихся рядов
Определение. Абсолютно сходящимся рядом называется сходящийся ряд , для которого сходится и ряд .
Легко доказать, что из сходимости ряда вытекает сходимость ряда . По критерию Коши, примененному к , получаем: . Из полученного неравенства следует, что и для исходного ряда также выполнен критерий Коши, следовательно он сходится.
Обозначим , т.е. , . Очевидны равенства: . Рассмотрим ряды и . Если они сходятся, то сходится и ряд , т.е. ряд абсолютно сходится. Если же сходятся ряды , то, т.к. , ряды и тоже сходятся. Таким образом, для абсолютной сходимости необходима и достаточна сходимость рядов и .
(признак Лейбница).
Если члены знакочередующегося ряда (9.4.1), будучи взяты по модулю, образуют не возрастающую бесконечно малую последовательность, т.е. и, то этот рядсходится.
Приведем примеры знакочередующихся рядов.
Исследовать сходимость ряда .
Этот ряд сходится по признаку Лейбница, так как его члены убывают по абсолютной величине и при.
Исследовать сходимость ряда .
Нетрудно убедиться, что данный ряд удовлетворяет условиям Теоремы 1 и потому сходится.
Замечание. В теореме Лейбница существенно не только условие , но и условие. Так, например, для рядавторое условие нарушено и, хотя, ряд расходится. Это видно, если данный ряд представить в виде, т.е. удвоенного гармонического ряда.
Под знакопеременным рядом будем понимать ряд, в котором любой его член может быть как положительным, так и отрицательным.
Рассмотрим случай ряда с членами, имеющими произвольные знаки:
. (9.4.2)
Одновременно рассмотрим ряд
, (9.4.3)
где — члены ряда (9.4.2).
(достаточный признак сходимости знакопеременного ряда). Из сходимости ряда (9.4.3) следует сходимость ряда (9.4.2).
Признак Даламбера сходимости знакоположительного ряда
Пусть дан
знакоположительный ряд 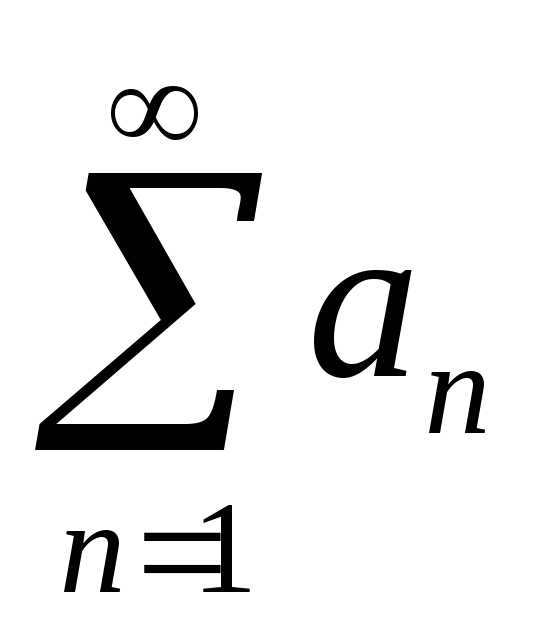 и существует
и существует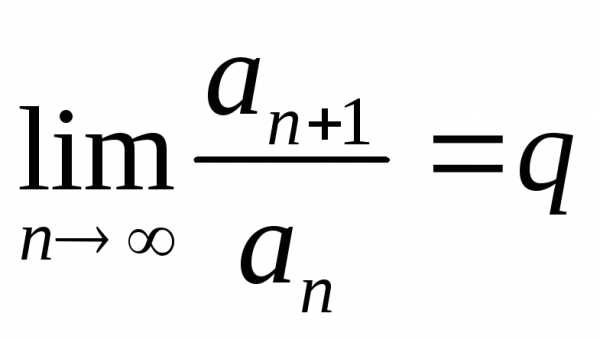 .
Тогда, еслиq
< 1, то ряд сходится; если q
> 1, то ряд расходится.
.
Тогда, еслиq
< 1, то ряд сходится; если q
> 1, то ряд расходится.
Доказательство:
1) пусть q
< 1, докажем, что ряд сходится. Поскольку
существует предел 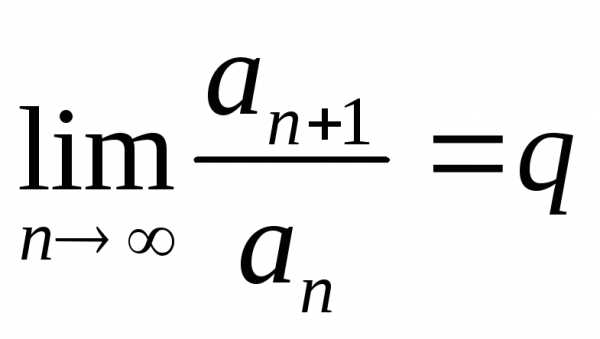 ,
можно записатьили
,
можно записатьили an (q
— )
< an+1 < an (q
+ ).
Выберем
таким образом, чтобы q
+
< 1. Из полученного двойного неравенства
и неравенства q
+
< 1 следует, что
an (q
— )
< an+1 < an (q
+ ).
Выберем
таким образом, чтобы q
+
< 1. Из полученного двойного неравенства
и неравенства q
+
< 1 следует, что
aN+2 < (q + ) aN+1;
aN+3 < (q + ) aN+2 < (q + )2 aN+1;
aN+4 < (q + ) aN+3 < (q + )3 aN+2 < (q + )3 aN+1.
Итак, члены ряда
aN+2 + aN+3 + aN+4 +… меньше соответствующих членов
бесконечной геометрической прогрессии
aN+1 (q
+ )
+ aN+2 (q
+ )2 + aN+3 (q
+ )3 +… Знаменатель прогрессии меньше
единицы, поэтому прогрессия представляет
собой сходящийся ряд (см. №1). По признаку
сравнения, ряд 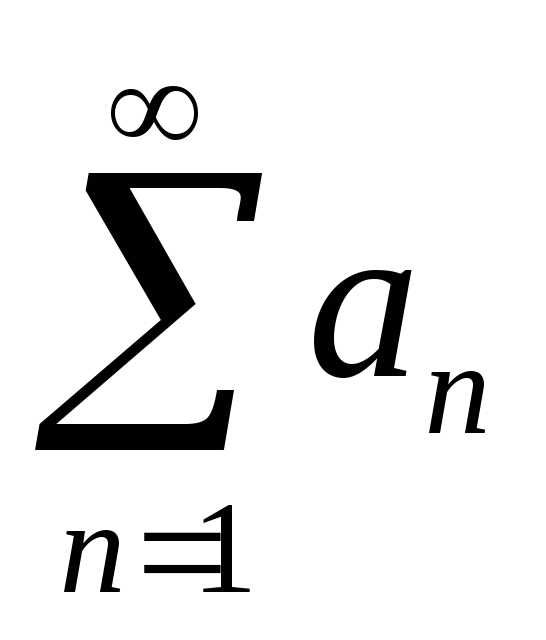 также является сходящимся.
также является сходящимся.
2) Пусть теперь q > 1. Возьмем такое число , что q — будет также больше единицы. Тогда для достаточно больших n, на основании выведенного в пункте 1) данного доказательства двойного неравенства, мы будем иметь
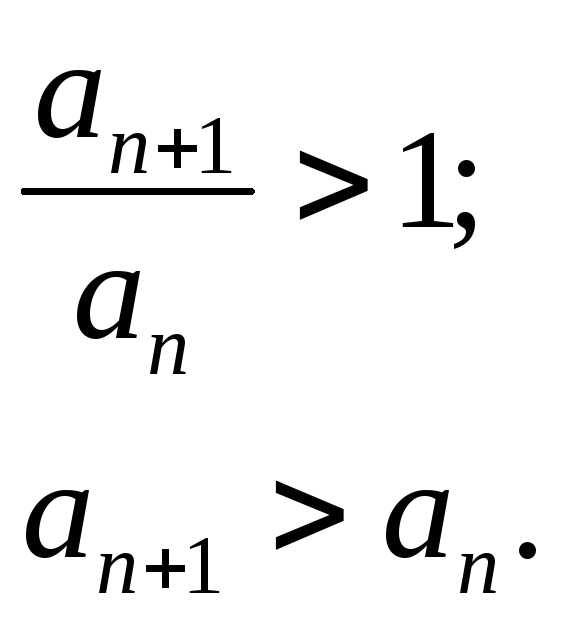
Отсюда aN < aN+1 < aN+2.
Следовательно члены ряда 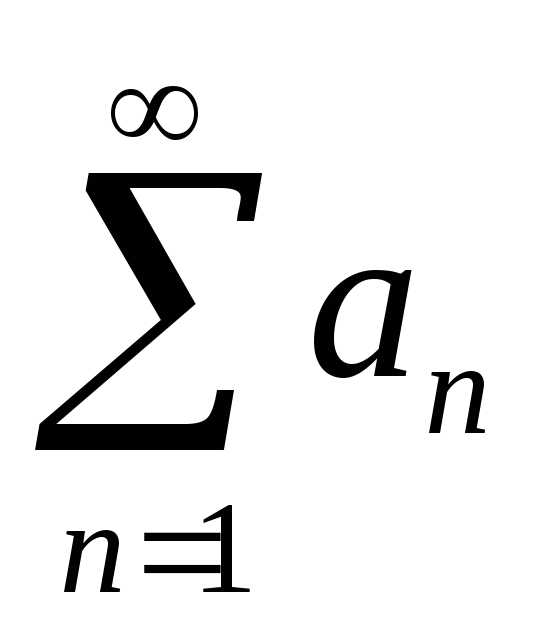 возрастают при увеличении их номера,
не выполняется необходимый признак
сходимости. Поэтому ряд
возрастают при увеличении их номера,
не выполняется необходимый признак
сходимости. Поэтому ряд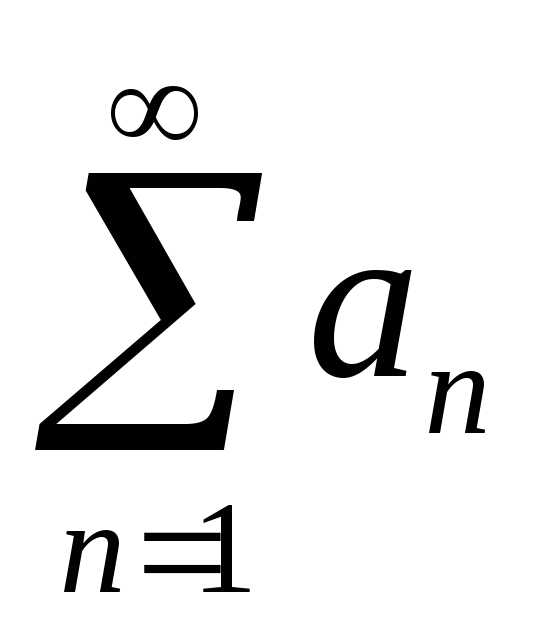 расходится. Теорема полностью доказана.
расходится. Теорема полностью доказана.
Если q
= 1, то нельзя определить характер
сходимости ряда. Например, ряд 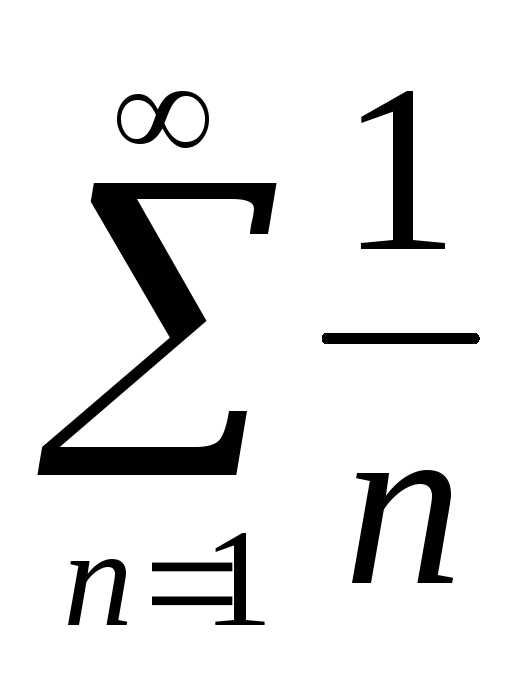 сходится, а ряд
сходится, а ряд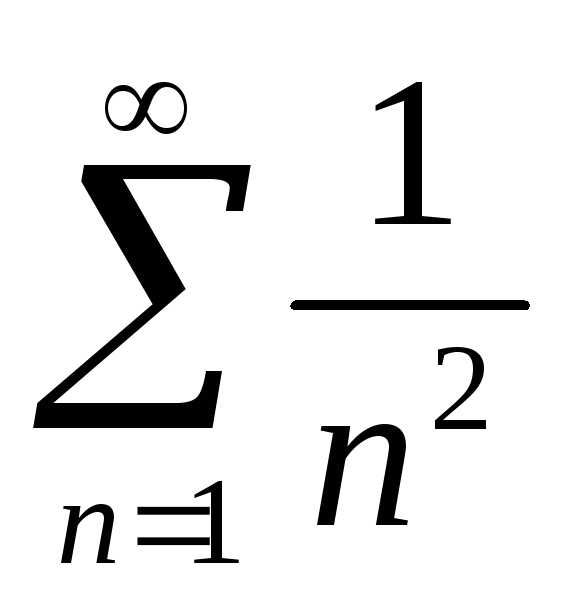 расходится.
расходится.
Знакочередующиеся ряды. Признак сходимости Лейбница. Понятие об абсолютно и условно сходящихся рядах
Знакочередующиеся ряды. Признак сходимости Лейбница. Знакочередующийся ряд – ряд, у которого любые рядом стоящие члены имеют противоположные знаки.
Признак сходимости Лейбница: если абсолютные величины членов знакочередующегося ряда монотонно убывают при возрастании их номера и n-й член ряда при неограниченном возрастании n стремится к нулю, т.е.
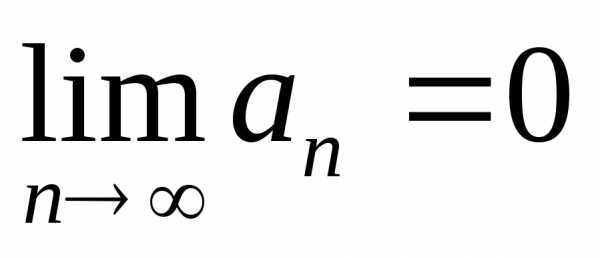 ,
,
то этот ряд сходится.
Доказательство:
возьмем сумму S2m первых членов ряда 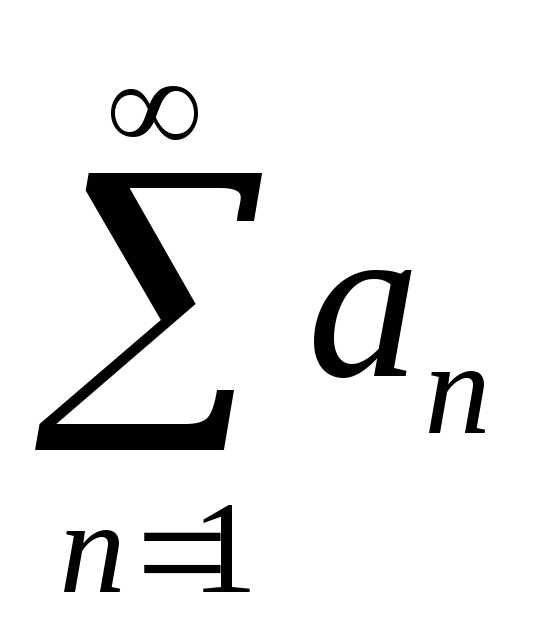 и запишем ее следующим образом:
и запишем ее следующим образом:
S2m = (a1 – a2) + (a3 + a4) +…+ (a2m-1 + a2m).
Так как разности, стоящие в скобках, на основании условия монотонности убывания абсолютных величин членов ряда, положительны, то
S2m 0.
Если 2m возрастает, то S2m не убывает, т.к. каждый раз прибавляются положительные или равные нулю слагаемые.
С другой стороны ту же сумму можно представить в виде:
S2m = a1 – (a2 – a3) – (a4 – a5) -…- (a2m-2 – a2m-1) – a2m.
В скобках стоят положительные числа, поэтому
S2m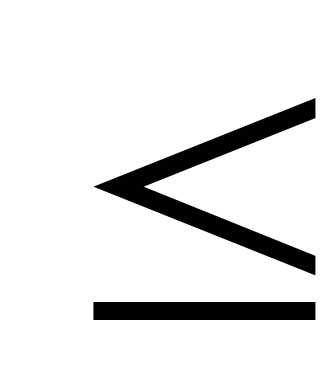 a1.
a1.
Следовательно, S2m, будучи монотонно возрастающей (точнее, не убывающей) и ограниченной последовательностью, имеет при m конечный предел S:
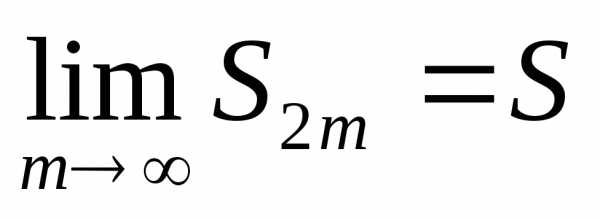 .
.
Но очевидно, что
S2m+1 = S2m + а2m+1.
На основании условия о стремлении n-го члена к нулю, имеем также
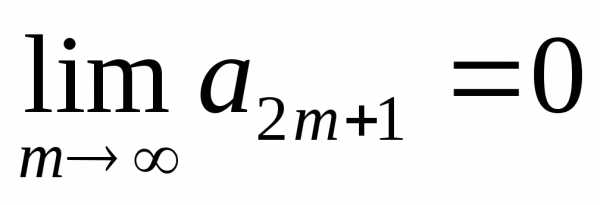 .
.
Таким образом, получаем
.
Мы получили, что
при неограниченном возрастании n
частные суммы Sn стремятся к одному и тому же пределу S,
независимо от того, будет ли n
четное или нечетное. Поэтому ряд 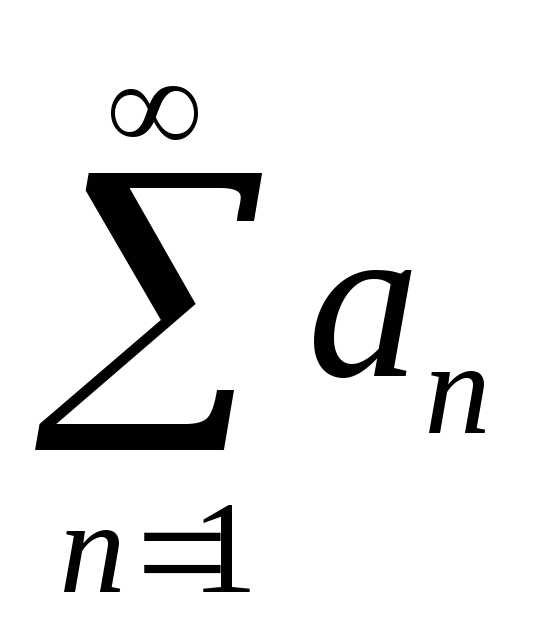 сходится.
сходится.
Понятие об абсолютно и условно сходящихся рядах. Ряд, состоящий из членов разных знаков, называется знакопеременным. Знакопеременный ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Теорема: если для
знакопеременного ряда 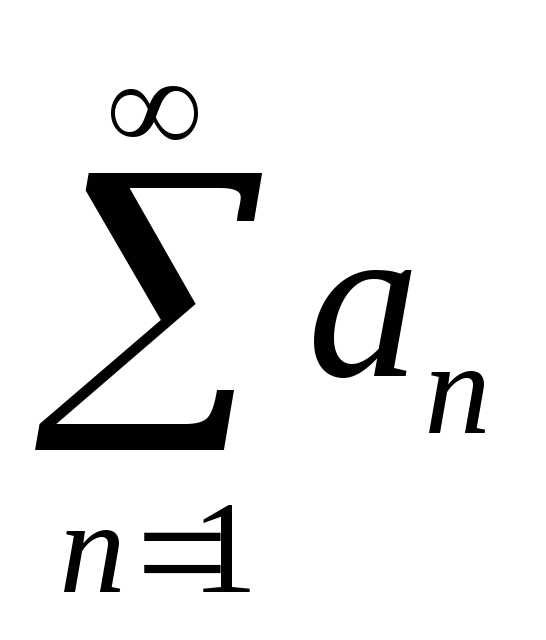 сходится ряд, составленный их абсолютных
величин его членов
сходится ряд, составленный их абсолютных
величин его членов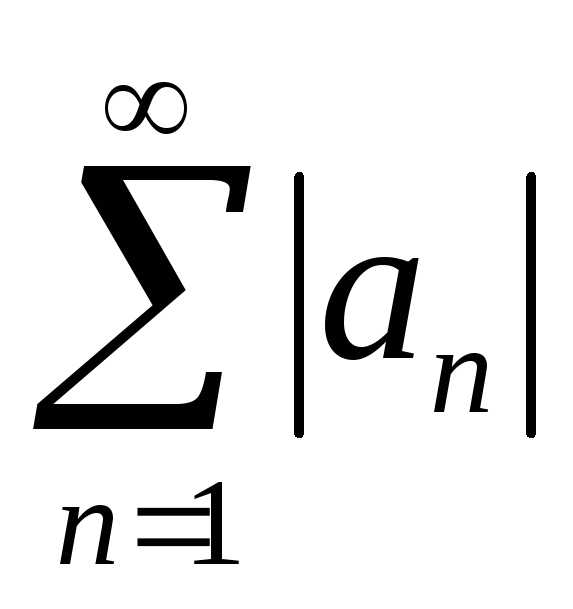 ,
то данный ряд также сходится.
,
то данный ряд также сходится.
Доказательство: рассмотрим вспомогательный ряд
Так как 1) 0
и 2) ряд в силу заданной по условию сходимости
ряда
в силу заданной по условию сходимости
ряда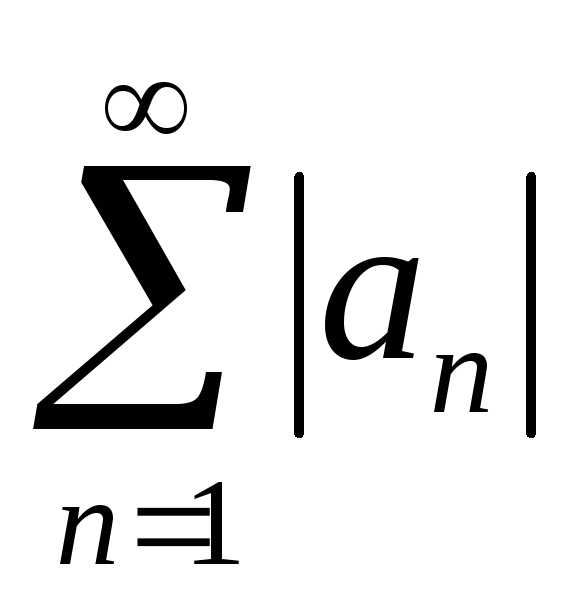 также сходится, то на основании признака
сравнения и рассматриваемый вспомогательный
ряд сходится. Поэтому наш ряд
также сходится, то на основании признака
сравнения и рассматриваемый вспомогательный
ряд сходится. Поэтому наш ряд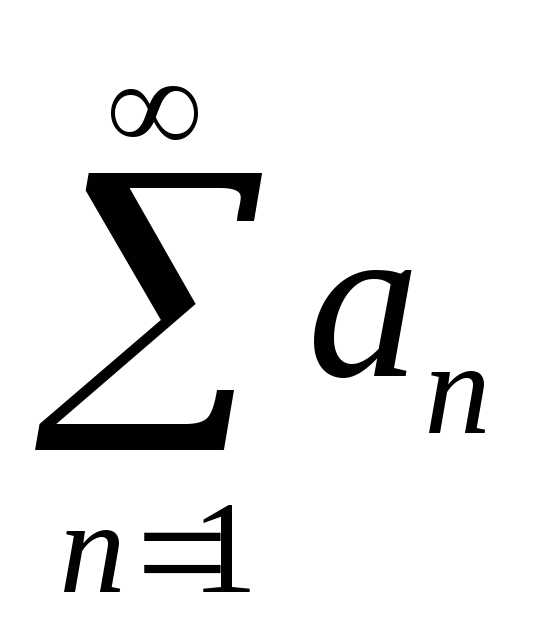 представляет собой разность двух
сходящихся рядов
представляет собой разность двух
сходящихся рядов
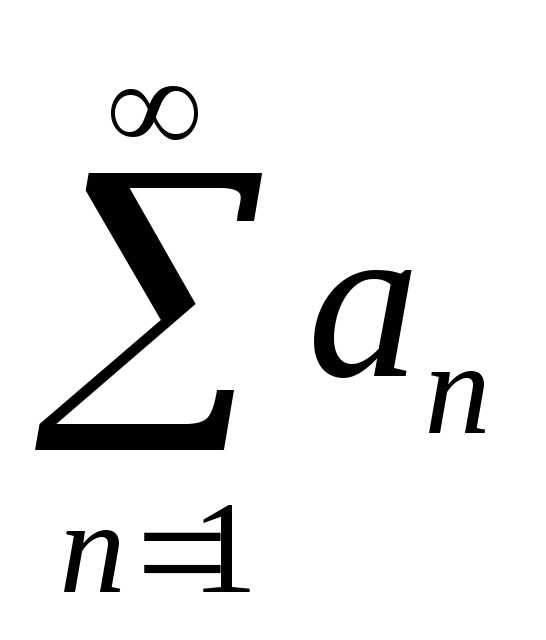 =
=
и, следовательно, сходится, ч. т. д. Обратное утверждение не верно.
Степенные ряды.
Определение. Степенным рядом называется ряд вида
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример. Исследовать на сходимость ряд
Применяем признак Даламбера:
.
Получаем,
что этот ряд сходится при 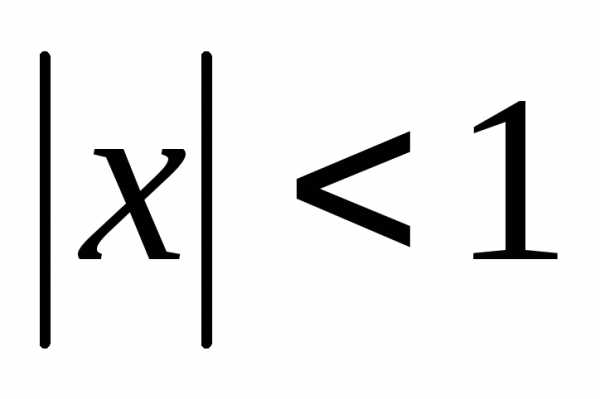 и
расходится при
и
расходится при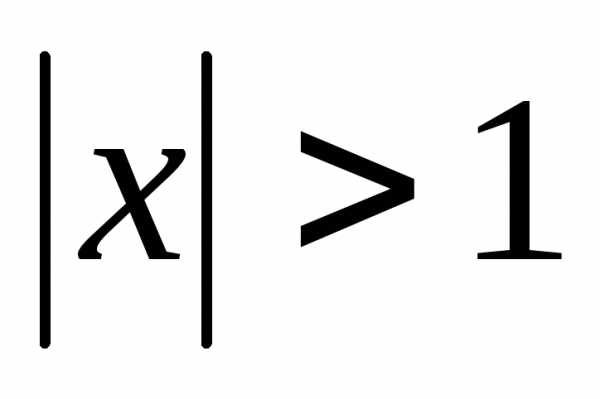 .
.
Теперь определим сходимость в граничных точках 1 и –1.
При х = 1: ряд сходится по признаку Лейбница (см. Признак Лейбница.).
При х = -1: ряд расходится (гармонический ряд).
Теоремы Абеля.
(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)
Теорема. Если степенной
ряд
сходится приx = x1 , то он сходится и притом абсолютно для
всех 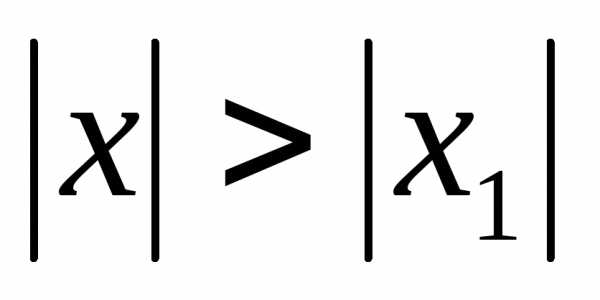 .
.
Доказательство. По условию теоремы, так как члены ряда ограничены, то
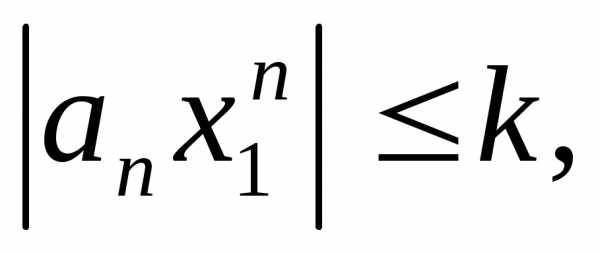
где k— некоторое постоянное число. Справедливо следующее неравенство:
Из этого неравенства
видно, что при x<x1 численные величины членов нашего ряда
будут меньше ( во всяком случае не больше
) соответствующих членов ряда правой
части записанного выше неравенства,
которые образуют геометрическую
прогрессию. Знаменатель этой прогрессии 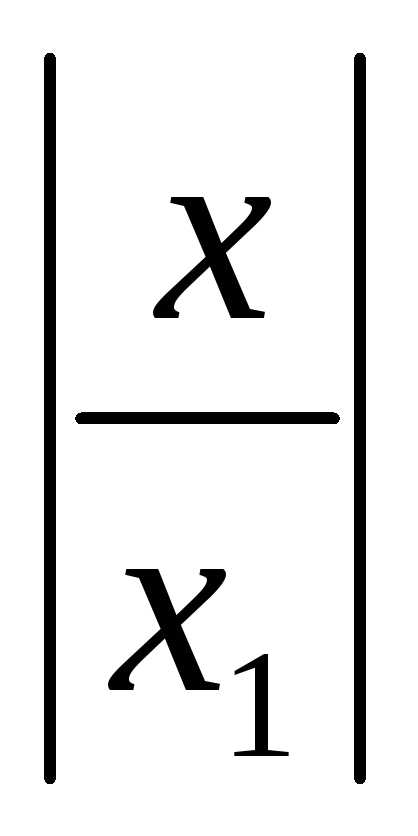 по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.
по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.
Поэтому на основании
признака сравнения делаем вывод, что
ряд 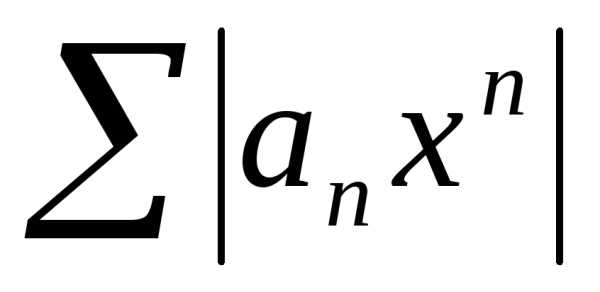 сходится, а значит ряд
сходится, а значит ряд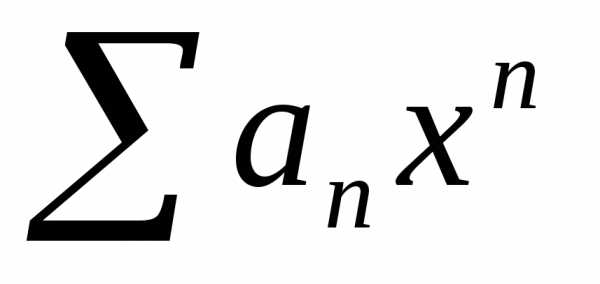 сходится абсолютно.
сходится абсолютно.
Таким образом, если
степенной ряд 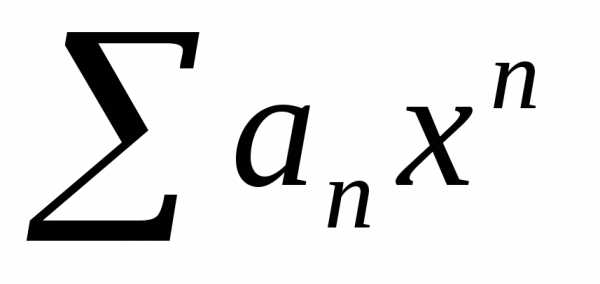 сходится
в точкех1,
то он абсолютно сходится в любой точке
интервала длины 2
сходится
в точкех1,
то он абсолютно сходится в любой точке
интервала длины 2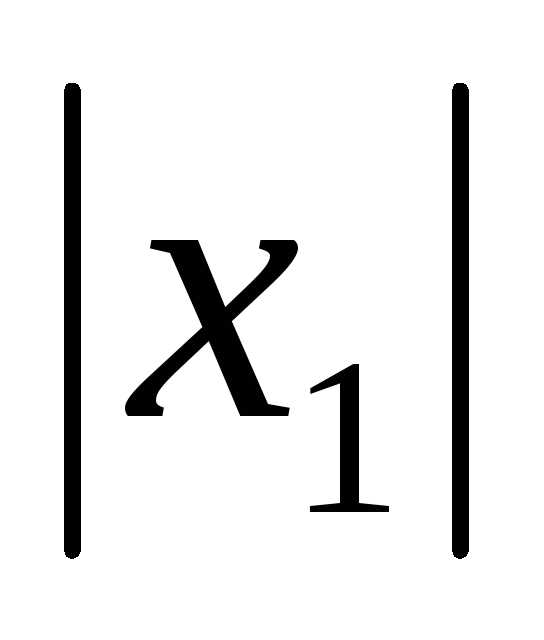 с центром в точкех = 0.
с центром в точкех = 0.
Следствие. Если при х =
х1 ряд расходится, то он расходится для
всех 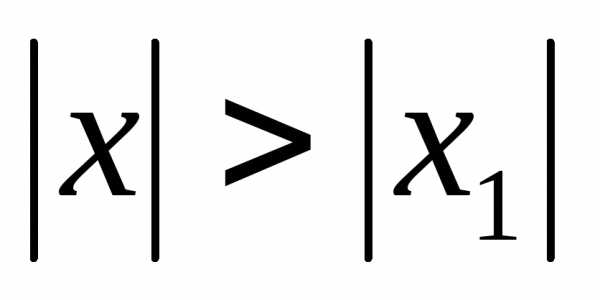 .
.
Таким образом, для
каждого степенного ряда существует
такое положительное число R,
что при всех х таких, что 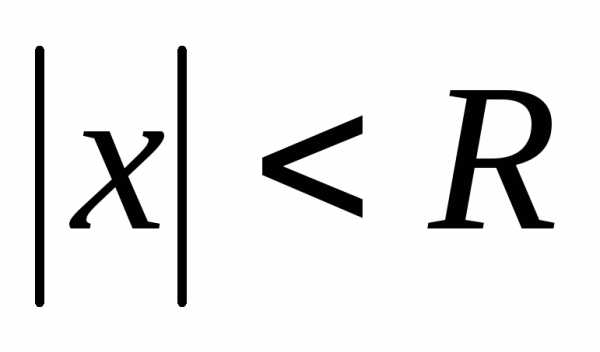 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех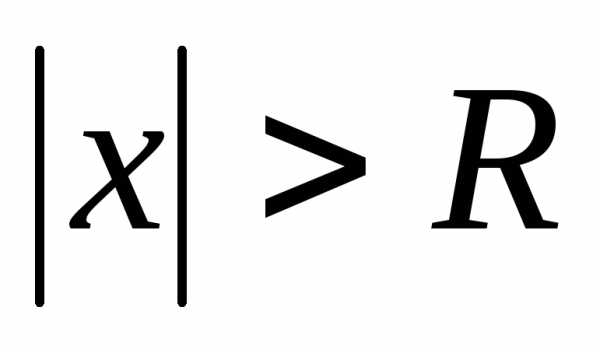 ряд
расходится. При этом числоR
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
ряд
расходится. При этом числоR
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
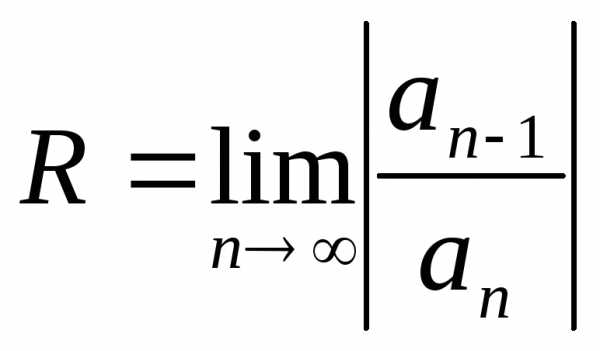
Пример. Найти область сходимости ряда
Находим радиус сходимости .
Следовательно, данный ряд сходится прилюбом значении х. Общий член этого ряда стремится к нулю.
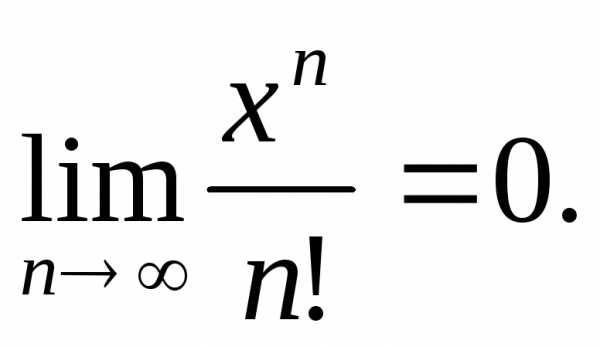
Теорема. Если степенной ряд 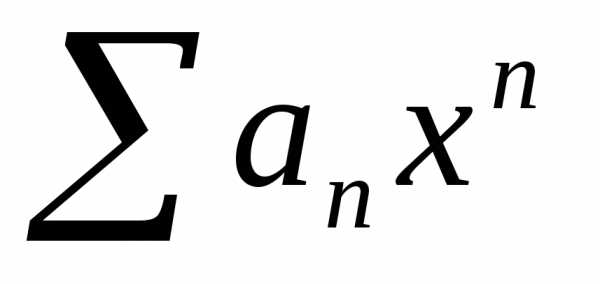 сходится для положительного значениях=х1 , то он сходится равномерно в любом
промежутке внутри
сходится для положительного значениях=х1 , то он сходится равномерно в любом
промежутке внутри 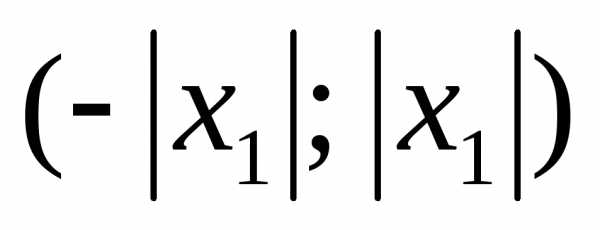 .
.
Действия со степенными рядами.
studfiles.net

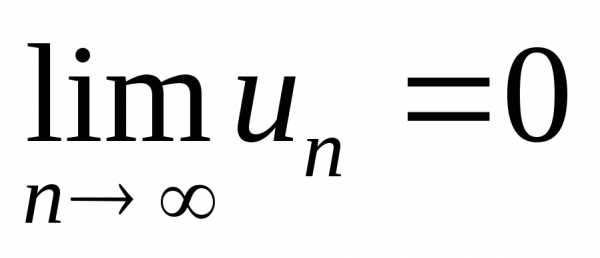 .
При этом сумма
.
При этом сумма ряда
удовлетворяет неравенствам
ряда
удовлетворяет неравенствам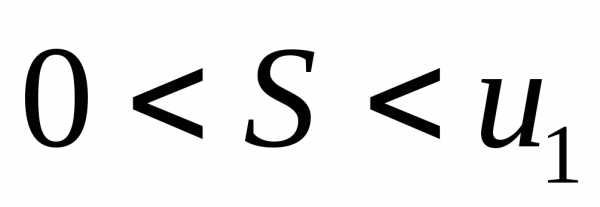 .
.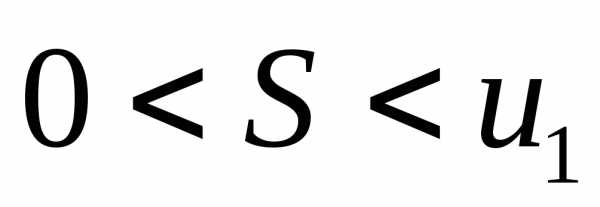
 данного ряда его частичной суммой
данного ряда его частичной суммой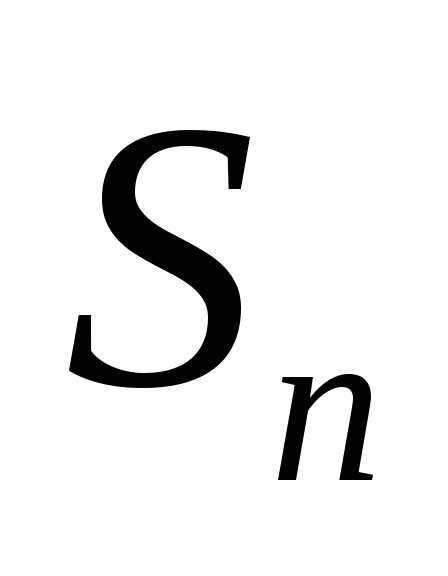 .
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е.
.
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е. поэтому
ошибка меньше модуля первого из
отброшенных членов.
поэтому
ошибка меньше модуля первого из
отброшенных членов.