Измерение углов. Транспортир
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов
и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34‘19»
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
naobumium.info
Измерение углов. Транспортир. Видеоурок. Математика 5 Класс
Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.
Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.
В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.
Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).
Рис. 1. Окружность, разделенная на 360 равных углов
Один такой маленький угол назовем углом в 1° (см. Рис. 2).
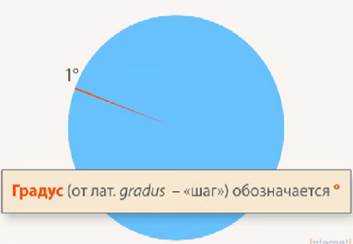
Рис. 2. 1 градус
Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).
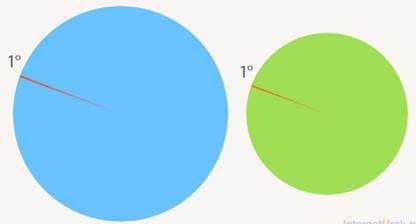
Рис. 3. Углы равны
Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).
Рис. 4. Более явный пример равенства углов
Величина любого угла – это сколько раз в него умещается угол в 1°.
Вот мы видим угол 13° (см. Рис. 5).
Рис. 5. Угол 13°
Понятно, что полный угол состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).
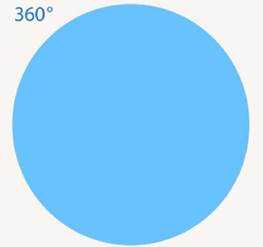
Рис. 6. Полный угол
Развернутый угол – это половина полного угла. Он равен (см. Рис. 7).
Рис. 7. Развернутый угол
Прямой угол является половиной развернутого и равен 90° (см. Рис. 8).
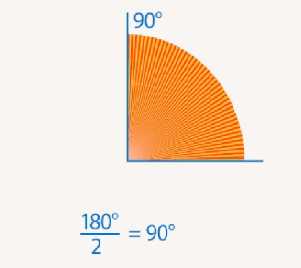
Рис. 8. Прямой угол
Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый – на 180, или прямой – на 90.
Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).
Рис. 9. Транспортир
Единицы измерения на ней – градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, – это 180°, развернутый.
Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.
1. Измерим пару углов.
Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, – 54° (см. Рис. 10, 11).
Рис. 10. Измерение угла
Проделаем то же самое со вторым углом, 137°.
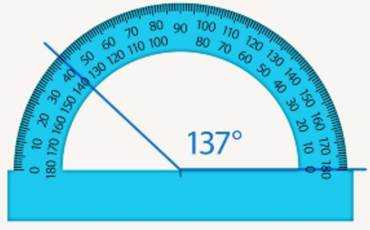
Рис. 11. Измерение угла
Если сторона угла не достает до шкалы, то ее нужно сначала продлить.
2. Начертим углы 29°, 81° и 140°.
Сначала чертим одну сторону угла по линейке (см. Рис. 12).
Рис. 12. Построение одной стороны угла
Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла – 29° (см. Рис. 13).
Рис. 13. Использование транспортира для построения углов
Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).
Рис. 14. Угол 29°
Точно так же строим два других угла (см. Рис. 15).
Рис. 15. Построение углов
Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус – это полного угла.
Инструментом для измерения и построения углов является транспортир.
Можно не использовать названия углов – полный, развернутый, прямой. Мы можем просто говорить – 360 градусов, 180 или 90 градусов.
На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.
Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину – скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода – 5 км/ч, 5 минут – это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.
Точно по такому же принципу устроена другая единица измерения расстояния – световой год. Световой год – расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.
Очень распространенный пример использования «чужой» единицы измерения – это измерять вес в килограммах. На самом деле килограмм – единица измерения массы, а вес – это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.
Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).
Хотя для угла есть свои «родные» единицы измерения – градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.
Получим величину угла , которая называется тангенсом.
Если увеличить треугольник, то ничего не изменится (см. Рис. 16).
Рис. 16. Тангенс
Ведь во сколько раз увеличилась одна сторона, во столько и вторая.
То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.
Существуют и другие единицы измерения углов.
1. Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.
Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.
Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда – уже очень маленькая величина, но ее тоже можно делить дальше.
Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.
2. Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.
3. Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).
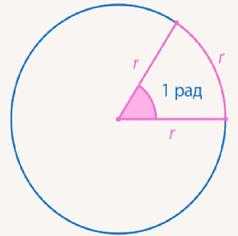
Рис. 17. Радианы
Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад – дуга 1 см, угол 2 рад – длина дуги 2 см.
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
- Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
- Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Shkolo.ru (Источник).
- Cleverstudents.ru (Источник).
- Festival.1september.ru (Источник).
Домашнее задание
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013. Стр. 144 № 522.
- Начертите углы: 23°, 167°, 84°.
- Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) – 2010. Стр. 163 № 3.
interneturok.ru
Чем и как измерить угол наклона на мониторе? Программа Транспортир
Содержание статьи
Общие положения
Часто бывает необходимость измерить углы наклона линий на экране монитора, например, угол наклона графика цены или каких-то линий на строительных чертежах. Для их определения можно, конечно, использовать школьный транспортир, прикладывая его к монитору, но это неудобно и не точно.
Поэтому был разработан целый ряд платных и бесплатных программ, которые способны измерять углы наклона графиков. Сегодня мы рассмотрим одну из таких программ – Protractor (Транспортир).
Сразу скажу, что эта программа не самая удобная, есть и более удобные программы, но они обладают существенным недостатком – они платные. Конструкторам и другим специалистам, конечно, надо задуматься об их приобретении, а нам, трейдерам Форекс и бинарных опционов, вполне достаточно функционала, заложенного в бесплатном образце.
Сама по себе эта программа несложная в освоении, но я все-таки расскажу как ее настраивать и как ею пользоваться, тем более что программа разработана программистами с Востока (Япония, Китай..), поэтому и в интерфейсе программы, и в ее описании используются иероглифы.
Я закачал программу Protractor в Яндекс. Диск, откуда ее можно скачать бесплатно и без всяких предварительных условий. СКАЧАТЬ. Она очень легкая (47 КБ) и заархивирована в архиваторе zip, поскольку имеет несколько вспомогательных файлов:
Рис.1
После того, как вы откроете архив (как и чем это сделать?), необходимо кликнуть по наименованию файла с программой Protractor.exe (стрелка), программа довольно быстро откроется. Важное замечание: программа не инсталлируется в ваш компьютер как бы «навсегда», поэтому перед каждым ее использованием ее необходимо открывать — как здесь рассказано. Но из этого следует, что архив с программой должен быть размещен в той папке, где вы его всегда можете легко найти.
После того, как программа откроется, у вас в трее (правый нижний угол монитора, там где часы) появится новый значок – кружок ярко зеленого цвета:
Рис.2
Через некоторое время он уже не будет виден в трее и искать его надо будет в скрытых значках (белый треугольник, показан левой стрелкой). Это происходит потому, что Windows (по крайней мере, Windows7) расценивает эту программу как редко используемую и очищает трей, чтобы не было захламленности на экране.
Я потому так подробно рассказываю об этом, что у Транспортира есть одна особенность: при сворачивании этот значок в трее может быть не виден, но теперь вы знаете где его искать. Начиная работать с программой и не зная об этом, я каждый раз запускал программу по-новой.
После запуска программы у вас на мониторе появится транспортир:
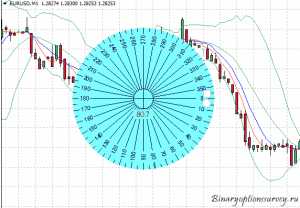 Рис.3
Рис.3
Прежде, чем приступать к работе с ним, его надо настроить.
Настройка программы
Сначала следует сделать так, чтобы транспортир был виден на каждой вкладке нашего торгового терминала, иначе при переключении с одной валютной пары на другую вам придется каждый раз кликать по значку в трее. Для этого нам надо кликнуть ПРАВОЙ кнопкой мыши по самому транспортиру, откроется меню:
Рис.4
Вам надо кликнуть по второй строчке (стрелка), той, где в скобках написана латинская буква F, я думаю, — от слова Forward (вперед, впереди). Теперь транспортир будет виден всегда на вашем мониторе, что бы вы ни открывали – вкладки терминала, браузер, игры, Word и т.д. Чтобы убрать программу с экрана, надо еще раз кликнуть по этой же строчке меню. Или можно кликнуть по следующей строчке, той, где буква (H) – hide, т.е скрыть. В последнем случае программа свернется и станет неактивной: в трее цвет значка станет другой – цвет «глухой зеленый в крапинку» ;-)). Чтобы она опять стала активной, надо ДВАЖДЫ кликнуть по этому значку.
Основные настройки программы расположены в первой строчке контекстного меню:
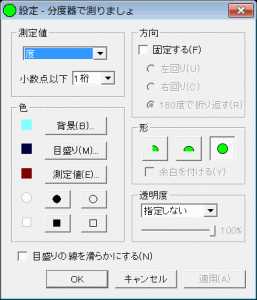 Рис.5
Рис.5
Сначала рассмотрим левую часть этого окна.
В самом верхнем окошке (там, где синий фон) вы можете выбрать форму представления данных, я думаю, что здесь ничего трогать не надо.
В следующем окне, вы можете определить точность измерений – один или два знака после запятой или вовсе без десятичных долей.
Далее идет выбор цветов – 5 строчек, где можно определить цвет фона, шрифта, окошек (о них чуть ниже). Все можно оставить по умолчанию.
Правая часть программы более интересна.
Первая часть настроек (один квадратик и три кружочка) определяют характер отображения информации. Если поставить галочку в квадратик, то активируются радиокнопки (так называются кружочки) и, кликая по ним, можно установить прямое и обратное отображение градусной шкалы, — попробуйте сами и вы поймете, о чем речь. Хотя честно сказать, нам это ни к чему: я вам предложу другой вариант работы.
Прежде всего, кликнем по самой нижней радиокнопке (той, где есть цифры 180), тогда увеличение шкалы идет и вверх, и вниз (от ноля), что очень удобно при определении угла наклона восходящих и нисходящих графиков:
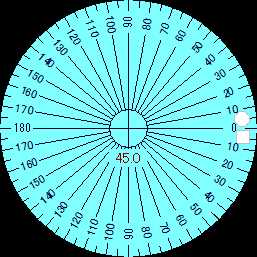 Рис.6
Рис.6
Сравните градуировку с рис.3.
Следующий раздел позволяет установить транспортир как круг, ½ и ¼ круга. Если хотите, можете себе установить то или иное изображение.
Следующий раздел довольно важный – он позволяет установить степень прозрачности транспортира.
Нажимаете на кнопку выпадающего списка (верхняя стрелка):
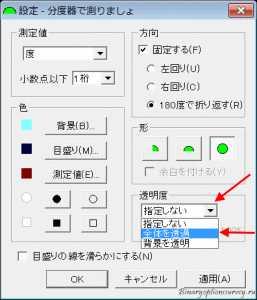 Рис.7
Рис.7
Теперь кликаете по второй строчке (ну, не знаю я что там написано!), активируется ползунок под этим окном. Передвигая его в ту или иную сторону, добиваетесь нужной прозрачности транспортира. Зачем это надо? Это надо для того, чтобы вы могли точно установить его центр в нужной точке.
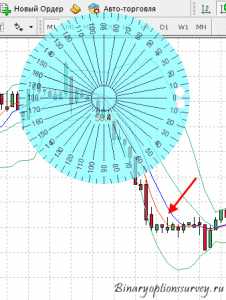 Рис.8
Рис.8
Предположим, я решил измерить величину угла наклона синей скользящей средней. Устанавливаю центр транспортира в начало падения и устанавливаю курсор в ту точку, на которую указывает стрелка. Программа показывает, что угол наклона 59,4 градуса (цифры в центре транспортира). Кстати, степень прозрачности транспортира на рис.8 составляет 70%.
Можно установить и полную прозрачность, без фона. На этого надо кликнуть не по второй, а по третьей строчке (см.рис.7). Но этот вариант мне очень не понравился – программа капризничает, при клике по ней – исчезает, невозможно даже кликнуть правой мышью, чтобы изменить настройки. В таком случае надо кликать правой мышью по значку программы в трее, появится контекстное меню и только тогда изменять настройки.
На этом я заканчиваю рассмотрение этого окна настроек (о чем не написал – того не знаю) и продолжаю говорить о контекстном меню (см.рис.4).
Четвертая строчка (с буквой R) позволяет изменить градуировку транспортира, т.е. если «0» у вас будет направлен вверх, то одно нажатие на эту строчку приведет к отсчету справа налево и повторное нажатие – наоборот. Иногда это может быть полезным, но я этой функцией вообще не пользуюсь.
Пятая строчка (с буквой D) позволяет направить начало отсчета в ту или иную сторону. Пояснять там нечего поскольку имеются указывающие стрелки:
Рис.9
Соответственно, ноль будет направлен туда, куда показывает стрелка: вверх (Up), вниз (Down), влево (Left) и вправо (Right).
Предпоследняя строчка – информация о программе.
Последняя строчка – закрытие программы (не сворачивание в трей, а полное закрытие).
Как использовать программу
Устанавливаете транспортир в исходную точку и курсором определяете угол, который вы хотите измерить.Изменяя положение курсора, вы тем самым изменяете угол. Величину измеряемого угла показывают цифры в середине транспортира, хотя, конечно, можно и смотреть и на бегающий по окружности указатель.
На самом этом приборе есть возможность изменить его размеры. Для этого надо навести курсор на квадратик, появится стрелка с двумя наконечниками, нажимаете курсор и, не отпуская его, двигаете вправо-влево, добиваясь нужного размера.
Кроме того, у него есть одна очень полезная функция – произвольная установка ноля. Иногда бывает необходимым измерить угол между двумя наклонными линиями, где фиксированная установка ноля вверх-вниз-вправо-влево, которую мы рассмотрели выше, не поможет.
Например, его (т.е. ноль) необходимо установить на 30 градусов к горизонту, в этом случае надо навести курсор на кружочек (около ноля), появится спираль, кликнуть по нему и, не отпуская мышь, поворачивать круг транспортира до нужного положения. Потом, двигая курсор, измеряете угол. А вот вернуть в исходное положение лучше всего с помощью настроек, показанных на рис.9. Лучше, потому что точнее.
Написано все это, конечно, ужасно косноязычно, но вы попробуйте это сделать и все сами поймете – ведь программа очень простая.
На этом рассмотрение этой программы я заканчиваю, будут вопросы – пишите в комментариях.
Понравилась статья? Оцените ее и… :
[starrater tpl=10 size=’46’]
Благодарю Вас! А еще Вы можете подписаться на рассылку — у меня в запасе есть много интересных индикаторов и прибыльных стратегий.Удачи!
Автор: Сергей Ваулин
Информация о статье
Чем и как измерить угол наклона на мониторе? Программа Транспортир
В статье подробно рассматривается программа для измерения углов, ее настройки, принцип работы с ней. Даются практические советы
Written by: Сергей Ваулин
Date Published: 09/22/2014
Программа Транспортир достаточно удобная для работы. Свои функции она выполняет исправно. И — она бесплатная!
5.0 / 5 stars
binaryoptionssurvey.ru
Использование транспортира
Использование транспортираМожно вставить на страницу транспортир, настроить его размер, поворот и положение, а затем рисовать вдоль его краев.
Вставка транспортира
Нажмите «Инструменты измерения» и выберите «Транспортир» .
Появится транспортир.
Перемещение транспортира
Нажмите на внутреннюю часть транспортира (отображается более темным синим полутоном), и перетащите его в другое место на странице.
Изменение размеров транспортира
Нажмите на внутренний круг чисел, а затем тащите в направлении от транспортира для его увеличения или в направлении к центру – для уменьшения.
Поворот транспортира
Нажмите на наружный круг чисел и тащите транспортир в том направлении, куда его нужно повернуть.
На транспортире отображается текущий угол поворота в градусах.
Отображение транспортира в виде полного круга
Нажмите на синий кружок около надписи 180 внутреннего круга чисел
Чтобы вернуться к отображению в виде полукруга, снова нажмите на синий кружок.
Рисование с помощью пера и транспортира
-
Нажмите на инструмент «Перо» , а затем выберите доступный тип линии.
-
Рисуйте вдоль края транспортира.
Цифровые чернила формируют дугу вдоль кромки транспортира.
Отображение углов с помощью транспортира
-
Двигайте зеленый кружок, пока он не покажет правильное значение угла первых двух пересекающихся линий.
-
Нажмите на зеленую стрелку в нижнем углу.
Появится первая линия.
-
Двигайте зеленый кружок, пока он не покажет правильное значение угла вторых двух пересекающихся линий.
-
Нажмите на зеленую стрелку в нижнем углу.
Появится вторая линия. SMART Notebook также отобразит угол между двумя линиями.
Удаление транспортира
-
Нажмите на транспортир.
-
Нажмите на стрелку меню транспортира и выберите «Удалить».
onlinehelp.smarttech.com
Угловой размер, линейный размер и расстояние
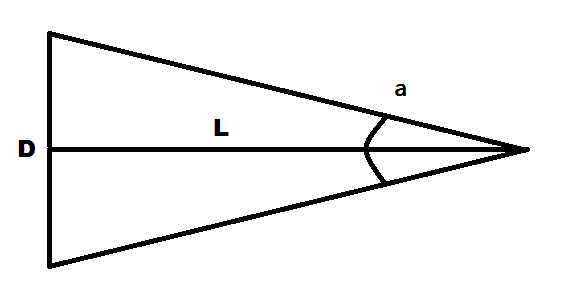
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):
Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.
Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.
Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.
Знаков после запятой: 2
Сохранить share extension
Угловой размерТочность вычисленияЗнаков после запятой: 2
Линейный размер
Сохранить share extension
Угловой размер
planetcalc.ru
Путевой угол и расстояние между двумя точками по локсодроме (линии румба).
В 16 веке фламандский географ Герхард Меркатор составил навигационную карту мира, изобразив поверхность Земли на плоскости таким образом, чтобы углы на карте не искажались. В настоящее время такой способ изображения Земли известен, как равноугольная цилиндрическая проекция Меркатора. Такая карта была очень удобна для мореплавателей, так как для того чтобы прийти из точки А в точку Б на карте Меркатора достаточно провести прямую линию между этими точками, замерить ее угол к меридиану и постоянно придерживаться этого направления, например используя секстант и полярную звезду в качестве ориентира или магнитный компас. (На самом деле с компасом не так все просто, так как он не всегда показывает на истинный север, но об этом как-нибудь в другой раз). Проекция Меркатора до сих пор широко применяется для составления навигационных карт.
Однако, еще древние мореплаватели начинали замечать, что линия румба не всегда является кратчайшим путем между двумя точками, особенно, это становилось заметно для дальних переходов. Если провести на глобусе линию, пересекающую все меридианы под одним и тем же углом, то станет понятно, отчего это происходит. Прямая линия на карте Меркатора превращается на глобусе в бесконечно закручивающуюся к полюсам спираль. Такую линию в современной науке принято называть греческим словом локсодромия, что означает «косой бег».
Следующий далее калькулятор вычисляет путевой угол и расстояние трансатлантического перехода из Лас Пальмаса (Испания) в Бриджтаун (Барбадос) по локсодромии. Полученное расстояние на десятки километров отличается от кратчайшего пути (см.Расстояние между двумя координатами).
Знаков после запятой: 2
Расстояние в километрах
Расстояние в морских милях
Сохранить share extension
Для вычисления путевого угла используются следующие формулы:
где
Длина локсодромии вычислена по следующей формуле:
, где — широта и долгота первой точки — широта и долгота второй точки
— эксцентиситет сфероида (a — длина большой полуоси, b — длина малой полуоси)
При углах 90° или 270° для вычисления длины дуги использовалась формула:
planetcalc.ru
