Автор тригонометрических функций – ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ | Энциклопедия Кругосвет

История тригонометрии: возникновение и развитие

История тригонометрии неразрывно связана с астрономией, ведь именно для решения задач этой науки древние ученые стали исследовать соотношения различных величин в треугольнике.

На сегодняшний день тригонометрия является микроразделом математики, изучающим зависимость между значениями величин углов и длин сторон треугольников, а также занимающимся анализом алгебраических тождеств тригонометрических функций.

Термин «тригонометрия»

Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник». Если быть точнее, то речь идет не о буквальном измерении этой фигуры, а об её решении, то есть определении значений её неизвестных элементов с помощью известных.

Общие сведения о тригонометрии

История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы.

Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятиричной, применяемой во многих прикладных науках.

Предполагается, что изначально тригонометрия существовала как часть астрономии. Затем она стала использоваться в архитектуре. А со временем возникла целесообразность применения данной науки в различных областях человеческой деятельности. Это, в частности, астрономия, морская и воздушная навигация, акустика, оптика, электроника, архитектура и прочие.

Тригонометрия в ранние века

Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.

Также одним из важнейших достижений тех времен является определение соотношения катетов и гипотенузы в прямоугольных треугольниках, которое позже получило название теоремы Пифагора.

История развития тригонометрии в Древней Греции связана с именем астронома Птоломея — автора геоцентрической системы мира, господствовавшей до Коперника.

Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.

Также исследования древних греков продвинули развитие сферической тригонометрии. В частности, Евклид в своих «Началах» приводит теорему о закономерностях соотношений объемов шаров различного диаметра. Его труды в этой области стали своеобразным толчком в развитии еще и смежных областей знаний. Это, в частности, технология астрономических приборов, теория картографических проекций, система небесных координат и т. д.

Средневековье: исследования индийских ученых

Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию.

История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.

Первые таблицы синусов были у Ариабхаты, они была проведены через 3^о, 4^о, 5^о. Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1^о.

Первый специализированный трактат по тригонометрии появился в X—XI веке. Автором его был среднеазиатский учёный Аль-Бируни. А в своем главном труде «Канон Мас‘уда» (книга III) средневековый автор еще более углубляется в тригонометрию, приводя таблицу синусов (с шагом 15′) и таблицу тангенсов (с шагом 1°).

История развития тригонометрии в Европе

После перевода арабских трактатов на латынь (XII-XIII в) большинство идей индийских и персидских ученых были заимствованы европейской наукой. Первые упоминания о тригонометрии в Европе относятся к XII веку.

По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.

История тригонометрии: Новое время

В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик — ученик Коперника — приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.

Франсуа Виет в «Математическом каноне» (1579) дает обстоятельную и систематическую, хотя и бездоказательную, характеристику плоской и сферической тригонометрии. А Альбрехт Дюрер стал тем, благодаря кому на свет появилась синусоида.

Заслуги Леонарда Эйлера

Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить обратные функции. Но и это еще не все.

Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого. Общая теория тригонометрических рядов и изучение сходимости полученных рядов не были объектами исследований Эйлера. Однако, работая над решением смежных задач, он сделал много открытий в этой области. Именно благодаря его работам продолжилась история тригонометрии. Кратко в своих трудах он касался и вопросов сферической тригонометрии.

Области применения тригонометрии

Тригонометрия не относится к прикладным наукам, в реальной повседневной жизни ее задачи редко применяются. Однако этот факт не снижает ее значимости. Очень важна, например, техника триангуляции, которая позволяет астрономам достаточно точно измерить расстояние до недалеких звезд и осуществлять контроль за системами навигации спутников.

Также тригонометрию применяют в навигации, теории музыки, акустике, оптике, анализе финансовых рынков, электронике, теории вероятностей, статистике, биологии, медицине (например, в расшифровке ультразвуковых исследований УЗИ и компьютерной томографии), фармацевтике, химии, теории чисел, сейсмологиии, метеорологии, океанологии, картографии, многих разделах физики, топографии и геодезии, архитектуре, фонетике, экономике, электронной технике, машиностроении, компьютерной графике, кристаллографиии и т. д. История тригонометрии и ее роль в изучении естественно-математических наук изучаются и по сей день. Возможно, в будущем областей ее применения станет еще больше.

История происхождения основных понятий

История возникновения и развития тригонометрии насчитывает не один век. Введение понятий, которые составляют основу этого раздела математической науки, также не было одномоментным.

Так, понятие «синус» имеет очень долгую историю. Упоминания о различных отношениях отрезков треугольников и окружностей обнаруживаются еще в научных трудах, датируемых III веком до нашей эры. Работы таких великих древних ученых, как Евклид, Архимед, Апполоний Пергский, уже содержат первые исследования этих соотношений. Новые открытия требовали определенных терминологических уточнений. Так, индийский учёный Ариабхата дает хорде название «джива», означающее «тетива лука». Когда арабские математические тексты переводились на латынь, термин заменили близким по значению синусом (т. е. «изгиб»).

Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус».

Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов – его заслуга. А переводится этот термин как «касающийся».

fb.ru

Тригонометрия — Циклопедия

Титульная страница «Тригонометрии» (переиздание 1612) В. Питиска, давшая название одноименному разделу математики Основы тригонометрии // KhanAcademyRussian (CC) [9:25] Основы тригонометрии Часть 2 // KhanAcademyRussian [12:22]

Тригонометрия — раздел классической математики, лежащий на пересечении алгебры и геометрии: система законов-функций, по которым на евклидовой плоскости соотносятся стороны и углы треугольников.

Тригонометрия основывается на соотношении подобия. Треугольники с двумя равными углами подобны, поэтому подобны прямоугольные треугольники, в которых равен один острый угол. Отношение длин сторон у подобных треугольников одинаковое, поэтому отношение сторон прямоугольных треугольников зависит только от одного параметра — величины острого угла. Это обстоятельство позволяет обозначить тригонометрические функции: синус, косинус, тангенс, котангенс, секанс и косеканс, через отношение различных сторон прямоугольного треугольника.

[править] Исторические сведения

Некоторые сведения о науке, позже получившей название «тригонометрия», были еще у древних египтян. В папирусе Ахмеса есть пять задач, касающихся измерения пирамид, в которых упоминается какая-то функция угла — «сект». Есть мнение, что «сект» обозначает котангенс угла. Применение этой функции носило сугубо практическую причину: египетские архитекторы строили пирамиды, строго придерживаясь одного и того же значения угла наклона боковой грани к основанию (52°) и угла между ребром и диагональю основания (42°). А для этого надо было знать соответствующие отношения между линейными элементами четырехугольной пирамиды.

Вавилоняне так же имели некоторые знания об этой области математики: они ввели разделение круга на 360° и разделение градуса на 60 частей, что соответствовало принятой в древней Месопотамии шестидесятеричной системе счисления. Для измерения углов вавилоняне пользовались примитивной астролябией.

Древние греки умели решать многие тригонометрические задачи, но они применяли геометрические, а не алгебраические методы.

Тригонометрическую функцию синус впервые ввели древние индийцы в трактате «Сурья-сиддханта». Свойства этой функции исследовал индийский математик 5 века Ариабхата

[1]. Дальнейший вклад в развитие тригонометрии сделали арабские математики. До 10 века они апеллировали всеми тригонометрическими функциями и протабулировали их. В Европу понятие тригонометрических функций пришло с переводами трудов ал-Баттани и Ат-Туси. Одной из первых работ европейской математики, посвященных тригонометрии была книга «De Triangulis» немецкого математика 15 века Региомонтана. Однако, еще в 16 веке тригонометрия была мало известна. Коперник вынужден был посвятить ее описанию 2 отдельных раздела в своей работе «Об обращении небесных сфер» (лат. «De revolutionibus orbium coelestium»).

Быстрое дальнейшее развитие тригонометрии было обусловлено требованиями навигации и картографии^[2]. Сам термин тригонометрия ввел, опубликовав в 1595 книгу под таким же названием, немецкий математик Варфоломей Питиск (нем. Bartholomäus Pitiscus, 1561—1613)^[3]. Гемма Фризий описал метод триангуляции.

Со становлением математического анализа тригонометрия получила новые методы. Благодаря трудам Брука Тейлора и Колина Маклорена тригонометрические функции получили представление в виде рядов

[4]. Формула Муавра установила связь между тригонометрическими функциями и экспонентой. Леонард Эйлер расширил определение тригонометрических функций на комплексную плоскость.

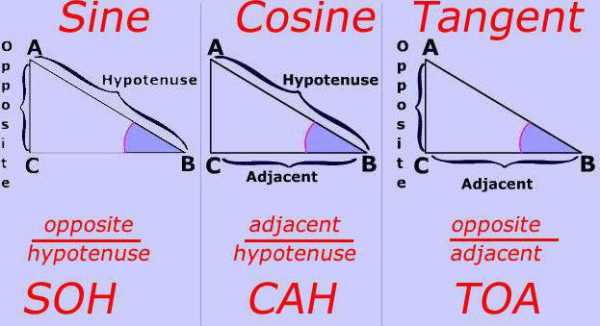
• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

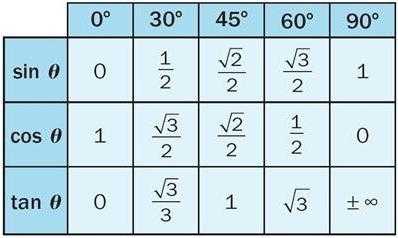
Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до [math]\pi \over 2[/math] радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол [math]\theta[/math] (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим

A. Тогда:

Для острых углов новые определения совпадают с прежними.

[править] Свойства функции синус

Синус

1. Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math].
2. Множество значений — промежуток [−1; 1]: [math]E(y)[/math] = [−1;1].
3. Функция [math] y = \sin \left( \alpha \right) [/math] является нечётной: [math] \sin \left( — \alpha \right) = — \sin \alpha[/math].
4. Функция периодическая, наименьший положительный период равен [math]2\pi[/math]: [math] \sin \left( \alpha + 2 \pi \right) = \sin \left( \alpha \right) [/math].
5. График функции пересекает ось
   Ох при [math] \alpha = \pi n \,, n \in Z[/math].
6. Промежутки знакопостоянства: [math]y \gt 0[/math] при [math] \left( 2\pi n + 0; \pi + 2\pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \pi + 2\pi n; 2\pi + 2\pi n \right) \,, n \in Z [/math].
7. Функция непрерывна и имеет производную при любом значении аргумента: [math]( \sin \alpha )’ = \cos \alpha[/math]
8. Функция [math] y = \sin \alpha [/math] возрастает при [math] \alpha \in \left( — \frac{\pi}{2} + 2\pi n; \frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math], и убывает при [math] \alpha \in \left( \frac{\pi}{2} + 2\pi n; 3\frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math].
9. Функция имеет минимум при [math] \alpha = -\frac{\pi}{2} + 2\pi n \,, n \in Z [/math] и максимум при [math] \alpha = \frac{\pi}{2} + 2\pi n \,, n \in Z [/math].

[править] Свойства функции косинус

Косинус

1. Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math].
2. Множество значений — промежуток [−1; 1]: [math]E(y)[/math] = [−1;1].
3. Функция [math] y = \cos \left( \alpha \right) [/math] является чётной: [math] \cos \left( — \alpha \right) = \cos \alpha[/math].
4. Функция периодическая, наименьший положительный период равен [math]2\pi[/math]: [math] \cos \left( \alpha + 2 \pi \right) = \cos \left( \alpha \right) [/math].
5. График функции пересекает ось Ох при [math] \alpha = \frac{\pi}{2} + \pi n \,, n \in Z[/math].
6. Промежутки знакопостоянства: [math]y \gt 0[/math] при [math] \left( -\frac{\pi}{2} + 2\pi n; \frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \frac{\pi}{2} + 2\pi n; 3\frac{\pi}{2} + 2\pi n \right) \,, n \in Z .[/math]
7. Функция непрерывна и имеет производную при любом значении аргумента: [math]( \cos \alpha )’ = -\sin \alpha[/math]
8. Функция [math] y = \cos \alpha [/math] возрастает при [math] \alpha \in \left( -\pi + 2\pi n; 2\pi n \right) \,, n \in Z ,[/math] и убывает при [math] \alpha \in \left( 2\pi n; \pi + 2\pi n \right) \,, n \in Z .[/math]
9. Функция имеет минимум при [math] \alpha = \pi + 2\pi n \,, n \in Z [/math] и максимум при [math] \alpha = 2\pi n \,, n \in Z .[/math]

[править] Свойства функции тангенс

Тангенс

1. Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math], кроме чисел [math] \alpha = \frac{\pi}{2} + \pi n . [/math]
2. Множество значений — множество всех действительных чисел: [math] E(y) = R . [/math]
3. Функция [math] y = \mathrm{tg} \left( \alpha \right) [/math] является нечётной: [math] \mathrm{tg} \left( — \alpha \right) = — \mathrm{tg}\ \alpha[/math].
4. Функция периодическая, наименьший положительный период равен [math]\pi[/math]: [math] \mathrm{tg} \left( \alpha + \pi \right) = \mathrm{tg} \left( \alpha \right) [/math].
5. График функции пересекает ось Ох при [math] \alpha = \pi n \,, n \in Z[/math].
6. Промежутки знакопостоянства: [math] y \gt 0 [/math] при [math] \left( \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( -\frac{\pi}{2} + \pi n; \pi n \right) \,, n \in Z [/math].
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: [math]( \mathop{\operatorname{tg}}\, x )’ = \frac{1}{\cos ^2 x}.[/math]
8. Функция [math] y = \mathrm{tg}\ \alpha [/math] возрастает при [math] \alpha \in \left( -\frac{\pi}{2} + \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math].

[править] Свойства функции котангенс

Котангенс

1. Область определения функции — множество всех действительных чисел: [math]D(y) = R,[/math] кроме чисел [math] \alpha = \pi n .[/math]
2. Множество значений — множество всех действительных чисел: [math] E(y) = R .[/math]
3. Функция [math] y = \mathop{\operatorname{ctg}} \left( \alpha \right) [/math] является нечётной: [math] \mathop{\operatorname{ctg}} \left( — \alpha \right) = — \mathop{\operatorname{ctg}}\ \alpha \,.[/math]
4. Функция периодическая, наименьший положительный период равен [math]\pi[/math]: [math] \mathop{\operatorname{ctg}} \left( \alpha + \pi \right) = \mathop{\operatorname{ctg}} \left( \alpha \right) .[/math]
5. График функции пересекает ось Ох при [math] \alpha = \frac{\pi}{2} + \pi n \,, n \in Z \,.[/math]
6. Промежутки знакопостоянства: [math] y \gt 0 [/math] при [math] \left( \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \frac{\pi}{2} + \pi n; \pi \left( n + 1 \right) \right) \,, n \in Z .[/math]
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: [math]( \mathop{\operatorname{ctg}}\, x )’ = -\frac{1}{\sin ^2 x}.[/math]
8. Функция [math] y = \mathop{\operatorname{ctg}}\ \alpha [/math] убывает при [math] \alpha \in \left( \pi n; \pi \left( n + 1 \right) \right) \,, n \in Z .[/math]

[править] Основные теоремы тригонометрии

Определенные для прямоугольного треугольника тригонометрические функции позволяют решать произвольные треугольники с использованием основных теорем: теоремы синусов, теоремы косинусов и теоремы тангенсов.

[править] Теорема синусов

Теорема синусов утверждает, что отношение синуса угла к длине противоположной стороны треугольника одинакова для всех углов треугольника. Для плоского треугольника со сторонами [math]a, b, c[/math] и соответствующими противоположными них углами [math]A, B, C[/math] можно записать:

[math]\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,[/math]

где [math]R[/math] — радиус описанной окружности вокруг треугольника.

[math]R = \frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}.[/math]

[править] Теорема косинусов

По теореме косинусов, квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами [math]a, b, c[/math] и углом [math]C[/math], между сторонами [math]a, b[/math]:

[math]c^2=a^2+b^2-2ab\cos C ,\,[/math]

или:

[math]\cos C=\frac{a^2+b^2-c^2}{2ab}.\,[/math]

Теорема косинусов позволяет определить длину третьей стороны треугольника, если известны длины двух сторон и значение угла между ними.

[править] Теорема тангенсов

Теорема тангенсов — теорема о соотношении между двумя сторонами произвольного треугольника и тангенса полусуммы и полуразности противоположных к ним углов, которая записывается уравнением (формула Региомонтана):

[math]\frac{a-b}{a+b}=\frac{\mathop{\operatorname{tg}}\left[\tfrac{1}{2}(A-B)\right]}{\mathop{\operatorname{tg}}\left[\tfrac{1}{2}(A+B)\right]}[/math]

[править] Площадь треугольника

Площадь треугольника тоже может быть определена через тригонометрические функции: она равна половине произведения прилегающих сторон на синус угла между ними:

[math]A = \frac{1}{2}ab\sin C .\,[/math]

[править] Простейшие тригонометрические уравнения

Уравнения, в которых фигурируют тригонометрические функции, называют тригонометрическими. Самые простые из них имеют аналитические решения, благодаря существованию обратных тригонометрических функций. Поскольку тригонометрические функции периодические, такие решения не единственные, а определяются с точностью до периода.

[math]\begin{matrix} \sin x=a & (|a|\le1) & x=(-1)^n \arcsin a + \pi n \\ \cos x=a & (|a|\le1)& x=\pm \arccos a + 2 \pi n \\ \text{tg}\, x=a & & x=\text{arctg}\, a + \pi n \\ \text{ctg}\, x=a & & x=\text{arcctg}\, a + \pi n \\ \end{matrix}[/math]

[править] Формулы преобразования тригонометрических выражений

Синус и косинус суммы/разности:

[math]\sin(x+y)=\sin x \cos y + \cos x \sin y \![/math]

[math]\sin(x-y)=\sin x \cos y — \cos x \sin y \![/math]

[math]\cos(x+y)=\cos x \cos y — \sin x \sin y \![/math]

[math]\cos(x-y)=\cos x \cos y + \sin x \sin y \![/math]

Сумма/разность синусов и косинусов:

[math]\sin x + \sin y = 2 \sin{\frac{x+y}{2}} \cos{\frac{x-y}{2}} \![/math]

[math]\sin x — \sin y = 2 \sin{\frac{x-y}{2}} \cos{\frac{x+y}{2}} \![/math]

[math]\cos x + \cos y = 2 \cos{\frac{x+y}{2}} \cos{\frac{x-y}{2}} \![/math]

[math]\cos x — \cos y =-2 \sin{\frac{x+y}{2}} \sin{\frac{x-y}{2}} \![/math]

Сферическая тригонометрия — раздел сферической геометрии, главными объектами которого являются многоугольники (особенно треугольники) на сфере и соотношение между сторонами и углами. Возникновение сферической геометрии связано с задачами сферической астрономии.

Основными элементами сферической геометрии являются точки и большие круги сферы. Большие круги являются геодезическими линиями сферы, поэтому они в сферической геометрии играют роль, аналогичную роли прямых в планиметрии. Расстояние между двумя точками в сферической геометрии измеряется углом между радиусами сферы, проведенными в эти точки. Угол между двумя «прямыми» равен двугранному углу между плоскостями больших кругов, которые определяют эти «прямые». Две любые «прямые» в сферической геометрии пересекаются в двух точках и разбивают поверхность сферы на 4 двуугольника. Три «прямые», пересекаясь попарно, образуют 8 сферических треугольников. Эти треугольники имеют много необычных свойств, которые отличают их от плоских треугольников. Например, сумма углов сферического треугольника всегда больше 180° и меньше 540°.

Стороны и углы сферического треугольника связаны зависимостями:

[math]\frac{\sin\frac{a}{R}}{\sin A}=\frac{\sin\frac{b}{R}}{\sin B}=\frac{\sin\frac{c}{R}}{\sin C};[/math]

[math]\cos\frac{c}{R}=\cos\frac{a}{R}\cos\frac{b}{R}+\sin\frac{a}{R}\sin\frac{b}{R}\cos C;[/math]

[math]\cos\frac{a}{R}=\frac{\cos A + \cos B\cos C}{\sin B\sin C}.[/math]

где [math]a, b, c[/math] — стороны сферического треугольника; [math]A, B, C[/math] — углы, противоположные этим сторонам; [math]R[/math] — радиус сферы.

Сферическая тригонометрия очень важна в астрономических вычислениях (небесной механике), а также в орбитальной, космической навигации и навигации на поверхности Земли.

• Андронов И. К., Окунев А. К. Курс тригонометрии, развиваемый на основе реальных задач. — М.: Просвещение, 1967. — 648 с.
• Волынский Б. А. Сферическая тригонометрия. — М.: Наука, 1977. — 136 с.
• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. — 830 c.

cyclowiki.org

Тригонометрические функции, формулы и примеры

Определения и формулы всех тригонометрических функций

Рассмотрим произвольный прямоугольный треугольник , углы и – острые. (рис. 1). Тогда – гипотенуза (это сторона противолежащая прямому углу), самая длинная сторона в прямоугольном треугольнике. Катет – это катет, являющийся противолежащим по отношению к углу . Катет – это катет, прилежащий к углу .

Рис. 1

Это отношение не зависит от выбора , содержащего угол , так как все такие треугольники подобны.

Подробнее про синус угла читайте по ссылке.

Подробнее про косинус угла читайте по ссылке.

Замечание 1. Катет AC, прилежащий к углу , является противолежащим по отношению к углу . Аналогично с катетом , он противолежащий для угла и прилежащий к углу . Таким образом, синус одного острого угла в треугольнике равен косинусу второго его острого угла, и наоборот:

   

Также тангенс выражается через косинус и синус следующим образом:

   

Котангенс выражается через косину и синус следующим образом:

   

Замечание 2. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго его острого угла, и наоборот:

   

Секансом угла называется отношение гипотенузы к прилежащему катету или

   

Косеканс можно выразить через синус:

   

Примеры решения задач

Примечание. Прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским треугольником». Это простейший треугольник из Героновых треугольников – треугольников с целочисленными сторонами и площадями.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Коротко о тригонометрических функциях. II

 

Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».

Чтобы скачать полный текст, пройдите по ссылке.

 

К началу

4. Обобщение тригонометрических функций на случай любых углов.

Убедитесь самостоятельно, что всё, сказанное выше о тригонометрических функциях, справедливо для ситуации, изображённой на рисунке:

 

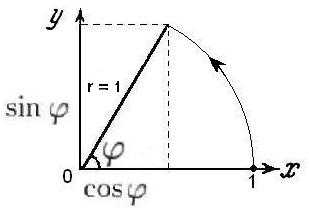
Здесь

— вершина угла φ прямоугольного треугольника совмещена с началом координат,

— гипотенуза треугольника, являющаяся также и радиусом окружности, равна единице, r = 1,

— косинус является проекцией радиуса на ось абсцисс,

— синус является проекцией радиуса на ось ординат.

Всё это правильно, но пока только для острых углов, когда радиус-гипотенуза находится в первой четверти.

Обобщение ситуации на случай любых углов очевидным образом следует из рисунка:

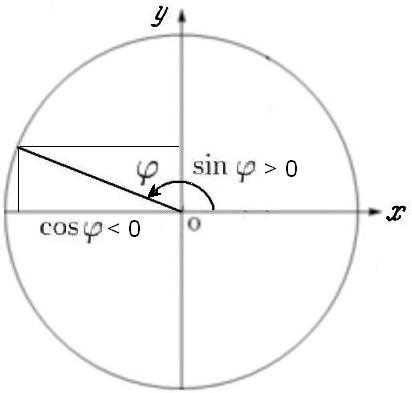
А именно, для любых углов косинус, — проекция единичного радиуса на ось абсцисс (Ox), синус — проекция единичного радиуса на ось ординат (Oy), причём в тех случаях, когда проекция попадает в отрицательную область координатных осей, функциям приписывается знак минус.

Все прочие тригонометрические функции выражаются через синус и косинус, соответствующие формулы приведены выше.

 

Наиболее важные свойства и графики тригонометрических функций

Функция	Область определения	Область значений	Чётность, нечётность	Период, Т	Графики функций
y  = sinx	(–∞, ∞)	[–1, 1]	нечётная	Т = 2π
y = cosx	(–∞, ∞)	[–1, 1]	чётная	Т = 2π
y  = tgx	(–∞, ∞) за исключением точек πn + π/2, здесь n целое	(–∞, ∞)	нечётная	Т = π
y = ctgx	(–∞, ∞) за исключением точек πn, здесь n целое	(–∞, ∞)	нечётная	Т = π

Функция f(x) называется чётной, если  f(–x) = f(x), и нечётной, если f(–x) = –f(x).

График чётной функции симметричен относительно оси ординат (Oy), а график нечётной функции симметричен относительно начала координат. Из графиков видно, что косинус является чётной функцией, а синус, тангенс и котангенс — нечётные.

Большинство функций не являются ни чётными, ни нечётными, они являются суммой двух слагаемых:

f(x)= [f(x) + f(–x 

)]/2 + [f(x) – f(–x)]/2

Первое слагаемое — чётная часть, второе слагаемое — нечётная часть.

Но основные тригонометрические функции имеют, как мы теперь убедились, вполне определённую чётность.

5. Что обязательно нужно помнить о тригонометрических функциях.

Прежде всего — обобщённое определение синуса и косинуса.

Отсюда сразу же следует, что, например, косинус в четвёртой четверти положителен, а синус отрицателен, или синус 180° равен нулю, а косинус равен минус единице. И т.п.

Полезно также уметь рисовать графики синуса, косинуса, тангенса и котангенса с обязательным указанием значений на осях абсцисс и ординат, так,  как это показано на рисунках, приведённых в таблице.

Ещё очень важные формулы:

sin²φ + cos²φ = 1.

А также

cos(φ + ψ) = cosφ  cosψ

  – sinφ  sinψ,

sin (φ + ψ) = sinφ cosψ + cosφ  sinψ.

Последние две формулы можно легко восстановить из равенства:

cos(φ + ψ) + i sin(φ + ψ) = (cosφ + i sinφ ) (cosψ + i sinψ). 

Кроме того, полезно помнить о чётности-нечётности тригонометрических функций и знать их периоды.

Полезны также формулы приведения, которые позволяют выразить значения тригонометрических функций для любых углов через значения тригонометрических функций углов первой четверти.

Например:

cos(180°+ α) =  cos 180°∙ cosα  – sin180°∙ sinα  = 

(–1) ∙ cosα – 0 ∙ sinα = – cosα.

Чтобы избежать необходимости пользоваться подобными расчётами, применяют мнемоническое правило:

1. Если вычисляется тригонометрические функции углов 90° ± α или 270° ± α , то синус меняется на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс. В случае углов 180° ± α или 360° ± α  функции остаются неизменными, т.е. синус остаётся синусом и т.п.

2. Знак результата такой же, как у исходной функции в той четверти, в которую попадает исходный угол.

Например: cos(180°– α) = – cosα.

Косинус остаётся косинусом, потому что 180°, а не 90° или 270°.

Исходный угол (180°– α) во второй четверти, где косинус, исходная функция, отрицательна, поэтому знак минус.

Вот, пожалуй, и всё!

Посмотрите, сколько всяких тригонометрических формул в справочнике! Но почти все основные формулы легко получаются за одно-два действия из тех соотношений, которые мы рассмотрели.

Поэтому проще всего тригонометрические формулы не заучивать, а выводить по мере необходимости.

Конечно, не мешало бы знать тригонометрию получше, но здесь приведён необходимый минимум. Если при дальнейшем чтении что-либо понадобится дополнительно, то будут даны необходимые разъяснения. 

К началу

©   А.А.Дмитриевский.

 

vestishki.ru

Math.ru

Израиль Моисеевич Гельфанд, Сергей Михайлович Львовский, Андрей Леонович Тоом

М., МЦНМО, 2002. 199 с.
ISBN ISBN 5-94057-050-X; Тираж 10000 экз.

Загрузить (Mb) djvu (-) pdf (1.74) ps (-) html (-) tex (-)

Эта книга, написанная группой авторов под руководством одного из крупнейших математиков 20 века академика И.М.Гельфанда, призвана опровергнуть расхожее мнение о тригонометрии как скучном и непонятном разделе школьного курса математики. Читателю предлагается взглянуть на знакомый предмет по-новому. Изложение, сопровождающееся большим количеством задач, начинается ?с нуля? и доходит до материала, выходящего довольно далеко за рамки школьной программы; тригонометрические формулы иллюстрируются примерами из физики и геометрии.

Отдельная глава посвящена типичным приемам решения тригонометрических задач, предлагаемых на вступительных экзаменах в высшие учебные заведения.

Книга будет незаменимым помощником для школьников старших классов, преподавателей, родителей и всех, интересующихся математикой.

---

Содержание

1. Первое знакомство с тригонометрией
  ? 1. Как измерить крутизну
    1.1. Синус
    1.2. Измерение углов
  ? 2. Тангенс
  ? 3. Косинус
  ? 4. Малые углы

2. Начальные свойства тригонометрических функций
  ? 5. Часы, или современный взгляд на тригонометрию
    5.1. Часы и процессы
    5.2. Скорость
  ? 6. Определение тригонометрических функций
    6.1. Ось тангенсов
    6.2. Знаки тригонометрических функций
  ? 7. Простейшие формулы
  ? 8. Периоды тригонометрических функций
  ? 9. Формулы приведения
  ? 10. Простейшие тригонометрические уравнения
  ? 11. Графики синуса и косинуса
  ? 12. Графики тангенса и котангенса
  ? 13. Чему равно sin x + cos x?

3. Решение треугольников
  ? 14. Теорема косинусов
  ? 15. Вокруг площади треугольника
  ? 16. Теорема синусов

4. Формулы сложения и их следствия
  ? 17. Векторы
    17.1. Направленные отрезки и векторы
    17.2. Сложение векторов
    17.3. Вычитание и умножение на число
    17.4. О векторах в физике
  ? 18. Скалярное произведение
  ? 19. Тригонометрические формулы сложения
  ? 20. Формула вспомогательного угла, или сложение колебаний равной частоты
  ? 21. Двойные, тройные и половинные углы
  ? 22. Преобразование произведения в сумму и суммы в произведение
  ? 23. Производные тригонометрических функций

5. Тригонометрия для абитуриентов
  ? 24. Как решать тригонометрические уравнения
  ? 25. Отбор чисел на тригонометрическом круге
  ? 26. Как решать тригонометрические неравенства
  ? 27. Задачи на повторение

6. Комплексные числа
  ? 28. Что такое комплексные числа
  ? 29. Модуль и аргумент комплексного числа
  ? 30. Показательная функция и формула Эйлера

Ответы и указания к некоторым задачам

Предметный указатель

---

Загрузить (Mb) djvu (-) pdf (1.74) ps (-) html (-) tex (-)

math.ru