Все формулы диагонали параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
www-formula.ru
Как найти диагональ параллелограмма?
Параллелограмм представляет собой геометрическую фигуру, характерной особенностью которой является то, что у нее противоположные стороны параллельны и попарно равны, а также диагонали в ней пересекаются, и точка пресечения делит их пополам. Квадрат, ромб и прямоугольник являются параллелограммами.
Диагональ параллелограмма
Рассмотрим, как найти диагональ параллелограмма. В параллелограмме:
- Сумма углов, которые прилегают к одной стороне, всегда будет составлять 180 градусов;
- Точка, в которой диагонали пересекаются, есть центр симметрии параллелограмма.
- В любом четырехугольнике, в том числе в параллелограмме сумма всех углов равна 360 градусов;
- Удвоенная сумма квадратов двух смежных сторон параллелограмма всегда равна сумме квадратов диагоналей.
Для того чтобы знать, как найти большую диагональ параллелограмма, надо определиться с буквенным обозначением. К примеру, мы имеем параллелограмм со сторонами АВ и ВС. Маленькой буквой «а» обозначим одну длину параллелограмма, а маленькой буквой «в» будет вторая его длина. Маленькими буквами d1 d2 обозначим диагонали. Для того чтобы найти диагональ параллелограмма надо:
- Значение свойств параллелограмма помогает найти нужное решение. Диагонали, которые в точке пресечения делятся пополам, называются биссектрисами. Меньшая биссектриса – для тупых углов, большая для острых углов. Таким образом, когда рассматриваются пары треугольников, получаемых из одной диагонали и двух смежных сторон геометрической фигуры, другая половина диагонали является еще и медианой.
- Треугольники, которые получаются в результате образования половинами диагонали и параллельными сторонами любого параллелограмм считаются подобными, также диагональ делит такую геометрическую фигуру на два треугольника, они симметричны относительно основания и абсолютно одинаковы.
- Для нахождения большой диагонали параллелограмма необ
elhow.ru
Диагонали параллелограмма | Онлайн калькулятор
Параллелограмм — это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ — напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы — это
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
allcalc.ru
Как найти диагональ параллелограмма зная его стороны
Как найти диагональ параллелограмма, зная его стороны
У параллелограмма есть две диагонали, причем чаще всего одна из них длинная, а другая короткая.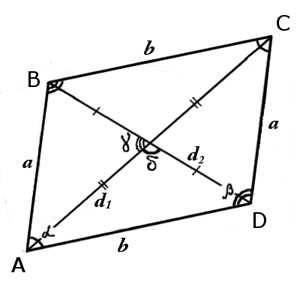
Запишем формулы для определения длины диагоналей параллелограмма через его стороны и не только ))
Используя теорему косинусов несложно получить следующую формулу:
Здесь ugol2 — тупой угол между сторонами параллелограмма. Соответственно ugol1 — это острый угол между сторонами.
Запишем еще несколько формул для нахождения диагонали параллелограмма:
Здесь ugol3 и ugol4 — острый и тупой угол между диагоналями параллелограмма.
Вторая диагональ находится аналогично:
ru.solverbook.com
Как найти диагональ в параллелограмме
Автор КакПросто!
Вычислить диагональ параллелограмма бывает необходимо не только при подготовке домашнего задания. Это может понадобиться, например, в бумажной пластике или при создании архитектурного проекта.

Статьи по теме:
Вам понадобится
- Оборудование Бумага Линейка Карандаш Транспортир Таблица синусов и косинусов Математические понятия: Свойства параллелограмма Свойства высоты треугольника Извлечение квадратного корня Теоремы синусов и косинусов
Инструкция
Постройте параллелограмм с заданными параметрами. В условиях должны быть заданы длины сторон параллелограмма и хотя бы один угол.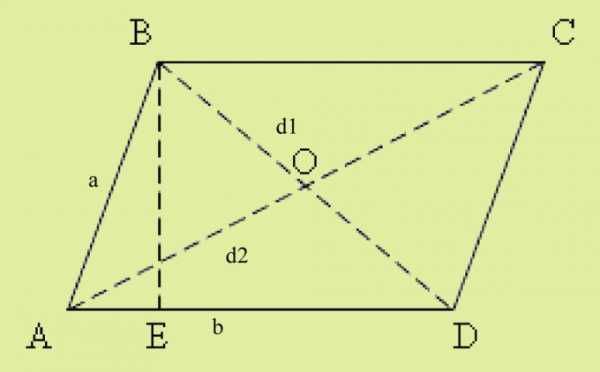 Вспомните, чему равна сумма квадратов диагоналей параллелограмма. Она равна удвоенной сумме квадратов его сторон, которые вам известны. Обозначьте параллелограмм АBCD. Стороны параллелограмма обозначьте как a и b. Диагонали обозначьте как d1 и d2. Из угла В к стороне АD опустите высоту и обозначьте точку ее пересечения со стороной AD как Е. Внутри параллелограмма у вас получился прямоугольный треугольник АВЕ.
Вспомните, чему равна сумма квадратов диагоналей параллелограмма. Она равна удвоенной сумме квадратов его сторон, которые вам известны. Обозначьте параллелограмм АBCD. Стороны параллелограмма обозначьте как a и b. Диагонали обозначьте как d1 и d2. Из угла В к стороне АD опустите высоту и обозначьте точку ее пересечения со стороной AD как Е. Внутри параллелограмма у вас получился прямоугольный треугольник АВЕ.Найдите высоту BЕ. Вам известен угол А и гипотенуза АВ. AE = a*sinА
Вычислите длину отрезка АЕ. Он равен AE=a*cosA.
Вычислите отрезок ЕD, который равен разности стороны AD и отрезка AE.
Вычислите гипотенузу прямоугольного треугольника BED, которая одновременно является диагональю d1. Она будет равна квадратному корню из суммы квадратов сторон BE и ED.
Найдите квадрат второй диагонали. Он будет равняться удвоенной сумме квадратов сторон минус квадрат уже известной диагонали. Извлеките квадратный корень.
Обратите внимание
При построении параллелограмма строго следуйте заданным параметрам и пользуйтесь инструментами. При расчетах пользуйтесь таблицами синусов и косинусов.
Полезный совет
В прямоугольнике и квадрате диагонали равны. Квадрат диагонали прямоугольника равен сумме квадратов его сторон. В квадрате диагональ равна квадратному корню, извлеченному из удвоенного квадрата стороны. Диагонали ромба являются биссектрисами его углов.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
По диагоналям параллелограмма найти его стороны
Чтобы по диагоналям параллелограмма найти его стороны, нужно использовать свойство диагоналей параллелограмма.
Задача 1.
Диагонали параллелограмма равны 18 см и 26 см, а одна из сторон на 10 см больше другой. Найти стороны параллелограмма.
Дано: ABCD — параллелограмм,
AC=26 см, BD=18 см,
AD на 10 см больше AB.
Найти: AB, AD.
Решение:
Пусть AB=x см, тогда AD=(х+10) см.
По свойству диагоналей параллелограмма,
Составим уравнение и решим его:
Делим обе части уравнения на 4, получаем:
Второй корень не подходит по смыслу задачи. Значит, AB=10 см, AD=10+10=20 см.
Ответ: 10 см, 20 см.
Задача 2.
Найти стороны параллелограмма, если они относятся как 8:19, а диагонали параллелограмма равны 30 см и 50 см.
Рисунок — аналогичный.
Дано: ABCD — параллелограмм,
AC=50 см, BD=30 см,
AB:AD=8:19.
Найти: AB, AD.
Решение.
Пусть k — коэффициент пропорциональности (k>0). Тогда AB=8k см, AD=19k см.
По свойству диагоналей параллелограмма,
Составляем уравнение:
Значит, AB=2∙8=16 см, AD=2∙19=38 см.
Ответ: 16 см, 38 см.
Найти угол между диагоналями параллелограмма
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
β — тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и диагонали:
Формулы соотношения острого и тупого углов между диагоналями:
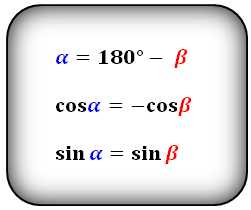
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
- Автор: Administrator
www-formula.ru
