Монотонность функции. Возрастание и убывание
Возрастающая и убывающая функции в промежутке
ОПРЕДЕЛЕНИЕ Функция называется возрастающей в промежутке , если большому значению аргумента соответствует большее значение функции, то есть для любой пары таких, что справедливо неравенство ОПРЕДЕЛЕНИЕ Функция называется убывающей в промежутке , если большому значению аргумента соответствует меньшее значение функции, то есть для любой пары таких что справедливоМонотонная функция
ОПРЕДЕЛЕНИЕФункция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.
Достаточное условие монотонности функции.Пусть функция определена и дифференцируема в промежутке . Для того чтобы функция была возрастающей в промежутке , достаточно, чтобы для всех
Для убывания функции достаточно, чтобы для всех
Для исследования функции на монотонность необходимо:
- найти её производную ;
- найти критические точки функции как решения уравнения ;
- определить знак производной на каждом из промежутков, на которые критические точки разбивают область определения функции;
- согласно достаточному условию монотонности функции определить промежутки возрастания и убывания.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
§ 4. Промежутки возрастания и убывания функций
Вспомним сначала определения возрастающей и убывающей функций.Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x1 < x2, то f(x1) < f(x2).
Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x1 <x2, то f(x1) > f(x2).
Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.
Функция
Рассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.
(-∞, a), (c, +∞) – убывает;
(a, b) – постоянная;
(b, c) – возрастает.
Применим понятие производной для исследования возрастания и убывания функции.
Теорема 1. (Необходимое и достаточное условия возрастания функции)
Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f ‘(x)≥ 0.
Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ‘ (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].
Доказательство.
Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) — f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
Переходя в этом равенстве к пределу при Δx→0, получим , то естьf ‘(x)≥0.
Докажем вторую часть теоремы. Пусть f ‘(x)>0при всех x Î (a,b). Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По теореме Лагранжа существует такое число c Î (x1, x2), что . По условиюf ‘(x)>
Аналогичная теорема имеет место и для убывающих функций.
Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Еслина (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].
Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривойy=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f ‘(x)≥0.
Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f ‘(x)>0 – для возрастания или f ‘(x)<0 – для убывания.
Примеры. Определить интервалы монотонности функции.
. Область определения заданной функции D(y) = (-∞; 0)È(0; +∞).
. Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).
Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
.
Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).
studfiles.net
Интервалы возрастания и убывания функции
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒
y = x^3-3*x^2+9*x+2
Область существования функции
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3 • x2-6 • x+9
Находим нули функции. Для этого приравниваем производную к нулю
3 • x2-6 • x+9 = 0
Для данного уравнения корней нет.
16.Дана функция . Тогда
(Укажите интервал выпуклости вверх (вниз) функции).
Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f»(x) = 6 • x-6
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
6 • x-6 = 0
Откуда точки перегиба:
x1 = 1
| (-∞ ;1) | (1; +∞) |
| f»(x) < 0 | f»(x) > 0 |
| функция выпукла | функция вогнута |
17.Найти наибольшее значение функции в интервале [4,5].
Экстремумы функции
y = x^2-11*x+28
[4;5]
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f»0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f»0(x*) < 0
то точка x* — локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y’ = 2 • x-11
Приравниваем ее к нулю:
2 • x-11 = 0
Вычисляем значения функции на концах отрезка
f(4) = 0
f(5) = -2
Ответ:
fmin = -2, fmax = 0
18.Пусть функции — непрерывны на интервале . Тогда (Основные свойства неопределенного интеграла).
Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то
Короче: постоянную можно выносить за знак интеграла.
Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то
Короче: интеграл суммы равен сумме интегралов.
Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:
Короче: производная от интеграла равна подынтегральной функции.
Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
19.Таблица интегралов. ( ).
Sinx+C
20.Найдите интеграл , , , ,
21.Вычислить , , ,
22.Пусть функции — непрерывны на интервале . Тогда (Основные свойства определенного интеграла, 9 свойств).
Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.
Теорема 1. Если f(x) и g(x) — две непрерывные функции, заданные на промежутке [a, b], то
т. е. интеграл суммы равен сумме интегралов слагаемых.
В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь
после чего остается перейти к пределу при λ → 0.
Аналогично доказывается
Теорема 2. Если f(x) — непрерывная функция, а c — постоянное число, то
т. е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.
Доказанную теорему можно высказать в более общей форме. Для этого нам понадобится расширить смысл символа интеграла.
Если f(x) — любая функция, определенная в точке a, то по определению полагаем
(11)
Таким образом, интеграл с совпадающими пределами равен нулю.
Пусть функция f(x) интегрируема на промежутке [a, b]. Тогда по определению полагаем
(12)
Таким образом, при перестановке пределов интегрирования определенный интеграл меняет знак.
Теперь можем привести упомянутую более общую форму теоремы 3:
Теорема 4. Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то
(13)
В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a, b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда
откуда
и остается дважды применить формулу (12).
Свойство интеграла, выражаемое теоремами 3 и 4, называется аддитивностью его, как функции промежутка интегрирования.
Теорема 5. Если f(x) — непрерывная функция, заданная на промежутке [a, b], то существует такая точка , что
(14)
В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму
Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 — xk) ≤ M(xk+1 — xk). Складывая такие неравенства и замечая, что
получим:
m(b — a) ≤ σ ≤ M(b — a).
Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b — a к новому неравенству
Таким образом, частное
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14).
Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет
Теорему 5 обычно называют теоремой о среднем значении. Из нее вытекает ряд свойств интеграла, выражающихся неравенствами.
Теорема 6. Если f(x) — неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего*, то и сам интеграл будет числом неотрицательным
Действительно, в этом случае оба сомножителя правой части формулы (14) неотрицательны.
___________________________________
* Если в интеграле будет a ≤ b, то будем говорить, что порядок пределов интегрирования — нормальный.
Последний результат можно несколько уточнить.
Теорема 7. Если a < b, а f(x) — непрерывная неотрицательная функция, которая хотя бы в одной точке [a, b] отлична от нуля, то
В самом деле, пусть x0 (a < x0 < b) — такая точка, что f(x0) > 0. Возьмем столь малое δ > 0, чтобы при | x — x0 | < δ было f(x) > 0, что, очевидно, возможно, благодаря непрерывности нашей функции. Не ограничивая общности, можно принять, что a ≤ x0 — δ, x0 + δ ≤ b. Тогда
Первый и третий интегралы правой части по предыдущей теореме неотрицательны, а второй интеграл по теореме о среднем представим в форме
и потому строго положителен.
Теорему 7 можно, очевидно, формулировать и так:
Теорема 8. Пусть f(x) — неотрицательная непрерывная функция, заданная в [a, b], причем a < b. Если
то f(x) всюду на [a, b] равна нулю.
В обеих теоремах 7 и 8 (в отличие от теоремы 6) нельзя отбросить условия непрерывности подинтегральной функции. Например, функция, которая в конечном числе точек [a, b] равна единице, а в остальных точках этого промежутка равна нулю, будет неотрицательной и нетождественной нулю, а интеграл от нее (как показано в пунктеОпределенный интеграл) равен нулю.
Теорема 9. Если a ≤ b, а f(x) и u·g(x) — две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то
(15)
т. е. при нормальном порядке пределов интегрирования неравенство можно интегрировать почленно.
Действительно,
Если бы мы допустили, что a < b и что хоть в одной точке оказывается f(x) < g(x), то смогли бы и в (15) исключить знак равенства.
Теорема 10. Если a ≤ b и f(x) непрерывна на [a, b], то
(16)
т. е. при нормальном порядке пределов интегрирования абсолютная величина интеграла не превосходит интеграла от абсолютной величины подинтегральной функции.
В самом деле, интегрируя неравенств
— | f(x) | ≤ f(x) ≤ | f(x) |,
находим:
а это равносильно неравенству (16).
23.Пусть — площадь фигуры, ограниченной линиями , . Тогда значение лежит в интервале
Приводим подобные:
2Решаем уравнение:
3Решаем уравнение:
4Решаем уравнение:
5Графики уравнений:
Ответ:
(Решение уравнения с учётом ОДЗ )
24.Формула для вычисления длины дуги плоской кривой, заданной явно и параметрически.
Если линия задана параметрическими уравнениями , то при выполнении некоторых условий, на которых я не буду останавливаться, длина дуги кривой , которая прочерчивается при изменении параметра в пределах , рассчитывается по формуле:
, где – значения, определяющие точки и .
25. ,
Частные производные
z = x^3/y^2+acos(sqrt(y))
Находим частные производные:
При нахождении ∂z/∂x считаем аргумент y постоянным:
При нахождении ∂z/∂y считаем аргумент x постоянным:
Находим вторые частные производные:
Найдем смешанные частные производные:
Для того, чтобы найти ∂2z/∂x∂y дифференцируем ∂z/∂x по у:
26. ;
Частные производные
z = x^3/y^2
Находим частные производные:
При нахождении ∂z/∂x считаем аргумент y постоянным:
При нахождении ∂z/∂y считаем аргумент x постоянным:
Найдем смешанные частные производные:
Для того, чтобы найти ∂2z/∂x∂y дифференцируем ∂z/∂x по у:
27. ;
z = 3*x^2*y*z^8+y^2*z^3/log(x)
Находим частные производные по формулам:
Для нашей функции F(x,y,z):
При нахождении ∂F/∂x считаем y и z постоянными:
При нахождении ∂F/∂y считаем x и z постоянными:
При нахождении ∂F/∂z считаем x и y постоянными:
По формулам находим частные производные:
∂z∂x=−6⋅x⋅y⋅z8−y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)∂z∂x=−6⋅x⋅y⋅z8−y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)
или
∂z∂x=−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)∂z∂x=−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)
или
Полный дифференциал функции.
dz=(−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dx+(−3⋅x2⋅z8−2⋅y⋅z3ln(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dydz=(−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dx+(−3⋅x2⋅z8−2⋅y⋅z3ln(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dy
28.Найти производную функции в точке М(1;-2) :
z = 5*x*y-y*y
Находим частные производные:
При нахождении ∂z/∂x считаем аргумент y постоянным:
При нахождении ∂z/∂y считаем аргумент x постоянным:
Полный дифференциал функции.
dz = (5 • y)dx + (5 • x-2 • y)dy
Найдем частные производные в точке А(1;-2)
или
или
Находим вторые частные производные:
Найдем вторые частные производные в точке А(1;-2)
или
или
Найдем смешанные частные производные:
Для того, чтобы найти ∂2z/∂x∂y дифференцируем ∂z/∂x по у:
Найдем значение производной в точке А(1;-2)
или
29.Найти градиент функции в точке .
z = 3*x^2+x*y-2*y^2
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.:
Находим частные производные:
Тогда величина градиента равна:
Найдем градиент в точке А(2;1)
или
Модуль grad(z) — наибольшая скорость возрастания функции:
Направление вектора-градиента задаётся его направляющими косинусами:
30.Укажите сходящийся несобственный интеграл 1-го рода.
Рекомендуемые страницы:
lektsia.com
Тема «Возрастание и убывание квадратичной функции» Найти по
Описание презентации Тема «Возрастание и убывание квадратичной функции» Найти по по слайдам
Тема «Возрастание и убывание квадратичной функции» Найти по графику промежутки возрастания и убывания квадратичной функции
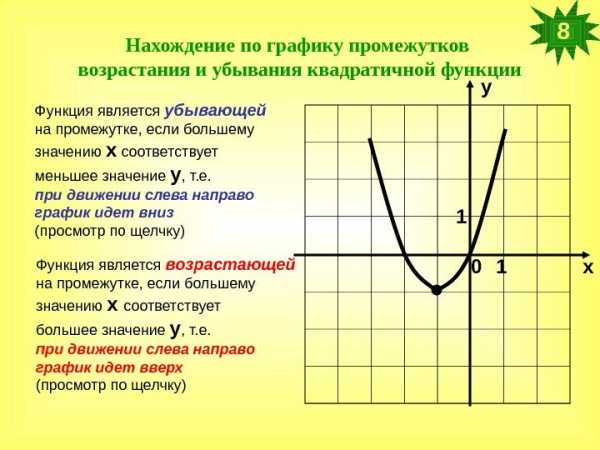Нахождение по графику промежутков возрастания и убывания квадратичной функции ху 0 11 Функция является убывающей на промежутке, если большему значению х соответствует меньшее значение у , т. е. при движении слева направо график идет вниз (просмотр по щелчку) Функция является возрастающей на промежутке, если большему значению х соответствует большее значение у , т. е. при движении слева направо график идет вверх (просмотр по щелчку)
8 у х0 11 Найти по графику и записать промежутки возрастания и убывания квадратичной функции Обратите внимание, что график квадратичной функции состоит из двух ветвей. Ветви соединяются между собой вершиной параболы. При записи промежутков возрастания и убывания самую главную роль будет играть абсцисса (х) вершины параболы Пример 1. Рассмотрим движение по каждой ветке параболы отдельно: • по левой ветке при движении слева направо график идет вниз, значит функция убывает ; • по правой ветке — график идет вверх, значит функция возрастает. Ответ: промежуток убывания (- ∞; -1 ] ; промежуток возрастания [ -1; +∞)
present5.com
Как найти промежутки возрастания и убывания функции примеры
ЕГЭ, ДОМАШНИЕ ЗАДАНИЯ Стереометрия Найдите V/S поверхности МНОГОГРАННИКА, изображенного на рисунке (все двугранные углы прямые)
Возрастание и убывание функции на интервале, экстремумы.
Очень важную информацию о поведении функции предоставляют промежутки возрастания и убывания. Их нахождение является частью процесса исследования функции и построения графика. К тому же точкам экстремума, в которых происходит смена с возрастания на убывание или с убывания на возрастание, уделяется особое внимание при нахождении наибольшего и наименьшего значения функции на некотором интервале.
В этой статье дадим необходимые определения, сформулируем достаточный признак возрастания и убывания функции на интервале и достаточные условия существования экстремума, применим всю эту теорию к решению примеров и задач.
Рекомендуем при необходимости обращаться к разделу дифференцирование функции, так как все признаки в этой статье основаны на нахождении производной.
Навигация по странице.
Возрастание и убывание функции на интервале.
Определение возрастающей функции.
Определение убывающей функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b) , то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
Точки экстремума, экстремумы функции.
Точки минимума и максимума называют Точками экстремума, а значения функции, соответствующие точкам экстремума, называют Экстремумами функции.
Не путайте экстремумы функции с наибольшим и наименьшим значением функции.
На первом рисунке наибольшее значение функции на отрезке [a;b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b, которая не является точкой максимума.
Достаточные условия возрастания и убывания функции.
На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.
Вот формулировки признаков возрастания и убывания функции на интервале:
- если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X ; если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
- найти область определения функции; найти производную функции; к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.
Переходим к нахождению производной функции:
В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы.
Приводим график функции для сопоставления с ним полученных результатов.
Достаточные условия экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Алгоритм нахождения точек экстремума по первому признаку экстремума функции.
- Находим область определения функции. Находим производную функции на области определения. Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют Точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак). Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала). Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак — они и являются точками экстремума.
Слишком много слов, рассмотрим лучше несколько примеров нахождения точек экстремума и экстремумов функции с помощью первого достаточного условия экстремума функции.
Областью определения функции является все множество действительных чисел, кроме x=2 .
Нулями числителя являются точки x=-1 и x=5 , знаменатель обращается в ноль при x=2 . Отмечаем эти точки на числовой оси
Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x=-2, x=0, x=3 и x=6 .
Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.
Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.
Областью определения функции является все множество действительных чисел. Саму функцию можно записать в виде:
Найдем производную функции:
В точке x=0 производная не существует, так как значения односторонних пределов при стремлении аргумента к нулю не совпадают:
В это же время, исходная функция является непрерывной в точке x=0 (смотрите раздел исследование функции на непрерывность):
Найдем значения аргумента, при котором производная обращается в ноль:
Отметим все полученные точки на числовой прямой и определим знак производной на каждом из интервалов. Для этого вычислим значения прои
poiskvstavropole.ru
3.2.1 Монотонность функции. Промежутки возрастания и убывания
Видеоурок: Возрастание и убывание функции
Лекция: Монотонность функции. Промежутки возрастания и убывания
Монотонность функцииНевозможно правильно построить охарактеризовать функцию и построить график без исследования её на монотонность.
Если у функции имеются диапазоны, на которых она постоянно убывает, или возрастает, такие функции называются монотонными.
Функция называется возрастающей, если на некотором промежутке большему значению функции соответствует большее значение аргумента, если же большему аргументы соответствует меньшее значение функции, то она называется убывающей.
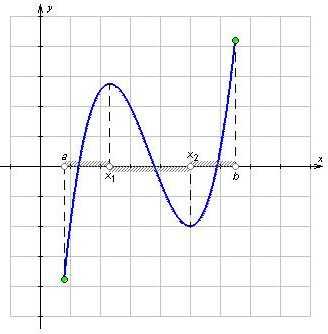
Обратите внимание на рисунок: на промежутке от а до х1 значение функции увеличивается, а значит, данный промежуток функции является возрастающим. На промежутке от х1 до х2 функция убывает. А на промежутке от х2 до b функция снова возрастает.
Постоянство, возрастание, убывание
Для того, чтобы знать, как ведет себя функция необходимо знать некоторые тонкости. В этом нам помогут теоремы:
1. Функция имеет постоянные значения на некотором промежутке в том случае, когда производная в каждой точке данного промежутка равна нулю.
При этом данный промежуток может иметь конечные значения, а может иметь и бесконечные значения аргумента.
2. Достаточным признаком возрастания функции считается то, что производная данной функции на заданном интервале принимает положительные значения.
3. Достаточным признаком убывания функции на некотором промежутке можно считать отрицательное значение производной в точках, выбранных из заданного диапазона.
cknow.ru