Вычислить площадь фигуры ограниченной линиями. Геометрический смысл определенного интеграла
Плоская фигура, ограниченная осью , прямыми и и графиком непрерывной на отрезке функции , которая не меняет знак на этом промежутке, называется криволинейной трапецией.
Площадь криволинейной трапеции численно равна определенному интегралу:
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
На основании геометрического смысла определенного интеграла покоится целый класс задач на нахождение площадей фигур, ограниченных линиями.
100task.ru
Вычислить площадь фигуры ограниченной линиями
Для того, чтобы вычислить площадь фигуры, которая ограничена указанными линиями, полезно сначала начертить графики заданных функций и определить какими функциями она ограничена сверху, снизу и на каком отрезке по оси Ох. Затем уже используют формулу нахождения площади фигуры:
Удобнее этот вопрос изучать на примерах.
Пример.
Найдем площадь фигуры, которая ограничена линиями , , , .
Решение.
Из условия видно, что площадь фигуры нужно найти на промежутке (на это указывают функции и ).
При построении графика функций определим, что сверху фигура будет ограничена функцией , а снизу — функцией .
Подставим полученные данные в формулу:
Ответ. кв. ед.
Встречаются случаи, когда отрезок, на котором нужно вычислить площадь фигуры, явно не задан. В таком случае сначала находят этот отрезок, а затем вычисляют определенный интеграл.
Пример.
Вычислить площадь фигуры, которая ограничена линиями и .
Решение.
Найдем точки пересечения данных функций. Для этого составим уравнение:
Запишем определенный интеграл для нахождения площади заданной фигуры:
Ответ. кв. ед.
ru.solverbook.com
Вычисление площади фигуры с помощью определенного интеграла
Вычисление площади фигуры с помощью определенного интеграла | |Пример 1.
Решение
Сделаем чертёж фигуры, ограниченной указанными линиями:
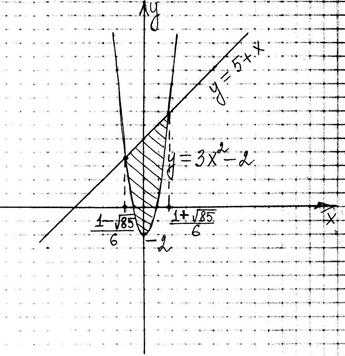
Найдём точки пересечения линий:
Найдём площадь фигуры с помощью определённого интеграла:
Ответ: кв.ед.
Пример 2.
Решение
Сделаем чертёж фигуры, ограниченной указанными линиями:
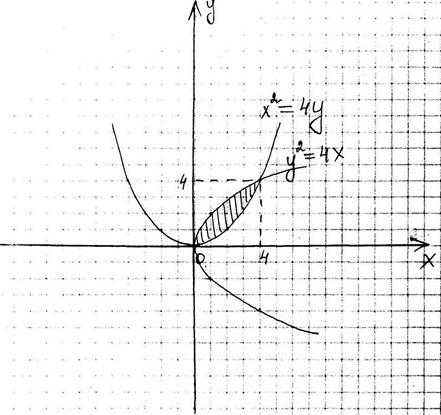
Найдём площадь фигуры с помощью определённого интеграла:
Ответ: кв.ед.
primer.by
Задание 3. Вычислить площадь фигуры, ограниченной линиями.
0. y = x2 – 2x + 2, y = x + 2.
Решение варианта 0.
Данная
фигура сверху ограничена прямойy = x + 2, снизу параболой y = x2 – 2x + 2.
Искомую
площадь вычислим по формуле S = 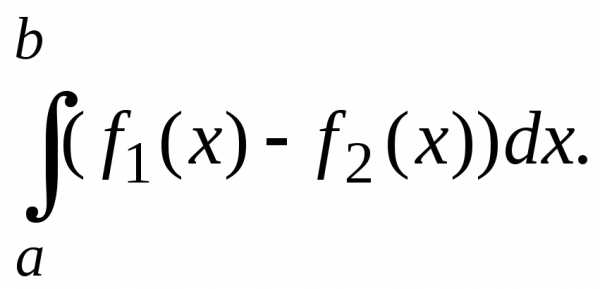 Пределами
интегрирования будут абсциссы точек
пересечения параболы и прямой. Решая
систему уравнений y = x2 – 2x + 2, y = x + 2 находим:
Пределами
интегрирования будут абсциссы точек
пересечения параболы и прямой. Решая
систему уравнений y = x2 – 2x + 2, y = x + 2 находим: 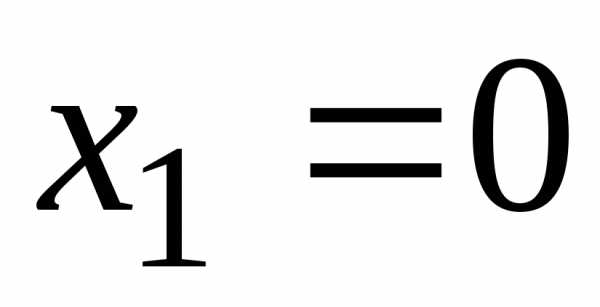
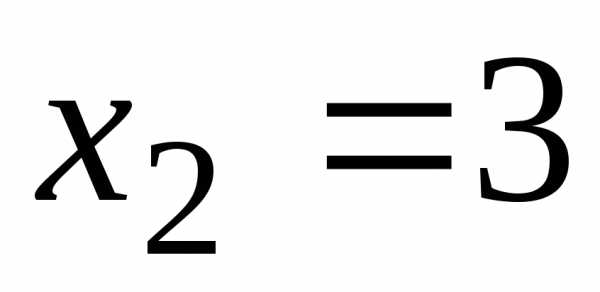 ,
т. е. a = 0, b = 3. Таким
образом получаем:
,
т. е. a = 0, b = 3. Таким
образом получаем: S
= 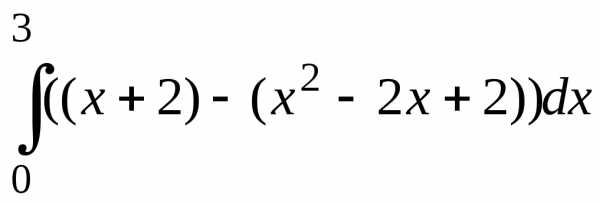 =
=  =
=
= 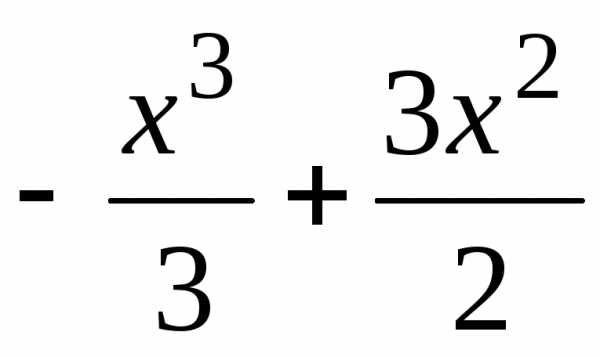
 =–9 +
=–9 + 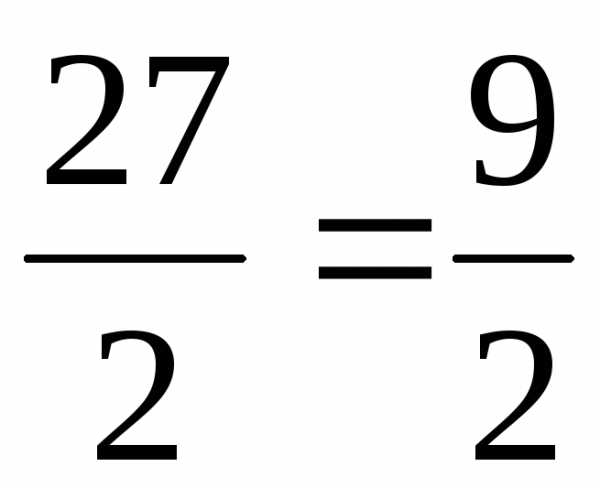
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4. Вычислить объем тела, образованного вращением вокруг указанной оси фигуры, ограниченной линиями:
0. y = sinx, (0≤x≤), y =
0, Ox.
Решение варианта 0.
Изобразим указанное тело на чертеже.
Искомый объем
вычислим по формуле V = 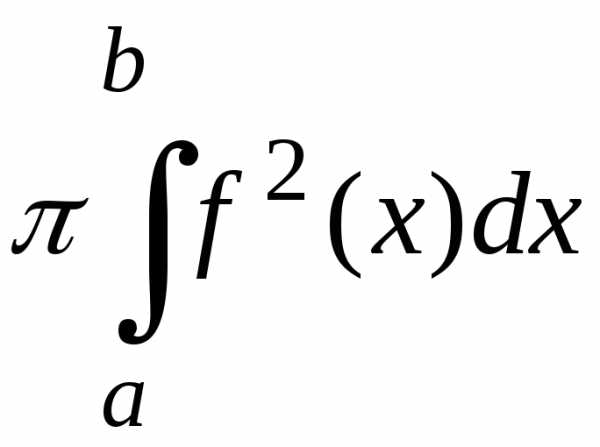 .
Имеем:
.
Имеем:
V =  =
=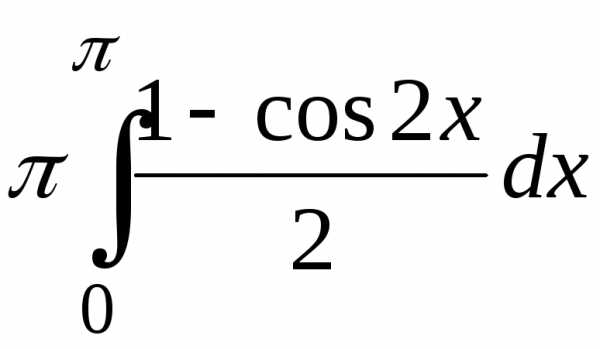 =
= 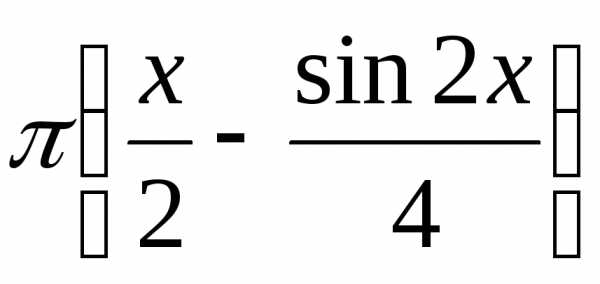
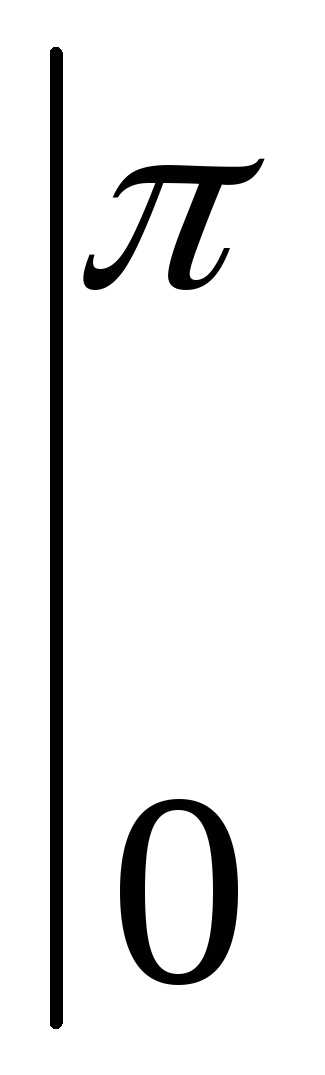 =
= 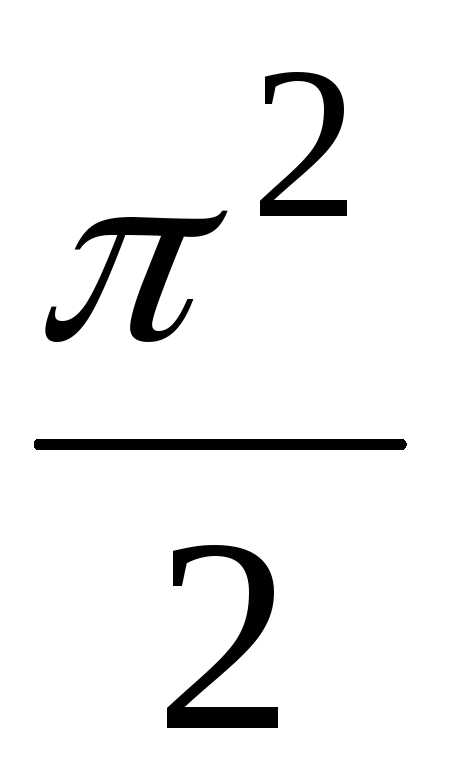 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
studfiles.net
Двойной интеграл. Вычисление площади плоской фигуры
Площадь плоской фигуры, ограниченной областью D, находится по формуле
$$S=\int \int _{D}dxdy.$$
Если область D определена, например, неравенствами \(a\leq x\leq b, \varphi _1(x)\leq y\leq \varphi _2(x)\), то
$$S=\int_{a}^{b}{dx\int_{\varphi _1}^{\varphi _2}{dy}}. $$
Если область D в полярных координатах определена неравенствами \(\alpha \leq \theta \leq \beta , \varphi (\theta )\leq \rho \leq f(\theta ),\) то
$$S=\int \int _{D}\rho d\rho d\theta=\int_{\alpha }^{\beta }{d\theta }\int_{\varphi (\theta )}^{f(\theta )}{\rho d\rho} .$$
Пример 1. Вычеслить площадь фигуры, ограниченной линиями \(x=4y-y^2, x+y=6.\)
Найдем координаты точек пересечения заданных линий, решая систему уравнений \(x=4y-y^2\) и \(x+y=6\) (чертеж рекомендуется выполнить самостоятельно). В результате получим \(А(4;2), В(3;3)\). Таким образом получим,
$$S=\int \int _{D}dxdy=\int_{2}^{3}{dy}\int_{6-y}^{4y-y^2}{dx}=\int_{2}^{3}{x}\mid \begin{matrix} 4y-y^2 \\ 6-y \end{matrix} dy=$$
$$=\int_{2}^{3}{(-y^2+5y-6)dy}=[-\frac{1}{3}y^3+\frac{5}{2}y^2-6y]_2^3=\frac{1}{6}.$$
Пример 2. Найти площадь фигуры, ограниченной данными линиями : \(y=3/x, y=4e^x, y=3, y=4.\)
Решение. Построим область интегрирования D и находим площадь ограниченной области D (заштрихованая область).
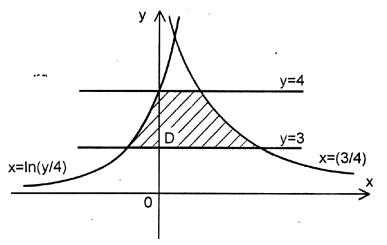
Пределы интегрирования для данной области определяются ее границами из неравенства \(3\leq y\leq 4; ln\frac{y}{4}\leq x\leq \frac{3}{y}\). Отсюда, применяя интегрирование по частям, получим
$$S=\int_{3}^{4}{dy}\int_{\ln (y/4)}^{3/y}{dx}=\int_{3}^{4}{\left[\frac{3}{y}-\ln \frac{y}{4}dy \right]}=\left[ 3\ln y-y\ln \frac{y}{4}+y\right]_3^4=1$$
Итак, площадь данной фигуры равна 1.
Пример 3. Найти площадь фигуры, ограниченной линией \(x^3+y^3=axy\)/
Решение. Область интегрирования есть площадь петли, симметричной относительно прямой \(x=y\). Преобразуем данное уравнение, используя полярные координаты.
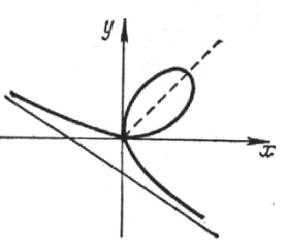
Имеем :
$$r^3(\sin ^3\varphi +\cos ^3\varphi )=r^2\cdot a\cdot \sin \varphi \cdot \cos \varphi, или r=\frac{a\sin \varphi \cdot \cos \varphi }{\sin ^3\varphi +\cos ^3}.$$
Осью симметрии петли является ось \(\varphi =\pi /4\), поэтому область интегрирования разделим на две равные части по оси симметрии и искомая площадь будет равна удвоенному интегралу:
$$S=2\int \int _{D} rdrd\varphi =2\int_{0}^{\pi /4}{d\varphi }\int_{0}^{a\sin \varphi \cdot \cos \varphi /(\sin ^3\varphi +\cos ^3\varphi) }{rdr}=a^2\int_{0}^{\pi /4}{\frac{\sin ^2\varphi \cdot \cos ^2\varphi }{(\sin ^3\varphi +\cos ^3\varphi)}d\varphi }=$$
$$=a^2\int_{0}^{\pi /4}{\frac{tg^2\varphi \cdot \cos ^4\varphi }{\cos ^6\varphi (1+tg^3\varphi )^2}d\varphi }=\frac{a^2}{3}\int_{0}^{\pi /4}{\frac{3tg^2\varphi d(tg\varphi )}{(1+tg^3\varphi )2}}=$$
$$=\frac{a^2}{3}\int_{0}^{\pi /4}{\frac{d(1+tg^3\theta )}{(1+tg^3\theta )^2}}=-\frac{a^2}{3}\left[\frac{1}{1+tg^3\theta } \right]_0^\pi /4=\frac{a^2}{6}$$
Итак, площадь данной фигуры равна \(S=\frac{a^2}{6}\) .
2012-12-05 • Просмотров [ 17839 ]
primat.org

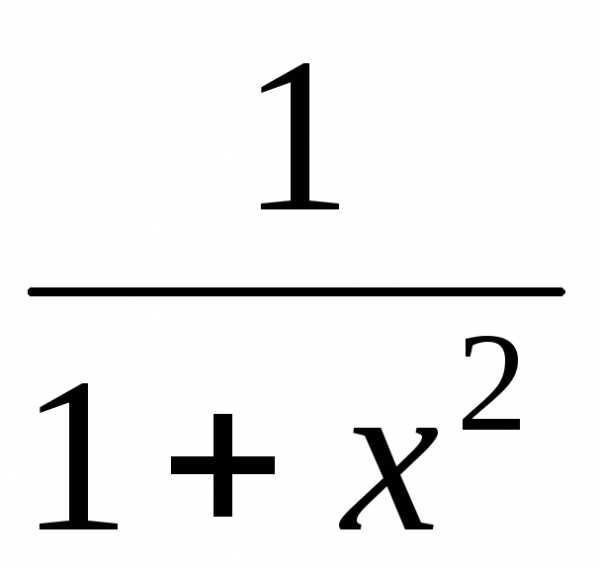
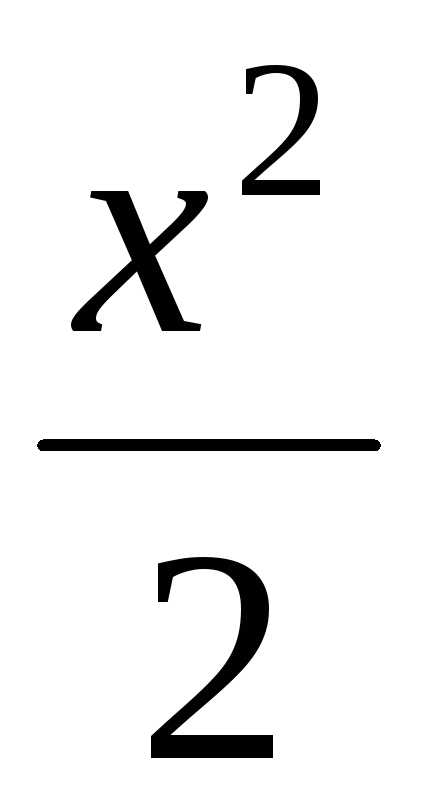 .
.
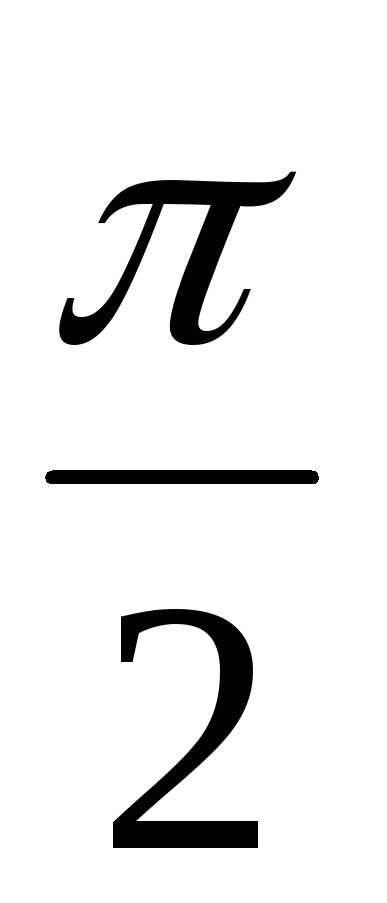 ,y = 0.
,y = 0. sinx.
sinx.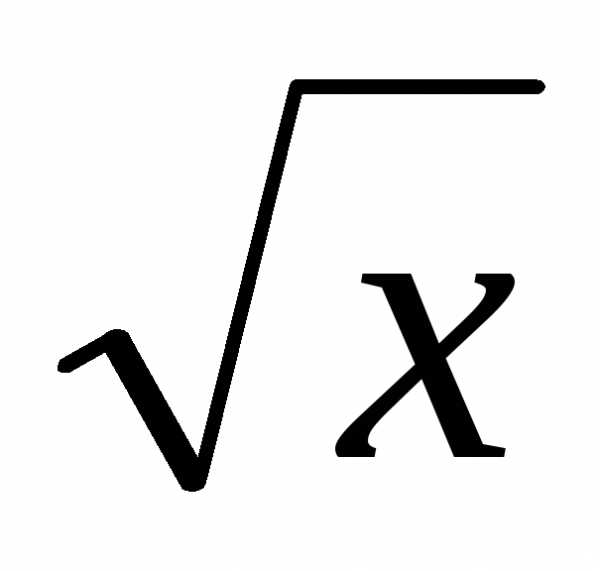 , y = x2,
Ox.
, y = x2,
Ox. ,
(1≤x≤2), y = 0, Ox.
,
(1≤x≤2), y = 0, Ox.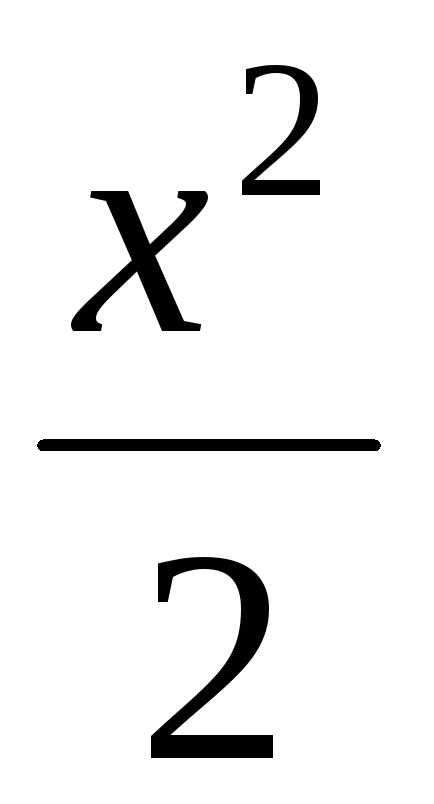 , x + y = 2, Oy.
, x + y = 2, Oy.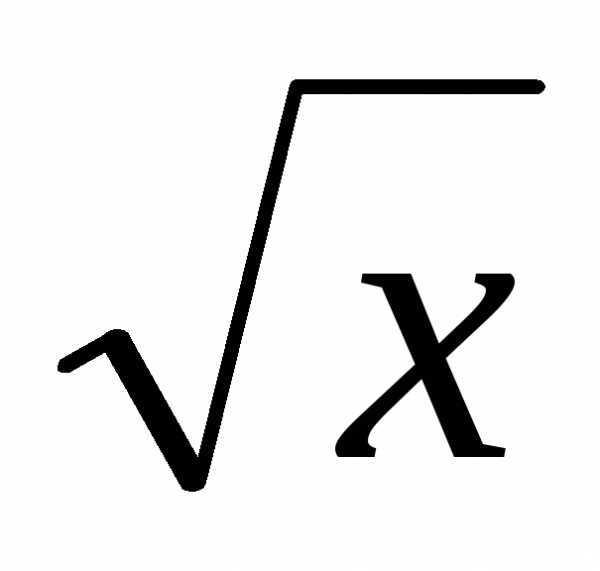 , y = x,
Ox.
, y = x,
Ox.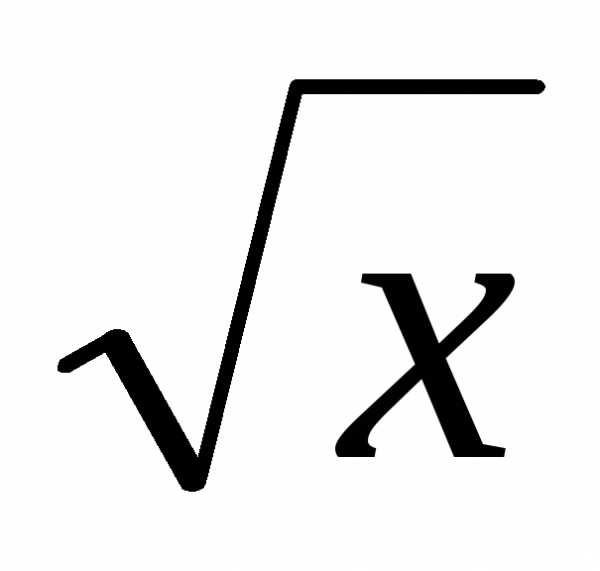 , (0≤x≤4), y = 0,
Ox.
, (0≤x≤4), y = 0,
Ox. , y = x, Ox.
, y = x, Ox. Oy.
Oy.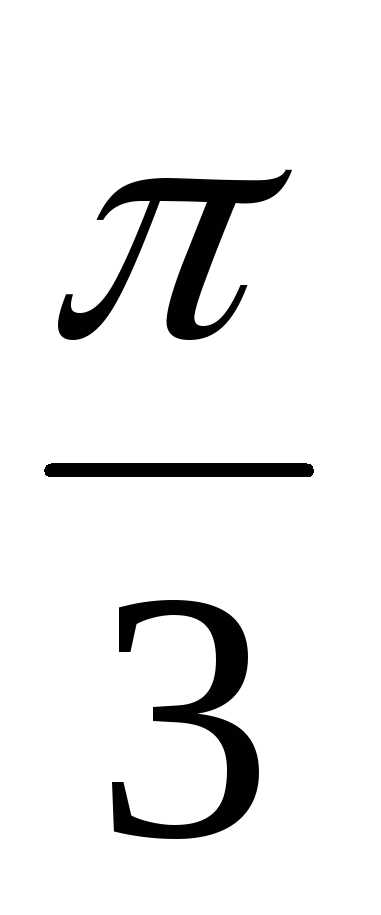 ), y = 0, Ox.
), y = 0, Ox.