Как найти наибольшее значение производной функции по графику – Дан график производной функции

Как найти наибольшее значение производной функции по графику

Как правильно написать программу для решения квадратного уравнения на Pascal.

Как найти наибольшее значение производной функции по графику

Тип 2. Определить точку, в которой функция принимает наибольшее (наименьшее) значение.

Задача: Дан график производной функции. Определить, в какой точке отрезка функция принимает наибольшее значение.

Отбросим лишнее (оставим на чертеже только отрезок )

Требуется определить точку, в которой функция принимает наибольшее значение.

Замечание 1: Вторая теорема Вейерштрасса: функция, непрерывная на отрезке, принимает на нем наибольшее и наименьшее значения.

Замечание 2: Это наибольшее и наименьшее значение она достигает или внутри отрезка или на его границах.

Замечание 3: В точке максимума производная функции равна нулю и меняет свой знак с плюса на минус.

В этом случае есть две точки, в которых производная равна нулю, но только при этот график переходит из верхней полуплоскости в нижнюю (т. е. производная меняет свой знак с «+» на «-»).

Вывод: — точка максимума функции на отрезке.

Ответ: в точке функция достигает своего наибольшего значения на отрезке

А зачем, собственно говоря, в условии задачи дано ограничение на рассматриваемый отрезок? И почему именно?

Рассмотрим и проанализируем отрезок.

1) на интервале производная (а это график производной ) отрицательна, т. е. функция убывает.

2) в точке производная равна 0 и меняет свой знак с «-» на «+», т. е. функция имеет в этой точке минимум.

3) на интервале производная положительна (график лежит выше оси ОХ) , т. е. функция возрастает.

4) в точке производная равна 0 и меняет свой знак с «+» на «-», т. е. функция имеет в этой точке максимум.

5) на отрезке производная отрицательна, т. е. функция убывает.

Построим пример графика, удовлетворяющий пунктам 1) — 6).

В данном случае наибольшее значение функция принимает наибольшее значение на границе интервала в точке, а не в точке максимума.

Только по графику производной сравнивать значение функции практически невозможно, поэтому и взят интервал, на котором функция сначала возрастает, а потом убывает, т. е. думать особо не надо.

Задача: Дан график производной функции. Определить, в какой точке отрезка функция принимает наибольшее значение.

Замечание: дан график ПРОИЗВОДНОЙ.

На рассматриваемом отрезке производная всюду отрицательна (лежит ниже оси ОХ ), т. е. функция всюду убывает на этом отрезке, типа вот такого:

Очевидно, что наибольшее значение функция принимает в левой точке рассматриваемого отрезка.

Ответ: Функция, определенная на отрезке принимает наибольшее значение в точке

Как найти наибольшее значение производной функции по графику

На рисунке изображён график производной функции

Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки. В конце поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами рассматривали задачи, в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее (или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции, принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Могут стоять и другие вопросы, но они не вызовут у вас затруднений, если вы поняли геометрический смысл производной и свойства производной для исследования функций (ссылки указаны на статьи, в которых представлена необходимая для решения информация, рекомендую повторить).

Основная информация (кратко):

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.

3. Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ох.

Это нужно чётко уяснить и помнить.

Многих график производной «смущает». Некоторые по невнимательности принимают его за график самой функции. Поэтому в таких зданиях, где видите, что дан график, сразу же акцентируйте своё внимание в условии на том, что дано: график функции или график производной функции?

Если это график производной функции, то относитесь к нему как бы к «отражению» самой функции, которое просто да

poiskvstavropole.ru

Как найти наибольшее значение производной по графику функции

Учебник: Л.Г. Петерсон, Математика, 4 класс, часть 1, урок 32. Как мы умеем измерять площадь фигуры, если нам не известна формула площади?. 2*5=10 (см?). – Можно ли с помощью полученного результата найти площадь прямоугольного треугольника? Как? (5*2):2=5 (см?). – Замените числа буквами.

На рисунке изображён график производной функции

Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки. В конце поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами рассматривали задачи, в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее (или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции, принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Могут стоять и другие вопросы, но они не вызовут у вас затруднений, если вы поняли геометрический смысл производной и свойства производной для исследования функций (ссылки указаны на статьи, в которых представлена необходимая для решения информация, рекомендую повторить).

Основная информация (кратко):

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.

3. Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ох.

Это нужно чётко уяснить и помнить.

Многих график производной «смущает». Некоторые по невнимательности принимают его за график самой функции. Поэтому в таких зданиях, где видите, что дан график, сразу же акцентируйте своё внимание в условии на том, что дано: график функции или график производной функции?

Если это график производной функции, то относитесь к нему как бы к «отражению» самой функции, которое просто даёт вам информацию об этой функции.

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–2;21).

Ответим на следующие вопросы:

1. В какой точке отрезка [7;15] функция f(х) принимает наибольшее значение.

На заданном отрезке производная функции отрицательна, значит функция на этом отрезке убывает (она убывает от левой границы интервала к правой). Таким образом, наибольшее значение функции достигается на левой границе отрезка, т. е. в точке 7.

2. В какой точке отрезка [3;6] функция f(х) принимает наименьшее значение.

По данному графику производной можем сказать следующее. На заданном отрезке производная функции положительна, значит функция на этом отрезке возрастает (она возрастает от левой границы интервала к правой). Таким образом, наименьшее значение функции достигается на левой границе отрезка, то есть в точке х = 3.

3. Найдите количество точек максимума функции f(х), принадлежащих отрезку [0;20].

Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Рассмотрим, где таким образом меняется знак.

На отрезке (3;6) производная положительна, на отрезке (6;16) отрицательна.

На отрезке (16;18) производная положительна, на отрезке (18;20) отрицательна.

Таким образом, на заданном отрезке [0;20] функция имеет две точки максимума х = 6 и х = 18.

4. Найдите количество точек минимума функции f(х), принадлежащих отрезку [0;4].

Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. У нас на интервале (0;3) производная отрицательна, на интервале (3;4) положительна.

Таким образом, на отрезке [0;4] функция имеет только одну точку минимума х = 3.

*Будьте внимательны при записи ответа – записывается количество точек, а не значение х, такую ошибку можно допустит из-за невнимательности.

5. Найдите количество точек экстремума функции f(х), принадлежащих отрезку [0;20].

Обратите внимание, что необходимо найти Количество точек экстремума (это и точки максимума и точки минимума).

Точки экстремума соответствуют точкам смены знака производной (с положительного на отрицательный или наоборот). На данном в условии графике это нули функции. Производная обращается в нуль в точках 3, 6, 16, 18.

Таким образом, на отрезке [0;20] функция имеет 4 точки экстремума.

6. Найдите промежутки возрастания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки возрастания данной функции f(х) соответствуют промежут

poiskvstavropole.ru

Как найти по графику производной функции наибольшее значение

Доказательство[править | править код]. Доказательство проводится для случая выпуклого n-угольника. В случае n=3 смотреть Теорема о сумме углов треугольника. Пусть A 1 A 2.. A n {\displaystyle A_{1}A_{2}. A_{n}} {\displaystyle A_{1}A_{2}. A_{ — данный выпуклый многоугольник и n > 3. Тогда проведем из.

На рисунке изображён график производной функции

Здравствуйте! Ударим по приближающемуся ЕГЭ качественной систематической подготовкой, и упорством в измельчении гранита науки. В конце поста имеется конкурсная задача, будьте первым! В одной из статей данной рубрики мы с вами рассматривали задачи, в которых был дан график функции, и ставились различные вопросы, касающиеся экстремумов, промежутков возрастания (убывания) и прочие.

В этой статье рассмотрим задачи входящие в ЕГЭ по математике, в которых дан график производной функции, и ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее (или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции, принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Могут стоять и другие вопросы, но они не вызовут у вас затруднений, если вы поняли геометрический смысл производной и свойства производной для исследования функций (ссылки указаны на статьи, в которых представлена необходимая для решения информация, рекомендую повторить).

Основная информация (кратко):

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.

3. Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ох.

Это нужно чётко уяснить и помнить.

Многих график производной «смущает». Некоторые по невнимательности принимают его за график самой функции. Поэтому в таких зданиях, где видите, что дан график, сразу же акцентируйте своё внимание в условии на том, что дано: график функции или график производной функции?

Если это график производной функции, то относитесь к нему как бы к «отражению» самой функции, которое просто даёт вам информацию об этой функции.

На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–2;21).

Ответим на следующие вопросы:

1. В какой точке отрезка [7;15] функция f(х) принимает наибольшее значение.

На заданном отрезке производная функции отрицательна, значит функция на этом отрезке убывает (она убывает от левой границы интервала к правой). Таким образом, наибольшее значение функции достигается на левой границе отрезка, т. е. в точке 7.

2. В какой точке отрезка [3;6] функция f(х) принимает наименьшее значение.

По данному графику производной можем сказать следующее. На заданном отрезке производная функции положительна, значит функция на этом отрезке возрастает (она возрастает от левой границы интервала к правой). Таким образом, наименьшее значение функции достигается на левой границе отрезка, то есть в точке х = 3.

3. Найдите количество точек максимума функции f(х), принадлежащих отрезку [0;20].

Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. Рассмотрим, где таким образом меняется знак.

На отрезке (3;6) производная положительна, на отрезке (6;16) отрицательна.

На отрезке (16;18) производная положительна, на отрезке (18;20) отрицательна.

Таким образом, на заданном отрезке [0;20] функция имеет две точки максимума х = 6 и х = 18.

4. Найдите количество точек минимума функции f(х), принадлежащих отрезку [0;4].

Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. У нас на интервале (0;3) производная отрицательна, на интервале (3;4) положительна.

Таким образом, на отрезке [0;4] функция имеет только одну точку минимума х = 3.

*Будьте внимательны при записи ответа – записывается количество точек, а не значение х, такую ошибку можно допустит из-за невнимательности.

5. Найдите количество точек экстремума функции f(х), принадлежащих отрезку [0;20].

Обратите внимание, что необходимо найти Количество точек экстремума (это и точки максимума и точки минимума).

Точки экстремума соответствуют точкам смены знака производной (с положительного на отрицательный или наоборот). На данном в условии графике это нули функции. Производная обращается в нуль в точках 3, 6, 16, 18.

Таким образом, на отрезке [0;20] функция имеет 4 точки экстремума.

6. Найдите промежутки возрастания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки возрастания данной функции f(х) соответствуют промежуткам, на которых ее производная положительна, то есть интервалам (3;6) и (16;18). Обратите вним

poiskvstavropole.ru

ЕГЭ по математике задание В8 (производные)

Прямая $y=-9x$ является касательной к графику функции $24x^2+bx+6$. Найдите b, учитывая, что абсцисса точки касания меньше 0.

На рисунке изображен график $y=f'(x)$ — производной функции f(x), определенной на интервале (-1;10). Найдите точку экстремума функции f(x), принадлежащую отрезку [0;7].

На рисунке изображен график $y=f'(x)$ — производной функции f(x), определенной на интервале (-10;5). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

На рисунке изображен график $y=f'(x)$ — производной функции f(x), определенной на интервале (-8;16). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-4;15].

На рисунке изображен график $y=f'(x)$ — производной функции f(x), определенной на интервале (-4;7). В какой точке отрезка [-3;1] функция f(x) принимает наименьшее значение?

На рисунке изображен график функции $y=f(x)$, определенной на интервале (-2;10). Определите количество целых точек, в которых производная функции положительна.

На рисунке изображен график функции $y=f(x)$, определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.

Прямая $y=9x-5$ является касательной к графику функции $12x^2-3x+c$. Найдите c.

Материальная точка движется прямолинейно по закону $x(t)=t^2+7t+27$, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3c.

Материальная точка движется прямолинейно по закону $x(t)=-t^3-8t^2+6t+2$, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3c.

bankege.ru

Как решать задачи B15 без производных

29 января 2012

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) < f (x₂).

Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) > f (x₂).

Другими словами, для возрастающей функции чем больше x,тем больше f (x). Для убывающей функции все наоборот: чем больше x,тем меньше f (x).

Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log_ax (a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:

f (x) = a ^x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax² + bx + c. Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x₀ тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x₀ для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы x₀, координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы y = ax² + bx + c и найти ее вершину по формуле: x₀ = −b/2a;
2. Найти значение исходной функции в этой точке: f (x₀). Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция y = x² + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке x₀ = −3 функция y = x² + 6x + 13 принимает наименьшее значение.

Корень монотонно возрастает, значит x₀ — точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

y = log ₂ (x² + 2x + 9)

Под логарифмом снова квадратичная функция: y = x² + 2x + 9. График — парабола ветвями вверх, т.к. a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −2/(2 · 1) = −2/2 = −1

Итак, в точке x₀ = −1 квадратичная функция принимает наименьшее значение. Но функция y = log ₂x — монотонная, поэтому:

y_min = y(−1) = log ₂ ((−1)² + 2 · (−1) + 9) = … = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция y = 1 − 4x − x². Перепишем ее в нормальном виде: y = −x² − 4x + 1.

Очевидно, что график этой функции — парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:

x₀ = −b/(2a) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x₀ = −2:

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

1. Аргумент логарифма должен быть положительным:

   y = log_af (x) ⇒ f (x) > 0

2. Арифметический квадратный корень существует только из неотрицательных чисел:

3. Знаменатель дроби не должен равняться нулю:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: y = 3 − 2x − x². Ее график — парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2x − x² ≥ 0 ⇒ x² + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒x ∈ [−3; 1]

Теперь найдем вершину параболы:

x₀ = −b/(2a) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Точка x₀ = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x₀, а также на концах ОДЗ:

y(−3) = y(1) = 0

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

y = log _0,5 (6x − x² − 5)

Внутри логарифма стоит квадратичная функция y = 6x − x² − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6x − x² − 5 > 0 ⇒ x² − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒x ∈ (1; 5)

Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.

Ищем вершину параболы:

x₀ = −b/(2a) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: x₀ = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x₀:

y_min = y(3) = log _0,5 (6 · 3 − 3² − 5) = log _0,5 (18 − 9 − 5) =log _0,5 4 = −2

Смотрите также:

1. Показательные функции в задаче B15: хитрости решения
2. Задача B15: работаем с показательной функцией без производной
3. Тест к уроку «Что такое числовая дробь» (средний)
4. Правила комбинаторики в задаче B6
5. Пример решения задачи 15
6. Задача B2 про комиссию в терминале

www.berdov.com

Задачи на производную и касательную

В этом году в Задании 7 из  Открытого банка заданий для подготовки к ЕГЭ  по математике появились новые задачи. Давайте разберем их решение.

Прототип задания B8 (№ 317543)

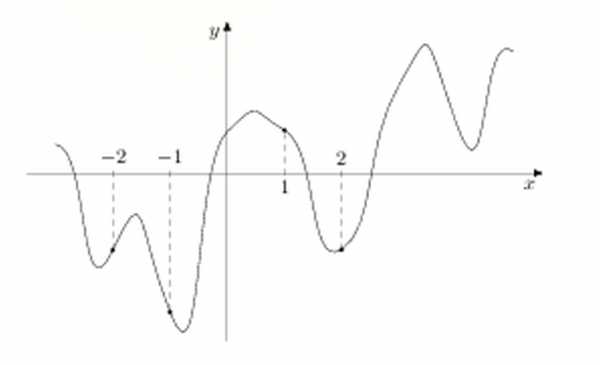
На рисунке изображен график функции y=f(x)  и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

 Как мы знаем, производной  называется

предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Производная в точке показывает скорость изменения функции в данной точке. Чем быстрее изменяется функция, то есть чем больше приращение функции, тем больше угол наклона касательной. Поскольку в задаче требуется определить точку, в которой значение производной наибольшее, исключим из рассмотрения точки с абсциссами -1 и 1 — в этих точках функция убывает, и производная в них отрицательна.

Функция возрастает в точках -2 и 2. Однако, возрастает она в них по-разному — в точке -2 график функции поднимается круче, чем в точке 2, и следовательно, приращение  функции в этой точки, а, значит и производная — больше.

Ответ: -2

И аналогичная задача:

Прототип задания B8 (№ 317544)

На рисунке изображен график функции  и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

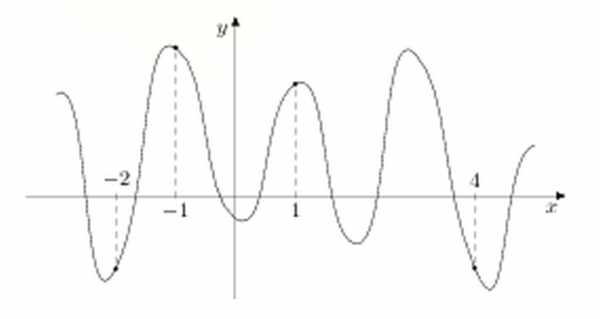
Решение этой задачи аналогично решению предыдущей «с точностью до наоборот»

Нас интересует точка, в которой производная принимает наименьшее значение, то есть мы ищем точку, в которой функция уменьшается наиболее быстро — на графике это точка, в которой самый крутой «спуск». Это точка с абсциссой 4.

Ответ: 4.

И.В. Фельдман, репетитор по математике.

ege-ok.ru