Как найти область значений функции 10 класс – Область значений функции

Содержание

Область значений функции

Всем здравствуйте! Тренируемся находить область значений функции! Кто еще не понял, что такое область определения (а она нам тоже понадобится непременно), тому сюда.

Что же такое область значений функции? Это та “часть” оси ординат, та область, где можно наткнуться на какие-либо точки, принадлежащие функции. То есть можно сказать, что если область значений найдена, то все точки функции находятся в ней, не выше и не ниже. Это почти тоже самое, что и область определения, только теперь это “область определения по оси ординат”. Здесь никаких особых ограничений нет, поэтому, чтобы найти область значений, нужно иметь представление об элементарных функциях – например, как выглядят парабола или гипербола, как определить, направлены ли ветви параболы вверх или вниз и т.п. Все это рассказано и показано здесь.

Ну, поехали!

Примеры.

1. Найдите область значений функции

Решение: функция – квадратичная, представляет собой параболу с положительным старшим коэффициентом, ветви направлены вверх. Понятно тогда, что весь график располагается выше координаты своей вершины (вершина – самая низшая точка). Ордината вершины: , тогда .

2. Найдите область значений функции

Решение: область определения функции ( ] [).

В точках (-7) и (3) двучлен обращается в ноль. Поскольку результат извлечения корня – величина положительная, то вся функция располагается выше оси абсцисс, и ее область значений [)

3. Найти область значений функции

Область определения – вся числовая ось, кроме ноля. Можем подставить любое число из области определения, при этом функция всегда отрицательна.

Из графика также видно, что

4. Найти область значений функции:

Решение. Область определения:

На концах отрезка функция принимает значение 1, под корнем имеем квадратный двучлен, наибольшее значение он принимает в вершине, при , значит, функция будет принимать в этой точке наименьшее значение.

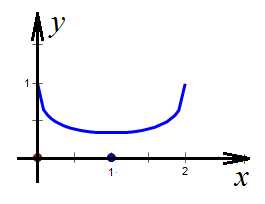
Подставив 1, получаем

Ответ:

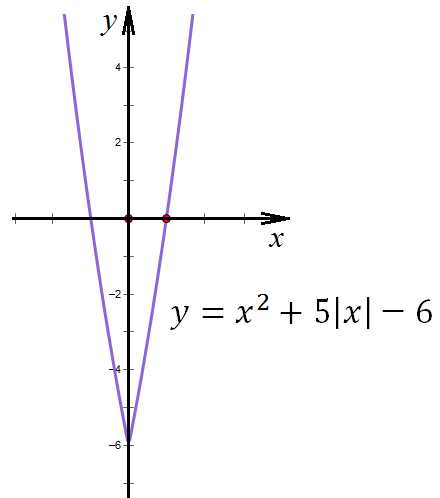
5. Найдите область значений функции:

Очевидно, что график данной функции может быть получен из графика обычной параболы , область значений которой легко найти: ветви направлены вверх, поэтому низшая точка – вершина параболы. Однако заметим также, что если аргумент функции под знаком модуля, то график такой функции может быть построен с помощью отражения части графика, лежащей в правой вертикальной полуплоскости, в левую полуплоскость(см. рисунок). Тогда от нашей параболы останется только часть, лежащая правее оси ординат, и именно она будет отражена относительно оси y, и тогда низшей точкой окажется та, в которой график пересечет ось ординат, а это – значение свободного члена (коэффициента с), который у нас равен (-6).

Область значений нашей функции [)

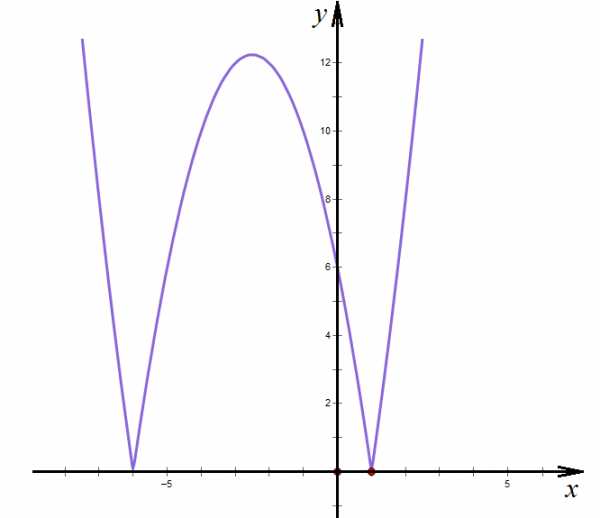
6. Найдите область значений функции:

Очевидно, что график данной функции может быть получен из графика обычной параболы . Так как все выражение находится под знаком модуля, то для того, чтобы построить такой график, нужно отразить всю часть графика, расположенную ниже оси х, вверх, поэтому [).

7. Найдите область значений функции:

Данная функция получена преобразованием обычной гиперболы. Данная функция не существует при , или . При второе слагаемое обращается в ноль, и функция стремится к значению , причем можно заметить, что при положительных больших значениях х данная функция приближается к 2 снизу, а при отрицательных – сверху.

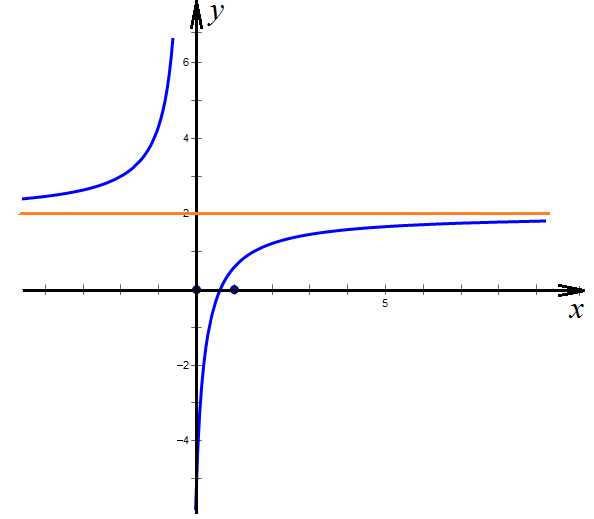
Ответ:

8. Найти область значений функции:
Решение. Область определения:
При функция принимает наибольшее значение ,
При x, стремящемся к бесконечности, функция стремится к нулю. Но мы запишем область значений от меньшего к большему:
Ответ: (]

easy-physic.ru
Область значений функции, теория и примеры
Область значений основных элементарных функций
Для линейной функции область значений .

Для обратной пропорциональности, то есть функции заданной формулой , область значений: .

Значение , где дискриминант, называется ординатой вершины параболы, задаваемой уравнением .

Действительно, абсцисса вершины параболы вычисляется по формуле , тогда

Итак, для квадратичной функции : если , то ветки параболы направлены вниз и значение является наибольшим значением функции, то есть ; если , то ветки направлены вверх и значение является наименьшим значением функции, то есть .

Для логарифмической функции область значений .

Для показательной функции область значений .

Для тригонометрических функции область значений , для область значений — множество всех действительных чисел.

Примеры решения задач
Понравился сайт? Расскажи друзьям!

ru.solverbook.com

область определения и область значений функций + ПРИМЕРЫ
Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая.

Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.
Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).
НАПРИМЕР у=5+х
1. Независимая -это х, значит берем любое значение, пусть х=3
2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)
Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).

НАПРИМЕР.
1.у=1/х. (наз.гипербола)
2. у=х^2. (наз. парабола)
3.у=3х+7. (наз. прямая)
4. у= √ х. (наз. ветвь параболы)
Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.
Область определения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (у) для 1.,2.,3.,4.
1. D (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
3. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
4. D (у)= [0; +∞)// мн-во неотрицат.чисел
Зависимая переменная (кот. мы обозначаем у ) имеет название значение функции.
Область значения функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).
Рассмотрим Е (у) для 1.,2.,3.,4.
1. Е (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. Е (у)= [0; +∞)// мн-во неотрицат.чисел
3. Е (у)=( ∞; +∞)//всё мн-во действит.чисел
4. Е (у)= [0; +∞)// мн-во неотрицат.чисел
Рассмотрим примеры подробнее
1) Постановка задачи. Найти функции у= 4х/(3+х)
Решение.
1. Найдем D (у)//т.е. какие значения может принимать х. для этого найдем ОДЗ(область допустимых значений дроби)
3+х≠0
х≠-3
значит D (у) данной функции ( ∞; 3) и (3;+∞)// всё множество действительных чисел, кроме 3.
2. Найдем Е (у)//т.е. какие значения может принимать у, при всех возможных х
решаем уравнение вида 4х/(3+х)=А, где А є Е (у)
(3+х)А=4х
3А=4х-хА
3А=х(4-А)
х=3А/(4-А)
значит Е (у) данной функции ( ∞; 4) и (4;+∞)// всё множество действительных чисел, кроме 4.
2) Постановка задачи. Найти D (у)и Е (у) функции, изображенной на графике

Область определения(значения х) смотрим по оси х- это промежуток [ 4; 7],
Областью значения(значения у) смотрим по оси у- это промежуток [ 4; 4].
Нужна помощь в учебе?

Предыдущая тема: Графический способ решения уравнений: алгоритм и примеры графиков
Следующая тема:&nbsp&nbsp&nbspСвойства функции: разбираем на примере
Все неприличные комментарии будут удаляться.
www.nado5.ru
Функция, область определения, множество значений, четность, периодичность, график, монотонность: возрастание, убывание, нули. Тесты

Тестирование онлайн
Понятие функции
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.
Обозначение:
Переменную x называют независимой переменной или аргументом, а переменную y — зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.
Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Обозначения:
D(f) — значения аргумента. E(f) — значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Если некоторому значению x=x₀ соответствуют несколько значений (а не одно) y, то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.

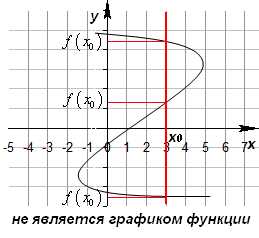
Способы задания функции
1) Функция может быть задана аналитически в виде формулы. Например,
2) Функция может быть задана таблицей из множества пар (x; y).
3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «взбираться» вверх по графику.
Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «скатываться» вниз по графику.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

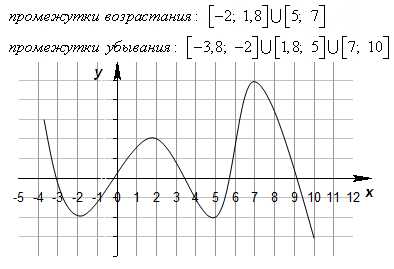
Нули функции и промежутки знакопостоянства
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.

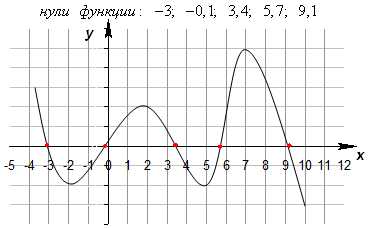
Такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

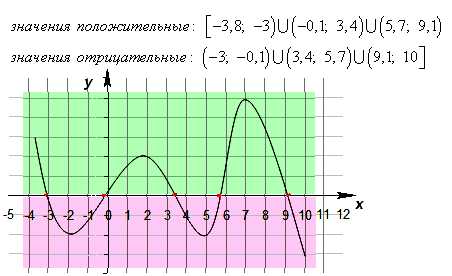
Четные и нечетные функции
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
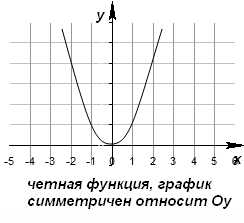
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
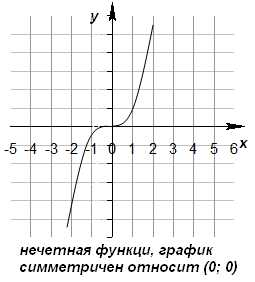
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
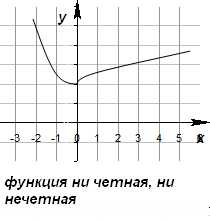
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

Периодические функции
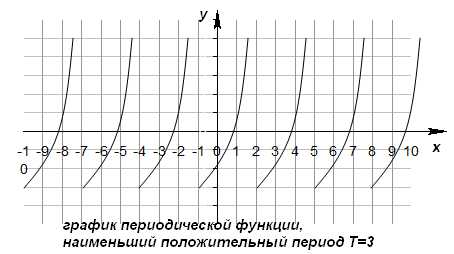
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T — это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.

fizmat.by
Область определения и область значения функции.

Тема урока: «Область определения и область значения функции».
Лаврентьева Н. С.
МБОУ «Гимназия»
г. Протвино

Что такое «функция»?
Определение функции:
Функцией называется зависимость между двумя переменными (У и Х) в которой каждому значению независимой переменной (Х) соответствует единственное значение зависимой переменной (У).
Независимую переменную называют — аргумент .
Значения зависимой переменной называют значениями функции .
Запись У=f (X) читается: У – функция от Х.

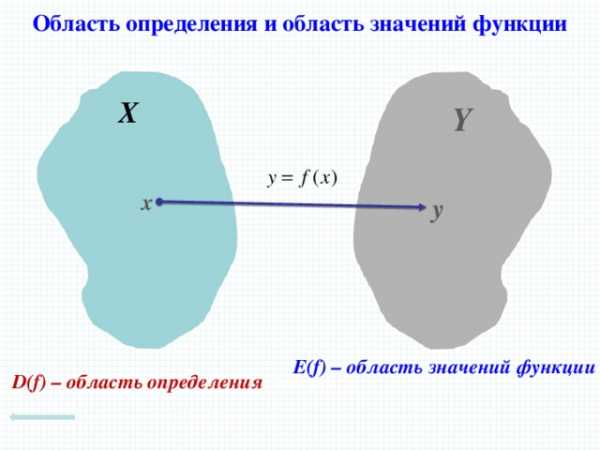
Область определения и область значений функции
Х
Y
x
y
Е(f) – область значений функции
D(f) – область определения функции

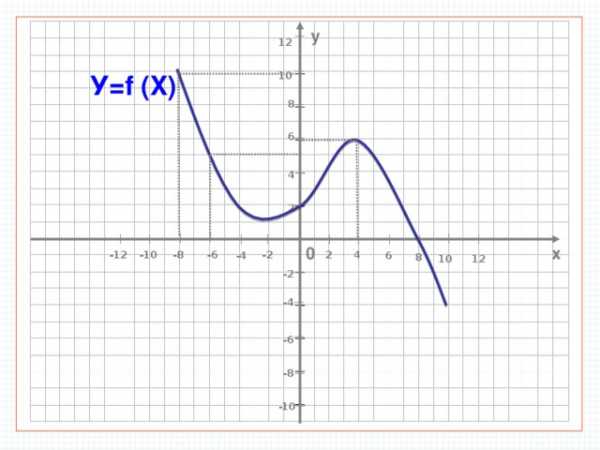
у
12
10
У=f (X)
8
6
4
2
0
х
-12
4
-2
-6
-10
2
-8
-4
6
8
12
10
-2
-4
-6
-8
-10

Область определения и множество значений функции.
Все значения независимой переменной образуют область определения функции — D (f).
Все значения, которые принимает зависимая переменная, образуют область значений функции – E (f).

у
12
10
8
6
4
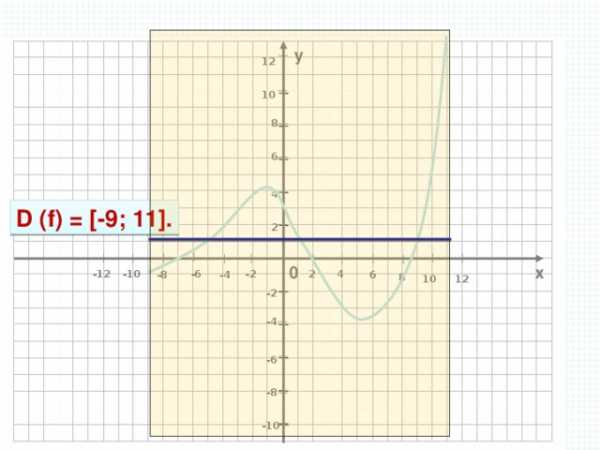
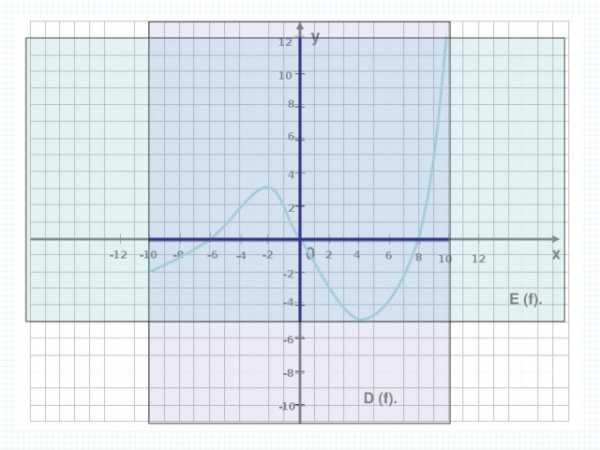
D (f) = [-9; 11].
2
0
х
-10
4
-2
-12
-6
2
-8
-4
6
8
12
10
-2
-4
-6
-8
-10

у
12
10
8
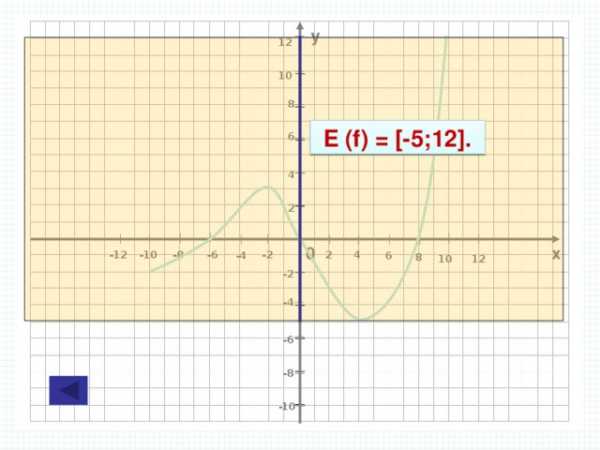
E (f) = [-5;12].
6
4
2
0
х
-12
4
-2
-10
-6
2
-8
6
-4
8
12
10
-2
-4
-6
-8
-10

у
12
10
8
6
4
2
0
х
-12
-10
-6
4
-2
2
-8
-4
6
8
10
12
-2
E (f).
-4
-6
-8
D (f).
-10

Область определения функции
Областью определения функции называют множество всех значений, которые может принимать ее аргумент (х) D(х)
Все действительные числа
Все действительные числа
Х+1 ≠0 ⇒ Х≠-1
2х-6 ≥0 ⇒ 2х≥6 ⇒ х≥3

Множество значений функции
Множеством значений функции называют множество всех значений которые может принимать переменная у Е(у)
Все действительные числа
у ≥0
у ≠0
у≥0

у
у
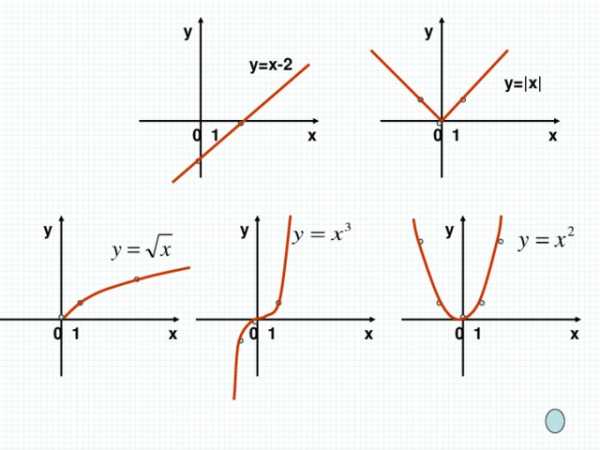
у=х-2
у= |х|
0 1 х
0 1 х
у
у
у
0 1 х
0 1 х
0 1 х

Тема урока: «Свойства функций».
16.09.2016 г.

1.Возрастание и убывание
функции
Функция называется возрастающей на
множестве Х , если большему значению
аргумента из множества Х соответствует
большее значение функции.
Если
Х 1 , то У 2 У 1. -10 «
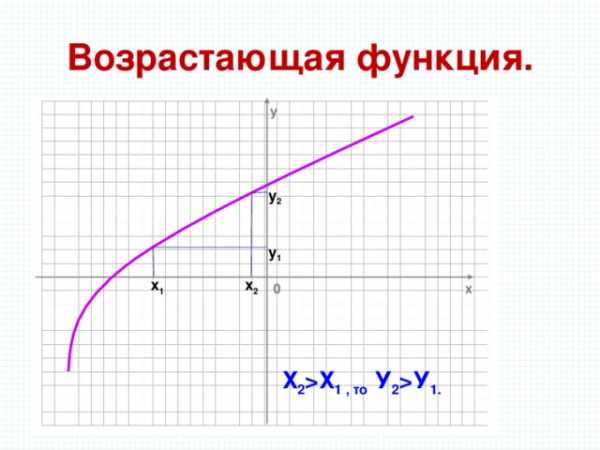
Возрастающая функция.
у
у 2
у 1
х 1
х 2
х
0
Х 2 Х 1 , то У 2 У 1.
-10

Возрастание и убывание
функции
Функция называется убывающей на
множестве Х , если большему значению
аргумента из множества Х соответствует
меньшее значение функции.
Если
Х 1 , то У 2 1. -10 «
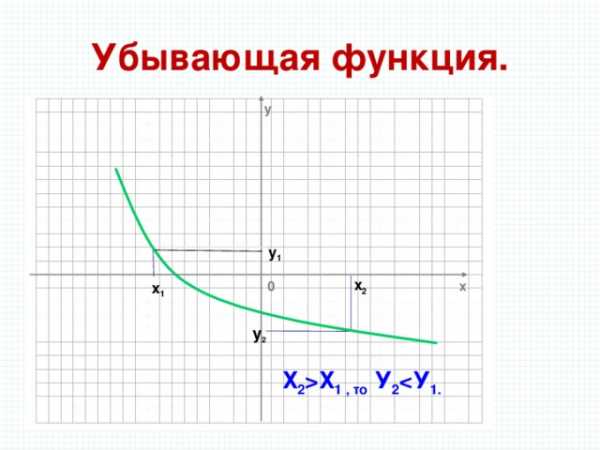
Убывающая функция.
у
у 1
х 2
х
0
х 1
у 2
Х 2 Х 1 , то У 2 1.
-10
1. -4 Возрастание и убывание квадратичной функции «
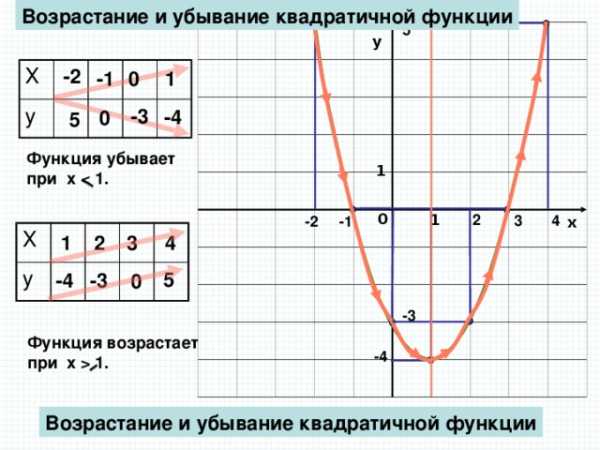
Возрастание и убывание квадратичной функции
5
у
Х
у
-2
-1
0
1
-3
-4
0
5
Функция убывает
при x
1
0
1
2
4
3
-1
-2
х
Х
у
4
2
1
3
5
-4
-3
0
-3
Функция возрастает
при x 1.
-4
Возрастание и убывание квадратичной функции

у
12
10
8
6
4
2
0
х
4
-12
-2
-6
-10
2
-8
-4
6
8
10
12
-2
-4
-6
-8
-10

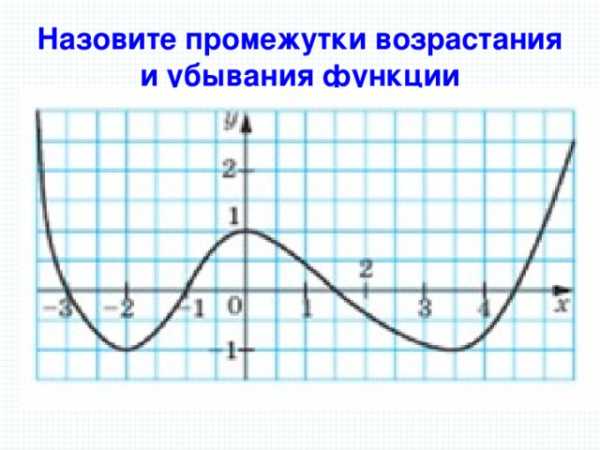
Назовите промежутки возрастания и убывания функции
0 (график расположен выше оси ОХ) при х  (- ∞; 1) U (3; +∞) , y (график расположен ниже OX) при х  (1;3) «
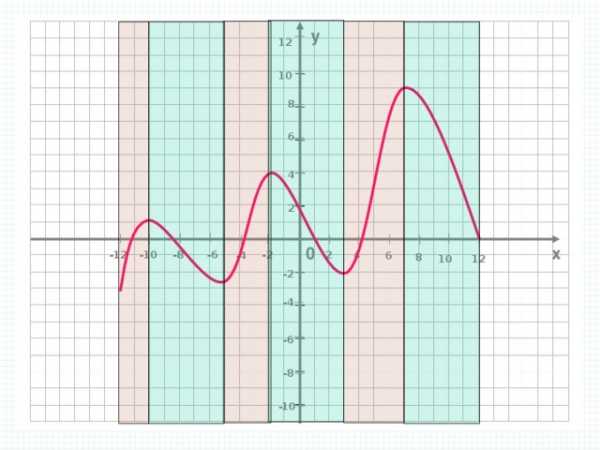
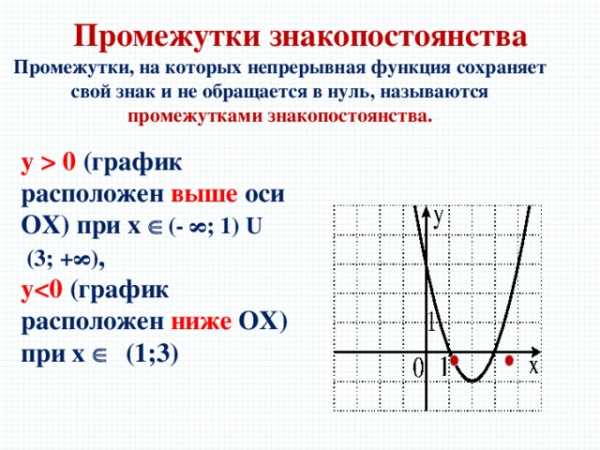
Промежутки знакопостоянства
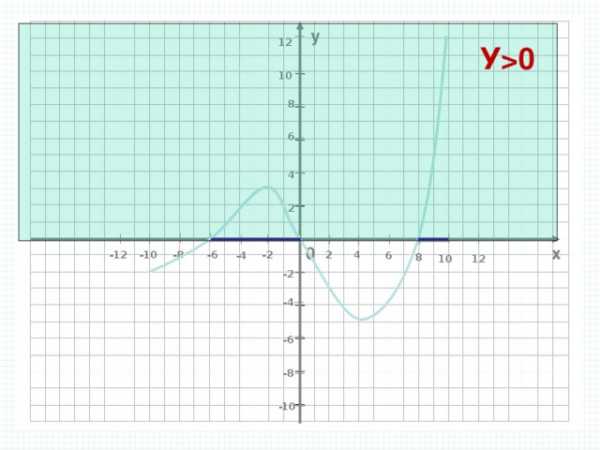
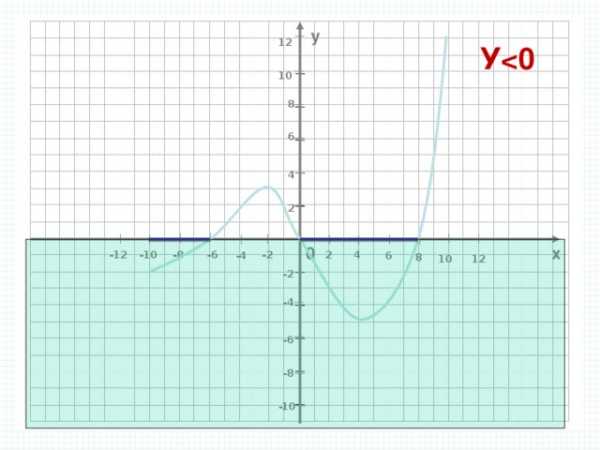
Промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства.
y 0 (график расположен выше оси ОХ) при х  (- ∞; 1) U
(3; +∞) ,
y (график расположен ниже OX) при х  (1;3)
0 10 8 6 4 2 0 х -12 -2 -10 4 -6 2 -8 -4 6 8 12 10 -2 -4 -6 -8 -10 «
у
12
У0
10
8
6
4
2
0
х
-12
-2
-10
4
-6
2
-8
-4
6
8
12
10
-2
-4
-6
-8
-10

у
12
У
10
8
6
4
2
0
х
-2
4
-12
-6
-10
2
-8
6
-4
8
12
10
-2
-4
-6
-8
-10

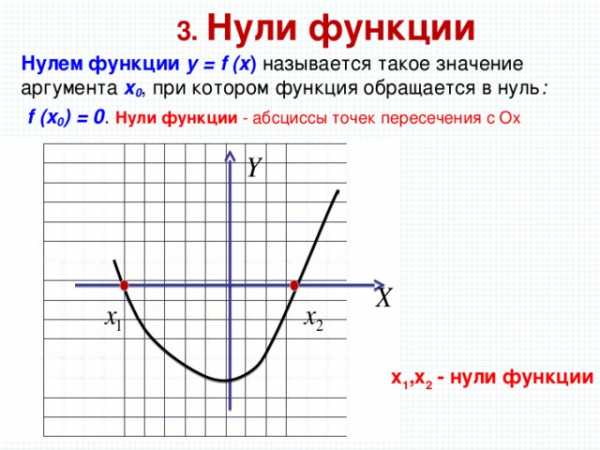
3. Нули функции
Нулем функции y = f (x ) называется такое значение аргумента x 0 , при котором функция обращается в нуль :
f (x 0 ) = 0 . Нули функции — абсциссы точек пересечения с Ох
x 1 ,x 2 — нули функции

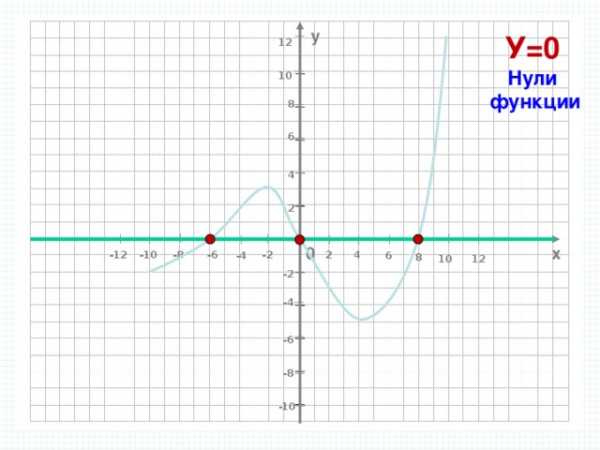
у
У=0
Нули
функции
12
10
8
6
4
2
х
0
-6
-12
-10
-2
4
2
-8
6
-4
8
12
10
-2
-4
-6
-8
-10

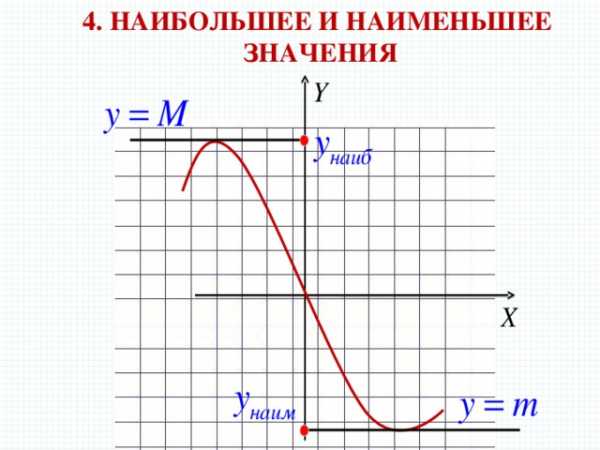
4. Наибольшее и наименьшее значения

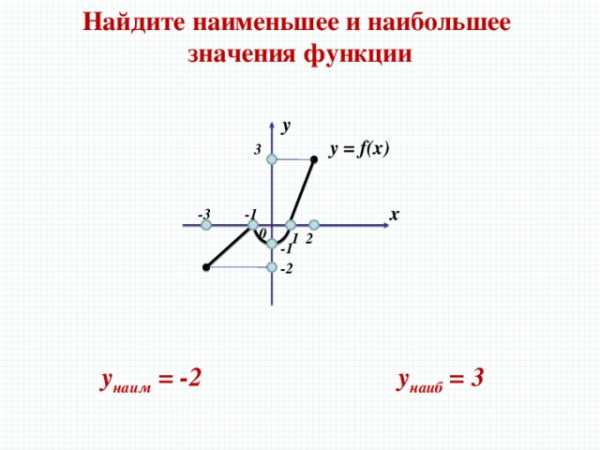
Найдите наименьшее и наибольшее
значения функции
y
y = f(x)
3
x
-1
-3
0
2
1
-1
-2
y наиб = 3
y наим = -2

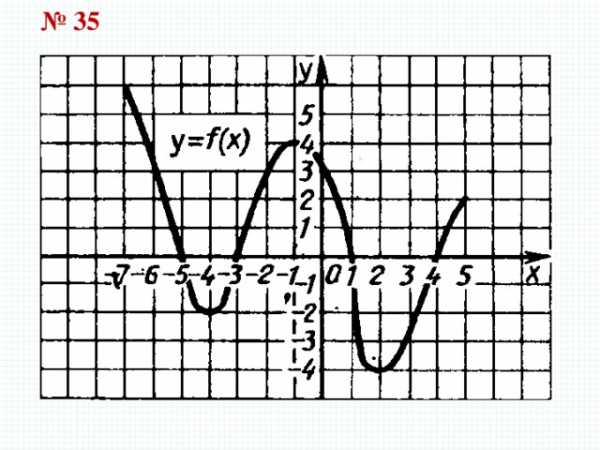
№ 35

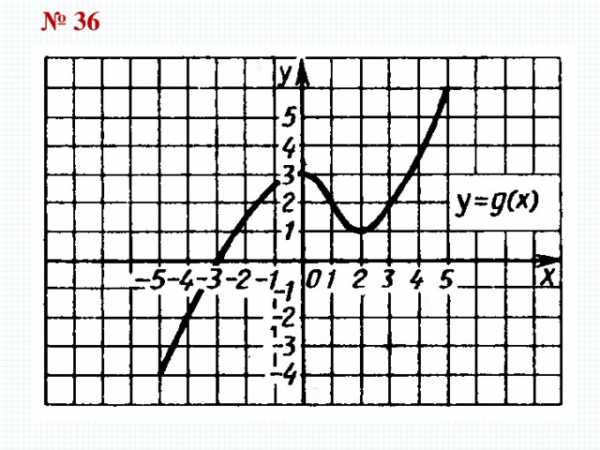
№ 36

Домашняя работа 1) пункт 2 ( Знать определения ) 2) Составить ОК

Спасибо за урок! Всем удачи!
multiurok.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Понятие функции. Область определения функции. Множество значений функции
Определение. Пусть X – некоторое множество чисел. Говорят, что на множестве X задана числовая функция, если указано правило, с помощью которого каждому числу x из множества X ставится в соответствие некоторое число.
Это принято обозначать так:
y = f (x),
причем в этой записи x называют аргументом функции или независимой переменной, а y называют значением функции, соответствующим аргументу x .
Множество X называют областью определения функции f и обозначают D ( f ) . Множество Y всех возможных значений функции y = f (x) называют множеством значений функции f и обозначают E ( f ) (рис. 1).
Рис.1
Примеры решения задач
Часто в задачах известна формула, задающая функцию f , и требуется найти наиболее широкое множество чисел, к которым данную формулу можно применить. В этом случае указанная задача формулируется так: «Найти область определения функции y = f (x)». В некоторых задачах требуется найти не только область опредения функции, но и множество ее значений.
Задача 1. Найти область определения функции
Решение. Указанная функцию представляет собой результат, полученный при делении числа x⁴ на число (3 + x) . Поскольку единственным ограничением является запрет деления на число 0 , то число (3 + x) не может равняться 0 , то есть .
Ответ. .
Задача 2. Найти область определения функции
Решение. Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством
которое эквивалентно неравенству
и может быть записано в виде
.
Решая это неравенство с помощью метода интервалов, получим
Ответ. .
Задача 3. Найти область определения функции
Решение. Исходя из определений логарифма и квадратного корня, область определения данной функции задается следующей системой неравенств
(1)
Решая второе неравенство системы с помощью метода интервалов,
получим
Таким образом, система (1) эквивалентна системе
Решением этой системы является интервал
Ответ. .
Задача 4 . Найти множество значений функции
y = 3sin x + 4cos x
Решение. Воспользовавшись формулой дополнительного угла (вспомогательного аргумента), получим
y = 5 sin (x + φ) ,
где
Поскольку множеством значений функции y = sin (x + φ) является отрезок [–1, 1], то множеством значений функции y = 5 sin (x +φ) будет отрезок [–5, 5].
Ответ. .
Задача 5 . Найти множество значений функции
y = x² + 6x + 8
Решение. Поскольку
и для каждого числа существуют решения уравнения
x² + 6x + 8 = y ,
определяемые формулой
то множеством значений функции y = x² + 6x + 8 будет множество .
Ответ. .

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными».
Запись по телефону (495) 509-28-10
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Понятие функции. Область определения и область значений функции. Свойства функций
Вопросы занятия:
· вспомнить основные сведения о координатной плоскости, функции;
· повторить основные свойства функции.
Материал урока
Начнём мы с вами с координатной плоскости.
Таким образом, мы задали на плоскости прямоугольную систему координат.
Определение.
Плоскость, на которой задана система координат, называют координатной плоскостью.
Повторим определение функции.
Определение.
Зависимость одной переменной у от переменной х, при которой каждому значению переменной х из определённого множества D соответствует одно определённое значение у, называется функцией от переменной х.
Перед нами графики двух зависимостей.
Мы должны определить, какая из них является функцией, а какая нет. В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции. Давайте посмотрим на первый график.
В общем виде любую функцию можно записать так y = f(x). Например, для функции y= 7x – 14 можно записать, что f(x) = 7x – 14, это одно и тоже. Под буквой f понимают некоторый набор действий над переменной x, в данном случае умножение на 7 и вычитание 14.
Переменную x называют независимой или аргументом функции, а y — зависимой (она зависит от x).
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции и аргументы названы разными буквами. Действительно, функцию и аргумент можно называть любой буквой латинского или греческого алфавитов.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
Возьмём, например, функцию y = 7x – 4. Можно записать f(x) = 7x – 4. Это линейная функция, графиком которой, является прямая. Для изображения прямой достаточно двух точек. Найдём значение этой функции, например, при x = 1 и x = -1. Для этого подставим в функцию вместо x сначала 1, затем -1. Тогда получим, что:
f(1) = 7 · 1 – 4 = 7 – 4 =3
Получаем точку с координатами (1; 3).
f(-1) = 7 · (-1) – 4 = -7 – 4 =-11
Получаем точку с координатами (-1; -11).
Проведём прямую через полученные точки. Мы изобразили график функции y = 7x – 4.
Взяв некоторое x, мы получаем соответствующее y. Эти значения и являются координатами точек графика. Если перебрать все возможные значения x, то мы получим множество точек, изображение которых на координатной плоскости и называют графиком.
Вспомним определение.
Определение.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Существует три способа задания функции.
Функция может быть задана формулой.
Например, f(x) = 5x + 1.
Функция может быть задана таблицей значений аргумента и функции.
Например,
Здесь сразу указаны координаты точек графика функции.
Функция можно задать словесно.
Например, каждому натуральному числу x, из отрезка [10; 20], поставлен в соответствие остаток от деления этого числа на пять. Построить график такой функции не составит труда. Для этого составим таблицу значений аргумента и функции.
Аргументами этой функции будут натуральные числа из отрезка от десяти до двадцати. А значениями функции будут остатки от деления соответствующих аргументов на пять.
Теперь давайте поговорим об основных свойствах функции.
Первое свойство о котором мы поговорим – это область определения.
Все значения аргумента, т.е. переменной x образуют область определения функции (пишут D(f)),
Следующее свойство – область значений функции. Все значения зависимой переменной, т.е. y, — область значений функции (пишут E(f)). В скобках указывают букву, которой названа функция.
Пример.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
Пример.
Следующее свойство, которое мы рассмотрим – нули функции.
Определение.
Значения аргумента, при которых функция принимает значение, равное нулю, называют нулями функции.
Рассмотрим пример.
Пример.
В данном случае функция задана графически и мы определили нули функции по графику. Нули функции можно находить по формуле, с помощью которой задана функция.
Пример.
Стоит обратить внимание на то, что не каждая функция имеет нули.
Например, функция y = x² + 6.
На графике это будет выглядеть так.
График не пересекает ось икс ни в одной точке.
Теперь поговорим о промежутках знакопостоянства функции.
Определение.
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.
Выполните задание. Запишите промежутки знакопостоянства функции.
Осталось рассмотреть ещё одно свойство. Промежутки монотонности функции.
Определение.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Определение.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Определение.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Пример.
Найдём промежутки монотонности данной функции.
Выполним задание, где нужно описать свойства функции.
Пример.
Итоги урока
Сегодня на уроке мы повторили такие понятия как координатная плоскость, функция, график функции, повторили основные свойства функции.
videouroki.net
No related posts.