Как найти площадь поверхности конуса – Площадь поверхности конуса | Формулы и расчеты онлайн

Содержание

Площадь поверхности конуса

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.

Так как площадь основания конуса равна πR² (как площадь круга), то площадь полной поверхности конуса будет равна: πR² + πRl = πR (R + l ).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

Получим ряд равных треугольников. Площадь каждого треугольника равна ^ah/₂, где а — длина основания треугольника, a h — его высота.

Сумма площадей всех треугольников составит:

ah/₂ • n = ^anh/₂ , где n — число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = ^Cl/₂, где С — длина окружности основания конуса, l — образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl.

Примечание. В формуле S = ^Cl/₂ поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = ^Cl/₂ точное, а не приближённое.

Теорема. Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р и l числа, выражающие длины периметра основания и апофемы этой пирамиды.

Тогда боковая поверхность её выразится произведением ¹/₂р • l .

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK

¹/₂

р• l, будет стремиться к пределу ¹/₂С• L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = ¹/₂С • L = С • ¹/₂L

Следствия.
1) Так как С = 2πR, то боковая поверхность конуса выразится формулой:

S = ¹/₂• 2πR • L = πRL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = πRL + πR²= πR(L + R)

Теорема. Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами

р, р₁ и l числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

Тогда боковая поверхность вписанной пирамиды равна ¹/₂ (р + р₁) • l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р и р₁ стремятся к пределам, принимаемым за длины С и С₁ окружностей оснований, а апофема l имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С₁) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = ¹/₂ (С + С₁) L

Следствия.
1) Если R и R₁ означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = ¹/₂ (2πR + 2πR₁) L = π (R + R₁) L.

2) Если в трапеции OO₁А₁А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = ¹/₂(OA + O₁A₁) = ¹/₂ • (R + R₁),

откуда

R + R₁ = 2ВС.

Следовательно,

S = 2πBC• L,

т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π( R² + R₁²+ RL + R₁L)

razdupli.ru

Площадь поверхности усеченного конуса

R — радиус нижнего основания

r— радиус верхнего основания

L — образующая усеченного конуса

π ≈ 3.14

Формула площади боковой поверхности усеченного конуса, (S_бок):

Калькулятор — вычислить, найти площадь боковой поверхности усеченного конуса

Формула площади полной поверхности усеченного конуса, (S):

Калькулятор — вычислить, найти площадь полной поверхности усеченного конуса

Подробности: Автор: Administrator; Опубликовано: 08 сентября 2011; Обновлено: 25 мая 2017

www-formula.ru

Как найти площадь боковой поверхности конуса

Как найти площадь боковой поверхности конуса
Поскольку конус получается в результате вращения прямоугольного треугольника вокруг его катета, изобразим конус, полученный в результате вращения вокруг катета visota прямоугольного треугольника с другим катетом radius и гипотенузой obrazuyuschaya.

Запишем формулу для вычисления площади боковой поверхности конуса:

Рассмотрим примеры применения этой формулы к решению задач на конус.
Задача 1.
Радиус основания конуса равен 3 см, а его образующая равна 5 см. Найти площадь боковой поверхности конуса.
Решение.
Запишем формулу боковой поверхности конуса:

Из условия известна длина радиуса и образующей, которые и подставим в эту формулу:
(кв. см).
Ответ. кв. см.
Задача 2.
Радиус основания конуса равен 1 см, а его высота равна 5 см. Найти площадь боковой поверхности конуса.
Решение.
Запишем выше рассмотренную формулу:

По условию задана длина радиуса основания. Необходимо найти длину образующей, чтобы воспользоваться данной формулой.
Рассмотрим рисунок, на котором отчетливо видно прямоугольный треугольник, в результате вращения которого получился данный конус. Это треугольник со сторонами visota, radius и obrazuyuschaya. Применим к этому треугольнику теорему Пифагора:

Подставим известные из условия значения:

(см)
Теперь полученные данные можно подставлять в формулу площади:
(кв. см).
Ответ. (кв. см).
ru.solverbook.com
Площадь поверхности конуса
На этом уроке мы выведем и научимся применять формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса.
Для начала давайте вспомним, что же это за геометрическое тело – конус.
Итак, тело, ограниченное конической поверхностью и кругом с границей , называется конусом.
Напомним, что боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.

На экране изображён конус, у которого радиус равен , а образующая равна . Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих.
Давайте представим, что боковую поверхность конуса разрезали по образующей и развернули таким образом, что получился круговой сектор .
Стороны и которого являются двумя краями разреза боковой поверхности конуса.
Развёрткой боковой поверхности конуса является круговой сектор. Обратите внимание, радиус сектора равен образующей конуса, т.е. . А длина дуги сектора равна длине окружности основания конуса, т.е. равна .
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через его образующую и радиус основания .
Площадь кругового сектора – развёртки боковой поверхности конуса – равна , где – градусная мера дуги .

Выразим через длину дуги и радиус окружности. Длина дуги окружности с градусной мерой и радиусом равна . С другой стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто восемьдесят равно . Отсюда, . Подставим это выражение в формулу площади боковой поверхности конуса. Тогда площадь боковой поверхности конуса равна . Т.е. площадь боковой поверхности конуса с образующей и радиусом основания выражается следующей формулой: .
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Теперь выведем формулу для вычисления площади полной поверхности конуса.
Вообще, площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Формулу для вычисления площади боковой поверхности конуса мы с вами выразили выше, а площадь круга равна . Подставим все данные в формулу.
Упростим. Отсюда, получаем, что площадь полной поверхности конуса равна .
А сейчас давайте решим несколько задач на применение выведенных формул.
Задача: образующая конуса равна см, а его высота – см. Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для вычисления площади боковой поверхности конуса.
Теперь внимательно рассмотрим рисунок.
Напомним, что высота конуса перпендикулярна его основанию. А, значит, она перпендикулярна любой прямой, лежащей в плоскости основания конуса. Следовательно, высота конуса .
Рассмотрим . Он прямоугольный. Применяя теорему Пифагора, найдём длину стороны , которая и является радиусом основания конуса. Получаем, что ОА равно .
Подставим длину образующей конуса и его радиус в формулу для вычисления площади боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности конуса равна .
Запишем ответ.
Задача: радиус основания конуса равен дм, а площадь его осевого сечения – дм². Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для вычисления площади боковой поверхности конуса.
Теперь рассмотрим рисунок.
Напомним, что осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось, и представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Значит, – равнобедренный.
Так как по условию задачи радиус основания конуса равен 9 дм, то основание осевого сечения равно .
Напомним, что площадь треугольника равна половине произведения длины основания на высоту . Выразим из формулы высоту . Получаем, что высота треугольника, а она является и высотой конуса, равна .
Рассмотрим . Он прямоугольный, так как . Применяя теорему Пифагора, найдём длину . Получаем, что . Обратите внимание, гипотенуза есть образующая нашего конуса.
Подставим найденную длину образующей конуса и его радиус в формулу для вычисления площади боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности конуса равна .
Не забудем записать ответ.
Задача: прямоугольный треугольник, длины катетов которого равны см и см, вращается вокруг меньшего катета. Вычислите площадь полной поверхности конуса, образованного при этом вращении.
Решение: запишем формулу для вычисления площади полной поверхности конуса.
Рассмотрим . Он прямоугольный по условию.
Воспользуемся теоремой Пифагора и найдём длину гипотенузы , которая и является образующей конуса. Имеем, .
Так как по условию задачи треугольник вращается вокруг меньшего катета, то радиус основания конуса, образованного при этом вращении, равен .
Подставим длину образующей конуса и его радиус в формулу для вычисления площади полной поверхности конуса. Посчитаем. Получим, что площадь полной поверхности нашего конуса равна .
Запишем ответ.
Итоги:
На этом уроке мы вывели формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса. А также научились их применять при решении задач.

videouroki.net
Боковая поверхность конуса: площадь как найти?
Каждая объемная фигура, которая имеет конечные линейные размеры, обладает в пространстве некоторой площадью поверхности. В статье рассмотрим, чему равна площадь боковой поверхности конуса, приведем соответствующие формулы и покажем, откуда они выводятся.
Что такое конус?
В общем случае конусом в геометрии называют любую пространственную фигуру, которая образована в результате соединения фиксированной точки пространства со всеми точками некоторой плоской кривой. Фиксированная точка называется вершиной фигуры. Отрезки, соединяющие ее с кривой, получили название генератрис, или образующих, поскольку их совокупность образует коническую поверхность. Кривая, на которую опирается эта поверхность, называется директрисой, то есть направляющей. Директрисой может быть произвольная кривая, например, гипербола, окружность, парабола, эллипс и так далее. Образованный на них конус будет гиперболическим, круглым, параболическим и эллиптическим, соответственно.

Выше рисунок демонстрирует пример двух одинаковых эллиптических конусов, обращенных друг к другу своими вершинами.
Круглый конус
Площадь боковой поверхности конуса будем рассматривать на примере круглой прямой фигуры. Такой конус представляет собой круглое основание, на которое опирается коническая поверхность. Эта фигура показана ниже.

Все генератрисы этой фигуры равны между собой. Их длина всегда больше радиуса основания. Расстояние от вершины конуса до его круглого основания называется высотой. Высота пересекает круг в его центре, поэтому конус называется прямым.
Получить этот конус не представляет никакой сложности. Для этого следует взять любой треугольник, имеющий прямой угол, и вращать его вокруг одного из катетов так, как показано ниже на схеме.

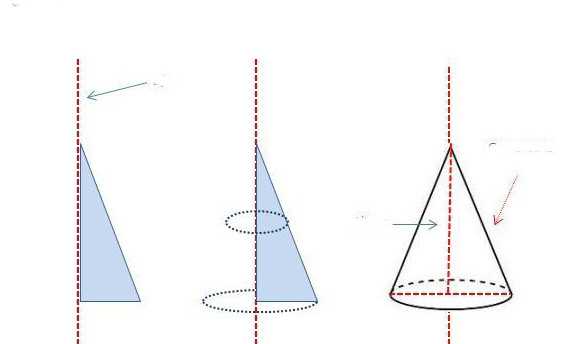
Если обозначить гипотенузу этого треугольника буквой g, а его катеты h и r, тогда будет справедливо равенство:
g² = h² + r².
Для полученного конуса g — это генератриса, h — высота, r — радиус круга.
Ответить на этот вопрос проще всего, если разрезать коническую поверхность вдоль одной из генератрис и развернуть ее на плоскости. Получившаяся фигура называется разверткой боковой поверхности. Она показана на главном фото к статье, где также приводится круг — основание фигуры.
Эта развертка показывает, что площадь боковой поверхности конуса равна площади соответствующего кругового сектора. Он ограничен двумя генератрисами g, которые представляют радиус полного круга, и дугой. Длина последней точно равна длине окружности основания. Получим формулу для площади этого сектора.
Сначала определим угол в радианах, соответствующий дуге сектора. Его можно найти с использованием следующей пропорции:
2*pi ==> 2*pi*g;
x ==> 2*pi*r.
Здесь 2*pi*g — это длина всей окружности, ограничивающей рассматриваемый сектор, 2*pi*r — это длина дуги сектора. Угол в радианах x сектора будет равен:
x = 2*pi*r*2*pi/(2*pi*g) = 2*pi*r/g.
Для определения площади рассматриваемого сектора, следует воспользоваться пропорцией через соответствующие площади. Имеем:
2*pi ==> pi*g²;
2*pi*r/g ==> S_b.
Здесь pi*g² является площадью круга, построенного с помощью образующей g, S_b — площадь боковой поверхности конуса, равная площади рассматриваемого кругового сектора. Результатом решения пропорции будет конечная формула для S_b:
S_b = pi*g²*2*pi*r/g/(2*pi) = pi*r*g.
Таким образом, чтобы найти площадь конической поверхности, достаточно умножить радиус фигуры на ее директрису и на число пи.
При получении конечной формулы для S_b через пропорции использовалось свойство равенства угла полной окружности числу 2*pi радиан.
Понятие о конусе усеченном
Пусть имеется круглый прямой конус. Возьмем плоскость и отсечем от этой фигуры верхнюю часть таким образом, чтобы секущая плоскость прошла параллельно основанию конуса. Оставшаяся под плоскостью фигура называется прямым усеченным конусом с параллельными основаниями. Он показан на рисунке ниже.

В отличие от исходной фигуры, усеченный конус образован тремя поверхностями:
малое круглое основание;
большое круглое основание;
часть конической поверхности.
Последняя в списке является боковой поверхностью для рассматриваемой фигуры.
Для усеченной фигуры справедливы те же понятия, что для полного конуса. Так, расстояние между его основаниями — это высота h, каждое основание имеет свой радиус (r₁ и r₂). Часть генератрисы исходного конуса теперь является генератрисой конуса усеченного. Обозначим ее буквой l.
Между отмеченными линейными параметрами существует следующая связь:
l² = h² + (r₁-r₂)².
Боковая поверхность усеченной фигуры
Выше было сказано, что представляет собой боковая поверхность для конуса усеченного. Разрезая ее вдоль одной из генератрис, получим следующий результат.

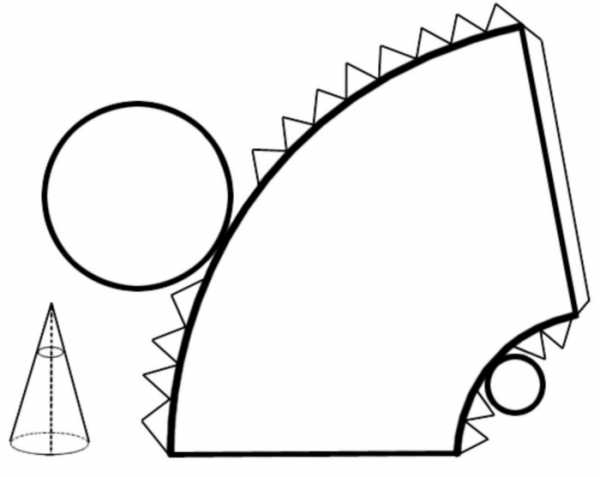
Два круга представляют собой основания. Четырехугольная фигура, ограниченная двумя прямыми отрезками и двумя дугами — это искомая боковая поверхность усеченного конуса, площадь которой необходимо найти. Решим эту задачу.
Заметим, что эта поверхность представляет собой сектор круга, у которого вырезана центральная часть. Обозначим радиус внешней дуги как g. Тогда радиус внутренней дуги будет равен g — l. Используя результаты решения предыдущей пропорции при определении угла сектора x, можно записать следующее равенство:
x = 2*pi*r₁/g = 2*pi*r₂/(g-l) =>
g = l*r₁/(r₁-r₂).
Искомая площадь S_b равна разнице площадей секторов, построенных с помощью радиусов g и g-l. Используя формулу для площади сектора, полученную выше, можно записать:
S_b = pi*g*r₁ — pi*(g-l)*r₂.
Подставляя в это выражение формулу для g, получаем конечное равенство для площади боковой поверхности конуса усеченного:
S_b = pi*l*(r₁+r₂).
Задача на определение площади конической поверхности
Решим простую задачу. Необходимо найти площадь боковой поверхности конуса, если известно, что его высота h равна диаметру основания, а генератриса составляет 15 см.
Запишем соответствующую формулу для S_b, из которой будет видно, какие величины следует рассчитать. Имеем:
S_b = pi*r*g.
Значение генератрисы g известно из условия задачи. Остается определить радиус фигуры.
Генератриса, высота и радиус связаны друг с другом следующим равенством:
g² = h² + r².
Из условия следует, что 2*r = h. Подставляя значение h в выражение, получим:
g² = (2*r)² + r² = 5*r² =>
r = g/√5.
Теперь формулу для радиуса основания подставляем в выражение для S_b, получаем:
S_b = pi/√5*g².
Мы получили конечную формулу, из которой видно, что площадь искомой поверхности зависит только от длины генератрисы. Подставляя g = 15 см, получаем ответ на задачу: S_b ≈ 315,96 см².
fb.ru
Площадь поверхности усеченного конуса — формула, пример расчета
Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии.Основаниями конуса являются геометрические круги.

Усеченный конус может быть получен в результате вращения прямоугольной трапеции вокруг ее боковой стороны, которая является ее высотой. Границей конуса является круг радиуса R, круг радиуса r и боковая поверхность конуса. Боковую поверхность конуса описывает боковая сторона трапеции во время ее вращения.
Площадь боковой поверхности усеченного конуса через направляющую и радиусы его оснований
При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса.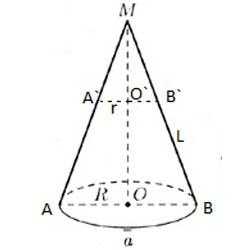

Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O`=r, образующая равна L.Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x).
Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB`:

Треугольники OMB и O`MB`– подобны по равенству углов ∠{MOB} = ∠{MO`B`} и ∠{OMB} = ∠{O`MB`}. Из подобия этих треугольников следует:
Воспользуемся производной пропорции. Имеем:
Отсюда находим x:
Подставив это выражение в формулу площади боковой поверхности, имеем:
Таким образом, площадь боковой поверхности усеченного конуса равна произведению числа π на его направляющую и сумму радиусов его оснований.
Формула площади боковой поверхности усеченного конуса имеет следующий вид:
Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3.
Имеем:
L=5
R=7
R=4
Формула площади боковой поверхности усеченного конуса имеет следующий вид:

Подставив значения, имеем:
Площади боковой поверхности усеченного конуса через направляющую и средний радиус
Средний радиус усеченного конуса равен половине суммы радиусов его оснований:

Тогда формула площади боковой поверхности усеченного конуса может быть представлена следующим образом:

Площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на его образующую.
Площади боковой поверхности усеченного конуса через радиусы его основания и угол наклона образующей к плоскости основания
Если меньшее основание ортогонально спроектировать на большее основание, то тогда проекция боковой поверхности усеченного конуса будет иметь вид кольца, площадь которого вычисляется по формуле:

Тогда:
Площади боковой поверхности усеченного конуса по Архимеду

Площадь боковой поверхности усеченного конуса равна площади такого круга, радиус которого является средней пропорциональной между образующей и суммой радиусов его оснований
Полная поверхность усеченного конуса
Полная поверхность конуса – это сумма площади его боковой поверхности и площади оснований конуса:
Основаниями конуса является круги с радиусом R и r. Их площадь равна произведению числа на квадрат их радиуса:

Площадь боковой поверхности вычисляется по формуле:

Тогда площадь полной поверхности усеченного конуса равна:

Формула имеет следующий вид:
2mb.ru
Калькулятор онлайн — Вычисление площади поверхности конуса
Этот математический калькулятор онлайн поможет вам вычислить площадь поверхности конуса. Программа для вычисления площади поверхности конуса не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)
www.math-solution.ru
No related posts.