Как решать дифференциальные уравнения – примеры решения диффуров (ДУ) в математике

Проблему нахождения решения дифференциального y’ = f(x,y) уравнения, которое удовлетворяет начальному условию y(x₀) = y₀, называют задачей Коши.

Теорема 1.1. Если в уравнении y’ = f(x,y)  функция f(x,y)  и ее частная производная f’_y(x,y)  непрерывны в некоторой области G плоскости Oxy, которая содержит точку (x₀,y₀), то существует и при этом единственное решение y=φ(x) такого уравнения, которое удовлетворяет условию y(x₀) = y₀.

Введем теперь еще несколько основных определений.

y = φ(x, C) (1.4)

которая зависит от одной произвольной постоянной С и удовлетворяет таким условиям:

1) она удовлетворяет уравнению при любом конкретном значении постоянной С;

2) каким бы не было начальное условие y(x₀) = y₀, всегда можно найти такое значение С = С₀, так что функция y= φ(x, C₀) будет удовлетворять этому начальному условию.

Замечание. При построении общего решения «дифура» очень часто приходят к соотношению вида

Ф(x, y, c) = 0 (1.5)

не решаемому относительно y.

Равенство Ф(x, y, c) = 0, которое неявно задает общее решение (в дальнейшем, для краткости ОР)

Определение 1.2. Частным решением дифференциального уравнения I-го порядка называется функцияy= φ(x, C₀), которую получаем из его общего решения y= φ(x, C) при определенном значении C = C₀.

Соотношение Ф(x, y, C₀) = 0называют частным интегралом дифференциального уравнения I-го порядка. 

§2. Дифференциальные уравнения I-го порядка с разделяющимися переменными

Определение 2.1. Дифференциальное уравнение I-го порядка вида

φ(y)dy = f(x)dx (2.1)

называется уравнением с переменными, которые можно разделить.

Непосредственно (дифференцированием) устанавливается, что

∫ φ(y)dy = ∫ f(x)dx (2.2)

где — C=const.

Пример 2.1. Решить “дифур” 2y²dy = 3xdx.

Решение. Найдем неопределенные интегралы от правой и, конечно же, левой части

Легко увидеть, что это решение, при желании, можно записать в явной форме , но обычно его оставляют в той форме, в которой получили, кое-что упростив получим 4y³ = 9x² + C.

Пример 2.2. Решить “дифур”  

Решение. Найдем неопределенные интегралы от правой и, конечно же, левой части

Поскольку C=const, то зачастую в такой форме решения для удобства записи, вместо C пишут ln |C|, а дальше выражение потенцируют

ln|y — 1| = ln|x| + ln C

ln|

y – 1 = Cx

y = Cx + 1. 

Определение 2.2. Дифференциальное уравнение I-го порядка называется уравнением с переменными, которые можно разделить, если его правая часть является произведением двух функций, одна из которых зависит лишь от аргумента х, а вторая от неизвестной функции у:

Здесь мы считаем, что функция φ(x) определена и непрерывна для всех x ϵ (a,b) а функция ѱ(y) определена и непрерывна и не равна нулю для всех y ϵ (c,d).

Если переписать уравнение (2.2) в виде  , то левая часть зависит только от переменной у, а правая часть зависит только от переменной х, то есть переменные отделены. Тогда общий интеграл запишется в виде

,

где С=const.

Пример 2.3.

Решение. Перед нами уравнение с переменными, которые можно разделить,. Запишем производную в виде соотношения дифференциалов: y’ = dy/dx, умножим обе части уравнения на dx  и разделим на y lny. В результате проделанной замены и “перемещения” переменных получим уравнение, в котором разделены переменные

После вычисления интегралов, имеем

y= e^Cx  ОР искомого уравнения.

Пример 2.4. Эффективность рекламы.

Пусть фирма продает продукцию B, про которую на момент времени tиз числа возможных клиентов знает лишь xклиентов. Далее, для увеличения продажи продукции, были сделаны рекламные объявления на радио и телевидении. Далее информация о товаре распространяется между клиентами через общение. После рекламы скорость изменения числа клиентов, которые знают о продукции

Если допустить, что счет времени начинается после рекламных объявлений, когда о продукции узнало N/ɣ  человек, то получаем дифференциальное уравнением с переменными, которые можно разделить

При таких начальных условиях: x = N/ɣ , если t = 0. Здесь k— положительной коэффициент пропорциональности.

Интегрируя уравнение, имеем:

В экономической литературе это выражение называют уравнением логистической кривой.

С учетом начальных условий, получим

Замечание. Уравнение с переменными, которые можно разделить, можно также задать в симметричной относительно x и y дифференциальной форме

M(x) · N(y)dx+ P(x) · Q(y)dy=0 (2.4)

где функции M(x),

Для нахождения решений необходимо разделить правую, (желательно, конечно) и левую части на произведение: N(y) · P(x).

и интегрируют полученное так соотношение

Если для x ϵ (a,b), y ϵ (c,d) функции P(x) и N(y) отличающиеся от нуля, то соотношение (2.6) является ОИ уравнения (2.4).

Пример 2.5. Решить “дифур” x(1 + y²)dx– y(1 + x²)dy = 0

Решение. Поступим также, как и в серии предыдущих примеров (разделим обе части уравнения на (1 + y²) · (1 + x²)

Интегрируя каждое из слагаемых (для этого не обязательно один из них переносить в правую часть), приравниваем сумму первообразных постоянной, которую обозначаем через ½ ln C, имеем:

Пример 2.6. Решить “дифур” y’ + 2x²y’ + 2xy– 2x = 0.

Решения. Представим производные в виде соотношения dy/dxи далее все члены уравнения домножим на dx:

Сгруппируем члены с разными дифференциалами и вынесем за скобки дифференциалы.

(1 + 2x²)dx +2x(y– 1)dx = 0

В результате деления на (1 + 2x²) (y– 1). Получим:

Интегрируем каждое из слагаемых:

Сумму первообразных приравниваем постоянной:

тогда

– ОИ уравнения.

В следующей своей статье я расскажу Вам об Однородных дифференциальных уравнениях I-го порядка и о Линейных дифференциальных уравнениях I-го порядка, уравнении Бернулли.

Если у Вас есть желание более детально изучить данный материал, научиться решать задания по данным разделам, записывайтесь на мои занятия на сайте. Буду рад Вам помочь. Онлайн репетитор Андрей Зварыч.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Дифференциальные уравнения первого порядка

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Как решать дифференциальные уравнения первого порядка

Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .

Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.

Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.

Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.

Если и это не помогает, то пытаемся найти интегрирующий множитель.

Уравнения с разделяющимися переменными

;
.
Делим на и интегрируем. При получаем:
.
Подробнее >>>

Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>

Однородные уравнения

Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>

Уравнения, приводящиеся к однородным

Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>

Обобщенные однородные уравнения

Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>

Линейные дифференциальные уравнения

Есть три метода решения линейных уравнений.

1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>

2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>

3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:

Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>

Уравнения Бернулли

Подстановкой уравнение Бернулли приводится к линейному уравнению.

Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .

Подробнее >>>

Уравнения Риккати

Оно не решается в общем виде. Подстановкой

уравнение Риккати приводится к виду:
,
где – постоянная;   ;   .
Далее, подстановкой:

оно приводится к виду:
,
где .

Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>

Уравнения Якоби

Решается подстановкой:
.
Подробнее >>>

Уравнения в полных дифференциалах

При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.

Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция, при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>

Уравнения, не решенные относительно производной y’

Уравнения, допускающие решение относительно производной y’

Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, допускающие разложение на множители

Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;

;
Подробнее >>>

Уравнения, не содержащие x и y

Здесь – постоянная:
,
где – корень уравнения
.
Подробнее >>>

Уравнения, не содержащие x или y

  или  
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
  или   .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .

Более общие уравнения:
  или  
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>

Уравнения, разрешенные относительно y

Уравнения Клеро

Такое уравнение имеет общее решение

Подробнее >>>

Уравнения Лагранжа

Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>

Уравнения, приводящиеся к уравнению Бернулли

Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 20-05-2016

1cov-edu.ru

Порядок дифференциального уравнения и его решения, задача Коши

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.

Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.

Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения, связывающие независимые переменные , неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».

Примеры дифференциальных уравнений:

(1) ;

(2) ;

(3) ;

(4) ;

(5) .

Уравнение (1) — четвёртого порядка, уравнение (2) — третьего порядка, уравнения (3) и (4) — второго порядка, уравнение (5) — первого порядка.

Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.

Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) — производной второго порядка и функции; в уравнении (4) — независимой переменной; в уравнении (5) — функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.

Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.

Процесс нахождения решения дифференциального уравнения называется его интегрированием.

Пример 1. Найти решение дифференциального уравнения .

Решение. Запишем данное уравнение в виде . Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть первообразная для , т. е.

.

Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.

Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.

Решение дифференциального уравнения в примере 1 является общим.

Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.

Пример 2. Найти общее решение дифференциального уравнения и частное решение при .

Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.

,

,

.

В результате мы получили общее решение —

данного дифференциального уравнения третьего порядка.

Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим

.

Если кроме дифференциального уравнения задано начальное условие в виде , то такая задача называется задачей Коши. В общее решение уравнения подставляют значения и и находят значение произвольной постоянной C, а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.

Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии .

Решение. Подставим в общее решение значения из начального условия y = 3, x = 1. Получаем

.

Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:

.

При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.

Пример 4. Найти общее решение дифференциального уравнения .

Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.

.

Применяем метод интегрирования заменой переменной (подстановкой). Пусть , тогда .

Требуется взять dx и теперь — внимание — делаем это по правилам дифференцирования сложной функции, так как x и есть сложная функция («яблоко» — извлечение квадратного корня или, что то же самое — возведение в степень «одна вторая», а «фарш» — самое выражение под корнем):

Находим интеграл:

Возвращаясь к переменной x, получаем:

.

Это и есть общее решение данного дифференциального уравнения первой степени.

Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.

Пример 5. Найти общее решение дифференциального уравнения .

Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального исчисления, что производная может быть записана также в виде . В результате уравнение приобретает вид

,

то есть, в нём в некотором виде появился x.

Теперь вспомнаем одно из свойств пропорции: из пропорции выткают следующие пропорции:

,

то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

Применяя это свойство, преобразуем уравнение к виду

,

после чего интегрируем обе части уравнения:

.

Оба интеграла — табличные, находим их:

и получаем решение данного дифференциалного уравнения первого порядка:

.

Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.

Всё по теме «Дифференциальные уравнения»

Поделиться с друзьями

function-x.ru

Линейные дифференциальные уравнения первого порядка

Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.

Общий вид линейного дифференциального уравнения первого порядка таков:

,

где и — непрерывные функции от x.

Как решить линейное дифференциальное уравнение первого порядка?

Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций

и линейное дифференциальное уравнения первого порядка примет вид

или

.  (*)

Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:

,

то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися переменными, отличное от нуля. Разделяя в уравнении переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v — решение уравнения, то её подстановка в уравнение даёт

.

Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.

Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.

Пример 1. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!

Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 2. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

.

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

В следующем примере — обещанная экспонента.

Пример 3. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находимu:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.

Пример 4. Решить линейное дифференциальное уравнение первого порядка

.

Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.

В интеграле , .

Тогда .

Интегрируем и находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.

Пример 5. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

В последних двух примерах требуется найти частное решение уравнения.

Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка

при условии .

Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на и получим

или

.

Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка

при условии .

Перенесём функцию «игрека» в левую часть и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

  (* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

.

Первый интеграл равен , второй находим интегрированием по частям.

В нём , .

Тогда , .

Находим второй интеграл:

.

В результате получаем функцию u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.

Всё по теме «Дифференциальные уравнения»

Поделиться с друзьями

function-x.ru

Дифференциальные уравнения. Что это? | Решатель

Вы уже имеете находить производные и интегралы? Тогда настало самое время, чтобы перейти к более сложной теме, а именно, решению дифференциальных уравнений (ДУ, в простонародье диффуров). Но не все так страшно, как кажется на первый взгляд.
 

Дифференциальное уравнение: что это такое?

Дифференциальное уравнение (ДУ) – это уравнение, которое вместе с самой функцией (и ее аргументами), содержит еще и ее производную или несколько производных.
 

Дифференциальное уравнение: что нужно знать еще?

Первое (и главное), что понадобится, это умение правильно определять тип дифференциального уравнения. Второе, но не менее важное, это умение хорошо интегрировать и дифференцировать.
 

Не секрет, что дифференциальные уравнения бывают разных типов. Но… для начала отметим, что ДУ бывают разных порядков. Порядок ДУ — это порядок высшей производной, входящей в дифференциальное уравнение. Классификацию ДУ согласно порядку уравнения можно посмотреть в следующей таблице:
 

Наиболее часто приходится иметь дело с ДУ первого и второго порядка, реже третьего. В 99% случаев в задачах встречаются три типа ДУ первого порядка: уравнения с разделяющимися переменными, однородные уравнения и линейные неоднородные уравнения. Иногда еще встречаются более редкие типы ДУ: уравнения в полных дифференциалах, уравнения Бернулли и др. Среди ДУ второго порядка часто встречаются уравнения, приводящиеся к ДУ первого порядка, линейные однородные и неоднородные уравнения с постоянными коэффициентами.
 

Дифференциальное уравнение: решение – что это значит и как его найти?

При решении ДУ нам предлагается найти либо общее решение (общий интеграл), либо частное решение. Общее решение y = f(x, C) зависит от некоторой постоянной (С — const), а частное решение не зависит: y = f(x, C₀).

С геометрической точки зрения общее решение – это семейство кривых на координатной плоскости, а частное решение – это одна прямая этого семейства, проходящая через некоторую точку.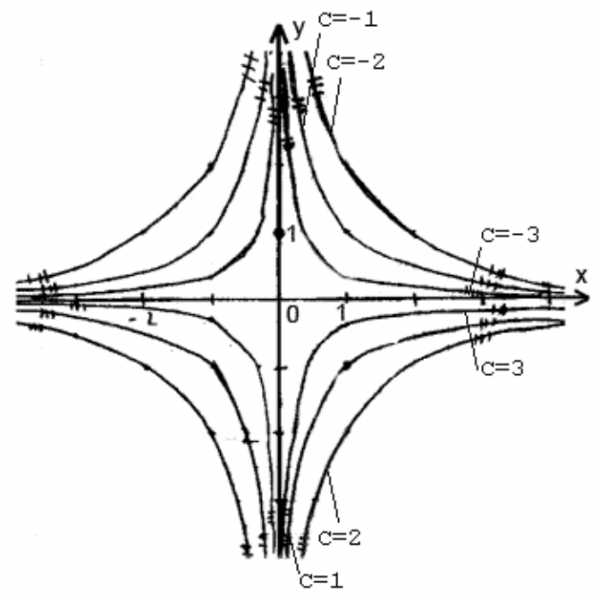

Давайте рассмотрим примеры решения некоторых ДУ. Начнем с ДУ первого порядка с разделяющимися переменными:

Здесь все очень просто как на уроке физкультуры, когда ученики класса делятся на две команды, в одну из которых входят только мальчики, а в другую – только девочки. Применительно к уравнению делаем следующее: в левую часть от знака равенства переносим все то, что содержит переменную y, а в правую часть – переменную x.
Получаем:

Далее интегрируем обе части:

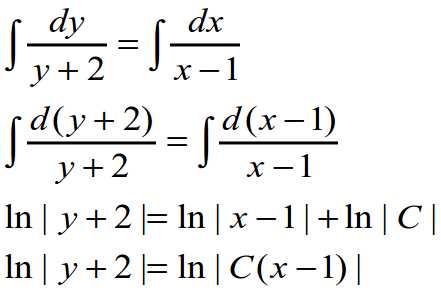
Итоговое общее решение выглядит следующим образом: y = C(x-1) — 2. Все оказалось очень просто, не правда ли?
 

Не сложнее и решение однородных ДУ второго порядка с постоянными коэффициентами. Здесь всего-то и нужно знать из курса школьной алгебры, как решаются квадратные уравнения, а из курса по ДУ, как правильно записать общее решение.
 

Для наглядности рассмотрим пример:

Составляем характеристическое уравнение, заменяя переменную y на переменную k, а количество штрихов соответствующей степенью (два штриха – степень 2, один штрих – степень 1, нет штрихов – степень 0). Получаем квадратное уравнение, решить которое можно с помощью дискриминанта или теоремы Виета:

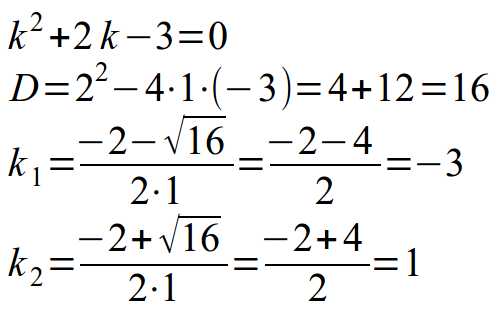
После того, как корни характеристического уравнения найдены, вспоминаем правила записи общего решения однородного ДУ:

1. Корни характеристического уравнения являются действительными и различными. Общее решение записывается в виде:
   
2. Корни характеристического уравнения являются комплексными. Общее решение записывается в виде:
   
3. Корни характеристического уравнения являются действительными и равными. Общее решение записывается в виде:
   

Вспоминаем, что наше уравнение имеет два различных действительных корня. Следовательно, общее решение запишем в виде:

Решение линейных неоднородных ДУ с постоянными коэффициентами выполняется в два этапа:
 

1. нахождение общего решения линейного однородного ДУ;
2. нахождение и частного решения линейного неоднородного ДУ.

Выполнение первого этапа рассмотрено на примере чуть раньше. То, в каком виде мы будем искать частное решение неоднородного ДУ, зависит от того, что стоит в уравнении справа от знака равенства. Все возможные случаи подробно рассматривают в учебной литературе.
 

Итак, тема «Решение задач по дифференциальным уравнениям» изучается в ВУЗах, но, как было показано выше, решить некоторые ДУ может и школьник.
 

Дифференциальные уравнения и методы их решения рассматриваются практически в каждом учебнике по высшей математике и математическому анализу. Особенно хорошо данная тема рассмотрена в учебнике автора Пискунов Н.С., а называется он «Дифференциальное и интегральное исчисления: Учеб. Для втузов. В 2-х т. Т. II». С помощью данного учебника можно самостоятельно изучить методы решения тех типов ДУ, которые не были рассмотрены в данной статье.
 
 

Решение дифференциальных уравнений на заказ

У нас вы можете выгодно заказать решение задач с дифференциальными уравнениями. Нами накоплен большой опыт решения заданий по данной дисциплине, которым мы готовы поделиться с вами. Работа будет оформлена очень подробно. При заказе большого количества задач действует скидка. Купить решение можно, сделав заказ у нас на сайте.

reshatel.org

Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»

Разделы: Математика

I. Обыкновенные дифференциальные уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

F(x,y,y’)=0, F(x,y,y»)=0, F(x,y,y’,y»,.., y⁽ⁿ⁾)=0

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение

Примеры.

1. Рассмотрим дифференциальное уравнение первого порядка

Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение, получим: , – тождество.

А это и значит, что функция – есть решение этого дифференциального уравнения.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

Примеры

1.Найти частное решение дифференциального уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения, получим

Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .

— общее решение дифференциального уравнения.

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3² + 4²= C²; C=5.

Подставляя С=5 в общее решение, получим x² +y² = 5².

Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.

2. Найти общее решение дифференциального уравнения

Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .

Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .

Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y)  удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x₀) = y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y)  при условии y(x₀) = y₀,, означает найти интегральную кривую уравнения y’ = f(x,y)  которая проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого порядка

2.1. Основные понятия

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.

Пример. Рассмотрим дифференциальное уравнение первого порядка .

Решением этого уравнения является функция .

Действительно, заменив в данном уравнении, его значением, получим

то есть 3x=3x

Следовательно, функция является общим решением уравнения при любом постоянном С.

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1  в общее решение уравнения , получим откуда C = 0.

Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.

2.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x)  и g(y)– заданные функции.

Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».

Уравнение вида называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными

1. Производную функции переписать через её дифференциалы
2. Разделить переменные.
3. Проинтегрировать обе части равенства, найти общее решение.
4. Если заданы начальные условия, найти частное решение.

Пример 1

Решить уравнение y’ = xy

Решение. Производную функции y’ заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Пример 2

Найти частное решение уравнения

2yy’ = 1- 3x², если y₀ = 3 при x₀ = 1

Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда

Интегрируя обе части последнего равенства, найдем

Подставив начальные значения x₀ = 1, y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл будет или

Пример 3

Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися переменными. Разделив переменные, получим:

 Проинтегрировав обе части уравнения, получим:

Используя начальные условия, x = 2  и y = — 3 найдем C:

Следовательно, искомое уравнение имеет вид

2.3. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)

где f(x) и g(x) — некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид:  y’ = f(x)y

Если то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.

В частности, если С =0, то решением является  y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .

Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.

Для линейного неоднородного уравнения вида y’ = kx + b,

где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно, где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.

 Алгоритм решения линейного дифференциального уравнения первого порядка

y’ = f(x)y + g(x)

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ = u’v + uv’

3. Подставить y и y’ в данное уравнение:   u’v + uv’ = f(x)uv + g(x) или u’v + uv’ +  f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:

5. Из скобки, приравняв ее к нулю, найти функцию

Это уравнение с разделяющимися переменными:

Разделим переменные и получим:

Откуда . .

6. Подставить полученное значение v в уравнение (из п.4):

и найти функцию Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: , т.е. .

Пример 1

Найти частное решение уравнения y’ = -2y +3 = 0  если y =1  при x = 0

Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’ в данное уравнение, получим

Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки

Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)

Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:

Подставим полученное значение v в уравнение Получим:

Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:

Ответ:

III. Дифференциальные уравнения высших порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0

Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C₁ и C₂.

Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.

2. Составить его характеристическое уравнение, обозначив y» через r², y’  через r, yчерез 1:r² + pr +q = 0

3.Вычислить дискриминант  D = p² -4q и найти корни характеристического уравнения; при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ — произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде

в) D < 0; следовательно, характеристическое уравнение имеет комплексные корни, Общее решение дифференциального уравнения выражается, в виде 

xn--i1abbnckbmcl9fb.xn--p1ai

Дифференциальные уравнения в полных дифференциалах

Дифференциальным уравнением в полных дифференциалах называется уравнение вида

P(x,y)dx + Q(x,y)dy = 0,

где левая часть является полным дифференциалом какой-либо функции двух переменных.

Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней.

Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.

Второе — должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах. Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.

Итак, неизвестную функцию, которую требуется найти, обозначили через F. Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению

dF = P(x,y)dx + Q(x,y)dy.

Вспоминаем формулу вычисления полного дифференциала функции двух переменных:

.

Решая два последних равенства, можем записать

.

Первое равенство дифференцируем по переменной «игрек», второе — по переменной «икс»:

.

Так как

,

получим

,

что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.

Шаг 1. Убедиться, что уравнение является уравнением в полных дифференциалах. Для того, чтобы выражение было полным дифференциалом некоторой функции F(x, y), необходимо и достаточно, чтобы . Иными словами, нужно взять частную производную по x одного слагаемого в левой части выражения и частную производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.

Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F:

Шаг 3. Проинтегрировать первое уравнение системы — по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:

,
где — пока неизвестная функция от y.

Альтернативный вариант (если так интеграл найти проще) — проинтегрировать второе уравнение системы — по y (x остаётся константой и выносится за знак интеграла). Таким образом так же восстанавливается функция F:

,
где — пока неизвестная функция от х.

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте — по x) и приравнять ко второму уравнению системы:

,

а в альтернативном варианте — к первому уравнению системы:

.

Из полученного уравнения определяем (в альтернативном варианте )

Шаг 5. Результат шага 4 интегрировать и найти (в альтернативном варианте найти ).

Шаг 6. Результат шага 5 подставить в результат шага 3 — в восстановленную частным интегрированием функцию F. Произвольную постоянную C чаще записывают после знака равенства — в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F(x, y) = C.

Какая ошибка возможна здесь с наибольшей вероятностью? Самые распространённые ошибки — принять частный интеграл по одной из переменных за обычный интеграл произведения функций и пытаться интегрировать по частям или заменной переменной а также принять частную производную двух сомножителей за производную произведения функций и искать производную по соответствующей формуле.

Это надо запомнить: при вычислении частного интеграла по одной из переменной другая является константой и выносится за знак интеграла, а при вычислении частной производной по одной из переменной другая также является константой и производная выражения находится как производная «действующей» переменной, умноженной на константу.

Среди уравнений в полных дифференциалах не редкость — примеры с экспонентой. Таков следующий пример. Он же примечателен и тем, что в его решении используется альтернативный вариант.

В следующем примере возвращаемся от альтернативного варианта к основному.

Всё по теме «Дифференциальные уравнения»

Поделиться с друзьями

function-x.ru