Урок по теме «Методы решения задач с параметрами»
Разделы: Математика
Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.
Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.
- Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
- Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
- Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
- Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Методы решений задач с параметрами.
1. Аналитический метод.
Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
Пример 1. Найдите все значения параметра a, при которых уравнение:
(2a – 1)x2 + ax + (2a – 3) =0 имеет не более одного корня.
Решение:
При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.
Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.
Если a ≠ 1/2, то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:
D = a2 – 4(2a – 1)(2a – 3) = -15a2 + 32a – 12;
Чтобы записать окончательный ответ, необходимо понять,
2. Графический метод.
В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).
Пример 2. Для каждого значения параметра a определите количество решений уравнения .
Решение:
Заметим, что количество решений уравнения равно количеству точек пересечения графиков функций и y = a.
График функции показан на рис.1.
Рис.1
Рис. 2
Рис. 3
y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).
Ответ: при a < 0 – решений нет; при a = 0 и a = 25/4 – четыре решения; при 0 < a < 6 – восемь решений; при a = 6 – семь решений; при
6 < a < 25/4 – шесть решений; при a > 25/4 – два решения.
3. Метод решения относительно параметра.
При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.
Пример 3. Найти все значения параметра а , при каждом из которых уравнение = —ax +3a +2 имеет единственное решение.
Решение:
Будем решать это уравнение заменой переменных. Пусть = t , t ≥ 0 , тогда x = t2 + 8 и уравнение примет вид
1) Если а = 0, то уравнение имеет единственное решение t = 2.
Решение некоторых типов уравнений и неравенств с параметрами.
Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.
Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.
Ⅰ
. Линейные уравнения.Задача № 1. При каких значениях параметра b уравнение не имеет корней?
Ⅱ
. Степенные уравнения, неравенства и их системы.Задача №2. Найти все значения параметра a, при которых множество решений неравенства:
содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.
Решение:
.
Преобразуем обе части неравенства.
Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:
Рис.4
При a > 6 множество решений неравенства: .
Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).
Это
Ⅲ
. Показательные уравнения, неравенства и системы.Задача № 3. В области определения функции взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.
Решение:
1) Графиком дробно-линейной функции является гипербола. По условию x > 0. При неограниченном возрастании х дробь монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.
Рис. 5
2) По определению степени область определения D(y) состоит из решений неравенства . При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.
3) При 0 < a < 1 показательная функция с основанием а убывает и неравенство равносильно неравенству . Так как x > 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства . Поэтому для таких а указанную в условии сумму нельзя найти.
4) При a > 1 показательная функция с основанием а возрастает и неравенство равносильно неравенству . Если a ≥ 5, то любое положительное число является его решением, и указанную в условии сумму нельзя найти. Если 1 < a < 5, то множество положительных решений – это интервал (0;x0) , где a = z(x0) .
5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим
суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3
= 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только
если число 3 лежит в интервале (0;x0),
а число 4 не лежит в этом интервале. Значит, 3 < x
Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.
Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.
По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.
7.05.2013
xn--i1abbnckbmcl9fb.xn--p1ai
Задачи с параметром. ЕГЭ по математике
Уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=x\log_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].
Построим графики этих функций.
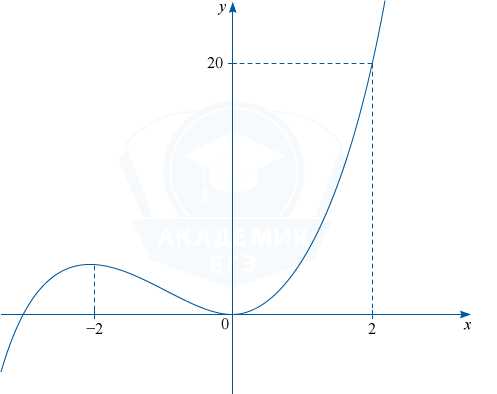
1) y=x^3+3x^2.
Найдём стационарные точки: y’=3x^2+6x=3x(x+2). y’=0 при x=0, x=-2
y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.
2) y=x\log_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=\log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).
Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.
Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),
2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.
2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).
Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.
Если x=1, то y=4, тогда 4=k-5, откуда k=9.
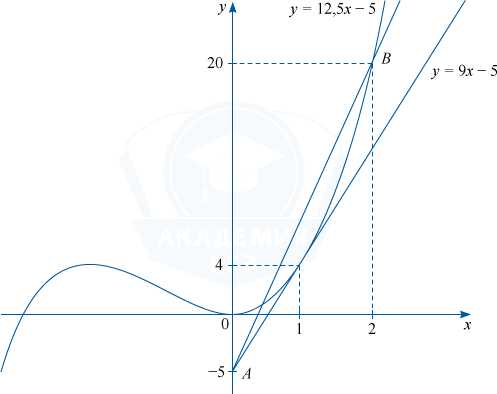
Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.
Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.
\log_{3}(a+1)=9, a+1=3^9, a=3^9-1.
\log_{3}(a+1) > 12,5, a+1 > 3^{\tfrac{25}{2}}. a > 3^{12,5}-1.
Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].
academyege.ru
Теория параметрических уравнений, задачи
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр . На самом деле с каждым параметрическим уравнением может быть написано множество уравнений. Мы рассмотрим модуль параметрического уравнения и решение простых параметрических уравнений.
Задача 1 Решите уравнения в отношении к $x$
A) $x + a = 7$
B) $2x + 8a = 4$
C) $x + a = 2a – x$
D) $ax = 5$
E) $a – x = x + b$
Решение:
A) $x + a = 7 \Leftrightarrow x = 7 – a$, то есть решение к данному уравнению найдено.
Для различных значений параметров, решения есть $x = 7 – a$
B) $2x + 8a = 4 \Leftrightarrow 2x = 4 — 8a \Leftrightarrow x = 2 – 4a$
C) $x + a = 2a – x \Leftrightarrow x + x = 2a – a \Leftrightarrow 2x = a \Leftrightarrow x = \frac{a}{2}$
D) $ax = 5$, когда а отличается от 0 мы можем разделить обе части на a и мы получим $x = 5$
Если $a = 0$, мы получим уравнение, такое как $0.x = 5$, и которое не имеет решения;
E) $a – x = x + b \Leftrightarrow a – b = x + x \Leftrightarrow 2x = a – b \Leftrightarrow x = \frac{a-b}{2}$
F) Когда a = 0 уравнение ax = 3a равно 0.x = 0
Поэтому, любое x является решением. Если a отличается от 0, тогда
$ax = 3a \Leftrightarrow x = \frac{3a}{a} \Leftrightarrow x = 3$
Задача 2 Если a является параметром, решите уравнение:
A) $(a + 1)x = 2a + 3$
B) $2a + x = ax + 4$
C) $a^2x – x = a$
D) $a^2x + x = a$
Решение:
A) Если $a + 1$ отлично от 0, то есть.. $a \neq -1$,
тогда $x = \frac{2a+3}{a+1}$;
если $a + 1 = 0$, i.e. $a = — 1$
уравнение принимает вид $0\cdot x = (2)\cdot(-1) + 3 \Leftrightarrow$
$0\cdot x = 1$, что не имеет решения;
B) $2a + x = ax + 4 \Leftrightarrow$
$x – ax = 4 — 2a \Leftrightarrow$
$(1 – a)\cdot x = 2(2 – a)$
Если $(1 – a) \neq 0$, то есть a $\neq 1$; решение будет
$x = \frac{2(2 — a)}{(1 — a)}$;
Если $a = 1$ уравнение примет вид $0\cdot x = 2(2 — 1) \Leftrightarrow$
$0\cdot x = 2$, что не имеет решения
C) $a^2x – x = a \Leftrightarrow$
$x(a^2 -1) = a \Leftrightarrow$
$(a — 1)(a + 1)x = a$
Если $a — 1 \neq 0$ и $a + 1 \neq 0$ то есть $a \neq 1, -1$,
решением есть is $x = \fra
www.math10.com
Примеры решения задач с параметрами
«Примеры решения задач с параметрами (С5 ЕГЭ)»
Симакина Елена Анатольевна,
учитель математики МБОУ «Лицей»
Новомосковск
март 2014
Цели и задачи:
1) оказание практической помощи учителям математики в решении задач с параметрами;
2) создание банка методических материалов, которые могут быть использованы учителями в практической деятельности;
3) повышение педагогического и методического мастерства, развитие и поддержка новых технологий в организации образовательного процесса;
4) обмен педагогическим опытом.
Задачи с параметрами традиционно считаются наиболее трудными. Это связано с тем, что часто они являются исследовательскими, то есть при их решении надо не просто применить те или иные формулы, а найти те значения параметра, при которых выполнено некоторое условие для корней. При этом не всегда требуется искать сами корни, а бывает, что их и вовсе невозможно найти.
Единого «рецепта» решения задач с параметром не существует. Как это обычно бывает, задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются:
— чисто алгебраический способ решения;
— способ решения, основанный на построении и исследовании геометрической модели данной задачи;
— функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Зачастую (но далеко не всегда) графический метод более ясно ведет к цели.
Далее рассмотрены некоторые способы решения заданий С5 , которые предлагались на ЕГЭ прошлых лет.


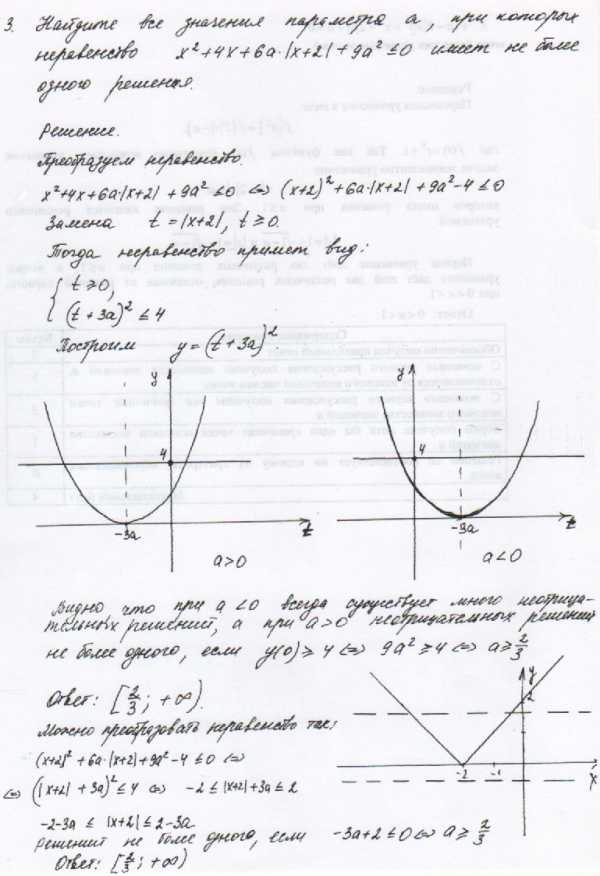

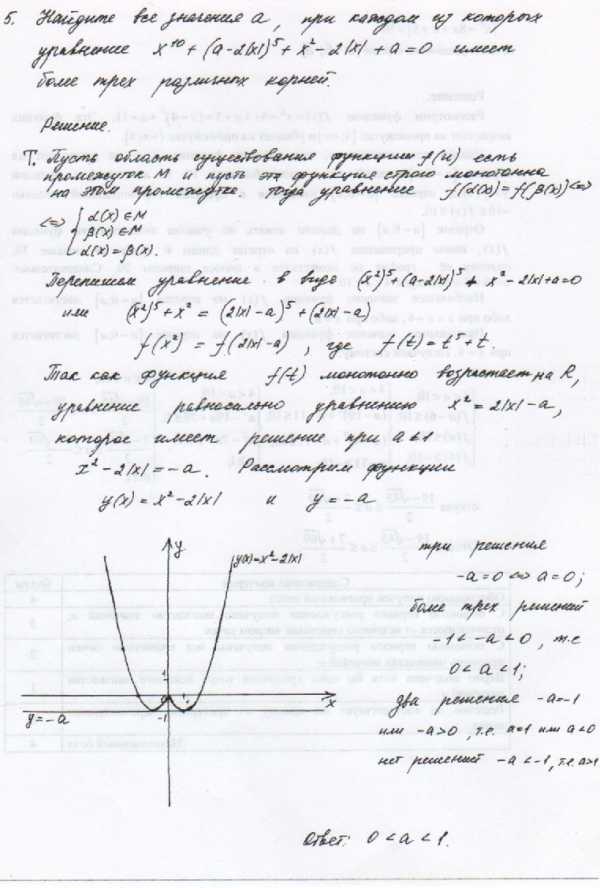

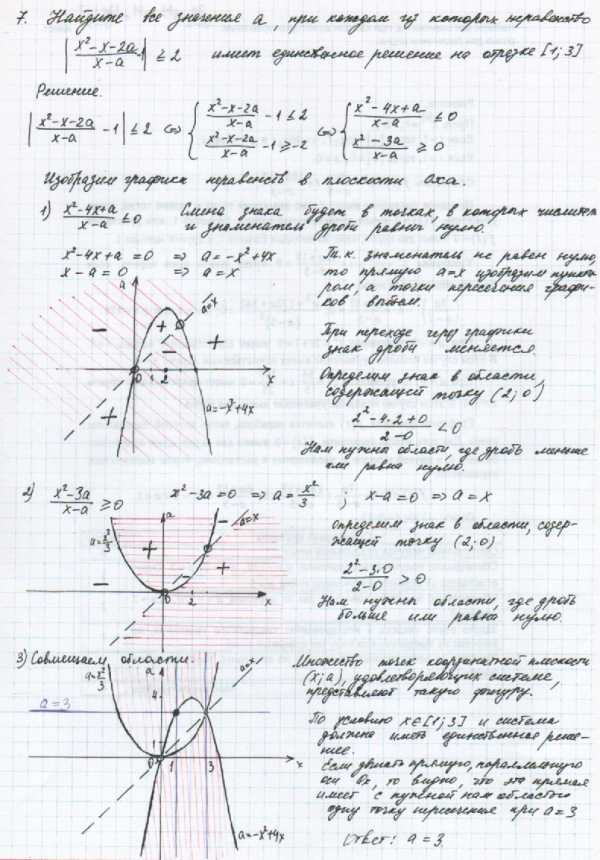



Заключение.
Выше разобранные задачи естественно не исчерпывают все возможные типы задач С5, которые могут быть предложены на экзамене. Показаны отдельные методические приемы решения задач данной направленности, которые могут быть использованы учителями математики при подготовке учащихся к успешной сдаче ЕГЭ.
Источники:
Задачи с параметром. ЕГЭ. Математика / С.И. Колесникова. – М.: ООО «Азбука – 2000», 2013. (Серия «МФТИ помогает готовиться к ЕГЭ», выпуск 8)
Математика – абитуриенту /В.В. Ткачук. – М.: МЦНМО, 2005.
Корянов А.Г., Прокофьев А.А. Различные подходы к решению задач С5 ЕГЭ // Математика. М.: Издательский Дом «Первое сентября», 2011, №5
Самое полное издание типовых ва- риантов реальных заданий ЕГЭ 2012: Математика / авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель, 2011. – 93 с. – (Федеральный институт педагогических измерений).
www.mathege.ru – Математика ЕГЭ 2012 (открытый банк заданий)
www.alexlarin.net – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучении различных разделов высшей математики
infourok.ru
Решение уравнений с параметром онлайн подробно
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В математике существуют задачи, в которых необходимо произвести поиск решений линейных и квадратных уравнений в общем виде или произвести поиск количества корней, которое имеет уравнение в зависимости от значения параметра. Все эти задачи с параметрами.

Так же читайте нашу статью «Решить уравнение пропорцией онлайн»
Рассмотрим следующие уравнения в качестве наглядного примера:
\[у = kx,\] где \[x, y\] — переменные, \[k \]- параметр;
\[у = kx + b,\] где \[x, y\] — переменные, \[k, b\] — параметр;
\[аx^2 + bх + с = 0,\] где \[x\] — переменная, \[а, b, с\] — параметр.
Решить уравнение с параметром значит, как правило, решить бесконечное множество уравнений.
Однако, придерживаясь определенного алгоритма, можно легко решить такие уравнения:
1. Определить «контрольные» значения параметра.
2. Решить исходное уравнение относительно [\x\] при значениях параметра, определенных в первом пункте.
3. Решить исходное уравнение относительно [\x\] при значениях параметра, отличающихся от выбранных в первом пункте.
Допустим, дано такое уравнение:
\[\mid 6 — x \mid = a.\]
Проанализировав исходные данные, видно, что a \[\ge 0.\]
По правилу модуля \[6 — x = \pm a, \] выразим \[x:\]
\[x = 6 \pm a. \]
Ответ: \[x = 6 \pm a,\] где \[a \ge 0.\]
Где можно решить уравнение с параметром онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Способы решения уравнений и неравенств с параметрами
Разделы: Математика
Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.
Имеется несколько способов решения параметрических уравнений и неравенств׃ алгебраический, аналитический, функционально-графический. А в некоторых задачах применяются методы математического анализа.
Суть каждого способа рассмотрена на примерах. (Приложение)
1. Алгебраический способ решения иррациональных уравнений с параметрами
Задача 1. При каких уравнение имеет единственное решение?
Решение: 1 способ. Обеспечим неотрицательность обеих частей, возведем в квадрат обе части уравнения:
Найдем дискриминант квадратного уравнения:
1) По условию уравнение должно иметь один корень, значит,
но надо проверить, удовлетворяет ли это значение ОДЗ уравнения:
.
2) Если , то только один корень уравнения должен удовлетворять условию .
а)
б) Ø
Ответ:
2 способ. Решим это задание аналитическим способом.
Проведем графический анализ менее трудоемкий, чем построение графика — полупараболы с вершиной х=-3; – множество параллельных прямых, с угловым коэффициентом 2.
Рассмотрим схему расположения графиков при различных значениях а, причем с ростом a прямая у=2х – a перемещается вправо.
Когда прямая является касательной к полупараболе и, начиная с положения, когда прямая проходит через вершину параболы (- 3; 0),мы имеем одну точку пересечения, т. е одно решение исходного уравнения. Напишем уравнение касательной в точке
Угловой коэффициент равен 2, т. е. =2 , — абсцисса точки касания
Тогда уравнение касательной , a =
При х=-3, у=0 графики пересекаются в двух точках. При этом .
А при имеем одну точку пересечения.
Ответ:
2. Аналитический способ решения тригонометрического уравнения с параметром
Задача 2. При каких значениях параметра a уравнение
имеет на промежутке не меньше 3 корней?
Решение:
1 способ. Заменим , причем |t| ≤ 1
при любом a.
Рассмотрим 2 случая:
1) , тогда уравнения будут иметь не больше 2 корней, но по условию должно быть не меньше 3 корней. Следовательно, этот случай не надо рассматривать.
2) ,
Рассмотрим расположение корней уравнения на тригонометрической окружности.
Видим, что при уравнение имеет два решения. Чтобы оно имело не меньше трех решений и .
Ответ:
2 способ. Пусть , , тогда . Рассмотрим график .
В промежутке при t= — 1 уравнение имеет один корень
При — два корня, при — один корень.
Поэтому чтобы исходное уравнение имело не меньше 3 корней необходимо выполнение условия:
| Первая система имеет 4 решения. | |
| Вторая система имеет 3 решения. |
Расположим корни квадратного трехчлена по этим двум условиям:
1)
2)
Объединяя 1) и 2) получаем
3. Два способа решения одного тригонометрического неравенства с параметром
Задача 3. При каких а неравенство верно для всех х?
Решение: 1 способ. Преобразуем неравенство и приведем его к виду
Пусть. Получим неравенство
Это значит, что парабола при 0≤t≤1 находится ниже оси ох
Рассмотрим 3 случая:
1)
Получаем условия для
2)
Но если .
Ø
3)
Полученное неравенство верно при любых 0≤t≤1; объединяем 3 случая и получаем ответ: .
2 способ. Уединяем параметр
,
Минимум f(x) достигается при ; т.к — минимум числителя, — максимум знаменателя. Значит,
Максимум f(x) достигается при ; т.е .
Схема:
Заметим, что минимум числителя и максимум знаменателя достигается при одном и том же х.
для всех х при
Ответ: .
4. Графически и аналитический способы решения неравенства с параметром, содержащего знак модуля
Задача 5. При каких a неравенство выполняется для всех ?
Решение: . Рассмотрим две функции
Построим эскизы графиков функций:
Найдем уравнение касательной в точке функции y= |x2-4x+3|
Тогда . Так как
Подставим значение точки х0 в производную рассматриваемой функции и получаем, что — —a=-2-4, a=4+2.
Следовательно, при a =4+2 y=1-ax – касательная к y=|x2-4x+3|. Значит, чтобы неравенство выполнялось, нужно, чтобы
II способ.
1 случай.
Это значит, что
2 случай.
А это значит, что
Чтобы неравенство выполнялось при всех x:
Ответ: .
Решение уравнений и неравенств с параметрами алгебраическим, аналитическим и графическим способами заключается в том, что при одном способе решение может быть громоздким, а при другом — более простым и наглядным. А это говорит о том, что нужно перед началом решения задания оценить его и выбрать тот путь, который проще.
Литература
- Сборник задач по математике для подготовки к вступительным экзаменам УГНТУ, Уфа-2003 г.
- Факультативный курс по математике, 10 класс. Шарыгин.И.Ф. Москва «Просвещение» 1989 г.
- Уравнение с параметрами на факультативных занятиях. С.Я.Постникова. «Математика в школе», №8, 2002 г.
- Математика абитуриенту. В.В.Ткачук, Москва, 2002 г.
22.07.2009
xn--i1abbnckbmcl9fb.xn--p1ai
Задачи с параметром
В этом разделе мы будем рассматривать задачи разного уровня сложности — от совсем простых до эксперт-уровня. Большинство из них будут взяты из открытых источников, некоторые составлены специально мной для того, чтобы показать работу с тем или иным специальным приёмом.
- § 1.
- Формула расстояния на плоскости и следствия из нее для решения сложных задач с параметром.
- § 2.
- Учёт специальных условий в задачах с параметром
- Глава 1.
- Уравнения с параметрами
- Глава 2.
- Аналитическое решение
- Глава 3.
- Графическое решение
- § 3.
- График модуля в задачах с параметром — учимся строить правильно
- § 7.
- Точные квадраты и корни в задачах с параметром
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
www.berdov.com
