1. Найдите долю, которая читается: «Одна третья». a. 1/2 b. 1/3 c. 3/1 d. 2/3 2. Как правильно читается доля 1/4? a. две четвертых b. одна вторая c. одна четвертая d. одна третья 3. Какая из этих долей является наибольшей? a. 1/2 b. 1/4 c. 1/6 d. 1/7 4. Какая из этих долей является наименьшей? a. 1/3 b. 1/5 c. 1/4 d. 1/9 5. Сколько шестых долей в целом торте? a. 1 b. 2 c. 6 d. 8 6. Торт разделили на четыре равные части и взяли одну такую часть. Какие доли получатся, если разделить на три равные части каждую четвертую часть торта? a. 1/4 b. 1/8 c. 1/12 d. 1/16 7. От куска ткани отрезали одну пятую часть, она равна 3 метра. Какова длина всего куска ткани? a. 5 метров b. 10 метров c. 15 метров d. 20 метров 8. Одна шестая часть от числа 24 равна … a. х = 2 b. х = 3 c. х = 4 d. х = 6 9. Начертили отрезок длиной 20 см. Чему равна 1/4 часть этого отрезка? a. 2 см b. 4 см c. 5 см d. 10 см 10. Длина одного куска ленты равна 30 см, а длина второго куска ленты составляет одну третью часть от первого куска ленты. Чему равна длина второго куска ленты? a. 5 см b. 10 см c. 15 см d. 20 см | 1. Найдите долю, которая читается: «Одна третья». a. 1/2 b. 1/3 c. 3/1 d. 2/3 2. Как правильно читается доля 1/4? a. две четвертых b. одна вторая c. одна четвертая d. одна третья 3. Какая из этих долей является наибольшей? a. 1/2 b. 1/4 c. 1/6 d. 1/7 4. Какая из этих долей является наименьшей? a. 1/3 b. 1/5 c. 1/4 d. 1/9 5. Сколько шестых долей в целом торте? a. 1 b. 2 c. 6 d. 8 6. Торт разделили на четыре равные части и взяли одну такую часть. Какие доли получатся, если разделить на три равные части каждую четвертую часть торта? a. 1/4 b. 1/8 c. 1/12 d. 1/16 7. От куска ткани отрезали одну пятую часть, она равна 3 метра. Какова длина всего куска ткани? a. 5 метров b. 10 метров c. 15 метров d. 20 метров 8. Одна шестая часть от числа 24 равна … a. х = 2 b. х = 3 c. х = 4 d. х = 6 9. Начертили отрезок длиной 20 см. Чему равна 1/4 часть этого отрезка? a. 2 см b. 4 см c. 5 см d. 10 см 10. Длина одного куска ленты равна 30 см, а длина второго куска ленты составляет одну третью часть от первого куска ленты. Чему равна длина второго куска ленты? a. 5 см b. 10 см c. 15 см d. 20 см |
infourok.ru
Проверочная работа по математике тема «Дроби» (3 класс)
Проверочная работа по теме «Дроби» 3 класс
Запишите, где возможно, соответствующие рисункам дроби.а) б)
в) г)
д)
Запишите, где возможно, соответствующие рисункам дроби:
а) б)
в) г)
д)
а) Запишите дроби, у которых:
числитель 5, знаменатель 8; —
знаменатель 4, числитель 1; —
знаменатель 7, числитель 11; —
числитель 7, знаменатель 12. —
б) Запишите цифрами дроби:
семь тринадцатых;
восемь одиннадцатых;
шесть девятых;
девять десятых;
двадцать шестых.
а) Запишите дроби, у которых:
числитель 9, знаменатель 9;
знаменатель 6, числитель 1;
знаменатель 5, числитель 9;
числитель 5, знаменатель 11.
б) Запишите цифрами дроби:
четыре четвертых;
девять шестых;
тридцать седьмых;
восемь одиннадцатых;
девять третьих.
Сравните дроби и поставьте знаки сравнения.
…
…
…
…
…
Сравните дроби и поставьте знаки сравнения:
…
…
…
…
…
4. Запишите данные дроби в порядке увеличения.
-
Запишите данные дроби в порядке убывания.
а) Решите задачу.
Шестая часть пути от дачи до реки 70 м. Найдите расстояние между дачей и рекой.
а) Решите задачу.
Пятая часть пути от дома до школы 80 м. Найдите расстояние между домом и школой.
infourok.ru
Урок математики в 3 классе. Сравнение дробей с одинаковым знаменателем.
Современный урок математики с учетом требований ФГОС 10.04.18г.
Урок математики в 3 классе УМК Л.В. Занкова.
Тема: Сравнение дробей с одинаковым знаменателем.
Цель: познакомить учащихся с правилом сравнения дробей с одинаковым знаменателем, научить учащихся применять данное правило при выполнении практических заданий.
Задачи урока:
Образовательные (формирование познавательных УУД):
Совершенствовать умения:
Применять правило сравнения дробей с одинаковыми знаменателями в процессе разрешения проблемной ситуации
Анализировать полученные результаты
Моделировать с помощью координатной прямой геометрическую интерпретацию отношения «больше-меньше»
Воспитательные (формирование коммуникативных и личностных УДД):
Воспитывать:
Познавательный интерес и навыки взаимоконтроля, взаимопроверки
Коммуникативные способности во время работы в парах
Понимание ответственности за индивидуальную деятельность и деятельность работы в паре
Положительный эффект настойчивости для достижения цели
Развивающие (формирование регулятивных УУД:
Развивать умения:
Анализировать, сравнивать, обобщать, делать выводы
Участвовать во взаимоконтроле, самоконтроле, вносить предложения.
Осуществлять рефлексию своей деятельности
Главная проблема урока: Как сравнить обыкновенные дроби.
Оборудование:
Учебник «Математика — 3 класс», автор И.И.Аргинская.
Рабочая тетрадь «Математика — 3 класс, 3 часть», автор Е.П.Бененсон.
Индивидуальный и групповой раздаточный материал
Ход урока
1.Организационный этап:
— Посмотрите на эти механические часы (висят в классе). Что будет, если мы уберем 1 деталь? Так же и знания человека состоят из маленьких «деталей». И только, когда эти «детали» собраны вместе и не упущена ни одна, тогда знания начинают действовать и их можно применить в жизни. То, что мы узнаем на уроке сегодня и являются такими «деталями» наших знаний. Девиз нашего урока ( слайд 1)
«Мудрым никто не родился, а научился»
— Как понимаете эти слова?
— Сегодня продолжим путь к мудрости
2. Актуализация знаний и умений
Математический диктант.
1) Запишите дроби: семь восьмых
2) Запишите дробь, девять одиннадцатых
3) Запишите дробь, у которой числитель 4, а знаменатель 5
4) Запишите дробь, у которой знаменатель 7, а числитель 2
5) Запишите дробь, у которой числитель 6, а знаменатель на 3 больше
6) четверть
7) Запишите дробь, у которой числитель 7, а знаменатель в 3 раза больше
8) Запишите дробь, у которой знаменатель в 18 а числитель в 2 раза меньше
10) четыре семнадцатых
Проверка (парами, соседи меняются тетрадями).
Критерии оценки:
«5» — без ошибок
«4» — 1 ошибки
«3» — 2-3 ошибки
Молодцы!
3.Постановка учебной проблемы, формулирование темы урока: Приложение1
1) На сколько равных квадратов разделен большой квадрат?
2) Какую часть большого квадрата составляет один маленький? Запишите ответ дробью.
3) Какие еще дроби можно составить по этому рисунку? Запиши их.
4) Закрасьте ту часть большого квадрата, которая соответствует дроби.
Найдите рисунок с наименьшей и наибольшей закрашенной площадью. Каким дробям они соответствуют?
5) Расположи все записанные дроби в порядке возрастания соответствующим им площадей.
1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 9/9
— Как сравнивают дроби?
— Тогда формулируем тему урока: «Сравнение дробей с одинаковыми знаменателями»
Поставьте каждый для себя цель урока.
Целеполагание: Научиться сравнивать дроби с одинаковым знаменателем.
4. Открытие нового знания
— Вернёмся к вопросу: как сравнить дроби;
Запишите в тетради примеры сравнения дробей с одинаковыми знаменателями.
1/9 ‹ 5/9, 7/9 ›4/9 и т. д.
Физкультминутка.
Дети делятся на группы и получают конверты с заданием: встать в порядке возрастания дробей.
5. Первичное закрепление.
Учебник с. 80 № 422Проверьте себя: насколько хорошо вы поняли материал; выполните следующее задание самостоятельно в паре. Оцените задание друг друга, укажите друг другу, что он сделал не так, опираясь на правило или алгоритм.
Самостоятельная работа (№422 (2)).
Проверка:
— Какие дроби вы записали?
— Как вы их расположили в порядке увеличения?
Парная работа (№422 (2))
Проверка:
— Какой отрезок у вас получился?
— Какие дроби вы записали?
— Как вы их расположили в порядке уменьшения?
Критерии оценки:
«5» — без ошибок
«4» — 1-2 ошибки
«3» — 3-4 ошибки
Молодцы!
6.Самостоятельная работа (карточка)
7. Повторение пройденного. Слайд.
Бабушка наказала внучке Оле за час полить 3 грядки: со свёклой, огурцами и горохом. Треть этого времени Оля ловила бабочек, четверть часа – поливала свёклу, шестую часть часа – потратила на полив грядки с огурцами. Сколько времени осталось у Оли, чтобы полить грядку с горохом?
Решение задачи
60 : 3 = 20 (мин.) ловила бабочек
60 : 4 = 15 (мин.) поливала свёклу
60 : 6 = 10 (мин.) поливала огурцы
20 + 15 + 10 = 45 (мин.) потратила Оля
60 – 45 = 15 (мин.) осталось на полив гороха
8.Рефлексия учебной деятельности на уроке (итог урока).
-Какова тема нашего урока?
— Какую цель ставили перед собой?
— Какую работу мы выполняли для достижения цели?
— Давайте оценим нашу работу на уроке: продолжите предложения
Я понял (а) тему урока и могу помочь товарищу…..
Я понял(а) тему урока, но немного сомневаюсь …..
Я не понял тему урока…
Девиз нашего урока.
9.Домашнее задание
infourok.ru
«Сравнение дробей с одинаковыми знаменателями»
Разделы: Начальная школа
Задачи урока:
- Уточнить представление детей о дробных числах.
- Подвести детей к осознанию того, что из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Оборудование:
- Учебник «Математика — 3 класс», автор И.И.Аргинская.
- Рабочая тетрадь «Математика — 3 класс, 3 часть», автор Е.П.Бененсон.
- Индивидуальный и групповой раздаточный материал
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
2.1. На доске:
— Кто может прочитать эти записи? Что вы можете о них сказать?
2.2. На партах индивидуальный раздаточный материал.
Приготовьте цветные карандаши, послушайте внимательно задание и выполните его.
Итак, проверяем. От каждого ряда выходит ученик к доске. Дети оценивают, сравнивают.
2.3. Три человека работают у доски
— Кто сможет записать дробью?
— Кто может прочитать дроби?
2.4. Фронтальный опрос.
— Как называется число под чертой? Над чертой?
— Сколько натуральных чисел использовано в записи каждой дроби?
— Какой знак показывает, что записано дробное число?
Итак, что обозначает в записи дроби каждое число?
3. Изучение нового материала.
3.1. Постановка проблемы.
На доске записаны дроби в общем виде.
> ? <
— Как вы думаете, верны ли эти записи?
— Докажите.
3.2. Новая тема.
На доске
— Какая из дробей больше, какая меньше?
— Почему мы не можем ответить на эти вопросы?
— А мы умеем сравнивать дроби?
— Чему сегодня будем учиться на уроке?
На доске учитель записывает тему:
Сравнение дробей.
3.3. Выдвижение гипотез.
— Как вы предлагаете сравнить данные дроби?
3.4. Физ. минутка.
3.5. Решение проблемы.
Класс делится на пять групп. Выдаётся групповой раздаточный материал.
Ученики записывают дроби, показывают на рисунке, сравнивают и записывают вывод.
Дети рассказывают у доски о проделанной работе.
Итак:
— Сравните дроби. Что не изменяется?
— Что изменяется?
— Как изменяются числители дробей?
Вывод: Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
3.6. Реализация продукта.
— Сформулируем правило сравнения дробей с одинаковыми знаменателями.
3.7. Физминутка.
4. Закрепление нового материала.
Ученики выполняют задание в рабочей тетради — стр.20 №42
— Раскрасьте часть торта Карлсона — жёлтым карандашом, а часть торта, которая досталась Малышу — коричневым.
— Какая дробь больше?
На доске:
>
5. Решение задачи.
Ученики читают текст задачи, записанный на доске:
В магазине в отделе фруктов было 80 кг яблок. Утром продали часть всех яблок. Вечером продали всех яблок. Когда продали яблок больше и на сколько килограммов?
Ученики решают задачу с пояснением.
Итак, не вычисляя можно было сравнить эти дроби?
6. Итог урока.
— Что узнали о сравнении дробей с одинаковыми знаменателями?
Приложения.
21.07.2009
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Опорная карточка к уроку математики. Тема «Сравнение дробей ».
Опорная карточка к уроку математики в 6 классе по теме «Сравнение дробей».Опорные карточки удобно использовать по системе Класс -комплект.
Просмотр содержимого документа
«Опорная карточка к уроку математики. Тема «Сравнение дробей ».»
Муниципальное бюджетное образовательное учреждение «Сидоровская школа» структурное подразделение «Лежская школа» Грязовецкого муниципального района Вологодской области
Опорная карточка к уроку математики.
Тема «Сравнение дробей ».
Работу выполнил учитель физики и математики
Смирнов Александр Николаевич.
д.Спасское
2018г
Урок 3 Сравнение дробей 6 кл
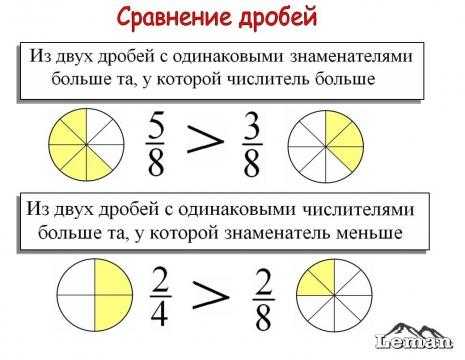
Пример: Сравнить дроби  . Приведем дроби к общему знаменателю 6. Первую дробь домножим на 3.
. Приведем дроби к общему знаменателю 6. Первую дробь домножим на 3. .
. 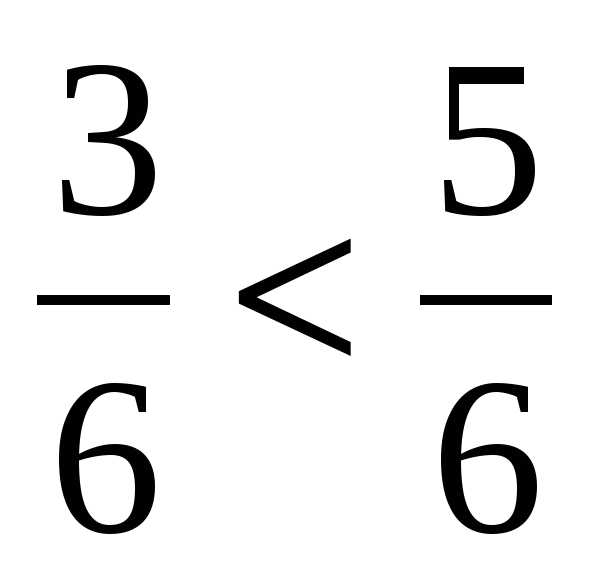
Задания в классе: № 9(а,в,д), 10, 12, 14(а)
Домашнее задание: № 9(б,г,е), 11, 14(б)
Урок 3 Сравнение дробей 6 кл

Пример: Сравнить дроби  . Приведем дроби к общему знаменателю 6. Первую дробь домножим на 3.
. Приведем дроби к общему знаменателю 6. Первую дробь домножим на 3. .
. 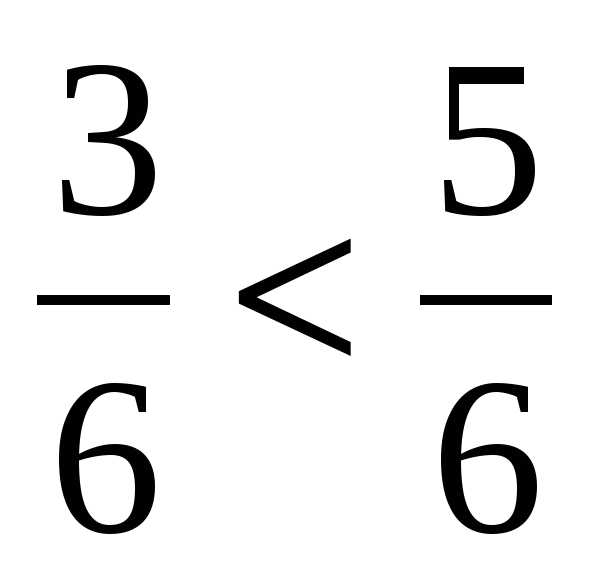
Задания в классе: № 9(а,в,д), 10, 12, 14(а)
Домашнее задание: № 9(б,г,е), 11, 14(б)
kopilkaurokov.ru
Сравнение обыкновенных дробей с одинаковыми знаменателями
Открытый урок по теме: Сравнение обыкновенных дробей с одинаковыми знаменателями
Цели урока:
Дидактическая цель: создать условия для формирования новой учебной информации.
Цели по содержанию:
— обучающие:
1. Познакомить учащихся с правилами сравнения обыкновенных дробей.
2. Научить учащихся формулировать данные правила и применять их на практике.
3. Моделировать с помощью координатной прямой геометрическую интерпретацию отношения «больше — меньше»
— развивающие: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание;
— воспитательные: развивать познавательный интерес, навыки взаимопроверки, развивать коммуникативные способности во время работы в парах, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.
Тип урока: изучение нового материала.
Образовательные технологии: технология критического мышления (на этапе открытия новых знаний), обучение в сотрудничестве (работа в парах), здоровье сберегающая технология (применена на этапе физкультминутка, а также на подготовительном этапе).
Ход урока:
I.Организационный момент – 3 минуты.
Девиз урока:”Добывай знания сам!” Отправляемся в экспедицию, а для этого проверим готовность. Ведь чтобы новых знаний набраться, надо на старые опираться!
II.Устные упражнения (5 минут):
А) Прочтите дроби:1/8,1/4,3/8,4/6,1/2,2/8,1/3,2/100,5/60(Слайд 3)
Б) Дробь 2/5.Назовите числитель и знаменатель этой дроби.(Слайд 2)
В) Какая часть фигуры заштрихована? (Слайд 4)
Г) Укажите координату мигающей точки. (Слайд 5)
III. Этап подготовки к активному и сознательному усвоению нового материала (5 минут)
Посмотрим, ребята, какой багаж знаний возьмет в дорогу каждый из вас?
1.У вас на столах лежат путевые листы с заданиями. На слайде (№6) изображены две фигуры. Нужно определить, какая часть каждой фигуры закрашена красным, какая зеленым, какая часть красным и зеленым вместе, а какая желтым. Заполнить таблицу.
Вопросы: Где в жизни мы встречаемся сразу с тремя названными цветами? Что означает каждый цвет?
Класс выполняет самостоятельную работу на листочках. Тем временем двое у доски выполняют индивидуальные задания по карточке.
Приложение 1.
Вариант 1.
Укажите дробью часть фигуры, закрашенную | ||
А | В | |
Красным цветом | ||
Зеленым цветом | ||
Зеленым и красным цветами | ||
Желтым цветом | ||
—
2.Индивидуальные задания.
1 ученик: На доске начерчены 4 равных прямоугольника. Закрасить половину первого, две четверти второго, три шестых третьего и шесть двенадцатых четвертого, начиная с левого края. Записать дроби рядом с прямоугольниками.
2 ученик: Начертить на доске координатный луч. Отметить точки с координатами А(3), О(0), В(7), Е(1), С(10). Отметьте точки , которые удалены от точки В на два единичных отрезка, обозначьте и найдите их координаты. Запишите на доске, какие точки лежат:
а) левее точки В:
б) правее точки В:
Сформулируйте правило сравнения натуральных чисел с помощью координатного луча.
IV. Открытие детьми нового знания (18 минут).
И так, проверим, что каждый из вас возьмет в путь? Не забыли девиз нашей экспедиции?
Открываем тетради и записываем дату и тему.
1. Проверим, как класс справился с заполнением путевых листов.
Беседа с классом (учитель задаёт вопросы и записывает ответы на доске, учащиеся ведут такие же записи в тетрадях).
. (Слайд 6)
1) Как называется фигура А?
На сколько равных долей разбит прямоугольник?
Какая его часть закрашена красным цветом, зеленым цветом, желтым цветом?
Какая часть фигуры больше: та, что закрашена красным цветом или та, что зеленым?
Что можно сказать о дробях и ? Запишите это неравенство в тетрадь.
Какая из дробей больше или ? Запишите. >.
Посмотрите на рисунок и скажите “Какая же из дробей с одинаковыми знаменателями больше?” Та дробь, которая показывает большую долю фигуры.
Посмотрим, как работает наше правило в других случаях?
2) Как называется фигура В?
На сколько долей разбит круг?
Какие дроби вы получили, выполняя задание?
Можно ли сказать, что дроби и равны? Запишите равенство.
А дробь больше дроби ? Почему? Взято больше долей. Запишите неравенство.
Вопрос учителя классу: есть ли ещё равные дроби? Запишите в тетрадь самостоятельно.
2. Что взял с собой в дорогу 1 ученик?
Ученик выходит к доске и объясняет, как он выполнил задание, какие дроби он записал.
Ученики должны заметить, что все заштрихованные части занимают половины прямоугольников. Так как прямоугольники равны, то и дроби равны. Записываем в тетрадь : задача №1.
Учитель на доске, а ученики в тетради записывают: 2/4=1/2, 3/6=1/2, 6/12=1/2, 3/6=6/12.
3. Что взял с собой в дорогу 2 ученик?
К доске выходит любой ученик из класса и проверяет задание с координатным лучом по карточке-заданию. Учитель стирает 0 у точки С (1), ученик записывает новые координаты точек.
Ученик, который выполнял задание на доске, устно формулирует правило сравнения натуральных чисел с помощью координатного луча.
Задание учащимся класса: записать в тетрадь точки с новыми координатами, которые лежат
а) левее точки В:
б) правее точки В:
Какая точка имеет координату равную 1/2? Изобразите ее на нашем луче.
Сформулируйте сами правило сравнения дробей с помощью координатного луча.
V. Физкультминутка (3 минуты)
1. Упражнение для глаз (влево смотрим, вправо, вверх, вниз — 3 раза)
2. “Кулачки”
Руки на коленях,
Кулачки сжаты,
Крепко с напряжением
Пальчики прижаты.
Пальчики сжимаем, сжимаем,
Отпускаем, разжимаем.
Знайте, девочки и мальчики,
Отдыхали ваши пальчики.
3. Учитель показывает выражения на слайдах №№10,11,12,13,14,15. Быстро и громко читает их. Если выражение “верно”, то дети поднимают руки вверх, если нет, то вытягивают перед собой:
а) 6/10 > 3/10,
б) 3/10 > 1,
в) 8/14 > 0,
г) 5/10 < 1/2,
д) А(2/12) лежит левее В (7/12),
е) С(2/5) правее Д(4/10)
VI. Закрепление нового материала (5 минут).
Откройте учебники на стр. 146 учебника, прочитайте оба правила сравнения дробей с одинаковыми знаменателями.
Вопрос: совпадают ли правила в учебнике с нашими открытиями?
Резерв. Продолжаем дальше получать новые знания, теперь уже по учебнику: №940(устно),№ 945 (в тетради).
VII. Проверка полученных знаний (5 минут)
Наша математическая экспедиция подходит к концу. Мы стоим у подножия высокой горы, название которой “Дроби”. Нам предстоит трудное восхождение. Для того чтобы проверить, как мы научились сравнивать дроби с одинаковыми знаменателями, проведем мини-тестирование. Тесты на столах
Правильность выполнения проверяется с помощью таблиц (слайд 12).
Результаты заносим в таблицу на путевых листах. Взаимопроверка: каждый проверяет работу соседа и подчеркивает ошибки. Без ошибок — оценка “5”одна ошибка- “4”, две ошибки-“3”, три и больше-“2”.
I вариант
Таблица ответов——————————————линия разреза———————————————————-
II Вариант
Таблица ответов
VIII. Итог урока(2 минуты).
1. Повторить ещё раз, чем занимались на уроке.
2. Выставить отметки за работу в экспедиции.
IX. Домашнее задание: № 965,№966,№969
/data/files/w1474742316.ppt
xn--j1ahfl.xn--p1ai
«Дроби. Получение и обозначение дробей. Сравнение дробей».
МБОУ Чымнайская средняя общеобразовательная школа имени Г.Д.Бястинова
Варламова Татьяна Спиридоновна учитель начальных классов
Урок математики в 3-м классе.
Тема: «Дроби. Получение и обозначение дробей. Сравнение дробей».
Цели:
1. Образовательные:
познакомить с тем, как образуются, называются и записываются дроби;
учить сравнивать дроби (доли).
2. Развивающие:
дать представление о том, как можно найти долю по числу и число по доле.
3. Воспитательные:
учить работать дружно, аккуратно;
учить отвечать полными предложениями.
Ход урока
I. Организационный момент.
Сегодня у нас необычный урок. Это будет урок-исследование. А мы с вами будем юными математиками, которым предстоит сделать открытие. Итак, начинаем работу.
2, 5, 12, 128
1/2 3/4 5/8 (Запись на доске.)
0,25 1,5 2,35
Посмотрите на ряд чисел…
— Что вы можете сказать о них?
Молодцы! Вы всё верно рассказали. Хотя мы и не о всех числах поговорили.
Устное решение задач.
— У бабушки было 8 яблок. Она разделила их поровну между 4 внуками. По сколько яблок досталось каждому? (По 2 яблока.)
— Как вы узнали? (8 / 4 =2)
— Что это за число? (Целое.)
Молодцы. Справились легко и быстро. Но на то мы и исследователи, чтобы от простого идти к сложному. Решите теперь такую задачу.
— У бабушки было 2 яблока. Она разделила их поровну между 4 внуками. По сколько яблок досталось каждому? (По половинке.)
— А как это записать?
II. Новое!
Цель. Вот сегодня на уроке мы и познакомимся с новыми числами. А вот как они называются?! Давайте попробуем придумать им названия.
1. Работа на предметном столике.
— У меня в руках яблоко. Какое оно? ( Целое.)
Правильно, одно целое. Разрезаю пополам (показываю).
— Сколько половин получилось? (2)
— На сколько равных частей делили? (На 2.)
Я взяла одну часть, одну из двух, одну вторую (показываю).
Посмотрите как это записать: — эта черта обозначаетделение.
1 пишу в числитель (показываю на доске).
2 пишу знаменатель (показываю на доске).
— На сколько частей делили? (На 2.)
— Сколько частей взяла?
— Как прочитать это число? (Одна вторая.)
— Но как же мы назовём это число? Что мы делали с яблоком? (Разделили на доли, раздробили, дробили.)
— Как же назовём такие числа? (Дроби. Доли.)
— Что такое 1/2? (Дробь.)
2. Работа на предметном столике.
У меня в руках яблоко. Разделим его на 4 части (показываю.)
— На сколько частей я разделила? (На 4.)
— Сколько частей я взяла? (Показ 1/2, 2/4, 3/4.)
— Покажите, где записаны эти дроби?
Запись на доске: 1/4, 2/4, 3/4.
— Как вы думаете, что больше1/2 или 1/4? (Показ долек яблока.)
www.prodlenka.org
