Касательная к графику функции параллельна прямой – Прямая является касательной к графику функции

Прямая является касательной к графику функции

   Продолжаем рассматривать задачи входящие в состав экзамена по математике. В курсе алгебры есть группа задач, где задаётся уравнение функции и уравнение прямой — касательной к графику данной функции или прямой параллельной этой касательной.

Задачи несложные, но они требуют чёткого понимания геометрического смысла производной. Это теоретическая основа для решения подобных задач (и подобных им), и без этой основы никак нельзя. Рекомендую ознакомиться со статьями «Геометричесий смысл произвоной. Часть 1» и «Геометрический смысл производной. Часть 2».

Рассмотрим две задачи:

Прямая у = 4х + 8 параллельна касательной к графику функции

у = х² – 5х + 7 

Найдите абсциссу точки касания.

Из геометрического смысла производной мы знаем, что значение производной  в точке касания равно угловому коэффициенту касательной.

Известно, что угловые коэффициенты параллельных прямых равны, значит  угловые коэффициенты прямой  у = 4х + 8 и касательной равны 4.

Угловой коэффициент прямой  вида у = kх + b это число  k.

Таким образом, абсцисса точки касания находится из уравнения:

Значит,

Ответ: 4,5

Второй способ: 

Он предельно прост, но не всегда работает. Строим на координатной плоскости график у = х² – 5х + 7, строим прямую у = 4х + 8, далее строим (параллельным переносом) параллельную ей прямую касающуюся параболы, и в некоторых задачах вы визуально сможете определить абсциссу точки касания.

Отмечу, что таким способом можно решить задачу, если абсцисса целое число или целое  с половиной, например  1,5; – 2,5; –3,5  и так далее. Если же точка пересечения «непонятна», то есть, нельзя точно и уверенно определить абсциссу (например, визуально сложно определить 3,2; 5,7 …), то точное решение  даст  первый способ. 

Если вы  решили задачу этим способом  и уверены в правильности решения, обязательно сделайте проверку. Подставьте полученную абсциссу в оба исходных уравнения, должны получится равные значения функций (ордината точки пересечения).

Решите самостоятельно:

Прямая у = 7х – 8 параллельна касательной к графику функции

у = х² + 6х – 8

Найдите абсциссу точки касания.

Посмотреть решение

Прямая у = 6х + 4  является касательной к графику функции 

у = х³ – 3х² + 9х + 3

Найдите абсциссу точки касания.

Из геометрического смысла производной функции известно, что  она (производная)  равна угловому коэффициенту касательной.

Известно, что угловой коэффициент прямой  вида у = kх + b это число  k.

Значит, угловой коэффициент прямой  у = 6х + 4   равен 6. Таким образом,

Решая квадратное уравнение, получим:

Получили два равных корня.  Таким образом, абсцисса точки касания равна 1.

Ответ: 1

Решите самостоятельно:

Прямая у = – 4х – 11  является касательной к графику функции

у = х³ + 7х² + 7х – 6 

Найдите абсциссу точки касания

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите! 

На этом все. Успехов Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Касательная к графику функции

​

Основные понятия и определения

    В общем случае уравнение прямой на плоскости записывается как , где  некоторые константы. График функции    приведен на рис. 1. Причем здесь  .  Если  , то будет уравнением прямой, параллельной числовой оси  

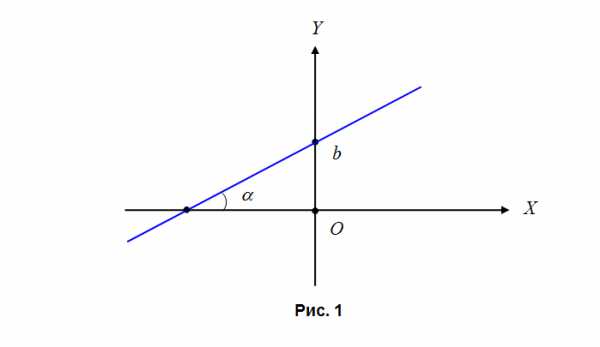
    Пусть имеются две прямые, заданные уравнениями и  . Если  , то данные прямые являются параллельными.

    Для того, чтобы эти прямые были взаимно перпендикулярны, требуется выполнение условия  .

    В частности, прямые и являются параллельными, а прямые и будут взаимно перпендикулярны.

 

Уравнение касательной

 

    Пусть некоторая функция, дифференцируемая в точке . На графике функции  , который приведен на рис. 2, выделена точка  , где  . Прямая    является секущей, а касательная есть предельное положение секущей при условии, что точка стремится к точке  

.

    Для составления уравнения касательной, проведенной к графику функции в точке с абсциссой , обычно используются формулы (1) и (2), известные из школьных учебников по математике:

 

                                                                                            (1)

или

                                      .                                      (2)

    Однако при решении задач на составление уравнений касательных данные формулы не отражают тот факт, что касательная является прямой линией. В этой связи уравнение касательной целесообразно представлять в виде  . Сделать это нетрудно, поскольку формула (2) равносильна формуле  

                              

    Формула (3) имеет вид уравнения прямой линии , где    и  .

    Рассмотрим примеры решения задач на применение формулы (3) при составлении уравнения касательной к графику функции  в точке с абсциссой .

Примеры решения задач

 

   

    Пример 1. Написать уравнение касательной, проведенной к графику функции   в точке с абсциссой  

 

   

    Решение. Воспользуемся формулой (3). Так как   и  , то    и  . В таком случае формула (3) принимает вид    или  .

    Ответ:  .

 

   

    Пример 2. Составить уравнение касательной, проведенной к графику функции    в точке с абсциссой  

 

   

    Решение.  Поскольку    и  ,  то  

,    и из формулы (3) получаем   .

    Ответ:  .

 

   

    Пример 3. Найти уравнение касательной, проведенной к графику функции  , при условии, что касательная параллельна прямой  .

 

   

    Решение.  Предположим, что точка касания имеет абсциссу

. Так как  , то формула (3) принимает вид

  или

                                          .                                       (4)

    По условию задачи касательная (4) должна быть параллельна к прямой , поэтому    или  . Если  значение    подставить в формулу (4), то получим уравнение искомой касательной.

    Ответ:  .

    Примечание. Если в условии данного примера потребовать, чтобы касательная была бы перпендикулярна прямой , то здесь необходимо положить  . Тогда   и из формулы (4) получим уравнение касательной  .

 

   

    Пример 5. Написать уравнение касательной к графику функции  , при условии, что касательная содержит точку с координатами  и

.

 

   

    Решение.  Так как  , то формула (3) принимает вид

 или

                                          .                                                  (5)

    Поскольку касательная (5) содержит точку с координатами  и , то подставим в эту формулу значения    и получим

  или   .

    Однако квадратное уравнение имеет два корня    и  

, поэтому рассматриваемая задача имеет два решения.  Если найденные значения    подставить в уравнение (5), то получим уравнения двух  касательных.

    Ответ:  , .  

   

    Пример 6. Провести касательную к графику функции   в точке с абсциссой   и вычислить площадь треугольника, образованного касательной и положительными полуосями системы координат.

 

    Решение.  Так как и , то   ,   и уравнение касательной (3) к графику функции   в точке с абсциссой принимает вид  .

    Пусть касательная    пересекает оси  

 и    в точках и , соответственно. Тогда нетрудно установить, что . Поскольку  , то  .

    Ответ:  .

   

    Пример 7. Составить уравнение  касательной к графику функции   при условии, что касательная проходит через начало координат.

 

   

    Решение.  Так как    и  , то уравнение касательной (3) принимает вид  

                                    ,                              (6)

где  абсцисса точки касания.

    Так как касательная    проходит через начало координат, то  . В этой связи из уравнения (6) следует, что

,      или   .

    Поскольку    и  , то  . Следовательно, уравнение искомой касательной имеет вид   .

    Ответ:  .

   

    Пример 8. Найти уравнение общей касательной к графикам функций    и  .

 

   

    Решение.  Если построить эскиз графиков функций  и  , то можно увидеть, что существует единственная общая для них касательная  . Поскольку эта прямая касается графиков обеих функций, то имеет место система уравнений

  или  

    Поскольку общая касательная к графикам функций  и  , является единственной, то каждое из уравнений системы должно иметь только по одному корню. А это означает, что дискриминанты уравнений системы должны быть равны нулю. Следовательно, имеем

   или   

    Если из второго уравнения системы вычесть первое, то   или  .  Если значение    подставить в любое из уравнений системы, то получим  .

    Ответ:  .

    С целью качественной подготовки к вступительным экзаменам по математике в области составления уравнений касательных целесообразно использовать учебные пособия, приведенные в списке рекомендованной литературы.  

   

Рекомендуемая литература

1.  Кушнир А.И. Шедевры школьной математики (задачи и решения в двух книгах). – Киев: Астарта, книга 2, 1995. – 512 с.

2. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.

3. Супрун В.П. Математика для старшеклассников: дополнительные разделы школьной программы. – М.: Ленанд / URSS, 2016. – 216 с.

 

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

   

   

blog.tutoronline.ru

В какой точке касательная к графику функции параллельна прямой

Острые углы прямоугольного треугольника равны 81 и 9 градусов.Найдите угол между высотой и биссектрисой , проведенными из вершины прямого угла.( если можно с полным объяснением). Попроси больше объяснений; Следить ? Отметить нарушение ? Юлия19210 14.03.2013. Войти чтобы добавить.

Совет 1: Как найти уравнение касательной к графику функции

Как найти уравнение касательной к графику функции Что такое парабола Как найти неизвестное уменьшаемое

Для начала дадим определение касательной. Касательной к кривой в данной точке М называется предельное положение секущей NM, когда точка N приближается вдоль кривой к точке М.

Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).

Координаты точки М (x; y), координаты точки N1(x+∆x; y+∆y).

Из полученного треугольника MN1N можно найти угловой коэффициент этой секущей:

Где (x0; y0) – координаты точки касания,

(x; y) – текущие координаты, т. е. координаты любой точки, принадлежащей касательной,

F`(x0) = k = tg α – угловой коэффициент касательной.

Совет 2: Как найти касательное уравнение

Для решения этой задачи воспользуйтесь алгоритмом составления уравнения. Но при этом учитывайте, что в данном примере дана функция f(x)=2-х-х3, а=0.

Совет 3: Как написать уравнение касательной

Kx1 + b = y1, kx2 + b = y2.

Решая эту систему двух линейных уравнений, получаем: kx2 — kx1 = y2 — y1. Таким образом, k = (y2 — y1)/(x2 — x1).

Y = 6*(x — 3) + 9 = 6x — 9.

Правильность этого уравнения легко проверить. График прямой y = 6x — 9 проходит через ту же точку (3;9), что и исходная парабола. Построив оба графика, вы сможете убедиться, что эта прямая действительно прилегает к параболе в этой точке.

Математика для школьников — уравнение касательной составить уравнение касательной

Совет 4: Как найти абсциссу точки касания

Совет 5: Как найти угловой коэффициент касательной

— математический справочник; — простой карандаш; — тетрадь; — транспортир; — циркуль; — ручка.

Касательная к графику функции

Совет 6: Как найти координаты точки касания

Совет 7: Как решать график функции и касательной

Совет 8: Как найти тангенс угла наклона касательной

В какой точке касательная к графику функции параллельна прямой

В какой точке касательная к графику функции параллельна прямой

В какой точке касательная проведенная к графику функции у=х^2-2х+1 параллельна прямой у=-4х-4

Попроси больше объяснений Следить Отметить нарушение

Snezhanna 22.11.2011

Ответы и объяснения

Уравнение касательной y=f'(x0)(x-x0)+f(x0)

Ищем производную f'(x)=(x^2-2x+1)’=2x-2

Угловые коэффициенты паралельных прямых равны k1=k2

В какой точке касательная к графику функции параллельна прямой

В какой точке касательная к графику функции параллельна прямой

В какой точке касательная проведенная к графику функции у=х^2-2х+1 параллельна прямой у=-4х-4

Попроси больше объяснений Следить Отметить нарушение

Snezhanna 22.11.2011

Ответы и объяснения

Уравнение касательной y=f'(x0)(x-x0)+f(x0)

Ищем производную f'(x)=(x^2-2x+1)’=2x-2

Угловые коэффициенты паралельных прямых равны k1=k2

poiskvstavropole.ru