Комплексного числа деление – Деление комплексных чисел | Математика

Деление комплексных чисел | Математика

Деление комплексных чисел определяется как действие, обратное умножению.

Определение

Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z , при умножении которого на z2 получается z1:

z=z1/z2, если z∙z2=z1 (z2≠0).

Для комплексных чисел, записанных в алгебраической форме:

   

и

   

   

На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю.

С помощью формулы правило деления комплексных  можно записать так:

   

   

Примеры.

Найти частное комплексных чисел:

   

   

   

   

Решение:

1) Чтобы выполнить деление комплексных чисел, записанных в алгебраической форме, и делимое, и делитель умножаем на число, комплексно-сопряженное делителю (вариант: и числитель, и знаменатель умножаем на число, сопряженное знаменателю):

   

Умножение комплексных чисел выполняем как умножение многочленов.

i² заменяем на -1.

   

 

   

   

 

   

 

   

   

 

Деление комплексных чисел, представленных в тригонометрической форме, будет рассмотрено позже.

www.matematika.uznateshe.ru

Деление комплексных чисел

Деление на число и деление заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.

Определение 1

Делением заданного комплексного числа $z=a+b\cdot i$ на некоторое действительное число $k\ne 0$ является комплексное число, которое определяется равенством \[\frac{z}{k} =\frac{a+b\cdot i}{k} =\frac{a}{k} +\frac{b}{k} \cdot i.\]

Пример 1

Выполнить деление заданных комплексных чисел на число $k=\sqrt{3} $:

1) $z_{1} =\sqrt{3} +\sqrt{3} \cdot i$; 2) $z_{2} =5-4\cdot i$; 3) $z_{3} =\sqrt{3} \cdot i$.

Решение:

Для деления заданных комплексных чисел на действительное число воспользуемся определением и получим:

1) $\frac{z_{1} }{k} =\frac{z_{1} }{\sqrt{3} } =\frac{\sqrt{3} +\sqrt{3} \cdot i}{\sqrt{3} } =\frac{\sqrt{3} }{\sqrt{3} } +\frac{\sqrt{3} }{\sqrt{3} } \cdot i=1+1\cdot i$;

2) $\frac{z_{2} }{k} =\frac{z_{2} }{\sqrt{3} } =\frac{5-4\cdot i}{\sqrt{3} } =\frac{5}{\sqrt{3} } -\frac{4}{\sqrt{3} } \cdot i$;

3) $\frac{z_{3} }{k} =\frac{z_{3} }{\sqrt{3} } =\frac{0+\sqrt{3} \cdot i}{\sqrt{3} } =\frac{0}{\sqrt{3} } +\frac{\sqrt{3} }{\sqrt{3} } \cdot i=0+1\cdot i=i$.

Примечание 1

При делении заданного комплексного числа $z=a+b\cdot i$ на действительное число $k\, \, (|k|>1)$ модуль этого числа уменьшается в $|k|$ раз:

\[\left|\frac{z}{k} \right|=\frac{\sqrt{a^{2} +b^{2} } }{|k|} .\]

Примечание 2

При умножении заданного комплексного числа $z=a+b\cdot i$ на действительное число $k\, \, (|k|

\[\left|\frac{z}{k} \right|=\left|\frac{1}{k} \right|\cdot \sqrt{a^{2} +b^{2} } .\]

Примечание 3

Графическая интерпретация операции деления заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, уменьшается в $|k|$ раз (радиус-вектор становится короче в $|k|$ раз).

Примечание 4

Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|

Иллюстрация примера деления заданного комплексного числа $z=a+b\cdot i$ на число $k_{1} =2,\, \, k_{2} =\frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.

Рис. 1

Рис. 2

Определение 2

Частным двух заданных комплексных чисел в тригонометрической форме представления $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ ($r_{2} \ne 0$) является комплексное число, которое определяется равенством

\[z_{1} \cdot z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )].\]

Пример 2

Выполнить деление заданных комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )$ и $z_{2} =2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )$; 2) $z_{1} =4\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$.

Решение:

Для деления заданных комплексных чисел воспользуемся определением и получим:

1) \[\begin{array}{l} {\frac{z_{1} }{z_{2} } =\left(\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )\right)\div \left(2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )\right)=\frac{\sqrt{3} }{2} \cdot [\cos (\frac{\pi }{4} -\frac{2\pi }{3} )+i\cdot \sin (\frac{\pi }{4} -\frac{2\pi }{3} )]=} \\ {=\frac{\sqrt{3} }{2} \cdot (\cos \left(-\frac{5\pi }{12} \right)+i\cdot \sin \left(-\frac{5\pi }{12} \right))} \end{array}\] 2) \[\begin{array}{l} {\frac{z_{1} }{z_{2} } =\left(4\cdot (\cos \pi +i\cdot \sin \pi )\right)\div \left(5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)=\frac{4}{5} \cdot [\cos (\pi -\frac{\pi }{2} )+i\cdot \sin (\pi -\frac{\pi }{2} )]=} \\ {=\frac{4}{5} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )} \end{array}\]

Определение 3

Частным двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ ($r_{2} =\sqrt{a_{2}^{2} +b_{2}^{2} } \ne 0)$ является комплексное число, которое определяется равенством

\[\frac{z_{1} }{z_{2} } =\frac{a_{1} +b_{1} i}{a_{2} +b_{2} i} =\frac{a_{1} a_{2} +b_{1} b_{2} }{a_{2}^{2} +b_{2}^{2} } +\frac{a_{2} b_{1} -a_{1} b_{2} }{a_{2}^{2} +b_{2}^{2} } \cdot i.\]

Равенство, указанное в определении 3, достаточно сложно для запоминания, поэтому на практике при делении заданных комплексных чисел, представленных в алгебраической форме, используют алгоритм, который описан в примечании 5.

Примечание 5

Чтобы выполнить операцию деления заданных комплексных чисел, представленных в алгебраической форме необходимо:

• представить запись операции деления в виде дроби;
• числитель дроби и знаменатель дроби умножить на число сопряженное знаменателю;
• привести полученное выражение к алгебраической записи.

Пример 3

Выполнить деление комплексных чисел:

1) $z_{1} =3+i$ и $z_{2} =2-i$; 2) $z_{1} =3+2i$ и $z_{2} =1+2i$.

Решение:

Для деления комплексных чисел воспользуемся алгоритмом, приведенным в примечании 5, и получим:

1) \[\frac{z_{1} }{z_{2} } =\frac{3+i}{2-i} =\frac{(3+i)(2+i)}{(2-i)(2+i)} =\frac{6+2i+3i+i^{2} }{2^{2} -i^{2} } =\frac{6+5i-1}{4+1} =\frac{5+5i}{5} =1+i\] 2)\[\frac{z_{1} }{z_{2} } =\frac{3+2i}{1+2i} =\frac{(3+2i)(1-2i)}{(1+2i)(1-2i)} =\frac{3+2i-6i-4i^{2} }{1^{2} -2^{2} \cdot i^{2} } =\frac{3-5i+4}{1+4} =\frac{7-5i}{5} =\frac{7}{5} -1\cdot i=\frac{7}{5} -i\]

Определение 4

Частным двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} \cdot e^{i\varphi _{1} } $ и $z_{2} =r_{2} \cdot e^{i\varphi _{2} } $ является комплексное число, которое определяется равенством

\[\frac{z_{1} }{z_{2} } =\frac{r_{1} \cdot e^{i\varphi _{1} } }{r_{2} \cdot e^{i\varphi _{2} } } =\frac{r_{1} }{r_{2} } \cdot e^{i(\varphi _{1} -\varphi _{2} )} .\]

Пример 4

Выполнить деление комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{3} } $; 2) $z_{1} =\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{2} } $.

Решение:

Для деления комплексных чисел воспользуемся определением и получим:

1) \[\frac{z_{1} }{z_{2} } =\left(\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } \right)\div \left(2\cdot e^{i\cdot \frac{\pi }{3} } \right)=\frac{\sqrt{3} }{2} \cdot e^{i\cdot (\frac{\pi }{4} -\frac{\pi }{3} )} =\frac{\sqrt{3} }{2} \cdot e^{i\cdot \left(-\frac{\pi }{12} \right)} \] 2) \[\frac{z_{1} }{z_{2} } =\left(\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } \right)\div \left(2\cdot e^{i\cdot \frac{\pi }{2} } \right)=\frac{\sqrt{5} }{2} \cdot e^{i\cdot (\frac{2\pi }{3} -\frac{\pi }{2} )} =\frac{\sqrt{5} }{2} \cdot e^{i\cdot \frac{\pi }{6} } \]

spravochnick.ru

Деление комплексных чисел в тригонометрической форме записи » Аналитическая геометрия f(x)dx.Ru

п.1.Формула Муавра.

Теорема. (Формула Муавра, 1707 г.)

Для любого целого числа n и любого действительного числа  имеет место следующее равенство:

             .                     (1)

   Доказательство. Разобьем доказательство на 3 этапа.

1) Пусть  – натуральное число. Так как комплексное число  имеет модуль , то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.

2) Пусть теперь . Тогда

, ч.т.д.

3) Пусть , где  – натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в поле комплексных чисел, имеем:

.

   Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).

Теорема доказана.

Следствие. (О целых степенях комплексного числа.)

Пусть . Тогда

               .

Доказательство предоставляется читателю.

п.2. Деление комплексных чисел в тригонометрической форме записи.

Теорема. (О делении комплексных чисел в тригонометрической форме)

Пусть , где  и , где  – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

             .                (2)

   Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:

 

, ч.т.д.

Пример 1. Запишите комплексные числа  и  в тригонометрической форме и найдите их произведение  и частное .

Решение. 1) Комплексное число  на комплексной плоскости находится во второй четверти, поэтому

, .

2) Комплексное число  на комплексной плоскости находится во четвертой четверти, поэтому

, .

3)

.

Ответ: , .

Пример 2. Вычислить .

Решение. Комплексное число  на комплексной плоскости находится в третьей четверти, поэтому ,

Применим формулу Муавра:

.

Возможно найдутся ответы здесь:

fxdx.ru

1 Вопрос. Комплексные числа. Определение комплексного числа. Свойства операций над комплексными числами.

Комплексным числом  называется число вида , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью () комплексного числа , число  называется мнимой частью () комплексного числа .

Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой  принято обозначать множество действительных чисел.Множество же 

комплексных чисел принято обозначать «жирной» или утолщенной буквой. Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

Сложение комплексных чисел

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

z₁ + z₂ = (a₁ + a₂) + i*(b₁ + b₂).

Для комплексных чисел справедливо правило первого класса: z₁ + z₂ = z₂ + z₁ – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

z₁ + z₂ = (a₁ – a₂) + i*(b₁ – b₂)

Умножение комплексных чисел

Основное равенство комплексных чисел:

Произведение комплексных чисел:

z₁ * z₂ = (a₁ + i*b₁)*(a₂ + i*b₂) = a₁*a₂ + a₁*i*b₂ + a₂*i*b₁ + i²*b₁*b₂ = a₁*a₂ — b₁*b₂ +i*(a₁*b₂ +a₂*b₁).

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

Деление комплексных чисел

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

2 Вопрос. Комплексная плоскость. Модуль и аргументы комплексных чисел

Каждому комплексному числу z = a + i*b  можно сопоставить точку с координатами (a;b) , и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + i*d . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют 

комплексной плоскостью.

Однако чаще комплексные числа изображают в виде вектора с началом в точке О , а именно, комплексное число z = a + i*b изображается радиус-вектором точки с координатами (a;b) . В этом случае изображение комплексных чисел из предыдущего примера будет таким:

Изображением суммы двух комплексных чисел , является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие.

Пусть комплексное число z = a + i*b  изображается радиус-вектором. Тогда длина этого вектора называется модулем числа z и обозначается |z| .

Угол, образованный радиус-вектором числа с осью, называетсяаргументом числа и обозначаетсяarg z . Аргумент числа определяется не однозначно, а с точностью до числа, кратного . Однако, обычно аргумент указывают в диапазоне от 0 доили в диапазоне от  -до. Кроме того у числааргумент не определен.

С помощью этого соотношения можно находить аргумент комплексного числа:

или

(17.7)

причем первая формула действует, если изображение числа находится в первой или четвертой четверти, а вторая, если — во второй или третьей. Если , то комплексное число изображается вектором на оси Oy и его аргумент равен /2или  3*/2.

Получим еще одну полезную формулу. Пусть z = a + i*b . Тогда ,

или .

studfiles.net

Деление комплексных чисел

Поиск Лекций

---

Пример 4:

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример подобран «хороший», если взять два произвольных числа, то в результате деления почти всегда получатся дроби, что-нибудь вроде .

 

Примеры решения задач

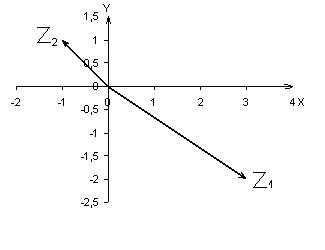
1) Построить на координатной плоскости числа Z₁ , Z₂, где Z₁=3-2i, Z₂=-1+i.

 

Решение

На координатной плоскости изобразим точки (3; -2), (-1; 1) и соединим их с началом

координат, получив векторы, конечными точками которых являются заданные точки.

2) Выполнить действия сложения, вычитания, умножения, деления над комплексными числами в алгебраической форме.

Z₁=3+4i, Z₂=2i¹⁸-5i¹⁵

Решение

Предварительно преобразуем второе число, используя значения степеней мнимой единицы. i¹⁸=i¹⁶⁺²=i¹⁶i²=1i²=-1, i¹⁵=i¹²⁺³=i¹²i³=i³=-i, Z₂=-2+5i

Выполним действия над числами:

Z₁+Z₂=(3+4i)+(-2+5i)=3+4i-2+5i=(3-2)+(4i+5i)=1+9i

Z₁-Z₂=(3+4i)-(-2+5i)=3+4i+2-5i=(3+2)+(4i-5i)=5-I

Z₁ ^.Z₂=(3+4i) ^. (-2+5i)=-6+15i – 8i +20i²=-6+7i – 20= — 26 + 7i

3) Представить число в тригонометрической форме Z=

Найдем модуль и аргумент комплексного числа

 

Раздел 4. Элементы теории вероятностей и математической статистики

Изучить по учебной литературе вопросы:

1. Случайные события, их виды. Вероятность случайного события, способы ее получения.

2. Комбинаторика. Применение элементов комбинаторики к вычислению вероятности.

3. Действия над случайными событиями, вычисление вероятностей результатов действий.

4. Случайные величины, их виды. Закон распределения случайной величины

5. Ряд и функция распределения дискретной случайной величины.

6. Математическое ожидание дискретной случайной величины.

7. Дисперсия дискретной случайной величины.

Случайные события и их вероятности.

Математическая статистика.

Применение комбинаторики к подсчету вероятности.

Пример 1:

В партии из N

деталей имеется n бракованных. Какова вероятность того, что среди наудачу отобранных k деталей окажется s бракованных?

Решение.

Количество всех элементарных исходов равно . Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей способами, а из N – nнебракованных можно выбрать

k – s небракованных деталей способами; по правилу произведения число благоприятных случаев равно . Искомая вероятность равна:

p = (1)

 

Замечание:

Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.

Число различных сочетаний из n элементов по k обозначается .

Справедлива формула

= , (2)

n! =1 2 3 4 … n

 

Пример 2:

В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.

Решение.

Искомую вероятность найдем по формуле (1) для случая

N =12, n =7, k = 6, s = 4.

p = = = = .

Пример 3:

Имеется набор разноцветных шариков, среди которых 5 синих, 3 красных и 2 зеленых. Наугад извлекают 4 шарика. Найти вероятность того, что среди извлеченных шариков 2 синих, 1 красный и 1 зеленый.

Решение

Для определения вероятности случайного события будем использовать классическую формулу , в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний.

Пример 4:

Из карточек разрезной азбуки составлено слово «панорама». Карточки перемешали и наудачу по одной извлекают 5 карточек, выкладывая их в порядке извлечения. Найти вероятность того, что окажется составленным слово «роман».

 

Решение

В этой задаче можно воспользоваться произведением зависимых случайных событий

А – получение слова «роман»; В₁ – извлечение первой карточки с буквой «р»;

В₂ – извлечение второй карточки с буквой «о»; и т.д. Тогда А=В₁ ^. В₂^. В₃^. В₄^. В₅

Р(А)=Р(В₁) ^. Р(В₂) ^. Р(В₃) ^. Р(В₄) ^. Р(В₅)=

 

Пример 5:

В трех ящиках имеется по 6 одинаковых изделий, среди которых соответственно 2,

1, 3 бракованных. Наугад из каждого ящика извлекают по одному изделию. Найти вероятность того, что среди них окажутся два качественных и одно бракованное изделия.

Решение

Для решения задачи рассмотрим события: А – извлечение двух качественных и одного бракованного изделий, В₁ – извлечение качественного изделия из первого ящика;

В₂ – извлечение качественного изделия из второго ящика; В₃– извлечение качественного изделия из третьего ящика; извлечение бракованного изделия для каждого ящика является событиями Составим событие А и вычислим его вероятность

 

Пример 6:

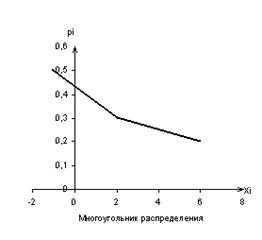
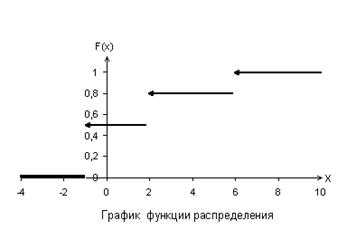
Вычислить математическое ожидание и дисперсию случайной величины, составить функцию распределения, начертить многоугольник распределения и график функции распределения. Имеется заданный ряд распределения дискретной случайной величины

 

 

Для вычисления математического ожидания воспользуемся формулой

Получим M(X)=(-1)^.0,5+2^.0,3+6^.0,2=1,3

Для вычисления дисперсии воспользуемся двумя соотношениями, одно из которых соответствует определению дисперсии, другое – ее свойству.

В примере получим: D(X)=(-1-1,3)^2. 0,5+(2-1,3)^2. 0,3+(6-1,3)^2. 0,2=7,21

M(X²)=(-1)^2. 0,5+2^2. 0,3+6^2. 0,2=8,9

D(X)= 8,9 – 1,3² =7,21 (значения должны совпадать)

Для построения многоугольника распределения нужно на координатной плоскости построить точки (x_i ;p_i) и последовательно их соединить отрезками.

Для построения функции распределения воспользуемся схемой:

В примере получим

Используя значения заданного примера получим графики:

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

Деление комплексных чисел | Математика

Деление комплексных чисел

Скачать или посмотреть оригинал
«АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Глава 16. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ» в формате PDF (323-341).

Ниже можете посмотреть текст для быстрого ознакомления (в них формулы отображаются не корректно). Эти тексты и форма поиска справа в колонке помогут Вам быстрее найти нужную информацию на этом сайте, а форма поиска ниже — по всему Интернету.

Двуличная сучность Ксении Собчак.

§ 196. Деление комплексных чисел.

Частным от деления двух комплексных чисел
а-\-Ы и а х-\-Ь]1 называется такое комплексное число
x — j- y i, которое, будучи умножено на делитель, дает в произведении
делимое (по определению действия деления).
Таким образом, если одновременно коэффициенты а х и Ьх
не равны нулю, то, полагая и —b■ i . = х 4- ~yt,, имеем

348 АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Деление комплексных чисел.

Проще этот результат можно получить умножением делимого
и делителя на сопряженное делителю число:

Этим правилом деления и будем руководствоваться
в дальнейшем.
Примеры.

349 АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Деление комплексных чисел.

§ 197. Степени мнимой единицы.

Пользуясь равенством /2 = — 1, легко определить любую
целую положительную степень мнимой единицы. Имеем:
/3 = /2 . г==_ 1 . /==_/; -‘Ц = р . г2= J. ;5 _ Ц . t _
/6==/4 -/2 — — 1; /7‘= — /; /8= 1 и т. д.
Это показывает, что значения степени /”, где п — целое
положительное число, периодически повторяются при увеличении
показателя на 4. Поэтому, чтобы возвести число /
в целую положительную степень, надо показатель степени
разделить на 4 и возвести / в степень, показатель которой
равен остатку от деления.
Примеры.

350 АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Деление комплексных чисел.

§ 198. Возведение в степень комплексного числа.

Возведение комплексного числа в целую положительную
степень производится по правилу возведения двучлена в соответствующую
степень, так как оно представляет собой частный
случай умножения одинаковых комплексных множителей.
Примеры .

§ 199. Извлечение квадратного корня
из комплексного числа

Пусть требуется извлечь квадратный корень из числа
a-\-bL Это значит, требуетея найти такое комплексное число
x — j- y f , квадрат которого равен а-\-Ы. Имеем

Уравнение 2ху — Ъ показывает, что произведете ху
имеет тот же знак, какой имеет число Ь. Следовательно,
если Ь > 0, то х а у имеют одинаковые знаки, если b < О,
то х и у имеют разные знаки. Поэтому для Ъ 0 имеем

В § 206 будет показан более удобный способ извлечения
корня из комплексного числа.

351 АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. Деление комплексных чисел.

Деление комплексных чисел

matematika.advandcash.biz

No related posts.