8. Численное решение задачи Коши для дифференциальных уравнений.
Постановка задачи Коши
Рассмотрим обыкновенное дифференциальное уравнение первого порядка: . (1.1)
Основная
задача, связанная с этим уравнением –
задача Коши состоит в следующем: найти
решение уравнения (1.1) в виде функции 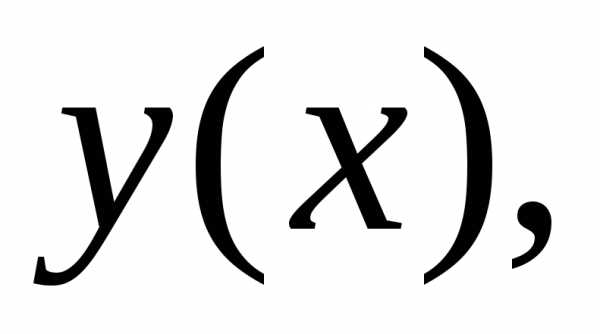 удовлетворяющей начальному условию:.
(1.2)
удовлетворяющей начальному условию:.
(1.2)
Геометрически это означает, что требуется найти интегральную кривую проходящую через заданную точкупри выполнения равенства (1.1). Существование и единственность решения уравнения (1.1) обеспечивается следующей теоремой.
Теорема Пикара: Если функция f определена и непрерывна в некоторой области
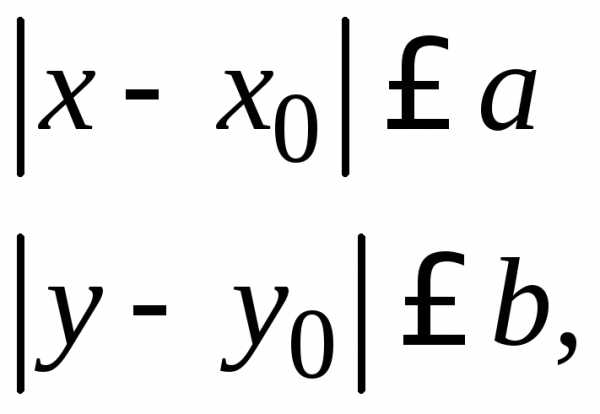 (1.3)
(1.3)
и удовлетворяет в этой области условию Липшица по у: , то на некотором отрезке, гдеh – положительное число, существует, и притом только одно, решение уравнения (1.1), удовлетворяющее начальному условию.
Здесь М – постоянная (константа Липшица), зависящая в общем случае от а и b.
Если f(x, y) имеет ограниченную в G производную 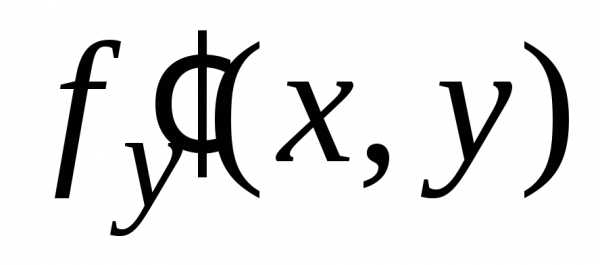 ,
то приможно принять.
,
то приможно принять.
В классическом анализе разработаны методы нахождения решений дифференциальных уравнений через элементарные (или специальные) функции. На практике эти методы очень часто оказываются либо совсем беспомощными, либо их использование требует трудных вычислений и времени.
Для
решения практических задач созданы
методы приближённого решения
дифференциальных уравнений. Пусть
требуется на отрезке  [х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2).
[х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2).
Разобьём отрезок на п равных частей точками: , где .
Численное
решение дифференциального уравнения
(1.1) заключается в том, что значение
искомой функции  вычисляется
в каждой точке
вычисляется
в каждой точке 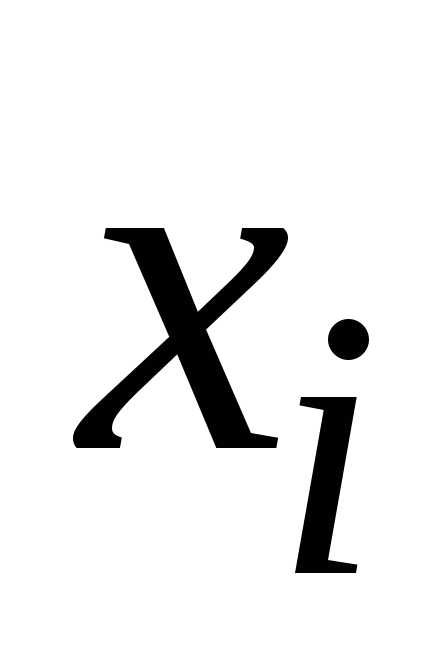 .
При этом, как правило, для вычисления
значения
.
При этом, как правило, для вычисления
значения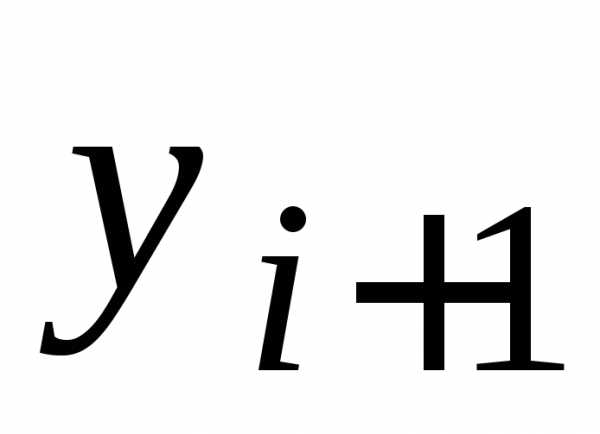 используется уже вычисленное значение
используется уже вычисленное значение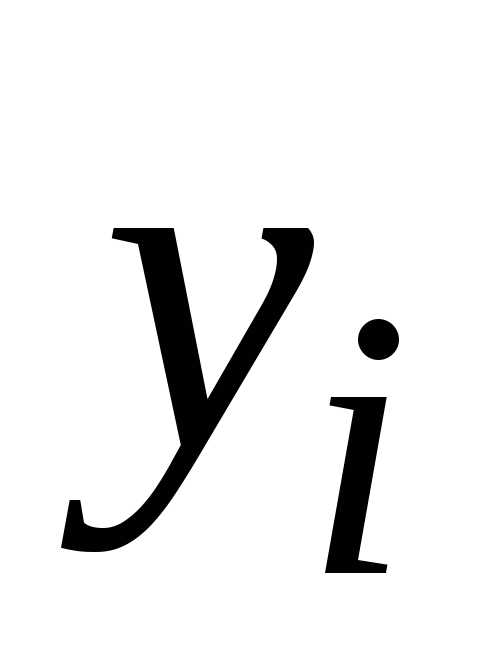
Для решения задачи Коши для обыкновенных дифференциальных уравнений существуют различные методы:
1. Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.
2. Графические методы, дающие приближенное решение в виде графиков.
3. Численные методы (табличные), при использовании которых искомая функция получается в виде таблицы.
Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений первого порядка вида (1.1).
Метод последовательных приближений
Рассмотрим задачу Коши для дифференциального уравнения первого порядка с начальным условием.
Метод
последовательных приближений состоит
в том, что решение 
 ,
которые находятся по рекурсивной формуле
,
которые находятся по рекурсивной формуле. (1.4)
Если
правая часть 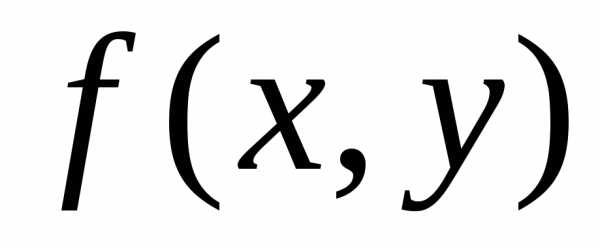 в некотором замкнутом прямоугольнике
в некотором замкнутом прямоугольнике ,
содержащем множество точек
,
содержащем множество точек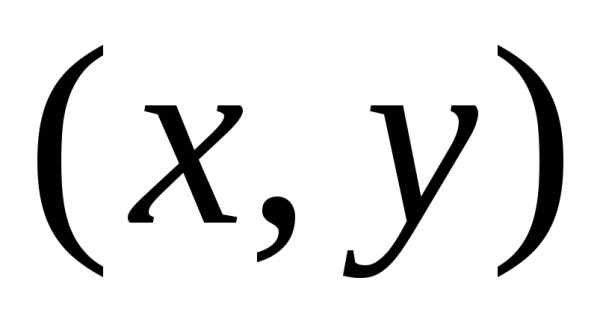 ,
для которых выполняются условияудовлетворяет условию Липшица по
,
для которых выполняются условияудовлетворяет условию Липшица по :
:
,
то
независимо от выбора начальной функции
последовательные приближения 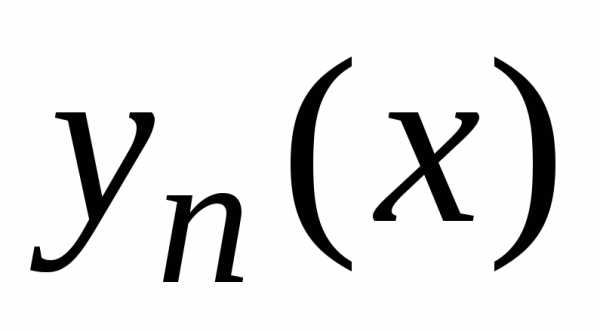
Если 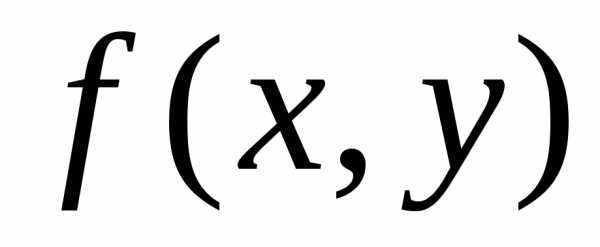 непрерывна в области
непрерывна в области ,
то оценка погрешности приближенного
решения
,
то оценка погрешности приближенного
решения 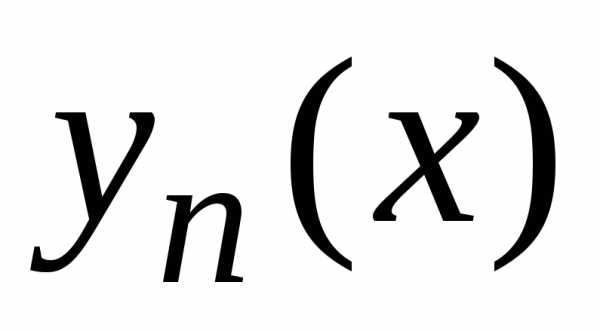 на отрезке дается неравенством:
на отрезке дается неравенством:
, (1.5)
где
,
а число 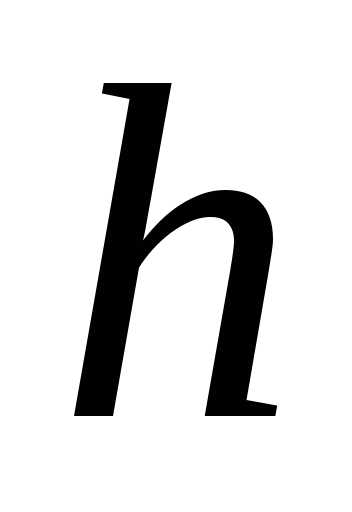 определяется из условия:
определяется из условия:
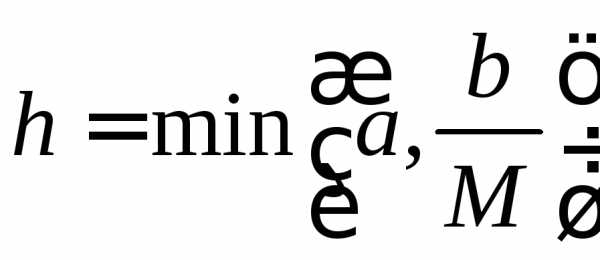 .
.
Метод Эйлера
Рассмотрим дифференциальное уравнение с начальным условием.
Выбрав
достаточно малый шаг 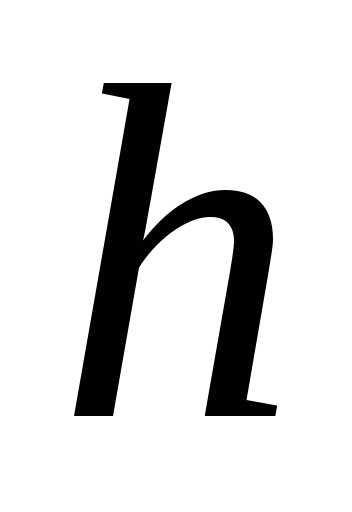
Приближенные значения по методу Эйлера вычисляются последовательно по формулам:
()
При оценке погрешности обычно используется двойной пересчет.
Если 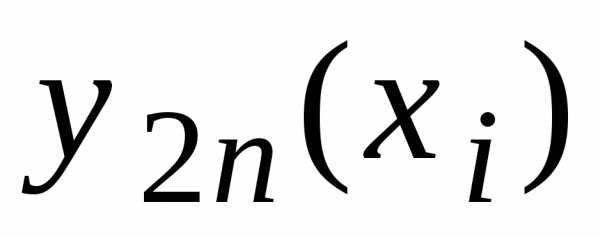 – вычисленное значение
– вычисленное значение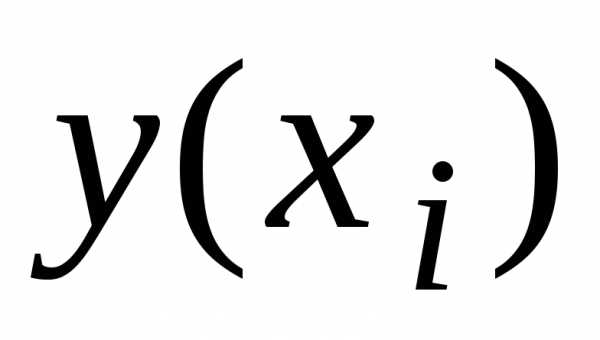 с шагом
с шагом ,
а
,
а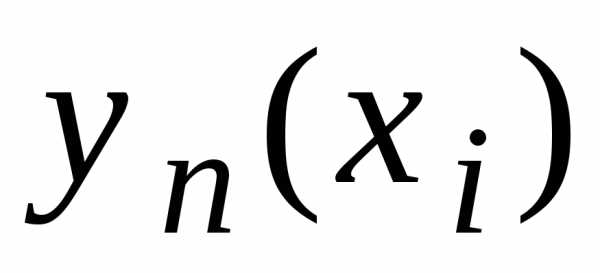 – соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:
– соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:
Метод
Эйлера–
Метод Эйлера–Коши является модификацией метода Эйлера. Вычисления табличных значений решения и оценка погрешности проводятся по следующим формулам.
,
,
,
где 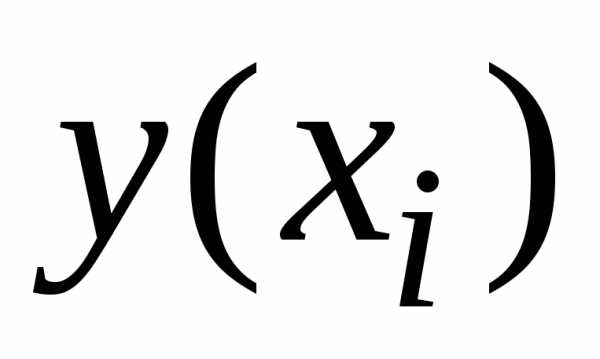 – точное
значение решения в узле
– точное
значение решения в узле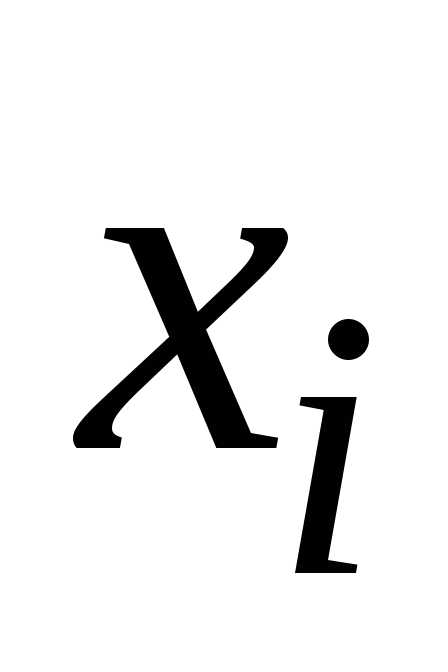 ,
,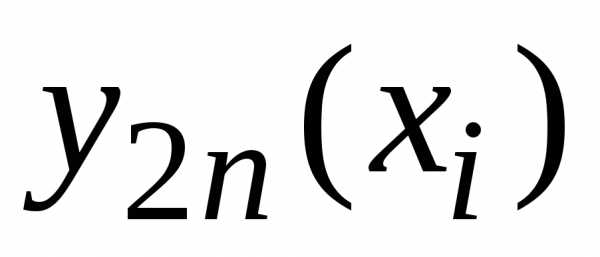 ,
,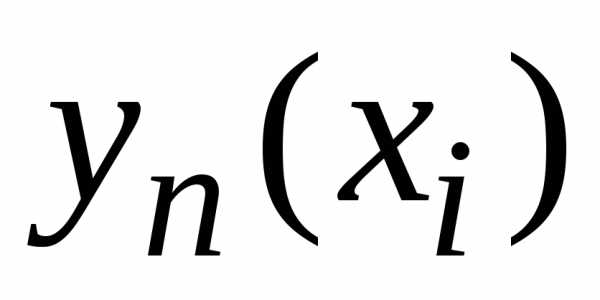 –
приближенные значения решения в узле
–
приближенные значения решения в узле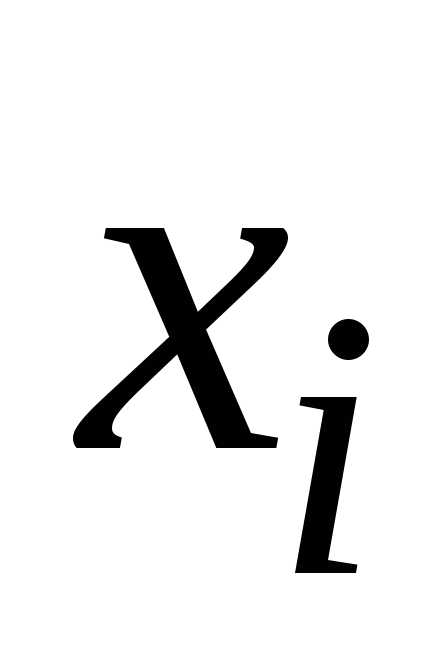 с шагом
с шагом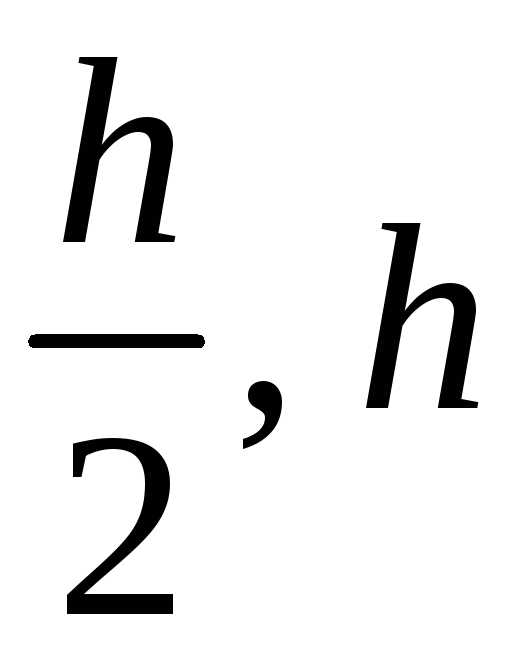 – соответственно.
– соответственно.
Метод Рунге–Кутта четвертого порядка
Рассмотрим метод Рунге–Кутта четвёртого порядка для нахождения численного решения уравнения (1.1) с начальным условием (1.2).
Пусть
является начальным условием (при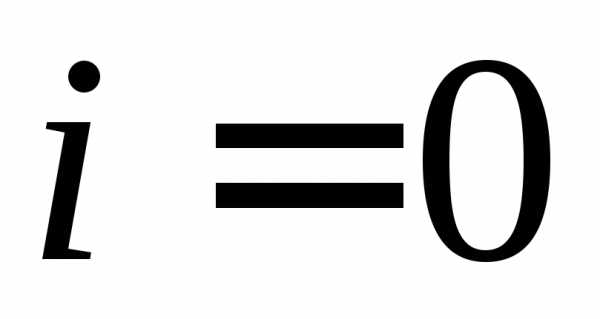 ),
либо получено как результат предыдущего
шага. Для получения следующего значения
),
либо получено как результат предыдущего
шага. Для получения следующего значения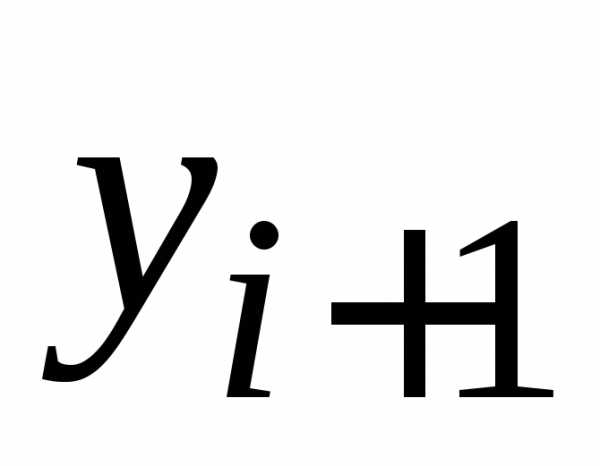 вначале вычисляются числа:
вначале вычисляются числа:
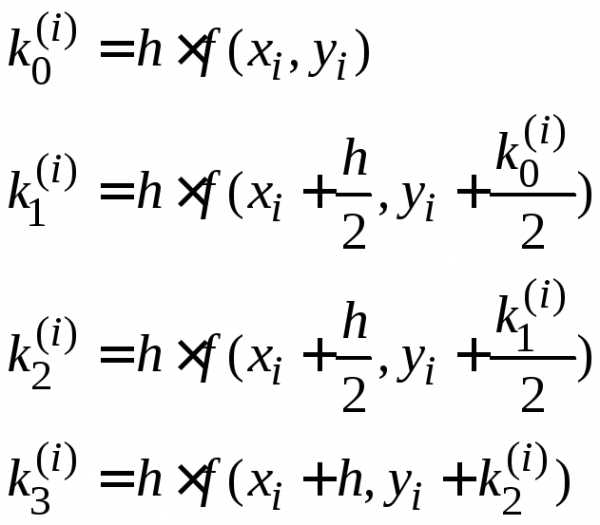 ,
(1.6)
,
(1.6)
где h – шаг интегрирования.
Затем вычисляют: .
Новое значение функции вычисляется по формуле:
. (1.7)
Метод Рунге–Кутта четвертого порядка является методом повышенной точности. На практике для контроля точности этого метода используется двойной счет пересчет.
Если 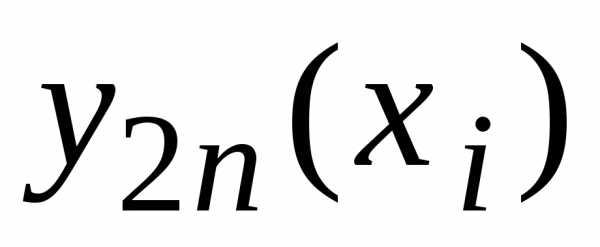 –
вычисленное значение
–
вычисленное значение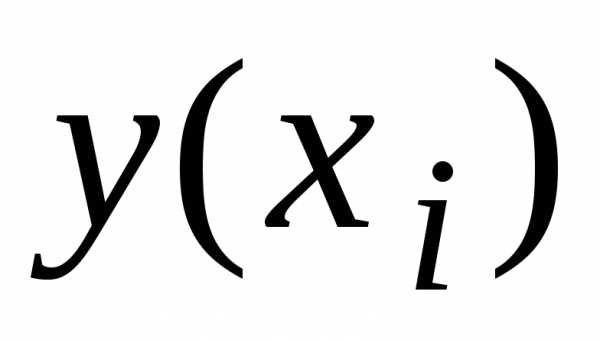 с
шагом
с
шагом ,
а
,
а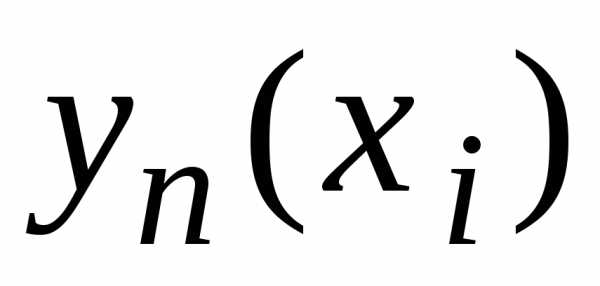 –
соответствующее узловое значение,
полученное с шагомh,
–
соответствующее узловое значение,
полученное с шагомh,
то
для приближенной оценки погрешности
значения 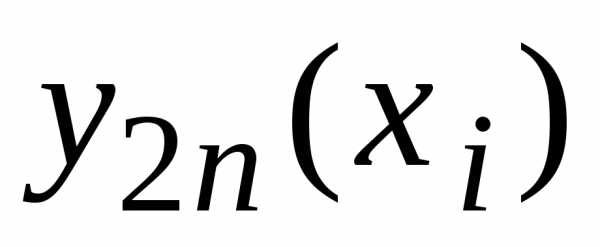 можно использовать формулу:
можно использовать формулу:
Многошаговые методы. Метод Адамса. Методы прогноза–коррекции
В
многошаговых методах для вычисления 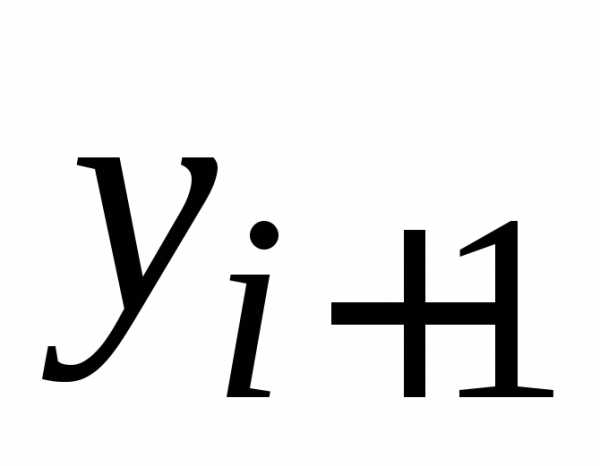 требуется не одно предыдущее значение
требуется не одно предыдущее значение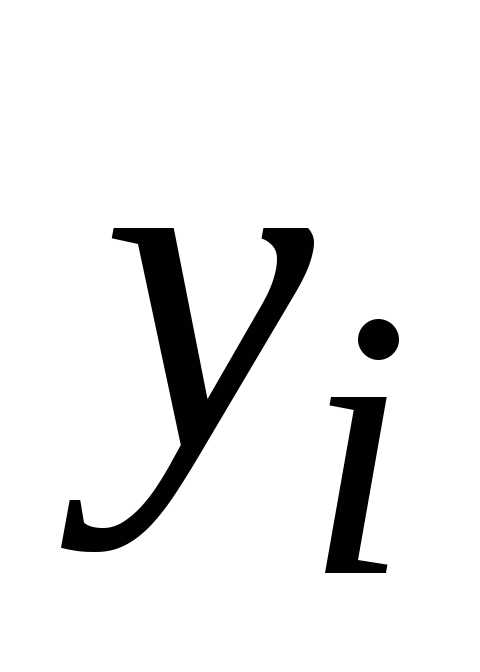
Метод
Адамса является примером многошаговых
методов решения обыкновенных
дифференциальных уравнений. Простейший
случай метода Адамса получается при 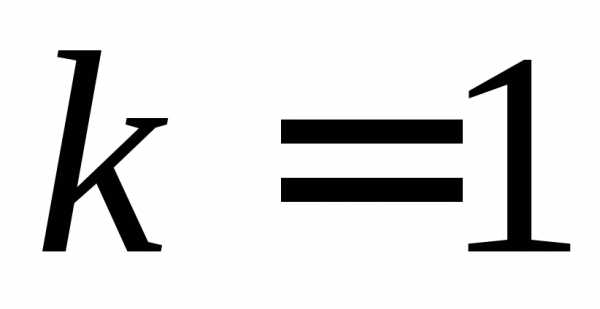 и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.
и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.
Пусть
вычислены значения в четырех последовательных узлах
.
Формула для вычисления значения 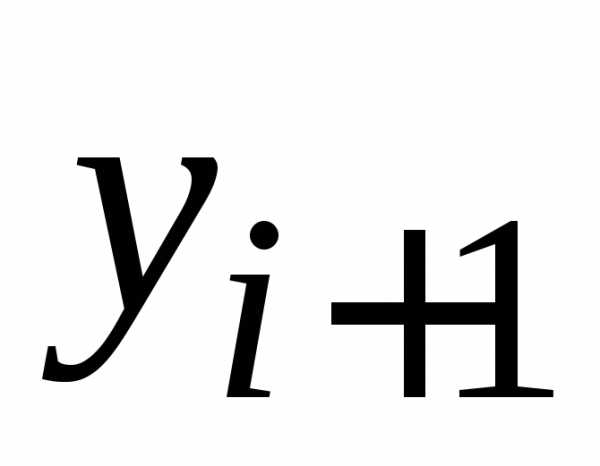 по методу Адамса имеет вид:
по методу Адамса имеет вид:
. (1.8)
Первые четыре значения для начала вычисления значений решения по методу Адамса получаются любым другим методом соответствующей точности, например, методом Рунге-Кутта четвертого порядка.
Сравнивая
метод Адамса с методом Рунге-Кутта той
же точности, следует отметить его
экономичность, так как он требует при
вычислении лишь одного значения правой
части на каждом шаге, а метод Рунге–Кутта
– четырех. Но метод Адамса неудобен
тем, что невозможно начать счет только
по известному значению 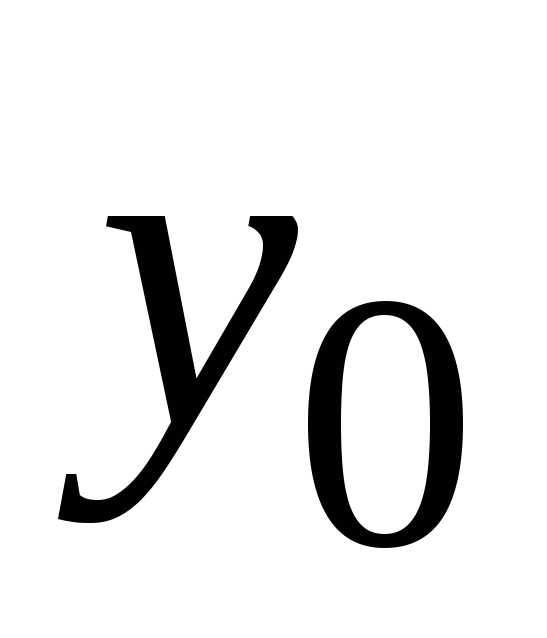 ,
надо вычислить еще
,
надо вычислить еще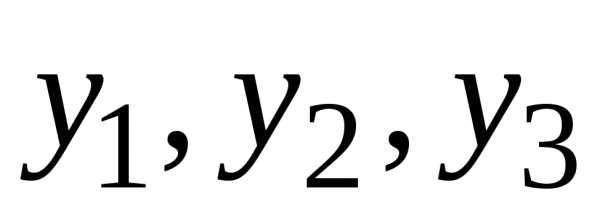 каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh в процессе
счета.
каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh в процессе
счета.
Существует еще одно семейство многошаговых методов, которые используют неявные схемы, — методы прогноза и коррекции. Суть этих методов состоит в следующем.
На каждом шаге вводятся два этапа, использующих многошаговые методы:
1)
с помощью явного метода (прогноза) по
известным значениям функции в предыдущих
узлах находятся начальное приближение 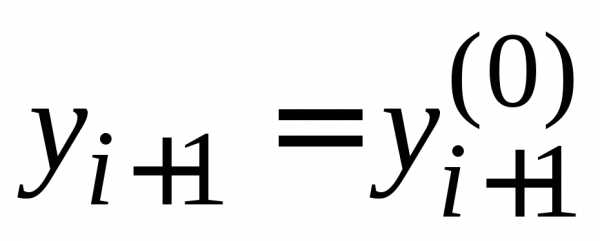 в новом узле;
в новом узле;
2)
используя неявный метод (корректор), в
результате итераций находятся приближения 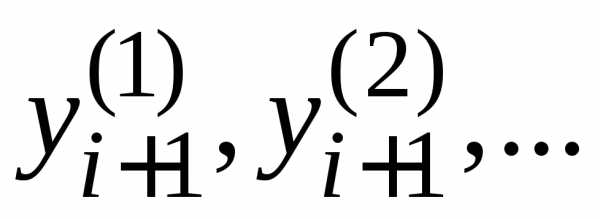
Один из вариантов метода прогноза и коррекции может быть получен на основе метода Адамса четвертого порядка. Для этого используются следующие расчетные формулы.
На этапе прогноза используется рассмотренная выше формула (1.8), а на этапе коррекции:
(1.9)
Явная
схема (1.8) используется на каждом шаге
один раз, а с помощью неявной схемы (1.9)
строится итерационный процесс вычисления 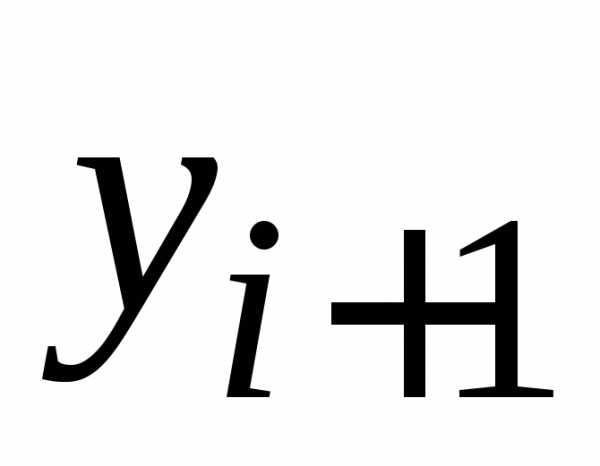 .
.
Итерации можно прекратить, если две последовательные итерации дают практически одинаковые результаты. На практике, если метод k -шаговый, то итераций должно быть не более k. Дальнейшее увеличение числа итераций порядок точности не увеличивает. Если точность мала, то надо менять шаг, что в многошаговых методах затруднительно.
Постановка краевой задачи для обыкновенного дифференциального уравнения
Пусть дано дифференциальное уравнение второго порядка
(1.10) |
Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.
Найти
функцию 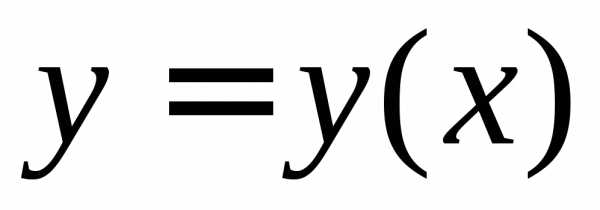 ,
которая внутри отрезка
,
которая внутри отрезка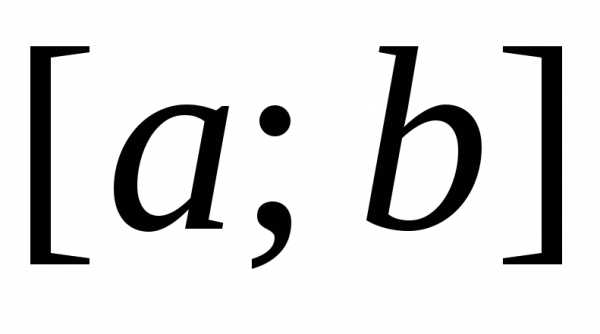 удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:
где
–
известные непрерывные на отрезке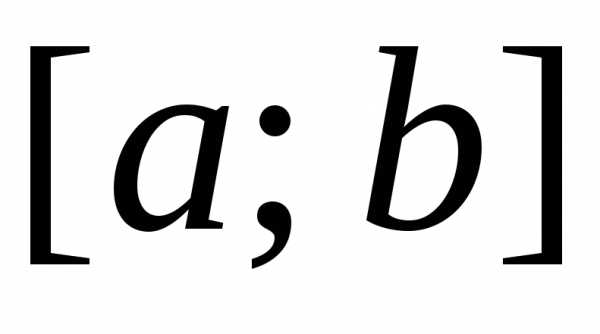 функции,–
заданные постоянные, причеми.
функции,–
заданные постоянные, причеми.
Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей
Данный метод заключается в следующем.
Разбиваем
отрезок 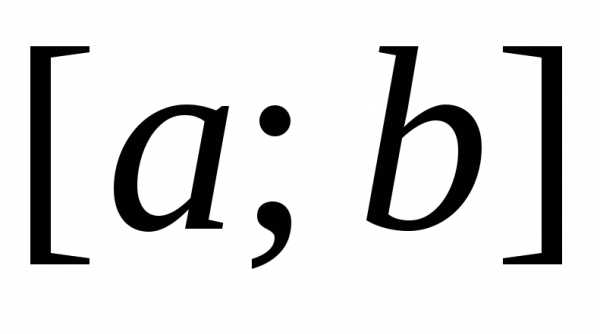 наn равных частей с шагом
наn равных частей с шагом 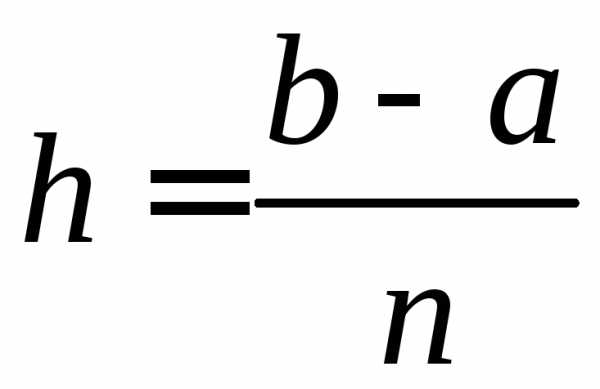 и получаем точки,
в которых требуется найти искомые
значения.
и получаем точки,
в которых требуется найти искомые
значения.
Введем обозначения:
Заменим приближенно в каждом внутреннем узле производные конечно-разностными схемами:
| (1.14) |
а на концах отрезка положим:
| (1.15) |
Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:
(1.16) |
Получим линейную алгебраическую систему, содержащую n+1 уравнение с n+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.
Более точные формулы получаются, если заменить центрально-разностными отношениями:
| (1.17) |
а на концах отрезка положить:
| (1.18) |
Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:
(1.19) |
Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.
Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.
Запишем уравнения системы (1.14) в виде:
,
где
(1.23) |
Полученную систему приводим к виду:
(1.24) |
Числа 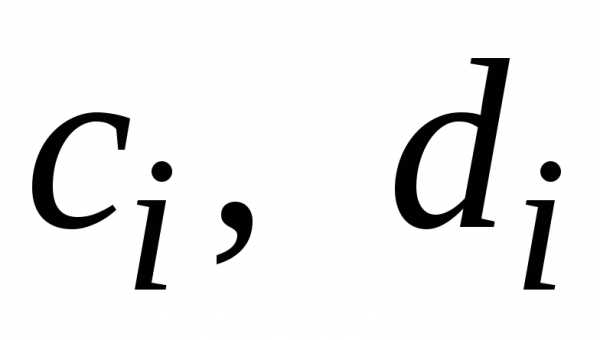 последовательно вычисляются по формулам:
последовательно вычисляются по формулам:
при 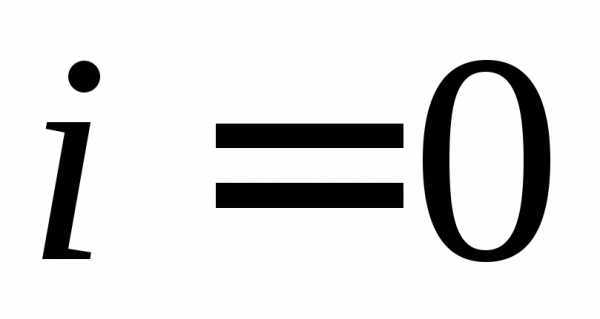
(1.25) |
При
| (1.26) |
Вычисления производятся в следующем порядке.
Прямой
ход. По
формулам (1.23) вычисляем значения 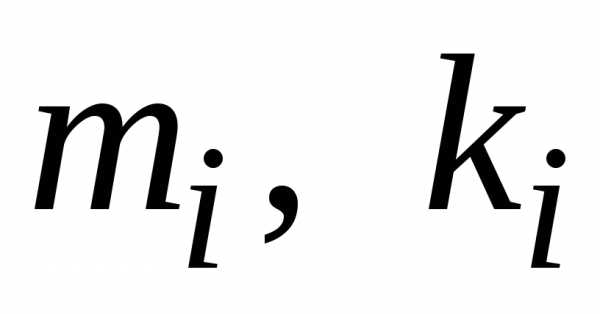 .
Находим
.
Находим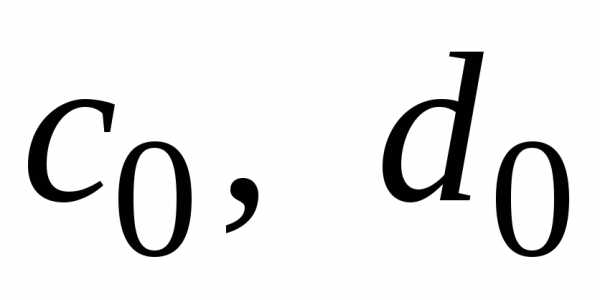 по формулам (1.25). Затем вычисляем
по формулам (1.25). Затем вычисляем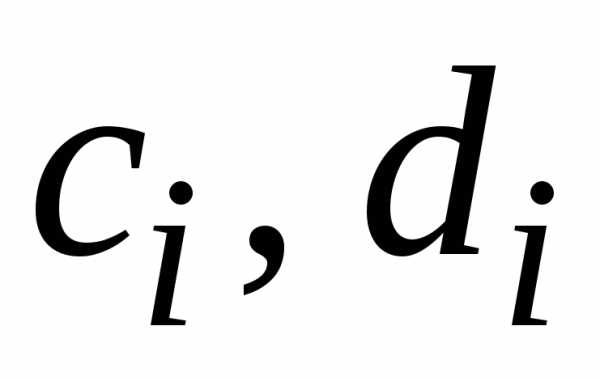 по формулам (1.26) для
по формулам (1.26) для
Обратный ход. Из уравнения (1.24) при и последнего уравнения системы (1.16) получаем:
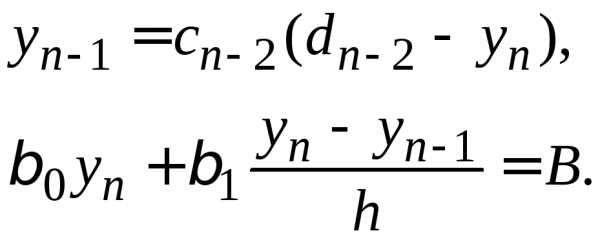
Решив
эту систему относительно 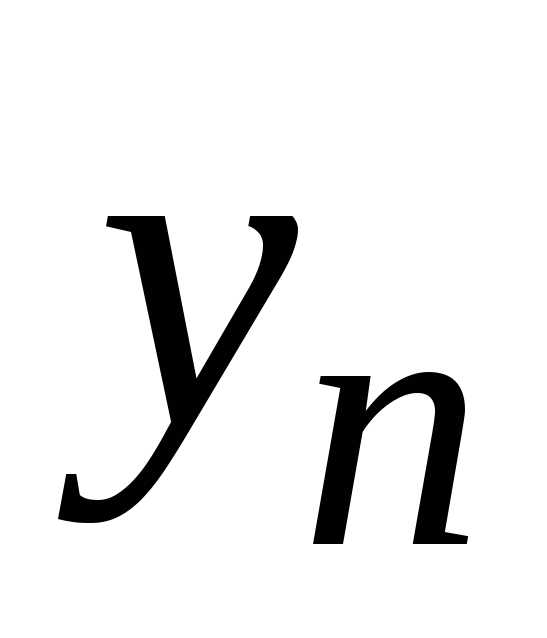 ,
будем иметь
,
будем иметь
(1.27) |
Используя
уже известные числа
,
находим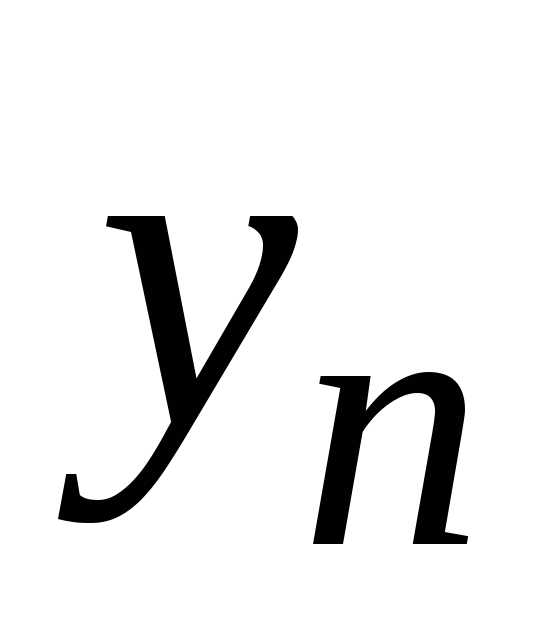 .
Затем вычисляем значения,
последовательно применяя рекуррентные
формулы (1.22):
.
Затем вычисляем значения,
последовательно применяя рекуррентные
формулы (1.22):
| (1.28) |
Значение 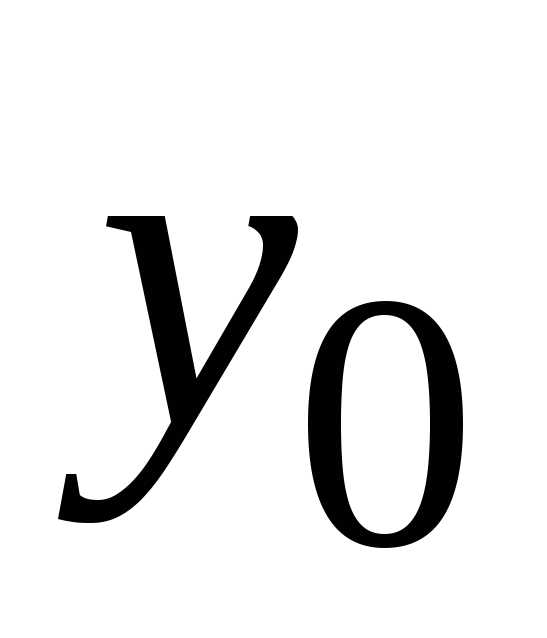 находим из предпоследнего уравнения
системы (1.16):
находим из предпоследнего уравнения
системы (1.16):
| (1.29) |
Таким образом, все вычисления «прогоняются» два раза.
Вычисления
прямого хода заготавливают вспомогательные
числа 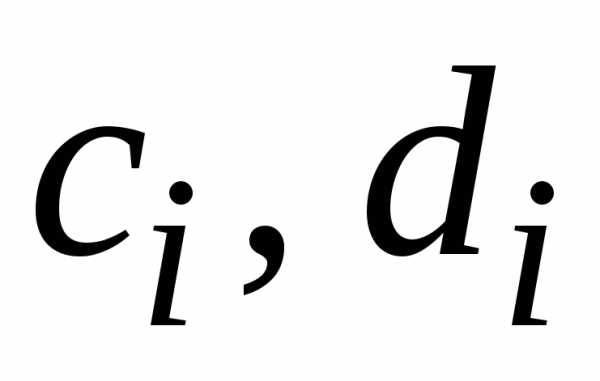 в порядке возрастания индекса
в порядке возрастания индекса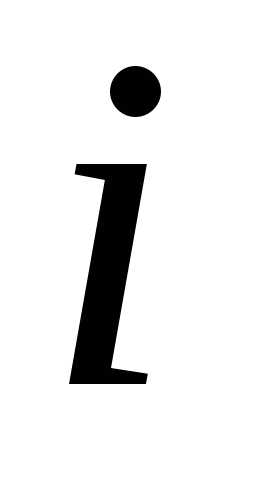 .
При этом для вычисления значений
.
При этом для вычисления значений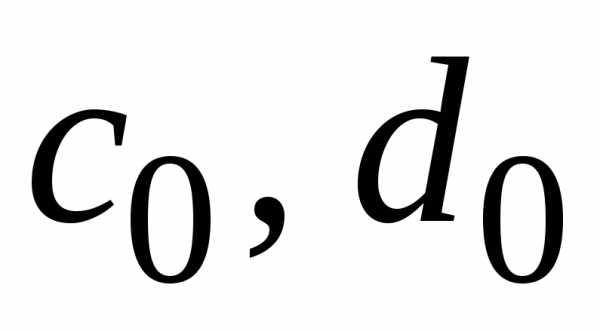 используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чиселс краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции
используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чиселс краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции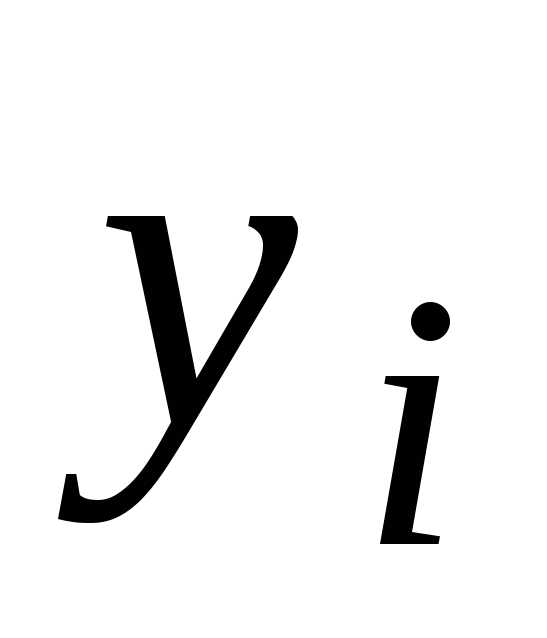 в порядке убывания индекса
в порядке убывания индекса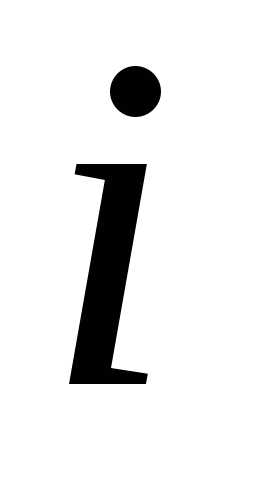 .
.
studfiles.net
1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
Уравнения, связывающие независимую переменную, неизвестную функцию и её производные называют дифференциальным. Если искомая функция зависит от одной переменной, то Д.У. называют обыкновенным.
Если искомая функция зависит от нескольких переменных, то Д.У. называют уравнение частных производных.
Наивысший порядок производной, входящий в Д.У. называют порядком этого уравнения. Д.У. первого порядка называют выражение вида F(x,y,)=0(1). Если это уравнение удаётся разрешить относительно производной, то записывают = f(x,y)(2). Решением уравнения (1) и (2) называют такую дифференцируемую функцию y=которая при подстановке её в уравнение обращает его в верное тождество.
Задачей Коши либо начальной задачей называют задачу нахождения решения y=уравнения(2), удовлетворяющего начальному условию y(xo)=yo (3).
Общим решением Д.У. (2) называется функция y=(4), зависящая от переменной x и произвольной постоянной c. Общее решение (4) удовлетворяет условию уравнения (2) при любых значениях константы с.
Каково бы ни было начальное условие (3) можно подобрать значение со константы с, так чтобы функция y=удовлетворяла заданному начальному условию(3)(если выполнены условия теоремы Коши).
Частным решением Д.У. называют решение, полученное из общего решения (4) либо вида (4) при каком либо определённом значении постоянной произвольной с.
2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
Теорема Коши (существования и единственности): если функция f(x,y) непрерывна и имеет непрерывную производную в областиD, то решение Д.У. = f(x,y) с начальным условием y(xo)=yo , где точка с координатами (xo,yo) принадлежит D, существует и единственно, то есть через точку (xo,yo) принадлежащую области D проходит единственная интегральная кривая данного уравнения.
Если во всех точках решения y = Ψ(x) уравнения = f(x,y) условие действительности не выполняется, то такое решение называется особым. При этом через каждую точку Мо(xo,yo) особого решения проходит также и другое решение уравнения= f(x,y), которое не совпадает с решением y =Ψ(x) в сколь угодно малой окрестности этой точки.
3.ДУ 1-го порядка,интегрируемые в квадратурах.
1.Ур-ия с разделяющимися переменними
P(xy)dx+Q(xy)dy=0 (1). Ур-е(1) наз. ур-ем,записанным в диф-лах.,где x-аргумент,y-искомая ф-я, dx,dy-диф-лы, P(xy), Q(xy)-заданные непрерывные в некот.области D ф-ии.
Пусть P(xy)=p(x),а Q(xy)=q(y),тогда (1) примет вид (2): p(x)dx+q(y)dy=0. (2)наз.ДУ с разделёнными переменнымы, интегрируя которое мы получим:+=C-общий ин-л у-я(2). Если хотя бы один из интегралов неберущ.,то ДУ(2) всё равно считается решённым, при этом говорят, что решение найдено в квадратурах.Пусть P(xy)=(x)*(y), Q(xy)=(x)*(y), тогда (1) примет вид(3):(x)*(y)dx+(x)*(y)dy=0.У-е (3)-ДУ с разделяющимися переменными.Разделив (3) на (x)*(y) получаем:dx+dy=0,которое является ур-ем с разделёнными переменными: dx+=C. При таком решении могут быть потеряны корни (x)=0 и (y)=0,которые необходимо рассматривать отдельно.
studfiles.net
6.7 Обыкновенные дифференциальные уравнения
Задача Коши для дифференциального уравнения первого порядка
Задача Коши для дифференциального уравнения первого порядка включает уравнение вида:
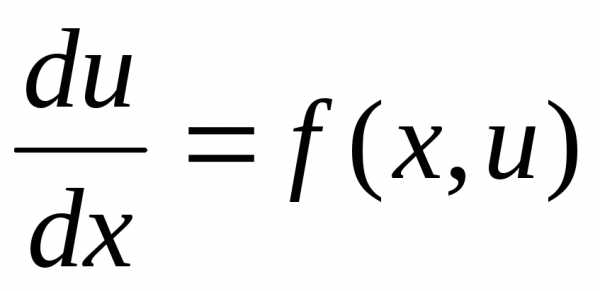 и начальное
условие:
.
и начальное
условие:
.
Существуют различные
методы численного решения задачи Коши:
методы рядов Тейлора, одношаговые методы
Рунге-Кутта, многошаговые разностные
методы. При решении уравнения численными
методами значения функции  находятся приближенно в виде дискретной
числовой последовательности {yi}, где
находятся приближенно в виде дискретной
числовой последовательности {yi}, где 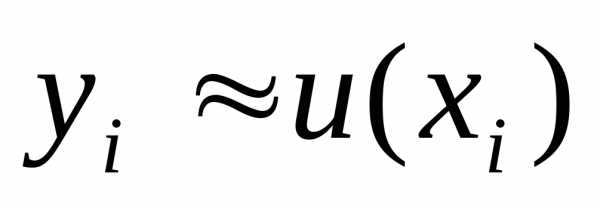 .
.
Методы Рунге-Кутта.
Простейшим вариантом методов Рунге-Кутта является метод Эйлера, при котором производная заменяется конечной разностью.
В случае 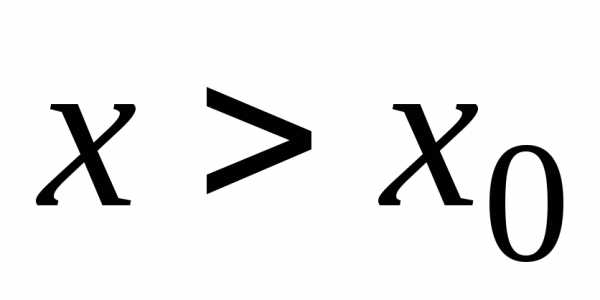 ,,
тогда,
,,
тогда,
где
,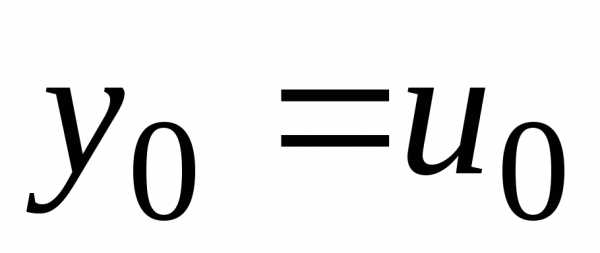 ,,.
,,.
Данный метод имеет
первый порядок точности по h,
погрешность нарастает с удалением от
точки 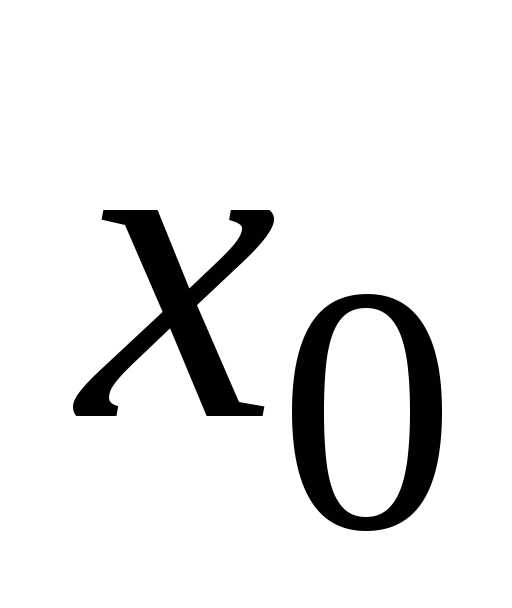 .
Метод Эйлера является методом Рунге-Кутта
первого порядка.
.
Метод Эйлера является методом Рунге-Кутта
первого порядка.
Общий вид методов
Рунге-Кутта (при 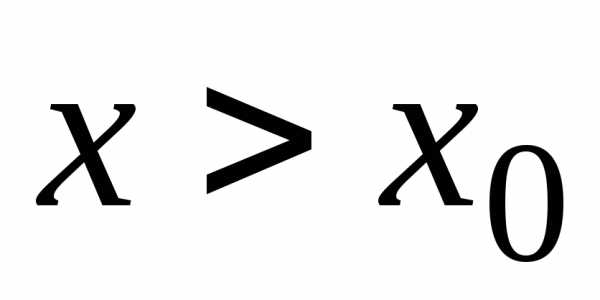 )
записывается с помощью формулы:
)
записывается с помощью формулы:
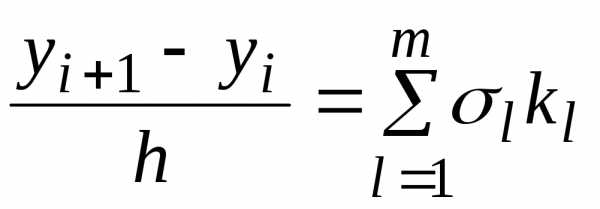 ,
где
порядок метода,
,
где
порядок метода, 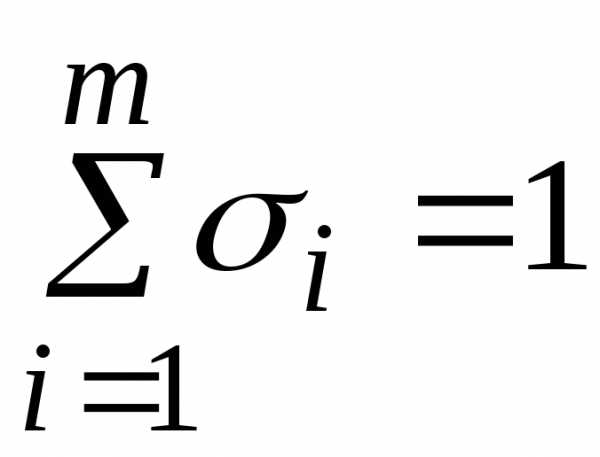 ,
,
,
,
,
. . . . . . . . ,
.
Коэффициенты  ,
,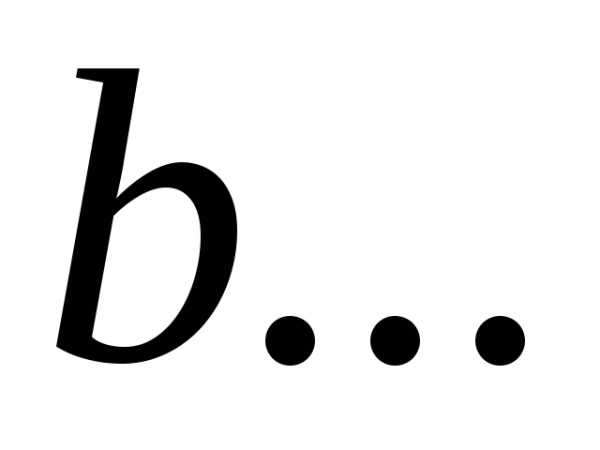 ,
, выбираются из соображений точности.
выбираются из соображений точности.
Метод Эйлера
получается при 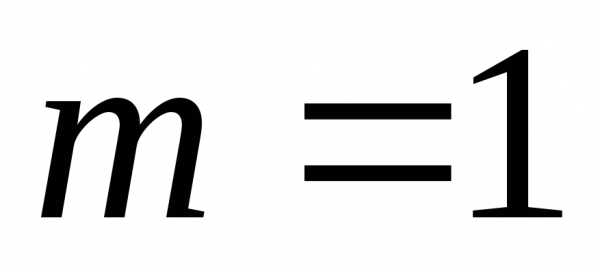 .
.
Для 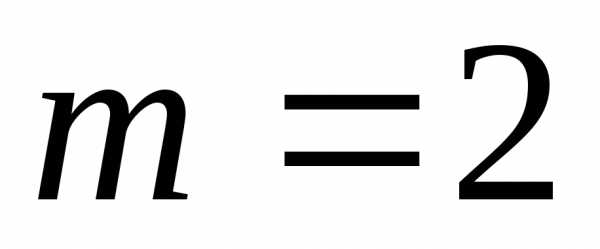 имеется уже семейство методов Рунге-Кутта
второго порядка, для которых должно
выполнятся условие.
имеется уже семейство методов Рунге-Кутта
второго порядка, для которых должно
выполнятся условие.
В частности при иполучается, так называемый,исправленный метод Эйлера:
.
При
,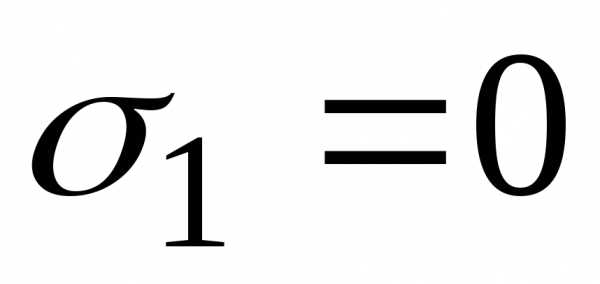 ,
,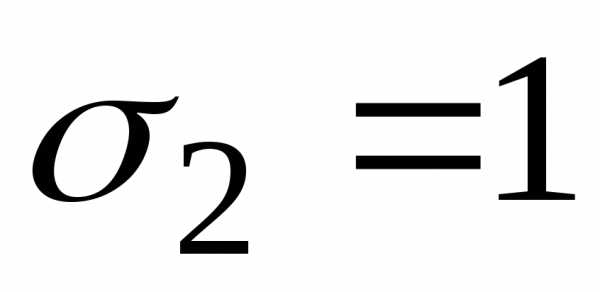 ,
получаетсямодифицированный
метод Эйлера:
,
получаетсямодифицированный
метод Эйлера:
.
Большое распространение
получили методы Рунге-Кутта четвертого
(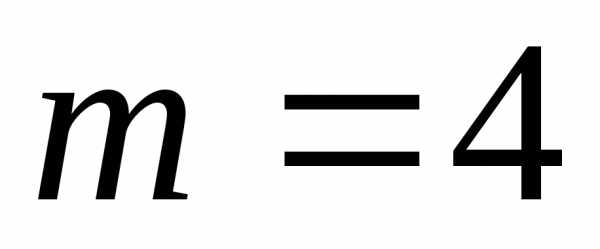 )
порядка точности. Ниже приведены примеры
методов четвертого порядка:
)
порядка точности. Ниже приведены примеры
методов четвертого порядка:
Пример 1.
, ,
, ,
.
Пример 2.
, ,
, ,
.
Для повышения
точности вычислений можно воспользоваться
итерационным методом уточнения. Он
заключается в том, что каждое значение  вычисляется с помощью последовательных
приближений. Например, для метода Эйлера
за начальное приближение берется,
найденное значение уточняется по формуле,
где
вычисляется с помощью последовательных
приближений. Например, для метода Эйлера
за начальное приближение берется,
найденное значение уточняется по формуле,
где
Уточнение продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут.
Задача Коши для дифференциального уравнения n-го порядка.
Каноническая форма обыкновенного дифференциального уравнения n-го порядка имеет вид: . Начальные условия для задачи Коши:
.
Уравнение порядка n сводится к эквивалентной системе n уравнений первого порядка путем замены переменных:
. Задача Коши сводится к решению системы n уравнений с начальными условиями:
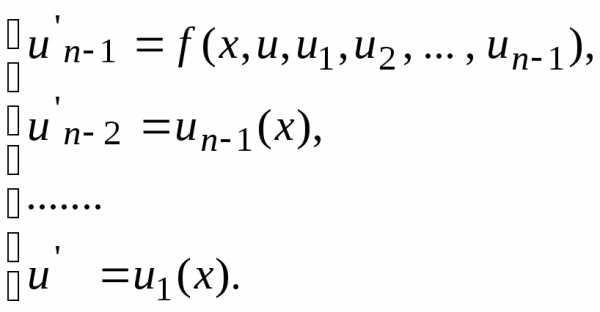
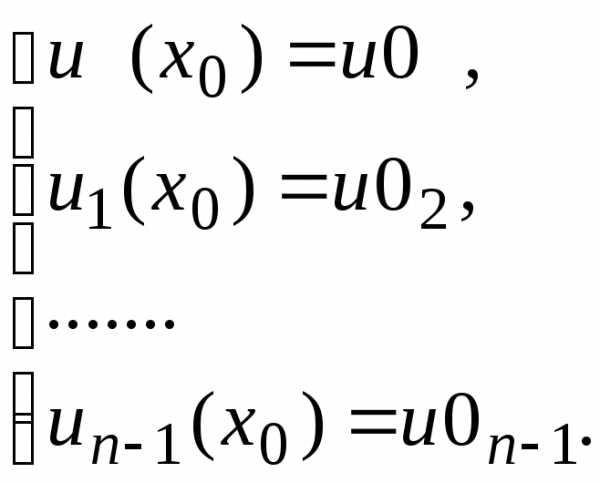
Для ее решения применимы те же методы, о которых говорилось выше. Численное решение этой задачи состоит в построении таблицы приближенных значений yi, y1,i, y2,i,…, yn-1,i, i=1,2,…,k решения u(x) и его производных: u1(x),…, un-1(x) на отрезке [ x0, xk] в точках x0,x1,…,xk.
Например, дано
уравнение 2-го порядка
,
удовлетворяющее начальным условиям,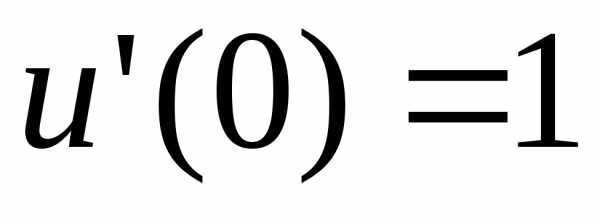 .
Введение дополнительной функциисводит задачу к эквивалентной системе
двух уравнений с начальными условиями
.
Введение дополнительной функциисводит задачу к эквивалентной системе
двух уравнений с начальными условиями
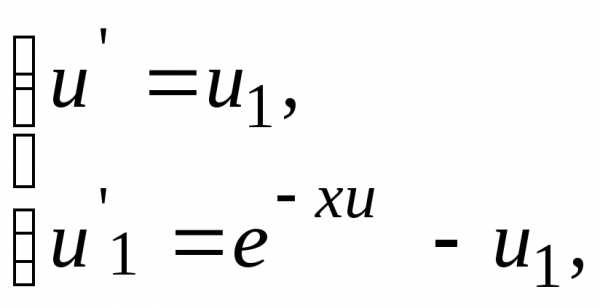
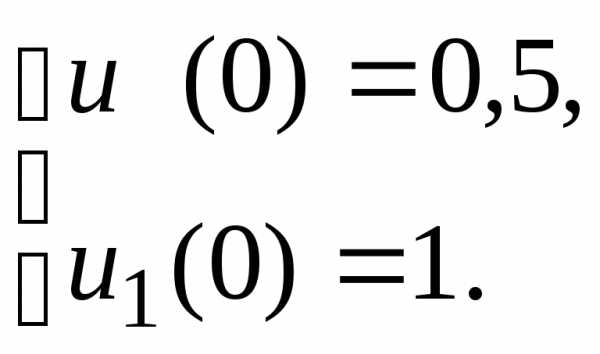
Ниже показано
решение этой задачи с помощью встроенной
в MathCAD функции rkfixed.
Здесь вектор-функция {u(x), u1(x)} обозначена
как {y1(x), y2(x)}. При вычислении
решения на отрезке 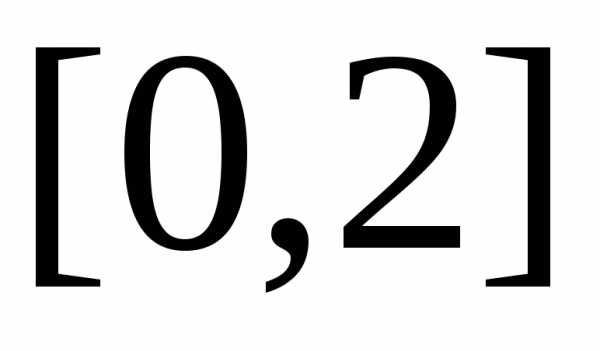 ,
на сетке с 15-ю равноотстоящими узлами
получается:
,
на сетке с 15-ю равноотстоящими узлами
получается:
Функция rkfixed имеет пятьаргументов. Первый аргумент вектор начальныхусловий. Два вторых аргумента задают начальное и конечное значение x. Четвертый определяет количество шагов интегрирования. Последний аргумент это вектор-функция, составленный из правых частей системы уравнений. Результатом вычислений является матрица, первый столбец которой задает координату х, следующие столбцы соответственно y, y’…
studfiles.net
2.2.Задача Коши для уравнения первого порядка, не разрешенного относительно производной
36 | Глава 2. Задача Коши |
ствование решения только на отрезке [t0 − h, t0 + h], где h = min{T,MA }
(см. рис. 2.1). Это объясняется тем, что мы должны следить за тем, чтобы точка (t, y(t)) не выходила за пределы прямоугольника Π, то есть чтобы выполнялось неравенство |y(t) − y0| 6 A, t [t0 − h, t0 + h]. Это необходимо, поскольку только в Π функция f(t, y) ограничена фиксированной постоянной M и удовлетворяет условию Липшица с фикси-
рованной константой L. Попытки увеличить число h = min{T, MA } за
счет увеличения A, вообще говоря, безрезультатны, поскольку при увеличении A в общем случае увеличивается постоянная M.
Приведем пример, показывающий, что без дополнительных предположений относительно функции f(t, y) решение существует только на достаточно малом отрезке.
Пример 2.1.1. Рассмотрим при a > 0 задачу Коши
y0(t) = a(y(t)2 + 1), y(0) = 0.
Функция f(t, y) = a(y2 + 1) определена при любых действительных t и y. Однако решение этой задачи y(t) = tg(at) существует только на
отрезке [−h2, h2], содержащемся в интервале −2πa,2πa .
2.2.1. Примеры постановки задачи Коши
Рассмотрим обыкновенное дифференциальное уравнение первого порядка, не разрешенное относительно производной
F (t, y(t), y0(t)) = 0. | (2.14) |
Всюду в этом параграфе будем считать, что функция F (t, y, p) определена в параллелепипеде D с центром в некоторой точке (t0, y0, y00 ) R3:
D = {(t, y, p) : |t − t0| 6 a, |y − y0| 6 b, |p − y00 | 6 c}, | (2.15) |
где a, b, c – фиксированные положительные числа.
Определение 2.2.1. Функция y(t) называется решением уравнения (2.14) на отрезке [t1, t2], если:

2.2.Задача Коши для уравнения, не разрешенного относительно y0 37
1.y(t) непрерывно дифференцируема на [t1, t2];
2.(t, y(t), y0(t)) D для всех t [t1, t2];
3.на отрезке [t1, t2] выполнено(2.14).
Если уравнение (2.14) разрешено относительно производной,
F (t, y, p) = p − f(t, y),
то при некоторых дополнительных условиях на функцию f(t, y) для получения единственного решения уравнения достаточно задать условие прохождения соответствующей интегральной кривой (графика решения) через некоторую точку (t0, y0). В общем случае приходим к задаче с дополнительным условием
F (t, y(t), y0(t)) = 0, y(t0) = y0. | (2.16) |
Проиллюстрируем особенности такой задачи для случая уравнения, квадратично зависящего от производной:
(y0(t))2 | − | (t + y(t))y0(t) + ty(t) = 0. | (2.17) |
|
|
Поскольку квадратное уравнение p2 − (t + y)p + ty = 0 имеет корни p1 = t, p2 = y, то исходное дифференциальное уравнение распадается на совокупность двух уравнений, разрешенных относительно производной:
|
| y0(t) = t, y0(t) = y(t). |
Получаем два семейства решений | ||
| t2 | |
y1(t) = |
| + C1, y2(t) = C2 exp{t}, C1, C2 R. |
2 | ||
Пример 2.2.1. Задача для уравнения (2.17) с дополнительным усло-
вием y(0) = 1 имеет два решения (см. рис. 2.2а): |
| |
| t2 |
|
y1(t) = | 2 + 1, y2(t) = exp{t}. | (2.18) |
Задача для уравнения (2.17) c дополнительным условием y(0) = 0 имеет четыре решения (см. рис.2.2б-г):
|
| y1(t) = | t2 | y2(t) = 0, |
|
|
| ||
|
|
| , |
|
|
| |||
|
| 2 |
|
|
| ||||
3 | y2 | e | e | y1 | (t), t > 0. |
| |||
| (t), t > 0, |
|
| ||||||
y (t) = | y1 | (t), t < 0, | y4 | (t) = | y2 | (t), t < 0, | (2.19) | ||
e | e |
|
|
| e |
| e |
|
|
e |
|
|
|
| e |
|
| ||
38 | Глава 2. Задача Коши |
Рис. 2.2. К примерам 2.2.1, 2.2.2: неединственность решения задачи Коши.
Рассмотренный пример показывает, что неединственность решения достаточно характерна для задачи (2.16). Для единственности необходимо задать еще одно дополнительное условие. Из геометрических соображений наиболее естественно потребовать, чтобы искомое решение проходило через заданную точку с данным наклоном касательной. В результате приходим к постановке задачи Коши
F (t, y(t), y0(t)) = 0, y(t0) = y0, y0(t0) = y00 . | (2.20) |
Пример 2.2.2. Задача Коши для уравнения (2.17) с начальными условиями y(0) = 1, y0(0) = 0, то есть
(t | , y | , y0 | ) = (0, 1, 0), F (0, 1, 0) = 0, | ∂F (0, 1, 0) | = 1 = 0, | (2.21) | ||
∂p |
| |||||||
0 | 0 | 0 |
| − 6 | ||||
имеет единственное решение y(t) = t2 + 1.
2
Задача Коши для уравнения (2.17) с начальными условиями y(0) = 1, y0(0) = 1, то есть
|
|
| (t | , y | , y0 | ) = (0, 1, 1), | F (0, 1, 1) = 0, | ∂F (0, 1, 1) | = 1 = 0, | (2.22) | |||||||
|
|
|
| ||||||||||||||
|
|
| 0 | 0 | 0 |
|
|
|
|
|
|
| ∂p |
| 6 | ||
имеет единственное решение y(t) = exp{t}. |
|
|
|
| |||||||||||||
|
| Задача Коши для уравнения (2.17) с начальными условиями y(0) = | |||||||||||||||
1 | , | y0 | (0) = y0 | y0 | 0; 1 | }, то есть |
|
|
|
|
|
|
| ||||
|
|
|
| 0, | 0 6 { |
|
|
|
|
|
|
| |||||
|
|
|
|
|
| (t | , y | , y0 | ) = (0, 1, y0 ), | F (t | , y | , y0 | ) = 0, | (2.23) | |||
|
|
|
|
|
| 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 6 |
| ||

2.2. Задача Коши для уравнения, не разрешенного относительно y0 39
не имеет ни одного решения.
Задача Коши для уравнения (2.17) с начальными условиями y(0) = 0, y0(0) = 0, то есть
(t | , y | , y0 | ) = (0, 0, 0), F (0, 0, 0) = 0, | ∂F (0, 0, 0) | = 0, | (2.24) |
| ||||||
0 | 0 | 0 |
| ∂p |
|
|
|
|
|
|
|
|
имеет четыре решения (2.19).
Приведенный пример показывает следующие особенности постановки задачи Коши (2.20):
1.тройка чисел (t0, y0, y00 ) R3 не может быть взята произвольно; для существования решения необходимо выполнения условия
F (t0, y0, y00 ) = 0;
2.двух дополнительных условий y(t0) = y0, y0(t0) = y00 может оказаться недостаточно для единственности решения в случае
∂F (t0, y0, y00 )= 0. ∂p
2.2.2.Теорема существования и единственности решения задачи Коши
Теорема 2.2.1. Пусть функция F (t, y, p) определена в параллелепипеде D, заданным (2.15), и выполнены следующие условия:
1. | F (t0, y0, y00 ) = 0; |
|
|
| (2.25) | ||||
2. | F (t, y, p), | ∂F (t, y, p) | , | ∂F (t, y, p) | непрерывны в D; (2.26) | ||||
|
| ∂y | ∂p |
| |||||
|
|
|
|
|
|
| |||
3. | ∂F (t0, y0, y00 ) | 6= 0. |
|
|
| (2.27) | |||
| ∂p |
|
|
|
|
| |||
Тогда найдется h > 0 такое, что на отрезке [t0 − h, t0 + h] существует единственное решение задачи Коши(2.20).
Доказательство. Рассмотрим в окрестности точки (t0, y0, y00 ) уравнение
Из условий (2.25)-(2.27) и теоремы о неявной функции следует, что найдется окрестность Ω0 точки (t0, y0), в которой существует единственная
40 | Глава 2. Задача Коши |
непрерывная функция p = f(t, y), имеющая в Ω0 непрерывную частную производную
∂f(t, y) | = − | ∂F (t, y, f(t, y))/∂y | , | (2.29) |
∂y | ∂F (t, y, f(t, y))/∂p |
и являющаяся решением уравнения (2.28). В частности, выполнено равенство
В окрестности Ω0 уравнение(2.14) эквивалентно дифференциальному уравнению y0(t) = f(t, y(t)), разрешенному относительно производной, а задача Коши(2.20) принимает вид
y0(t) = f(t, y(t)), y(t0) = y0. | (2.31) |
Отметим, что фигурирующее в (2.20) начальное условие на производную y0(t0) = y00 автоматически выполнено в силу равенства(2.30).
Рассмотрим задачу Коши (2.31) в прямоугольнике
Π = {(t, y) : |t − t0| 6 a0, |y − y0| 6 b0},
где положительные числа a0, b0 настолько малы, чтобы Π Ω0. Как уже установлено выше, функция f(t, y) непрерывна в Ω0, а значит и в Π. Условие Липшица для этой функции по переменной y на множестве Π с константой
(t,y) Π | ∂y |
|
|
| ||
L = max |
| ∂f (t, y) |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| ∂f |
|
вытекает из непрерывности в Π частной производной |
| (t, y), опреде- | ||||
∂y | ||||||
ленной в (2.29). Таким образом, в Π выполнены все условия теоремы2.1.2 существования и единственности решения задачи Коши для дифференциального уравнения, разрешенного относительно производной. Следовательно, найдется h > 0 такое, что на отрезке [t0 − h, t0 + h] существует единственное решение задачи Коши(2.31), а значит и задачи Коши(2.20).
Замечание 2.2.1. В приведенном выше примере 2.2.2 условия теоремы2.2.1 выполнены для задач Коши(2.21), (2.22) и не выполнены для задач Коши(2.23), (2.24).
studfiles.net
20 Обзор численных методов решения задачи Коши для обыкновенных дифференциальных уравнений
Лекция 26. Обзор численных методов решения задачи Коши для обыкновенных дифференциальных уравнений.
Будем рассматривать схемы численных методов для уравнения первого порядка
.
Это – самый простой случай, но к нему по аналогии сводятся схемы методов для системы дифференциальных уравнений и для дифференциального уравнения n- го порядка.
1. Методы, основанные на разложении функции в ряд Тейлора.
Запишем разложение функции в ряд Тейлора в окрестности точки
Рассмотрим равномерную сетку по
Пусть , тогда разложение функции в ряд Тейлора можно записать в виде
, где
Подставим в из дифференциального уравнения
Тогда
.
Это – основная расчетная формула.
Учитывая в слагаемые с производными высших порядков, получим более точные приближенные формулы.
Если взять , то получим метод Эйлера
2. Методы Рунге – Кутта.
Основная идея методов Рунге – Кутта – вместо вычисления производных высших порядков в вычислять значения функции в некоторых точках, отличных от .
Выберем
=
Разложим по h
= +=
Сравним с приведенной выше основной расчетной формулой
.
и определим коэффициенты
.
Пусть , тогда .
Если . Тогда
.
= .
Это – метод Хойна.
Если в формуле . выбрать ,
то получим явный m – шаговый (m – точечный) метод Рунге – Кутта.
Наиболее распространен явный четырехточечный метод Рунге – Кутта
В явных методах Рунге – Кутта значения вычисляются только по предыдущим значениям .
В неявных методах Рунге – Кутта значения вычисляются как по предыдущим, так и по последующим значениям . Поэтому в этих методах приходится еще решать систему уравнений относительно .
Неявный m – шаговый метод Рунге – Кутта можно записать в виде
.
,
3. Методы Адамса.
Идея методов Адамса – использовать не промежуточные вычисления значений правой части дифференциального уравнения внутри отрезка , а значения правой части на предыдущих шагах (сделать метод методом «с памятью»).
В формуле заменим интерполяционным полиномом Ньютона .
Явные методы Адамса (Адамса – Башфорта).
Возьмем , но интеграл будем брать по предыдущему отрезку . Тогда
Здесь — конечная разность — го порядка:
Подставляя эти разности, получим
(k – шаговый явный метод Адамса – Башфорта)
Пример. Получен явный метод Адамса – Башфорта второго порядка (двухшаговый)
.
Более точен метод Адамса – Башфорта четвертого порядка:
Заметим, если задано (в задаче Коши начальное условие задается), то для того, чтобы начал работать метод Адамса 4 порядка, нужно вычислить еще значения (каким-либо другим методом) . Тогда из системы формул Адамса Башфорта, выписанных для , вычисляются значения правых частей , необходимые для того, чтобы метод начал работать. Затем уже по этим значениям по формуле метода определяются .
Эта процедура называется «разгоном метода» и является обязательной в методах Адамса.
Неявные методы Адамса (Адамса – Мултона).
Возьмем , интеграл будем брать по отрезку . Тогда
Здесь — конечная разность — го порядка:
Подставляя эти разности, получим
(k – шаговый явный метод Адамса –Мултона)
Формально он записан в том же виде, что и метод Адамса – Башфорта, но разница существенна: в методе Адамса – Мултона в левой части уравнения присутствует , а в правой части присутствует . Поэтому приходится еще решать систему уравнений для явного определения .
Пример. . Поэтому имеем формулу
метода Адамса – Мултона второго порядка.
Более точен метод Адамса – Мултона четвертого порядка
.
Эти методы также требуют разгона.
Обобщением методов Адамса являются линейные многошаговые методы
Если , то метод – явный, если , то метод – неявный.
Есть методы, сочетающие явные и неявные этапы – методы. Таковы, например, методы типа предиктор – корректор (предиктор P – предсказатель – явный метод, корректор С – неявный метод). Эти методы содержат обычно и этапы вычисления функции Е. Распространены методы РЕСЕ и РЕС.
Рассмотрим в качестве метода Р метод Адамса – Башфорта 2 го порядка, а в качестве метода С – метод Адамса – Мултона 2 го порядка.
Схема метода может быть записана в виде.
Р .
Е
С
Е
Метод Р «предсказывает», прогнозирует , вычисляется значение правой части, которое используется в методе С – «корректоре» для коррекции приближения , затем вычисляется более точное значение правой части, которое вновь используется в методе Р.
Сходимость, устойчивость разностных схем, порядок точности методов.
Вообще-то это – тема отдельного курса, но нельзя говорить о методах решения дифференциальных уравнений и не сказать хотя бы несколько слов о сходимости численных алгоритмов, устойчивости вычислительных схем и точности методов.
Рассмотрим дифференциальное уравнение , равномерную сетку на отрезке интегрирования .
Рассмотрим сеточную функцию — правую часть уравнения, определенную на сетке .
Введем аппроксимации производной:
, , .
Задача Коши (дифференциальная задача) заменяется разностной задачей (разностной схемой)
или .
Разностная схема отличается от дифференциального уравнения тем, что функции заменены сеточными, производные заменены их аппроксимациями.
— решение разностной задачи, — решение дифференциальной задачи, — сеточная функция, построенная по .
Сходимость разностной схемы с порядком .
Решение сходится к с порядком , если .
.
Аппроксимация с порядком .
Пусть задача имеет единственное решение.
Пусть (- невязка).
Разностная задача аппроксимирует дифференциальную задачу на решении
с порядком , если .
Пример. Рассмотрим схему Эйлера для задачи .
Разностная задача , ,
. Поэтому
=. То есть, , следовательно, схема Эйлера дает аппроксимацию первого порядка.
Замечание. Ошибку аппроксимации можно оценить по правилу Рунге, решая дифференциальное уравнение с шагом , а затем с шагом и сравнивая решения: , где — порядок аппроксимации.
Устойчивость разностной схемы.
Разностная схема называется устойчивой, если разностная задача имеет единственное решение такое, что .
Другими словами, при малых возмущениях мало возмущается .
Теорема. Пусть разностная схема аппроксимирует дифференциальную задачу на решении с порядком и устойчива. Тогда решение разностной задачи сходится к с порядком , причем . Здесь — константа аппроксимации, С – константа устойчивости.
Доказательство. Пусть , тогда по единственности решения (определение устойчивости) и определению аппроксимации . Тогда
(при имеем ).
studizba.com
7.2. Решение задачи Коши для линейных дифференциальных уравнений
Методы операционного исчисления удобно применять при решении некоторых дифференциальных уравнений.
Пусть задано дифференциальное уравнение, например 2-го порядка с постоянными коэффициентами:
a0x«(t)+a1x'(t)+a2x(t)=f(t),
где а0, а1, а2=const. Требуется найти решение этого уравнения, удовлетворяющее начальным условиям: х(0)=х1, x‘(0)=x2. Предположим, что правая часть данного уравнения является оригиналом. Тогда и решение x(t) этого уравнения тоже будет оригиналом. Пусть x(t) X(p), тогда
x'(t)pX(p)-x(0)=pX(p)-x1
x»(t)p2X(p)-px(0)-x'(0)=p2X(p)-px1—x2.
Далее находим изображение функции f(t) F(p).
Наконец, применяя преобразование Лапласа к обеим частям уравнения и пользуясь свойством линейности преобразования Лапласа, получаем операторное уравнение:
a0(p2X(p)-px1-x2)+a1(pX(p)-x1)+a2X(p)=F(p).
Это уравнение является линейным относительно известной функции X(p). Решая его, находим Х(р) и затем по Х(р) восстанавливаем оригинал f(t).
_______________________
Средствами операторного исчисления решить линейные (однородные и неоднородные) дифференциальные уравнения (всюду x=x(t)):
x’+3x=0, x(0)=2.
x’-4x=1-4t, x(0)=1.
x»+ 4x’-5x=0, x(0)=3, x’(0)=-3.
x»-6 x’+9x=0, x(0)=1, x’(0)=2.
x»- x’=sint, x(0)=-1, x’(0)=0.
x»+2x’+x=t+2, x(0)=0, x’(0)=2.
x»- x’=et, x(0)=x’(0)=4.
x»-3x’+10x=9sint-3cost, x(0)=0, x’(0)=-2.
x»+2 x’+x=t, x(0)=x’(0)=0.
x»+2x’+10x=sin3t+6cos3t, x(0)=x’(0)=1.
Ответы:
1. 2е-3t; 2. е4t+t; 3. 2еt+е-5t; 4. е3t—tе3t ; 5. ;
6. tе—t+t; 7. tеt+3еt+1; 8. е2t—е5t+sint; 9. tе-t+2е—t+t-2 ;
10. е-tcos3t-е-tsin3t+sin3t.
Глава 8. Интегрирование однородных систем с постоянными коэффициентами
Найти общее решение систем дифференциальных уравнений и, где указано, выделить частное решение, удовлетворяющее поставленным начальным условиям:
1.
2.
3.
4.
5.
6.
Ответы:
1. 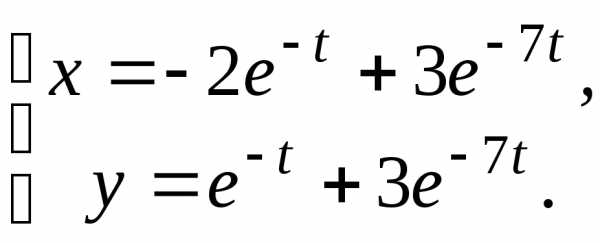 2.
2.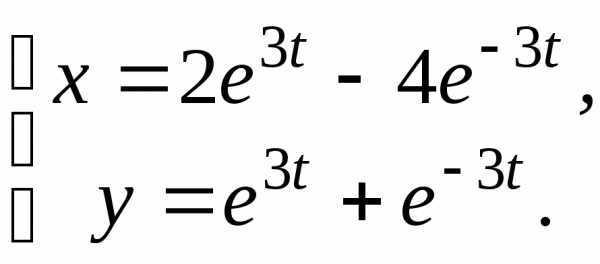 3.
3.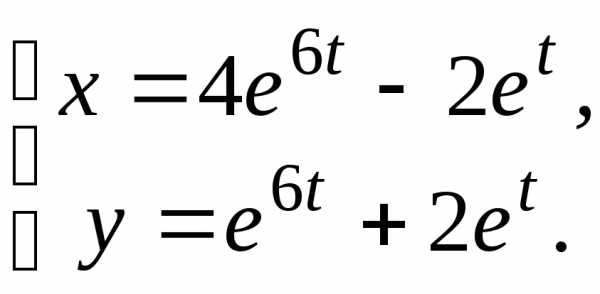
4. 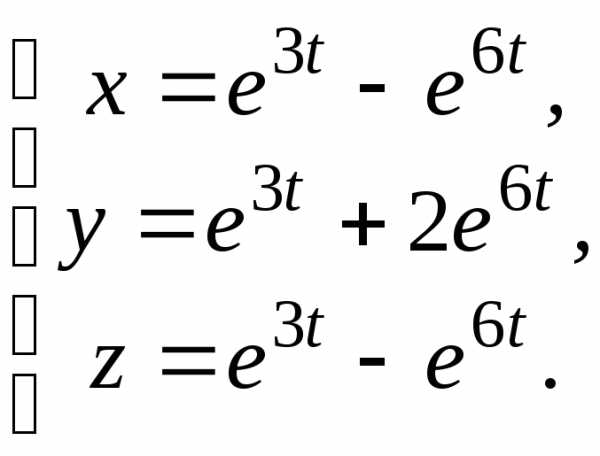 5.
5.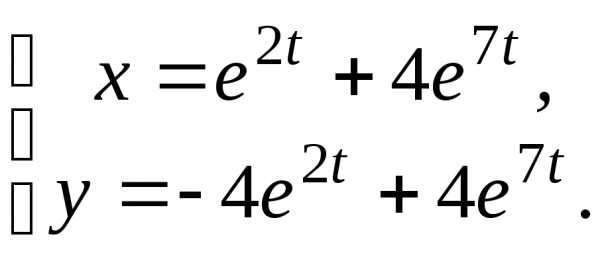 6.
6.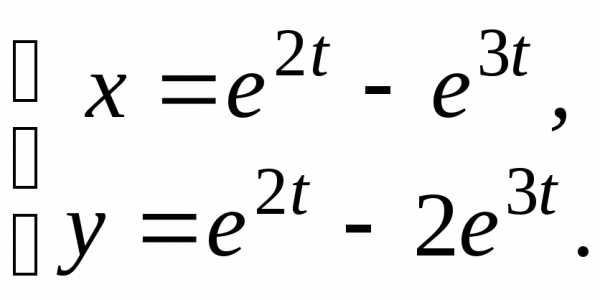
Глава 9. Ряды
9.1. Числовые ряды с положительными членами
Пусть задана бесконечная последовательность чисел а1, а2,…, аn,… .
Числовым рядом называется выражение вида
а1+а2+ а3+ аn+…
=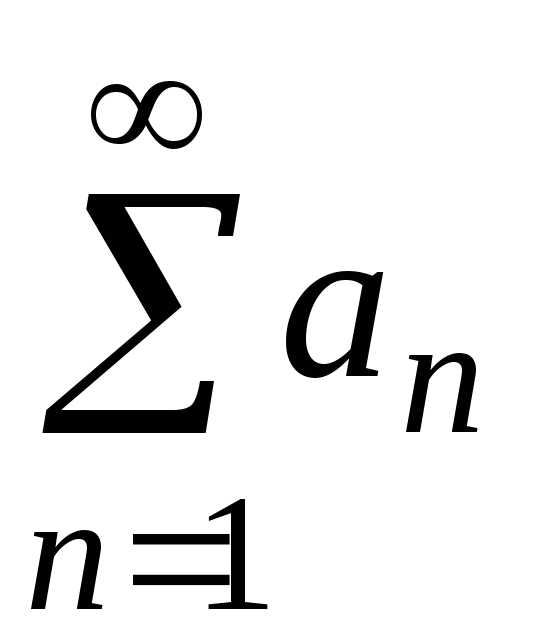 .
.
Числа а1, а2,…, аn,… называются членами ряда, число аn – общим членом ряда.
Суммы вида S1= а1, S2= а1 + а2, S3= а1 + а2 +а3,…, Sn= а1 + а2 +…+аn называются частичными суммами.
Числовой ряд
называется сходящимся, если существует
конечный предел последовательности
его частичных сумм 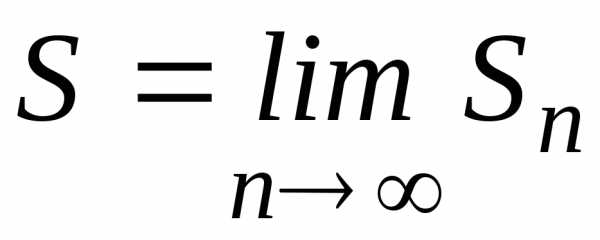 ,
в противном случае ряд называется
расходящимся.
,
в противном случае ряд называется
расходящимся.
Необходимый признак сходимости
Если ряд 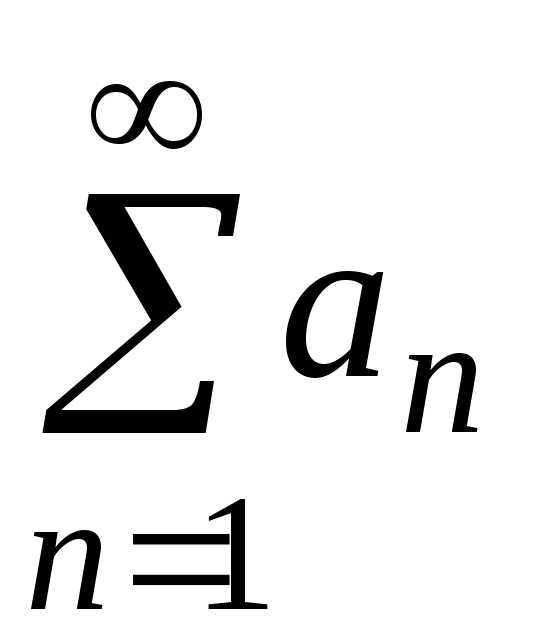 сходится,
то общий член рядаn
стремится к нулю, т.е.
сходится,
то общий член рядаn
стремится к нулю, т.е. 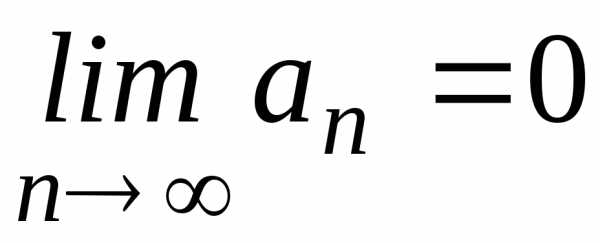 .
.
Если 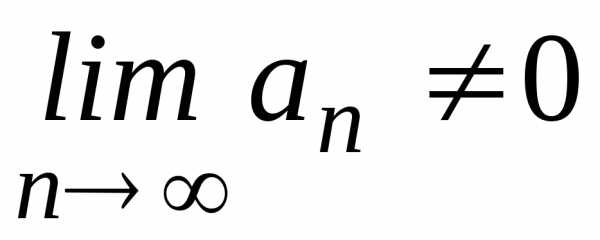 ,
то ряд расходится.
,
то ряд расходится.
Признаки сходимости рядов с положительными членами
1-й признак сравнения
Пусть 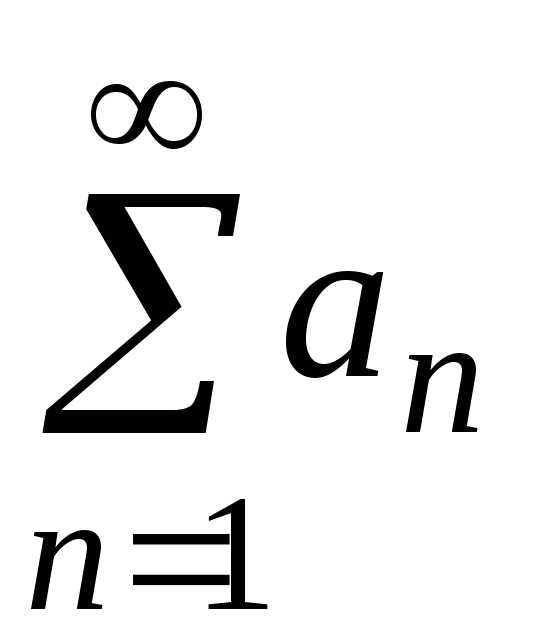 и
и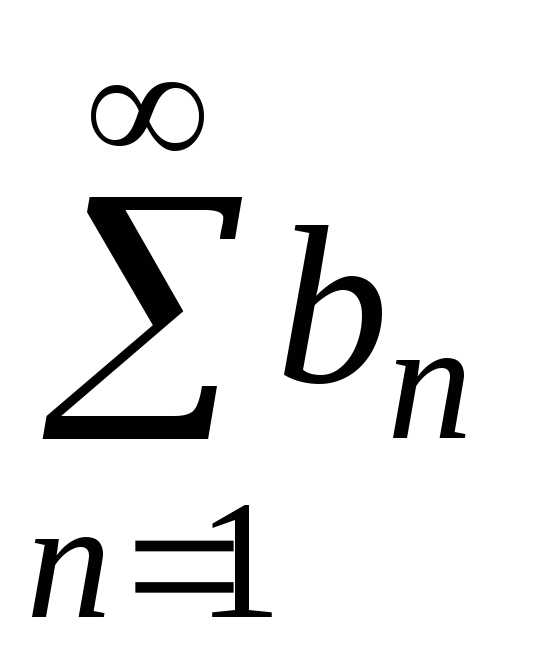 — ряды с положительными членами, причемanbn для всех номеров, начиная с некоторого n=k.
Тогда
— ряды с положительными членами, причемanbn для всех номеров, начиная с некоторого n=k.
Тогда
если ряд
 сходится,
то сходится и ряд
сходится,
то сходится и ряд ;
;если ряд
 расходится, то расходится и ряд
расходится, то расходится и ряд .
.
2-й признак сравнения
Пусть 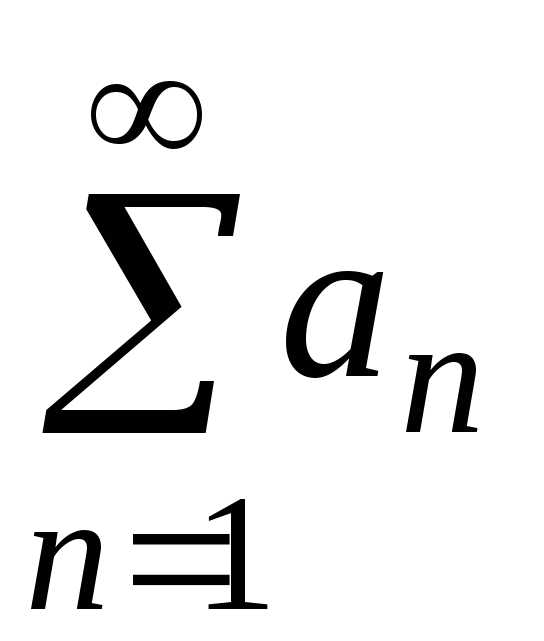 и
и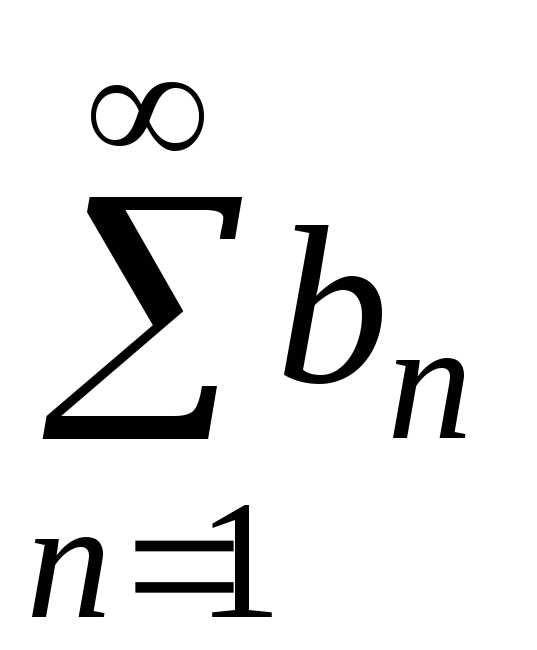 —
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел
—
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел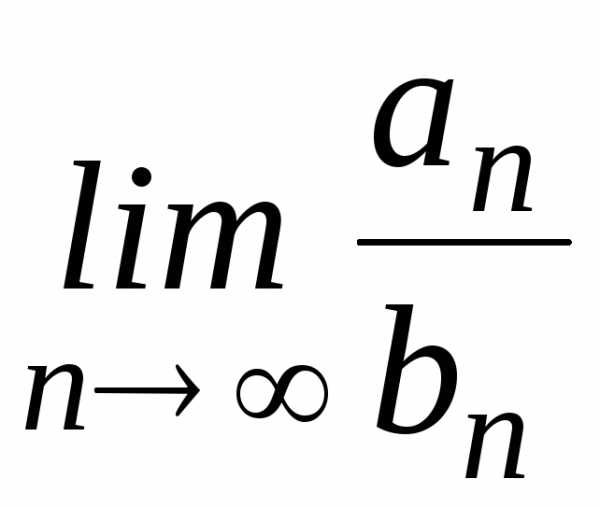 .
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.
.
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.
Для сравнения часто используются следующие ряды:
1) 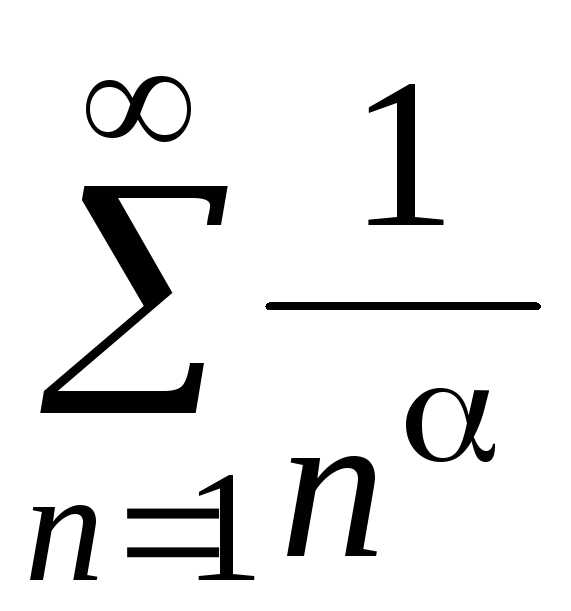 ,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;
,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;
2) 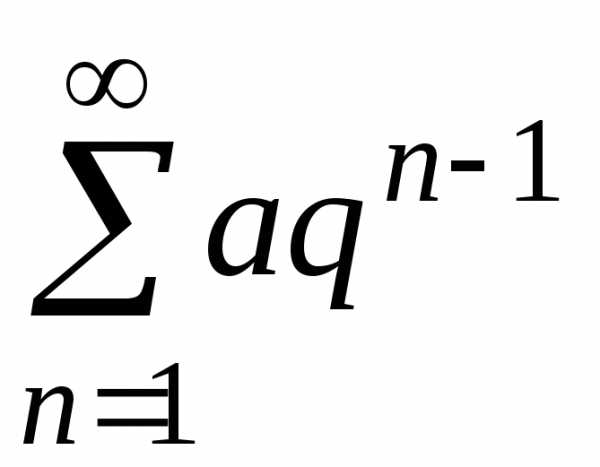 ,
если |q|<1,
то ряд сходится; в противном случае –
расходится.
,
если |q|<1,
то ряд сходится; в противном случае –
расходится.
Признак Даламбера
Пусть 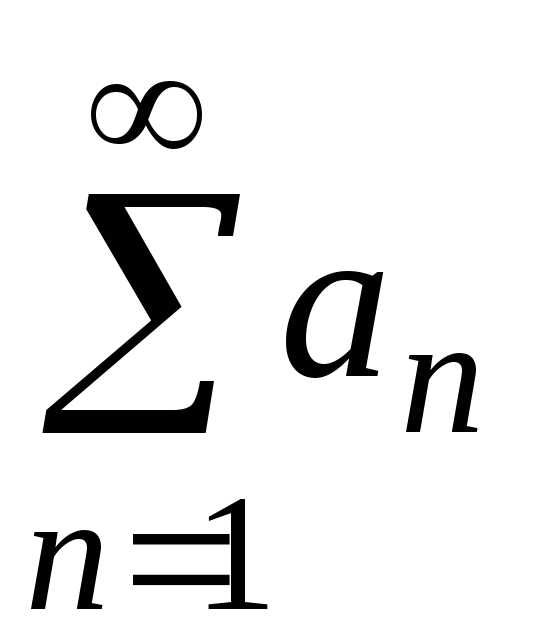 — ряд с положительными членами, и
существует конечный предел.
— ряд с положительными членами, и
существует конечный предел.
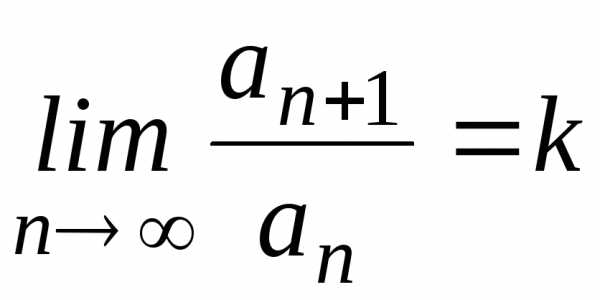 ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
Признак Коши
Пусть 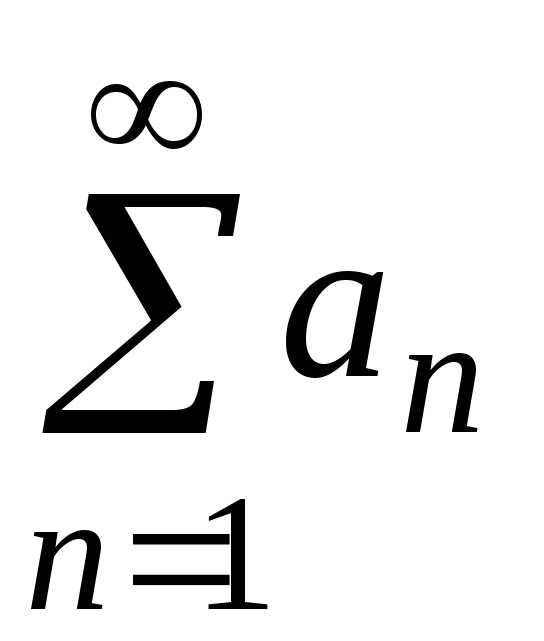 — ряд с положительными членами и существует
конечный предел:
— ряд с положительными членами и существует
конечный предел:
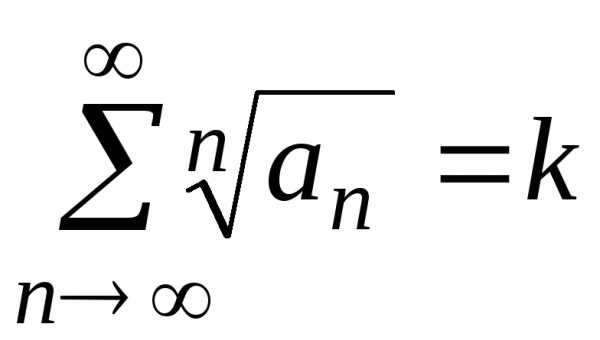 ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
Интегральный признак сходимости
Пусть 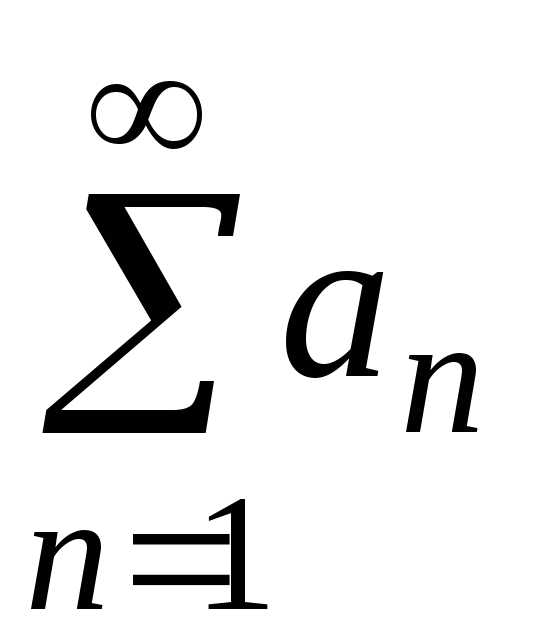 — ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x) такая, что f(n)=an, n=1;2;….
Тогда ряд
— ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x) такая, что f(n)=an, n=1;2;….
Тогда ряд 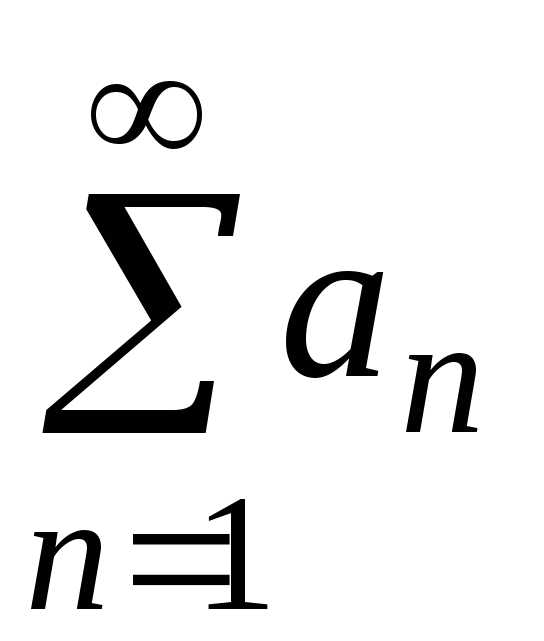 и несобственный интеграл
и несобственный интеграл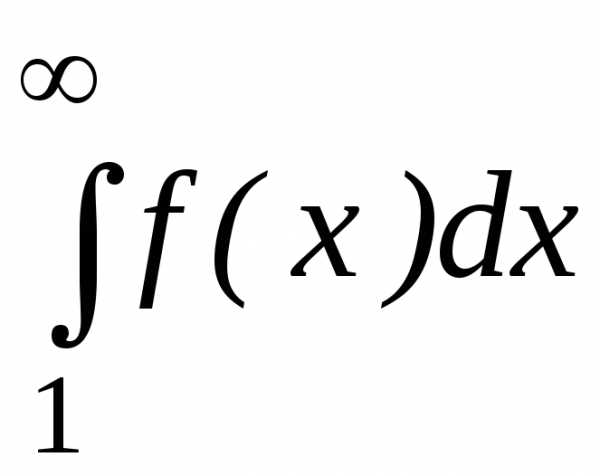 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
1. Для следующих рядов проверить необходимый признак сходимости:
а) 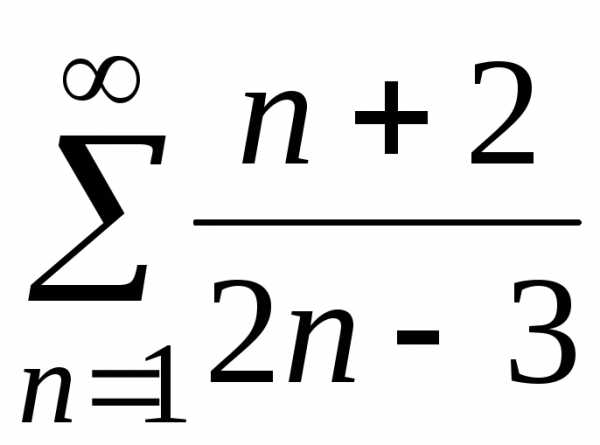 ;
б)
;
б)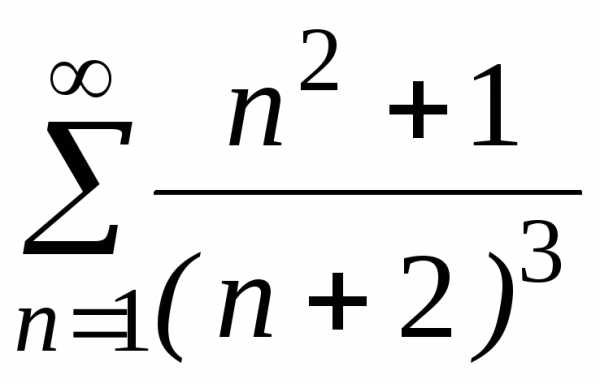 ;
в)
;
в)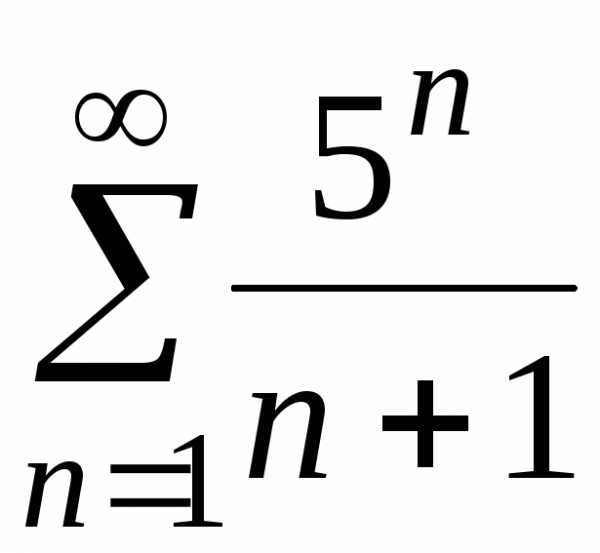 ;
г)
;
г)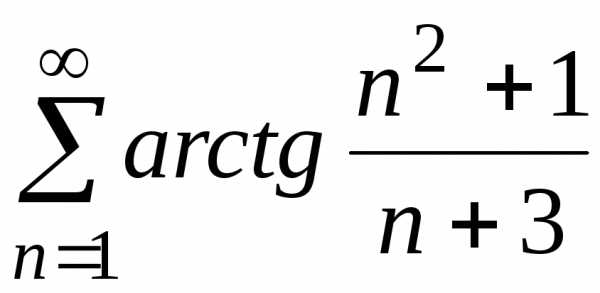 ;
;
д) 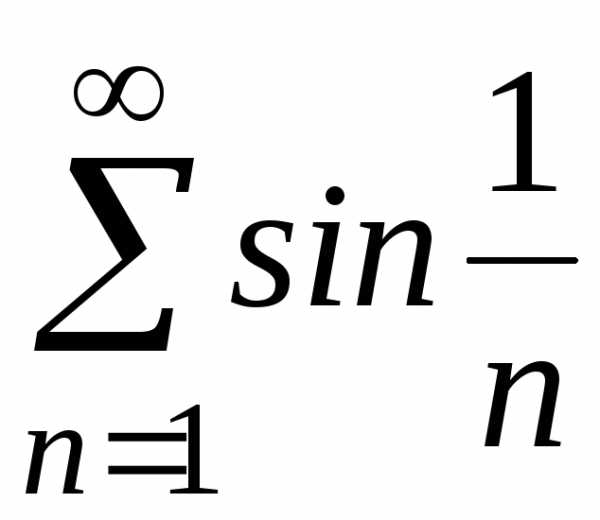 ;
е)
;
е)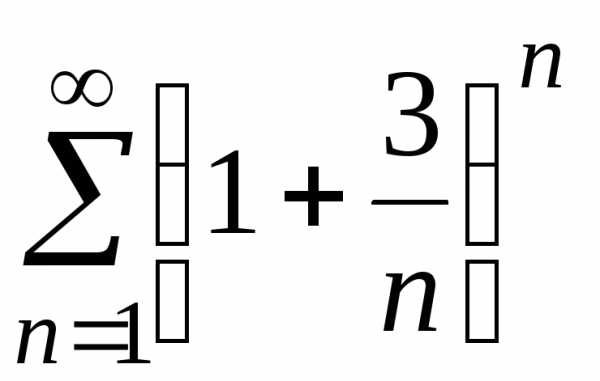 .
.
2. Исследовать на сходимость ряд, применяя 1-й признак сравнения
а) 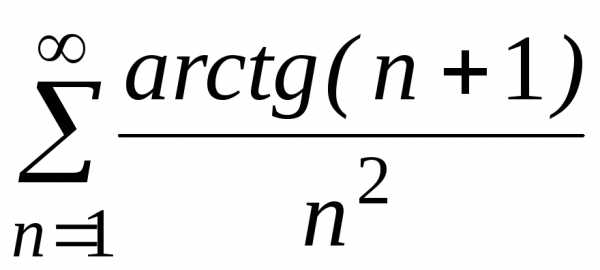 ;
б)
;
б)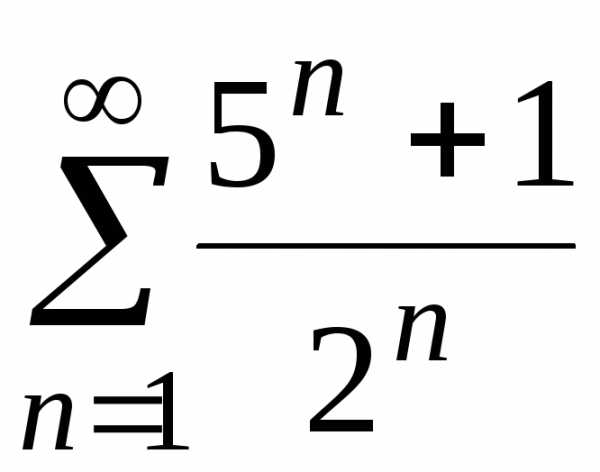 ;
в)
;
в)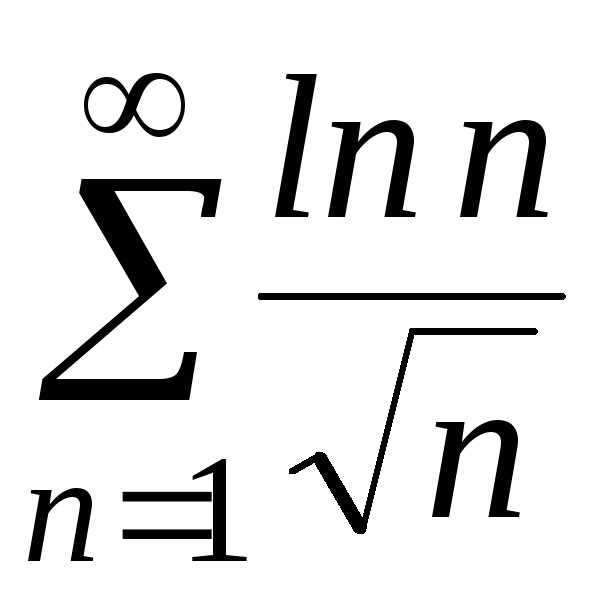 ;
г)
;
г)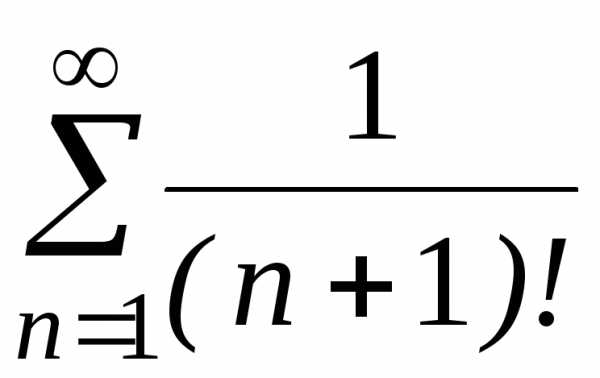 ;
;
д) 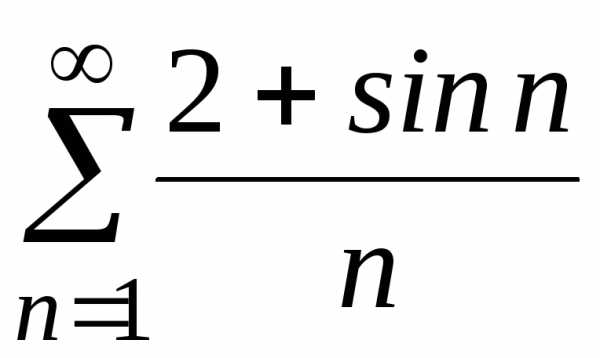 .
.
3. Исследовать ряд на сходимость, применяя 2-й признак сравнения:
а) 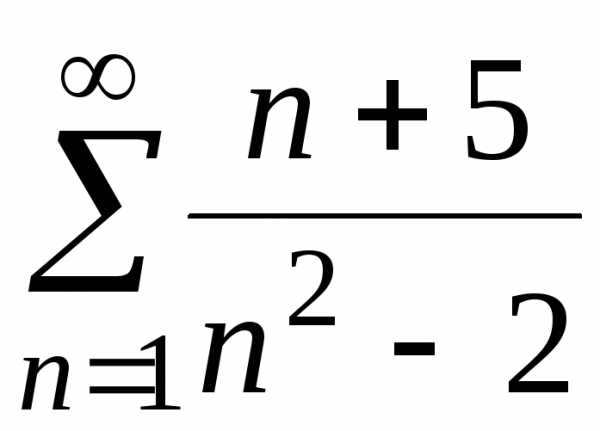 ;
б)
;
б)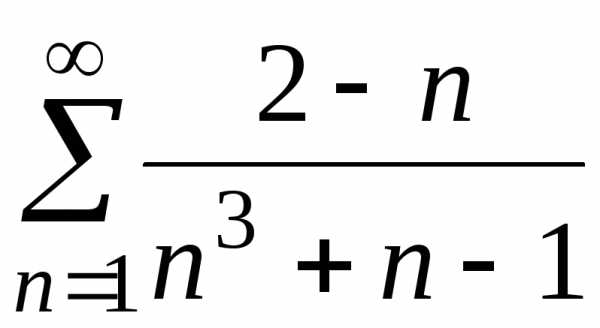 ;
в)
;
в)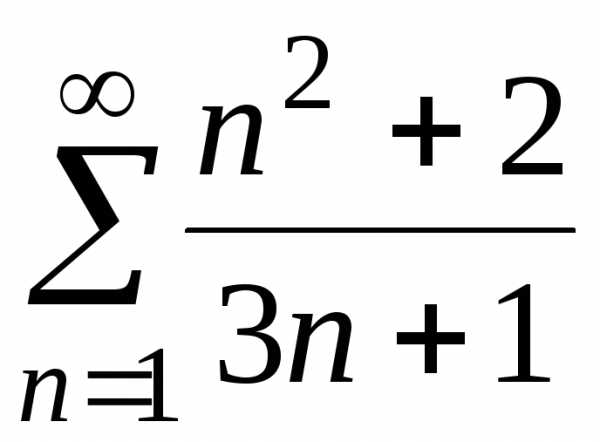 ;
г)
;
г)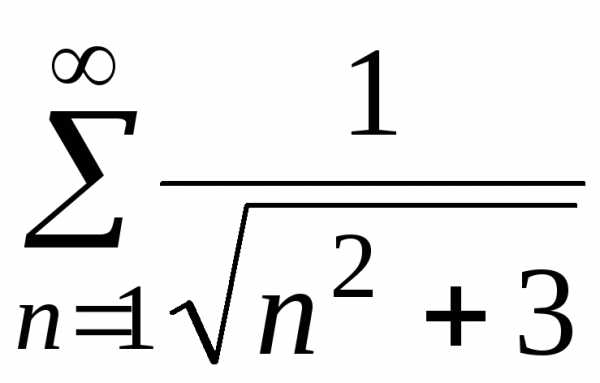 ;
;
д) 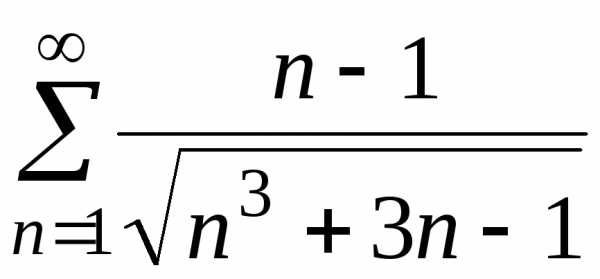 ;
е)
;
е)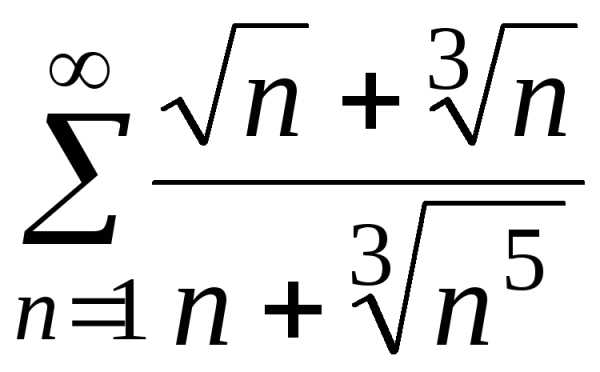 ;
ж)
;
ж)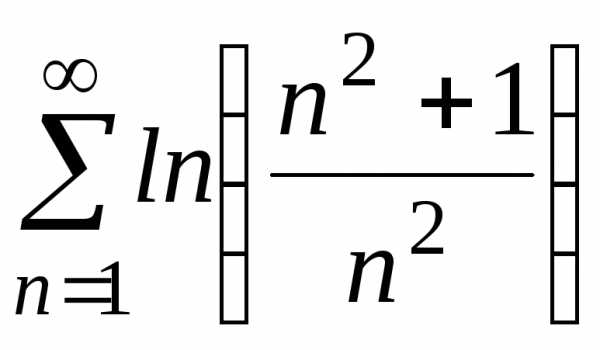 ;
з)
;
з)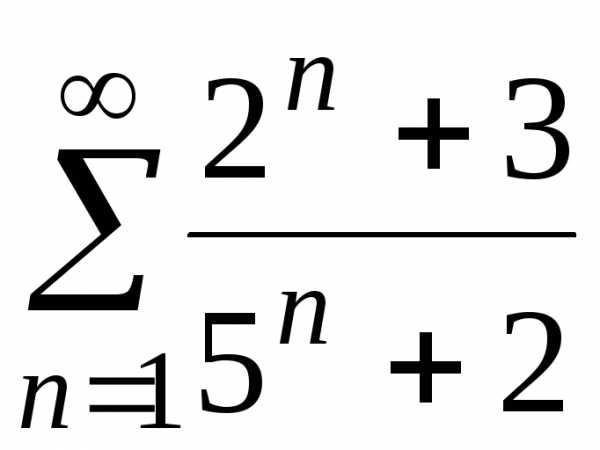 .
.
4. Исследовать ряд на сходимость, используя признак Даламбера
а) 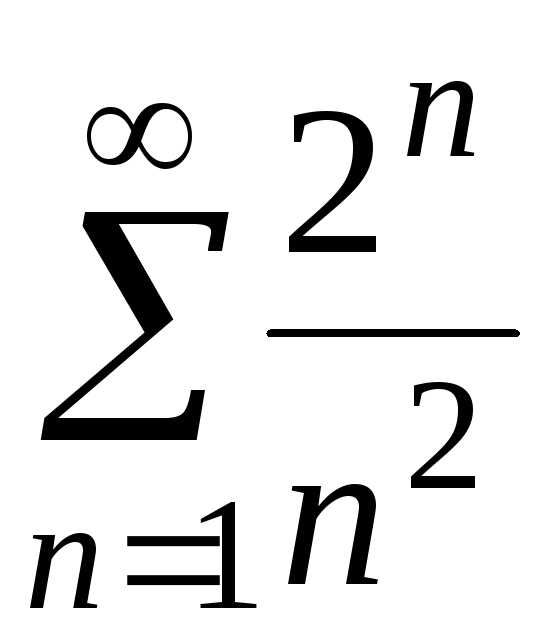 ;
б)
;
б)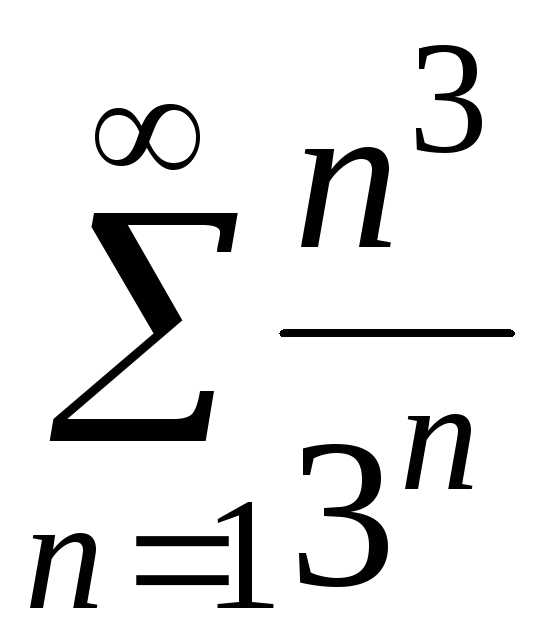 ;
в)
;
в)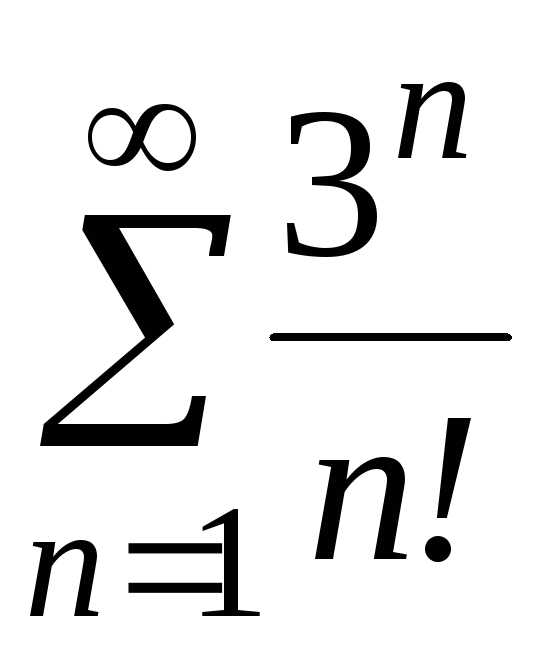 ;
г)
;
г)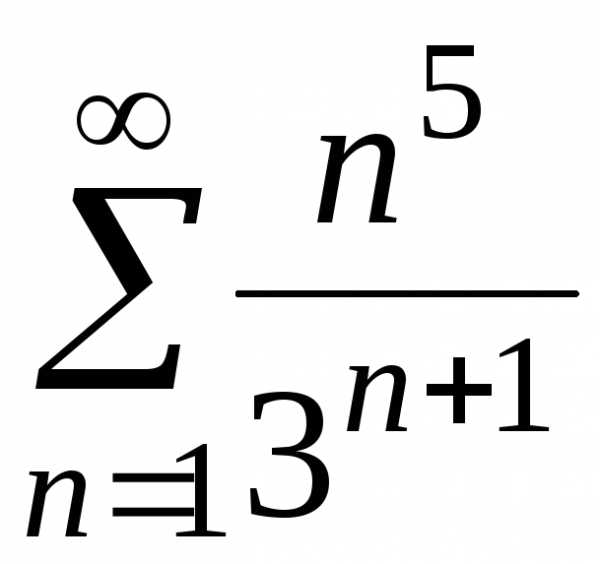 ;
д)
;
д)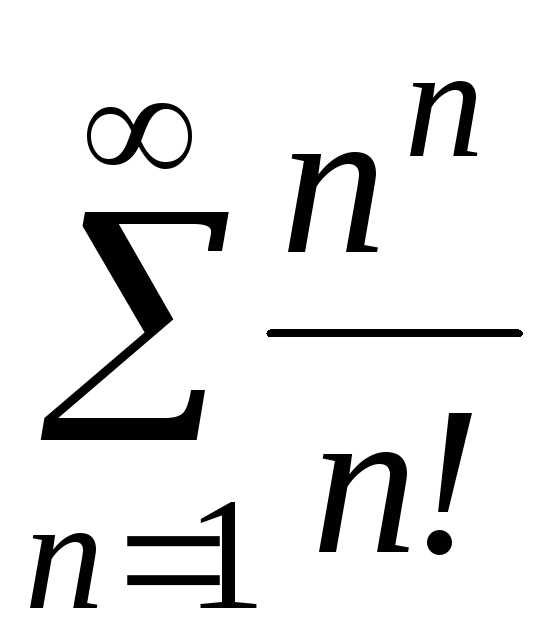 ;
е)
;
е)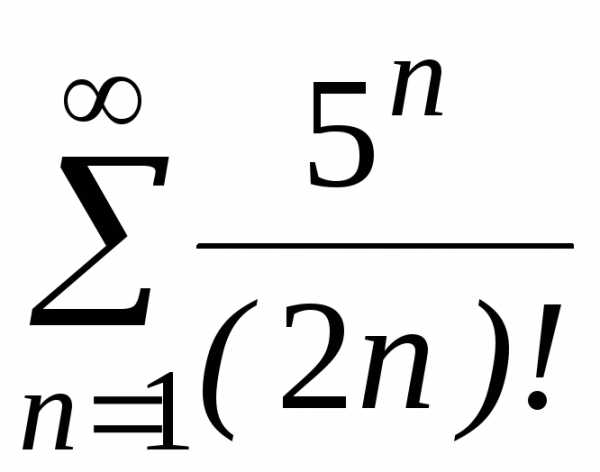 .
.
5. Исследовать ряды на сходимость, применяя признак Коши:
а) 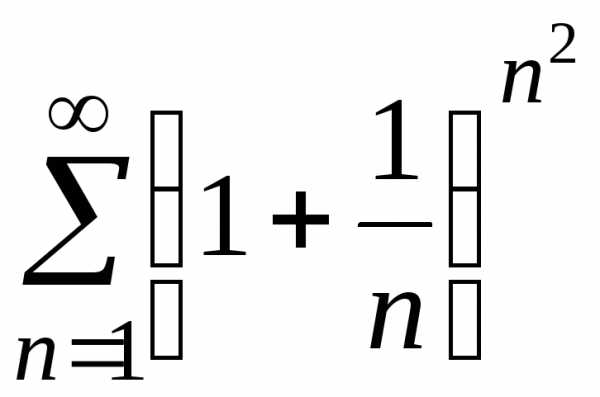 ;
б)
;
б)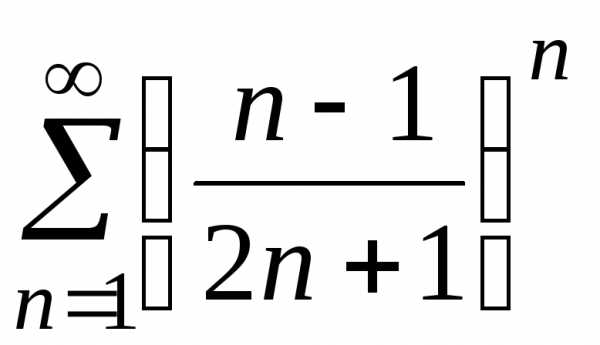 ;
в)
;
в)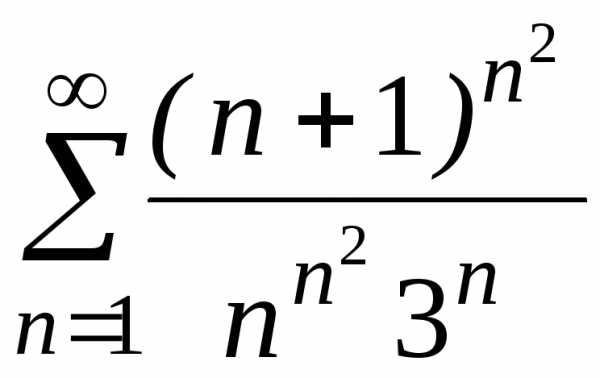 .
.
6. Применяя интегральный признак, исследовать ряды на сходимость:
а) 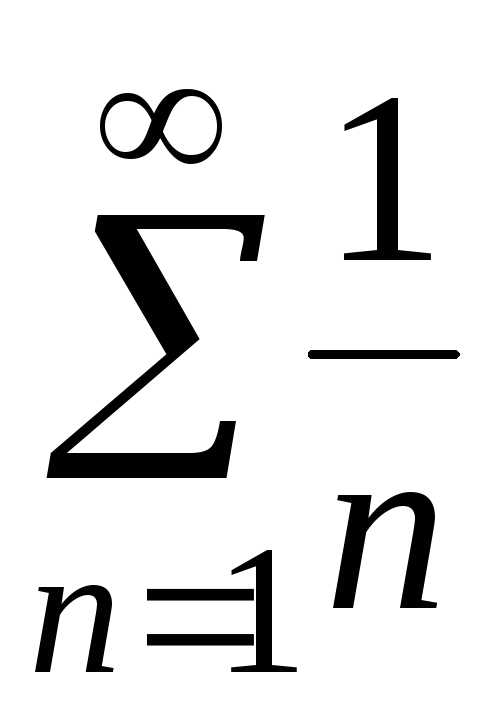 ;
б)
;
б) ;
в)
;
в)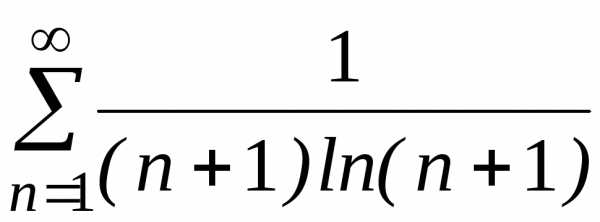 .
.
7. Исследовать на сходимость следующие ряды:
а) 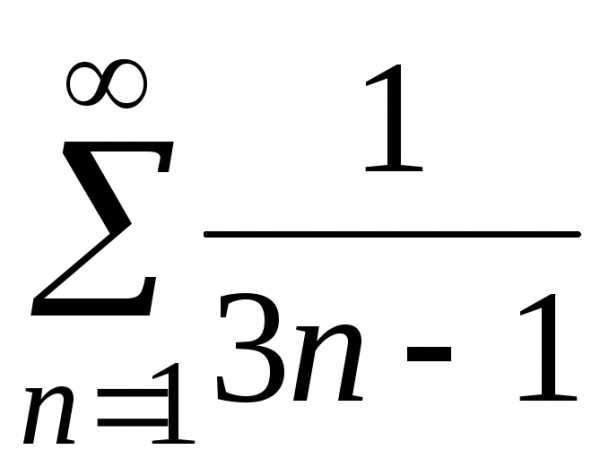 ;
б)
;
б)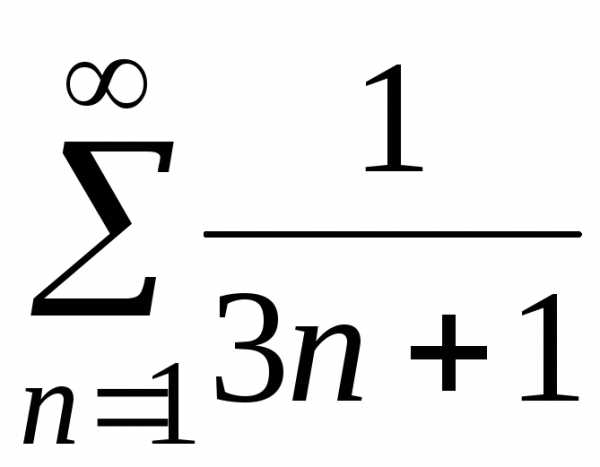 ;
в)
;
в)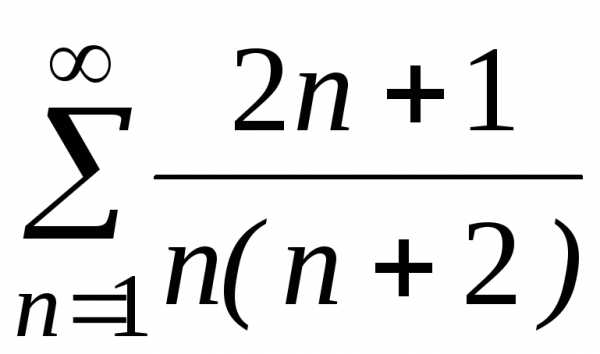 ;
г)
;
г)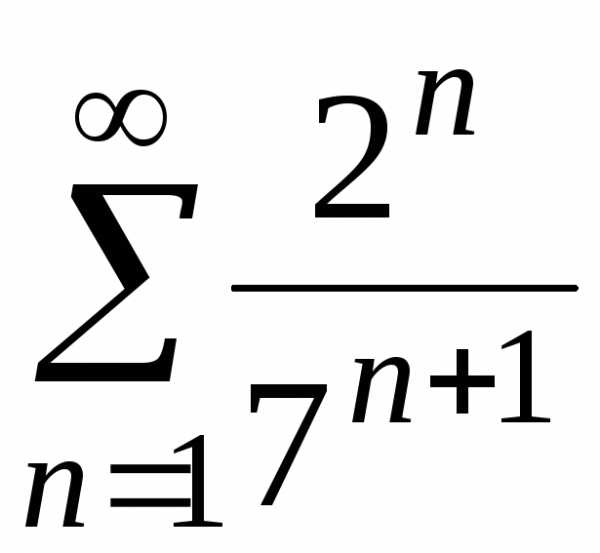 ;
д)
;
д)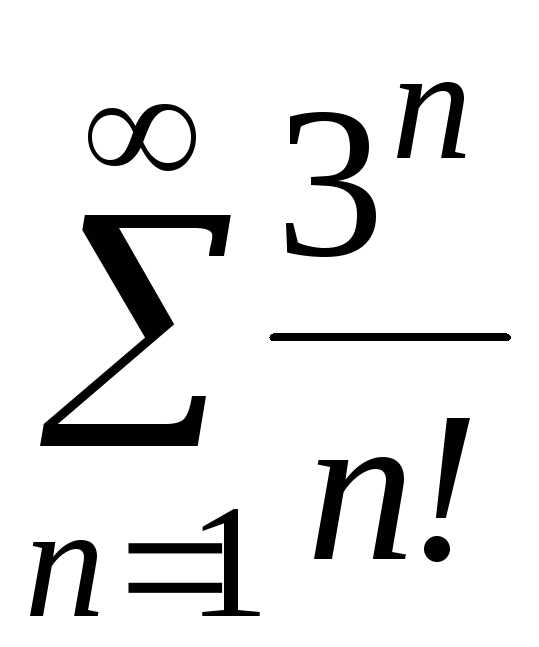 ;
;
е) 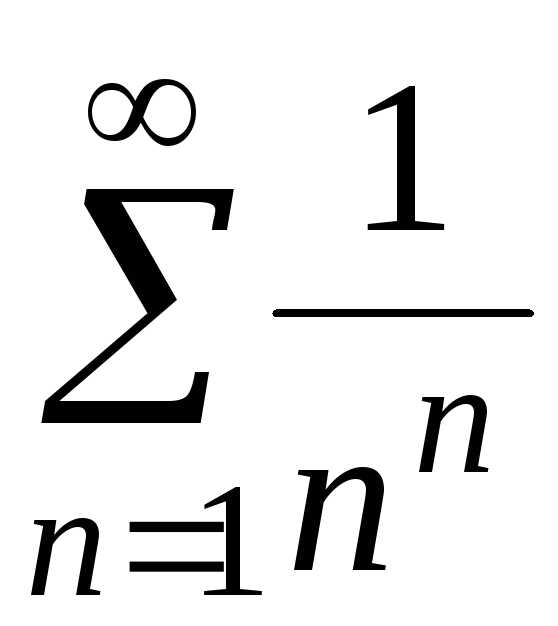 ;
ж)
;
ж)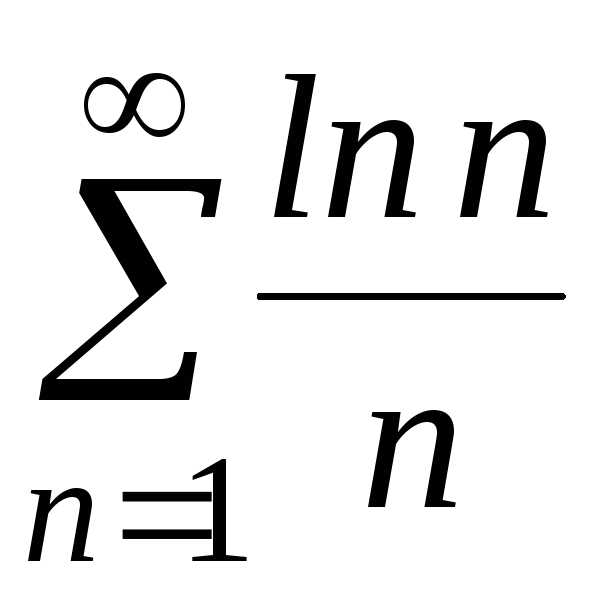 ;
з)
;
з)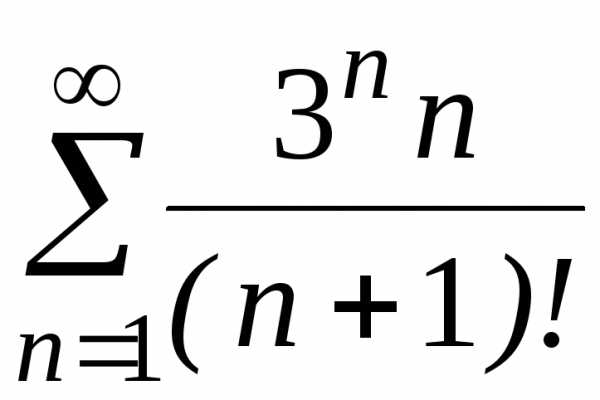 ;
и)
;
и)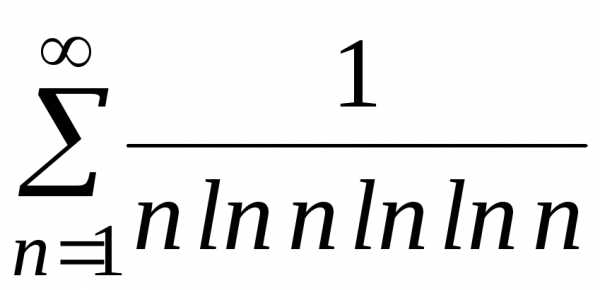 .
.
_______________________
Ответы:
1. а) расходится;
б) 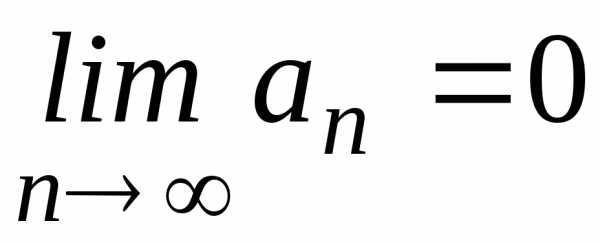 ;
в) расходится; г) расходится;
;
в) расходится; г) расходится;
д) 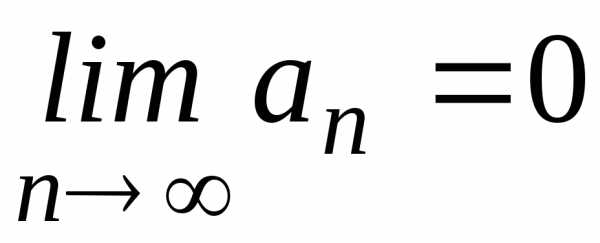 ;
е) расходится.
;
е) расходится.
2. а) сходится; б) расходится; в) расходится; г) сходится;
д) расходится.
3. а) расходится; б) сходится; в) расходится; г) расходится;
д) расходится; е) сходится; ж) сходится; з) сходится.
4. а) расходится; б) сходится; в) сходится; г) сходится;
д) расходится; е) сходится.
5. а) расходится; б) сходится; в) сходится.
6. а) расходится; б) расходится; в) расходится.
7. а) расходится; б) расходится; в) расходится; г) сходится;
д) сходится; е) сходится; ж) расходится; з) сходится;
и) расходится.
studfiles.net
Решение задачи Коши для дифференциального уравнения
Добрый вечер!
Я считаю, что будет лучше всё это показывать сразу на конкретном примере. Нам задано дифференциальное уравнение 1- порядка
А также дано одно начальное условие:
Исходя из известного, мы понимаем, что нам задана задача Коши. Теперь будем разбираться с последовательностью действий, чтоб понять, какое решение задачи Коши для дифференциального уравнения может быть.
Решить задачу Коши — значит найти такое решение заданного дифференциального уравнения, которое сможет удовлетворить начально заданное условие, т.е. нам следует найти частное решение данного дифференциального уравнения.
Первым делом найдём общее решение, а также определим тип уравнения.
Мы знаем, что
Выполним замену:
Домножим на :
Это уравнение с разделяющимися переменными.
Теперь:
Получим:
Теперь у нас дифференциальное уравнение с разделёнными переменными. И мы уже можем проинтегрировать обе части:
Получаем общее решение данного дифференциального уравнения:
Обратимся к начально заданному условию:
Из чего получаем, что:
Подставим в общее решение:
Подставляем уже значение искомого в общее решение дифференциального уравнения:
Это и будет наше решение
Ответ:
ru.solverbook.com

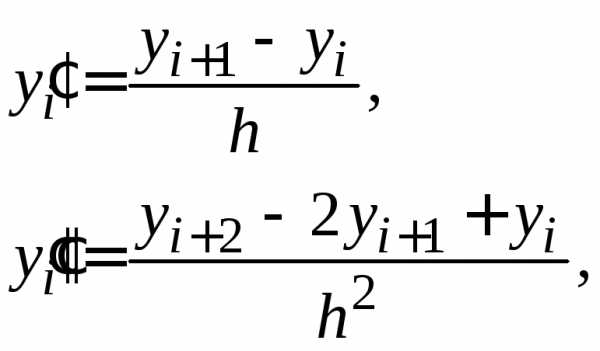
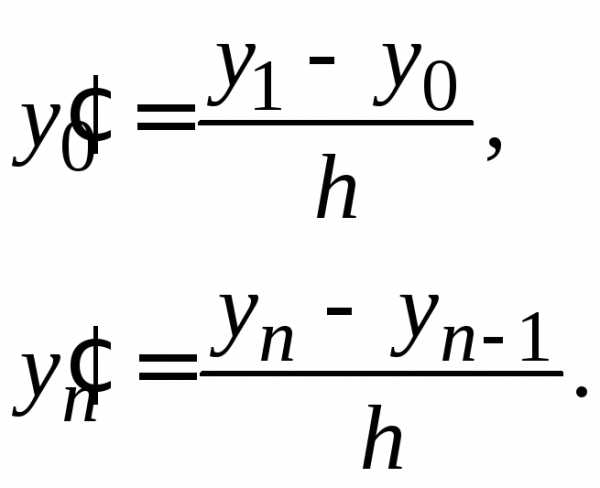
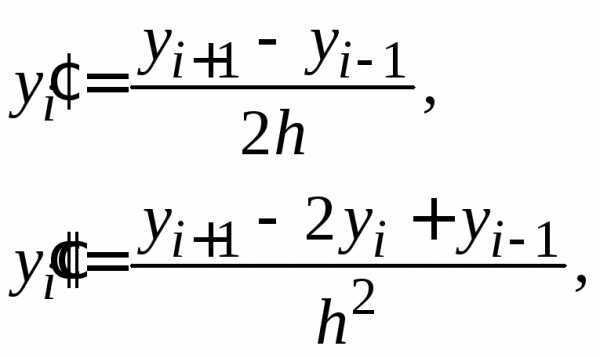
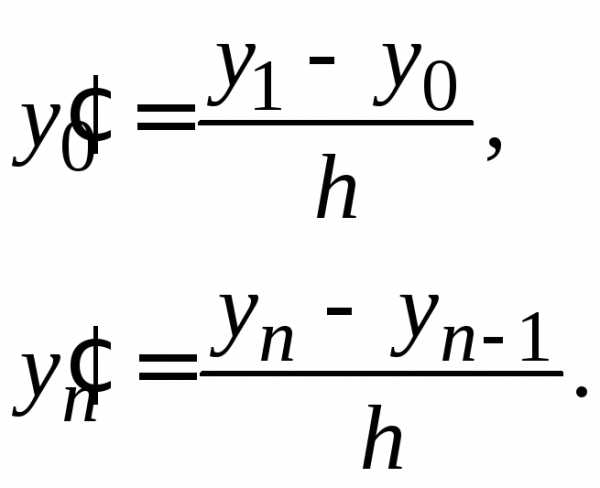
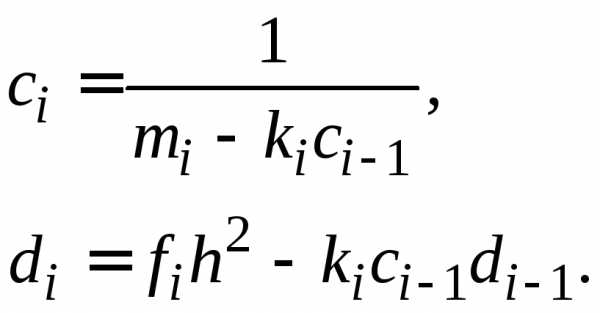
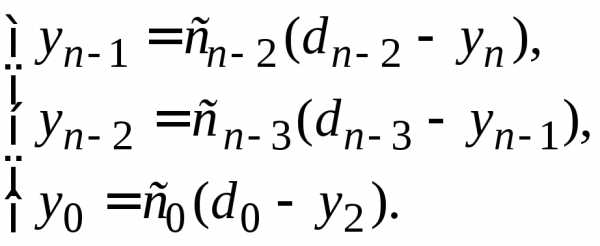
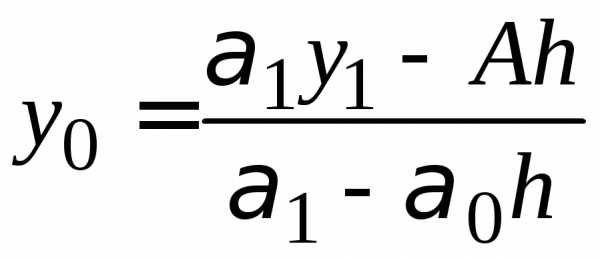
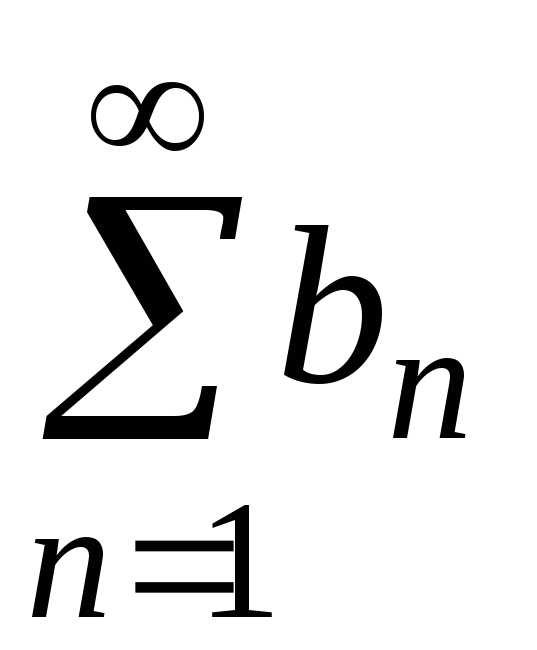 сходится,
то сходится и ряд
сходится,
то сходится и ряд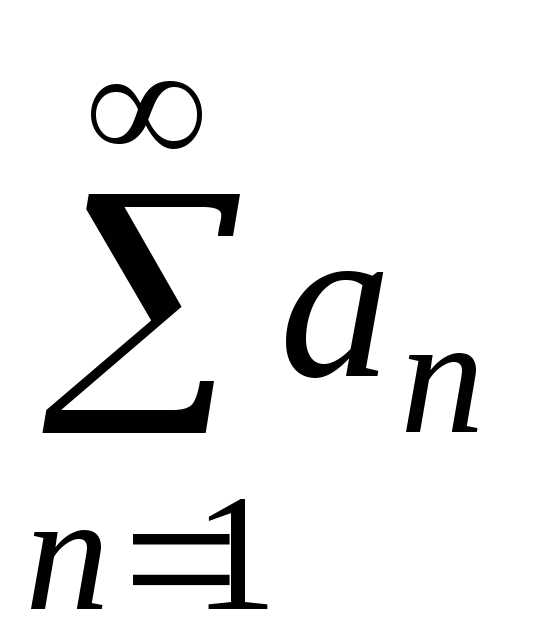 ;
;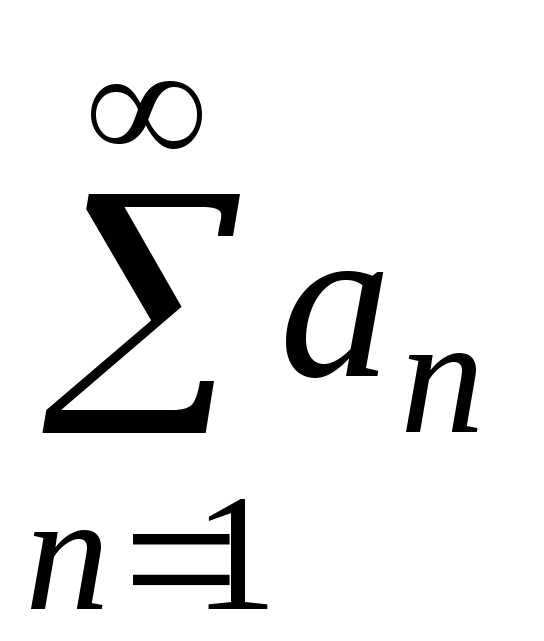 расходится, то расходится и ряд
расходится, то расходится и ряд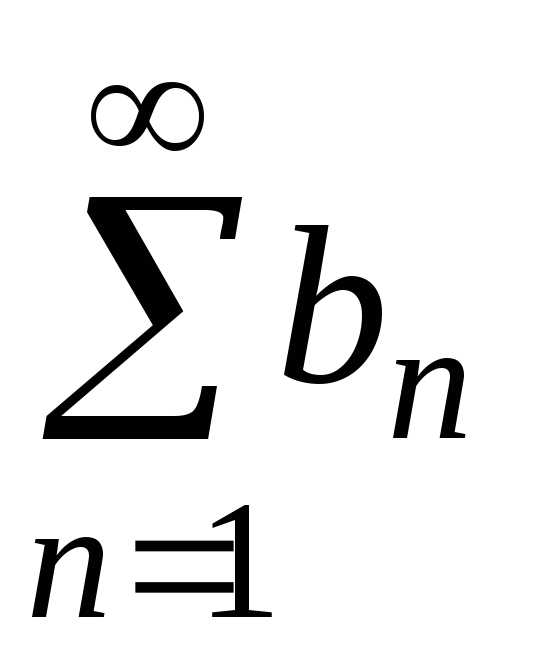 .
.