Логарифмические уравнения простые – Логарифмические уравнения Решения. Разбор примеров..

2.1.6 Логарифмические уравнения

Видеоурок 1: Логарифмические уравнения

Видеоурок 2: Логарифмические уравнения с заменой переменных

Лекция: Логарифмические уравнения

            

Если Вам попалось выражение, функция или уравнение, содержащее логарифмы, то для их упрощения или решения необходимо четко знать и использовать определение и свойства логарифмов.

            

Следует помнить, что логарифм любого положительного числа b по основанию положительного числа а, не равного единице, называется некоторый показатель степени с, в который возводят число а, для получения b.

log_ab = c <=> a^c = b.

            

Также следует помнить основное тождество:

Свойства логарифмов

1. Если имеется логарифм произведения двух чисел больших нуля, то данный логарифм можно записать в виде суммы:

Данное свойство вытекает из основного свойства степени — при умножении степеней их показатели складываются.

2. Логарифм частного двух чисел равен разности двух логарифмов:

Данное свойство было получено из свойства деления степеней — при делении степеней, показатели вычитаются.

3. Если некоторое число в степени находится под знаком логарифма, то показатель степени можно вынести вперед, тем самым, умножив логарифм на показатель:

Данное свойство вытекает из одного из основных свойств степенной функции — при возведении степени в степень показатели степеней перемножаются.

4. Если число и основание логарифма совпадает, то значение такого логарифма равно единице:

5. Логарифм по любому основанию равен нулю, если число равно единице:

6. При любом логарифме можно перейти от одного основания к другому. Для этого необходимо просто воспользоваться формулами:

Основная ошибка, которую допускают большинство — использование некоторого логарифма суммы. Запомните, не существует данной формулы: log_a(b±c) ≠ log_ab ± log_ac.

Свойства логарифмической функции

Для любой логарифмической функции с положительным основанием, не равным единице, справедливы следующие свойства:

• Областью определения данной функции являются все положительные числа.

• Значением логарифмической функции является множество действительных чисел.

• Для основания степени, большего единицы, функция возрастает на всем промежутке рассмотрения.

• Если основание находится в пределах от нуля до единицы, то функция убывает на всем рассматриваемом промежутке.

• Данная функция не является парной или непарной.

• Если переменная равна единице, то функция превращается в ноль, то есть точка, в которой график функции пересекает ось ОХ — это (1;0).

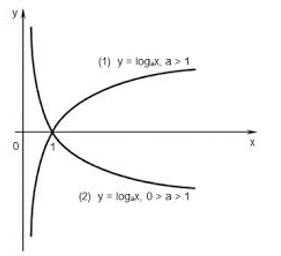
Так как логарифмические функции являются обратными к показательны, то и решения логарифмических уравнений сводится по аналогии к решению показательных уравнений.

Существует три основных вида простейших логарифмических уравнений. Ниже представлены способы их решения:

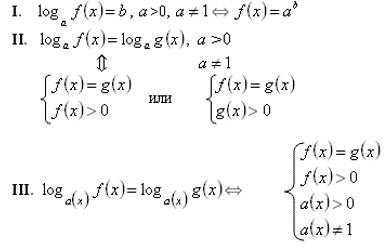
cknow.ru

Логарифмические уравнения

Факт 1.
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\):\[{\color{blue}{a^t=b \quad\Leftrightarrow\quad \log_a{b}=t}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in \mathbb{R}\).
Примеры:

 

1) \(\log_24\) – степень, в которую нужно возвести \(2\), чтобы получить \(4\). Следовательно, \(\log_24=2\).

 

2) \(\log_3\frac13\) – степень, в которую нужно возвести \(3\), чтобы получить \(\dfrac13\). Следовательно, \(\log_3\frac13=-1\).   \(\bullet\) Некоторые важные формулы:

 

(0) при \(a>0, \ a\ne 1, \ b>0\) выполняется основное логарифмическое тождество \[a^{\log_ab}=b\]

(1) при \(a>0,\ a\ne 1\) \[\log_a1=0, \qquad \log_aa=1\]

(2) при \(a>0,\ a\ne 1,\ b>0\) \[\log_{a}{b^m}= m\log_ab\]
\[\log_{a^n}{b}=\frac 1n\log_ab\]
\[\log_{a^n}{b^m}=\frac mn\log_ab\]

при четных \(m\) и \(n\) и \(a\ne 0,\ a\ne 1,\ b\ne 0\) \[\log_{a^n}{b^m}=\dfrac mn\log_{|a|}{|b|}\]

(3) при \(a>0,\ a\ne 1,\ b>0,\ c>0\) \[b^{\log_ac}=c^{\log_ab}\]

(4) при \(a>0,\ a\ne 1,\ bc>0\) \[\log_a{bc}=\log_a{|b|}+\log_a{|c|} \qquad \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\]

(5) при \(a>0,\ a\ne 1,\ b>0,\ b\ne 1,\ c>0\) \[\log_ab\cdot \log_bc=\log_ac \quad\Leftrightarrow\quad \log_bc=\dfrac{\log_ac}{\log_ab}\]
\[\log_ab\cdot \log_ba=1 \quad\Leftrightarrow\quad \log_ba=\dfrac{1}{\log_ab}\]
\(\bullet\) Частный случай формул (2): \[m=\log_a{a^m}\]
С помощью нее нагляднее видно, как заменить число на логарифм по нужному основанию:
\(4=\log_2{2^4}=\log_2{16}\).   \(\bullet\) Формулу (0) удобно использовать, чтобы заменить число на степень с нужным основанием:
\(4=3^{\log_34}\).   \(\bullet\) С помощью формулы \(\log_ba=\dfrac1{\log_ab}\) из (5) можно “менять” основание и аргумент логарифма местами:
\(\log_52=\dfrac1{\log_25}\).

 

\(\bullet\) Логарифмическое уравнение – уравнение, содержащее переменную \(x\) в основании и/или аргументе логарифма.
Простейшее логарифмическое уравнение:

\[\log_a{f(x)}=\log_a{g(x)} \quad \Leftrightarrow \quad \begin{cases} f(x)=g(x)\\ f(x)>0 \ (\text{или }g(x)>0) \end{cases}\] где \(a>0, a\ne 1\).
Неравенства \(f(x)>0\) и \(g(x)>0\) составляют ОДЗ данного уравнения.  

Примеры решения уравнений:
1) Решить уравнение \(\log_{\frac13}(4x+1)=-3\).
Решение.
ОДЗ уравнения: \(4x+1>0\).
Пользуясь определением логарифма, уравнение можно переписать в виде \(\left(\frac13\right)^{-3}=4x+1\). Так как \(\left(\frac13\right)^{-1}=3\), то \(\left(\frac13\right)^{-3}=3^3=27\). Следовательно, получаем уравнение \(27=4x+1\), откуда \(x=6,5\). Данный корень подходит по ОДЗ.   2) Решить уравнение \(\log_{\sqrt5}(2x+15)=4\log_{\sqrt5}2\).
Решение.
ОДЗ уравнения: \(2x+15>0\).
Так как \(m\log_ab=\log_ab^m\), то \(4\log_{\sqrt5}2=\log_{\sqrt5}2^4=\log_{\sqrt5}16\). Следовательно, получаем уравнение \(\log_{\sqrt5}(2x+15)=\log_{\sqrt5}16\). Получили простейшее логарифмические уравнение, которое преобразуется в \(2x+15=16\), откуда \(x=0,5\). Данный корень подходит по ОДЗ.   3) Решить уравнение \(\log_3(2x+1)=\log_3(3-x)+1\).
Решение.
ОДЗ уравнения: \(2x+1>0\) и \(3-x>0\).
Так как \(1=\log_33\), то правая часть равна \(\log_3(3-x)+\log_33=\log_3(3(3-x))\), следовательно, уравнение примет вид \(\log_3(2x+1)=\log_3(9-3x)\). Данное уравнение преобразуется в \(2x+1=9-3x\), откуда \(x=1,6\). Данный корень подходит по ОДЗ.  

Факт 2.
\(\bullet\) Объясним, зачем нужны модули в формулах (2) и (4).

 

1) Рассмотрим частный случай формулы (2) при четном \(m\): \(\log_a{b^m}=m\log_a{|b|}\) на примере.
Рассмотрим: \(\log_3{b^2}=2\log_3{|b|}\).
Зачем модуль? Заметим, что в левую часть равенства можно подставлять вместо \(b\) все числа \(b\ne 0\). Если в правой части не поставить модуль (т.е. \(\log_3b\)), то вместо \(b\) можно подставлять только \(b>0\). Таким образом, теряется часть возможных значений числа \(b\).

 

2) В формулах (4): \[\log_a{bc}=\log_a{|b|}+\log_a{|c|} \ \ \ \ \ \ \text{и} \ \ \ \ \ \ \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\] аналогичная причина: в левую часть равенств можно подставлять как одновременно положительные \(b\) и \(c\), так и одновременно отрицательные (так как произведение двух отрицательных чисел является положительным числом). А вот в правые части, если в них убрать модули, отрицательные \(b\) и \(c\) уже подставлять будет нельзя (так как аргумент логарифма – всегда положительное выражение). Таким образом, не поставив модули, мы значительно сузим возможные значения для \(b\) и \(c\).
Пример:
Если не поставить модули, а записать, например, \(\log_2{bc}=\log_2b+\log_2c\), то значения \(b=-1\) и \(c=-1\) не удовлетворяют равенству. Тогда как с модулями числа \(b\) и \(c\) могут одновременно быть отрицательными.

shkolkovo.net

Логарифмические уравнения

Главный принцип решения логарифмических уравнений состоит в том, чтобы избавиться от этих самых логарифмов:

Если логарифмы обоих чисел по одному и тому же основанию равны, то их подлогарифмические выражения тоже равны:

Также следует помнить основные логарифмические свойства:

Пример 1.

Решите уравнение:

Число 8 обозначает показатель степени, в который нужно возвести основание (2), чтобы получить число (х)

Ответ: x=256..

Пример 2.

Решите уравнение:

Число  обозначает показатель степени, в которой нужно возвести основание (3), чтобы получить число (x)

По свойству логарифмов: получаем:

Ответ: x=9.

Пример 3.

Решите уравнение:

Число  обозначает показатель степени, в которой нужно возвести основание (3), чтобы получить число

По свойству логарифмов:  получаем:

— по Т Виета

Ответ: .

Пример 4.

Решите уравнение:

 

Воспользуемся формулой :

Приводим к общему знаменателю:

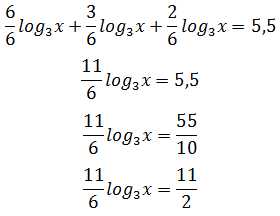
Приводим к общему знаменателю:

Число 3 обозначает показатель степени, в который нужно возвести основание (3), чтобы получить число (х)

Ответ: x=27.

Пример 5.

Решите уравнение:

Приведём логарифмы к общему основанию (5) с помощью формулы :

Сокращаем:

Раскроем  по формуле суммы логарифмов

По свойству логарифмов :

Замена:

Ответ: .

Пример 6.

Решите уравнение:

По формуле  преобразуем левую часть:

Число 0 обозначает показатель степени, в который нужно возвести основание (4), чтобы получить число

Вычислим корень из правой и из левой части:

Ответ: .

Пример 7.

Решите уравнение:

Замена:

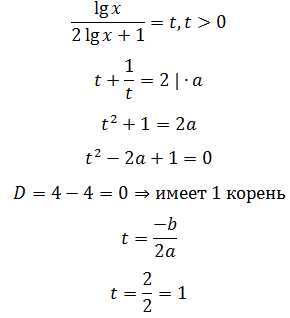
Обратная замена:

Число -1 обозначает показатель степени, в который нужно возвести основание (10), чтобы получить число (x)

Ответ: .

Пример 8.

Решите уравнение:

О.Д.З:

 

3)  – это условие выполняется при любом x, т.к. число в чётной степени. Остаётся только учесть строгость неравенства:

Если дробь равна 0, значит её числитель равен 0:

Произведение равно 0, когда один из его множителей равен 0:

 

По О.Д.З нам подходят корни:

Ответ:

Автор статьи: Дьяков Александр Дмитриевич

Редакторы статьи: Гаврилина Анна Викторовна, Агеева Любовь Александровна

www.teslalab.ru

Логарифмические уравнения — Мои файлы — Каталог файлов

1.  Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся внутри логарифмов. И только там! Это важно.

Вот вам примеры логарифмических уравнений:

log₂х = 32

log₃х = log₃9

log₃(х²-3) = log₃(2х)

log_х+1(х²+3х-7) = 2

lg²(x+1)+10 = 11lg(x+1)

Обратите внимание! Самые разнообразные выражения с иксами располагаются исключительно внутри логарифмов. Если, вдруг, в уравнении обнаружится икс где-нибудь снаружи, например:

log₂х = 3+х ,

это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Кстати, попадаются уравнения, где внутри логарифмов только числа. Например:

х+1 = lg4+lg25

Что тут сказать? Повезло вам, если попалось такое! Логарифм с числами — это какое-то число. И всё. Достаточно знать свойства логарифмов, чтобы решить такое уравнение. Знания специальных правил, приёмов, приспособленных именно для решения логарифмических уравнений, здесь не требуется.

Итак, что такое логарифмическое уравнение — разобрались.

 

2. Решение логарифмических уравнений — штука, вообще-то, не очень простая.Требуется приличный запас знаний по всяким смежным темам. Кроме того, существует в этих уравнениях особая фишка. И фишка это настолько важная, что её смело можно назвать ОДЗ!

Начнём с самых элементарных, простейших уравнений.

Простейшие логарифмические уравнения.

Это уравнения вида:

1.   log₃х = log₃9

2.   log₇(2х-3) = log₇х

3.   log₇(50х-1) = 2

4.   log_х-18 = 1

И так далее.

Процесс решения любого логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них. В простейших уравнениях этот переход осуществляется в один шаг. Потому и простейшие.)

И решаются такие логарифмические уравнения на удивление просто. Смотрите сами.

Решаем первый пример:

log₃х = log₃9

Для решения этого примера почти ничего знать и не надо, да… Чисто интуиция!) Что нам особо не нравится в этом примере? Что-что… Логарифмы не нравятся! Правильно. Вот и избавимся от них. Пристально смотрим на пример, и у нас возникает естественное желание… Прямо-таки непреодолимое! Взять и выкинуть логарифмы вообще. И, что радует, это можно сделать! Математика позволяет. Логарифмы исчезают, получается ответ:

х = 9

Здорово, правда? Так можно (и нужно) делать всегда. Ликвидация логарифмов подобным образом — один из основных способов решения логарифмических уравнений и неравенств. В математике эта операция называется потенцирование. Есть, конечно, свои правила на такую ликвидацию, но их мало. Запоминаем:

Ликвидировать логарифмы безо всяких опасений можно, если у них:

а) одинаковые числовые основания

в) логарифмы слева-справа чистые (безо всяких коэффициентов) и находятся в гордом одиночестве.

Поясню последний пункт. В уравнении, скажем,

log₃х = 2log₃(3х-1)

убирать логарифмы нельзя. Двойка справа не позволяет. Коэффициент, понимаешь… В примере

log₃х+log₃(х+1) = log₃(3+х)

тоже нельзя потенцировать уравнение. В левой части нет одинокого логарифма. Их там два.

Короче, убирать логарифмы можно, если уравнение выглядит так и только так:

log_а(…..) = log_а(…..)

Теперь легко можно решить второй пример:

log₇(2х-3) = log₇х

Собственно, в уме решается. Потенцируем, получаем:

2х-3 = х

х=3

Ну что, очень сложно?) Как видите, логарифмическая часть решения уравнения заключается только в ликвидации логарифмов… А дальше идёт решение оставшегося уравнения уже без них. Пустяшное дело.

Последующие примеры уже так не решить… Тут уже надо знать, что такое логарифм.

Решаем третий пример:

log₇(50х-1) = 2

Видим, что слева стоит логарифм:

log₇(50х-1)

Вспоминаем, что этот логарифм — какое-то число, в которое надо возвести основание (т.е. семь), чтобы получить подлогарифменное выражение, т.е. (50х-1).

Но это число равно двум! По уравнению. Стало быть:

7² = 50х-1

Вот, в сущности, и всё. Логарифм исчез, осталось безобидное уравнение:

50х-1 = 49.

х = 1.

Мы решили это логарифмическое уравнение исходя только из смысла логарифма. Что, ликвидировать логарифмы всё-таки проще?) Согласен. Между прочим, если из двойки логарифм сделать, можно этот пример и через ликвидацию решить. Из любого числа можно логарифм сделать. Причём, такой, какой нам надо. Очень полезный приём в решении логарифмических уравнений и (особо!) неравенств.

Совершенно аналогично (по определению) решается и четвёртое уравнение:

log_х-18 = 1

(х-1)¹ = 8

х-1 = 8

х = 9

Вот и все дела.

Подведём итоги этого урока. Мы рассмотрели на примерах решение простейших логарифмических уравнений. Это очень важно. И не только потому, что такие уравнения бывают на контрольных-экзаменах. Дело в том, что даже самые злые и замороченные уравнения обязательно сводятся к простейшим!

Собственно, простейшие уравнения — это финишная часть решения любых уравнений. И эту финишную часть надо понимать железно! И ещё. Обязательно дочитайте эту страничку до конца. 

 

Решаем теперь самостоятельно. Набиваем руку, так сказать…)

Найти корень (или сумму корней, если их несколько) уравнений:

ln(7х+2) = ln(5х+20)

log_{2(х²+32) = log2(12x)}

log₂х = 4

log₁₆(0,5х-1,5) = 0,25

log_0,2(3х-1) = -3

ln(е²+2х-3) = 2

log_х5 = 0,5

log_{2(14х) = log27 + 2}

Ответы (в беспорядке, разумеется): 42; 12; 9; 25; 7; 1,5; 2; 16.

Всё получилось!? Все примеры «одной левой»?) Поздравляю!

Но…

Пришло время открыть вам горькую правду. Успешное решение этих примеров вовсе не гарантирует успех в решении всех остальных логарифмических уравнений. Даже простейших, подобных этим. Увы.

Дело в том, что решение любого логарифмического уравнения (даже самого элементарного!) состоит из двух равноценных частей. Решение уравнения, и работа с ОДЗ. Одну часть — решение самого уравнения — мы освоили. Не так уж и трудно, верно?

Для этого урока я специально подобрал такие примеры, в которых ОДЗ никак на ответе не сказывается. Но не все такие добрые, как я, правда?…)

Посему надо обязательно освоить и другую часть. ОДЗ. Это и есть главная проблема в решении логарифмических уравнений. И не потому, что трудная — эта часть ещё проще первой. А потому, что про ОДЗ просто забывают. Или не знают. Или и то, и другое). И падают на ровном месте…

В следующем уроке мы расправимся с этой проблемой. Вот тогда можно будет уверенно решать любые несложные логарифмические уравнения и подбираться к вполне солидным заданиям.

u4ilki.ucoz.ru

Лекция по математике тема: «Логарифмические уравнения»

Лекция

Тема: Логарифмические уравнения

План

1. Определение логарифмического уравнения

2. Решение простейших уравнений

3. Потенцирование.

4. Cведение уравнений к виду log _a f(x) = log _a g(x) с помощью свойств логарифмов по одному основанию.

5. Уравнения вида Alog _a f(x) + Blog _b g(x) + C = 0.

6. Введение новой переменной

Определение логарифмического уравнения

Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение вида log_a x = b (где а>0, и а ≠1).

Функция у=log _a x является возрастающей (или убывающей) на промежутке

(0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне) для любого b это уравнение имеет корень, и только один.

Решение простейших уравнений

Простейшими логарифмическими уравнениями будем называть уравнения следующих видов:

log _a x = b, a > 0, a  1.

log _a f(x) = b, a > 0, a  1

.

log _f(x) b = c, b > 0.

Эти уравнения решаются на основании определения логарифма:

если log_b a = c, то a = b^c.

Пример 2.1.

Решение. Область определения уравнения x > 0. По определению логарифма x = 2³, x = 8 принадлежит области определения уравнения.

Ответ: x = 8.

Уравнения вида log_a f(x) = b, a > 0, a ≠ 1.

Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x). Уравнение равносильно следующей системе

Обычно область определения находится отдельно, и после решения уравнения

f(x) = a^b проверяется, принадлежат ли его корни области определения уравнения.

Пример 2.2. log₃(5х – 1) = 2.

Решение: ОДЗ: 5х – 1 > 0; х > 1/5. log₃(5х– 1) = 2, log₃(5х – 1) = log₃3², 5х — 1 =9,
х = 2. Ответ: 2.

Пример 2.3.

Решение. Область определения уравнения находится из неравенства 2х² – 2х – 1 > 0. Воспользуемся определением логарифма:

Применим правила действий со степенями, получим 2х² – 2х – 1 = 3. Это уравнение имеет два корня х = –1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х² – 2х – 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями.

Ответ. х₁

= –1, х₂ = 2.

Уравнения вида log_f(x) b = с, b > 0.

Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе

Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения (f(x))^c = b или равносильного уравнения

проверяется, принадлежат ли его корни найденной области.

Пример 2.4. log_x–19 = 2.

Решение. Данное уравнение равносильно системе

Ответ. x = 4.

Потенцирование.

Суть метода заключается в переходе от уравнения

log _a f(x) = log _a g(x) к уравнению f(x) = g(x), которое обычно

не равносильно исходному.

Уравнения вида log_a f(x) = log_a g(x) , а > 0, а  1.

На основании свойства монотонности логарифмической функции заключаем, что f(x) = g(x).

Переход от уравнения log_a f(x) = log_a g(x) к уравнению f(x) = g(x) называется потенцированием.

Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении

f(x) > 0, g(x) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними.

Пример 3.1 log₃ (x² – 3x – 5) = log₃ (7 – 2x).

Решение. Область определения уравнения найдётся из системы неравенств

Потенцируя данное уравнение, получаем х² – 3х – 5 = 7 – 2х,

х² – х – 12 = 0, откуда х₁ = –3, х₂ = 4. Число 4 не удовлетворяет системе неравенств. Ответ. х = –3.

Cведение уравнений к виду log _a f(x) = log _a g(x) с помощью свойств логарифмов по одному основанию.

Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log _a f(x) = log _a g(x) используются следующие свойства логарифмов:

• log_b a + log_b c = log_b (ac), где a > 0; c > 0; b > 0, b  1,

• log_b a – log_b c = log_b (a/c), где a > 0; c > 0; b > 0, b  1,

• m log_b a = log_b a ^m, где a > 0; b > 0, b  1; mR.

  Пример 4. 1. log₆ (x – 1) = 2 – log₆ (5x + 3).

Решение. Найдём область определения уравнения из системы неравенств

Применяя преобразования, приходим к уравнению

log₆ (x – 1) + log₆ (5x + 3) = 2,

log₆ ((x – 1)(5x + 3)) = 2, далее, потенцированием, к уравнению

(х – 1)(5х + 3) = 36, имеющему два корня х = –2,6; х = 3. Учитывая область определения уравнения, х = 3. Ответ. х = 3.

  Пример 4.2.

Решение. Найдём область определения уравнения, решив неравенство

(3x – 1)(x + 3) > 0 методом интервалов.

Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log₅ (x + 3) ² = 0. По определению логарифма

(х + 3) ² = 1, х = –4, х = –2. Число х = –2 посторонний корень.

Ответ. х = –4.

  Пример 4. 3. log₂ (6 – x) = 2log₆ x.

Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 – x = x², откуда х = –3, х = 2. Число х = –3 посторонний корень.

Ответ. х = 2.

Уравнения вида Alog _a f(x) + Blog _b g(x) + C = 0.

Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы:

 

Пример 5.1.

Решение. Область определения уравнения 1 < x < 2. Используя формулу (3), получим

Так как 3 = log₂8, то на области определения получим равносильное уравнение (2–x)/(x–1) = 8, откуда x = 10/9. Ответ. x = 10/9.

  Пример 5.2.

Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4).Ответ. х = 6.

  Пример 5. 3.

Решение. Область определения уравнения x > –1, x  0. Приведём логарифмы к основанию 3, используя формулу (2).

Умножим обе части уравнения на log ₃(x + 1)  0 и перенесем все слагаемые в левую часть уравнения. Получим (log ₃(x + 1)–1)² = 0, откуда log ₃(x + 1) = 1 и

x = 2. Ответ. x = 2..

Введение новой переменной

Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным.

Уравнения видагде a > 0, a  1, A, В, С – действительные числа.

Пусть t = log_a f(x), tR. Уравнение примет вид t² + Bt + C = 0.

Решив его, найдём х из подстановки t = log_a f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.

Пример 6. 1. lg ² x – lg x – 6 = 0.

Решение. Область определения уравнения – интервал (0; ).Введём новую переменную t = lg x, tR.

Уравнение примет вид t ² – t – 6 = 0. Его корни t₁ = –2, t₂ = 3.

Вернёмся к первоначальной переменной lg x = –2 или lg x = 3,

х = 10 ^–2 или х = 10 ³. Оба значения x удовлетворяют области определения данного уравнения (х > 0).Ответ. х = 0,01; х = 1000.

Пример 6. 2.

Решение. Найдём область определения уравнения

Применив формулу логарифма степени, получим уравнение

Так как х < 0, то | x | = –x и следовательно

Введём новую переменную t = log₃ (–x), tR. Квадратное уравнение

t ² – 4t + 4 = 0имеет два равных корня t_1,2 = 2. Вернёмся к первоначальной переменной log₃ (–x) = 2, отсюда –х = 9, х = –9. Значение неизвестной принадлежит области определения уравнения. Ответ. х = –9.

 Уравнения вида где a > 0, a  1, A, В, С – действительные числа , A0, В0.

Уравнения данного вида приводятся к квадратным умножением обеих частей его на log_a f(x) 0. Учитывая, что log_a f(x) log_f(x) a=1

(свойство log_b a = 1/ log_a b), получим уравнение

Замена log_a f(x)=t, tR приводит его к квадратному At² + Ct + B = 0.

Из уравнений log_a f(x)= t₁ , log_b f(x)= t₂ найдем значения x и выберем среди них принадлежащие области определения уравнения: f(x) > 0, f(x) 1.

 Пример.6.3

Решение. Область определения уравнения находим из условий x+2>0, x+2  1, т.е. x >–2, x  –1.Умножим обе части уравнения на log₅ (x+2) 0, получим

или, заменив log₅ (x+2) = t, придем к квадратному уравнению t ² – t – 2 = 0, t₁ = –1, t₂ =2.

Возвращаемся к первоначальной переменной:

log₅ (x+2) = –1, x+2 = 1/5, x = –9/5,

log₅ (x+2) = 2, x+2 = 25, x = 23.

Оба корня принадлежат области определения уравнения.

Ответ: x = –9/5, x = 23.

Упражнения для закрепления материала

Решить уравнения

1); 2); 3);

4); 5);

Контрольные вопросы

1. Сформулировать определение логарифмического уравнения.

2. Назвать основные методы решения логарифмических уравнений

Литература

1.Ш.А.Алимов, стр.105-111 2 О.Н.Афанасьева, стор.2753-279 3.А.Г.Мерзляк, стор.202-2

infourok.ru

Примеры решения простейших логарифмических уравнений

Рассмотрим примеры решения простейших логарифмических уравнений.

   

ОДЗ: 3x-2>0.

Пока её не ищем.

Далее,

   

   

Возведём 0,5 в степень -2:

   

   

Так как 3x-2=4>0, то условие 3x-2>0 выполняется автоматически, то есть посторонние корни в ходе решения данного уравнения не появятся, и неравенство из ОДЗ можно не решать.

   

   

   

Ответ:2.

   

Запишем ОДЗ, но искать её пока не будем:

ОДЗ: x²+15x>0.

   

   

Так как x²+15x=16>0, то условие x²+15x>0 выполняется автоматически и ОДЗ можно не искать.

   

Корни уравнения можно найти по теореме, обратной теореме Виета:

   

Ответ: -16;1.

   

ОДЗ записываем, но пока не решаем:

   

Далее

   

   

Так как x+1>0, то и (x+1)²>0, поэтому условие 2x²+5x-3>0 выполняется автоматически и первое неравенство можно не решать. Таким образом, для нахождения ОДЗ решаем систему из двух неравенств:

   

Возвращаемся к уравнению. Правая часть — квадрат суммы:

   

   

   

Первый корень не входит в ОДЗ.

Ответ:1.

   

ОДЗ:

   

По определению логарифма,

   

   

Ответ: 2.

   

ОДЗ:

   

   

   

ОДЗ удовлетворяет только x=1.

Ответ: 1.

www.logarifmy.ru

Решение логарифмических уравнений. Часть 1.

Решение логарифмических уравнений. Часть 1.

Логарифмическим уравнением называется уравнение, в котором неизвестное содержится под знаком логарифма ( в частности, в основании логарифма).

Простейшее логарифмическое уравнение имеет вид:

Решение любого логарифмического уравнения предполагает переход от логарифмов к выражениям, стоящим под знаком логарифмов. Однако это действие расширяет область допустимых значений уравнения и может привести к появлению посторонних корней. Чтобы избежать появления посторонних корней, можно поступить одним из трех способов:

1. Сделать равносильный переход от исходного уравнения к системе, включающей область допустимых значений уравнения:

   

или

   

,

в зависимости от того, какое неравенство  или проще.

Если уравнение содержит неизвестное в основании логарифма:

,

то мы переходим к системе:

   

 

2. Отдельно найти область допустимых значений уравнения, затем решить уравнение и проверить, удовлетворяют ли найденные решения ОДЗ уравнения.

3. Решить уравнение, и потом сделать проверку: подставить найденные решения в исходное уравнение, и проверить, получим ли мы верное равенство.

Логарифмическое уравнение любого уровня сложности в конечном итоге всегда сводится к простейшему логарифмическому уравнению.

Все логарифмические уравнения можно  условно разделить на четыре типа:

1. Уравнения, которые содержат логарифмы только в первой степени. Они с помощью  преобразований и использования свойств логарифмов  приводятся к виду

или

Пример. Решим уравнение:

Решение.

Выпишем ОДЗ уравнения:

   

 

Внимание! Мы всегда ищем ОДЗ исходного уравнения, а не того, которое получится в процессе преобразований. То есть ОДЗ записываем перед тем, как переходим к решению уравнения. 

Для упрощения вычислений давайте перенесем логарифмы с отрицательными коэффициентами в противоположную часть уравнения — из соображений, что умножать проще, чем делить:

Представим число 2 в виде логарифма по основанию 4:

Получим уравнение:  

Воспользуемся свойствами логарифмов:

Приравняем выражения, стоящие под знаком логарифма:

Проверим, удовлетворяет ли наш корень ОДЗ уравнения:

   

Да, удовлетворяет.

Ответ: х=5

2. Уравнения, которые содержат логарифмы в степени, отличной от 1 (в частности, в знаменателе дроби). Такие уравнения решаются с помощью введения замены переменной.

Пример. Решим уравнение:

Решение.

Найдем ОДЗ уравнения:

Уравнение содержит логарифмы в квадрате, поэтому решается с помощью замены переменной.

Важно! Прежде чем вводить замену, нужно «растащить» логарифмы, входящие в состав уравнения на «кирпичики», используя свойства логарифмов.

При «растаскивании» логарифмов важно очень аккуратно применять свойства логарифмов:

Кроме того, здесь есть еще одно тонкое место, и, чтобы избежать распространенной ошибки, воспользуемся промежуточным равенством: запишем степень логарифма в таком виде:

Аналогично,

.

Подставим полученные выражения в исходное уравнение. Получим:

Теперь мы видим, что неизвестное  содержится в уравнении в составе . Введем замену: . Так как может принимать любое действительное значение, на переменную мы никаких ограничений не накладываем.

Получили уравнение:

Раскроем скобки, приведем подобные члены и решим квадратное уравнение:

,

Вернемся к исходной переменной:

,  

Отсюда:

,  

Ответ: ,  

Решение  логарифмических уравнений остальных типов мы рассмотрим здесь и здесь.

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru