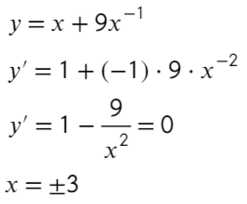Максимум функции это – Максимум и минимум функции

Значения функции и точки максимума и минимума

Значения функции и точки максимума и минимума

Наибольшее значение функции 

Наменьшее значение функции 

Точки max 

Точки min

 

---

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

1. Найти точку максимума / минимума (просят найти значения «x»).
   
2. Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

1. Взять производную от предложенной функции.
2. Приравнять ее к нулю.
3. Найденный или найденные «х» и будут являться точками минимума или максимума.
4. Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

Задания с ЕГЭ: 

Найдите точку максимума функции 

• Берем производную:

• Приравняем ее к нулю:
• Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15

Найдите точку минимума функции

• Преобразуем и возьмем производную: 

• Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

• Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

1. Взять производную от предложенной функции.
   
2. Приравнять ее к нулю.
   
3. Найденный «х» и будет являться точкой минимума или максимума.
   
4. Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
5. В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
6. Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции. 

Задания с ЕГЭ: 

Найдите наибольшее значение функции на отрезке [−4; −1] 

• Преобразуем и возьмем производную: 
• «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

• Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6

Найдите наибольшее значение функции на отрезке [0; 1,5π]

• Берем производную:
• Находим, чему равняется sin(x):
• Но такое невозможно! Sin(x)…
• Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:

• Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
  

Ответ: 11

Выводы:

1. 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
   
2. Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
3. Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
4. В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
5. А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.

ik-study.ru

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут

точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

         

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с \(-13\): до \(-13\) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что \(-13\) – точка максимума.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

\(-7\): минимум.

\(3\): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции \(f'(x)\). 
2. Найдите корни уравнения \(f'(x)=0\). 
3. Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
4. Определите знак производной в каждом промежутке (методом интервалов). 
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью). 
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   — если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума;
   — если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума;
   — если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

\(15x^4-60x^2=0\)      \(|:15\)
\(x^4-4x^2=0\)
\(x^2 (x^2-4)=0\)
\(x=0\)       \(x^2-4=0\)
               \(x=±2\)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Ответ. \(-2\).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

cos-cos.ru

Максимум функции · Как пользоваться Контрольная Работа РУ

Максимум функции определяется как экстремум функции, но добавляются дополнительные условия.

Воспользуйтесь калькулятором по нахождению максимума функции:

Получим результат:

Максимум равен y=1/e, в точке x=1

Для того, чтобы найти экстремумы, нужно решить уравнение $$\frac{d}{d x} f{\left (x \right )} = 0$$ (производная равна нулю), и корни этого уравнения будут экстремумами данной функции: $$\frac{d}{d x} f{\left (x \right )} = $$ Первая производная $$- x e^{- x} + e^{- x} = 0$$ Решаем это уравнение
Корни этого ур-ния: $$x_{1} = 1$$ Зн. экстремумы в точках:
-1 (1, e )
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумов у функции нет.
Максимумы функции в точках: $$x_{1} = 1$$ Убывает на промежутках
(-oo, 1]
Возрастает на промежутках
[1, oo)

Определение максимума функции

Максимум функции — это максимальное значение на данном промежутке. Максимум находится так:
Решается уравнение : «Производная функции равна 0» для неизвестной x (если функция зависит от x) и смотрится при найденном x как меняет точка знак производной функции, проходя через эту точку

Другой простой пример максимума функции

Рассмотрим функцию -x^2. Ее производная равна -2*x (Кстати производная функции находится здесь) — решаем уравнение -2*x = 0 — значит x = 0.

Смотрим — производная -2x при x > 0 — меньше 0, а при x < 0 производная больше 0.

Значит при x=0 функция -x^2 имеет максимум. Вот такой простой пример.

www.kontrolnaya-rabota.ru

Экстремумы функции, максимум и минимум

ОПРЕДЕЛЕНИЕ

Экстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.

Точки экстремума функции

Говорят, что в точке максимум (минимум), если существует такая -окрестность точки — , что для всех из этой окрестности, отличных от выполняется неравенство .

ОПРЕДЕЛЕНИЕ

Точки максимума и минимума называются точками экстремума.

ОПРЕДЕЛЕНИЕ Точки области определения, в которых производная функции равна нулю или не существует, называются критическими точками.

Необходимое условие существования экстремума функции. Пусть функция дифференцируема в промежутке . Если в некоторой точке функция имеет экстремум, то в этой точке производная равна нулю: .

Достаточное условие существования экстремума функции. Если производная функции равна нулю в точке и при переходе через эту точку в сторону возрастания меняет знак с «+» («-») на «-» («+»), то в точке функция имеет максимум (минимум). Если же при переходе через точку производная функции не меняет знак, то в этой точке функция экстремума не имеет.

Для исследования функции на экстремум необходимо:

1. найти критические точки функции;
2. проверить, изменяет ли знак производная функции при переходе через критическую точку;
3. вычислить значения максимума или минимума .

Примеры исследования функции на экстремум

ПРИМЕР 1

Задание	Найти экстремум функции
Решение	Найдем критические точки функции, для этого вычислим производную заданной функции     приравняем её к нулю и найдем корни полученного квадратного уравнения     Получили две критические точки . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах. В точке производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума     В точке производная меняет знак с «-» на «+», значит, — точка минимума. Значение минимума соответственно равно
Ответ

ПРИМЕР 2

Задание	Найти экстремум функции
Решение	Область определения функции — вся числовая прямая, за исключением точки , то есть . Вычислим производную заданной функции и найдем критические точки     Приравниваем к нулю производную     Получаем одну критическую точку . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах В точке производная меняет знак с «-» на «+», значит, в этой точке минимум. Значение минимума соответственно равно
Ответ

Читайте также:

Монотонность функции

Нули функции

Наибольшее и наименьшее значение функции

Точки перегиба функции

Промежутки выпуклости и вогнутости функции

Исследование функции

ru.solverbook.com

матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек

Экстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Определения

Пусть дана функция и— внутренняя точка области определенияТогда

Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.

Значение функции называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

Достаточные условия существования локальных экстремумов

 является точкой строгого локального максимума. А если

то является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке 

 и 

 является точкой локального максимума. А если

 и 

то является точкой локального минимума.

Если чётно и, то- точка локального максимума. Есличётно и, то- точка локального минимума. Еслинечётно, то экстремума нет.

Максимум и минимум функции.

Приведем точные определения точек экстремума.  Определение. Точка x₀ называется точкой минимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≥ f(x₀.  Это наглядно показано на рисунке 1:    рисунок 1  Определение. Точка x₀ называется точкой максимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≤ f(x₀.  Это наглядно показано на рисунке 2:    рисунок 2  По определению значение функции f в точке x₀ является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x₀ имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно).  В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис. 2 а) и б) соответственно).  Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже:    Слева направо: a — точка максимума; a — точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума.  Для точек минимума и максимума функции есть общее определение — точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название — экстремум функции. Точки максимума обычно обозначают x_max, а точки минимума — x_min.

Критической точкой дифференцируемой функции , где  — область в , называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.

studfiles.net

Как найти экстремум (точки минимума и максимума) функции

Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.

• Находим производную функции
• Приравниваем эту производную к нулю
• Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
• Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
• Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.

Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.

Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.

https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru

Рассмотрим пример
Находим производную и приравниваем её к нулю:

Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.

Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.

Смотрите также:

Еще больше материалов для подготовки к ЕГЭ

bugaga.net.ru

МАКСИМУМ И МИНИМУМ ФУНКЦИИ — это… Что такое МАКСИМУМ И МИНИМУМ ФУНКЦИИ?



МАКСИМУМ И МИНИМУМ ФУНКЦИИ

наибольшее и соответственно наименьшее значения функции, принимающей действительные значения. Точку области определения рассматриваемой функции, в к-рой она принимает максимум или минимум, наз. соответственно точкой максимума или точкой минимума (см. Максимума и минимума точки).Если нек-рая точка является точкой абсолютного (локального) максимума или минимума, строгого или нестрогого, то значение функции в этой точке наз. абсолютным (локальным), соответственно строгим или нестрогим максимумом или минимумом. Если функция непрерывна на компакте, то она всегда принимает на нем максимальное и минимальное значения.

М. и м. ф. называется ее экстремумом.

Л. Д. Кудрявцев.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

• МАКСИМИННЫИ КРИТЕРИЙ
• МАКСИМУМА И МИНИМУМА ТОЧКИ

Смотреть что такое «МАКСИМУМ И МИНИМУМ ФУНКЦИИ» в других словарях:

• МАКСИМУМ И МИНИМУМ ФУНКЦИИ — соответственно наибольшее и наименьшее значения функции по сравнению с её значениями во всех достаточно близких точках. Точки максимума и минимума называются точками экстремума …   Большая политехническая энциклопедия

• МАКСИМУМ И МИНИМУМ — (от латинского maximum и minimum наибольшее и наименьшее) (математическое), наибольшее и наименьшее значения функции по сравнению с ее значениями в достаточно близких точках. Точки максимума и минимума называются точками экстремума …   Современная энциклопедия

• МАКСИМУМ И МИНИМУМ — (лат. maximum и minimum букв. наибольшее и наименьшее), в математике наибольшее и наименьшее значения функции по сравнению с ее значениями в достаточно близких точках. Точки максимума и минимума называются точками экстремума …   Большой Энциклопедический словарь

• Максимум и минимум — (от латинского maximum и minimum наибольшее и наименьшее) (математическое), наибольшее и наименьшее значения функции по сравнению с ее значениями в достаточно близких точках. Точки максимума и минимума называются точками экстремума.   …   Иллюстрированный энциклопедический словарь

• максимум и минимум — (лат. maximum и minimum, буквально  наибольшее и наименьшее) (матем.), наибольшее и наименьшее значения функции по сравнению с её значениями в достаточно близких точках. На рисунке функция у = f(х) имеет в точках x1 и х3 максимум, а в точке х2 … …   Энциклопедический словарь

• МАКСИМУМ И МИНИМУМ — (лат. maximum и minimum, букв. наибольшее и наименьшее) (матем.), наибольшее и наименьшее значения функции по сравнению с её значениями в достаточно близких точках. На рис. функция y = f(x) имеет в точках х1 и х3 максимум, а в точке х2 минимум.… …   Естествознание. Энциклопедический словарь

• Локальный максимум, локальный минимум — (local maxi­mum, local minimum) см. Экстремум функции …   Экономико-математический словарь

• МИНИМУМ — см. Максимум и минимум функции, Максимума и минимума точки …   Математическая энциклопедия

• МАКСИМУМ — (maximum) самое большое число (величина или ценность), наибольший предел, до которого что либо может достигнуть. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МАКСИМУМ наибольшая величина из рассматриваемых… …   Словарь иностранных слов русского языка

• МАКСИМУМ — МАКСИМУМ, максимума, муж. (лат. maximum наибольшее). 1. Наибольшее, предельное количество; ант. минимум. Проявить максимум энергии. Максимум знаний. Максимум и минимум (наибольшее и наименьшее значение функции; мат.). 2. в знач. нареч. Самое… …   Толковый словарь Ушакова

Книги

• Математическое просвещение. Выпуск 4, Р. Н. Бончковский, Сборники Математическое просвещение содержат оригинальные статьи по элементарным разделам математики, по методике и истории математики, отделы текущей жизни, задач, библиографии и т. д.… Издатель: Книга по Требованию, Производитель: Книга по Требованию, Подробнее  Купить за 2591 грн (только Украина)
• Математическое просвещение. Выпуск 4, Р. Н. Бончковский, Сборники «Математическое просвещение» содержат оригинальные статьи по элементарным разделам математики, по методике и истории математики, отделы текущей жизни, задач, библиографии и т. д.… Серия: — Издатель: ЁЁ Медиа, Подробнее  Купить за 2003 руб
• чистоПитание. Книга о чистой, простой и сильной пище (подарочное издание), Вадим Зеланд, Роскошное полноцветное издание в бархатном переплете с фотографиями автора — это настоящее воплощение мечты для всех последователей `Трансерфинга реальности` и отличный подарок для вас и… Серия: Трансерфинг реальности Издатель: ИГ Весь, Производитель: ИГ Весь, Подробнее  Купить за 1055 грн (только Украина)

Другие книги по запросу «МАКСИМУМ И МИНИМУМ ФУНКЦИИ» >>

dic.academic.ru

No related posts.