Двойной интеграл, формулы и примеры
Определение двойного интеграла
Пусть в замкнутой области , принадлежащей плоскости , задана непрерывная функция . Разобьем эту область на элементарных областей , площади которых будем обозначать как , а наибольшее расстояние между точками соответствующей области – через (рис. 1).
В каждой элементарной области выберем произвольную точку . Значение функции в этой точке умножим на площадь соответствующей элементарной области и все такие произведения просуммируем:
Полученная сумма называется интегральной суммой функции в области .
Найдем предел указанной интегральной суммы при таким образом, чтобы . Если такой предел существует и не зависит ни от способа разбиения области на элементарные области, ни от способа выбора в них точек , то он называется двойным интегралом от функции по области и обозначается . Итак, двойной интеграл определяется равенством
Область называется областью интегрирования, и – переменные интегрирования, функция – подынтегральной функцией, которая является интегрируемой в области ; – элементом площади.
Свойства двойного интеграла
1. Константу можно выносить за знак двойного интеграла:
где
2. Двойной интеграл суммы/разности двух функций равен сумме/разности интегралов от каждой из них:
3. Если область интегрирования можно разбить на две области и , например, как это показано на рисунке 2, то
4. Если в области интегрирования функция , то и двойной интеграл .
5. Если функции и в области удовлетворяют неравенству , то справедливо и неравенство
6. , где – это площадь области .
7. Если функция непрерывна в замкнутой области , площадь которой равна , то
где и – наименьшее и наибольшее значения подынтегральной функции в области соответственно.
8. Если функция непрерывна в замкнутой области , площадь которой равна , то в этой области существует такая точка , что имеет место равенство:
Величина называется средним значением функции в област .
Пусть область интегрирования – это прямоугольник со сторонами, параллельными координатным осям и которые определяются уравнениями , ; , (рис. 3). В этом случае двойной интеграл вычисляется по одной из формул:
или
Интегралы, стоящие в правых частях этих формул, называются повторными или двукратными. В первой формуле интеграл называется внутренним. Он вычисляется в предположении, что переменная сохраняет на отрезке интегрирования постоянное фиксированное значение (то есть является константой). При таком предположении подынтегральная функция – функция одной переменной . В результате вычисления этого интеграла получаем функцию переменной .
После того, как эта функция определена, нужно выполнить внешнее интегрирование – проинтегрировать полученную функцию по переменной . В результате второго интегрирования получаем уже число.
Примеры решения задач
ru.solverbook.com
Как вычислить двойной интеграл
Как вычислить двойной интеграл? Примеры решений
Прозвучал удар гонга, который открывает второй раунд в бою с двойными интегралами. Если вы недавно надели перчатки или вообще боксируете с грушей, то, пожалуйста, начните с первого раунда Двойные интегралы для чайников. Настоятельно рекомендую разобраться со всеми примерами вводного урока без халтуры, это очень важно. К тому же, добрый дядя Саша нарисовал много картинок, которые можно распечатать и наклеить у себя в туалете. Помните, что Коперник свои блестящие открытия в астрономии делал именно там.
Однако задорное получилось вступление…. Задумался вот… почему? Да потому что мне хорошо. А отчего хорошо, поясню в конце статьи.
Вспоминаем общую запись двойного интеграла:
В первой статье Двойные интегралы для чайников я очень подробно рассмотрел понятие двойного интеграла, алгоритм его решения, важнейшие задачи на обход области интегрирования. Также были прорешаны простейшие двойные интегралы в примерах на нахождение площади плоской фигуры.
Снова посмотрим на общую запись двойного интеграла и заметим, что в нём притаилась функция двух переменных . А когда речь заходит о функции двух переменных, то это часто попахивает сероводородом частными производными второго порядка. Поэтому для освоения примеров вам необходимо уметь более или менее уверенно их находить.
В большинстве практических задач требуется формально вычислить двойной интеграл, но, помимо этого, он обладает отличным геометрическим смыслом – с помощью двойного интеграла помимо площади можно вычислить еще и объём. Геометрический смысл двойного интеграла поясню ниже на конкретных примерах.
Начинаем набивать наш двойной интеграл разнообразной начинкой:
Пример 1
Вычислить двойной интеграл , Изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Решение: Изобразим
область интегрирования на
чертеже: 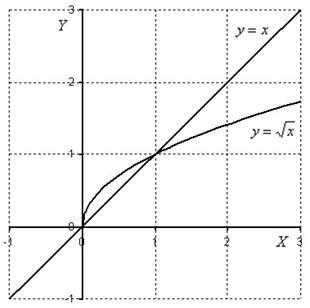
Напоминаю, что выполнение чертежа – необходимый начальный этап решения. Чертёж крайне важно выполнить правильно и точно, поскольку ошибка в графике незамедлительно запорет всё задание.
Выберем следующий порядок обхода:
Вопросы порядка обхода области интегрирования, я комментировать практически не буду, пожалуйста, смотрите статью Двойные интегралы для чайников.
Таким образом:
Обратите внимание на следующее действие: в данном случае можно вынести «икс» из внутреннего интеграла во внешний интеграл. Почему? Во внутреннем интеграле интегрирование проводится по «игрек», следовательно, «икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
С интегралами настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
Вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл , при этом ни в коем случае не забываем про «икс», который там уже находится:
Готово.
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
Для
наглядности еще раз приведу чертёж, он
будет точно таким же, но с другими
обозначениями графиков: 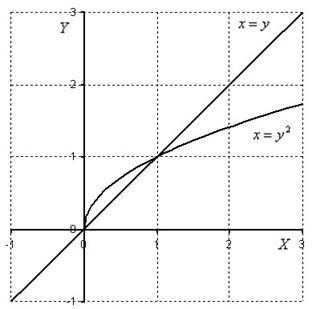
Второй способ обхода области:
Таким образом:
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
Вместо «икса» подставляются функции! Всегда проявляйте повышенное внимание при подстановке пределов интегрирования.
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
Результаты совпали, значит, задание выполнено верно.
Если есть время, постарайтесь всегда проводить проверку, даже если этого не требуется в условии: вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Ответ:
Пример 2
Вычислить двойной интеграл , Выполнить проверку: изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Это пример для самостоятельного решения. Обратите внимание, что в двойном интеграле изначально присутствует константа. А константу можно вынести за знак двойного интеграла, в данном случае: В ходе решения вынесение константы целесообразно проводить в момент перехода к повторным интегралам.
Как видите, свойство линейности справедливо не только для «обычных», но и для кратных интегралов. Интеграл от интеграла недалеко падает.
Самое главное потом при вычислениях вынесенную константу не потерять. А забывают о ней часто.
Примерный образец чистового оформления примера в конце урока.
Двойной интеграл как объем тела
Рассмотрим основной геометрический смысл двойного интеграла . Предполагаем, что функция существует в каждой точке плоской области .
Геометрически функция двух переменных задаёт некоторую поверхность в трехмерном пространстве. Для определенности считаем, что , то есть поверхность располагается над плоскостью .
Тогда
двойной интеграл численно равен
объёму цилиндрического
бруса : 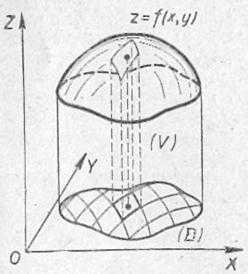
Что такое цилиндрический брус, думаю, всем понятно из чертежа. Плоская фигура (заштрихована на чертеже) полностью лежит в плоскости и брус ограничен областью снизу. Сверху брус как раз ограничен поверхностью , которая представляет собой такую шапку. Образно говоря, плоская область по своей границе перпендикулярными лучами вырезает из поверхности эту шапочку.
Дополнительно
поясню геометрический смысл на Примере
1. В нём мы рассматривали двойной
интеграл ,
причём область интегрирования имела
следующий вид: 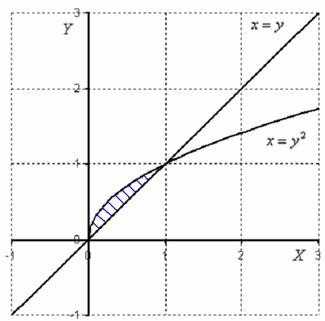
Подынтегральная функция задаёт плоскость в пространстве. Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси . В данном примере плоскость располагается в пространстве над областью , поэтому объем тела получился положительным: . Возможно, не всем до конца понятно, о каком объеме идёт речь: из границы области направьте на себя лучи. Эти лучи вырежут кусочек из плоскости , которая лежит над областью .
Двойной интеграл может быть и отрицательным, в таких случаях график функции полностью (или бОльшей частью) лежит под областью . Это тоже объем тела, только со знаком минус, поскольку поверхность полностью (или бОльшей частью) лежит подкоординатной плоскостью .
Прошу прощения, пока не подыскал программы для построения трехмерных чертежей, которая бы меня устраивала, пришлось объяснять на пальцах.
Однако на практике почти всегда встречаются задачи на формальное вычисление двойных интегралов, поэтому мы продолжим совершенствовать технику вычислений:
Пример 3
Вычислить двойной интеграл ,
Решение: Изобразим
область интегрирования на чертеже: 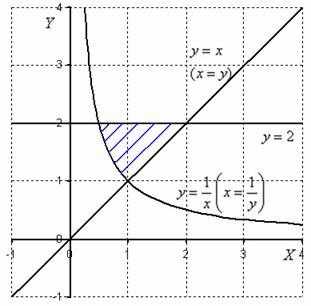
После того, как корректно выполнен чертеж и правильно найдена область интегрирования, самое время разобраться с порядком обхода.
Согласно первому способу обхода, область придется разделить на две части, при этом необходимо будет вычислить следующие интегралы:
Энтузиазма, прямо скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным функциям, переход здесь элементарен:
Порядок обхода области:
Таким образом:
Ну вот, совсем другое дело. И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу можно сразу вынести во внешний интеграл
1) Найдём внутренний интеграл:
Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначалавместо «икса» мы подставили верхний предел интегрирования , затем вместо «икса» подставили нижний предел интегрирования . Будьте внимательны при подстановках!
2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про , который там уже находится:
Ответ:
Для тренировки можете попробовать вычислить двойной интеграл менее рациональным способом: . Результаты должны совпасть.
Пример 4
Вычислить двойной интеграл ,
Это пример для самостоятельного решения. Постройте область и проанализируйте, какой способ обхода области выгоднее использовать. Полное решение и ответ в конце урока.
Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов:
Пример 5
Вычислить двойной интеграл ,
Решение: Сначала рассмотрим то, чего делать не нужно – в данном случае не следует использовать свойства линейности кратного интеграла и представлять его в виде: Почему? Вычислений заметно прибавится!
Решение,
как обычно, начинаем с построения области
интегрирования: 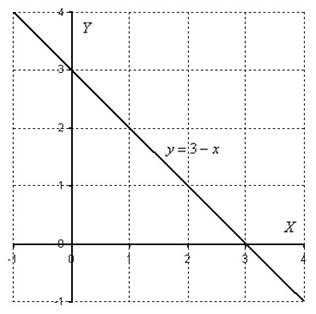
Область незамысловата, даже штриховать не буду. В данном примере, как легко заметить, не имеет особого значения порядок интегрирования, поэтому выберем первый, более привычный вариант обхода области:
Таким образом:
Здесь, в отличие от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является сумма.
С повторными интегралами опять разбираемся по отдельности. Да, кстати, кто хочет посмотреть, как решать повторные интегралы одной строкой, пожалуйста, зайдите на страницу Готовые решения по высшей математике и закачайте архив с примерами решений кратных интегралов.
1) Сначала берём внутренний интеграл:
Хотелось бы остановиться на нескольких существенных моментах. Во-первых, о частном интегрировании. О нём я уже подробно рассказывал в статье Дифференциальные уравнения в полных дифференциалах. Вкратце повторюсь:
Если интегрирование проводится по «игрек», то переменная «икс» считается константой. И наоборот.
Тем не менее, вот нашли вы первообразную и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»: Получена исходная подынтегральная функция, значит, всё в порядке.
Момент второй, подстановка пределов интегрирования. По стандартной формуле Ньютона-Лейбница сначала вместо «игреков» мы подставили , а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
И, наконец, может показаться странным результат: Ведь можно раскрыть скобки и привести подобные слагаемые! В данном случае это сделать несложно, и чайникам, вероятно, лучше так и поступить. Но если будет не вторая, а 3-я или 4-ая степень? На самом деле линейную функцию в степени выгоднее проинтегрировать, не раскрывая скобок! Данный прием я уже применял и подробно комментировал во втором параграфе урока Как вычислить объем тела вращения? Ещё раз посмотрим, как он работает:
2) Берём оставшийся внешний интеграл:
При нахождении интеграла использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
Ответ:
Пример 6
Вычислить двойной интеграл ,
Это пример для самостоятельного решения. В образце решения, как и в разобранном примере, использован первый способ обхода области.
На практике немало примеров, где трудно (а то и невозможно) обойтись без микрокалькулятора-«дробовика». Рассмотрим практический пример на данную тему:
Пример 7
Вычислить двойной интеграл по области
Задача будет решена двумя способами, так как готовое решение у меня уже есть =) А если серьезно, второй способ будет нужен для дополнительных важных комментариев.
Решение: Изобразим область интегрирования на чертеже:
Область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях.
Выберем следующий порядок обхода области: Таким образом:
1)
Начинающим чайникам всегда рекомендую выполнять проверку, особенно в подобных примерах: возьмите частную производную по «игрек» от первообразной и получите подынтегральную функцию .
Будьте предельно внимательны в подстановке пределов интегрирования: сначала вместо«игреков» подставляем , затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
2) Второй шаг прост:
Перейдём к обратной функции и изменим порядок обхода области:
Таким образом:
1) Вычислим внутренний интеграл:
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Не лишней будет и промежуточная проверка, возьмём частную производную по «икс» от найденной первообразной: Получена подынтегральная функция, что и хотелось увидеть.
Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем вместо «иксов» подставляем . После подстановки должны остаться только «игреки».
Степени рекомендую оставить в виде , а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
2)
Результаты совпали, как оно и должно быть.
Легко заметить, что первый способ решения был заметно проще. Всегда перед решением анализируйте – какой путь легче и короче.
Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю вручную. Но не удивляйтесь, если на практике получится ответ вроде , по крайне мере, в своей коллекции я нашел немало диких примеров, где без микрокалькулятора-«дробовика» фактически не обойтись.
Ответ:
Ответ получился отрицательным. Геометрически это обозначает, что график подынтегральной функции (поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования под плоскостью .
Пример 8
Вычислить двойной интеграл по области
Это пример для самостоятельного решения. Ответ будет целым – чтобы от своего хорошего настроения не запугать вас окончательно =). Похожие двойные интегралы встречаются в известном задачнике Кузнецова, и по этой причине пример тоже уместен. Полное решение и ответ в конце урока.
Студенты-заочники почти всегда сталкиваются с двойными интегралами наподобие тех, которые уже рассмотрены, но никто не застрахован от творческих примеров, где в подынтегральной функции есть какие-нибудь синусы, косинусы, экспоненты и т.п.
Рассмотрим заключительные примеры на данную тему:
Пример 9
Вычислить двойной интеграл по области
Решение: В ходе выполнения чертежа может возникнуть трудность с построением прямой , которая параллельна оси . Ничего сложного: если , то – примерно на этом уровне и следует провести прямую.
Выполним чертёж:
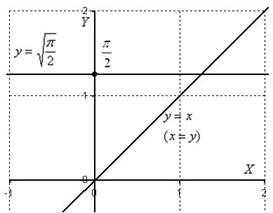
После выполнения чертежа нужно выяснить, какой порядок обхода области выгоднее применить.
Рассмотрим первый способ обхода: Тогда:
Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл придётся дважды брать по частям.
Но есть еще и второй способ обхода области: Следовательно:
Выглядит гораздо привлекательнее, начинаем вычисления:
1) По формуле Ньютона-Лейбница разберемся с внутренним интегралом:
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Если возникают трудности с интегрированием, можно прибегнуть даже к такому способу: временно замените «игрек» конкретным числом, например, «пятёркой»: . Теперь замените «пятёрку» обратно – «игреком»:
И, конечно же, лучше сделать проверку, продифференцировав первообразную по «икс»:
Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем , затем – ноль. После подстановки должны остаться только «игреки».
2) Полученный результат перемещаем во внешний интеграл, не забывая, что там уже есть и константа 4:
Второй интеграл взят методом подведения функции под знак дифференциала.
Ответ:
Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от подынтегральной функции.
Пример 10
Вычислить двойной интеграл по области
Это пример для самостоятельного решения.
Хочется привести ещё примеры, но в первом раунде я обещал не маньячить, поэтому скрепя сердце, заканчиваю статью. Множество других примеров на вычисление двойных интегралов можно найти в соответствующем архиве на странице Готовые решения по высшей математике. Если тема проработана качественно, то рискну предположить, что многие читатели самостоятельно смогут разобраться и в тройных интегралах – принципы решения очень похожи!
Раскрою секрет хорошего настроения – в аккурат перед вторым раундом на ринг вышла симпатичная девушка с табличкой 222. С вашего позволения, заключительное мудрое пожелание:
Хорошо должно быть каждый день!
Решения и ответы:
studfiles.net
Вычисление двойного интеграла. Двукратный интеграл / Двойной интеграл / 3dstroyproekt.ru
Определение простой { правильной } области
Область $ \mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Oxy } } $будем называть $\textbf { простой { правильной } в направлении оси } \quad \mathbf { \textit { Oy } } $, если любая прямая, проходящая через внутреннюю точку области $\mathbf { \textit { D } } $ и параллельная оси $\mathbf { \textit { Oy } } $, пересекает границу $\mathbf { \textit { D } } $ в двух точках.
Аналогично определяется область, $\textbf { простая { правильная } в направлении оси } \mathbf { \textit { Ox } } $: любая прямая, проходящая через внутреннюю точку области $\mathbf { \textit { D } } $ и параллельная оси $\mathbf { \textit { Oх } } $, пересекает границу $\mathbf { \textit { D } } $ в двух точках.
Область, правильную { простую } в направлении обеих осей, будем называть $\textbf { правильной } $.

$y=\varphi _1 (x) y=\varphi _2 (x)$ Ограниченную замкнутую область $\mathbf { \textit { D } } $, правильную в направлении оси $\mathbf { \textit { Oy } } $, можно описать неравенствами
$D:\left[ \begin{array} { l } a\leqslant x\leqslant b, \newline \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \newline \end{array} \right].$
Числа $\mathbf { \textit { a } } $ и $\mathbf { \textit { b } } $ существуют вследствие ограниченности области $\mathbf { \textit { D } } $, функция $\varphi _1 (x)$ образована нижними точками пересечения прямой $\mathbf { \textit { x } } =\mathbf { \textit { x } } _ { 0 } $ при $a<x_0 <b$ с границей области $\mathbf { \textit { D } } $, функция $\varphi _2 (x)$ — верхними точками пересечения этой прямой с границей области $\mathbf { \textit { D } } $.
Аналогичным образом область $\mathbf { \textit { D } } $, ограниченную, замкнутую и правильную в направлении оси $\mathbf { \textit { Oх } } $, можно описать неравенствами
$D:\left[ \begin{array} { l } c\leqslant y\leqslant d, \newline \psi _1 (y)\leqslant x\leqslant \psi _2 (y) \newline \end{array} \right].$
Функция $\psi _1 (y)$ образована левыми точками пересечения прямой $\mathbf { \textit { y } } =\mathbf { \textit { y } } _ { 0 } $ при $c<y_0 <d$ с границей области $\mathbf { \textit { D } } $, функция $\psi _2 (y)$ — правыми точками пересечения этой прямой с границей области $\mathbf { \textit { D } } $.
$x=\psi _2 (y) x=\psi _1 (y)$ Для правильной области { т.е. области, правильной в направлении обеих осей } существуют оба способа представления:
$D:\left[ \begin{array} { l } a\leqslant x\leqslant b, \newline \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \newline \end{array} \right]$ и $D:\left[ \begin{array} { l } c\leqslant y\leqslant d, \newline \psi _1 (y)\leqslant x\leqslant \psi _2 (y) \newline \end{array} \right].$
Двукратный { повторный } интеграл
Пусть $\mathbf { \textit { D } } $ — область, простая в направлении оси $\mathbf { \textit { Oy } } $. Рассмотрим выражение $J(D)=\int\limits_a^b { \left( { \int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } }\right)dx } $. Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по $\mathbf { \textit { у } } $ во внутреннем интеграле { переменная $\mathbf { \textit { х } } $ при этом рассматривается как постоянная } и подстановки по $\mathbf { \textit { у } } $ в пределах от $\varphi _1 (x)$ до $\varphi _2 (x)$ получается функция, зависящая только от $\mathbf { \textit { х } } $, которая интегрируется в пределах от $\mathbf { \textit { a } } $ до $\mathbf { \textit { b } } $. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
$$ J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } . $$
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области $\mathbf { \textit { D } } $: $\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { dy } } =\int\limits_a^b { dx\cdot \left. y \right|_ { \varphi _1 (x) } ^ { \varphi _2 (x) } } =\int\limits_a^b { \left[ { \varphi _2 (x)-\varphi _1 (x) }\right]dx } =s(D)$;
$y=\varphi _1 (x) y=\varphi _2 (x)$ теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться — это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область $\mathbf { \textit { D } } $ разбита на две подобласти $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $ прямой, параллельной одной из координатных осей, то двукратный интеграл по области $\mathbf { \textit { D } } $ равен сумме интегралов по $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $: $\mathbf { \textit { J } } (\mathbf { \textit { D } } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.
Первый случай:
прямая $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 1 } $ параллельна оси $\mathbf { \textit { Oy } } $. Тогда $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } $ { аддитивность внешнего интеграла } = $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.
$y=\varphi _2 (x) y=\varphi _2 (x)$
Второй случай:
прямая $\mathbf { \textit { y } } =\mathbf { \textit { c } } _ { 1 } $ параллельна оси $\mathbf { \textit { Oх } } $. Воспользуемся сначала аддитивностью внешнего интеграла: $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } = y=\varphi _1 (x) =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =$ { теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом } $\textbf { = } \int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\left[ { \int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } +\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } }\right] } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } = $ { применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму } =$ =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =$ $ =\left [ { \int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } + } \int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } }\right ]+ \left [ { \int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } }\right ] $
первая скобка даёт повторный интеграл по $\mathbf { \textit { D } } _ { 1 } $, вторая — по $_ { } \mathbf { \textit { D } } _ { 2 } =\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.
Понятно, что возможны различные случаи взаимного расположения прямых $\mathbf { \textit { y } } =\mathbf { \textit { c } } _ { 1 } $, $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 1 } $, $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 2 } $ и функций $y=\varphi _1 (x)$, $y=\varphi _2 (x)$, но логика доказательства во всех случаях такая же.
Обобщим доказанное свойство. Пусть прямая разбивает область $\mathbf { \textit { D } } $ на две подобласти $\mathbf { \textit { D } } _ { 1,1 } $ и $\mathbf { \textit { D } } _ { 1,2 } $. Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает $\mathbf { \textit { D } } _ { 1,1 } $ на $\mathbf { \textit { D } } _ { 1 } $ и$\mathbf { \textit { D } } _ { 2 } $; $\mathbf { \textit { D } } _ { 1,2 } $ — на $\mathbf { \textit { D } } _ { 3 } $ и $\mathbf { \textit { D } } _ { 4 } $. По доказанному, $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,1 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$, $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,2 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 3 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 4 } )$, поэтому $\mathbf { \textit { J } } (\mathbf { \textit { D } } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,2 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 3 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 4 } )$. Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область $\mathbf { \textit { D } } $ с помощью прямых, параллельных координатным осям, разбита на подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } , { \ldots } , \mathbf { \textit { D } } _ { n } $, то $J(D)=J(D_1 )+J(D_2 )+\ldots +J(D_n )=\sum\limits_ { i=1 } ^n { J(D_i ) } $.
Теорема о переходе от двойного интеграла к повторному
Пусть $\mathbf { \textit { D } } $ — простая в направлении оси $\mathbf { \textit { Oy } } $ область. Тогда двойной интеграл от непрерывной функции по области $\mathbf { \textit { D } } $ равен повторному интегралу от той же функции по области $\mathbf { \textit { D } } $: $\iint\limits_D { f(x,y)dxdy } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } $.
Док-во: Разобьём область $\mathbf { \textit { D } } $ с помощью прямых, параллельных координатным осям, на подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } $, { \ldots } , $\mathbf { \textit { D } } _ { n } $. По доказанному выше, $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\sum\limits_ { i=1 } ^n { J(D_i ) } $. К каждому из интегралов $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { i } )$ применим теорему о среднем: в любой области $\mathbf { \textit { D } } _ { i } $ найдётся точка $\mathbf { \textit { P } } _ { i } $ такая, что $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { i } )=\mathbf { \textit { f } } (\mathbf { \textit { P } } _ { i } ) \quad \mathbf { \textit { s } } (\mathbf { \textit { D } } _ { i } )$. Следовательно, $J(D)=\sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } $. В последнем равенстве справа стоит интегральная сумма для двойного интеграла $\iint\limits_D { f(x,y)dxdy } $. Будем мельчить разбиение области так, чтобы $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )\to 0$. Вследствие непрерывности функции $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$ по теореме существования интегральная сумма при этом стремится к двойному интегралу $\iint\limits_D { f(x,y)dxdy } $, т.е. в пределе получим $\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\iint\limits_D { f(x,y)dxdy } $, что и требовалось доказать.
Если область $\mathbf { \textit { D } } $ правильная в направлении оси $\mathbf { \textit { Oх } } $, то аналогично доказывается формула $\iint\limits_D { f(x,y)dxdy } =\int\limits_с^d { dy\int\limits_ { \psi _1 (y) } ^ { \psi _2 (y) } { f(x,y)dx } } $. Если $\mathbf { \textit { D } } $ правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул: $\iint\limits_D { f(x,y)dxdy } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\int\limits_с^d { dy\int\limits_ { \psi _1 (y) } ^ { \psi _2 (y) } { f(x,y)dx } } $.
Если область не является правильной, её разбивают на правильные подобласти.
3dstroyproekt.ru
