степенные ряды — ПриМат
Пусть дан степенной ряд вида $\sum\limits_{n=0}^{\infty}c_{n}z^n$ с радиусом сходимости $R$, где $c_n$,$z^{n}\in \mathbb{C}$. Тогда для этого ряда справедлива следующая теорема:
Теорема о вычислении радиуса сходимости степенного ряда
- Если существует конечный или бесконечный предел$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_n \right |}$, то $$\frac{1}{R}=\lim\limits_{n\to\infty}\sqrt[n]{\left | c_n \right |}. (1)$$
- Если существует конечный или бесконечный предел $\lim\limits_{n \to\infty} \left | \frac{c_{n}}{c_{n+1}} \right |$, то $$R=\lim\limits_{n \to\infty} \left | \frac{c_{n}}{c_{n+1}} \right | .(2)$$
Доказательство:
- Докажем формулу (1). Пусть $\lim\limits_{n\to\infty}\sqrt[n]{\left | c_n \right |} = \rho$.
- Если $0<\rho<+\infty$, и $z_0$ — произвольная точка из круга $K=\left \{z:\left |z\right | < \frac{1}{\rho}\right \}$, то $$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_{n} \cdot z_{0}^{n} \right |} = \left | z_{0} \right | \cdot \lim\limits_{n\to\infty}\sqrt[n]{\left |c_{n} \right |} = \left |z_{0} \right | \cdot \rho < 1.$$ По признаку Коши сходимости ряда, ряд сходится в точке $z_{0}$. В силу того, что точка $z_{0}$ — произвольная точка круга $K$, исходный ряд сходится в $K$.
Предположим, что точка $z_{m}$ не принадлежит кругу $K$, то есть $\left |z_{m} \right | > \frac{1}{\rho}$.Тогда $$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_{n} \cdot z_{m}^{n} \right |} = \left | z_{m} \right | \cdot \lim\limits_{n\to\infty}\sqrt[n]{\left |c_{n} \right |} = \left |z_{m} \right | \cdot \rho > 1.$$ По признаку Коши, ряд расходится.
Значит, ряд сходится в круге $K$, и расходится вне его замыкания. Это значит, что $\frac{1}{\rho}$ — радиус сходимости исходного ряда.Круг сходимости $K$ c нанесенными точками $z_{0}$ и $z_{m}$
[свернуть]
- Если $\rho = 0$, то $\forall z \in \mathbb{C}$ выполняется следующее: $$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_{n} \cdot z^{n} \right |} = \left | z \right | \cdot \rho = 0 .$$ По признаку Коши ряд сходится в точке $z$. В силу произвольности точки $z$ ряд сходится на всей комплексной плоскости. И это значит, что радиус сходимости ряда $R=+\infty$.
- Пусть $\rho = +\infty$. Тогда $\forall z \neq 0$ $$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_{n} \cdot z^{n} \right |} = \left | z \right | \cdot \rho = +\infty. $$ По признаку Коши, ряд расходится в точке $z$. Отсюда выходит, что радиус сходимости $R = 0$.
- Если $0<\rho<+\infty$, и $z_0$ — произвольная точка из круга $K=\left \{z:\left |z\right | < \frac{1}{\rho}\right \}$, то $$\lim\limits_{n\to\infty}\sqrt[n]{\left | c_{n} \cdot z_{0}^{n} \right |} = \left | z_{0} \right | \cdot \lim\limits_{n\to\infty}\sqrt[n]{\left |c_{n} \right |} = \left |z_{0} \right | \cdot \rho < 1.$$ По признаку Коши сходимости ряда, ряд сходится в точке $z_{0}$. В силу того, что точка $z_{0}$ — произвольная точка круга $K$, исходный ряд сходится в $K$.
- Доказательство (2) по сути идентично доказательству (1). Различие в том, что будет использоваться признак Даламбера сходимости ряда. Для этого выполним следующие преобразования: $$ R=\lim\limits_{n \to\infty} \left | \frac{c_{n}}{c_{n+1}} \right | = \frac{\lim\limits_{n \to \infty}\left | c_{n} \right |}{\lim\limits_{n \to \infty}\left | c_{n+1} \right |} = \frac{1}{(\frac{\lim\limits_{n \to \infty}\left | c_{n+1} \right |}{\lim\limits_{n \to \infty}\left | c_{n} \right |})} = \frac{1}{\lim\limits_{n \to\infty} \left | \frac{c_{n+1}}{c_{n}} \right |}.$$
Пусть $\lim\limits_{n \to \infty}\left | \frac{c_{n+1}}{c_{n}} \right | = \rho$- Если $0<\rho<+\infty$, и $z_0$ — произвольная точка из круга $K=\left \{z:\left |z\right | < \frac{1}{\rho}\right \}$, то $z_0$ так же по модулю меньше, чем $\frac{1}{\rho}$. Отсюда следует, что $$\lim\limits_{n \to \infty}\left | \frac{c_{n+1} \cdot z_{0}^{n+1}}{c_{n} \cdot z_{0}^{n}}\right |=\left | z \right | \cdot \lim\limits_{n \to \infty}\left | \frac{c_{n+1}}{c_{n}}\right |=\left |z \right | \cdot \rho < 1.$$ По признаку Даламбера сходимости ряда, ряд сходится в точке $z_{0}$. В силу того, что точка $z_{0}$ — произвольная точка круга $K$, исходный ряд сходится в $K$.
Значит, ряд сходится в круге $K$, и расходится вне него. А это значит, что $\frac{1}{\rho}$ — радиус сходимости исходного ряда. - Пусть $\rho = 0$, то $\forall z \in \mathbb{C}$ выполняется следующее:$$\lim\limits_{n \to \infty}\left | \frac{c_{n+1} \cdot z_{0}^{n+1}}{c_{n} \cdot z_{0}^{n}}\right |=\left |z \right | \cdot \rho = 0. $$ По признаку Даламбера, ряд сходится в точке $z$. В силу произвольности $z$ ряд сходится на всей комплексной плоскости. И это значит, что радиус сходимости ряда $R=+\infty$.
- Пусть $\rho = +\infty$. Тогда $\forall z \neq 0$ $$\lim\limits_{n \to \infty}\left | \frac{c_{n+1} \cdot z_{0}^{n+1}}{c_{n} \cdot z_{0}^{n}}\right |=\left |z \right | \cdot \rho = +\infty. $$ По признаку Даламбера, ряд расходится в точке $z$. Отсюда выходит, что радиус сходимости $R = 0$.
- Если $0<\rho<+\infty$, и $z_0$ — произвольная точка из круга $K=\left \{z:\left |z\right | < \frac{1}{\rho}\right \}$, то $z_0$ так же по модулю меньше, чем $\frac{1}{\rho}$. Отсюда следует, что $$\lim\limits_{n \to \infty}\left | \frac{c_{n+1} \cdot z_{0}^{n+1}}{c_{n} \cdot z_{0}^{n}}\right |=\left | z \right | \cdot \lim\limits_{n \to \infty}\left | \frac{c_{n+1}}{c_{n}}\right |=\left |z \right | \cdot \rho < 1.$$ По признаку Даламбера сходимости ряда, ряд сходится в точке $z_{0}$. В силу того, что точка $z_{0}$ — произвольная точка круга $K$, исходный ряд сходится в $K$.
Пример 1
Условие:
Найти радиус сходимости ряда
$$\sum\limits_{n=1}^{\infty}\frac{x^{n}}{3^{n} \cdot (n+1)}.$$
Решение:
$$R = \lim\limits_{n \to\infty} \left | \frac{c_{n}}{c_{n+1}} \right | = \lim\limits_{n \to\infty}\frac{3^{n+1}\cdot ((n+1)+1)}{3^{n} \cdot (n+1)} =$$ $$= \lim\limits_{n \to\infty} \frac{3 \cdot (n+2)}{n+1} = 3 \cdot \lim\limits_{n \to\infty} \frac{n+2}{n+1} = 3.$$
[свернуть]
Пример 2
Условие:
Найти радиус сходимости степенного ряда
$$\sum\limits_{n=0}^{\infty}\frac{\sqrt{2}^{n} \cdot z^{n}}{n \cdot 12^{n}}.$$
Решение:
$$\frac{1}{R} = \lim\limits_{n\to\infty}\sqrt[n]{\left | c_n \right |} = \lim\limits_{n\to\infty}\sqrt[n]\frac{\sqrt{2}^{n} }{n \cdot 12^{n}} = \frac{\sqrt{2}}{12} \cdot \lim\limits_{n\to\infty}\frac{1}{\sqrt[n]{n}} = \frac{\sqrt{2}}{12}. $$ Отсюда следует, что $$R = \frac{12}{\sqrt{2}}=6 \cdot \sqrt{2}.$$
[свернуть]
Замечание
Пределы в формулах (1) и (2) могут не существовать. Однако существует универсальная формула для вычисления радиуса сходимости.
Теорема
Радиус сходимости$R$ степенного ряда $\sum\limits_{n=0}^{\infty}c_{n}z^n$ высчитывается по формуле:
$$R = \frac{1}{\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \right |}},$$
где $\frac{1}{0}=+\infty$ и $\frac{1}{+\infty}=0.$
Доказательство
Доказательство данной теоремы основано на применении обобщенного признака Коши: $$\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \cdot z^{n} \right |} = \left | z \right | \cdot \varlimsup\limits_{n \to \infty}\sqrt[n]{\left |c_{n} \right |}. $$
Предположим, что ряд сходится в точке $z_{0}$, тогда из обобщенного признака Коши сходимости числового ряда с неотрицательными членами следует, что $\left | z_{0} \right | \cdot \varlimsup\limits_{n \to \infty}\sqrt[n]{\left |c_{n} \right |}<1$. Отсюда получаем, что $$\left | z_{0} \right | < \frac{1}{\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \right |}}.$$
Пусть ряд расходится в точке $z_{m}$. Тогда $\left | z_{m} \right | \cdot \varlimsup\limits_{n \to \infty}\sqrt[n]{\left |c_{n} \right |}>1$. Отсюда $$\left | z_{m} \right | > \frac{1}{\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \right |}}.$$
То есть, если $z$ по модулю меньше чем $\frac{1}{\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \right |}}$, то ряд сходится в данной точке, а если $z$ по модулю больше, то ряд в данной точке расходится. Из определения радиуса сходимости следует, что
$$R=\frac{1}{\varlimsup\limits_{n \to \infty}\sqrt[n]{\left | c_{n} \right |}}.$$
Список использованной литературы:
- Лысенко З.М., Конспект лекций по математическому анализу, 2015-2016 гг., 1-ый курс, семестр 2
- Тер-Крикоров А.М., Шабунин М.И., Курс математического анализа. 3-е изд., испр. – М.:ФИЗМАТЛИТ, 2001. — 672 с — стр 427-430.
- Кудрявцев Л.Д., Курс математического анализа, том 2.- 720 с. — стр. 104-110
- Коляда В.И., Кореновский А.А., Курс лекций по математическому анализу в 2-х частях, часть 2. — Одесса: Астропринт, 2009.- 292с. — стр.56-60.
Вычисление радиуса сходимости, формула Коши-Адамара
Лимит времени: 0
Информация
Тест по материалу данной статьи
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 3
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
- Математический анализ 0%
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Таблица лучших: Вычисление радиуса сходимости, формула Коши-Адамара
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
Если функция $f$ определена в некоторой окрестности точки $x_{0}$ и является бесконечно дифференцируемой (имеет в данной точке производные всех порядков), то степенной ряд вида $$\sum\limits_{n=0}^{\infty}a_{n}\left(x-x_{0}\right)^n$$ называется рядом Тейлора функции $f$ в окрестности точки $x_{0}$, где числа $$a_{n}=\frac{{f}^{\left(n \right)}\left(x_{0} \right)}{n!} \;\;\; \left(n=0,1,2,\ldots \right)$$ это коэффициенты Тейлора функции $f$ в окрестности точки $x_{0}$.
Спойлер
Представим в виде ряда Тейлора функцию $$f\left(x \right)=\begin{cases}&e^{\frac{-1}{x^{2}}},\;\;x\neq0\\&0,\;\;x=0\end{cases}$$
Найдем производные функции вне нуля: $${f}^{\left(1\right)}\left(x \right)=e^{\frac{-1}{x^{2}}}\cdot \frac{2}{x^{3}},$$ $${f}^{\left(2\right)}\left(x \right)=\left(\frac{4}{x^{6}}-\frac{6}{x^{4}} \right)e^{\frac{-1}{x^{2}}},$$ $$\ldots$$ $${f}^{\left(k\right)}\left(x\right)=e^{\frac{-1}{x^{2}}}Q_{3k}\left(\frac{1}{x}\right).$$
Рассмотрим производные функции в нуле. Докажем по индукции, что $${f}^{\left(k\right)}\left(0 \right)=0 \;\;\; \forall k \in N.$$ Имеем,
- ${f}^{\left(1\right)}\left(0 \right)=\lim\limits_{ n \to 0}\frac{e^{\frac{-1}{x^{2}}}}{x}=0.$
- ${f}^{\left(n\right)}\left(0 \right)=0 \;\;\; \forall n \in N.$
- ${f}^{\left(n+1\right)}\left(0 \right)=$$\lim\limits_{ n \to 0}\frac{{f}^{n}\left(x \right)-{f}^{n}\left(0 \right)}{x}=$$\lim\limits_{ n \to 0}\frac{1}{x}e^{\frac{-1}{x^{2}}}Q_{3k}\left(\frac{1}{x} \right)=$$0.$
Следовательно, для данной функции коэффициенты формулы Тейлора в точке $x_{0}$ равны нулю. Но, с другой стороны, $f\left(x \right)=e^{\frac{-1}{x^{2}}}\neq0,\;\;\; x\neq0$. Таким образом, функция не представима в виде своего ряда Тейлора.
[свернуть]
Пусть функция $f\left(x\right)$ бесконечно дифференцируема в точке $x_{0}$. Поставим ей в соответствие формулу Тейлора: $$f\left(x\right)=\sum\limits_{n=0}^{n}\frac{{f}^{\left(n\right)}\left(x_{0}\right)}{n!}\left(x-x_{0}\right)^{n}+r_{n}\left(x\right),$$ где $r_{n}\left(x \right)$ — остаток в формуле Тейлора. Обозначим, $$S_{n}\left(x\right)=\sum\limits_{n=0}^{n}\frac{{f}^{\left(n \right)}\left(x_{0} \right)}{n!}\left(x-x_{0}\right)^{n},$$ где $S_{n}\left(x\right)$— частичная сумма данного ряда Тейлора данной функции. Следовательно, можем записать равенство: $$f\left(x \right)=S_{n}\left(x \right)+r_{n}\left(x \right).$$ Тогда для того, чтобы $\lim\limits_{ n \to \infty}s_{n}\left(x \right)=f\left(x\right)$, функция $f\left(x\right)$ на заданном интервале должна быть равной сумме своего ряда Тейлора.
Таким образом, для сходимости ряда Тейлора функции $f\left(x\right)$ к функции $f\left(x\right)$ на некотором интервале необходимо и достаточно , чтобы для всех $x$ из этого интервала ее остаточный член в формуле Тейлора стремился к нулю: $$\lim\limits_{ n \to \infty}r_{n}\left(x \right)=0. $$
Коэффициенты Тейлора
Лимит времени: 0
Информация
Предлагаю пройти Вам данный тест на закрепление материала по данной статье.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 2
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Таблица лучших: Коэффициенты Тейлора
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
ib.mazurok.com
Степенные ряды
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«МАТИ» РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
имени К.Э. ЦИОЛКОВСКОГО
Кафедра «Моделирование систем и информационные технологии»
Методические указания к практическим занятиям
по дисциплине «Высшая математика»
Составители: Егорова Ю.Б.
Мамонов И.М.
Челпанов А.В.
Москва 2009
Степенные ряды:Методические указания к практическим занятиям по дисциплине «Высшая математика»/ Ю.Б. Егорова, И.М. Мамонов, А.В Челпанов. М.: МАТИ, 2009. – 20 с.
Егорова Ю.Б.,
Мамонов И.М.,
Челпанов А.В.,
составление, 2009
МАТИ, 2009
Введение
Методические указания предназначены для студентов дневного и вечернего отделений факультета № 14 специальностей 150601, 160301, 220301, 230102.
1. Основные понятия
Степенным рядом, разложенным по степеням x, называется функциональный ряд вида:
(1)
или
в сокращенном (свернутом) виде 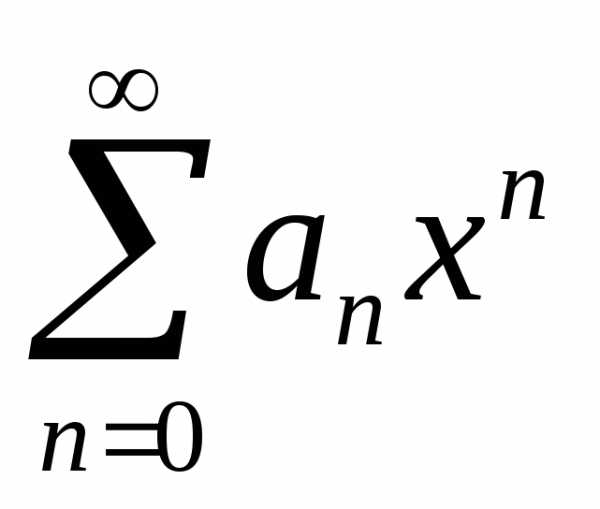 ,
гдеan – коэффициенты степенного ряда.
,
гдеan – коэффициенты степенного ряда.
Степенным рядом, разложенным по степеням (x—a), называется функциональный ряд вида:
(2)
или
в сокращенном (свернутом) виде 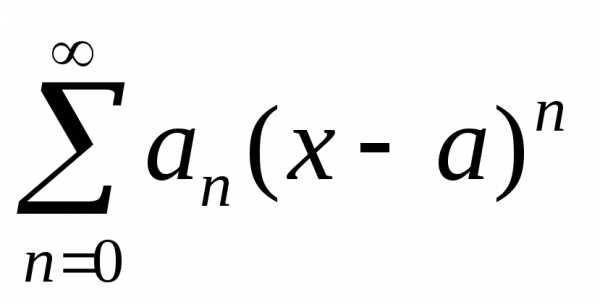 ,
гдеа — константа.
,
гдеа — константа.
Давая х числовые значения, ряды (1) и (2) становятся числовыми рядами, которые могут как сходиться, так и расходиться. Совокупность значений х, при которых степенной ряд сходится, называется областью сходимости.
2. Степенные ряды, разложенные по степеням х
Теорема
Абеля. Если
степенной ряд (1) сходится при некотором х=х0,
то он сходится абсолютно при всех х,
для которых 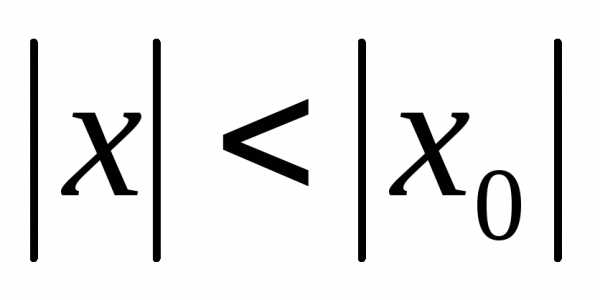 .
.
Из теоремы Абеля следует, что областью сходимости степенного ряда, разложенного по степеням х, является интервал сходимости (-R; R) с центром в т. х=0.
Число R называется радиусом
сходимости степенного ряда. Внутри интервала
степенной ряд сходится абсолютно, вне
интервала – расходится. На концах
интервала ряд может, как сходиться, так
и расходиться. Если R=0,
то степенной ряд сходится только в одной
точке
Для отыскания радиуса и интервала сходимости необходимо сначала составить ряд из абсолютных величин (модулей) членов степенного ряда (1):
(3)
Теорема. Степенной ряд (1) сходится абсолютно, если сходится ряд (3), составленный из абсолютных величин (модулей) членов степенного ряда (1).
Ряд (3) – это ряд с положительными членами, поэтому для исследования его сходимости (определения радиуса и интервала сходимости) можно применять признаки сходимости рядов с положительными членами, например признак Даламбера или радикальный признак Коши.
Для нахождения радиуса сходимости можно также использовать следующие формулы:
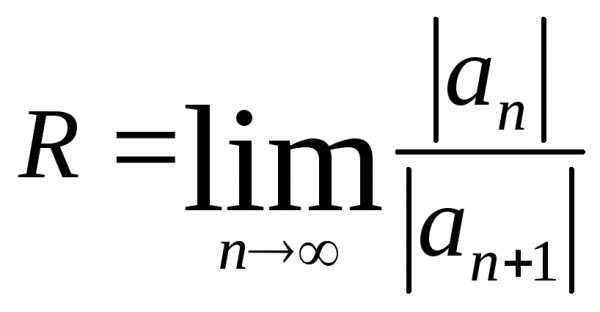 ,
(4)
,
(4)
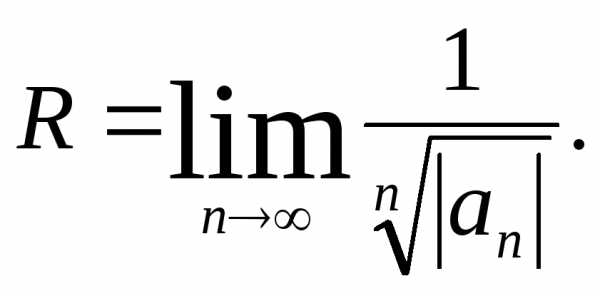 (5)
(5)
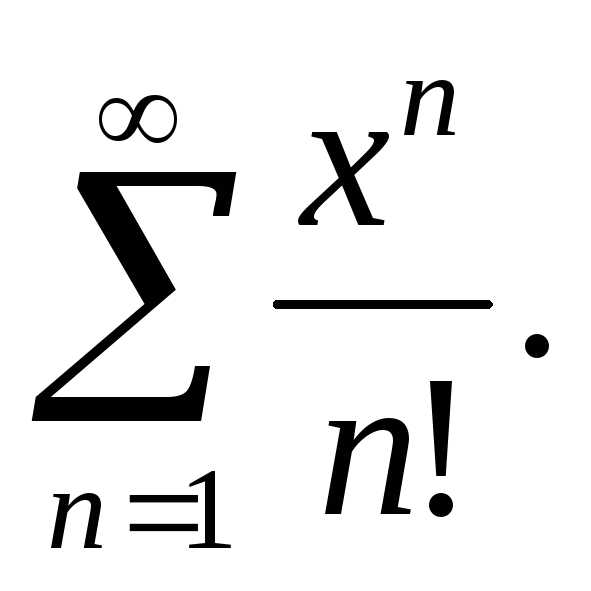
Решение. Имеем коэффициенты степенного ряда:
Найдем радиус сходимости по формуле (4):
Следовательно, интервал сходимости (-∞; +∞), т.е. данный ряд сходится при всех значениях х.
Пример
2. Исследовать
сходимость ряда 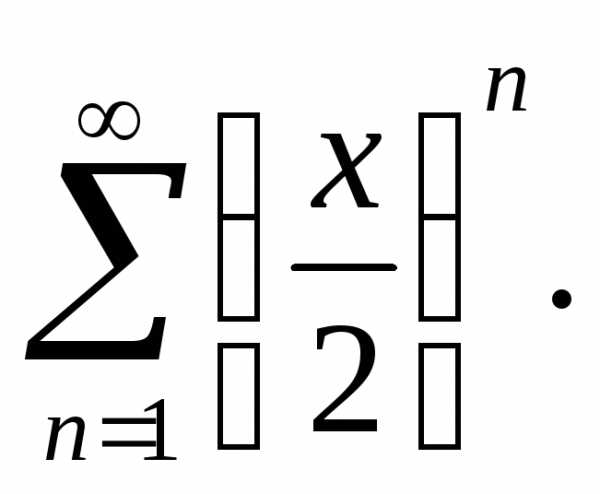
Решение. Имеем
коэффициент степенного ряда: 
Найдем радиус сходимости по формуле (5):
Следовательно, интервал сходимости (-2; 2). Исследуем сходимость ряда на концах интервала.
При х=2 получим ряд с положительными членами:
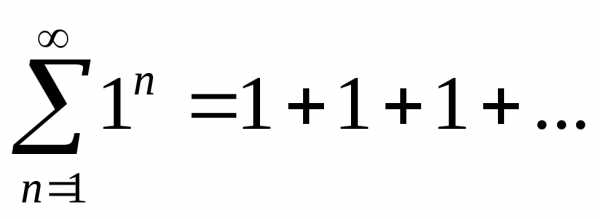
Для исследования его сходимости применим необходимый признак сходимости. Так как то ряд расходится (не выполняется необходимое условие сходимости).
При х=-2 получим знакочередующийся ряд:
Для исследования его сходимости можно также применить необходимый признак сходимости. Так как то ряд расходится.
Таким
образом, область сходимости степенного
ряда 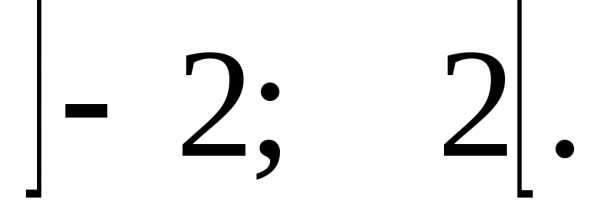
Пример
3. Исследовать
сходимость ряда 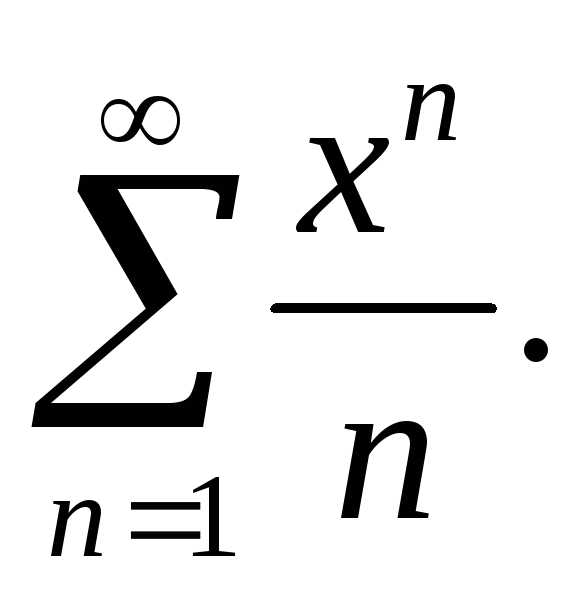
Решение. Имеем коэффициенты степенного ряда:
Найдем радиус сходимости по формуле (4):
Следовательно, интервал сходимости (-1; 1). Исследуем сходимость ряда на концах интервала.
При х=1
получим ряд с положительными членами
(гармонический ряд) .
Для исследования его сходимости можно
применить интегральный признак сходимости
Коши. Имеем:
.
Для исследования его сходимости можно
применить интегральный признак сходимости
Коши. Имеем:
Интеграл расходится, поэтому расходится и гармонический ряд.
При х=-1
получим знакочередующийся ряд: 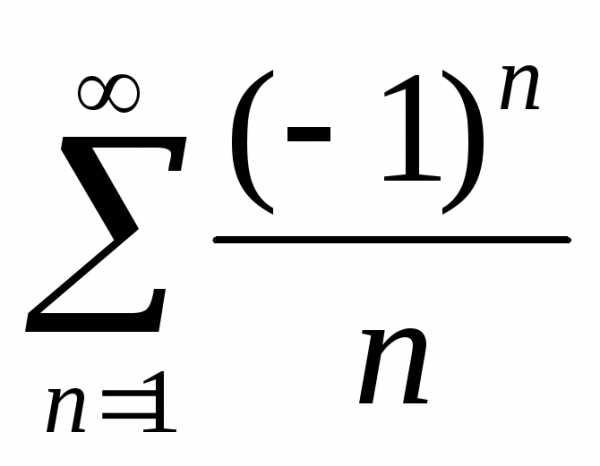 .
.
Для исследования его сходимости применим признак Лейбница. Все условия теоремы Лейбница выполнены:
члены ряда монотонно убывают (по модулю): ;
общий член ряда (по модулю) стремится к нулю:
Следовательно, ряд сходится. Причем этот ряд сходится условно, так как ряд из абсолютных величин членов данного ряда (гармонический ряд) расходится.
Таким
образом, область сходимости степенного
ряда 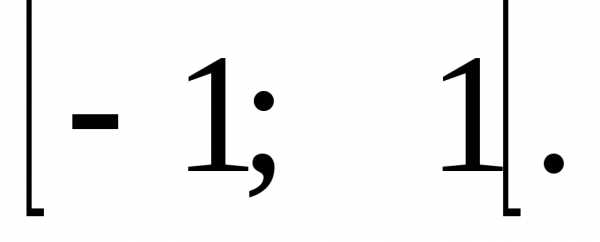
studfiles.net
Лекция 14. Степенные ряды
Степенным рядом называется ряд вида
Степенной ряд заведомо сходится при — центр сходимости ряда.
Теорема Абеля.
1)
Пусть степенной ряд сходится в точке 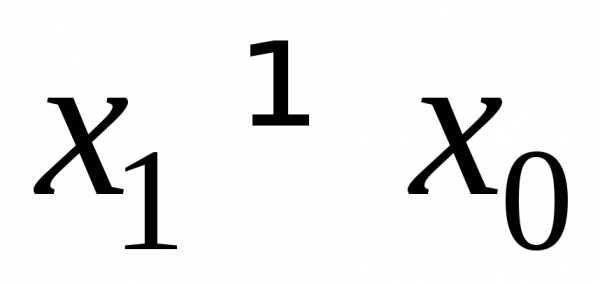 .
Тогда он абсолютно сходится в интервале
.
Тогда он абсолютно сходится в интервале
,
симметричном относительно 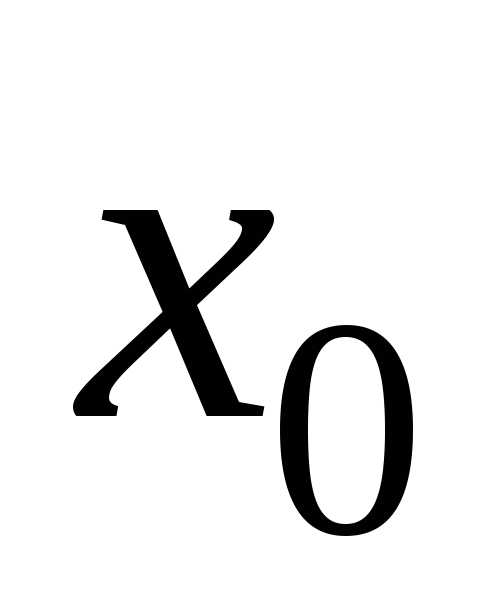 .
.
2)
Пусть степенной ряд расходится в точке 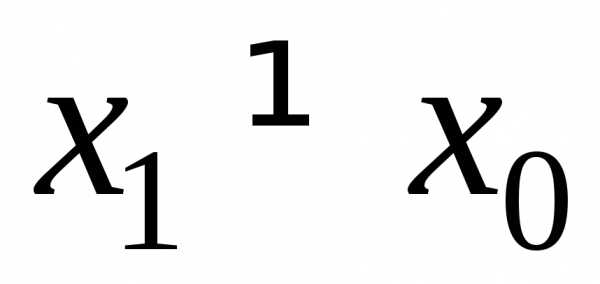 .
Тогда он расходится в области.
.
Тогда он расходится в области.
Доказательство.
Пусть степенной ряд сходится в точке
 ,
тогда числовой ряд
,
тогда числовой ряд сходится.
Тогда по необходимому признаку сходимости
ряда.
сходится.
Тогда по необходимому признаку сходимости
ряда.
Тогда .
Рассмотрим произвольное, но фиксированное .
Оценим ,
где .
По
первому признаку сравнения числовых
знакоположительных рядов ряд 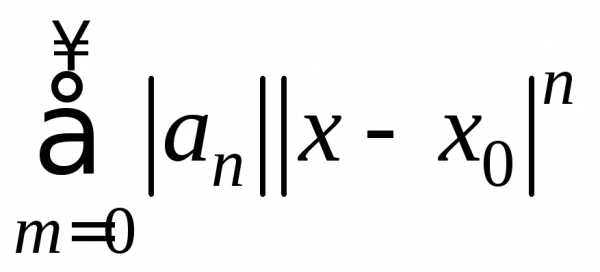 сходится в указанной области (сравнение
с бесконечно убывающей геометрической
прогрессией
сходится в указанной области (сравнение
с бесконечно убывающей геометрической
прогрессией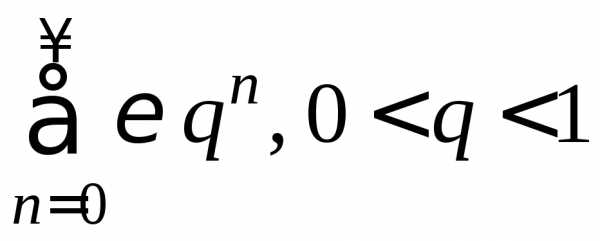 .
Следовательно, в областистепенной ряд абсолютно сходится.
.
Следовательно, в областистепенной ряд абсолютно сходится.
Пусть степенной ряд расходится в точке
 .
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке
.
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке  .
Противоречие.
.
Противоречие.
Замечание. Для каждой точки x константа q(x) своя. Может не найтись константы, меньшей единицы и ограничивающей сверху константы q(x) для всех точек области V.
Поэтому абсолютная сходимость есть, но равномерной сходимости степенного ряда в области V не гарантируется.
Если такая константа найдется, то гарантируется равномерная сходимость ряда.
Радиус сходимости и интервал сходимости степенного ряда
Рассмотрим монотонно убывающую последовательность 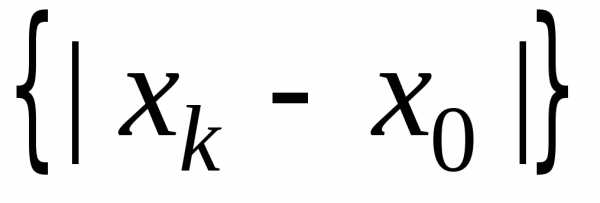 ,
такую, что в точке
,
такую, что в точке степенной
ряд
степенной
ряд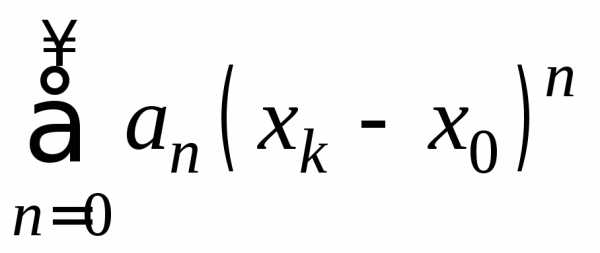 расходится.
Если выбрать
расходится.
Если выбрать 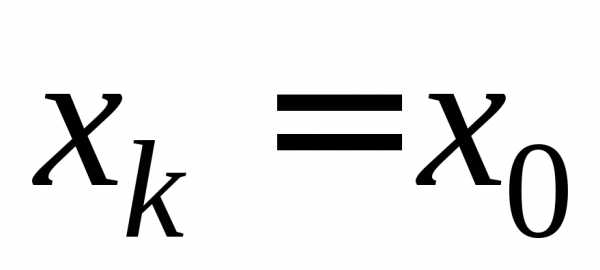 ,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
Такое
число  называетсярадиусом
сходимости степенного ряда. Следовательно, степенной
ряд (по
теореме Абеля) абсолютно
сходится в интервале сходимости
степенного ряда.
называетсярадиусом
сходимости степенного ряда. Следовательно, степенной
ряд (по
теореме Абеля) абсолютно
сходится в интервале сходимости
степенного ряда.
Определение радиуса и интервала сходимости степенного ряда
Зафиксируем
некоторое значение x
и запишем ряд из модулей членов степенного
ряда 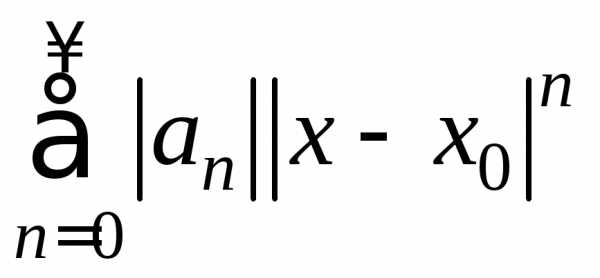 .
Это – знакоположительный числовой ряд.
Применим к нему признак Даламбера или
радикальный признак Коши.
.
Это – знакоположительный числовой ряд.
Применим к нему признак Даламбера или
радикальный признак Коши.
Применяя признак Даламбера, имеем
.
Отсюда 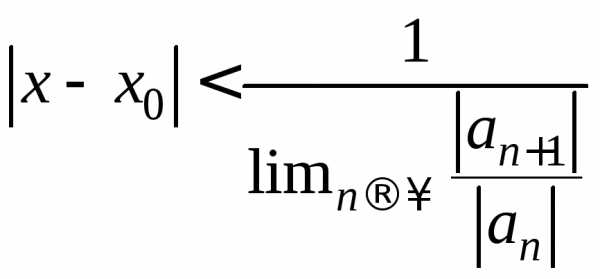 .
.
Поэтому 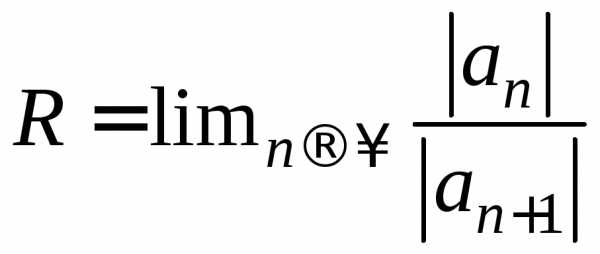 .
.
Применяя радикальный признак Коши, имеем
.
Так определяется радиус сходимости степенного ряда.
Затем исследуется сходимость ряда на границе интервала сходимости, в точках Эти точки подставляются в исходный ряд, ряд становится обычным числовым рядом и исследуется стандартными методами для числовых рядов.
Пример.  .
.
Составим ряд из модулей , применим радикальный признак Коши.
Радиус сходимости R=5, интервал сходимости (-2, 8). Исследуем сходимость ряда на границе, подставляя точки x= -2, в исходный ряд..
В
точке x
= -2 имеем ряд 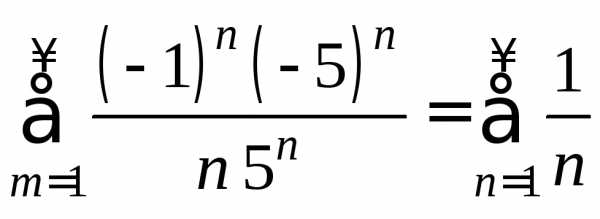 —
гармонический ряд, он расходится.
—
гармонический ряд, он расходится.
В точке x = 8 имеем ряд — сходящийся (по признаку Лейбница) знакочередующийся ряд.
Область сходимости исходного ряда (-2, 8].
Теорема. Степенной ряд равномерно сходится внутри интервала сходимости.
Доказательство. Пусть
.
Выберем,
например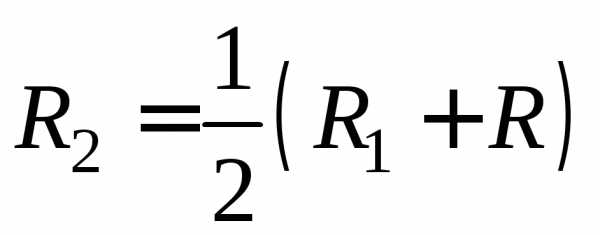 .
На интервалеи в точкеx1 степенной ряд сходится абсолютно, так
как этот интервал лежит внутри интервала
сходимости. Тогда (точно так же, как в
доказательстве теоремы Абеля оценим
,
.
На интервалеи в точкеx1 степенной ряд сходится абсолютно, так
как этот интервал лежит внутри интервала
сходимости. Тогда (точно так же, как в
доказательстве теоремы Абеля оценим
,
где
(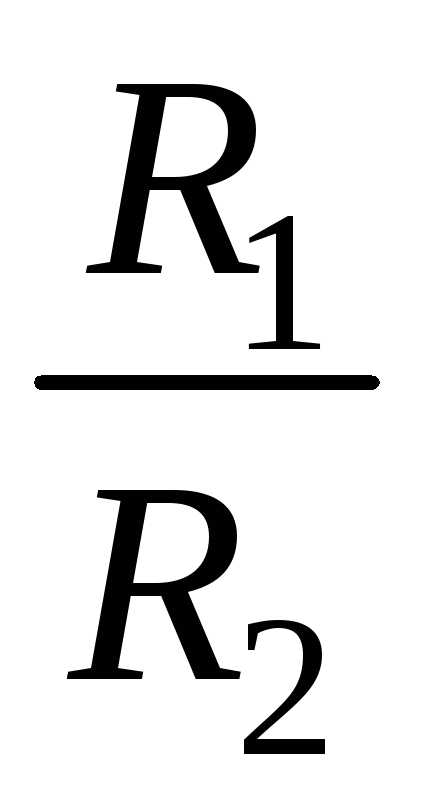 не зависит от
не зависит от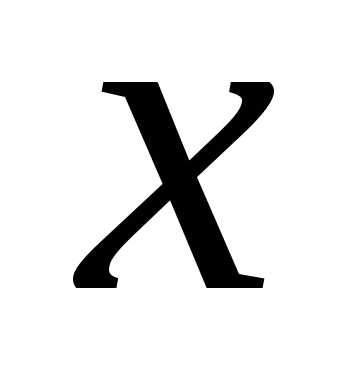 ).
).
Тогда в области степенной ряд будет сходиться равномерно по признаку Вейерштрасса (члены ряда мажорируются членами бесконечно убывающей геометрической прогрессии).
Следствие. Внутри интервала сходимости справедливы теоремы о непрерывности суммы ряда, о почленном интегрировании и дифференцировании ряда.
Теорема. При почленном дифференцировании и интегрировании степенного ряда его радиус сходимости не меняется.
Доказательство. Рассмотрим ряд из модулей членов степенного ряда (это – знакоположительный числовой ряд в конкретной точке) и определим радиус сходимости по признаку Даламбера.
.
Продифференцируем
почленно степенной ряд 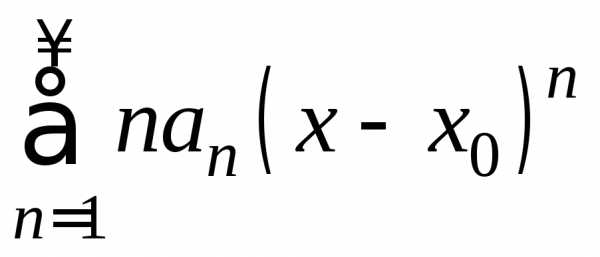 ,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
.
Таким образом, при почленном дифференцировании радиус сходимости степенного ряда не меняется. Он не меняется и при почленном интегрировании, иначе он изменился бы при почленном дифференцировании.
studfiles.net
Тема 2. Функциональные ряды
Тема 2. Функциональные ряды. Степенные ряды
2.1. Функциональные ряды
До сих пор мы рассматривали ряды, членами которых были числа. Перейдем теперь к изучению рядов, членами которых являются функции.
Функциональным рядомназывается ряд
,
членами которого являются функции одного и того же аргумента, определенные на одном множестве Е.
Например,
1. ;
2. ;
3. .
Если
придать аргументу хнекоторое
числовое значение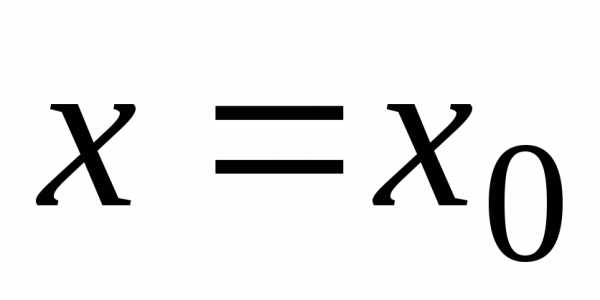 ,
,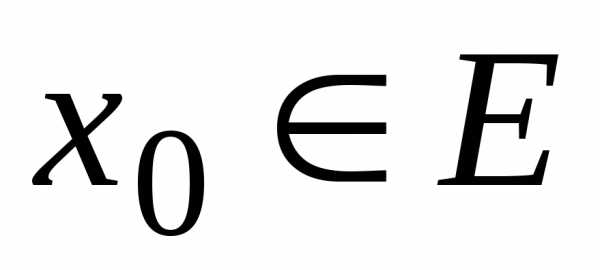 ,
то получим числовой ряд
,
то получим числовой ряд
,
который может сходиться (сходиться абсолютно) или расходиться.
Если
при 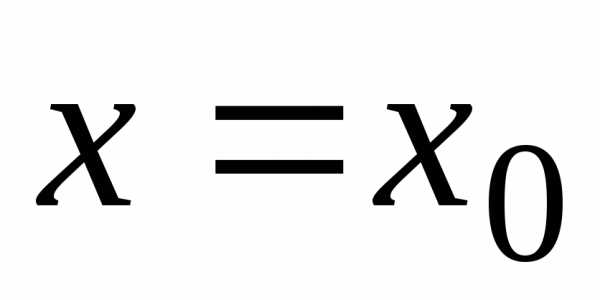 полученный числовой ряд сходится, то
точка
полученный числовой ряд сходится, то
точка 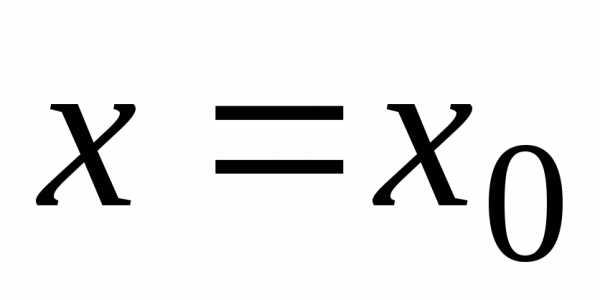 называется точкой сходимости функционального ряда. Совокупность
всех точек сходимости называется областью сходимости функционального ряда. Обозначим
область сходимостиХ, очевидно,.
называется точкой сходимости функционального ряда. Совокупность
всех точек сходимости называется областью сходимости функционального ряда. Обозначим
область сходимостиХ, очевидно,.
Если для числовых знакоположительных рядов ставится вопрос: «Сходится ряд или расходится?», для знакопеременных – вопрос: «Сходится как – условно или абсолютно,– или расходится?», то для функционального ряда основной вопрос звучит так: «Сходится (сходится абсолютно) при каких х?».
Функциональный
ряд 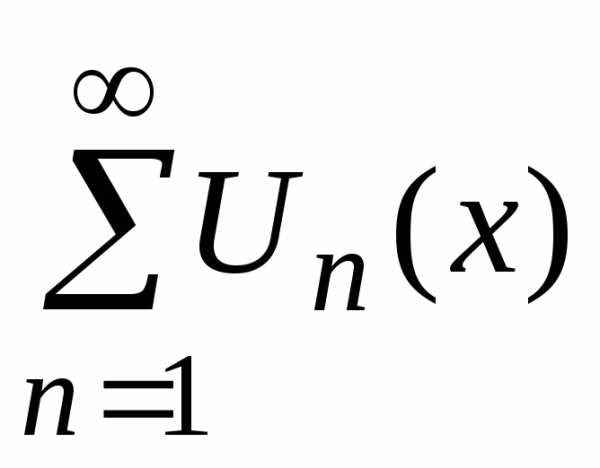 устанавливает закон, по которому каждому
значению аргумента
устанавливает закон, по которому каждому
значению аргумента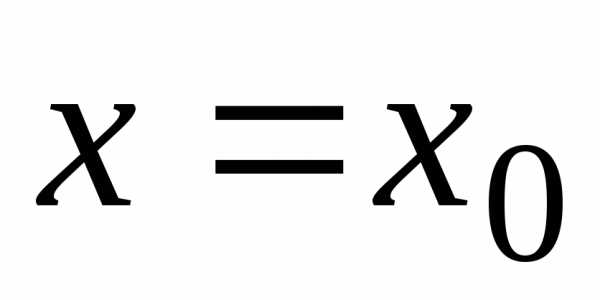 ,
,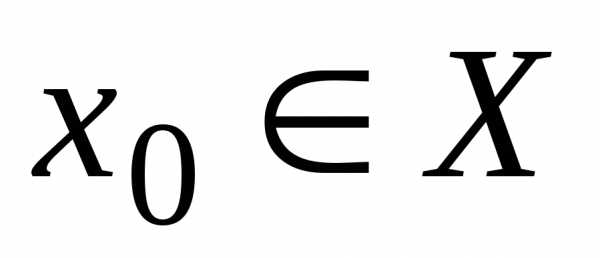 ,
ставится в соответствие число, равное
сумме числового ряда
,
ставится в соответствие число, равное
сумме числового ряда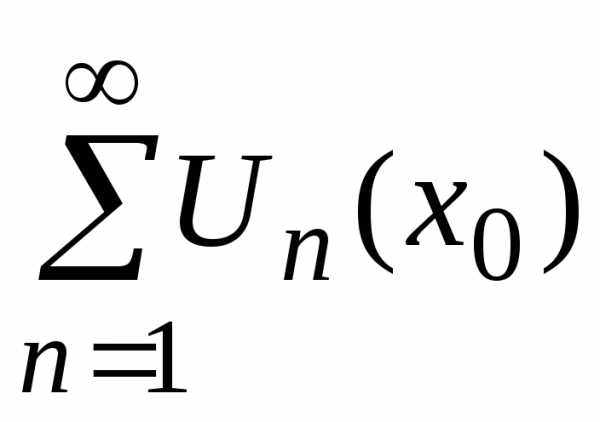 .
Таким образом, на множествеХзадается
функция
.
Таким образом, на множествеХзадается
функция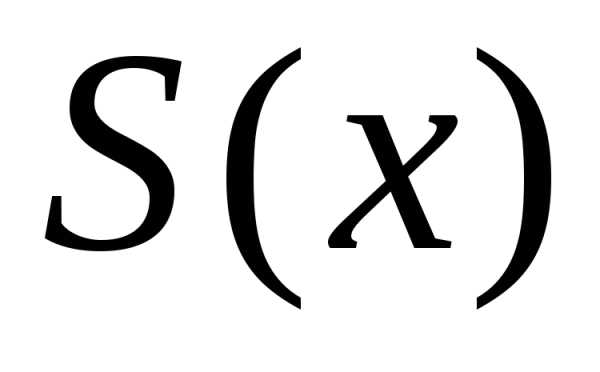 ,
которая называетсясуммой функционального
ряда.
,
которая называетсясуммой функционального
ряда.
Пример 16.
Найти область сходимости функционального ряда
.
Решение.
Пусть х– фиксированное число,
тогда данный ряд можно рассматривать
как числовой ряд, знакоположительный
при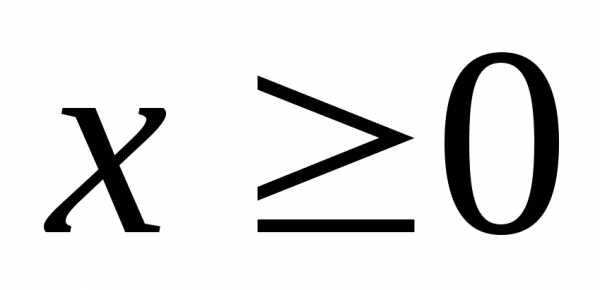 и знакопеременный при
и знакопеременный при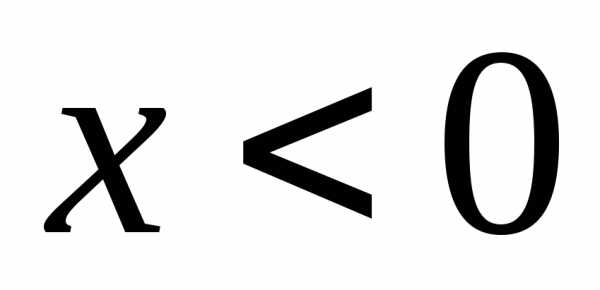 .
.
Составим ряд из абсолютных величин членов данного ряда:
и применим к нему признак ДАламбера.
т.е для любого значения хэтот предел меньше единицы, значит данный ряд сходится, причем абсолютно (так как исследовали ряд из абсолютных величин членов ряда) на всей числовой оси.
Таким образом, областью абсолютной сходимости является множество .
Пример 17.
Найти область сходимости функционального
ряда 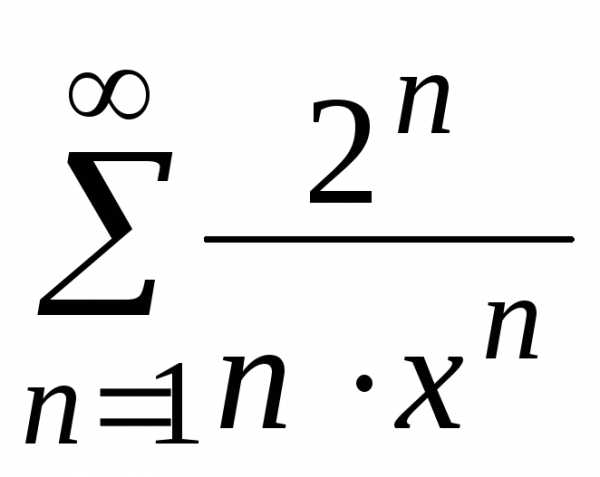 .
.
Решение.
Пусть х– фиксированное число,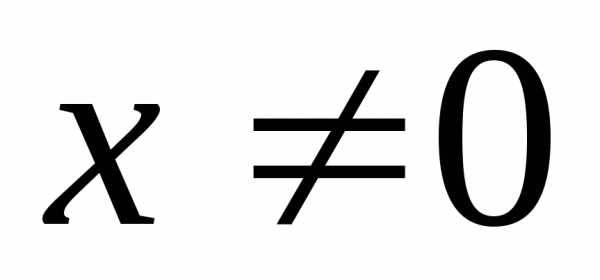 ,
тогда данный ряд можно рассматривать,
как числовой ряд, знакоположительный
при
,
тогда данный ряд можно рассматривать,
как числовой ряд, знакоположительный
при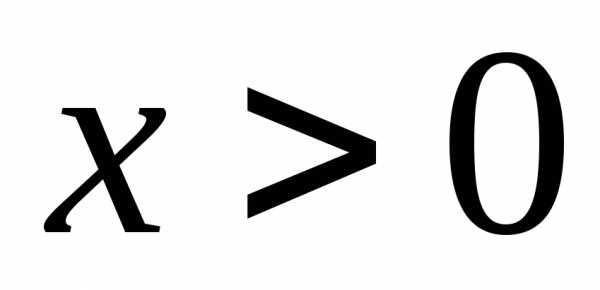 и знакопеременный при
и знакопеременный при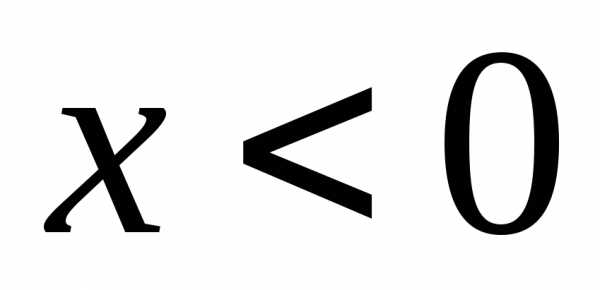 .
.
Рассмотрим ряд из абсолютных величин членов данного ряда:
и применим к нему признак ДАламбера.
По признаку ДАламбера
ряд сходится, если величина предела
меньше единицы, т.е. данный ряд будет
сходиться, если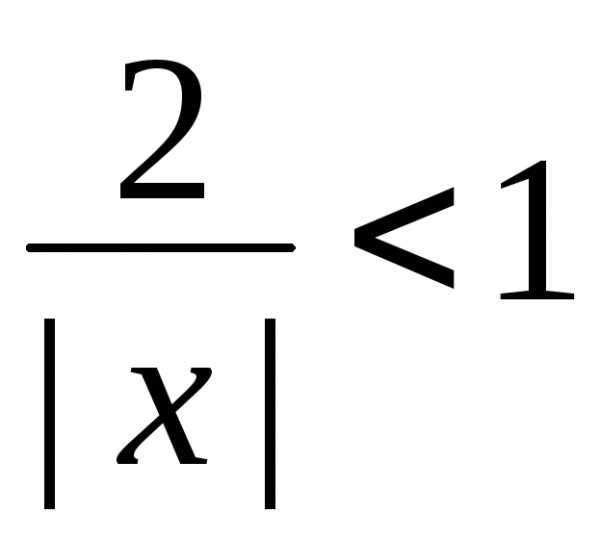 .
.
Решив это неравенство, получим:

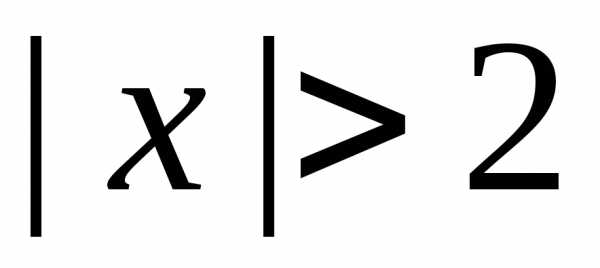 .
.
Таким образом, при , ряд, составленный из абсолютных величин членов данного ряда, сходится, значит, исходный ряд сходится абсолютно, а приданный ряд расходится.
При 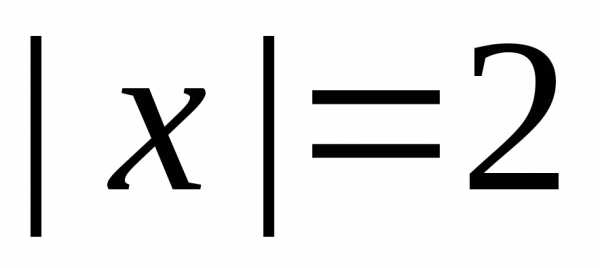 ряд может сходится или расходится, так
как при этих значенияххвеличина
предела равна единицы. Поэтому
дополнительно исследуем сходимость
ряда точках
ряд может сходится или расходится, так
как при этих значенияххвеличина
предела равна единицы. Поэтому
дополнительно исследуем сходимость
ряда точках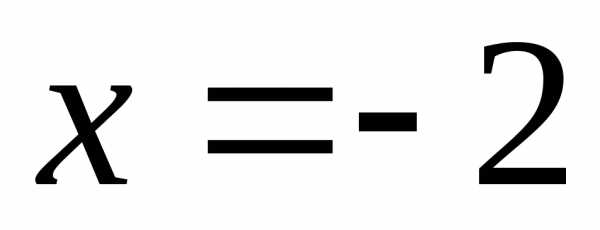 и
и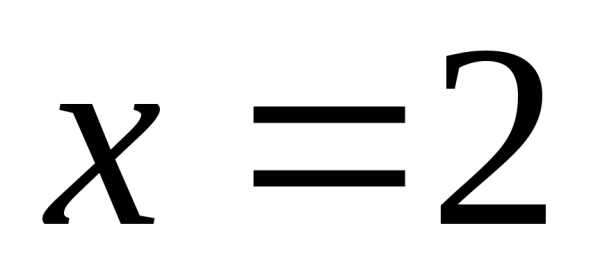 .
.
Подставляя
в данный ряд 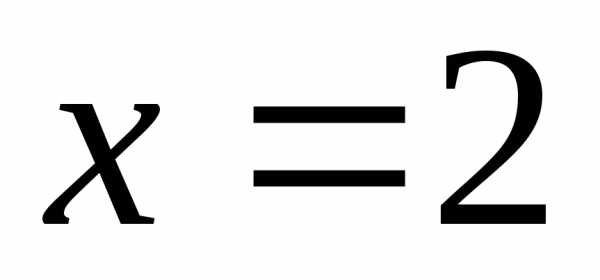 ,
получим числовой ряд
,
получим числовой ряд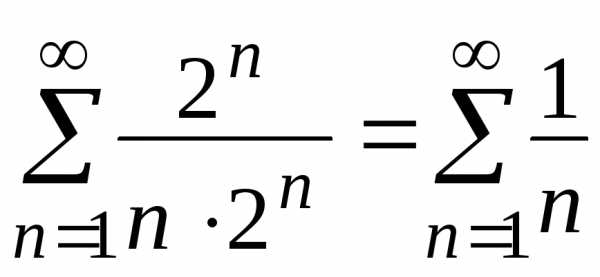 ,
про который известно, что он является
гармоническим расходящимся рядом,
значит, точка
,
про который известно, что он является
гармоническим расходящимся рядом,
значит, точка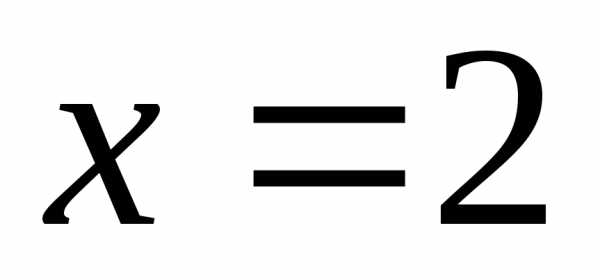 –
точка расходимости заданного ряда.
–
точка расходимости заданного ряда.
При 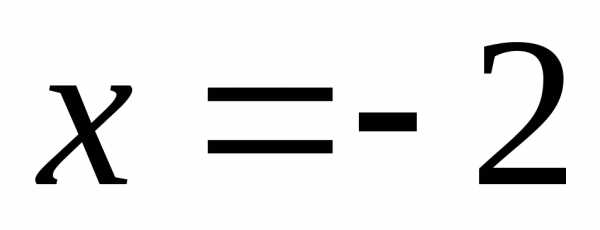 получается знакочередующийся числовой
ряд
получается знакочередующийся числовой
ряд
про который известно, что он сходится
условно (смотри пример 15), значит, точка 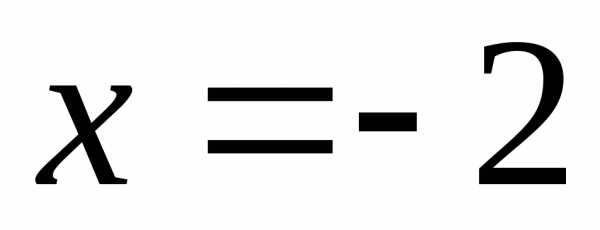 – точка условной сходимости ряда.
– точка условной сходимости ряда.
Таким образом, область сходимости данного ряда , причем ряд сходится абсолютно при.
Функциональный ряд
называется мажорируемым в некоторой области изменения х, если существует такой сходящийся знакоположительный ряд
,
что для всех х из данной области
выполняется условие  при.
Рядназываетсямажорантой.
при.
Рядназываетсямажорантой.
Иначе говоря, ряд является мажорируемым, если каждый его член по абсолютной величине не больше соответствующего члена некоторого сходящегося знакоположительного ряда.
Например, ряд
является мажорируемым для любого х, так как для всеххвыполняется соотношение
 при ,
при ,
а ряд  ,
как известно, является сходящимся.
,
как известно, является сходящимся.
Теорема Вейерштрасса
Ряд, мажорируемый в некоторой области, абсолютно сходится в этой области.
Рассмотрим
для примера функциональный ряд  .
Этот ряд является мажорируемым при,
так как при
.
Этот ряд является мажорируемым при,
так как при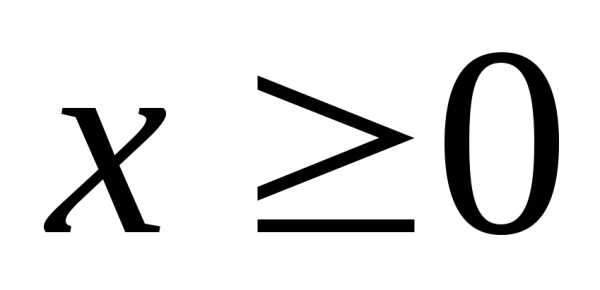 члены ряда не превосходят соответствующих
членов знакоположительного ряда
члены ряда не превосходят соответствующих
членов знакоположительного ряда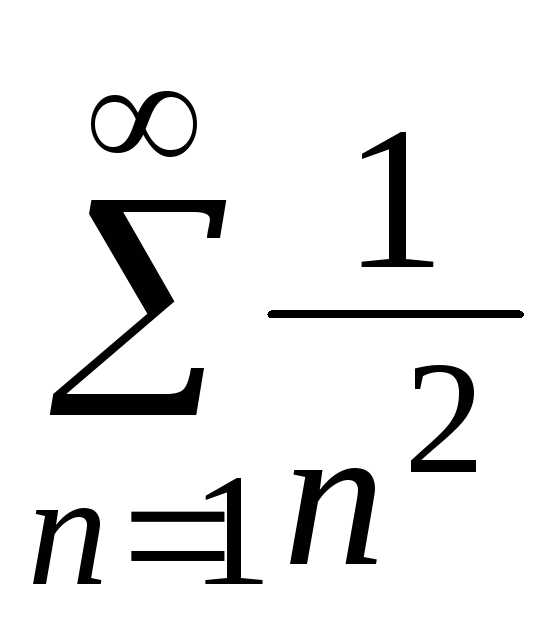 .
Следовательно, по теореме Вейерштрасса,
рассмотренный функциональный ряд
абсолютно сходится при.
.
Следовательно, по теореме Вейерштрасса,
рассмотренный функциональный ряд
абсолютно сходится при.
2.2. Степенной ряд. Теорема Абеля. Область сходимости степенного ряда
Среди всего многообразия функциональных рядов наиболее важными с точки зрения практического применения являются степенные и тригонометрические ряды. Рассмотрим такие ряды подробнее.
Степенным
рядом по степеням 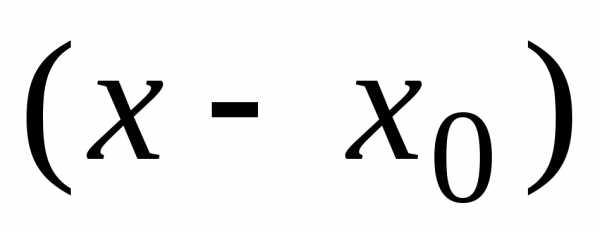 называется функциональный ряд вида
называется функциональный ряд вида
,
где 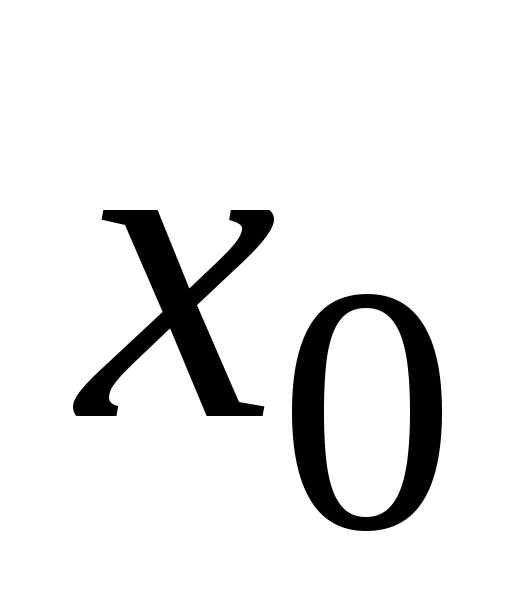 –
некоторое фиксированное число,–
числа, называемые коэффициентами ряда.
–
некоторое фиксированное число,–
числа, называемые коэффициентами ряда.
При  получаем степенной ряд по степенямх,
который имеет вид
получаем степенной ряд по степенямх,
который имеет вид
.
Для
простоты будем рассматривать степенные
ряды по степеням х, так как из такого
ряда легко получить ряд по степеням 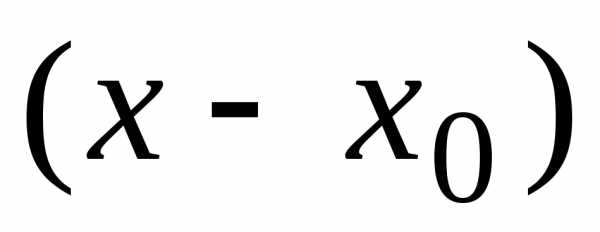 ,
подставив вместохвыражение
,
подставив вместохвыражение 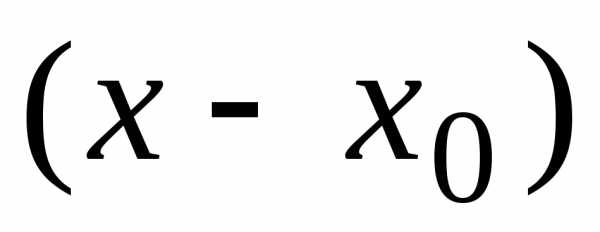 .
.
Простота и важность класса степенных рядов обусловлены в первую очередь тем, что частичная сумма степенного ряда
является многочленом – функцией, свойства которой хорошо изучены и значения которой легко вычисляются с помощью только арифметический операций.
Поскольку степенные ряды являются частным случаем функционального ряда, то для них так же необходимо находить область сходимости. В отличие от области сходимости произвольного функционального ряда, которая может быть множеством произвольного вида, область сходимости степенного ряда имеет вполне определенный вид. Об этом говорит следующая теорема.
Теорема Абеля.
Если
степенной ряд
сходится при некотором значении,
то он сходится, причем абсолютно, при
всех значениях х, удовлетворяющих
условию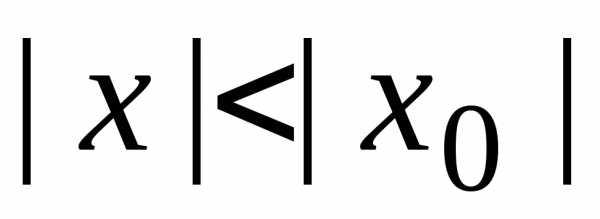 .
Если степенной ряд расходится при
некотором значении,
то он расходится и при значения,
удовлетворяющих условию
.
Если степенной ряд расходится при
некотором значении,
то он расходится и при значения,
удовлетворяющих условию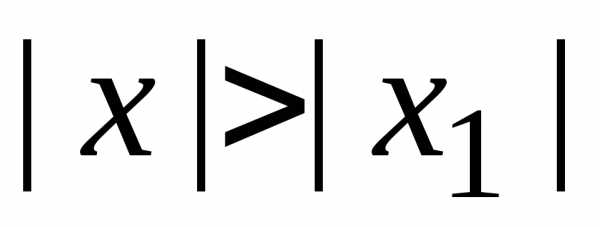 .
.
Из теоремы Абеля следует, что всеточки сходимости степенного ряда по степенямх расположены от начала координат не далее, чем любая из точек расходимости. Очевидно, что точки сходимости заполняют некоторый промежуток с центром в начале координат. справедлива теорема об области сходимости степенного ряда.
Теорема.
Для всякого степенного ряда
существует числоR (R>0) такое, что
при всех х, лежащих внутри интервала 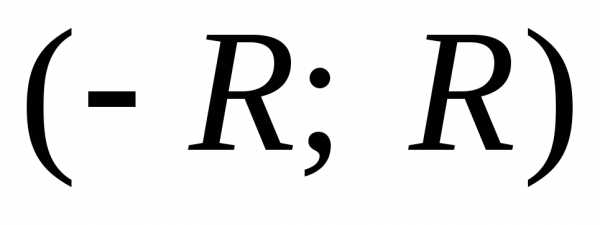 ,
ряд сходится абсолютно и при всех х,
лежащих вне интервала
,
ряд сходится абсолютно и при всех х,
лежащих вне интервала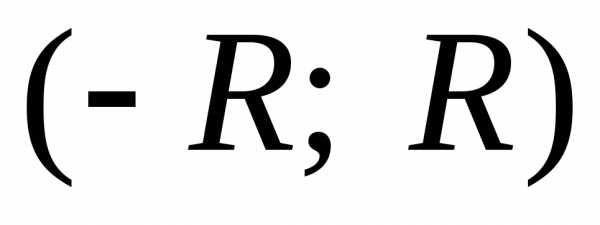 ,
ряд расходится.
,
ряд расходится.
Число R называется радиусом сходимости степенного
ряда, а интервал 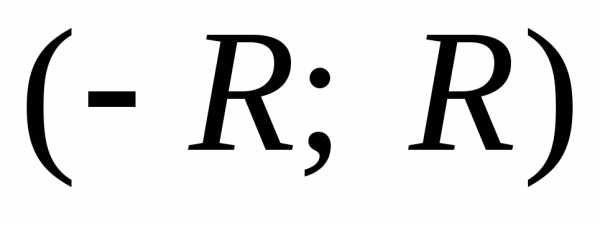 –интервалом сходимости степенного ряда по степеням х.
–интервалом сходимости степенного ряда по степеням х.
Заметим,
что в теореме ничего не говорится о
сходимости ряда на концах интервала
сходимости, т.е. в точках 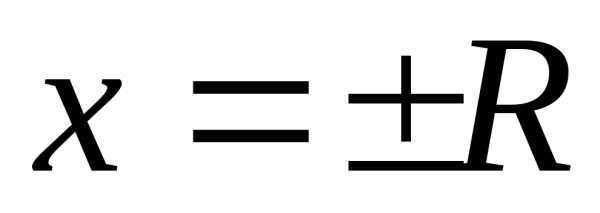 .
В этих точках различные степенные ряды
ведут себя по-разному: ряд может сходиться
(абсолютно или условно), а может
расходиться. Поэтому сходимость ряда
в этих точках следует проверять
непосредственно по определению.
.
В этих точках различные степенные ряды
ведут себя по-разному: ряд может сходиться
(абсолютно или условно), а может
расходиться. Поэтому сходимость ряда
в этих точках следует проверять
непосредственно по определению.
В частных
случаях радиус сходимости ряда может
быть равен нулю или бесконечности. Если 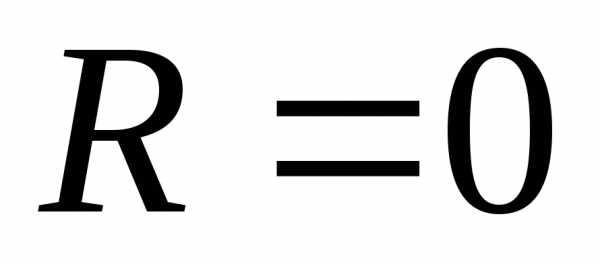 ,
то степенной ряд по степенямхсходится лишь в одной точке
,
то степенной ряд по степенямхсходится лишь в одной точке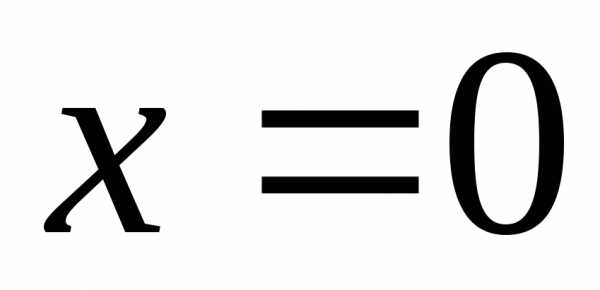 ;
если же
;
если же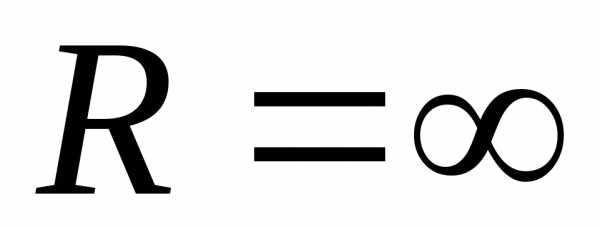 ,
то степенной ряд сходится на всей
числовой оси.
,
то степенной ряд сходится на всей
числовой оси.
Еще раз
обратим внимание на то, что степенной
ряд  по
степеням
по
степеням 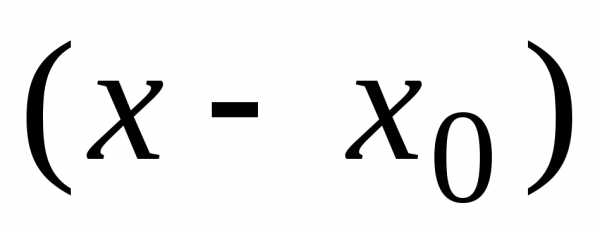 может
быть сведен к степенному ряду
может
быть сведен к степенному ряду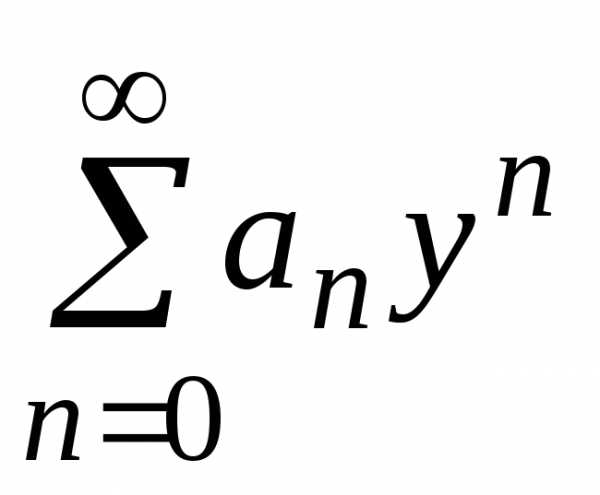 с помощью замены.
Если ряд
с помощью замены.
Если ряд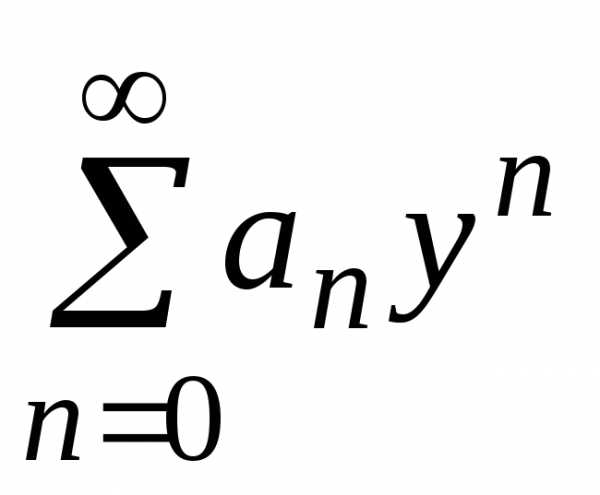 сходится при,
т.е. для,
то после обратной замены получим
сходится при,
т.е. для,
то после обратной замены получим
или.
Таким
образом, интервал сходимости степенного
ряда 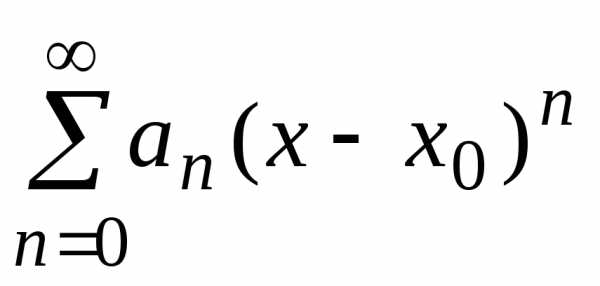 имеет вид .
Точку
имеет вид .
Точку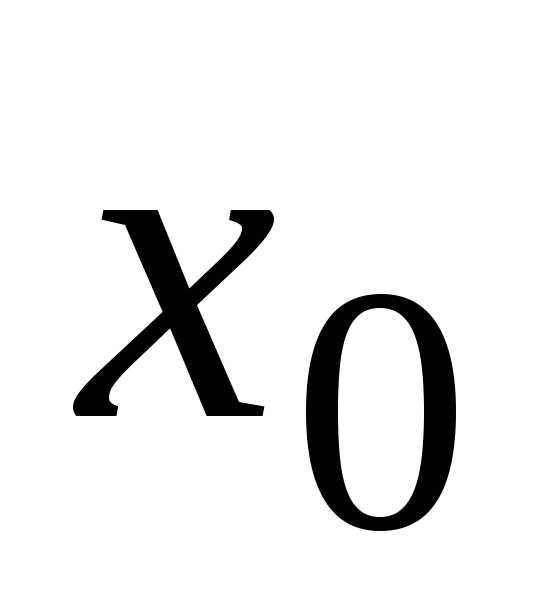 называютцентром сходимости. Для
наглядности принято интервал сходимости
изображать на числовой оси (рисунок 1)
называютцентром сходимости. Для
наглядности принято интервал сходимости
изображать на числовой оси (рисунок 1)
Таким
образом, область сходимости состоит из
интервала сходимости, к которому могут
быть добавлены точки  ,
если в этих точках ряд сходится. Интервал
сходимости можно находить, применяя
непосредственно признак ДАламбера
или радикальный признак Коши к ряду,
составленному из абсолютных величин
членов данного ряда.
,
если в этих точках ряд сходится. Интервал
сходимости можно находить, применяя
непосредственно признак ДАламбера
или радикальный признак Коши к ряду,
составленному из абсолютных величин
членов данного ряда.
Пример 18.
Найти
область сходимости ряда 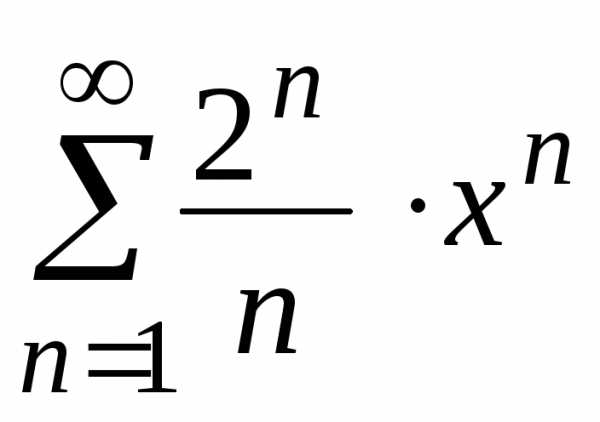 .
.
Решение.
Данный
ряд является степенным рядом по степеням х, т.е.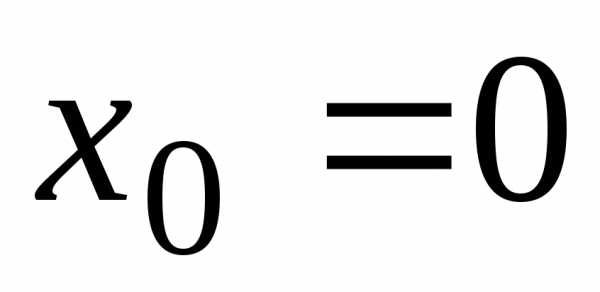 .
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда, и воспользуемся
признаком ДАламбера.
.
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда, и воспользуемся
признаком ДАламбера.
Ряд будет сходиться, если величина предела меньше 1, т.е.
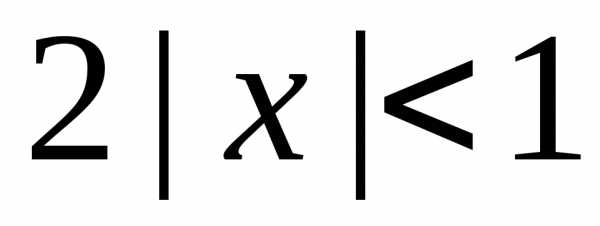 ,откуда
,откуда 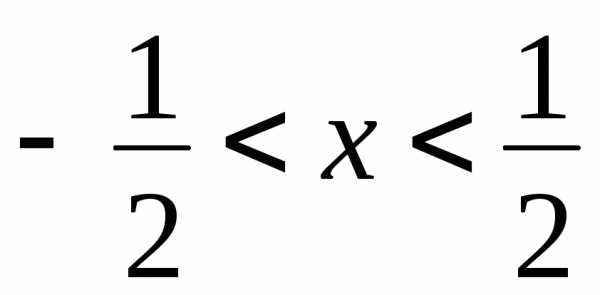 .
.
Таким
образом, интервал сходимости данного
ряда 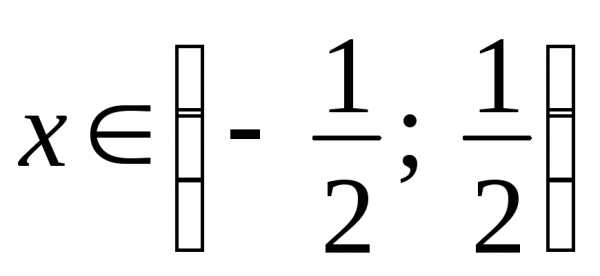 ,
радиус сходимости
,
радиус сходимости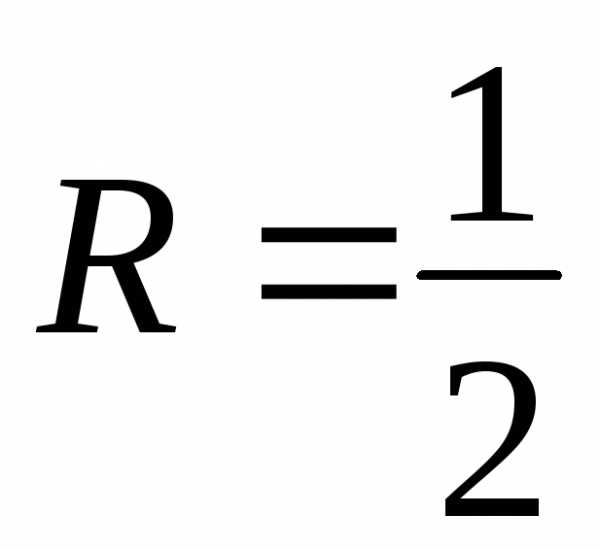 .
.
Исследуем сходимость
ряда на концах интервала, в точках 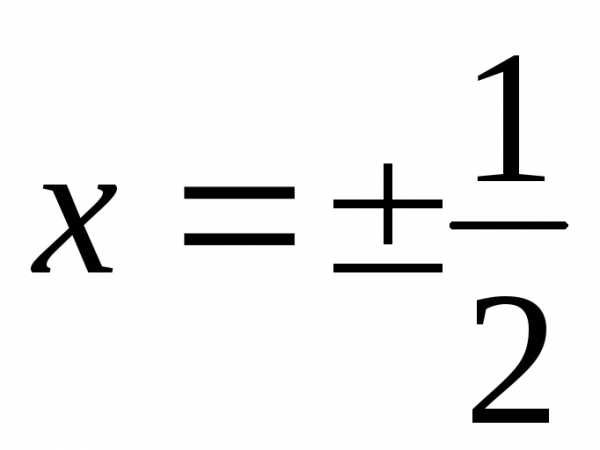 .
Подставляя в данный ряд значение
.
Подставляя в данный ряд значение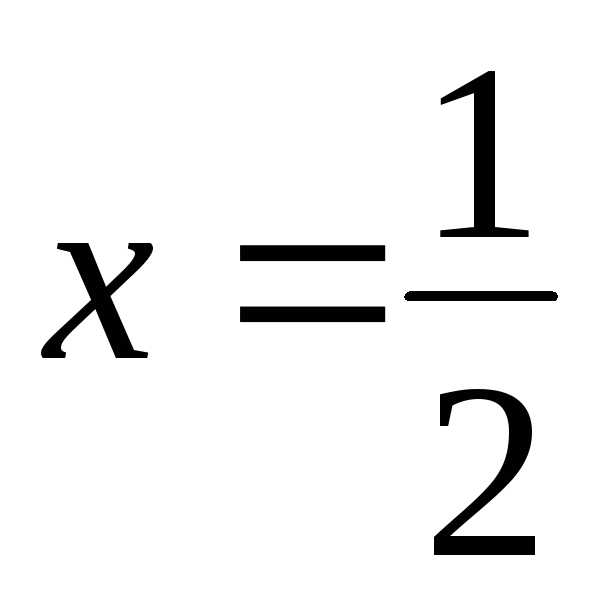 ,
получим ряд
,
получим ряд
.
Полученный ряд
является гармоническим расходящимся
рядом, следовательно, в точке 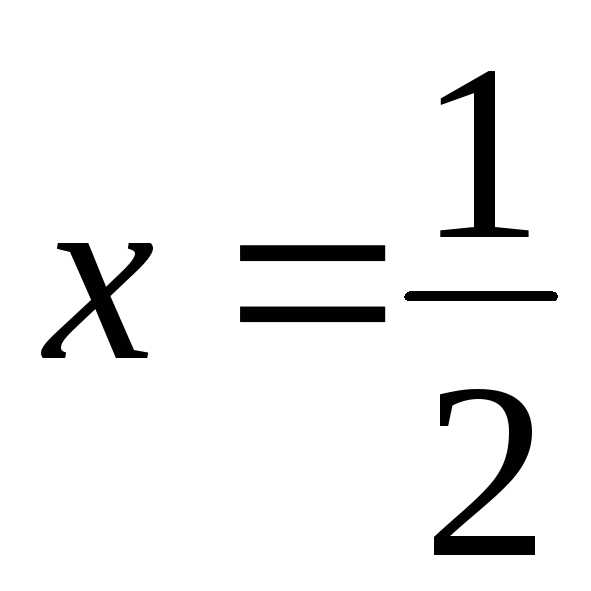 ряд расходится, значит, точка
ряд расходится, значит, точка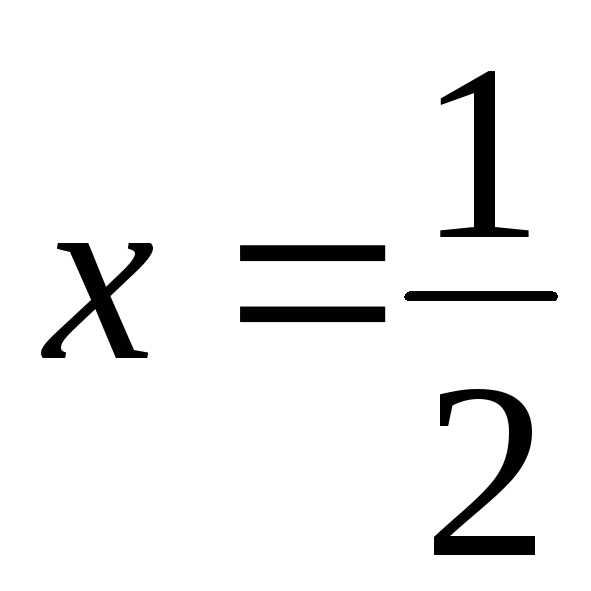 не входит в область сходимости.
не входит в область сходимости.
При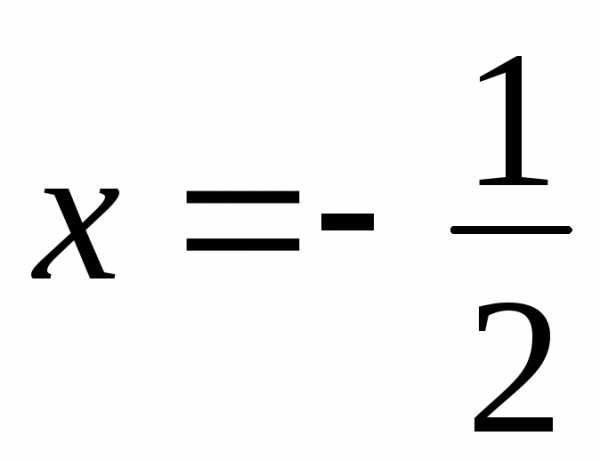 получим знакочередующийся ряд
получим знакочередующийся ряд
,
который является
условно сходящимся (пример 15), следовательно,
точка 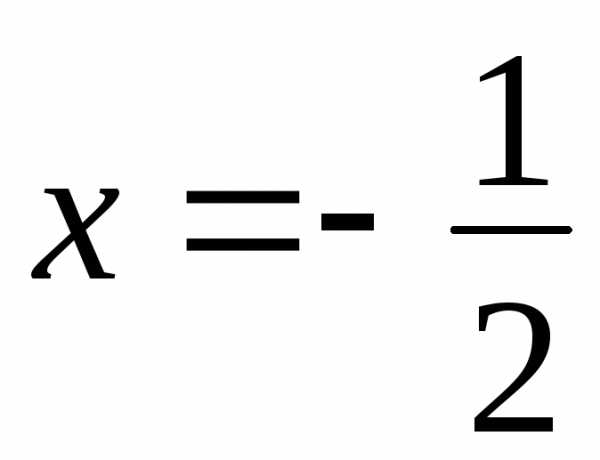 – точка
сходимости (условной).
– точка
сходимости (условной).
Таким образом,
область сходимости ряда 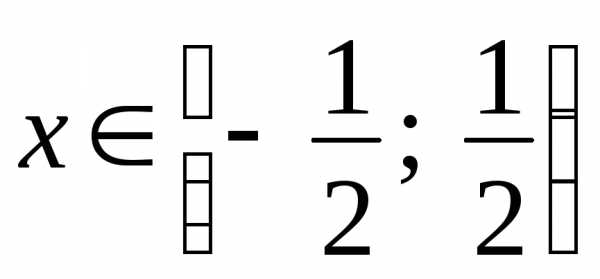 ,
причем в точке
,
причем в точке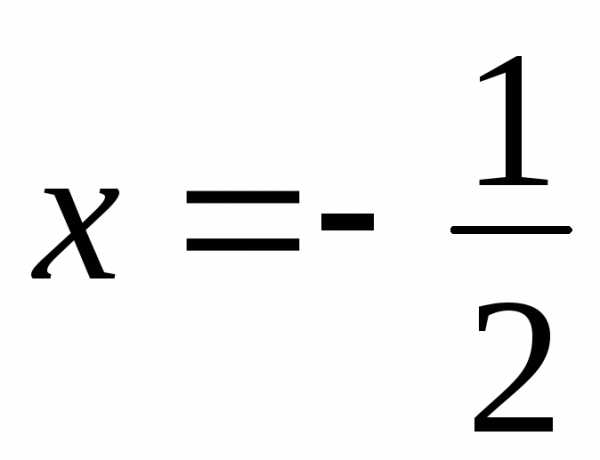 ряд сходится условно, а в остальных
точках — абсолютно.
ряд сходится условно, а в остальных
точках — абсолютно.
Рассуждениям, использованным при решении примера, можно придать общий характер.
Рассмотрим степенной ряд
Составим ряд из абсолютных величин членов ряда и применим к нему признак Д’Аламбера.
Если существует (конечный или бесконечный) предел, то по условию сходимости признака Д’Аламбера ряд будет сходиться, если
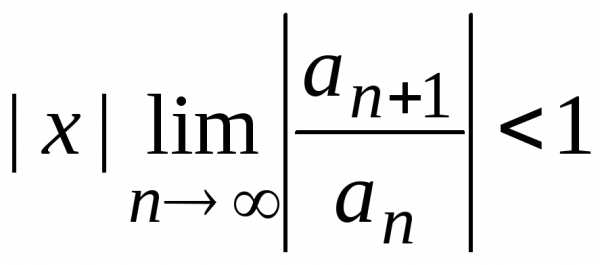 ,
,
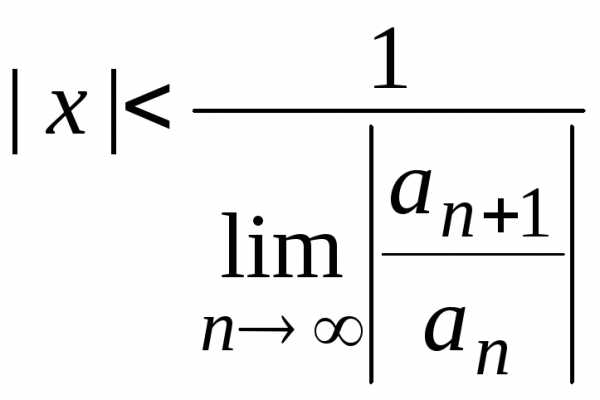 ,
,
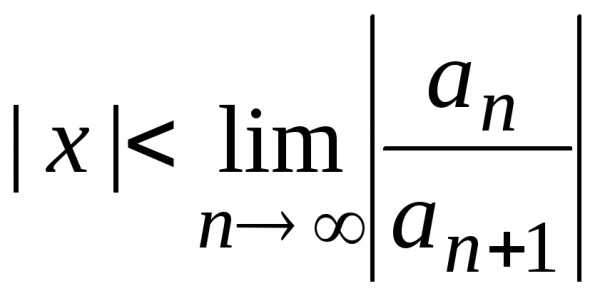 .
.
Отсюда из определения интервала и радиуса сходимости имеем
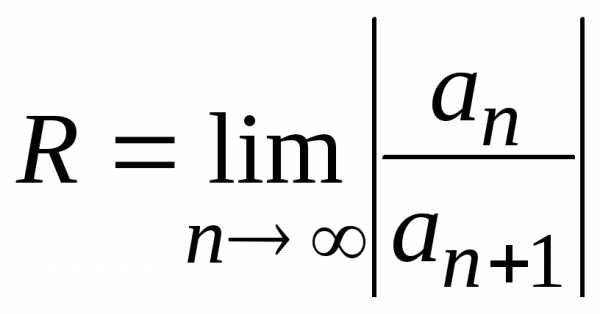
Применяя радикальный признак Коши и рассуждая аналогично, можно получить еще одну формулу для нахождения радиуса сходимости
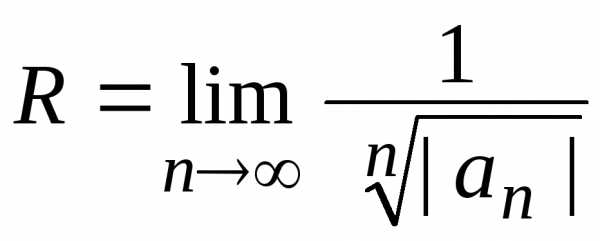
Пример 19
Найти область
сходимости ряда 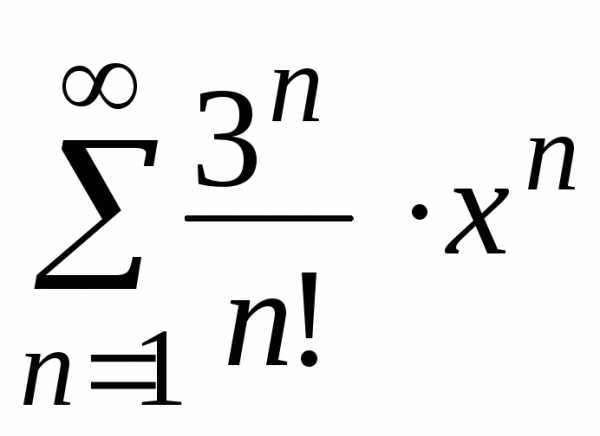
Решение.
Ряд является степенным по степеням х. Для нахождения интервала сходимости вычислим радиус сходимости по приведенной выше формуле. Для данного ряда формула числового коэффициента имеет вид
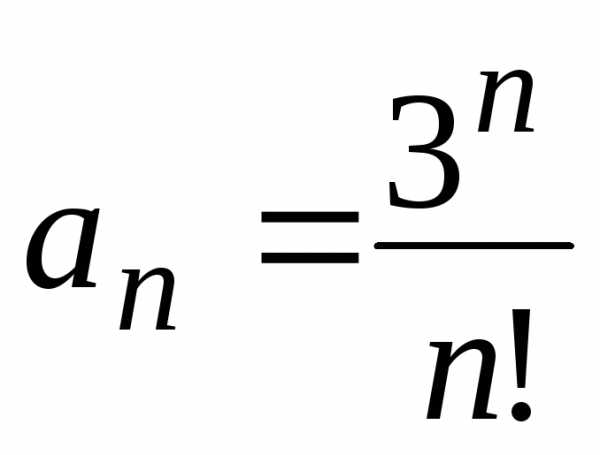 ,
тогда
,
тогда
Следовательно,
.
Так как R = , то ряд сходится (причем абсолютно) при всех значения х, т.е. область сходимости х (–; +).
Заметим, что можно было бы найти область сходимости без использования формул, а применяя непосредственно признак Д’ Аламбера:
Так как величина предела не зависит от х и меньше 1, то, значит, ряд сходится при всех значениях х, т.е. при х(-;+).
Пример 20
Найти область сходимости ряда
1!(х+5)+2!(х + 5)2 +3!(х + 5)3 +… + п!(х + 5)п +…
Решение.
Данный ряд является степенным рядом по степеням (х + 5), т.е. центр сходимости х0 = —5. Числовой коэффициент ряда ап = п!.
Найдем радиус сходимости ряда
.
Таким образом, интервал сходимости состоит из одной точки – центра интервала сходимости х = —5.
Пример 21
Найти область
сходимости ряда 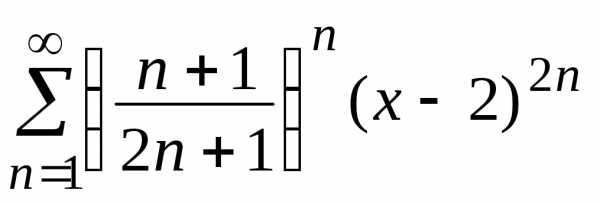 .
.
Решение.
Данный ряд является степенным рядом по степеням (х–2), т.е.
центр сходимости х0 = 2. Заметим, что ряд является знакоположительным при любом фиксированном х, так как выражение (х-2) возводится в степень 2п. Применим к ряду радикальный признак Коши.
Ряд будет сходиться, если величина предела меньше 1, т.е.
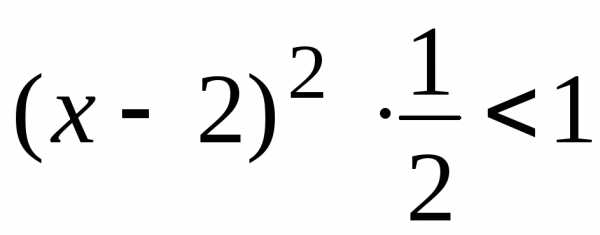 ,,,
,,,
значит, радиус
сходимости 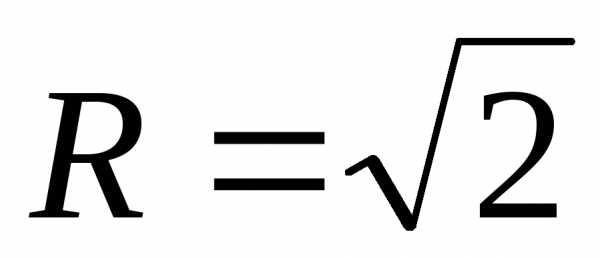 ,
тогда интеграл
сходимости
,
тогда интеграл
сходимости
, .
Таким образом, ряд сходится абсолютно при х . Обратим внимание, что интеграл сходимости симметричен относительно центра сходимости хо = 2.
Исследуем сходимость ряда на концах интервала сходимости.
Полагая , получим числовой знакоположительный ряд
Воспользуемся необходимым признаком сходимости:
,
следовательно, числовой ряд расходится, и точка является точкой расходимости. Заметим, что при вычислении предела использовали второй замечательный предел.
Полагая , получим тот же числовой ряд (проверить самостоятельно!), значит, точка также не входит в интервал сходимости.
Итак, область абсолютной сходимости данного ряда х.
2.3. Свойства сходящихся степенных рядов
Мы знаем, что конечная сумма непрерывных функций непрерывна; сумма дифференцируемых функций дифференцируема, причем производная суммы равна сумме производных; конечную сумму можно интегрировать почленно.
Оказывается, для «бесконечных сумм» функций – функциональных рядов в общем случае свойства не имеют места.
Например, рассмотрим функциональный ряд
Очевидно, что все члены ряда – непрерывные функции. Найдем область сходимости этого ряда и его сумму. Для этого найдем частичные суммы ряда
,
тогда сумма ряда
Таким образом, сумма S(х) данного ряда, как предел последовательности частичных сумм, существует и конечна при х (-1;1), значит, этот промежуток является областью сходимости ряда. При этом его сумма является разрывной функцией, так как
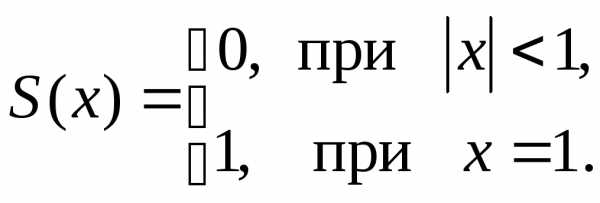

Итак, этот пример показывает, что в общем случае свойства конечных сумм не имеют аналога для бесконечных сумм – рядов. Однако для частного случая функциональных рядов – степенных рядов – свойства суммы аналогичны свойствам конечных сумм.
Свойства сходящихся степенных рядов
Рассмотрим степенной ряд
Для него справедливо
1. Сумма степенного ряда непрерывна в интервале сходимости ряда.
2. Степенной ряд можно почленно дифференцировать в интервале сходимости, т.е.
— сумма ряда S(х) дифференцируема в интервале сходимости;
— ряд, составленный из производных членов ряда
сходится в интервале сходимости исходного ряда, причем его сумма
равна S(х).
3. Степенной ряд
можно почленно интегрировать по любому
отрезку 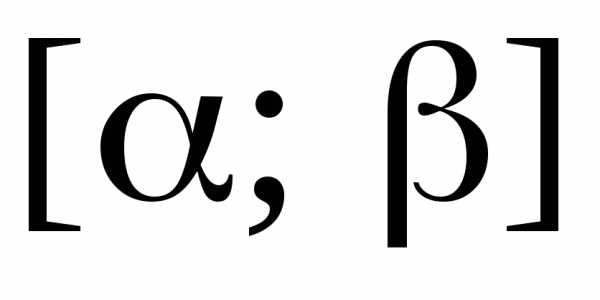 ,
принадлежащему интервалу сходимости,
т.е.
,
принадлежащему интервалу сходимости,
т.е.
В частности,
очевидно, что степенной ряд 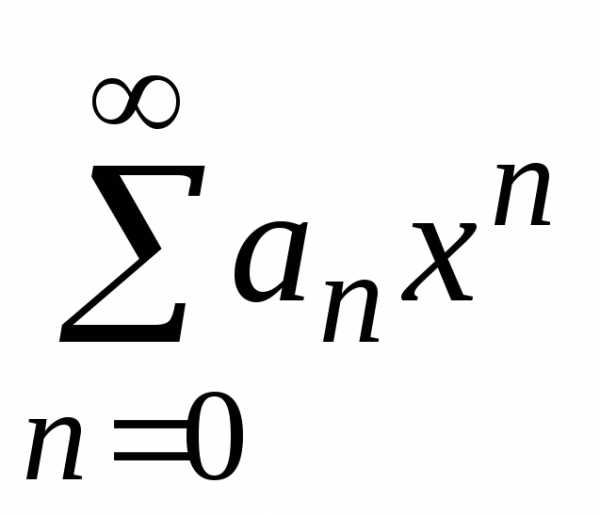 можно почленно
интегрировать по отрезку [0,х] для любого х из
интервала сходимости ряда. При этом
получим
можно почленно
интегрировать по отрезку [0,х] для любого х из
интервала сходимости ряда. При этом
получим
.
Заметим, что ряды, полученные из данного степенного ряда почленным дифференцированием или интегрированием, являются так же степенными рядами, сходящимися в том же интервале, что и исходный ряд.
Из приведенных свойств следует, что степенной ряд в интервале сходимости можно почленно дифференцировать любое число раз, причем получающиеся при этом ряды имеют тот же интеграл сходимости, а суммы соответственно равны S‘(х), S«(х), S«(х),…. Аналогичное утверждение можно сформулировать для почленного интегрирования ряда.
Пример 22
Найти сумму ряда
Решение.
Данный ряд является степенным по степеням х, центр сходимости х0=0, числовой коэффициент ап = п. Найдем радиус и интервал сходимости ряда:
,
следовательно, интервал сходимости х (–1;1).
Обозначим за S(х) сумму данного ряда и проинтегрируем ряд почленно по отрезку [0; x] для любого х из интервала сходимости ряда:
Полученный ряд составлен из членов бесконечной геометрической прогрессии со знаменателем q= х и первым членом а= х.
Нам известно, что
при знаменателе |q|<1 сумма
бесконечной геометрической прогрессии 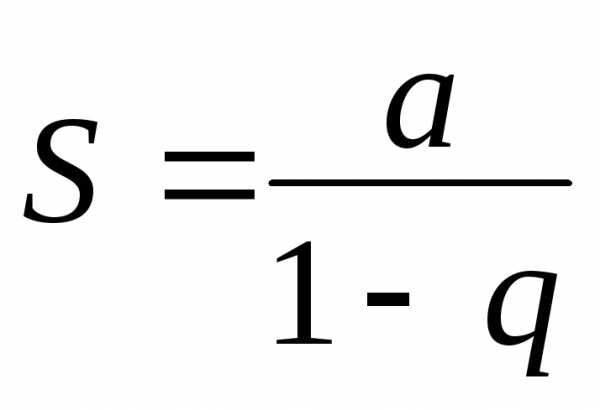 .
Таким образом, при |х|
< 1
.
Таким образом, при |х|
< 1
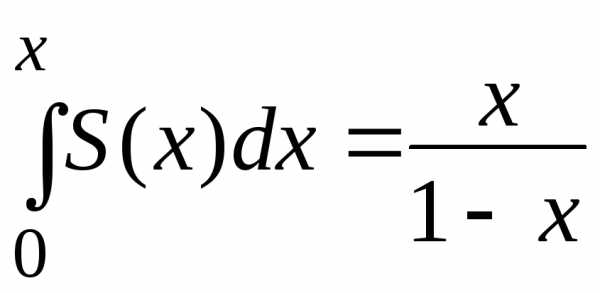
Чтобы найти искомую сумму ряда S(х), необходимо продифференцировать полученное равенство
.
Итак, внутри
интервала сходимости степенной ряд 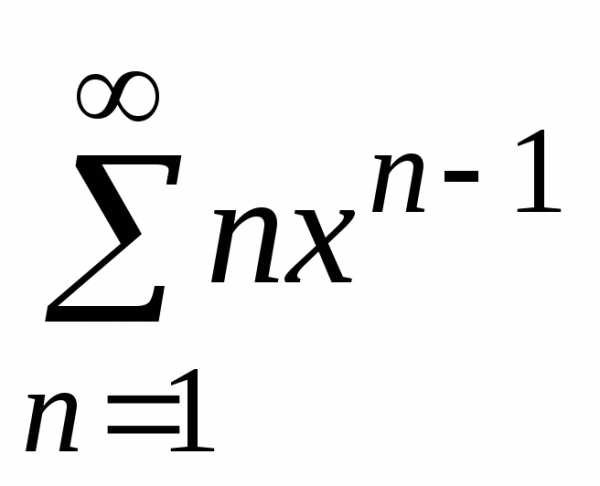 сходится
к функции
сходится
к функции 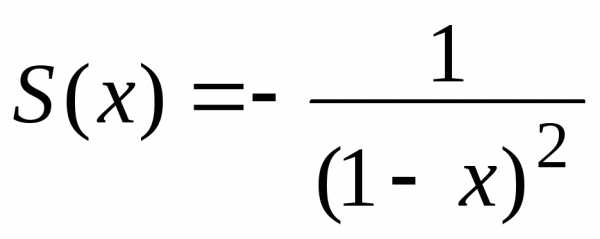 ,
т.е.
,
т.е.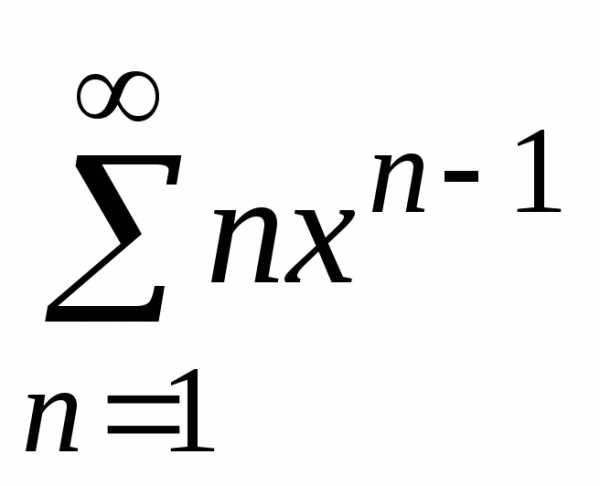 =
=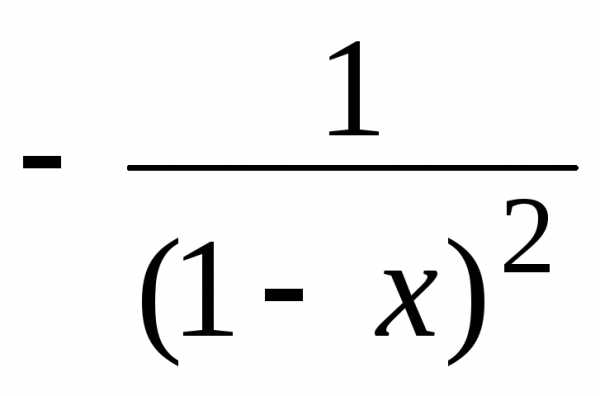 длях
(–1;1).
длях
(–1;1).
37
studfiles.net

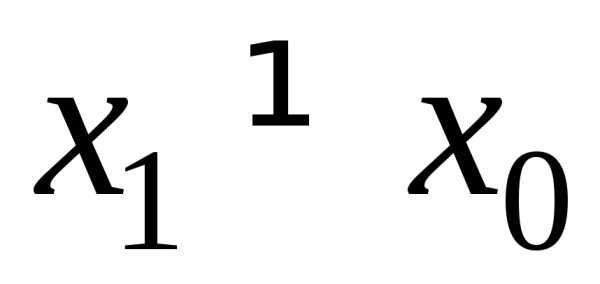 ,
тогда числовой ряд
,
тогда числовой ряд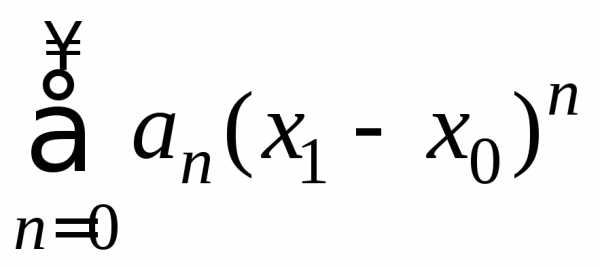 сходится.
Тогда по необходимому признаку сходимости
ряда.
сходится.
Тогда по необходимому признаку сходимости
ряда.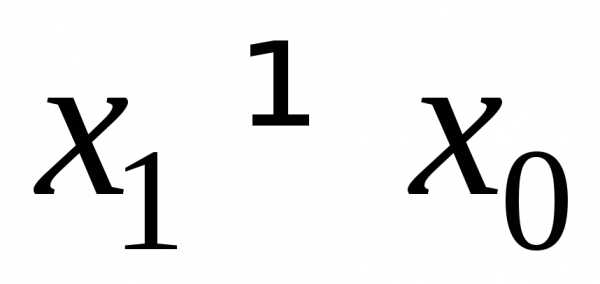 .
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке
.
Рассмотрим.
Если бы ряд сходился в точкеx,
то он по п. 1 доказательства сходился
бы в точке 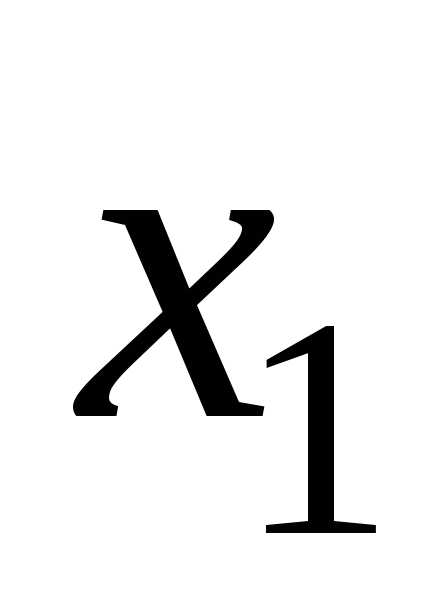 .
Противоречие.
.
Противоречие.