по сторонам треугольника найти медиану
Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.
Для начала рассмотрим задачу в общем виде.
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.
AB=a, AC=b, BC=c.
Решение.
На луче BF отложим отрезок FD, FD=BF.
Соединим точку D с точками A и C.
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.
Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),
BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,
Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:
Переходим к рассмотрению конкретной задачи.
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.
Решение:
Применяя аналогичные рассуждения, получаем:
AC²+BD²=2(AB²+BC²).
Отсюда
14²+BD²=2(13²+15²)
BD²=2(169+225)-196=592
Ответ:
www.uznateshe.ru
Калькулятор расчета длины медианы треугольника
Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.
Калькулятор длины медианы треугольника
Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника
Формула расчета длины медианы
где,
- a,b,c — Длина сторон треугольника.
Пример расчета медиан:
Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.
Получаем:
A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )
Решение:
Шаг 1:
Найдем длину сторон a,b,c используя формулу
d = √((x2 — x1)2 + (y2 — y1)2)
Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )
a = √((5 — 8)2 + (6 — 9)2 )= 4.242
Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )
Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )
c = √((8 — 1)2 + (9 — 5)2) = 8.062
Шаг 2:
Полученные значения a,b,c применяем в формулы
ma = (1/2) √2c2 + 2b2 — a2
mb = (1/2) √(2c2 + 2a2 — b2 )
mc = (1/2) √(2a2 + 2b2 — c2 )
- ma = (1/2)√(2(8.062)2 + 2(4.123)2 — 4.2422 )= 6.042
- mb = (1/2)√(2(8.062)2 + 2(4.242)2 — 4.1232 )= 6.103
- mc = (1/2)√2(4.242)2 + 2(4.123)2 — 8.0622 = 1.118
Свойства Медиан Треугольника
- Медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
- В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равняется половине гипотенузы.
- Из отрезков, образующих медианы, можно составить треугольник, то есть их длины удовлетворяют неравенству треугольника.
wpcalc.com
Как найти длину медианы треугольника
Рассмотрим произвольный треугольник АВС. Длины его сторон обозначим следующим образом:
АВ через storona1;
BC — storona2;
AC — storona3.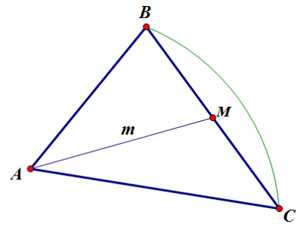
Проведем из вершины А медиану к стороне ВС и обозначим ее через m1.
Выведем формулу для расчета длины медианы треугольника через стороны этого треугольника.
- Достроим треугольник АВС так, чтобы получить параллелограмм ABDC.
- Рассмотрим треугольник АВС. Используя теорему косинусов, найдем косинус угла ВАС:
Выразим из этой формулы косинус ВАС:
- Согласно свойству односторонних углов четырехугольника их сумма равна 180 градусов. Следовательно, сумма углов ВАС и ABD также равна 180 градусов.
Тогда .
- Рассмотрим треугольник ABD. Используя теорему косинусов, найдем сторону АD:
Согласно свойству параллелограмма его противоположные стороны равны, поэтому:
BD = AC = storona3.
Поскольку для косинуса угла ВАС у нас уже есть готовое выражение, то подставим его в данное:
Итак, получили формулу для вычисления длины медианы через стороны треугольника.
ru.solverbook.com
Как построить медиану треугольника с помощью циркуля 🚩 картинки медиана треугольника 🚩 Математика
Автор КакПросто!
Медианой треугольника называется отрезок, соединяющий любую из вершин треугольника с серединой противоположной стороны. Поэтому задача построения медианы с помощью циркуля и линейки сводится к задаче нахождения середины отрезка.
Вам понадобится
- — циркуль
- — линейка
- — карандаш
Инструкция
Постройте треугольник ABC. Пусть необходимо провести медиану из вершины С к стороне AB.
Найдем середину стороны AB. Установите иглу циркуля в точке A. Другой конец циркуля поставьте в точку B. Тем самым ножками циркуля вы отмерили длину AB. Проведите окружность с центром в точке A и радиусом R, равным AB.
Затем, не меняя расстояния между ножкам циркуля, установите иглу циркуля в точке B. Проведите окружность с центром в точке В и тем же радиусом AB.
Окружности, проведенные из точек А и В, должны пересечься в двух точках. Назовите их, например, М и Т. Соедините линейкой точки М и Т. Точка, в которой отрезок МТ пересечет отрезок АВ, и будет являться серединой отрезка АВ. Назовем эту точку точкой Е.Кстати, прямая МТ будет не только делить отрезок АВ пополам, но и являться перпендикуляром к нему. Так что если перед вами стоит задача построить перпендикуляр к отрезку, действуйте по той же схеме, что и для нахождения середины отрезка.Итак, поскольку Е — середина стороны АВ, то отрезок СЕ будет являться искомой медианой треугольника, проведенной из вершины С к стороне АВ. Соедините при помощи линейки точки С и Е.
Если необходимо провести также медианы из вершин треугольника А и В к сторонам ВС и АС соответственно, проделайте аналогичную процедуру. Помните, что все три медианы треугольника должны пересечься в одной точке. В стороне от чертежа описывайте свои действия. Последовательно отмечайте, что вы строите. Какие линии, окружности вы проводите, и какими буквами обозначаете точки, получаемые на пересечениях. В задачах на построение циркулем и линейкой обычно требуется не только построить что-либо, но и доказать, что используемая последовательность действий привела к нужному результату.По построению четырехугольник АМВТ является ромбом (АМ=ВМ=АТ=ВТ=AB). Ромб — частный случай параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам (свойство параллелограмма). То есть, точка Е, полученная на пересечении диагоналей ромба АВ и МТ, дает середину АВ. Т.к. точка Е — середина АВ, то СЕ — медиана треугольника АВС (по определению). Что и требовалось доказать.Под медианами треугольника подразумеваются отрезки, которые проведены от соответствующих им вершин треугольника к противоположным сторонам и делят их на 2 равные части. Чтобы построить медианы в треугольнике, нужно сделать 2 шага.
Вам понадобится
- -Предварительно начерченный треугольник, размеры сторон произвольны;
- -Линейка;
- -Карандаш и ручка.
Инструкция
Берется карандаш и линейка, а затем с их помощью на сторонах треугольника отмечаются точки так, чтобы они делили соответствующие им стороны треугольника пополам. Один из вариантов, как их нужно отмечать, есть на рисунке 1.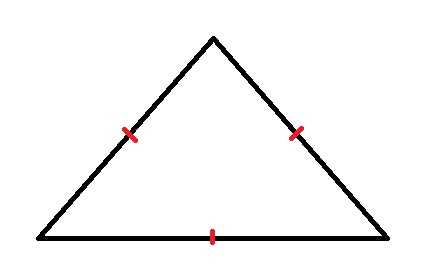
Теперь, с помощью красной/синей или другой цветной ручки и линейки из каждой вершины треугольника проводится отрезок, причем таким образом, чтобы он соединял вершины треугольника с соответствующими им противоположными прямыми в точках, которые были построены в первом шаге. Примерный вариант, как это должно получиться, показан на рисунке 2.
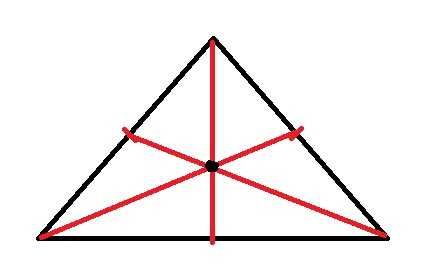
Видео по теме
Обратите внимание
Чтобы проверить правильность построения, необходимо учесть, что все медианы треугольника пересекаются в одной точке, которая называется центровой.
Медиана — это отрезок, проведенный из некоторого угла многоугольника к одной из его сторон таким образом, что точка пересечения медианы и стороны является серединой этой стороны.

Вам понадобится
- — циркуль
- — линейка
- — карандаш
Инструкция
Пусть задан треугольник ABC, надо построить медиану, падающую из угла C на сторону AB. По сути, задача сводится к разбиению стороны AB пополам с помощью циркуля. Отдельно будет рассмотрено разбиение этого отрезка пополам, а потом будет представлена общая картина. Сначала установите иглу циркуля в точку A, растворите циркуль так, чтобы он доставал грифелем до точки B. Проведите циркулем окружность с центром в точке A радиусом AB. Затем установите иглу циркуля в точку B и проведите такую же окружность с центром в точке B. Эти окружности пересекаются в двух точках, которые на рисунке обозначены как P и Q. Соедините точки P и Q по линейке. Точка пересечения отрезков PQ и AB будет серединой отрезка AB. Обозначьте ее D.
На рисунке изображена общая картина построений вокруг треугольника ABC. Теперь соедините найденную середину отрезка D с вершиной треугольника C. Отрезок CD является медианой треугольника.
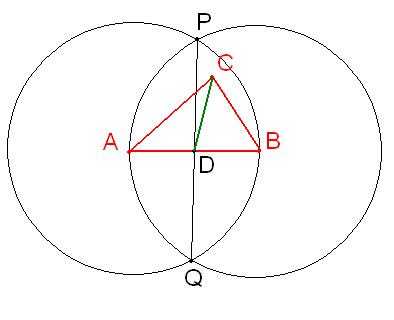
Видео по теме
Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы пересекаются в одной точке всегда внутри треугольника. Эта точка делит каждую медиану в отношении 2:1.
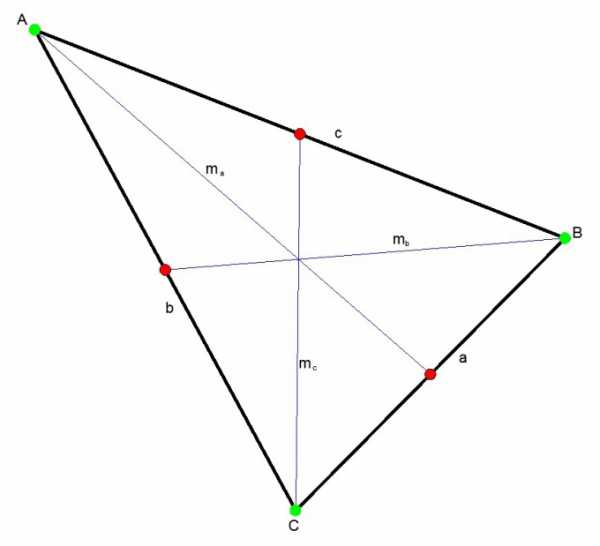
Инструкция
Медиану можно найти используя теорему Стюарта. Согласно которой, квадрат медианы равен четверти суммы удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана.mc^2 = (2a^2 + 2b^2 — c^2)/4,
где
a, b, c — стороны треугольника.
mc — медиана к стороне с;
Задача по нахождению медианы может быть решена через дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.Продлим стороны треугольника и медиану, достроив их до параллелограмма. Таким образом, медиана треугольника будет равна половине диагонали получившегося параллелограмма, две стороны треугольника — его боковым сторонам (a, b), а третья сторона треугольника, к которой была проведена медиана, является второй диагональю получившегося параллелограмма. Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
2*(a^2 + b^2) = d1^2 + d2^2,
где
d1, d2 — диагонали получившегося параллелограмма;
отсюда:
d1 = 0.5*v(2*(a^2 + b^2) — d2^2)
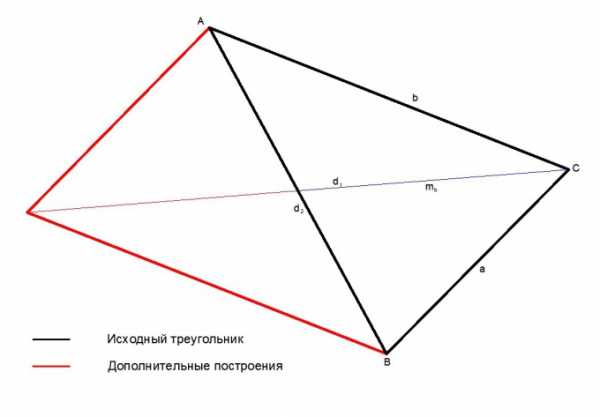
Вычислить медиану может понадобиться в самый неожиданный момент. Например, при планировке садового участка.
Вам понадобится
- Инструменты: Карандаш Линейка Транспортир Математические формулы и понятия: Медиана Теоремы синусов и косинусов
Инструкция
Постройте треугольник с заданными параметрами — по трем сторонам, по двум сторонам и углу между ними, по двум углам и расположенной между ними стороне.Обозначьте вершины углов, углы и стороны. Вершины углов обозначаются А, B, C, сами углы — греческими символами ?,?,?. Стороны обозначаются строчными латинскими буквами a,b,c.
Вычислите длины всех углов и сторон по теоремам синусов и косинусов.
 Вспомните, что такое медиана. Медиана — это линия, проведенная из заданного угла треугольника к середине его противолежашей стороны.
Вспомните, что такое медиана. Медиана — это линия, проведенная из заданного угла треугольника к середине его противолежашей стороны.Разделите стороны треугольника пополам и обозначьте получившиеся точки латинской M с соответствующими сторонам нижниими индексами a,b,c.
Вычислите длину медианы по формуле: медиана равна квадратному корню из суммы удвоенных квадратов двух других сторон треугольника минус квадрат стороны, к которой проведена медиана, деленному на четыре.Вычислите по этой же формуле размеры остальных медиан
Видео по теме
Обратите внимание
Все медианы треугольника пересекаются в одной точке. Эта точка называется центроидом. Самой длинной стороне треугольника соответствует самая короткая медиана. В прямоугольном треугольнике медиана, проведенная из прямого угла, является одновременно высотой к этой же стороне.
Полезный совет
Для определения синусов и косинусов пользуйтеся математическими таблицами.
Источники:
- пїЅпїЅпїЅ пїЅпїЅпїЅпїЅпїЅ, пїЅпїЅпїЅпїЅпїЅ найти длину медианы
Определение медианы прямоугольного треугольника — это одна из базовых задач в геометрии. Часто ее нахождение выступает в роли вспомогательного элемента в решение какой-либо более сложной задаче. В зависимости от имеющихся данных, поставленную задачу можно решить несколькими способами.

Вам понадобится
- учебник по геометрии.
Инструкция
Стоит напомнить, что треугольник является прямоугольным, если один и его углов равен 90 градусов. А медиана — это отрезок опущенный из угла треугольника на противолежащую сторону. Причем он делит ее на две равные части. В прямоугольном треугольнике ABC, у которого угол АВС является прямым, медиана BD, опушенная из вершины прямого угла, равняется половине гипотенузы AC. То есть, для того, чтобы найти медиану, поделите значение гипотенузы на два: BD=AC/2.Пример: Пусть в прямоугольном треугольнике АВС (АВС-прямой угол), известны значения катетов AB=3 см., BC=4 см., найдите длину медианы ВD, опущенной из вершины прямого угла. Решение:1) Найдите значение гипотенузы. По теореме Пифагора AC^2 = AB^2+BC^2. Следовательно AC = (AB^2+BC^2)^0,5 = (3^2+4^2)^0,5 = 25^0,5 = 5 см
2) Найдите длину медианы по формуле: BD = AC/2. Тогда BD = 5 см.
Совершенно другая ситуация возникает при нахождение медианы, опущенной на катеты прямоугольного треугольника. Пусть у треугольника АВС, угол В прямой, а АЕ и СF медианы опущенные на соответствующие катеты ВС и АВ. Тут длинна этих отрезков находится по формулам: АЕ=(2(АВ^2+AC^2)-BC^2)^0,5/2
СF=(2(BC^2+AC^2)-AB^2)^0,5/2 Пример: У треугольника АВС, угол АВС является прямым. Длина катета АВ = 8 см, угол BCA = 30 градусов. Найдите длины медиан, опущенных из острых углов.Решение:
1) Найдите длину гипотенузы АС, ее можно получить из соотношения sin(BCA)=AB/AC. Отсюда AC=AB/sin(BCA). AC=8/sin(30)=8/0,5=16 см.
2) Найдите длину катета АС. Проще всего ее можно найти по теореме Пифагора: AC = (AB^2+BC^2)^0,5, AC = (8^2+16^2)^0,5 = (64+256)^0,5 = (1024)^0,5 = 32 см.
3) Найдите медианы по выше приведенным формулам
АЕ=(2(АВ^2+AC^2)-BC^2)^0,5/2 = (2(8^2+32^2)-16^2)^0,5/2 = (2(64+1024)-256)^0,5/2 = 21,91 см.
СF=(2(BC^2+AC^2)-AB^2)^0,5/2 = (2(16^2+32^2)-8^2)^0,5/2 = (2(256+1024)-64)^0,5/2 = 24,97 см.
Обратите внимание
Медиана всегда разбивает треугольник на два других треугольника, равных по площади.
Точка пересечения всех трех медиан называется центром тяжести.
Полезный совет
Очень часто значение катетов и гипотенуз проще всего найти по тригонометрическим формулам.
Источники:
- что такое медиана прямоугольника
Медиана — это отрезок, соединяющий вершину треугольника и середину противолежащей стороны. Зная длины всех трех сторон треугольника, можно найти его медианы. В частных случаях равнобедренного и равностороннего треугольника, очевидно, достаточно знания, соответственно, двух (не равных друг другу) и одной стороны треугольника. Медиану также можно найти и по другим данным.
Вам понадобится
- Длины сторон треугольника, углы между сторонами треугольника
Инструкция
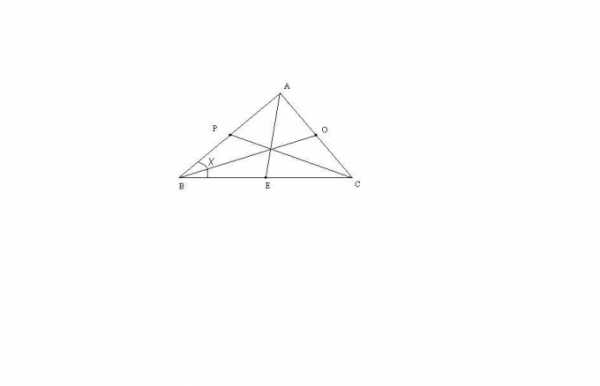
Рассмотрим самый общий случай треугольника ABC с тремя не равными друг другу сторонами. Длину медианы AE этого треугольника можно вычислить по формуле: AE = sqrt(2*(AB^2)+2*(AC^2)-(BC^2))/2. Остальные медианы находятся абсолютно аналогично. Эта формула выводится через теорему Стюарта, либо через достроение треугольника до параллелограмма. Если треугольник ABC — равнобедренный и AB = AC, то медиана AE будет являться одновременно и высотой этого треугольника. Следовательно, треугольник BEA будет прямоугольным. По теореме Пифагора, АЕ = sqrt((AB^2)-(BC^2)/4). Из общей формулы длины медианы треугольника, для медиан BO и СP справедливо: BO = CP = sqrt(2*(BC^2)+(AB^2))/2.Если треугольник ABC — равносторонний, то, очевидно, что все его медианы равны друг другу. Так как угол при вершине равностороннего треугольника равен 60 градусам, то AE = BO = CP = a*sqrt(3)/2, где a = AB = AC = BC — длина стороны равностороннего треугольника.
Медиану треугольника можно найти и по другим данным. Например, если заданы длины двух сторон, к одной из которых проведена медиана, например, длины сторон AB и BC, а также угол x между ними. Тогда длину медианы можно найти через теорему косинусов: AE = sqrt((AB^2+(BC^2)/4)-AB*BC*cos(x)).
Источники:
- Медианы и биссектрисы треугольника
- как находить длину медианы
В ряде планиметрических задач требуется построить медиану. Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианой называют прямую, содержащую этот отрезок.

Вам понадобится
- линейка
- циркуль
- карандаш
- ластик
Инструкция
Чтобы провести медиану, необходимо соединить вершину треугольника с серединой противоположной стороны. Поэтому основная сложность задачи состоит в нахождении середины этой самой стороны. Как же найти середину стороны? Сразу приходит в голову измерить ее линейкой и отложить половину от одного из концов — вот и будет медиана! Совершенно верно! Но если мы выполняем чертеж, и точность даже в полмиллиметра для нас существенна? То-то и оно! Придется прибегнуть к другому, более точному способу. Нам понадобятся циркуль и линейка. Оцениваем длину нашего отрезка на глазок и открываем циркуль на любую длину. Главное, чтобы эта длина была больше половины отрезка. Теперь необходимо провести две окружности из концов разбиваемого отрезка.Ставим иглу циркуля в один из концов отрезка, проводим окружность. То же самое проделываем для другого конца отрезка. Особенно нас интересуют точки, где эти окружности пересекутся. Поэтому имеет смысл в местах пересечения окружностей прорисовать их сильнее.
Итак, найдем точки пересечения окружностей. Видно, что они лежат по разные стороны нашего отрезка. Теперь соединим их между собой. Видим, новый отрезок он пересекает сторону треугольника. Оказывается, что точка пересечения и есть точная середина нашего отрезка. Соединив эту точку с противоположной вершиной, мы и получим искомую медиану.
Есть третий способ еще сложнее. В этом случае нам также понадобятся линейка и циркуль. Пусть мы имеем треугольник ABC. Пусть к стороне AC этого треугольника мы хотим построить медиану. Чтобы это сделать, нужно провести две окружности по следующим правилам. Вокруг вершины C нужно провести окружность радиуса AB. А вокруг вершины A нужно провести окружность радиуса BC.
Измеряем длину отрезка AB. Теперь не меняя положения ножек циркуля, чертим окружность из вершины С. То же самое проделываем для отрезка BC и вершины A. Получаем две окружности. Точку их пересечения необходимо соединить с вершиной B. Таким образом, мы получили медиану.
Видео по теме
Медиана – отрезок, который берет начало в одной из вершин треугольника и заканчивается в точке, делящей противолежащую сторону треугольника на две равные части. Построить медиану, не проводя математических вычислений, довольно просто.

Вам понадобится
- Лист бумаги, линейка, циркуль и карандаш.
Инструкция
Нарисуйте на плоскости произвольный треугольник, обозначьте его вершины буквами А, В и С. Необходимо, к примеру, построить с помощью циркуля медиану ВМ. Для этого установите циркуль в вершине треугольника А. Начертите окружность (с центром в точке А) радиусом, равным стороне треугольника АС. Теперь переставьте циркуль в вершину треугольника С и начертите еще одну окружность тем же радиусом (АС). Точки пересечения окружностей обозначьте буквами E и D.Через точки Е и D проведите прямую. Точку пересечения прямой ED и стороны АС треугольника обозначьте буквой М. Это искомая точка – середина стороны АС. Теперь соедините вершину треугольника В с точкой М. ВМ – одна из медиан треугольника АВС.
Используя вышеуказанный метод построения медианы при помощи циркуля, постройте самостоятельно медианы АМ1 и СМ2.
Чтобы проверить правильность избранного метода, обратите внимание на фигуру АЕСD. Соедините последовательно по линейке вершины А, Е, С и D. Полученная фигура – ромб по определению., т.к. ромбом называется четырехугольник с равными сторонами. По одному из свойств ромба диагонали ромба точкой пересечения делятся пополам, следовательно, АМ равно АС. Что и требовалось доказать.
Видео по теме
Медиана — геометрическое определение, которое связано с понятием треугольника. Она представляет собой отрезок, соединяющий вершину произвольного треугольника с серединой противоположной стороны. Найти или вычислить длину медианы можно, зная длины сторон произвольного треугольника. Рассмотрим решение задачи на примере.
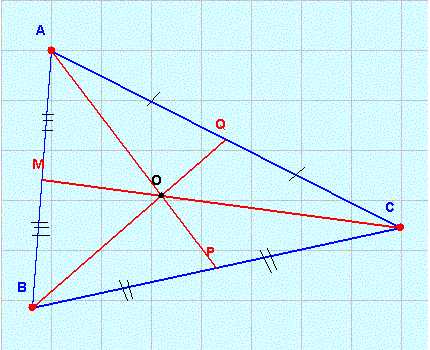
Вам понадобится
- Геометрическая формула для вычисления длины медианы произвольного треугольника ABC:
- m = √(2·(b2 + c2) — a2)/2,
- где m — длина медианы О,
- а — длина стороны ВС произвольного треугольника(к этой стороне проведена медиана),
- b — длина стороны АВ треугольника,
- c — длина сторон АС треугольника.
Инструкция
Измерьте с помощью линейки длины сторон АВ, АС и ВС данного треугольника. Длины сторон могут быть даны в условиях геометрической задачи. Пусть а=7 см — длина стороны ВС(сторона, к которой проведена медиана О), b=5 см — длина стороны АВ и с=6 см — длина стороны АС. Итак, по условиям задачи a=7 см, b=5 см, c=6 см. Вычислите длину медианы треугольника ABC по указанной формуле. Подставьте значения длин сторон треугольника ABC в формулу и произведите следующие вычисления.Возведите длины всех сторон треугольника ABC в квадрат:
— 5×5=25 см(квадрат длины b стороны АВ), 6×6=36 см(квадрат длины c стороны АС), 7×7=49 см(квадрат длины а стороны ВС).
Сложите полученные суммы квадратов длин сторон АВ и АС треугольника ABC (b2+c2):
— 25+36=61 .
Умножьте полученную сумму квадратов длин сторон b и c на число 2 ((b2+c2)х2) :
— 61×2=122.
— 122-49=73.
Извлеките квадратный корень из полученного результата. Разделите полученное число на 2(√(2·(b2 + c2) — a2)/2):
√73/2=4,27 см — искомая длина m медианы O треугольника ABC. Так, используя указанную геометрическую формулу и зная длины сторон треугольника ABC, вы вычислили длину его медианы.
Видео по теме
Обратите внимание
Медиана треугольника делит его на две равновеликие части. Из двух медиан треугольника большей является медиана, проведенная к меньшей стороне треугольника.В треугольнике существует три медианы. Они всегда пересекаются в одной точке внутри треугольника. Эта точка называется центром тяжести треугольника (или центроидом).
Треугольник разделяется тремя медианами на шесть равновеликих треугольников. В равнобедренном треугольнике медиана, поведенная к его основанию, является одновременно биссектрисой и высотой.
Источники:
- Формулы онлайн
www.kakprosto.ru
Как найти длину медианы треугольника
Примечание. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.Задача. Найти длину медианы треугольника через его стороны
Стороны треугольника равны 8, 9 и 13 сантиметров. К наибольшей стороне треугольника проведена медиана. Определите медиану треугольника исходя из размеров его сторон.Решение.
Задача имеет два способа решения. Первый, который не нравится учителям средней школы, но является наиболее универсальным.
Способ 1.
Применим Теорему Стюарта, согласно которой квадрат медианы равен одной четвертой от суммы удвоенных квадратов сторон из которой вычли квадрат стороны, к которой проведена медиана.
mc2 = ( 2a2 + 2b2 — c2 ) / 4
Соответственно
mc2 = ( 2 * 82 + 2 * 92 — 132) / 4
mc2 = 30,25
mc = 5,5 см
Способ 2.
Второй способ решения, который преподаватели в школе любят — это дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.
Продлим стороны треугольника и медиану достроив их до параллелограмма. В этом случае медиана BO треугольника ABC будет равна половине диагонали получившегося параллелограмма, а две стороны треугольника AB, BC — его боковым сторонам. Третья сторона треугольника AC, к которой была проведена медиана, является второй диагональю получившегося параллелограмма.

Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
2(a2+b2)=d12+d22
Обозначим диагональ параллелограмма, которая образована продолжением медианы исходного треугольника как х, получим:
2( 82 + 92 ) = 132 + x2
290 = 169 + x2
x2 = 290 — 169
x2 = 121
х = 11
Поскольку искомая медиана равна половине диагонали параллелограмма, то величина медианы треугольника составит 11 / 2 = 5,5 см
Ответ: 5,5 см
profmeter.com.ua
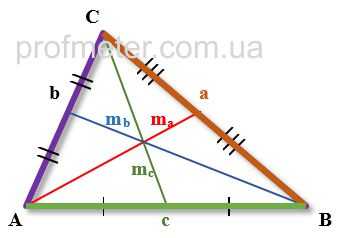
Найти сторону треугольника, зная медиану
В равностороннем треугольнике •все его углы равны, их величина составляет 60 градусов; •биссектрисы, высоты и медианы, проведенные из каждой вершины, совпадают. Значит, медиана делит треугольник на 2 прямоугольных треугольника, где углы равны 90, 60,30 гр. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов, а если один из углов равен 30 гр., то катет, лежащий напротив, равен 1/2 гипотенузы. Тогда получаем: а*=в*(медиана) +1/2а*
Допустим, имеем равносторонний треугольник ABC. Медиана, опущенная из вершины, делит сторону, на которую опускается, пополам. Т. е. медиана BM= \frac{1}{2} AC. Помимо этого, медиана будет являться и высотой. Получаем два прямоугольных треугольника: ΔAMB и ΔBMC. Из них и узнаем сторону. По теореме Пифагора: BC²=BM²+MC² BC²=BM²+BC²/4 BC²-BC²/4=BM² 3BC²/4=BM² 3BC²=4BM² BC²=4BM²/3 BC= \sqrt{ \frac{4BM^{2} }{3} }
touch.otvet.mail.ru
Разузнай! — Медиана треугольника — Уравнение длины медианы — Точка пересечения медиан треугольника
 |
Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.
Свойства медианы треугольника
- Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
- Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
- Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
- Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).
Уравнение длины медианы треугольника
Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны. В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.
Точка пересечения медиан треугольника
Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности. А другие геометрические фигуры имеют собственные центры.
Координаты точки пересечения медиан треугольника
Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x1;y1), B(x2;y2), C(x3;y3),
и вычисляем координаты центра треугольника по формуле: x0 = (x1 + x2 + x3)/3; y0 = (y1 + y2 + y3)/3.
Площадь треугольника через медиану
Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1. Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.
В случае с прямоугольным треугольником поступаем так. Вокруг треугольника описываем окружность, а еще одну вписываем в него. Помним, что площадь треугольника равна сумме квадрата радиуса внутренней окружности и двойного произведения радиуса описанной и вписанной окружности. При этом, радиус описанной равен длине медианы, которая идет к середине гипотенузы. А радиус вписанной вычисляем через свойство центра треугольника делить каждую медиану на две части в соотношении 2:1. Все полученные значения вставляем в формулу и получаем площадь прямоугольного треугольника.
- < Денежное дерево
- Мерчендайзер >
razuznai.ru
