Вычисление ранга матрицы методом элементарных преобразований (алгоритм Гаусса).
Под элементарными преобразованиями понимают те преобразования матрицы, которые не изменяют её ранга. К ним относят:
- Транспонирование ($\rang A=\rang A^T$).
- Перемена мест двух строк (столбцов).
- Умножение всех элементов строки (столбца) на некоторое число $a\neq 0$.
- Суммирование всех элементов одной строки (столбца) с соответствующими элементами иной строки (столбца), умноженными на некое действительное число.
Если применить к матрице $A$ некое элементарное преобразование, то получим матрицу $B$, при этом $\rang A=\rang B$.
Если $\rang A=\rang B$, то матрицы $A$ и $B$ называются эквивалентными. Тот факт, что матрица $A$ эквивалентна матрице $B$, записывают так: $A\sim B$.
Часто используется и такая запись: $A\rightarrow B$, которая означает, что матрица $B$ получена из матрицы $A$ применением некоего элементарного преобразования. Конечная цель преобразований матрицы – сделать её трапециевидной или ступенчатой.
Если матрица приведена к трапециевидной форме, то ранг матрицы будет равен количеству ненулевых элементов, стоящих на главной диагонали.
Если после преобразований исходная матрица стала ступенчатой, то ранг матрицы будет равен количеству ненулевых строк.
Отмечу, что при нахождении ранга методом Гаусса работать можно как со строками, так и со столбцами. Удобнее работать со строками, поэтому в примерах на этой странице преобразования выполняются именно над строками матриц. Впрочем, первое свойство (транспонирование не изменяет ранга) позволяет при необходимости вмиг строки сделать столбцами и наоборот.
Пример №1
Найти ранг матрицы $A=\left(\begin{array}{ccccc} 3 & 1 & 2 & 0 & 4 \\ -4 & -2 & -7 & 1 & -3 \\ -1 & -1 & 2 & -3 & 7 \\ 9 & 1 & 7 & -5 & 31 \\ 5 & 3 & 5 & 2 & -4 \end{array} \right)$.
Решение
Для начала отмечу, что первым элементом первой строки желательно поставить единицу (или (-1), не суть важно). Это не обязательно, но очень упрощает расчёты. У нас первым элементом первой строки есть тройка. Чтобы «поставить» единицу (или (-1)) на первое место в первой строке есть несколько вариантов. Можно поменять местами строки №1 и №3. Можно поменять местами столбцы №1 и №2. Можно даже поменять местами строки №1 и №2, а потом столбцы №1 и №4. Вариантов немало, выбираем любой. Остановимся на смене мест столбцов №1 и №2. При этом получим новую матрицу, эквивалентную матрице $A$:
$$ \left(\begin{array}{ccccc} 3 & 1 & 2 & 0 & 4 \\ -4 & -2 & -7 & 1 & -3 \\ -1 & -1 & 2 & -3 & 7 \\ 9 & 1 & 7 & -5 & 31 \\ 5 & 3 & 5 & 2 & -4 \end{array} \right)\sim \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ -2 & -4 & -7 & 1 & -3 \\ -1 & -1 & 2 & -3 & 7 \\ 1 & 9 & 7 & -5 & 31 \\ 3 & 5 & 5 & 2 & -4 \end{array} \right) $$Чтобы обнулить нужные элементы, будем выполнять операции со строками матрицы. Римскими цифрами будем обозначать строки матрицы: $I$ – первая строка, $II$ – вторая строка и так далее. «Красный элемент» расположен в первой строке, поэтому обнуление станем производить с помощью первой строки. Действия, которые нужно выполнить со строками, показаны на рисунке:
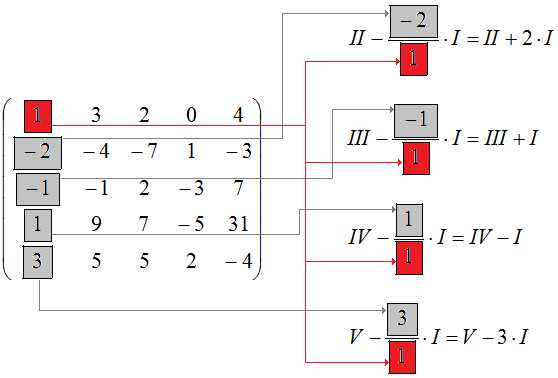
Что означает, например, запись $II+2\cdot I$? Она означает, что к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на два. Результат записывают на место второй строки в новую матрицу. Это преобразование можно выполнить отдельно:
$$ II+2\cdot I=\left(\begin{array}{ccccc} -2 & -4 & -7 & 1 & -3 \end{array} \right)+2\cdot \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \end{array} \right)=\\=\left(\begin{array}{ccccc} -2 & -4 & -7 & 1 & -3 \end{array} \right)+\left(\begin{array}{ccccc} 2 & 6 & 4 & 0 & 8 \end{array} \right)=\left(\begin{array}{ccccc} 0 & 2 & -3 & 1 & 5 \end{array} \right). $$ Результат выполненных преобразований записывается так: $$ \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ -2 & -4 & -7 & 1 & -3 \\ -1 & -1 & 2 & -3 & 7 \\ 1 & 9 & 7 & -5 & 31 \\ 3 & 5 & 5 & 2 & -4 \end{array} \right) \begin{array} {l} \phantom{0}\\ II+2\cdot I\\ III+I \\ IV-I \\ V-3\cdot I \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 2 & 4 & -3 & 11 \\ 0 & 6 & 5 & -5 & 27 \\ 0 & -4 & -1 & 2 & -16 \end{array} \right) $$Конечно, хорошо бы на месте диагонального «красного элемента» получить единицу, но в данной ситуации это не так уж и критично. В самом деле, все «серые элементы» нацело делятся на «красный», т.е. на 2. Поэтому изменять порядок строк или столбцов не станем. «Красный элемент» расположен во второй строке, поэтому именно её мы станем использовать для обнуления. Преобразования, которые нужно выполнить со строками матрицы, показаны на рисунке:
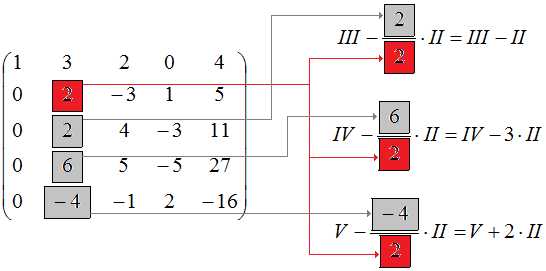
Выполняя все требуемые преобразования, будем иметь:
$$ \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 2 & 4 & -3 & 11 \\ 0 & 6 & 5 & -5 & 27 \\ 0 & -4 & -1 & 2 & -16 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ III-II \\ IV-3\cdot II \\ V+2\cdot II \end{array} \sim \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 7 & -4 & 6 \\ 0 & 0 & 14 & -8 & 12 \\ 0 & 0 & -7 & 4 & -6 \end{array} \right) $$ Заметьте, что все элементы четвёртой строки делятся на 2. Разделим их на 2. Это действие не изменит ранга матрицы, так как деление на 2 равносильно умножению на $\frac{1}{2}$, а умножение всех элементов строки на некое число, не равное нулю, не изменяет ранга матрицы. $$ \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 7 & -4 & 6 \\ 0 & 0 & 14 & -8 & 12 \\ 0 & 0 & -7 & 4 & -6 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ IV:2 \\ \phantom{0} \end{array} \sim \left(\begin{array}{ccccc} 1 & 3 & 2 & 0 & 4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 7 & -4 & 6 \\ 0 & 0 & 7 & -4 & 6 \\ 0 & 0 & -7 & 4 & -6 \end{array} \right) $$Пример №2
Решение
Для начала поменяем местами первый и четвёртый столбцы, чтобы первым элементом первой строки стала (-1):
$$ A=\left(\begin{array}{cccc} 5 & 2 & -3 & -1\\ -18 & -15 & 16 & 5\\ 9 & 18 & -14 & -4. \end{array} \right)\sim \left(\begin{array}{cccc} -1 & 2 & -3 & 5\\ 5 & -15 & 16 & -18\\ -4 & 18 & -14 & 9. \end{array} \right) $$Теперь начнём выполнять преобразования, аналогичные тем, что мы делали в примере №1:
$$ \left(\begin{array}{cccc} -1 & 2 & -3 & 5\\ 5 & -15 & 16 & -18\\ -4 & 18 & -14 & 9. \end{array} \right) \begin{array} {l} \phantom{0}\\ II+5\cdot I \\ III-4\cdot I \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & -3 & 5\\ 0 & -5 & 1 & 7\\ 0 & 10 & -2 & -11 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ III+2\cdot II \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & -3 & 5\\ 0 & -5 & 1 & 7\\ 0 & 0 & 0 & 3 \end{array} \right) $$Полученная нами матрица не является трапециевидной, так как на месте диагонального элемента в третьей строке стоит 0. Мы получили ступенчатую матрицу, у которой три ненулевых строки. Вывод: ранг равен 3. В принципе, при желании можно полученную матрицу сделать и трапециевидной. Для этого достаточно поменять местами третий и четвёртый столбцы:
$$ \left(\begin{array}{cccc} -1 & 2 & -3 & 5\\ 0 & -5 & 1 & 7\\ 0 & 0 & 0 & 3 \end{array} \right)\sim \left(\begin{array}{cccc} -1 & 2 & 5 & -3\\ 0 & -5 & 7 & 1\\ 0 & 0 & 3 & 0 \end{array} \right). $$Имеем трапециевидную матрицу, на главной диагонали которой расположены три ненулевых элемента (-1, -5, 3). Вывод: ранг равен 3.
Ответ: $\rang A=3$.
Пример №3
Найти ранг матрицы $A=\left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 1 & -2 & 3 & -4\\ -2 & 2 & -3 & 14\\ 4 & -2 & -1 & -20\\ 3 &-6 & 4 & -16\\ 1 & -2 & 0 & -5 \end{array} \right)$.
Решение
Начнём осуществлять те же преобразования, что и в предыдущих примерах:
$$ \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 1 & -2 & 3 & -4\\ -2 & 2 & -3 & 14\\ 4 & -2 & -1 & -20\\ 3 &-6 & 4 & -16\\ 1 & -2 & 0 & -5 \end{array} \right) \begin{array} {l} \phantom{0} \\ II+I \\ III-2\cdot I \\ IV+4\cdot I \\ V+3\cdot I \\VI+I \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 0 & 0 & 3 & 1\\ 0 & -2 & -3 & 4\\ 0 & 6 & -1 & 0\\ 0 &0 & 4 & -1\\ 0 & 0 & 0 & 0 \end{array} \right) $$Матрица трапециевидной формы не допускает, чтобы диагональным элементом в ненулевой строке был ноль. В свою очередь ступенчатая матрица не допускает, чтобы строка, которая расположена ниже, имела меньше нулей (расположенных в начале строки), чем строка, находящаяся выше. Иными словами, к какой бы форме мы не приводили заданную матрицу, вместо нуля во второй строке требуется расположить некий ненулевой элемент. Для этого можно пойти разными путями. Можно, к примеру, поменять местами второй и четвёртый столбцы. А можно просто поменять местами вторую и третью строки, а затем продолжить преобразования:
$$ \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 0 & 0 & 3 & 1\\ 0 & -2 & -3 & 4\\ 0 & 6 & -1 & 0\\ 0 &0 & 4 & -1\\ 0 & 0 & 0 & 0 \end{array} \right)\sim \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 0 & -2 & -3 & 4\\ 0 & 0 & 3 & 1\\ 0 & 6 & -1 & 0\\ 0 &0 & 4 & -1\\ 0 & 0 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ IV+3\cdot II \\ \phantom{0} \\ \phantom{0} \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 0 & -2 & -3 & 4\\ 0 & 0 & 3 & 1\\ 0 & 0 & -10 & 12\\ 0 &0 & 4 & -1\\ 0 & 0 & 0 & 0 \end{array} \right) $$Для дальнейших преобразований хотелось бы на месте диагонального элемента (т.е. на месте числа 3) получить единицу. Это легко осуществить, поменяв местами третий и четвёртый столбцы. После смены мест продолжим элементарные преобразования:
$$ \left(\begin{array}{cccc} -1 & 2 & 0 & 5\\ 0 & -2 & -3 & 4\\ 0 & 0 & 3 & 1\\ 0 & 0 & -10 & 12\\ 0 &0 & 4 & -1\\ 0 & 0 & 0 & 0 \end{array} \right)\sim \left(\begin{array}{cccc} -1 & 2 & 5 & 0\\ 0 & -2 & 4 & -3\\ 0 & 0 & 1 & 3\\ 0 & 0 & 12 & -10\\ 0 &0 & -1 & 4\\ 0 & 0 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ IV-12\cdot III \\ V+III \\ \phantom{0} \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & 5 & 0\\ 0 & -2 & 4 & -3\\ 0 & 0 & 1 & 3\\ 0 & 0 & 0 & -46\\ 0 &0 & 0 & 7\\ 0 & 0 & 0 & 0 \end{array} \right) $$В принципе, это уже практически готовый результат. Для формального приведения матрицы к трапециевидной форме поступим так: разделим четвёртую строку на (-46), а пятую – на 7. Затем вычтем из пятой строки четвёртую:
$$ \left(\begin{array}{cccc} -1 & 2 & 5 & 0\\ 0 & -2 & 4 & -3\\ 0 & 0 & 1 & 3\\ 0 & 0 & 0 & -46\\ 0 &0 & 0 & 7\\ 0 & 0 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ IV:(-46) \\ V:7 \\ \phantom{0} \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & 5 & 0\\ 0 & -2 & 4 & -3\\ 0 & 0 & 1 & 3\\ 0 & 0 & 0 & 1\\ 0 &0 & 0 & 1\\ 0 & 0 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ V-IV \\ \phantom{0} \end{array} \sim \left(\begin{array}{cccc} -1 & 2 & 5 & 0\\ 0 & -2 & 4 & -3\\ 0 & 0 & 1 & 3\\ 0 & 0 & 0 & 1\\ 0 &0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{array} \right). $$Матрица приведена к трапециевидной форме. На главной диагонали находятся 4 элемента, не равных нулю (-1, -2, 1, 1). Вывод: ранг равен 4.
Ответ: $\rang A=4$.
math1.ru
Элементарные преобразования матриц, с примерами
К элементарным преобразованиям над строками матриц относятся следующие преобразования:
- перестановка местами двух строк;
- умножение каждого элемента строки на одно и тоже, отличное от нуля, число;
- добавление к элементам строки соответствующих элементы другой строки, умноженные на некоторое ненулевое число.
Если матрица получена в результате элементарных преобразований строк матрицы , то матрицы и называются эквивалентными и обозначают .
Примеры элементарных преобразований матриц
Продемонстрируем элементарные преобразования строк на примере матрицы
1. Переставим местами первую и третью строки, при этом получится эквивалентная матрица, поэтому между ними ставим знак эквивалентности
2. Умножим первую строку последней матрицы на :
3. Прибавим к первой строке третью, умноженную на 4
Элементарные преобразования строк используются при нахождении ранга матрицы и лежат в основе метода Гаусса.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
2.6. Метод элементарных преобразований
Теорема 2.2. Определитель треугольной матрицы равен произведению элементов главной диагонали:
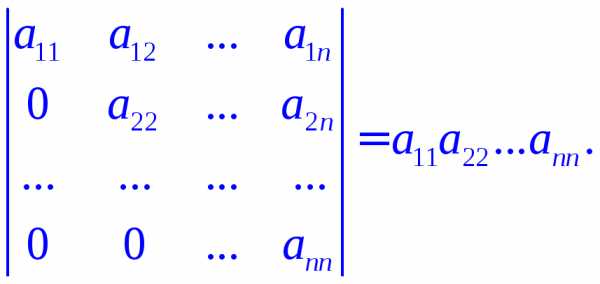
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки (столбца) на число, не равное нулю; 2) прибавление одной строки (столбца) к другой; 3) перестановка двух строк (столбцов).
Метод элементарных преобразований заключается в том, чтобы при помощи элементарных преобразований, учитывая свойства определителей, привести матрицу к треугольному виду.
Пример 2.5. Вычислить определитель при помощи элементарных преобразований, приведя их к треугольному виду:
Пример 2.6. Вычислить определитель:
 .
.
Решение. Упростим данный определитель, а затем вычислим его:
.
Пример
2.7. Вычислить
определитель  .
.
Решение. Способ 1.При помощи элементарных преобразований матрицы, учитывая свойства определителей, будем получать в какой-либо строке или столбце нули, а затем будем разлагать полученный определитель по этой строке или столбцу:
–6
7
-2
-2
.
Способ 2.При помощи элементарных преобразований матрицы, учитывая свойства определителей, приведем матрицу к треугольному виду:
.
Вычисление определителей при помощи элементарных преобразований, путем приведения его к треугольному виду, является одним из самых распространенных методов. Это связано с тем, что он является основным методом при реализации вычислений определителей на ЭВМ. Точнее он является одной из модификаций метода Гаусса, который обычно используется при решении систем линейных уравнений.
Пример 2.8. Вычислить определитель методом Гаусса:

Решение. Рассмотрим первый столбец и выберем в нем ту строку, которая содержит 1. Если единиц нет, то нужно эту единицу создать при помощи элементарных преобразований: переставляя строки или столбцы, складывая или вычитая их друг с другом, умножая или деля их на какое-либо число (учитывая при этом, конечно свойства определителей). Возьмем за основу вторую строку и получим при помощи ее нули в первом столбце:
После этого на первую строку больше внимания не обращаем. Рассмотрим 2-й столбец. Здесь единиц нет, однако ее можно легко создать, например, если поменять местами 2-й и 3-й столбцы, или если от второй строки отнять четвертую. Далее повторяем предыдущую операцию, т.е. создаем нули во втором столбце:
Сейчас рассматриваем 3-й столбец, в котором уже имеется единица, при этом на первые две строки не обращаем внимание. Переставляем третью и четвертую строки и при помощи отмеченной единицы получаем нули в четвертой и пятой строках третьего столбца:
Осталось рассмотреть четвертый столбец. Вынесем общий множитель четвертой строки, равный 2, за знак определителя и поменяем местами две последние стоки. Далее воспользуемся тем, что 99 кратно 33:
В результате, получилась треугольная матрица. Для того чтобы вычислить определитель, осталось только перемножить элементы матрицы, находящиеся на главной диагонали. Таким образом, получаем ответ: –2(–1)(–1)1334 = –264.
studfiles.net
