Метод интервалов примеры решения неравенств – Метод интервалов. Примеры

Метод интервалов. Примеры

Продолжаем рассматривать метод интервалов. Примеры, в которых в ходе решения квадратного уравнения получаем дискриминант, равный нулю — следующие.

   

Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:

   

Ищем дискриминант:

   

Поскольку дискриминант равен нулю, квадратное уравнение имеет один корень:

   

В точке x=3 на числовой прямой — «петля»:

Неравенство нестрогое, точка — закрашенная. Знак неравенства — больше либо равно, поэтому нам нужны промежутки с «+». Ответ:

   

   

От предыдущего неравенства это отличается только тем, что является строгим. Соответственно, точка x=3 — выколотая, и в ответ ее не включаем:

Ответ:

   

   

Поскольку знак неравенства — меньше либо равно, нам нужны промежутки с «-»  а их нет. Отдельно стоящие закрашенные точки включаем в ответ. Здесь такая точка есть —  x=3 (напоминаю, знак в петле — «виртуальный», на самом деле при x=3 выражение, стоящее в правой части,  равно нулю, а нуль не является ни положительным, ни отрицательным числом).

Ответ:

   

   

Здесь нет ни одной точки удовлетворяющей условию неравенства.

Ответ:

   

   

Приравниваем к нулю левую часть. Получаем:

   

Поскольку в ходе решения уравнения x²-10x+25=0 получили дискриминант, равный нулю, в соответствующей точке x=5  — «петля». Отмечаем полученные точки на числовой прямой:

Знак неравенства — меньше либо равно, поэтому выбираем промежутки со знаком «-«. Точка х=5 — закрашенная, поэтому ее включаем в ответ (то есть разрывать промежуток от -3 до 6 не нужно).

Ответ: х∈(-3;6).

   

От предыдущего примера данный отличается только тем, что неравенство — строгое. Соответственно, все точки выколотые и в ответ х=5 уже не входит (промежуток от -3 до 6 разбивается на два).

Ответ: х∈(-3;5)U(5;6).

   

Здесь выбираем промежутки с «+». Отдельно стоящую закрашенную точку также включаем в ответ:

Ответ:

   

   

Поскольку неравенство — строгое, ни одну из точек в ответ не включаем:

Ответ:

   

Следует заметить, что если бы мы решали квадратные уравнения, в которых дискриминант равен нулю, используя теорему Виета, то получили бы два одинаковых корня (то есть один и тот же корень встречается четное число раз). Если бы свернули квадратный трехчлен по формулам квадрата суммы или квадрата разности, то получили бы кратный корень четной степени. То есть, при любом подходе пришли бы к «петле».

www.uznateshe.ru

Метод интервалов в рациональных неравенствах. Примеры, тест

 

 

Чтобы оценить все могущество метода интервалов, давайте сначала решим несложное неравенство так, как если бы мы его решали, не зная метода интервалов. + показать

 

Решим неравенство .

Как мы будем рассуждать?

Произведение двух множителей дает знак «+», когда

1) оба множителя положительны;

2) оба множителя отрицательны.

Поэтому предстоит решить совокупность двух систем неравенств:

Решение первой системы:

 

Решение второй системы:

Итак, нам осталось объединить решения первой и второй систем:

Ответ:

 

А теперь представьте, если бы у нас было не два множителя, как выше, а три-четыре, а если бы при этом множители представляли из себя многочлены второй степени, например.

Представляете, сколько было бы перебора различных ситуаций?

Метод интервалов для рациональных неравенств

 

Метод интервалов выручит! Избавит нас от рутины!

Мы ведь понимаем, что любое число – либо отрицательное (-), либо положительное (+), либо ноль.  Где «переход» из одной зоны (+или – ) в другую (- или +)? В нуле!

               

На рисунке 1 функция обращается в нуль в точках -2; 1; 5  и 7. Именно при переходе через них она и меняет свой знак с одного на другой.

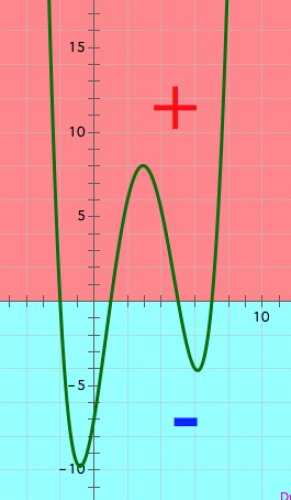
Функция может также коснуться оси (ох), и «не перескочить» в другую зону (как на рисунке 2). В данном случае  точка – корень четной кратности (мы еще поговорим об этом).

В любом случае, если функция попала из одной «зоны» («+,-») в другую («-,+»), – значит она в какой-то точке должна  была обратиться в ноль.

Поэтому-то нули функции и помогут нам!

Итак, давайте выработаем алгоритм, которого будем придерживаться при решении рациональных неравенств.

Алгоритм решения рациональных неравенств

 

Пусть нам дано неравенство вида , где – один из знаков .

1. Раскладываем на множители (если это возможно*).

2. Находим нули .

3. Отмечаем корни (нули) функции на оси в порядке возрастания.  Эти числа разбивают числовую ось на  интервалы. На каждом из этих интервалов  выражение сохраняет знак, а, переходя через отмеченные точки, меняет знак на противоположный (или не меняет, если корень – четной кратности, например, в неравенстве     – корень четной кратности, корень – обычный).

4. Расставляем  знаки на интервалах, начиная от крайнего правого. Советую брать «миллиончик» – не промахнетесь (шучу). Нам не важно само значение функции в выбранной точке, но только ЗНАК в ней, поэтому не утруждайте себя подсчетами  – только грубая прикидка.

5. Выбираем подходящие нам промежутки, записываем ответ. Например, если неравенство со знаком «>», то берем интервалы со знаком «+», если неравенство со знаком «<», то берем интервалы со знаком «-», если неравенство со знаком (), то берем промежутки со знаком «+» («-») c закрытыми концами.

Практика

Пример 1.

Решить неравенство:

Решение: + показать

1) Разложим вторую скобку неравенства на множители по формуле «разность квадратов»: 

2) Нули:

3)

4) Взяв «миллиончик» и «подставив» в  , конечно же будем иметь знак «-». Далее знаки чередуются.

5) Выбираем подходящие нам промежутки, записываем ответ:

Ответ: . 

Пример 2.

Решить неравенство:

Решение: + показать

1)

Попадаем в ситуацию (*) – на множители-то не раскладывается, так как .

2) –

3) А отмечать-то нечего на оси 🙁

4) Так значит, меняться знаку негде! Он – либо «+» либо «-» всюду! Берем любое число, например, 0 и смотрим, какой знак в нем принимает выражение . Очевидно, это «+». Поэтому 

5) Ответ: . 

 

Пример 3.

Решить неравенство:

Решение: + показать

1) Раскладываем первую скобку на множители по формуле разность кубов:

. Заметим, дальше на множители не раскладывается, так как для этого квадратного трехчлена. А значит, эта скобка несет в себе только один знак (не трудно понять, что «+»). То есть, вообще говоря, мы можем поделить обе части исходного неравенства на  . Полученное тогда неравенство равносильно исходному.

Будем дальше решать именно это неравенство:

2) Нули: .

3)-4) Обратите внимание: корень – четной кратности, при переходе через него не будет происходить смена знаков! Ну действительно, знак неравенства определяется только выражением , ведь принимает только «+» (то есть не влияет на знак произведения) или обращается в ноль.

Далее

Обратите внимание – в ответ пойдет и точка {-5}! Так как знак неравенства  нестрогий, мы должны взять и все точки, лежащие на оси.

5) Ответ: {}. 

Пример 4.

Решить неравенство:

Решение: + показать

Пример 5.

Решить неравенство:

Решение: + показать

Надеюсь, у вас не возникает желания разложить  на множители каждую из скобок? Ни в коем случае! Должен быть  «0» справа!

Поэтому, первое, что нужно сделать, – перенести «-5» в левую сторону. Но раскрывать скобки и выходить на 4-ю степень не хотелось бы.

Замечаем, что есть одинаковые компоненты () в скобках, поэтому, можно сделать замену переменной. Обозначим за . Тогда получаем следующее неравенство: .

Далее: .

1) Раскладываем на множители:

2) Нули: 1; 5

3)-5) Ось у нас будет называться :

.

Теперь нам предстоит сделать обратную замену: .

Перепишем двойное неравенство в виде системы:

Нам предстоит решить два неравенства, а потом пересечь их решения.

Решаем первое неравенство: 

Раскладываем на множители: .

Решение первого неравенства:

Решаем второе неравенство:

Раскладываем на множители: 

Решение второго неравества: .

Пересекаем решения неравенств:

Ответ: . 

 

 

Пример 6.

Решить неравенство: (|x|-3)(|x|-7)>0.

Решение: + показать

Введем переменную: , заметим, при этом .

Или, что тоже самое:

Обратная замена:

Тогда (как раскрывать модуль)

Ответ: . 

 

Здесь предлагаю ознакомиться с решением дробно-рациональных неравенств методом интервалов.

Вы можете пройти тест  тест по теме «Метод интервалов для рациональных неравенств»

 

 

 

egemaximum.ru

Примеры решений неравенств методом интервалов

I. Примеры решения иррациональных неравенств

1. .

Решение. Введем функцию f(x) = – 3. Необходимо определить промежутки, на которых f(x) 0. Очевидно, что D(f) = [0;). Нули f(x): x = 9.

f(16) >0,
f(4) < 0.

Ответ: [0; 9].

2. < 2 – x.

Решение. Традиционное решение этого неравенства приводит к системе неравенств

Решение этого неравенства можно осуществить, положив = y, где y  0. Получаем

y < 20 – y²,  y² + y – 20 < 0,  (y + 5)(y – 4) < 0,

откуда y < 4, поскольку y0. Итак, < 4 и – 18 x  –2.

Интересен и такой вариант (графический) решения примера. Если заметить, что f(x) = – функция возрастающая на луче [– 18; + ), а g(x) = 2 – x – убывающая на R и x = 2 – абсцисса их точки пересечения и при этом f(– 14) < g(– 14), то ясен и

ответ: [– 18; – 2).

Обратимся к теме статьи. Пусть f(x) =+ x – 2. Надо решить неравенство f(x)< 0. Заметим, что D(f)=[– 18; +). Нули функции найдем, решив уравнение  = 2 – x, откуда x = – 2.

Применяем метод интервалов:

f(– 14) < 0,
f(7) > 0.

Ответ: [– 18; – 2).

3.  < 20.

Решение. Область допустимых значений определяется системой неравенств

.      x

Для функции f(x) = – 20   D(f) = [4; +). Далее находим нули f(x):

откуда x = 29 и x = 13 – посторонний корень.

f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10 < 0.

Ответ: [4; 29).

Примечание. Это неравенство можно решить, например, выполнив замену переменной  = y, где y 0.

4.   < 1.

Решение. Область определения функции f(x) = – 1 найдем, решив систему неравенств

Легко видеть, что    .

Находим нули функции f(x):

1 – 2x = ,  – 4x + 12x² = 0, x = 0 – посторонний корень, x = ;

f(– 0,1) = – 1 = – 1 < 0,
f(0,1) = – 1 = < 0,
f(0,34) = – 1 = > 0.

Ответ:.

Примечание. Этот пример показывает, что для двух чисел, «близко» расположенных на координатной прямой, применение метода интервалов осуществимо.

5.  >x – 1.

Решение. Пусть f(x) = – x + 1. Найдем область определения этой функции, для чего решим неравенство x³ + x² – 2x  0  методом интервалов:

D(f) =.

Ищем нули функции f, решив уравнение

= x – 1, x³ = 1 и x = 1,

где x = 1 удовлетворяет уравнению, но не удовлетворяет исходному неравенству.

Далее применяем метод интервалов:

f(– 1) = + 2 > 0,
f(2) = – 1 > 0.

Ответ: .

Традиционное решение данного неравенства сводится к совокупности двух систем:

Примечание. Отметим, что не идет речь о преимуществах того или иного способа решения неравенств, а показывается применение метода интервалов на более широком классе неравенств.

Упражнения

Решите неравенства методом интервалов:

1.  .
2.   .
3.   .
4.  .

II. Примеры решения показательных неравенств

1. 4^x < 2^x+1 + 3.

Решение. Если f(x) = 4^x – 2•2^x – 3, то D(f) = R и необходимо решить неравенство f(x) < 0. Найдем нули                 

f:  4^x–2•2^x – 3 = 0, откуда 2^x = 3, x = log₂3.

Далее применяем метод интервалов:

f(0) < 0,  f(2) > 0.

Ответ: (– ; log₂3).

2.  – 3  0.

Решение. Пусть f(x) =  – 3. Решаем неравенство f(x) 0. Заметим, что D(f) = (– ; 0)(0; + ). Для нахождения нулей функции f решаем уравнение:

 – 3 = 0.

Полагая = t, где t > 0, приходим к уравнению t² – t – 3 = 0 с положительным корнем t = 2. Следовательно,   = 2 и x = .

Применяем метод интервалов:

f(1) < 0,
f > 0,
f(– 1) < 0.

Ответ: (–  ; 0) .

3. 4^x  .

Решение. Рассмотрим функцию

f(x) = 4^x – () .

Область определения функции f есть луч [0; + ). Найдем теперь нули функции f:

4^x – () = 0.

Разделив обе части последнего уравнения на , получим

,    

откуда   = 4, x– = 2, а это уравнение имеет единственный корень x = 4.

f(1) < 0, f(9) = 4⁹ – 3•2¹² – 4⁴ = 2⁸(2¹⁰ – 2•2⁴ – 1) > 0.

Ответ: [0; 4].

4.   < 1.

Решение. Введем в рассмотрение функцию f(x) = – 1. Легко видеть, что D(f) = . Находим нули функции f(x): 4^x – 2 – 2^2x += 0. Уравнение корней не имеет.

 

f(0) => 0,
f(1) =  < 0.

Ответ: .

Упражнения

Решите методом интервалов неравенства:

5. 9^x < 3^x + 2.
6.  .
7.  .
8. 3•4^x – 7•10^x + 2•25^x > 0.
9..

III. Примеры решения логарифмических 
неравенств методов интервалов.

1. lg² x – 2lg x – 8  0.

Решение. f(x) = lg² x – 2lg x – 8, D(f) = (0; +). Для нахождения нулей функции f решаем уравнение

lg² x – 2lg x – 8 = 0,

откуда lg x = – 2, lg x = 4 и x = , x = 10000.

f(10⁵) = 25 – 10 – 8 = 7 > 0,
f(1) < 0,
f(10^–3) = 9 + 6 – 8 = 7 > 0.

Ответ:  .

2. log_0,3 (x² – x – 20) – log_0,3 (x + 4) > 0.

Решение. Найдем область определения функции f в левой части неравенства, решив систему неравенств

   x > 5.

Решая уравнение log _0,3 (x² – x – 20) – log_0,3 (x + 4) = 0, находим нули функции f: x² – x – 20 = x + 4, x² – 2x – 24 = 0, x = – 4 – посторонний корень и x = 6.

 

f(7) = log_0,3 22 – log_0,3 7 <0,
f(5,5) = log_0,3 4,75 – log_0,3 9,5>5.

Ответ: (5; 6).

3.  .

Решение. Пусть f(x) = – 1. Необходимо решить неравенство f(x)  0.

Область определения функции f определяется системой неравенств

Итак, D(f) =  .

Найдем нули функции f:

log₃ (5x + 1) = log₃ (7x – 1)²,

откуда 49x² – 19x = 0, x = 0 – посторонний корень, x = – корень уравнения.

f(1) = < 0,
f(0,3) = > 0,
f(0,2) = – 1 < 0, так как log₃ 2 > 0, log₃ 0,4 < 0.
f(0,1) = < 0,
f(– 0,1) = < 0.

Ответ:  .

4. log_3x+1  0.

Решение. Для функции f(x) = log_3x+1   находим область определения. Решаем систему неравенств:

.

Найдем нули функции: log_3x+1 = 0, = 1, но последнее уравнение корней не имеет.

Применяем метод интервалов:

f(5) = log₁₆ 3 > 0,
f(1) = log₄< 0,
f(– 0,2) = log_0,4 > 0.

Ответ: (4; + ).

5. log_x2 2.

Решение. Для функции f(x) = log_x 2 – 2 имеем D(f) = (0; 1) (1; + ). Очевидно, что для нахождения нулей f необходимо решить уравнение x = , откуда x = 2.

Применяем метод интервалов:

f(4) = log₄ 2 – log₂ 2 < 0,

f(1,5) = ,

f = .

Ответ: (0; 1)  [2; +).

Упражнения

Решите методом интервалов неравенства:

10. 
11.  log₂ (x + 1) < 1 – 2log₄ x.
12.  .
13.  log_x < 1.
14.  log_x 3  log_2x+3 9.
15.  log_x (1 – 2x) < 1.
16.  log₃ log₂₇ log₂ (x² + x + 2)  –1.

IV. Примеры на применение метода интервалов 
к неравенствам, содержащим знак модуля.

1. x² > | 5x + 6 |.

Решение. Функция f(x) = x² – | 5x + 6 | определена при любом x. Найдем ее нули, решив уравнение 
x²=| 5x + 6 |, откуда x² = 5x + 6 или x² = – (5x + 6), т. е.

x² – 5x – 6 = 0 или x² + 5x + 6 = 0.

Корни этих уравнений – 1, 6, – 2, – 3.

Далее применяем метод интервалов:

f(7) > 0, f(0) < 0, f(– 1,5) > 0, f(– 2,5) < 0, f(– 4) > 0.

Ответ: (–; – 3)  (– 2; – 1)  (6; + ).

Примечание. Неравенство можно также решить, заменив его на равносильное (x² – 5x – 6)(x² + 5x + 6) > 0.

2. y² – 4| y | < 12.

Решение. Здесь положим f(y) = y² – 4| y | – 12. Заметим, что D(y) = R и найдем нули функции f: y² – 4| y | – 12=0, откуда | y | = 6, | y | = – 2. Последнее уравнение корней не имеет.

Ответ: – 6 < y < 6.

3.  .

Решение. Заменим неравенство на равносильное  0 и положим f(x) = . Ясно, что D(f) = (– ; – 2)  (– 2; 2)  (2; + ). Находим нули функции f, решая уравнение | 3x | = | x² – 4 |, которое распадается на два:

x² – 3x – 4 = 0 и x² + 3x – 4 = 0.

Корни этих уравнений соответственно равны – 1; 4 и 1; – 4.

Далее применяем метод интервалов:

Ответ: (– ; – 4]  [ – 1; 1]  [4; + ).

Замечание. Конечно, при решении этого неравенства можно было учесть, что |x² – 4 | > 0 при x ±2.

4. x² + 2| x – 1 | + 7  4| x – 2 |.

Решение. Если f(x) = x² + 2| x – 1 | + 7 – 4| x – 2 |, то D(f) = R и необходимо решить неравенство f(x)  0.

Находим нули f:

а) 

x = – 1 – нуль функции;

б) 

система решений не имеет;

в) 

система не имеет решений.

Применяем метод интервалов:

f(0) > 0,
f(– 2) > 0.

Ответ: – 1.

5. + 3 > | x – 1 |.

Решение. Для f(x) = + 3 – | x – 1 | находим D(f) = .

Находим нули функции f(x).

Если x , то

+3 – x + 1 = 0,  = x – 4, 8x = 21,

x = 2 – не корень.

Если x , то

+3+x–1 = 0,  = – x – 2,  4x = – 9,

x = – 2,25 – корень.

Итак, функция f имеет один нуль x = –2,25.

Применяем метод интервалов:

f(3) >0,

f(– 2,24) = + 3 – 3,24 < 0,1 – 0,24 < 0,

f(– 3) > 0.

Ответ: (–  ; – 2,25)  [5; +  ).

Упражнения

Решите методом интервалов неравенства:

17. | x – 6 | > x² – 5x + 9.
18. 16| x² – 2(x + | x | + 1 | < 1.
19. | x² – | x + 1 ||  2x – 3.

20. 

Ответы

1. (– ; – 6] 
2.  [0; 2).  
3. (– ; 0]  [5; 7)  (9; + ).  
4. [3; 4].  
5. (– ; log₃ 2).  
6. (– ; 2)  .  
7. [0; 16].  
8.
9. 
10.^^;10²⁵]

11. (0;1)
12.[;2]
13.(0;1)
14. (0;1) (3;+)  
15.
16.[-3;-1)
17.(1;3)
18. 
19. 
20.

А. Смоляков,
г. Нефтекумск

infourok.ru

Метод интервалов

Метод интервалов — универсальный метод решения неравенств. С его помощью можно решить неравенства самого разного вида. Рассмотрим алгоритм метода интервалов, а затем перейдем к примерам решения неравенств этим методом.

Алгоритм решения неравенств методом интервалов.

Прежде чем применить метод интервалов для решении неравенства, необходимо все дроби привести к наименьшему общему знаменателю и все слагаемые перенести в левую часть, чтобы справа остался нуль. Для начала рассмотрим алгоритм решения неравенств вида

   

1. Приравниваем к нулю левую часть:

   

(Таким образом мы находим нули функции

   

а также ее область определения).

2.Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:

   

   

3. Полученные точки отмечаем на числовой прямой с учетом области определения функции. Точки разбивают числовую прямую на промежутки, в каждом из которых рассматриваемая функция имеет определенный знак. Выбираем любое число из любого промежутка (удобнее всего брать нуль, если он не входит в отмеченные точки), и подставляем это число в последнее неравенство (то есть в упрощенное неравенство, в котором все слагаемые стоят в левой части и дроби приведены к наименьшему общему знаменателю). В результате определяем знак на выбранном промежутке. Остальные знаки расставляем в шахматном порядке.

4. «Петля»

1)Если есть кратный корень четной степени, то в нем — «петля»:

   

2)Если дискриминант равен нулю, то в соответствующем корне x=-b/2a — «петля».

3) Если один и тот же корень встречается четное число раз, то в нем — «петля»:

   

так как корень x2 встречается четное количество раз (два раза).

5. Выбираем промежутки с нужным знаком: если в неравенстве знак > или ≥, берем промежутки с «+»; если < или ≤ — с «-«. Точки, в которых знаменатель обращается в нуль, всегда выколотые.  В остальных случаях запомнить, выколотая точка или закрашенная, можно с помощью ассоциации.

Замечание

Отдельно стоящие закрашенные точки включаем в решение:

   

(Знаки в «петлях» — «виртуальные». В этих точках функция обращается нуль либо не определена. «Петля» служит только для сохранения  порядка чередования знаков).

Далее рассмотрим различные примеры решения неравенств с помощью этого метода.

www.uznateshe.ru

Решение методом интервалов

Теперь рассмотрим решение методом интервалов более сложных неравенств. Начнем с неравенств, содержащих кратные корни четных степеней.

   

Используем алгоритм решения неравенств методом интервалов. Приравниваем к нулю левую часть:

   

   

   

Полученные точки отмечаем на числовой прямой. Неравенство строгое, все точки — выколотые. Корни х=1 и х=5 — кратные корни четной степени, поэтому в них — «петля»:

Для проверки знака берем нуль и подставляем его в последнее неравенство. Получаем (+)∙(+)∙(+)∙(-), итого (-). Остальные знаки расставляем в шахматном порядке. Нам нужен знак «+», соответственно, выбираем промежутки с «+».

Ответ:

   

Рассмотрим еще три варианта решения этого же примера с разными знаками неравенства.

   

В отличие от предыдущего примера, данное неравенство нестрогое, поэтому точки в этом случае — закрашенные:

Отдельно стоящие закрашенные точки включаем в решение!

Ответ:

   

   

Неравенство строгое, точки — выколотые. В этом неравенстве нам нужен знак «-«:

Ответ:

   

 

   

От предыдущего неравенства это отличается только тем, что является нестрогим. Соответственно, точки в нем — закрашенные, и они входят в решение:

Ответ:

   

   

Приравниваем к нулю левую часть:

   

 

   

Полученные точки отмечаем на числовой прямой. Неравенство нестрогое, точки — закрашенные. Только точка, в которой знаменатель обращается в нуль, выколотая (всегда!).

Для проверки знака берем нуль. Подставляем его в последнее неравенство. Получаем

   

в итоге — «+». Нам нужен «-«, заштриховываем соответствующий промежуток. Не забываем включить в ответ отдельно стоящую закрашенную точку.

Ответ:

   

www.uznateshe.ru

Обобщенный метод интервалов | Подготовка к ЕГЭ по математике

Продолжение

Ранее мы рассмотрели как работает метод интервалов при решении рациональных (часть 1) и дробно-рациональных неравенств (часть 2).

 Будем рассматривать неравенства вида , где один из знаков , а  логарифмическая, показательная, иррациональная или тригонометрическая функция. И вот здесь самое время применить обобщенный метод интервалов.

Наши действия будут такими:

1) Находим область определения

2) Находим нули

3) Определяем знаки на ОДЗ (которая разделена на промежутки нулями функции),  подставляя удобные значения, принадлежащие каждому промежутку.

4) Записываем ответ, указывая объединение промежутков (из ОДЗ), на которых имеет соответствующий знак.

Если же перед нами неравенство , где   логарифмические, показательные, иррациональные или тригонометрические функции, то мы будем переходить к неравенству: , при условии, что

Пример 1. 

Решить неравенство:

Решение:

Рассмотрим функцию .

Найдем ОДЗ данной функции:

Найдем нули функции, решив уравнение: 

Из данного уравнения следует:

Рассмотрим знаки функции на образовавшихся промежутках :

Находим знак на крайнем правом промежутке:

Определяем знак на  :

Определяем знак на :

Ответ:

 

Пример 2. 

Решить неравенство:

Решение:

Перейдем к  равносильному неравенству:

 

Рассмотрим функцию .

ОДЗ данной функции: , то есть

Нули функции:

.

Из равенства следует:

Образовались следующие промежутки:

Заметим, функция – четная, поэтому нам достаточно определить знаки лишь на правой, например, половине рассматриваемых промежутков.

Определяем знак на :

Определяем знак на :

Определяем знак на :

Ответ:

Пример 3.

Решить неравенство: 

Решение:

Рассмотрим функцию .

ОДЗ данной функции:

Мы видим квадратное неравенство относительно :

Раскладываем на множители, найдя предварительно дискриминант:

Имеем: или

Значит:  или

или

Найдем нули функции:

Откуда следует: или

Стало быть, или или

Корень выпадает из ОДЗ.

Будем рассматривать знаки функции  на следующих промежутках:

Определяем знак на

Определяем знак на

Ответ: {}

Надо сказать, что у обобщенного метода интервалов есть свои минусы. Потому что не всегда удобно определять знаки на промежутках, тем более когда они малы, когда на них нет целых значений.

Попробуйте, вот например, решить обобщенным методом интервалов следующее неравенство:

Вы столкнетесь с трудностями при определении знаков вот на таких промежутках:

Не из приятных занятие, правда? Поэтому, конечно, метод интервалов здесь неоправдан. Советую решить данное неравенство методом рационализации.

Да и еще, надеюсь вы понимаете, что  не есть ? В данном случае . Поэтому, подумайте, нужно ли понижать степень в подлогарифмном выражении…

Да, ответ такой:  (лучше порешать самостоятельно, но если что, – смотрим решение здесь).

 

 

egemaximum.ru

Решение неравенств методом интервалов

Решение неравенств методом интервалов

В этой статье мы постараемся показать применение методов интервалов для решения иррациональных, показательных, логарифмических и других неравенств.
Универсальность метода интервалов заложена уже в его содержании. Находим область определения функции, затем отмечаем в этой области нули функции, которые разбивают область определения на несколько промежутков, внутри каждого из которых функция определена, непрерывна и сохраняет знак. Для определения знака функции на конкретном промежутке находим знак в любой (удобной) точке этого промежутка.
Иллюстрацию изменения знаков функции будем осуществлять с помощью координатной прямой.
Естественно, что показ учащимся метода интервалов для решения более широкого класса неравенств можно давать после рассмотрения традиционных приемов их решения.
Все рассматриваемые упражнения взяты из вариантов вступительных экзаменов в различные вузы страны.
Материал представляет, по мнению автора, интерес для проведения факультативных занятий.

I. Примеры решения иррациональных неравенств

1. .

Решение. Введем функцию f(x) = – 3. Необходимо определить промежутки, на которых f(x)Ј 0. Очевидно, что D(f) = [0;Ґ). Нули f(x): x = 9.

f(16) >0,
f(4) < 0.

Ответ: [0; 9].

2. < 2 – x.

Решение. Традиционное решение этого неравенства приводит к системе неравенств

Решение этого неравенства можно осуществить, положив = y, где y і 0. Получаем

y < 20 – y²,  y² + y – 20 < 0,  (y + 5)(y – 4) < 0,

откуда y < 4, поскольку yі0. Итак, < 4 и – 18Ј x Ј –2.

Интересен и такой вариант (графический) решения примера. Если заметить, что f(x) = – функция возрастающая на луче [– 18; +Ґ ), а g(x) = 2 – x – убывающая на R и x = 2 – абсцисса их точки пересечения и при этом f(– 14) < g(– 14), то ясен и

ответ: [– 18; – 2).

Обратимся к теме статьи. Пусть f(x) =+ x – 2. Надо решить неравенство f(x)< 0. Заметим, что D(f)=[– 18; +Ґ). Нули функции найдем, решив уравнение  = 2 – x, откуда x = – 2.

Применяем метод интервалов:

f(– 14) < 0,
f(7) > 0.

Ответ: [– 18; – 2).

3.  < 20.

Решение. Область допустимых значений определяется системой неравенств

.      Ю xі 4.

Для функции f(x) = – 20   D(f) = [4; + Ґ). Далее находим нули f(x):

откуда x = 29 и x = 13 – посторонний корень.

f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10 < 0.

Ответ: [4; 29).

Примечание. Это неравенство можно решить, например, выполнив замену переменной = y, где y і 0.

4.   < 1.

Решение. Область определения функции f(x) = – 1 найдем, решив систему неравенств

Легко видеть, что   .

Находим нули функции f(x):

1 – 2x = ,  – 4x + 12x² = 0, x = 0 – посторонний корень, x = ;

f(– 0,1) = – 1 = – 1 < 0,
f(0,1) = – 1 = < 0,
f(0,34) = – 1 = > 0.

Ответ:.

Примечание. Этот пример показывает, что для двух чисел, «близко» расположенных на координатной прямой, применение метода интервалов осуществимо.

5.  >x – 1.

Решение. Пусть f(x) = – x + 1. Найдем область определения этой функции, для чего решим неравенство x³ + x² – 2x і 0  методом интервалов:

D(f) =.

Ищем нули функции f, решив уравнение

= x – 1, x³ = 1 и x = 1,

где x = 1 удовлетворяет уравнению, но не удовлетворяет исходному неравенству.

Далее применяем метод интервалов:

f(– 1) = + 2 > 0,
f(2) = – 1 > 0.

Ответ: .

Традиционное решение данного неравенства сводится к совокупности двух систем:

Примечание. Отметим, что не идет речь о преимуществах того или иного способа решения неравенств, а показывается применение метода интервалов на более широком классе неравенств.

Упражнения

Решите неравенства методом интервалов:

1.  .
2.  .
3.  .
4.  .

II. Примеры решения показательных неравенств

1. 4^x < 2^x+1 + 3.

Решение. Если f(x) = 4^x – 2•2^x – 3, то D(f) = R и необходимо решить неравенство f(x) < 0. Найдем нули                 

f:  4^x–2•2^x – 3 = 0, откуда 2^x = 3, x = log₂3.

Далее применяем метод интервалов:

f(0) < 0,  f(2) > 0.

Ответ: (– Ґ; log₂3).

2. – 3 Ј 0.

Решение. Пусть f(x) =  – 3. Решаем неравенство f(x)Ј 0. Заметим, что D(f) = (– Ґ; 0)И(0; + Ґ). Для нахождения нулей функции f решаем уравнение:

– 3 = 0.

Полагая = t, где t > 0, приходим к уравнению t² – t – 3 = 0 с положительным корнем t = 2. Следовательно,  = 2 и x = .

Применяем метод интервалов:

f(1) < 0,
f > 0,
f(– 1) < 0.

Ответ: (–  Ґ; 0) И .

3. 4^xЈ .

Решение. Рассмотрим функцию

f(x) = 4^x – () .

Область определения функции f есть луч [0; + Ґ). Найдем теперь нули функции f:

4^x – () = 0.

Разделив обе части последнего уравнения на , получим

,   

откуда   = 4, x– = 2, а это уравнение имеет единственный корень x = 4.

f(1) < 0, f(9) = 4⁹ – 3•2¹² – 4⁴ = 2⁸(2¹⁰ – 2•2⁴ – 1) > 0.

Ответ: [0; 4].

4.   < 1.

Решение. Введем в рассмотрение функцию f(x) = – 1. Легко видеть, что D(f) = . Находим нули функции f(x): 4^x – 2 – 2^2x += 0. Уравнение корней не имеет.

 

f(0) => 0,
f(1) = < 0.

Ответ: .

Упражнения

Решите методом интервалов неравенства:

5. 9^x < 3^x + 2.
6. .
7. .
8. 3•4^x – 7•10^x + 2•25^x > 0.
9..

III. Примеры решения логарифмических
неравенств методов интервалов.

1. lg² x – 2lg x – 8 Ј 0.

Решение. f(x) = lg² x – 2lg x – 8, D(f) = (0; + Ґ). Для нахождения нулей функции f решаем уравнение

lg² x – 2lg x – 8 = 0,

откуда lg x = – 2, lg x = 4 и x = , x = 10000.

f(10⁵) = 25 – 10 – 8 = 7 > 0,
f(1) < 0,
f(10^–3) = 9 + 6 – 8 = 7 > 0.

Ответ: .

2. log_0,3 (x² – x – 20) – log_0,3 (x + 4) > 0.

Решение. Найдем область определения функции f в левой части неравенства, решив систему неравенств

   Ю x > 5.

Решая уравнение log _0,3 (x² – x – 20) – log_0,3 (x + 4) = 0, находим нули функции f: x² – x – 20 = x + 4, x² – 2x – 24 = 0, x = – 4 – посторонний корень и x = 6.

 

f(7) = log_0,3 22 – log_0,3 7 <0,
f(5,5) = log_0,3 4,75 – log_0,3 9,5>5.

Ответ: (5; 6).

3.  .

Решение. Пусть f(x) = – 1. Необходимо решить неравенство f(x) Ј 0.

Область определения функции f определяется системой неравенств

Итак, D(f) = .

Найдем нули функции f:

log₃ (5x + 1) = log₃ (7x – 1)²,

откуда 49x² – 19x = 0, x = 0 – посторонний корень, x = – корень уравнения.

f(1) = < 0,
f(0,3) = > 0,
f(0,2) = – 1 < 0, так как log₃ 2 > 0, log₃ 0,4 < 0.
f(0,1) = < 0,
f(– 0,1) = < 0.

Ответ: .

4. log_3x+1і 0.

Решение. Для функции f(x) = log_3x+1   находим область определения. Решаем систему неравенств:

.

Найдем нули функции: log_3x+1 = 0, = 1, но последнее уравнение корней не имеет.

Применяем метод интервалов:

f(5) = log₁₆ 3 > 0,
f(1) = log₄< 0,
f(– 0,2) = log_0,4 > 0.

Ответ: (4; + Ґ).

5. log_x2 Ј 2.

Решение. Для функции f(x) = log_x 2 – 2 имеем D(f) = (0; 1) И (1; + Ґ). Очевидно, что для нахождения нулей f необходимо решить уравнение x = , откуда x = 2.

Применяем метод интервалов:

f(4) = log₄ 2 – log₂ 2 < 0,

f(1,5) = ,

f = .

Ответ: (0; 1) И [2; +Ґ).

Упражнения

Решите методом интервалов неравенства:

10.
11.  log₂ (x + 1) < 1 – 2log₄ x.
12.  .
13.  log_x < 1.
14.  log_x 3 Ј log_2x+3 9.
15.  log_x (1 – 2x) < 1.
16.  log₃ log₂₇ log₂ (x² + x + 2) Ј –1.

IV. Примеры на применение метода интервалов
к неравенствам, содержащим знак модуля.

1. x² > | 5x + 6 |.

Решение. Функция f(x) = x² – | 5x + 6 | определена при любом x. Найдем ее нули, решив уравнение
x²=| 5x + 6 |, откуда x² = 5x + 6 или x² = – (5x + 6), т. е.

x² – 5x – 6 = 0 или x² + 5x + 6 = 0.

Корни этих уравнений – 1, 6, – 2, – 3.

Далее применяем метод интервалов:

f(7) > 0, f(0) < 0, f(– 1,5) > 0, f(– 2,5) < 0, f(– 4) > 0.

Ответ: (– Ґ; – 3) И (– 2; – 1) И (6; + Ґ).

Примечание. Неравенство можно также решить, заменив его на равносильное (x² – 5x – 6)(x² + 5x + 6) > 0.

2. y² – 4| y | < 12.

Решение. Здесь положим f(y) = y² – 4| y | – 12. Заметим, что D(y) = R и найдем нули функции f: y² – 4| y | – 12=0, откуда | y | = 6, | y | = – 2. Последнее уравнение корней не имеет.

Ответ: – 6 < y < 6.

3. .

Решение. Заменим неравенство на равносильное Ј 0 и положим f(x) = . Ясно, что D(f) = (– Ґ; – 2) И (– 2; 2) И (2; + Ґ). Находим нули функции f, решая уравнение | 3x | = | x² – 4 |, которое распадается на два:

x² – 3x – 4 = 0 и x² + 3x – 4 = 0.

Корни этих уравнений соответственно равны – 1; 4 и 1; – 4.

Далее применяем метод интервалов:

Ответ: (– Ґ; – 4] И [ – 1; 1] И [4; + Ґ).

Замечание. Конечно, при решении этого неравенства можно было учесть, что |x² – 4 | > 0 при x№ ±2.

4. x² + 2| x – 1 | + 7 Ј 4| x – 2 |.

Решение. Если f(x) = x² + 2| x – 1 | + 7 – 4| x – 2 |, то D(f) = R и необходимо решить неравенство f(x) Ј 0.

Находим нули f:

а)

x = – 1 – нуль функции;

б)

система решений не имеет;

в)

система не имеет решений.

Применяем метод интервалов:

f(0) > 0,
f(– 2) > 0.

Ответ: – 1.

5. + 3 > | x – 1 |.

Решение. Для f(x) = + 3 – | x – 1 | находим D(f) = .

Находим нули функции f(x).

Если x , то

+3 – x + 1 = 0,  = x – 4, 8x = 21,

x = 2 – не корень.

Если x , то

+3+x–1 = 0,  = – x – 2,  4x = – 9,

x = – 2,25 – корень.

Итак, функция f имеет один нуль x = –2,25.

Применяем метод интервалов:

f(3) >0,

f(– 2,24) = + 3 – 3,24 < 0,1 – 0,24 < 0,

f(– 3) > 0.

Ответ: (–  Ґ; – 2,25) И [5; +  Ґ).

Упражнения

Решите методом интервалов неравенства:

17. | x – 6 | > x² – 5x + 9.
18. 16| x² – 2(x + | x | + 1 | < 1.
19. | x² – | x + 1 || Ј 2x – 3.

20.

Ответы

А. Смоляков,
г. Нефтекумск

mat.1sept.ru