Урок 1. область определения и множество значений тригонометрических функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №1. Область определения и множество значений тригонометрических функций.
Перечень вопросов, рассматриваемых в теме
- Овладение понятиями «область определения», «область определения тригонометрических функций», «множество значений функции», «множество значений тригонометрических функций»;
- Нахождение области определения и множества значений тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.;
- Объяснение зависимости области определения и множества значений функции вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.
Глоссарий по теме
Областью определения функций y = sin x и y = cos x является множество
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Вопросы:
- Что такое функция?
- Что такое область определения функции? Чем является область определения функции геометрически?
- Что такое множество значений функции? Чем является множество значений функции геометрически?
Ответы на вопросы:
- Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а
- Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.
Найдите область определения функции и множество значений функции:
1) ; 2) ; 3) .
Ответы:
D(f): 1) ; 2) ; 3)
E(f): 1); 2) ; 3) .
Объяснение нового материала
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.
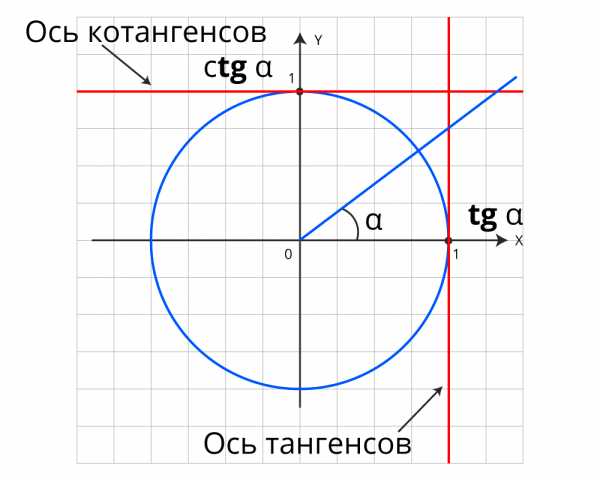
Заполните таблицу:
Функция | Область определения | Множество значений |
Ответ:
Функция | Область определения | Множество значений |
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найти область определения функции .
;
;
;
Ответ: −.
Пример 2. Найти все решения уравнения
;
;
Ответ:
.
resh.edu.ru
Тема урока | Область определения и множество значений тригонометрических функций | |
Класс | 11 класс | |
Тип урока | Урок изучения нового учебного материала | |
Номер урока по данной теме | Первый урок | |
Цель урока | Введение понятий тригонометрических функций и формирование умения исследовать область определения и множество значений тригонометрических функций | |
Учитель | Лобанова Виктория Михайловна | |
Учебник | Алгебра и начала математического анализа. 11 класс (базовый и профильный уровни). Авторы: Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Издательство «Просвещение», 2009 | |
Деятельность учителя | Деятельность учащихся | Время |
Организационный этап урока | 0,5 мин | |
Здравствуйте, дорогие ребята! Начну урок с высказывания британского физика и механика Уильяма Томсона (лорда Кельвина): Если Вы в состоянии измерить и выразить то, о чём Вы говорите, в числах, то Вы кое-что об этом знаете, но если вы не можете измерить это и выразить в числах, Ваши знания скудны и неудовлетворительны. | ||
Актуализация опорных знаний | ||
Повторим элементарные функции, изученные в курсе алгебры 7-10 классов. Вопросы: Что такое функция? Что такое область определения функции? Чем является область определения функции геометрически? Что такое множество значений функции? Чем является множество значений функции геометрически? | Ответы на вопросы: Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают y=f(x). Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох. Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy. | 2 мин |
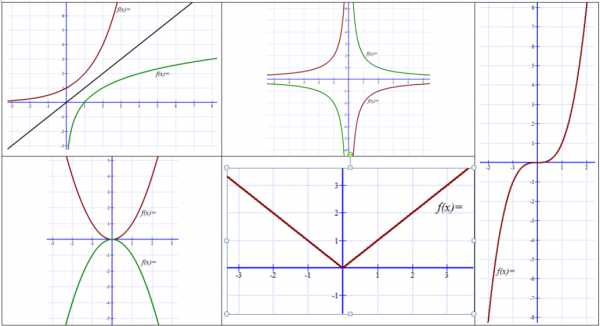
Индивидуальная работа. Задание 1. На выданных карточках подпишите графики функций соответствующими формулами. Укажите область определения и множество значений каждой функции.
После выполнения задания учитель демонстрирует соответствующие слайды, учащиеся дают ответы, проверяют свои записи. |
Пример ответа: формула задаёт показательную функцию, область определения образуют положительные числа, множество значений – все действительные числа; формула задает обратную пропорциональность, область определения данной функции – все действительные числа, кроме нуля, множество значений функции – также все действительные числа, кроме нуля. | 6 мин. |
Вопрос: Как найти область определения функции, заданной формулой? | Ответ на вопрос: Чтобы найти область определения функции y=f(x), заданной формулой, нужно установить, при каких значениях х выражение f(x) имеет смысл, т. е. выполнимы все действия в правой части формулы. | 5 мин. |
Задание 2. Фронтальная работа. Найдите область определения функции: 1) ; 2) ; 3) 4) ; 5) ; 6) ; 7) ; 8) ; 9) . | Примеры ответов: 1) Действие извлечения корня четной степени выполнимо, когда подкоренное выражение неотрицательно, т. е., в данном случае ; 5) Действие деления выполнимо, когда знаменатель не равен нулю, таким образом, 9) Логарифмом положительного числа b по основанию a, где , называется показатель степени, в которую надо возвести a,чтобы получить b. Значит, имеем | |
Изучение нового материала | ||
В десятом классе мы изучали логарифмическую функцию, ей обратную показательную функцию, степенную функцию и перешли к изучению важного раздела алгебры – тригонометрии. В этом разделе рассмотрели понятия синуса, косинуса, тангенса, основные тригонометрические тождества, тригонометрические уравнения и неравенства. Скажите, что еще важно рассмотреть и изучить? Какова цель сегодняшнего урока? | Мы должны изучить тригонометрические функции. Цель: ввести понятие тригонометрических функций. | 1 мин. |
А как ввести понятие тригонометрических функций? | Установить взаимно-однозначное соответствие между действительными числами и значениями их синусов, косинусов, тангенсов. | |
II. Вспомним, как устанавливается соответствие между действительными числами и точками окружности с помощью поворота точки окружности (для презентации используются плакаты из книги для учителя «Изучение алгебры и начал математического анализа в 11 классе» Федоровой Н. Е., издательство Просвещение, 2009). Вопрос: Расскажите, как получена точка М? Какая точка получится при повороте точки Р(1; 0) на угол ; ; ; ?
| Учащийся отвечает у доски. Рассмотрим окружность слева. Пусть х>0. Предположим, что точка, двигаясь по единичной окружности от точки Р против часовой стрелки, прошла путь длиной х (рис. 1). Конечную точку пути обозначим М. В этом случае говорим, что точка М получена из точки Р поворотом вокруг начала координат на угол х радиан. Рассмотрим окружность справа. Пусть х<0. В этом случае поворот на угол х радиан означает, что движение совершалось по часовой стрелке и точка прошла путь длиной . Поворот на 0 радиан означает, что точка остается на месте. При повороте точки Р на угол получается (0; 1). При повороте точки Р на угол получается точка (0; -1). При повороте точки Р на угол получается точка (0; -1). При повороте точки Р на угол получается точка (-1; 0). | 4 мин. |
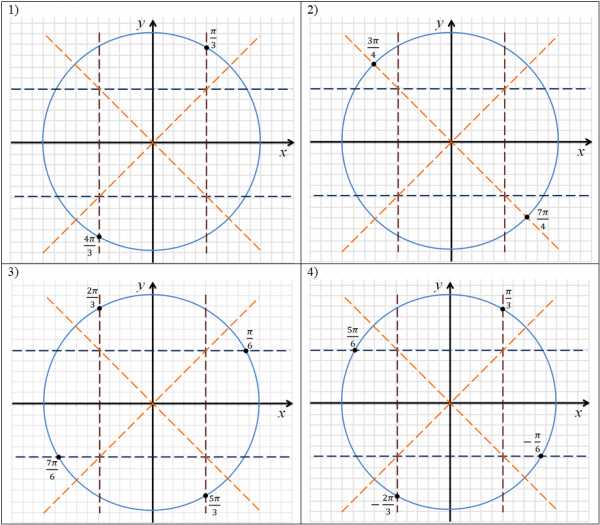
Задание 3. Индивидуальная работа (по шаблонам тригонометрической окружности). Выяснить, в какой четверти расположена точка, полученная поворотом точки Р(1; 0) вокруг начала координат на угол, равный х радиан, если: 1) х = 1,09; 2) х = — 2,9; 3) х = 4,1; 4) х = — 6. | 1) Точка, полученная поворотом точки Р вокруг начала координат на угол, равный х = 1,09 радиан расположена в I четверти; 2) х = — 2,9, точка в III четверти; 3) х = 4,1, точка в III четверти 4) х = — 6, точка в I четверти. | 4 мин. |
Изобразить на единичной окружности точки, полученные поворотом точки Р (1; 0) на угол х: 1) 2) 3) 4) Примерный ответ ученика: 1) . При , этому числу соответствует точка М, при , этому числу соответствует точка М1, при , этому числу также соответствует точка М и т. д. Учитель акцентирует внимание учащихся на том, что каждому числу соответствует единственная точка на числовой окружности, но каждой точке на числовой окружности соответствует бесконечно много чисел. |
| |
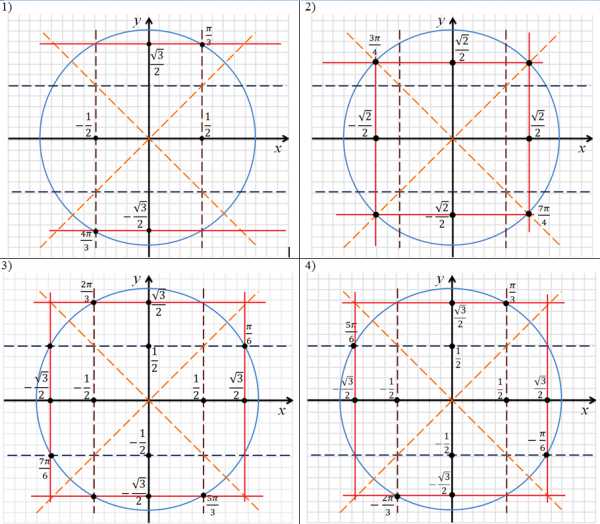
Фронтальная работа. Сформулируйте определения синуса, косинуса, тангенса и котангенса. На каждой единичной окружности подпишите значения синуса и косинуса точек, отмеченных в предыдущем задании.
| Формулируют определения.
| 2 мин. |
Итак, можно ли синус и косинус толковать как функции? | Да. Если х — любое действительное число, то этому числу соответствует определенный угол, измеряющийся числом х, а полученному углу соответствует определенное значение синуса – sin x. В конечном итоге получается соответствие между числами: каждому действительному числу х соответствует определенное действительное число y = sin x. Следовательно, sin x можно толковать как функцию. | 1 мин. |
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями. Какие задачи вы сегодня поставите перед собой? | Изучить свойства тригонометрических функций. Научиться решать задачи, где требуется знать свойства тригонометрических функций. | 2 мин. |
Сегодня мы научимся находить область определения и множество значений тригонометрических функций в случае их аналитического задания. На следующих уроках изучим другие свойства по общей схеме исследования и построим графики функций. Запишите тему урока: «Область определения и множество значений тригонометрических функций». | Записывают тему урока. | |
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций. Заполните таблицу. | Делают выводы, заполняют таблицу. | |
Проанализируйте решение задач №1, №2 учебника стр. 4. Оформите решения в тетради. Решение задачи 2 представьте в виде таблицы, где каждый из способов запишите в отдельный столбец. Попробуйте сформулировать приемы решения типичных задач. Какие необходимы умения и навыки при решении задач данного типа? Какие способы нахождения множества значений функции? | Чтобы найти область определения функции, заданной формулой, нужно установить, при каких значениях х выражение в правой части формулы имеет смысл. При этом необходимо уметь решать уравнения известных нам видов. Чтобы найти множество значений нужно выяснить, какие значения может принимать y при различных значениях х, т. е. установить при каких значениях параметра а уравнение имеет корни. А можно использовать метод оценки, основанный на применении свойств числовых неравенств. | 4 мин. |
Физминутка Кончиками пальцев рук помассировать виски круговыми движениями (12 — 15 сек). Руки на поясе: поднимая прямые руки вверх — подняться на носочки — вернуться в и.п. Наклоняясь вперед сделать глубокий выдох — выпрямляясь, руки поднять вверх, вдох; Руки «в замок»: энергичное вращение кистями в обе стороны (12 — 15 сек). Руки на поясе: полуприсесть — вернуться в и.п. Указательный палец «ведущей» руки на расстоянии 20 — 25 см перед глазами: посмотреть на палец — перевести взгляд на классную доску — вновь посмотреть на палец и т.д. | 2 мин. | |
На конкретных примерах оформим способы нахождения множества значений в виде алгоритмов. 1. Найти множество значений функции через уравнение с параметром. 2. Используя метод оценки, найти множество значений функции . | Оформляют в тетради таблицу. | 4 мин. |
| ||
Закрепление. Работа в парах | 5,5 мин. | |
Выполните упражнения № 1 — № 4 (нечетные), обсуждая решение с соседом по парте. Будьте готовы обосновать свое решение. | Выполняют упражнения в тетрадях. | |
Проверка решения упражнений № 1. Найти область определения функции. Решение: № 2. Найти множество значений функции. Решение: [0; 2]. № 3. Найти область определения функции. Решение: № 4. Найти область определения функции f(x) и вычислить её значение в заданных точках. Решение: | ||
Подведение итогов урока | 2 мин. | |
Что повторили? Что узнали нового? Что следует запомнить? На следующем уроке мы научимся исследовать область определения и множество значений функций, имеющих более сложное аналитическое задание. Вспомним способы решения тригонометрических уравнений и неравенств. | Повторили свойства элементарных функций; повторили, как исследовать свойства функций по графику и формуле. Ввели понятия тригонометрических функций. Познакомились со способами нахождения области определения и множества значений тригонометрических функций. Следует запомнить способ исследования множества значений через решение уравнений с параметром и метод оценки. | |
Рефлексия. Сегодня я узнал… было трудно… я понял, что… я научился… я смог… было интересно узнать, что… меня удивило… мне захотелось… . | Каждый ученик выбирает по 1-2 предложения и заканчивает их. | |
Домашнее задание | ||
Повторить изученные свойства тригонометрических функций. Выполнить упражнения: стр. 6, № 1 — № 4 (четные). | Записывают задание в дневники. | |
Решение домашних упражнений № 1. Найти область определения функции. Решение: № 2. Найти множество значений функции. Решение: № 3. Найти область определения функции. Решение: № 4. Найти область определения функции f(x) и вычислить её значение в заданных точках. Решение: | — | |
xn--j1ahfl.xn--p1ai
Тригонометрические функции
Область определения и множество значений тригонометрических функций
Каждому действительному числу x соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол x радиан. Для этого угла определены sin x и cos x. Тем самым каждому действительному числу x поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции
y = sin x и y = cos x Таким образом, областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.Чтобы найти множество значений функции y = sin x, нужно выяснить, какие значения может принимать y при различных значениях x, т.е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнение sin x = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a| > 1. Следовательно, множеством значений функции y = sin x является отрезок -1 ≤ y ≤ 1. Аналогично множеством значений функции y = cos x также является отрезок -1 ≤ y ≤ 1.
Функция y = tg x определяется формулой y = tg x = sin x/cos x. Эта функция определена при тех значениях x, для которых cos x ≠ 0 Известно, что cos x = 0 при x = π/2 + πn, n Є Z. Следовательно, областью определения функции y = tg x является множество чисел x ≠ π/2 + πn, n Є Z. Так как уравнение tg x = a имеет корни при любом действительном значении a, то множеством значений функции y = tg x является множество R всех действительных чисел.
Функции y = sin x, y = cos x, y = tg x называют тригонометрическими функциями.
Четность, нечетность, периодичность тригонометрических функций
Известно, что для любого значение x верны равенства
sin (-x) = -sin x, cos (-x) = cos x Следовательно, y = sin x — нечетная функция, а y = cos x — чётная функция. Так как для любого значения x из области определения функции y = tg x верно равенство tg (-x) = -tg x, то y = tg x — нечетная функция.Известно, что для любого значения x верны равенства
sin (x + 2π) = sin x, cos (x + 2π) = cos x. Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на 2π. Такие функции называются периодическими с периодом 2π.Функция f (x) называется периодической, если существует такое число T ≠ 0, что для любого x из области определения этой функции выполняется равенство f (x — T) = f (x) = f (x + T). Число T называется периодом функции f (x). Из этого определения следует, что если x принадлежит области определения функции f (x), то числа x + T, x — T и вообще числа x + Tn, n Є Z, также принадлежат области определения этой периодической функции и f (x + Tn) = f (x), n Є Z
Число 2π является наименьшим положительным периодом функции y = cos x, также и для функции
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
Решение типовых задач
страница 1Занятие 3
«Область значений функции»
Цели:- Применять понятие области значений к решению конкретной задачи;
решение типовых задач .
В течение нескольких лет на экзаменах регулярно появляются задачи, в которых из данного семейства функций требуется выделить те, чьи множества значений удовлетворяют объявленным условиям.
Рассмотрим такого рода задачи.
-
Актуализация знаний.
Проводится в форме диалога с учащимися.
Что мы понимаем под множеством значений функции?
Как обозначается множество значений функции?
-
По каким данным мы можем найти множество значений функции? (По аналитической записи функции или ее графику)
— Используя рисунок, по графикам найдите область значений функции.
(см задания ЕГЭ, часть А)
-
Множества значений каких функций мы знаем? (Перечисляются основные функции с записью их на доске; для каждой из функций записывается ее множество значений). В результате на доске и в тетради учащихся
| Функция | Множество значений |
| y = x2 y = x3 y = y = | x | y = | E(y) = [0, + ∞) E(y) = ( – ∞, + ∞) E(y) = [0, + ∞) E(y) = [0, + ∞) E(y) = ( – ∞, 0) (0, + ∞) |
| y = y = cos x y = tg x y = ctg x y = logax y = ax | E(y) = [- 1, 1] E(y) = [- 1, 1] E(y) = ( – ∞, + ∞) E(y) = ( – ∞, + ∞) E(y) = ( – ∞, + ∞) E(y) = ( 0, + ∞) |
-
Можем ли мы, используя эти знания, сразу найти множества значений записанных на доске функций? ( см. таблицу 2). -
Что может помочь в ответе на данный вопрос? (Графики этих функций). -
Как построить график первой функции? (Опустить параболу на 4 единицы вниз).
Аналогично беседуем по каждой функции из таблицы.
| Функция | Множество значений |
| y = x2 – 4 | E(y) = [-4, + ∞) |
| y = + 5 | E(y) = [5, + ∞) |
| y =3 sin x | E(y) = [- 3, 3] |
| y = – 5 cos x | E(y) = [- 5, 5] |
| y = tg (x + / 6) – 1 | E(y) = ( – ∞, + ∞) |
| y = sin (x + / 3) – 2 | E(y) = [- 3, — 1] |
| y = | x – 1 | + 3 | E(y) = [3, + ∞) |
| y = cos2x | E(y) = [0, 1] |
| y = | ctg x | | E(y) = [0, + ∞) |
| y = sin2x – 3 | E(y) = [- 3, — 2] |
| y = = | cos (x + /4) | | E(y) = [0, 1] |
| y = (x – 5)2 + 3 | E(y) = [3, + ∞) |
| y = x2 – 6x + 2 | E(y) = [– 7, + ∞) |
-
Последнюю функцию давайте запишем в тетрадь и найдем ее множество значений. Как это можно сделать? (Проанализировать ее график). -
Что мы можем сказать о графике данной функции? (Парабола, ветви направлены вверх, абсцисса вершины которой находится по формуле:
(xв = )
-
Можем ли мы теперь найти множество значений функции? Что еще нужно найти? (Ординату вершины: yв = – 7)
Впишем в таблицу результат.
-
А можем ли мы по-другому найти множество значений этой функции? (Можем выделить квадрат двучлена и записать функцию в виде
у = (х – 3)2 – 7.) -
Изменится ли при этом множество её значений? (Нет, оно останется прежним.)-
Найдите область значений функции:
-
-
Зная множество значений функции, восстановите формулу:
;
;
.
-
Пусть множество значений функции у=f(x) есть отрезок [-3;5].
Найдите множество значений функции:
.
-
Пусть множество значений функции y=f (x-5) есть отрезок [-3;5].
Найдите множество значений функции:
.
-
Найдите множество значений функции: . -
Найдите множество значений функции:
.
-
Пусть множество значений функции y=f(x) есть отрезок [-3;5]. Найдите все целочисленные значения функции:
-
Постройте схематически график функции и найдите область ее значений:
Введение алгоритма решения задач на нахождение множества значений тригонометрических функций.
Давайте посмотрим, как мы можем применить имеющийся опыт для решения различных заданий, включаемых в варианты единого экзамена.
1. Нахождение значений функций при заданном значении аргумента.
Пример. Найти значение функции у = 2 cos(π/2+ π/4) – 1, если х = — π/2.
Решение.
y(-π/2) = 2 cos(-π/2 – π/4)-1=2 cos(π/2 + π/4)-1 = — 2 sin π/4 – 1 = — 2 – 1 =
= – – 1.
2.Нахождение области значений тригонометрических функций
-
Найдите все целые значения функции у=+2 sin х
Решение.
-1≤ sin х ≤ 1
-2 ≤ 2 sin х ≤ 2
9 ≤ 11+2sin х ≤ 13
3 ≤ +2∙ sinх ≤ , т.е. Е (у)= [3; ].
Выпишем целые значения функции на промежутке [3; ]. Это число 3.
Ответ: 3.
-
Найдите множество значений функции у = sin2х + 6sin х + 10.
| Решение. | Алгоритм |
| 1. Перепишем функцию в виде у = sin2x + 6sin x + 9 + 1, 2. у = ( sin x + 3)2 + 1. 3. Е(sin x) = [-1;1], 4. Е(sin x + 3) = [2;4], Е(sin x + 3)2 = [4;16], Е(у) = [5;17]. |
2. Преобразовать это выражение, выделив квадрат двучлена. 3. Найти множество значений внутренней основной тригонометрической функции. 4. Найти множество значений всей функции, последовательно оценивая каждую промежуточную функцию, получаемую операцией из исходной. |
-
Найдите множество значений функции: у = sin2 х — 6 sin х + 8. (самостоятельно)
Решение.
у = sin2х- 2 3 sin х +32 — 32+ 8,
у = (sin х-3)2-1.
Е (sin х ) = [-1;1];
Е (sin х -3) = [-4;-2];
Е (sin х -3)2 = [4;16];
Е (у) = [3;15].
Ответ: [3;15].
-
Найдите наименьшее значение функции у = соs 2x + 2sin x – 2.
Решение.
Можем ли мы найти множество значений этой функции? (Нет.)
Что нужно сделать? (Свести к одной функции.)
Как это сделать? (Использовать формулу cos2x = 1—sin2x.)
Итак, у = 1—sin2x + 2sin x –2,
y = -sin2x + 2sin x –1,
у = -(sin x –1)2.
Ну, а теперь мы можем найти множество значений и выбрать из них наименьшее.
-1 ≤ sin x ≤ 1,
-2 ≤ sin x – 1 ≤ 0,
0 ≤ (sin x – 1)2 ≤ 4,
-4 ≤ -(sin x -1)2 ≤ 0.
Значит, наименьшее значение функции унаим = –4. Ответ: -4.
-
Найдите произведение наибольшего и наименьшего значений функции
у = sin2 x + cos x + 1,5.
Решение.
у = 1-cos2x + cos x + 1,5,
у = -cos2x + 2∙0,5∙cos x — 0,25 + 2,75,
у = -(cos x— 0,5)2 + 2,75.
Е(cos x) = [-1;1],
Е(cos x – 0,5) = [-1,5;0,5],
Е(cos x – 0,5)2 = [0;2,25],
Е(-(cos x-0,5)2 ) = [-2,25;0],
Е(у) = [0,5;2,75].
Наибольшее значение функции унаиб = 2,75; наименьшее значение унаим = 0,5. Найдём произведение наибольшего и наименьшего значения функции:
унаиб ∙ унаим = 0,5∙2,75 = 1,375.
Ответ: 1,375.
-
Найдите сумму всех целых значений функции у = .
Решение.
Перепишем функцию в виде у =,
у = ,
у = ,
Найдем теперь множество значений функции.
E(sin x) = [-1, 1],
E(6sin x) = [-6, 6],
E(6sin x + 1) = [-5, 7],
E((6sin x + 1)2) = [0, 49],
E(– (6sin x + 1)2) = [-49, 0],
E(– (6sin x + 1)2 + 64) = [15, 64],
E(y) = [, 8].
Найдем сумму целых значений функции: 4 + 5 + 6 + 7 + 8 = 30.
Ответ: 30.
-
Найдите множество значений функции если
Решение.
1) то есть х принадлежит I четверти.
2)
Следовательно, 2х принадлежат II четверти.
3) Во II четверти функция синус убывает и непрерывна. Значит, данная функция принимает все значения от до
4) Вычислим эти значения:
Ответ: .
-
Найдите множество значений функции
Решение.
1) Так как а синус принимает значения от -1 до 1, то множество значений разности . При умножении на этот отрезок перейдет в отрезок .
2) Арккосинус – монотонно убывающая и непрерывная функция. Значит, множество значений выражения — это отрезок .
3) При умножении этого отрезка на получим .
Ответ: .
-
Найдите множество значений функции , если .
Решение.
Так как арктангенс является возрастающей функцией, то .
2) При возрастании х от до аргумент 2х возрастает от до . Так как синус на таком промежутке возрастает, то функция принимает значения от до 1.
3) При возрастании от до аргумент 2х возрастает от до . Так как синус на таком промежутке убывает, то функция принимает значения от до 1.
4) Используя формулу, выражающую синус через тангенс половинного угла, находим, что
.
Значит, искомое множество значений – это объединение отрезков и , то есть отрезок .
Ответ: .
Данный прием (Введение вспомогательного угла) применяется для нахождения множества значений функций вида
у = a sin x + b cos x или у = a sin (рx) + b cos (р x).
-
Найдите множество значений функции
у = 15 sin 2x + 20 cos 2x.
Решение.
Найдем значение = = 25.
Преобразуем выражение
15 sin 2x + 20 cos 2x = 25 () = 25 () =
25 sin (2x +), где cos= , sin=.
Множество значений функций у = sin (2x +): -1 sin (2x +) 1.
Тогда множество значений исходной функции -25 25 sin (2x +) 25.
Ответ: [-25; 25].
3. Задания на нахождение наибольшего и наименьшего значения функции на промежутке.
-
Найдите наибольшее и наименьшее значение функции у = сtg х на отрезке [π/4; π/2].
Решение.
Функция у = сtg х является убывающей на отрезке [π/4; π/2], следовательно, наименьшее значение функция будет принимать при х = π/2, то есть у(π/2) = сtg π/2 = 0; а наибольшее значение – при х= π/4, то есть у(π/4) = сtg π/4 = 1.
Ответ: 1, 0.
-
Найти все значения параметра а, при каждом из которых функция на промежутке [-1; 1] принимает все значения из отрезка
[0; 1].
Решение.
Выделим в равенстве целую часть: .
Отсюда следует, что графиком функции f(x) является либо гипербола (а≠ 0), либо прямая без точки.
При этом если а ; 2а) и (2а; ) и, если а > 0, монотонно возрастает на этих лучах.
Если а = 0, то f(x) = -2 на всей области определения х ≠ 0. Поэтому очевидно, что искомые значения параметра не равняются нулю.
Поскольку нас интересуют значения функции только на отрезке [-1; 1], то классификация ситуаций определяется тем, что асимптота х = 2а гиперболы (а≠0) располагается относительно этого отрезка.
Случай 1. Все точки промежутка [-1; 1] находятся справа от вертикальной асимптоты х = 2а, то есть когда 2а
Случай 2. Вертикальная асимптота пересекает промежуток [-1; 1], и функция убывает (как и в случае 1), то есть когда
Случай 3. Вертикальная асимптота пересекает промежуток [-1; 1] и функция возрастает, то есть -1
.
Случай 4. Все точки промежутка [-1; 1] находятся слева от вертикальной асимптоты, то есть 1 а > .
Далее на каждом этапе находим множество значений функции на отрезке [-1;1] в точках, где она определена. Это делается на основе свойства монотонности.
Ответ: -2≤ а
-
Найти все а, при которых множество значений функции не пересекается с промежутком [3 ;∞).
Решение.
Имеем
Очевидно
Отсюда 0
Следовательно, область значений функции f – промежуток (0; ]. Полученный промежуток не должен иметь общих точек с лучом [3 ;∞). Понятно, что для этого достаточно потребовать
Отсюда а2 — За — 1 > — 1, то есть а 3.
Ответ: а 3.
-
Решите уравнение
Решение: Выделим в правой части уравнения полный квадрат:
Так как , , то равенство достигается, если
Решая второе уравнение системы, получаем Подстановкой убеждаемся, что является и решением первого уравнения системы. Следовательно, -решение системы.
Ответ:4.
-
Решите уравнение
Решение. Поскольку , произведение может равняться единице лишь при выполнении одной из двух систем уравнений:
Решая первую систему, найдем из первого уравнения и . Очевидно, решения первого уравнения входят в решение второго при то есть являются решениями системы. Решая вторую систему, убедимся, что она несовместна: решения первого уравнения и второго не имеют общих корней.
Ответ:
4. Задания на нахождение наибольшего и наименьшего значения функции через обратную функцию.
-
Какого значения функция не достигает ни при каком х
Решение Выразим функцию обратную данной от переменной y и найдем ее область определения, которая и будет областью значений заданной функции.
2ху-5у=3х+6
2ху-3х=6+5у
х=, где у. Итак D(x)=(-; )(;+).
Е(у)
Ответ: 1,5
-
Найти наибольшее целое значение функции у =
х2-5=ух2+2у
х2(1-у)=5+2у
х2 =, где у1, х20
Ответ: 0
5. Задания на последовательное нахождение значения функции (пошаговое )
-
Найти область значения функции f(x)=
Решение: Пусть f(x)=, где g(x)=
g(x)=sinx-cosx+2=sin(x-)+2.
Тогда 1 g(x) 3/
Функция y= убывающая, а значит
-20
-16у0. Итак, Е(у)= -16;0
Ответ: -16;0.
Итак, существует несколько приемов нахождения множеств значений функций, заданных аналитически.
Прием 1. Нахождение множества значений функции по её графику.
Прием 2. Нахождение множества значений функции с помощью производной. (см занятие 12)
Прием 3. Последовательное нахождение множества значений функций, входящих в данную композицию функций (прием пошагового нахождения множества значений функции).
Прием 4. Выражение х через у. (Поиск области определения обратной функции)
Прием 5. Упрощение формулы, задающей дробно-рациональную функцию
Прием 6. Нахождение множества значений квадратичных функций (с помощью нахождения вершины параболы и установления характера поведения её ветвей).
Прием 7. Введение вспомогательного угла для нахождения множества значений некоторых тригонометрических функций.
страница 1
Смотрите также:
Решение задач по классической генетике Этапы решения типовых генетических задач
1003.38kb. 8 стр.
Решение типовых задач. Методы обучения: лекция, письменные упражнения
109.4kb. 1 стр.
Решение типовых задач
124.87kb. 1 стр.
moglobi.ru
Деятельность учителя | Деятельность ученика |
1. Мотивационно-ориентировочная часть | |
1.1. Мотивация | |
— Начало урока посвятим обзору элементарных функций, изученных в курсе алгебры 7-10 классов. Вспомните, какими формулами они задаются, как называются соответствующие графические образы. — Установите соответствие между графиком функции и формулой. | Слайд 1 (объекты в движении). Ученики перетаскивают формулы на соответствующие им графики, параллельно повторяя, как выглядит график, название соответствующей кривой. Например, Учащиеся повторяют аналитическое задание функций и графические образы. Учитель может добавить следующее: каждому значению аргумента соответствует по определенному закону единственное значение функции, т.е. существует взаимно-однозначное соответствие между x и y. |
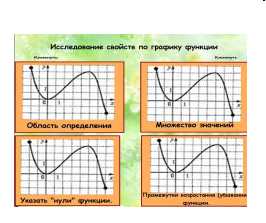
— Какие свойства функции можно исследовать свойства по графику?
| Слайд 2 (инструмент «штора»). Свойства:
Учитель, постепенно опуская «штору», повторяет с учениками очередное свойство функции, исследуемое или по графику, или по формуле. |
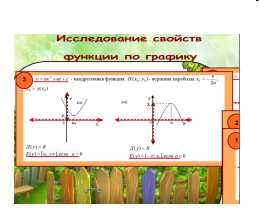
— Что такое область определения функции? — Что называется множеством значений функции? — Укажите область определения и множества значений по графическим образам. | Слайд 3 (выдвижные объекты). Область определения функции – это все значения, которые может принимать ее аргумент. Множество значений – это те значения, которые может принимать переменная y. По графическим образам ответ такой: Например, на фрагменте представлен график квадратичной функции в двух случаях: старший коэффициент положительный – х-любое, значения функции ограничены значением в вершине параболы, не меньше значения в вершине параболы; старший коэффициент отрицательный – х-любое, значения функции не больше значения функции в вершине параболы Учитель вытягивает выдвижные объекты с определениями, на которых приклеены ярлыки «Повторим теорию». Ученики вытягивают фрагменты с графиками и комментируют, как определить область определения и множество значений функций, представленных на графиках. |
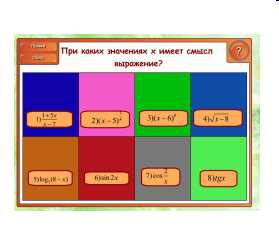
— При каких значениях x имеют смысл выражения? (самостоятельная работа, запись ответов в тетради, один ученик за крыльями доски). — С какими действиями связаны ограничения по возможным значениям переменной x? Вспомним, когда возможно деление? Когда возможно извлечение корня четной степени? Когда существует степень с дробным показателем? Когда существует степень с нулевым показателем? Когда существует логарифм? Когда существует синус, косинус, тангенс? | Слайд 4 (интерактивное упражнение) Ученики дают комментарии к упражнениям. Например: Не всегда возможно деление. Деление возможно на неравное нулю число. Логарифмы существуют только для положительных чисел. Корни четной степени существуют только для неотрицательных чисел. Степень с дробным показателем существует для положительных чисел. Синус, косинус существует для любого действительного числа, т.к. это координаты точки единичной окружности, на которой изображаются действительные числа. Тангенс не существует на концах вертикального диаметра единичной окружности. Котангенс не существует на концах горизонтального диаметра. При проверке ученик комментирует ответ, объясняя, когда возможно данное действие. Учитель для обратной связи с целью усиления наглядности использует интерактивное средство СМАРТ доски. При нажатии на домино появляется правильный ответ. Это упражнение является пропедевтическим для изучения области определения функций. По завершении необходимо сделать акцент на прием нахождения допустимых значений x. |
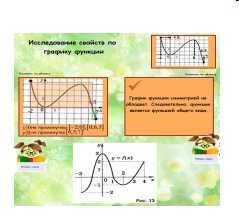
— Какая функция называется четной (нечетной)? Учитель после ответов учеников вытягивает объект с формулировкой (для наглядного закрепления). — Установите соответствие между графиком и свойством четности (нечетности).
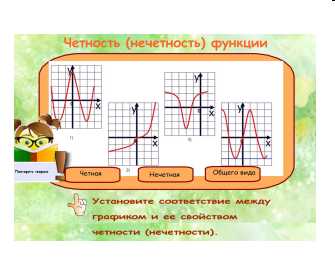
| Слайд 5. Выдвижной объект «повтори теорию». — Функция называется четной, если ее область определения симметрична относительно начала координат и значения функции в противоположных точках равны. График обладает симметрией относительно начала координат. — Функция называется нечетной, если ее область определения симметрична относительно начала координат и в противоположных точках значения противоположны. График обладает симметрией относительно начала координат. Повторяются определения, устанавливается соответствие между графиком и названием (четная, нечетная, общего вида). Слайд служит для пропедевтики изучения темы «Четность, нечетность тригонометрических функций». |
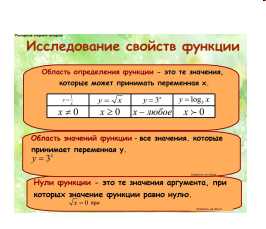
— Как найти область определения и множество значений функций, заданной формулой?
| Слайд №6 — Чтобы найти область определения функции, надо определить допустимые значения переменной x, учитывая ограничения, связанные с алгебраическими действиями. — Чтобы найти множество значений, надо определить возможные значения переменной у, учитывая свойства арифметических действий. На слайде заданы эффекты анимации «Появление». Учащиеся имеют возможность наглядно проверить свою версию ответа. |
— Исследуйте свойства функции, заданной графиком. На слайде задана анимация «вращение». Ответы указаны на обороте картинки. Проверка осуществляется сразу после предложенного ответа. | Слайд №7 Ученики работают в парах, делают краткие записи в тетрадях. Проверяют правильность друг у друга, вырабатывают одну правильную версию и озвучивают ее при фронтальной проверке. Возможный ответ: «Нуль» функции – это значение аргумента, при котором функция равна нулю. Функция равна нулю в точках пересечения с ось абсцисс. Поэтому нули функции: 0 и 6,5. Функция на двух промежутках убывает, на одном – возрастает. Убывает – с увеличением аргумента линия падает вниз. Возрастает – при увеличении аргумента линия поднимается вверх. График простирается не на всей действительной оси, поэтому область определения ограничена отрезком. По оси ординат график тоже ограничен, поэтому область значений тоже ограничена отрезком. На слайде предусмотрены подсказки — выдвижные фрагменты «повтори теорию», эффекты анимации «Поворот»: при наведении на объект он поворачивается и появляется ответ. Эффект хорош для обеспечения обратной связи. |
— Итак, мы привели знания в систему, повторив основные свойства элементарных функций, которые были изучены в курсе алгебры 7-10 классы. Еще раз акцентируем внимание на том, что свойства можно исследовать как по формуле, так и по графику. — Сегодня на уроке и на последующих уроках мы будем изучать новый вид функций и их свойства. | |
1.2 Постановка учебной задачи (цели) урока | |
— В десятом классе мы изучали логарифмы и связанную с ними логарифмическую функцию и ей обратную показательную функцию, степень и связанную с ней степенную функцию; важный раздел алгебры – тригонометрия. В этом разделе рассмотрели понятия синуса, косинуса, тангенса, основные тригонометрические тождества, тригонометрические уравнения. — По логике вещей, скажите, что еще важно рассмотреть и изучить? Сделайте предположение. | — Мы изучили основные понятия тригонометрии. Возможно, в природе существуют тригонометрические функции. И это нетрудно проверить, если попробовать установить взаимно-однозначное соответствие между действительными числами и значениями их синусов, косинусов, тангенсов. |
— Как сформулировать цель урока? | — Ввести понятия тригонометрических функций. |
— Поскольку с каждым видом функции связаны свои свойства, то, наверное, интересно будет познакомиться со свойствами тригонометрических функций. — Какие еще цели можно поставить? | — Изучить свойства тригонометрических функций, заданных формулами. Исследование возможно только по формуле, поскольку не известны графические образы. |
1.3 Планирование учебной деятельности | |
— Мы введем понятия тригонометрических функций и научимся находить их область определения и множество значений в случае их аналитического задания. Далее, на последующих уроках, изучим другие свойства по общей схеме исследования. Используя свойства, построим графические образы. Запишите тему урока. | Записывают тему урока «Тригонометрические функции. Область определения и множество значений». |
— Перед вами на партах лежит канва таблицы, такая же заготовка фрагментарно сделана на экране интерактивной доски. В ходе урока мы должны заполнить таблицу полностью. — Все согласны принять правила работы? — Тогда начинаем постепенно заполнять графы таблицы. Как только таблица будет заполнена, мы постараемся связать ее графы и обсудим результаты работы. | Слайд №8 На парте лежит канва таблицы. Такой образец заполнения, возможно, будет в тетради у ученика, при выполнении следующих указаний учителя.
|
2. Операционно-познавательная часть | |
2.1 Введение понятий тригонометрических функций. | |
— Самостоятельная работа с учебником по плану:
| Слайд №9 (для демонстрации для введения понятий тригонометрических функций) После работы с книгой ученики должны объяснить по данному слайду как вводятся тригонометрические функции. |
2.2. Рассмотрение области определения и множества значений. Формирование приемов нахождения области определения и множества значений функций, заданных формулами. | |
— Как с помощью тригонометрического круга определить, какова область определения и множество значений тригонометрических функций? — Вспомните определение тангенса и котангенса. Выпишите соответствующие соотношения. — Сделайте выводы об области определения и множестве значений. | Слайд №10. (для демонстрации области определения и множества значений) Параллельно идет заполнение таблицы со свойствами тригонометрических функций. |
— Итог: ввели понятия тригонометрических функций и рассмотрели их область определения и множество значений. | |
— Попробуйте выделить типы задач по новой теме. | — Найти область определения функции, заданной формулой; — Найти множество значений функций, заданных формулой. |
— Проанализируйте решение задач №1, №2 учебника стр. 4. Оформите решения в тетради. — Попробуйте сформулировать приемы решения типичных задач. — Какие необходимы умения и навыки при решении задач данного типа? — Какие способы нахождения области значений?
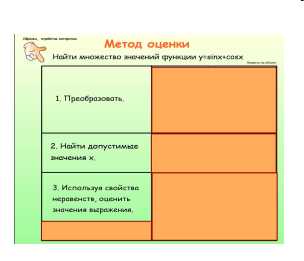
| — Чтобы найти область определения функции, надо определить допустимые значения переменной x, учитывая ограничения, связанные с алгебраическими действиями. При этом сталкиваемся с решением уравнений или неравенства. Необходимо уметь решать уравнения и неравенства известных нам видов. Поэтому хорошо бы повторить приемы решения. — Чтобы найти область значений можно использовать метод оценки, основанный на применении свойств числовых неравенств. Поэтому желательно повторить свойства числовых неравенств. |
— Вывод: Метод оценки заключается в следующем:
| Слайд №11 (демонстрирует приемы нахождения области значений функции). Учащиеся оформляют метод решения и образец задания на закрепление.
|
— Второй способ: через уравнение с параметром. Учитель объясняет на конкретном примере и дает под запись прием.
| Ученики оформляют вместе с учителем решение задания.
|
2.3. Закрепление. Решение упражнений на отработку навыков. | |
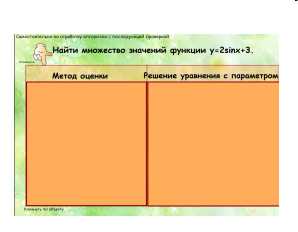
— Отработка алгоритма. Учитель предлагает выполнить задание самостоятельно.
| Ученики, сотрудничая в парах, пытаются решить задание двумя способами, оформляя решение по предложенной схеме в два столбика. По завершению осуществляется проверка по слайду (задана анимация объекта). |
— Итак, подведем итоги нашей работы.
| — Повторили:
— Ввели понятия тригонометрических функций. — Познакомились со способами исследования на область определения и множество значений. — Взять на заметку, запомнить:
|
3. Рефлексивно-оценочная часть | |
3.1. Оценка и самооценка учебной деятельности | |
Прошу вас на маленьких листочках: поставить себе оценку за работу на уроке; что показалось сложным; какие моменты вызывают трудности. Что понравилось, что не понравилось на уроке? | Ученики выставляют себе оценку за работу на уроке, указывают на сложности восприятия нового материала. |
3.2. Подведение итогов урока | |
— Итак, при постановке цели урока мы использовали оборот «привести знания свойств элементарных функций в систему», ввести понятия тригонометрических функций, исследовать область определения и множество значений и привести эти знания в систему, сформировать приемы исследования данных свойств. — Достигнута ли поставленная нами цель или нет, зависит от того, построена ли система знаний. Как вы считаете? | — Да, действительно, мы привели знания в систему, потому что повторили и систематизировали знания о свойствах функций. — Мы ввели понятия тригонометрических свойств и исследовали область определения и множество значений. Привели и эти знания в систему. Доказательством является заполненная таблица. — На конкретных задачах сформировали приемы нахождения области определения и множества значений (метод оценки, через уравнение с параметром). И эти знания привели в систему, т.к. оформили приемы в виде таблицы. |
3.3. Планирование предстоящей учебной деятельности | |
— На следующем уроке мы научимся исследовать область определения и множество значений функций, имеющих более сложное аналитическое задание. Возможно, предстоит вспомнить способы решения тригонометрических уравнений и неравенств, некоторые тригонометрические формулы. Поэтому в домашнее задание необходимо включить вопросы для повторения этих важных моментов. | Ученики записывают домашнее задание. |
videouroki.net
Занятие 3 «Область значений функции»
Занятие 3«Область значений функции»
Цели:- Применять понятие области значений к решению конкретной задачи;
решение типовых задач .
В течение нескольких лет на экзаменах регулярно появляются задачи, в которых из данного семейства функций требуется выделить те, чьи множества значений удовлетворяют объявленным условиям.
Рассмотрим такого рода задачи.
-
Актуализация знаний.
Проводится в форме диалога с учащимися.
Что мы понимаем под множеством значений функции?
Как обозначается множество значений функции?
-
По каким данным мы можем найти множество значений функции? (По аналитической записи функции или ее графику)
— Используя рисунок, по графикам найдите область значений функции.
(см задания ЕГЭ, часть А)
-
Множества значений каких функций мы знаем? (Перечисляются основные функции с записью их на доске; для каждой из функций записывается ее множество значений). В результате на доске и в тетради учащихся
| Функция | Множество значений |
| y = x2 y = x3 y = y = | x | y = | E(y) = [0, + ∞) E(y) = ( – ∞, + ∞) E(y) = [0, + ∞) E(y) = [0, + ∞) E(y) = ( – ∞, 0) (0, + ∞) |
| y = sin x y = cos x y = tg x y = ctg x y = logax y = ax | E(y) = [- 1, 1] E(y) = [- 1, 1] E(y) = ( – ∞, + ∞) E(y) = ( – ∞, + ∞) E(y) = ( – ∞, + ∞) E(y) = ( 0, + ∞) |
-
Можем ли мы, используя эти знания, сразу найти множества значений записанных на доске функций? ( см. таблицу 2). -
Что может помочь в ответе на данный вопрос? (Графики этих функций). -
Как построить график первой функции? (Опустить параболу на 4 единицы вниз).
Аналогично беседуем по каждой функции из таблицы.
| Функция | Множество значений |
| y = x2 – 4 | E(y) = [-4, + ∞) |
| y = + 5 | E(y) = [5, + ∞) |
| y =3 sin x | E(y) = [- 3, 3] |
| y = – 5 cos x | E(y) = [- 5, 5] |
| y = tg (x + / 6) – 1 | E(y) = ( – ∞, + ∞) |
| y = sin (x + / 3) – 2 | E(y) = [- 3, — 1] |
| y = | x – 1 | + 3 | E(y) = [3, + ∞) |
| y = cos2x | E(y) = [0, 1] |
| y = | ctg x | | E(y) = [0, + ∞) |
| y = sin2x – 3 | E(y) = [- 3, — 2] |
| y = = | cos (x + /4) | | E(y) = [0, 1] |
| y = (x – 5)2 + 3 | E(y) = [3, + ∞) |
| y = x2 – 6x + 2 | E(y) = [– 7, + ∞) |
-
Последнюю функцию давайте запишем в тетрадь и найдем ее множество значений. Как это можно сделать? (Проанализировать ее график). -
Что мы можем сказать о графике данной функции? (Парабола, ветви направлены вверх, абсцисса вершины которой находится по формуле:
(xв = )
-
Можем ли мы теперь найти множество значений функции? Что еще нужно найти? (Ординату вершины: yв = – 7)
Впишем в таблицу результат.
-
А можем ли мы по-другому найти множество значений этой функции? (Можем выделить квадрат двучлена и записать функцию в виде
у = (х – 3)2 – 7.) -
Изменится ли при этом множество её значений? (Нет, оно останется прежним.)-
Найдите область значений функции:
-
-
Зная множество значений функции, восстановите формулу:
;
;
.
-
Пусть множество значений функции у=f(x) есть отрезок [-3;5].
Найдите множество значений функции:
.
-
Пусть множество значений функции y=f (x-5) есть отрезок [-3;5].
Найдите множество значений функции:
.
-
Найдите множество значений функции: . -
Найдите множество значений функции:
.
-
Пусть множество значений функции y=f(x) есть отрезок [-3;5]. Найдите все целочисленные значения функции:
-
Постройте схематически график функции и найдите область ее значений:
Введение алгоритма решения задач на нахождение множества значений тригонометрических функций.
Давайте посмотрим, как мы можем применить имеющийся опыт для решения различных заданий, включаемых в варианты единого экзамена.
1. Нахождение значений функций при заданном значении аргумента.
Пример. Найти значение функции у = 2 cos(π/2+ π/4) – 1, если х = — π/2.
Решение.
y(-π/2) = 2 cos(-π/2 – π/4)-1=2 cos(π/2 + π/4)-1 = — 2 sin π/4 – 1 = — 2 – 1 =
= – – 1.
2.Нахождение области значений тригонометрических функций
-
Найдите все целые значения функции у=+2 sin х
Решение.
-1≤ sin х ≤ 1
-2 ≤ 2 sin х ≤ 2
9 ≤ 11+2sin х ≤ 13
3 ≤ +2∙ sinх ≤ , т.е. Е (у)= [3; ].
Выпишем целые значения функции на промежутке [3; ]. Это число 3.
Ответ: 3.
-
Найдите множество значений функции у = sin2х + 6sin х + 10.
| Решение. | Алгоритм |
| 1. Перепишем функцию в виде у = sin2x + 6sin x + 9 + 1, 2. у = ( sin x + 3)2 + 1. 3. Е(sin x) = [-1;1], 4. Е(sin x + 3) = [2;4], Е(sin x + 3)2 = [4;16], Е(у) = [5;17]. |
2. Преобразовать это выражение, выделив квадрат двучлена. 3. Найти множество значений внутренней основной тригонометрической функции. 4. Найти множество значений всей функции, последовательно оценивая каждую промежуточную функцию, получаемую операцией из исходной. |
-
Найдите множество значений функции: у = sin2 х — 6 sin х + 8. (самостоятельно)
Решение.
у = sin2х- 2 3 sin х +32 — 32+ 8,
у = (sin х-3)2-1.
Е (sin х ) = [-1;1];
Е (sin х -3) = [-4;-2];
Е (sin х -3)2 = [4;16];
Е (у) = [3;15].
Ответ: [3;15].
-
Найдите наименьшее значение функции у = соs 2x + 2sin x – 2.
Решение.
Можем ли мы найти множество значений этой функции? (Нет.)
Что нужно сделать? (Свести к одной функции.)
Как это сделать? (Использовать формулу cos2x = 1—sin2x.)
Итак, у = 1—sin2x + 2sin x –2,
y = -sin2x + 2sin x –1,
у = -(sin x –1)2.
Ну, а теперь мы можем найти множество значений и выбрать из них наименьшее.
-1 ≤ sin x ≤ 1,
-2 ≤ sin x – 1 ≤ 0,
0 ≤ (sin x – 1)2 ≤ 4,
-4 ≤ -(sin x -1)2 ≤ 0.
Значит, наименьшее значение функции унаим = –4. Ответ: -4.
-
Найдите произведение наибольшего и наименьшего значений функции
у = sin2 x + cos x + 1,5.
Решение.
у = 1-cos2x + cos x + 1,5,
у = -cos2x + 2∙0,5∙cos x — 0,25 + 2,75,
у = -(cos x— 0,5)2 + 2,75.
Е(cos x) = [-1;1],
Е(cos x – 0,5) = [-1,5;0,5],
Е(cos x – 0,5)2 = [0;2,25],
Е(-(cos x-0,5)2 ) = [-2,25;0],
Е(у) = [0,5;2,75].
Наибольшее значение функции унаиб = 2,75; наименьшее значение унаим = 0,5. Найдём произведение наибольшего и наименьшего значения функции:
унаиб ∙ унаим = 0,5∙2,75 = 1,375.
Ответ: 1,375.
-
Найдите сумму всех целых значений функции у = .
Решение.
Перепишем функцию в виде у =,
у = ,
у = ,
Найдем теперь множество значений функции.
E(sin x) = [-1, 1],
E(6sin x) = [-6, 6],
E(6sin x + 1) = [-5, 7],
E((6sin x + 1)2) = [0, 49],
E(– (6sin x + 1)2) = [-49, 0],
E(– (6sin x + 1)2 + 64) = [15, 64],
E(y) = [, 8].
Найдем сумму целых значений функции: 4 + 5 + 6 + 7 + 8 = 30.
Ответ: 30.
-
Найдите множество значений функции если
Решение.
1) то есть х принадлежит I четверти.
2)
Следовательно, 2х принадлежат II четверти.
3) Во II четверти функция синус убывает и непрерывна. Значит, данная функция принимает все значения от до
4) Вычислим эти значения:
Ответ: .
-
Найдите множество значений функции
Решение.
1) Так как а синус принимает значения от -1 до 1, то множество значений разности . При умножении на этот отрезок перейдет в отрезок .
2) Арккосинус – монотонно убывающая и непрерывная функция. Значит, множество значений выражения — это отрезок .
3) При умножении этого отрезка на получим .
Ответ: .
-
Найдите множество значений функции , если .
Решение.
Так как арктангенс является возрастающей функцией, то .
2) При возрастании х от до аргумент 2х возрастает от до . Так как синус на таком промежутке возрастает, то функция принимает значения от до 1.
3) При возрастании от до аргумент 2х возрастает от до . Так как синус на таком промежутке убывает, то функция принимает значения от до 1.
4) Используя формулу, выражающую синус через тангенс половинного угла, находим, что
.
Значит, искомое множество значений – это объединение отрезков и , то есть отрезок .
Ответ: .
Данный прием (Введение вспомогательного угла) применяется для нахождения множества значений функций вида
у = a sin x + b cos x или у = a sin (рx) + b cos (р x).
-
Найдите множество значений функции
у = 15 sin 2x + 20 cos 2x.
Решение.
Найдем значение = = 25.
Преобразуем выражение
15 sin 2x + 20 cos 2x = 25 () = 25 () =
25 sin (2x +), где cos= , sin=.
Множество значений функций у = sin (2x +): -1 sin (2x +) 1.
Тогда множество значений исходной функции -25 25 sin (2x +) 25.
Ответ: [-25; 25].
3. Задания на нахождение наибольшего и наименьшего значения функции на промежутке.
-
Найдите наибольшее и наименьшее значение функции у = сtg х на отрезке [π/4; π/2].
Решение.
Функция у = сtg х является убывающей на отрезке [π/4; π/2], следовательно, наименьшее значение функция будет принимать при х = π/2, то есть у(π/2) = сtg π/2 = 0; а наибольшее значение – при х= π/4, то есть у(π/4) = сtg π/4 = 1.
Ответ: 1, 0.
-
Найти все значения параметра а, при каждом из которых функция на промежутке [-1; 1] принимает все значения из отрезка
[0; 1].
Решение.
Выделим в равенстве целую часть: .
Отсюда следует, что графиком функции f(x) является либо гипербола (а≠ 0), либо прямая без точки.
При этом если а ; 2а) и (2а; ) и, если а > 0, монотонно возрастает на этих лучах.
Если а = 0, то f(x) = -2 на всей области определения х ≠ 0. Поэтому очевидно, что искомые значения параметра не равняются нулю.
Поскольку нас интересуют значения функции только на отрезке [-1; 1], то классификация ситуаций определяется тем, что асимптота х = 2а гиперболы (а≠0) располагается относительно этого отрезка.
Случай 1. Все точки промежутка [-1; 1] находятся справа от вертикальной асимптоты х = 2а, то есть когда 2а
Случай 2. Вертикальная асимптота пересекает промежуток [-1; 1], и функция убывает (как и в случае 1), то есть когда
Случай 3. Вертикальная асимптота пересекает промежуток [-1; 1] и функция возрастает, то есть -1
.
Случай 4. Все точки промежутка [-1; 1] находятся слева от вертикальной асимптоты, то есть 1 а > .
Далее на каждом этапе находим множество значений функции на отрезке [-1;1] в точках, где она определена. Это делается на основе свойства монотонности.
Ответ: -2≤ а
-
Найти все а, при которых множество значений функции не пересекается с промежутком [3 ;∞).
Решение.
Имеем
Очевидно
Отсюда 0
Следовательно, область значений функции f – промежуток (0; ]. Полученный промежуток не должен иметь общих точек с лучом [3 ;∞). Понятно, что для этого достаточно потребовать
Отсюда а2 — За — 1 > — 1, то есть а 3.
Ответ: а 3.
-
Решите уравнение
Решение: Выделим в правой части уравнения полный квадрат:
Так как , , то равенство достигается, если
Решая второе уравнение системы, получаем Подстановкой убеждаемся, что является и решением первого уравнения системы. Следовательно, -решение системы.
Ответ:4.
-
Решите уравнение
Решение. Поскольку , произведение может равняться единице лишь при выполнении одной из двух систем уравнений:
Решая первую систему, найдем из первого уравнения и . Очевидно, решения первого уравнения входят в решение второго при то есть являются решениями системы. Решая вторую систему, убедимся, что она несовместна: решения первого уравнения и второго не имеют общих корней.
Ответ:
4. Задания на нахождение наибольшего и наименьшего значения функции через обратную функцию.
-
Какого значения функция не достигает ни при каком х
Решение Выразим функцию обратную данной от переменной y и найдем ее область определения, которая и будет областью значений заданной функции.
2ху-5у=3х+6
2ху-3х=6+5у
х=, где у. Итак D(x)=(-; )(;+).
Е(у)
Ответ: 1,5
-
Найти наибольшее целое значение функции у =
х2-5=ух2+2у
х2(1-у)=5+2у
х2 =, где у1, х20
Ответ: 0
5. Задания на последовательное нахождение значения функции (пошаговое )
-
Найти область значения функции f(x)=
Решение: Пусть f(x)=, где g(x)=
g(x)=sinx-cosx+2=sin(x-)+2.
Тогда 1 g(x) 3/
Функция y= убывающая, а значит
-20
-16у0. Итак, Е(у)= -16;0
Ответ: -16;0.
Итак, существует несколько приемов нахождения множеств значений функций, заданных аналитически.
Прием 1. Нахождение множества значений функции по её графику.
Прием 2. Нахождение множества значений функции с помощью производной. (см занятие 12)
Прием 3. Последовательное нахождение множества значений функций, входящих в данную композицию функций (прием пошагового нахождения множества значений функции).
Прием 4. Выражение х через у. (Поиск области определения обратной функции)
Прием 5. Упрощение формулы, задающей дробно-рациональную функцию
Прием 6. Нахождение множества значений квадратичных функций (с помощью нахождения вершины параболы и установления характера поведения её ветвей).
Прием 7. Введение вспомогательного угла для нахождения множества значений некоторых тригонометрических функций.
takya.ru

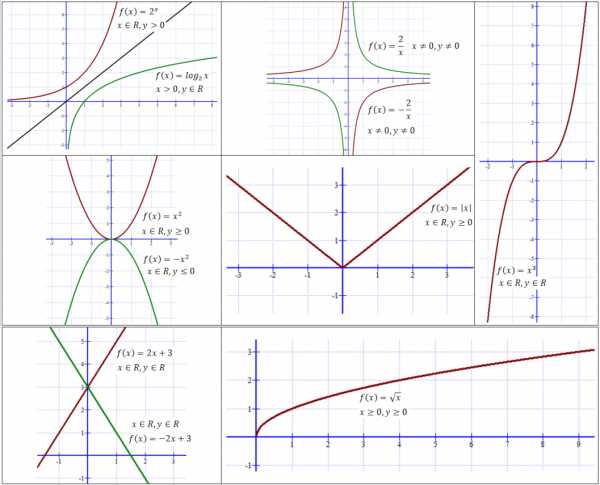


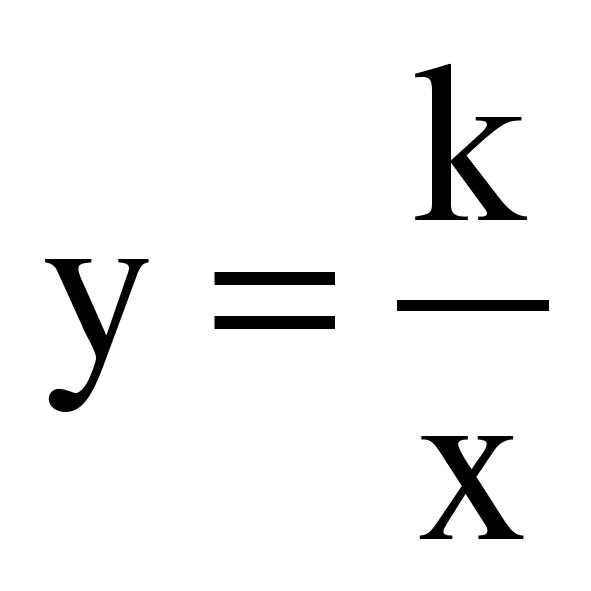 — эта формула описывает степенную функцию. График представляет собой две ветви гиперболы. В зависимости от k, ветви располагаются в 1,3 или 2,4 координатных углах.
— эта формула описывает степенную функцию. График представляет собой две ветви гиперболы. В зависимости от k, ветви располагаются в 1,3 или 2,4 координатных углах.