Модуль в алгебре – CGI script error

МОДУЛЬ (в математике) — это… Что такое МОДУЛЬ (в математике)?



МОДУЛЬ (в математике)

МОДУЛЬ (в математике) МО́ДУЛЬ комплексного числа, см. Абсолютная величина (см. АБСОЛЮТНАЯ ВЕЛИЧИНА). Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/log_ab.

Энциклопедический словарь. 2009.

• МОДУЛЬ (в архитектуре)
• МОДУЛЬ (в радиоэлектронике)

Смотреть что такое «МОДУЛЬ (в математике)» в других словарях:

• Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… …   Большая советская энциклопедия

• МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… …   Словарь иностранных слов русского языка

• Модуль (значения) — Модуль (от лат. modulus  «маленькая мера»)  составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… …   Википедия

• Модуль без кручения — Модуль без кручения  модуль над кольцом без делителей нуля такой, что из равенства , где и , следует или . Примерами таких модулей (левых) являются само кольцо …   Википедия

• Модуль — I Модуль (от лат. modulus мера)         в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строительной техники и композиции зданий за М.… …   Большая советская энциклопедия

• Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… …   Википедия

• Модуль автоморфизма — Связать? Модуль автоморфизма  вещественное положительное число, ставящееся в соответствие автоморфизму, локально компактной группы. Если   такая группа и …   Википедия

• Модуль — I м. 1. Название некоторых коэффициентов, мерил каких либо величин (в точных науках). 2. Число, на которое нужно умножить логарифм одной системы при данном основании, чтобы получить логарифм другой системы при другом основании (в математике). II… …   Современный толковый словарь русского языка Ефремовой

• Модуль — I м. 1. Название некоторых коэффициентов, мерил каких либо величин (в точных науках). 2. Число, на которое нужно умножить логарифм одной системы при данном основании, чтобы получить логарифм другой системы при другом основании (в математике). II… …   Современный толковый словарь русского языка Ефремовой

• Ряд в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Книги

• ОГЭ 2019 по математике от А до Я Модульный курс Геометрия, Ященко И., Шестаков С., Настоящее пособие является второй частью модульного курса «ОГЭ по математике от А до Я» и предназначено для подготовки к Основному государственному экзамену (ОГЭ)по математике, модуль… Производитель: МЦНМО, Подробнее  Купить за 154 руб
• ОГЭ 2018. По математике от А до Я. Модульный курс. Алгебра. ФГОС, Ященко И.В., Настоящее пособие является первой частью модульного курса «ОГЭ по математике от А до Я» и предназначено для подготовки к Основному государственному экзамену (ОГЭ)по математике, модуль… Серия: — Издатель: Московский центр непрерывного математического образования (МЦНМО), Подробнее  Купить за 113 руб
• ОГЭ 2018. По математике от А до Я. Модульный курс. Геометрия. ФГОС, Ященко И.В., Настоящее пособие является третьей частью модульного курса 171;ОГЭ по математике от А до Я 187;и предназначено для подготовки к Основному государственному экзамену (ОГЭ) по математике,… Серия: — Издатель: Московский центр непрерывного математического образования (МЦНМО), Подробнее  Купить за 102 руб

Другие книги по запросу «МОДУЛЬ (в математике)» >>

dic.academic.ru

Что такое модуль числа в математике, модули алгебра 7 класс

Модуль числа (абсолютная величина числа), определения, примеры, свойства.

В этой статье мы детально разберем модуль числа. Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.

Модуль числа – определение, обозначение и примеры

Сначала введем обозначение модуля числа. Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль целого числа−7 можно записать как ; модуль рационального числа4,125 записывается как , а модуль иррационального числа имеет запись вида .

Так мы определились с обозначением, теперь пришло время дать

определение модуля числа. Чтобы хорошо понять определение модуля числа необходимо хорошо владеть материалом статьи положительные и отрицательные числа, а также статьи противоположные числа.

Следующее определение модуля относится к действительным числам, а следовательно, и к натуральным числам, и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в последнем пункте этой статьи.

Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0, , если a=0, и , если a<0.

Запись можно представить в более компактной форме . Эта запись означает, что , если (a больше или равно 0), и , если a<0.

Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0. В этом случае имеем , но −0=0, так как нуль считают числом, которое противоположно самому себе.

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как — отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .

В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака, а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа. Так модуль числа и абсолютная величина числа – это одно и то же.

К началу страницы

Модуль числа как расстояние

Геометрически модуль числа можно интерпретировать как

расстояние. Приведем определение модуля числа через расстояние.

Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.

Например, модуль числа 9 равен 9, так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25, поэтому .

Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.

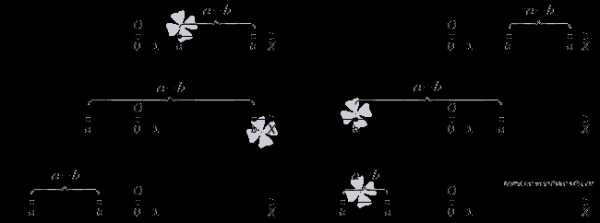
То есть, если даны точки на координатной прямой A(a) и B(b), то расстояние от точки A до точки B равно модулю разности чисел a и b. Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.

К началу страницы

Определение модуля числа через арифметический квадратный корень

Иногда встречается определение модуля через арифметический квадратный корень.

Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .

Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0, то .

К началу страницы

Свойства модуля

Модулю присущ ряд характерных результатов — свойства модуля. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

• Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом. В буквенном виде это свойство имеет запись вида для любого числа a. Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

• Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O, не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

• Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a. Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

• Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел, то есть, . По определению модуль произведения чисел a и b равен либо a·b, если , либо −(a·b), если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b, , либо −(a·b) , если , что доказывает рассматриваемое свойство.

• Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b, то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

• Следующее свойство модуля записывается в виде неравенства: , a, b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника. Чтобы это стало понятно, возьмем точки A(a), B(b), C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС, у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ, — длине отрезка АС, а — длине отрезка СВ. Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

• Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b, и принять c=0.

К началу страницы

Модуль комплексного числа

Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z, а – мнимая единица.

Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .

Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .

Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.

По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.

Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z, если оно записано в тригонометрической форме как или в показательной форме . Здесь . Например, модуль комплексного числа равен 5, а модуль комплексного числа равен .

Можно также заметить, что произведение комплексного числа на комплексно сопряженное число дает сумму квадратов действительной и мнимой части. Действительно, . Полученное равенство позволяет дать еще одно определение модуля комплексного числа.

В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.

Профиль автора статьи в Google+

К началу страницы

Модуль числа a – это либо само число a, если a – положительное число, либо число −a, противоположное числу a, если a – отрицательное число, либо 0, если a=0.

Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.

Модуль разности двух чиселa и b равен расстоянию между точками координатной прямой с координатами a и b.

Модулем комплексного числаz=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.

Модуль комплексного числаz – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.

Модуль комплексного числаz – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного: учебник для вузов.
• Привалов И.И. Введение в теорию функций комплексного переменного.

laservirta.ru

модуль над алгеброй — это… Что такое модуль над алгеброй?



модуль над алгеброй

мат. algebra module

Большой англо-русский и русско-английский словарь. 2001.

• модуль на пространстве
• модуль над кольцом

Смотреть что такое «модуль над алгеброй» в других словарях:

• МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… …   Математическая энциклопедия

• Алгебра над кольцом — У этого термина существуют и другие значения, см. Алгебра (значения). Пусть произвольное коммутативное кольцо с единицей. Модуль над кольцом , в котором для заданного билинейного отображения определено произведение согласно равенству …   Википедия

• НЕПРИВОДИМЫЙ МОДУЛЬ — простой модуль, ненулевой унитарный модуль Мнад кольцом Д с единицей, содержащий лишь два подмодуля нулевой и сам М. Примеры: 1) если кольцо целых чисел, то неприводимые R модули это абелевы группы простого порядка; 2) если R тело, то… …   Математическая энциклопедия

• БАНАХОВ МОДУЛЬ — (левый) над банаховой алгеброй А банахово пространство X вместе с непрерывным билинейным оператором т: , задающим на структуру левого модуля над Ав алгеб раич. смысле. Аналогично определяется правый Б. м. и банахов бимодуль над А. Морфизмом двух… …   Математическая энциклопедия

• ВЕКТОРНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ — локально тривиальное аналитич. расслоение над аналитич. ространством, слои к рого обладают структурой n мерного векторного пространства над основным полем k(если иоле комплексных чисел, то аналитич. расслоение наз. также голоморфны м). Число пназ …   Математическая энциклопедия

• ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА — 1) Д. ф. степени р, р форма на дифференцируемом многообразии М р раз ковариантное тензорное поле на М. Ее можно интерпретировать также как р линейное (над алгеброй F(M)гладких вещественных функций на М)отображение F(M), где есть Р(М) модуль… …   Математическая энциклопедия

• Алгебра Ли — Алгебра Ли  объект абстрактной алгебры. Естественно появляется при изучении инфинитезимальных свойств групп Ли. Названа по имени норвежского математика Софуса Ли (1842 1899). Содержание 1 Определение 1.1 Замечания …   Википедия

• ПОЛИЛИНЕЙНАЯ ФОРМА — n линейная форма, на унитарном A модуле Е полилинейное отображение (здесь А ассоциативно коммутативное кольцо с единицей). П. ф. наз. также полилинейной функцией ( п л инейной функцией). Поскольку П. ф. частный случай полилинейных отображений,… …   Математическая энциклопедия

• УНИВЕРСАЛЬНАЯ ОБЕРТЫВАЮЩАЯ АЛГЕБРА — алгебры Ли над коммутативным кольцом kс единицей ассоциативная k алгебра с единицей, снабженная отображением для к рой выполнены следующие свойства: 1) о является гомоморфизмом алгебр Ли, т. е. Ус линейно и 2) для любой ассоциативной k алгебры Ас …   Математическая энциклопедия

• ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — обобщение оператора дифференцирования. Д. о. (вообще говоря, не непрерывный, не ограниченный и не линейный) оператор, определенный нек рым дифференциальным выражением и действующий в пространствах (вообще говоря, векторнозначных) функций (или… …   Математическая энциклопедия

• МНОГОЧЛЕНОВ КОЛЬЦО — кольцо, элементами к рого являются многочлены с коэффициентами из нек рого фиксированного поля к. Рассматриваются также М. к. над произвольным ассоциативно коммутативным кольцом R, напр, над кольцом целых чисел. М. к. от конечного множества… …   Математическая энциклопедия

dic.academic.ru