РЯДЫ — Стр 2
Пример 7
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Это пример для самостоятельного решения.
Кто утомился, может сходить покурить, а мы рассмотрим еще два примера.
Пример 8
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала
Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера: 
Предел по той причине, что числитель и знаменательодного порядка роста. Более подробно об этом моменте и «турбо»-методе решения читайте в статьеПризнак Даламбера. Признаки Коши.
Итак, ряд сходится при
Умножаем обе части неравенства на 9: Извлекаем из обеих частей корень, при этом помним старый школьный прикол:Раскрываем модуль:И прибавляем ко всем частям единицу:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если , то получается следующий числовой ряд:
Множитель бесследно пропал, поскольку при любом натуральном значении «эн».
И в третий раз обращаю внимание на то, что в результате подстановки сократились степени , а значит, интервал сходимости найден правильно.
По всем признакам для полученного числового ряда следует применить предельный признак сравнения. Какой ряд подобрать для сравнения? Об этой методике я уже рассказывал на уроке Ряды для чайников. Повторим.
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого: . Таким образом, старшая степень знаменателя равна. Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:.
Таким образом, наш ряд нужно сравнить со сходящимся рядом . Используем предельный признак сравнения:
Получено конечное, отличное от нуля число, значит, ряд сходится вместе с рядом.
2) Что происходит на другом конце интервала? При – сходится.
А вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область сходимости исследуемого степенного ряда:
Чуть менее сложный пример для самостоятельного решения:
Пример 9
Найти область сходимости ряда
Достаточно для начала =)
В заключение остановлюсь на одном моменте. Во всех примерах мы использовали признак Даламбера и составляли предел . Всегда ли при решении заданий такого типа нужно применять признак Даламбера? Почти всегда. Однако в редких случаях невероятно выгодно использовать радикальный признак Коши и составлять предел, при этом техника и алгоритм решения задачи остаются точно такими же! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени.
Следующий урок по теме – Разложение функций в степенные ряды. Примеры решений.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера: Ряд сходится при Слева нужно оставить только модуль, поэтому умножаем обе части неравенства на 7 – интервал сходимости исследуемого степенного ряда. Исследуем сходимость ряда на концах найденного интервала. 1) При Используем признак Лейбница. – Ряд является знакочередующимся. – члены ряда не убывают по модулю. Вывод: Ряд расходится 2) При Ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Ответ: – область сходимости исследуемого степенного рядаПример 5: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера: Ответ: Ряд сходится при
Почему получилась двойка, а не ноль? Перечитайте классификацию области сходимости степенного ряда. Хотя, наверное, многие уже понимают, почему.
Пример 7: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера: Ряд сходится при Слева нужно оставить только модуль, умножаем обе части неравенства на : В середине нужно оставить только «икс», вычитаем из каждой части неравенства 3: – интервал сходимости исследуемого степенного ряда. Исследуем сходимость ряда на концах найденного интервала: 1) При Степень сократилась, значит, мы на верном пути. Используем признак Лейбница. Ряд является знакочередующимся.
Пример 9: Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера: Ряд сходится при – интервал сходимости исследуемого степенного ряда. Исследуем сходимость ряда на концах найденного интервала.
1) При Сравним данный ряд с расходящимся гармоническим рядом . Используем предельный признак сравнения. Получено конечное число, отличное от нуля, значит, полученный числовой ряд расходится вместе с гармоническим рядом. 2) При – расходится (по доказанному). Ответ: область сходимости исследуемого степенного ряда:studfiles.net
Пример 1. Исследовать сходимость степенного ряда
Решение
Здесь 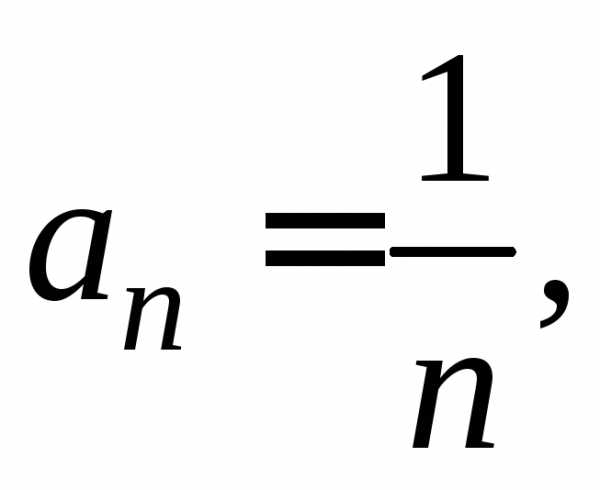

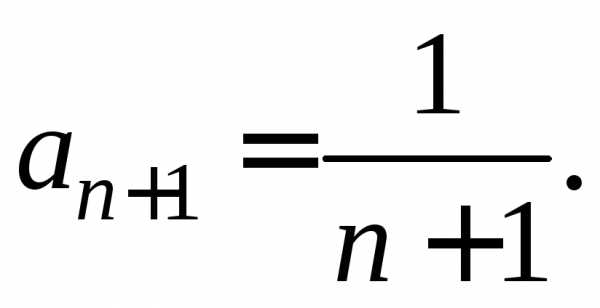
Следовательно, ряд сходится для значений х, удовлетворяющих неравенству х<1 или -1<х<1.
Исследуем сходимость ряда на концах промежутка. Подставляя в данный ряд вместо х число 1, получим гармонический ряд , который, как известно, расходится.
Если х=-1, получаем числовой знакочередующийся ряд Этот ряд сходится, так как удовлетворяет условиям признака Лейбница:
1) 
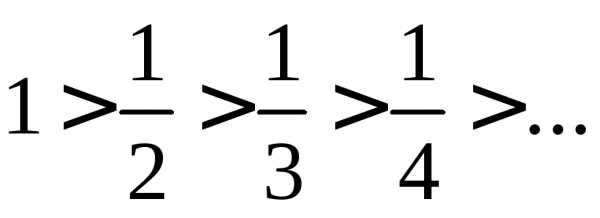 ;
2).
;
2).
Таким образом, данный ряд сходится при всех значениях х, удовлетворяющих неравенствам -1х<1, и его промежуток сходимости представляет собой полузамкнутый интервал [-1;1).
Геометрически это выглядит так:
Пример 2. Найти область сходимости ряда:
Решение.
Найдем радиус сходимости этого ряда по
формуле 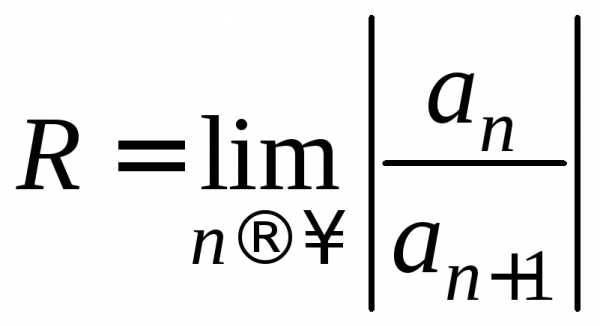 .
.
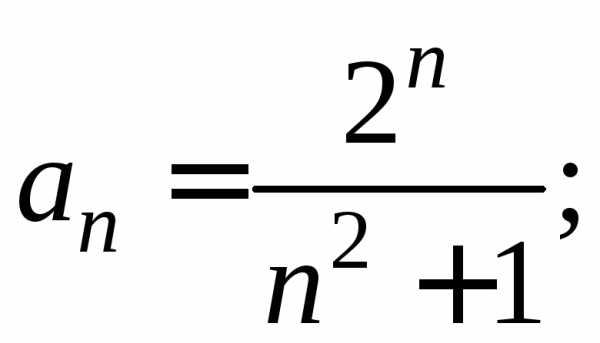
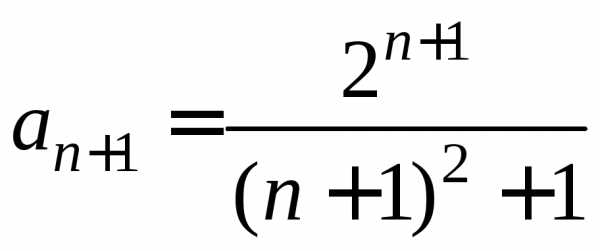 ;
;
Следовательно,
радиус сходимости 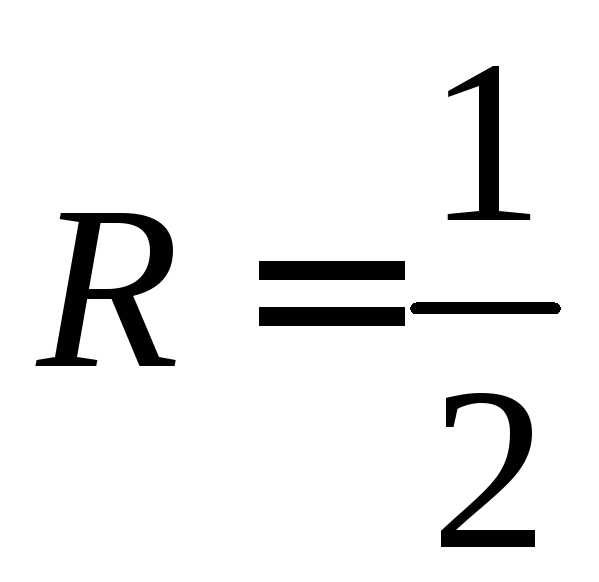 ,
а интервал сходимости (-
,
а интервал сходимости (-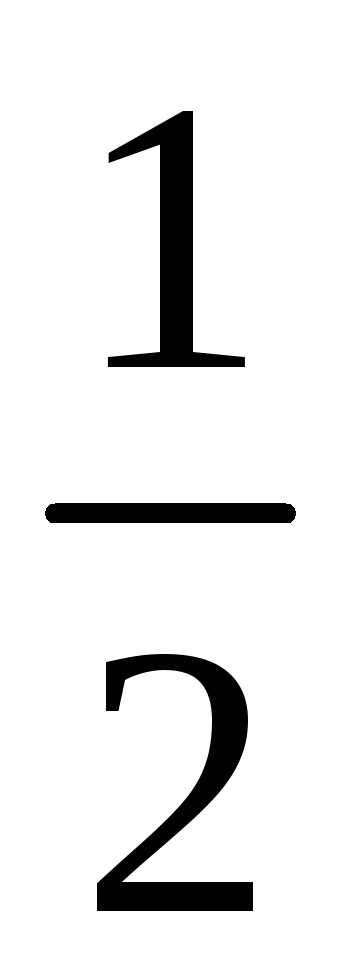 ;
;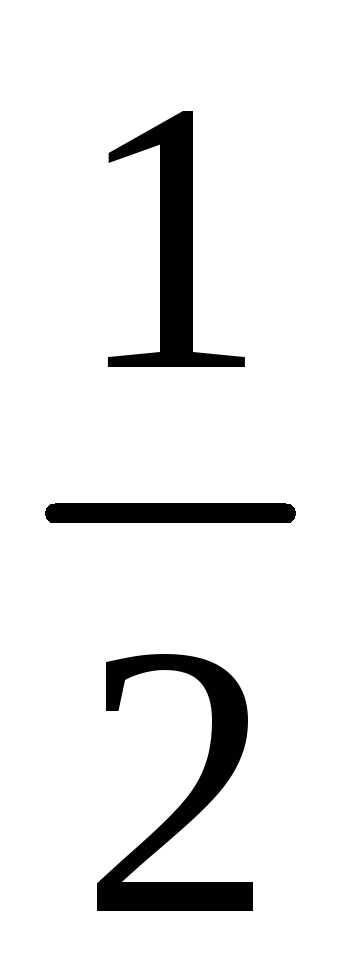 ).
Геометрически это выглядит так:
).
Геометрически это выглядит так:
Теперь выясним поведение ряда на концах интервала сходимости. В правом конце, при
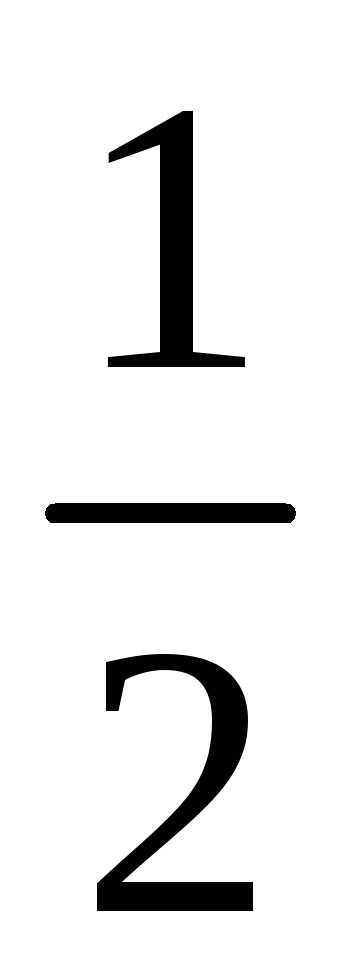 , данный степенной ряд превращается в
числовой ряд вида:
, данный степенной ряд превращается в
числовой ряд вида:Выше сходимость этого ряда была доказана при помощи интегрального признака.
В
левом конце, при х=— ,
данный степенной ряд превращается в
знакочередующийся рядкоторый сходится абсолютно, так как
сходится соответствующий ряд из
абсолютных величин:.
,
данный степенной ряд превращается в
знакочередующийся рядкоторый сходится абсолютно, так как
сходится соответствующий ряд из
абсолютных величин:.
Таким
образом, данный степенной ряд сходится
в обоих концах интервала сходимости,
значит, областью сходимости будет
отрезок 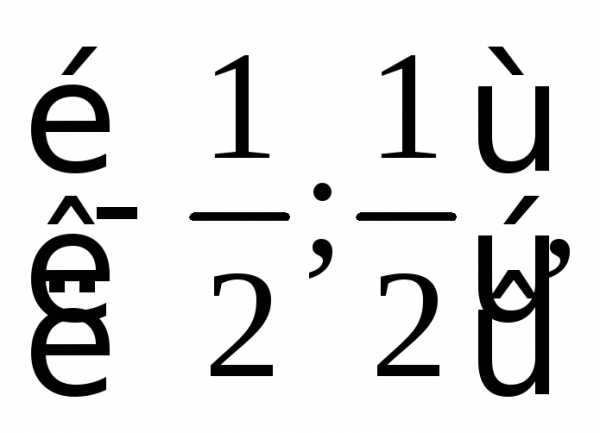 т.е.
т.е.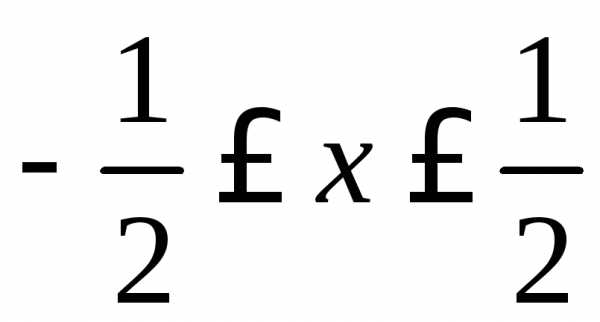
Графически:
Пример 3. Найти промежуток сходимости ряда:
Решение.
Радиус
сходимости ряда находим по формуле 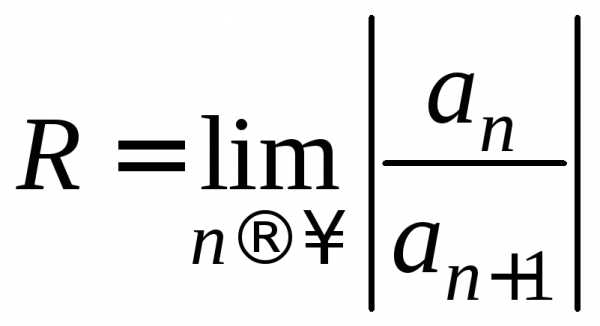 .
.
В
нашей задаче 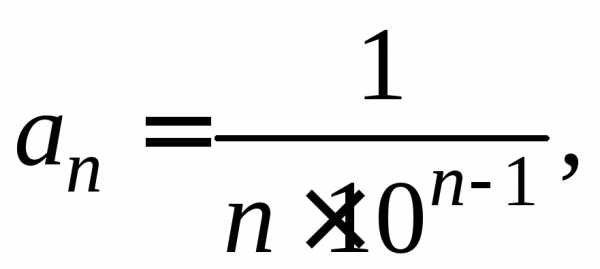
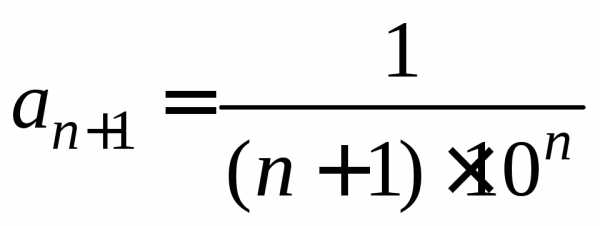
Поэтому .
Значит, данный ряд сходится при значениях х, удовлетворяющих неравенству х<10 или -10<х<10.
Исследуем теперь поведение ряда на концах промежутка. Подставляя в данный ряд вместо х число 10 получаем ряд:
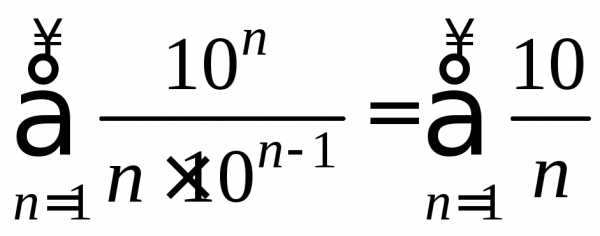
который расходится как гармонический (отличаясь от него лишь постоянным множителем)
При х=-10 получим числовой знакочередующийся ряд:
, который сходится условно.
Таким образом, данный степенной ряд сходится при всех значениях х, удовлетворяющих неравенствам -10х<10, и его промежуток сходимости представляет собой полузамкнутый интервал [-10;10).
Графически:
Пример 4. Найти радиус и интервал сходимости степенного ряда
Решение.
;
Радиус сходимости ряда равен нулю. Ряд сходится в единственной точке х=0
Замечание.
1.
При вычислении предела использовали
второй замечательный предел 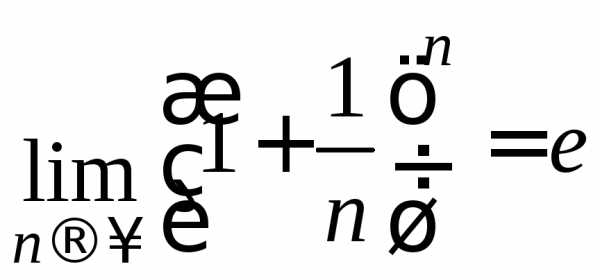 .
.
2.
Тот же результат можно получить и по
формуле 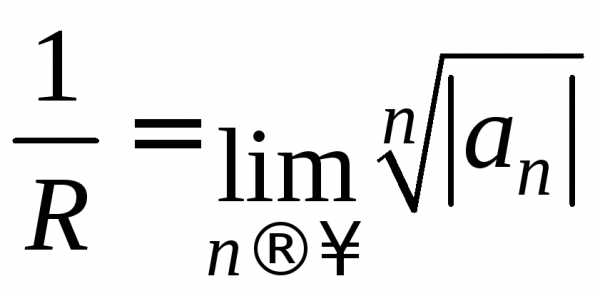 :
:
.
Пример 5. Найти радиус и интервал сходимости степенного ряда . Решение
Так как ,
то  .
Ряд сходится при всехх,
т.е. в интервале (-;
+).
.
Ряд сходится при всехх,
т.е. в интервале (-;
+).
Пример 6. Найти промежуток сходимости ряда
Решение.
Здесь
мы не вправе применять формулу 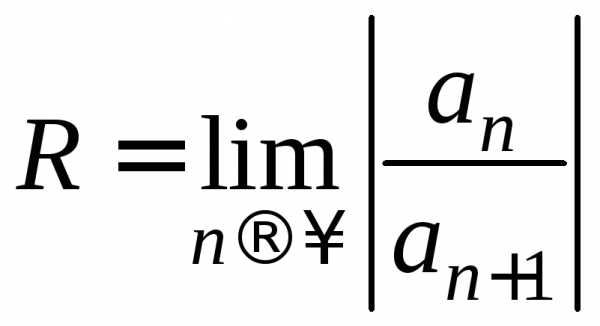 для отыскания радиуса сходимости ряда,
так как он не содержит четных степенейх.
Поэтому промежуток сходимости ряда
найдем, воспользовавшись признаком
Даламбера.
для отыскания радиуса сходимости ряда,
так как он не содержит четных степенейх.
Поэтому промежуток сходимости ряда
найдем, воспользовавшись признаком
Даламбера.
Данный ряд будет сходиться при всех значениях х, удовлетворяющих
неравенству
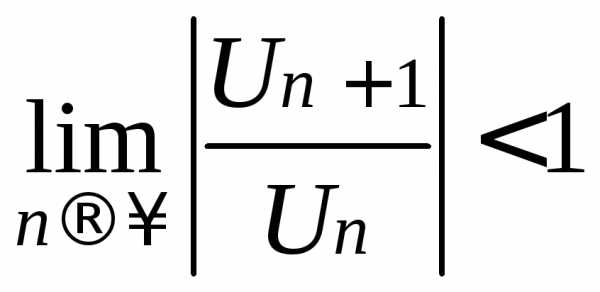 т.е.
т.е. 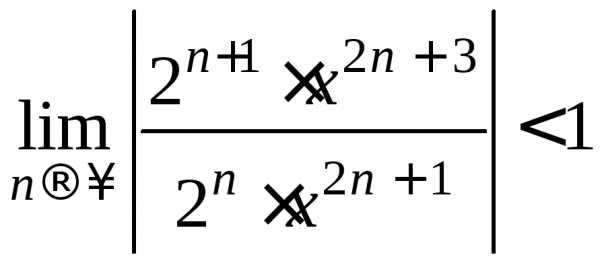 .
.
Отсюда
получаем 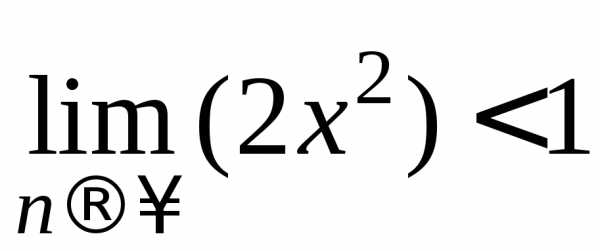 .
.
Выражение
в скобках не зависит от n,
поэтому 2х2<1,
или х2<1/2.
Окончательно получаем 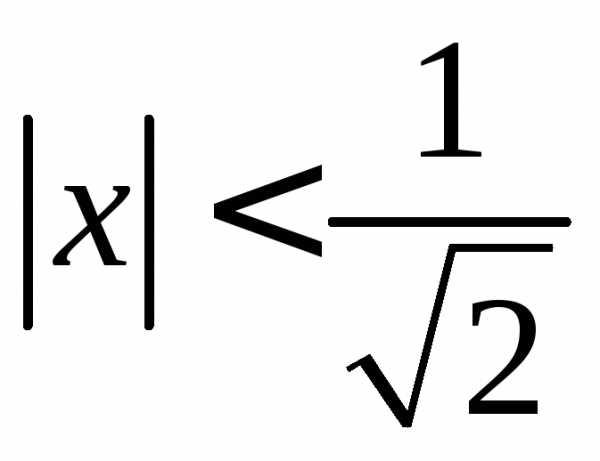 ,
т.е.
,
т.е.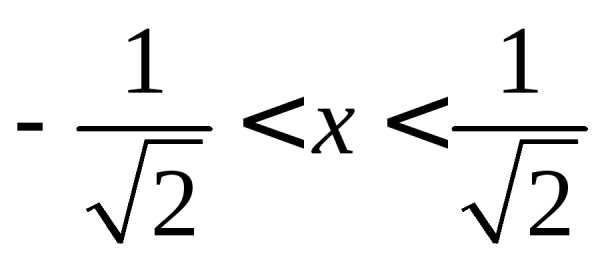 .
.
Исследуем поведение ряда на концах промежутка.
При 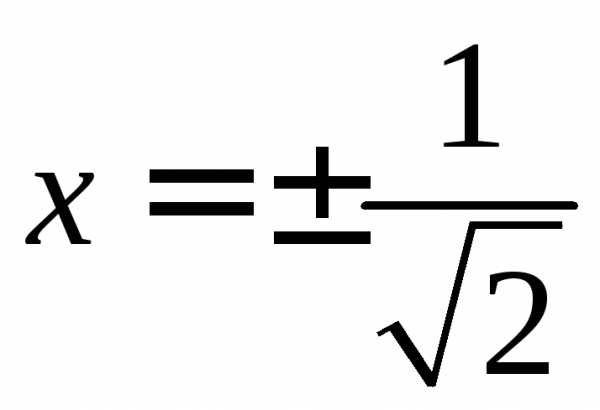 получим расходящийся числовой ряд
1+1+1+1+…+1+…
получим расходящийся числовой ряд
1+1+1+1+…+1+…
Таким образом, на концах интервала данный ряд расходится. Промежутком сходимости является интервал .
Замечание. Тот же результат можно было получить, воспользовавшись радикальным признаком Коши.
Пример 7 Найти область сходимости степенного ряда
.
Решение: Применим признак Даламбера.
В данном случае .
Ряд сходится при (х+3)2<1, т.е. х+3<1, -1<х+3<1, т.е. -4<х<-2.
Исследуем
сходимость ряда на концах промежутка
(-4; -2). При х=-4
получаем ряд
— гармонический ряд, который расходится.
Прих=-2
также получаем расходящийся гармонический
ряд 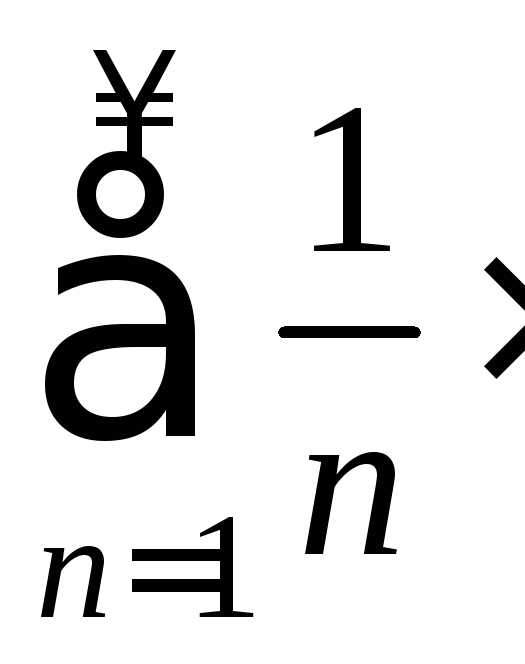
Следовательно, областью сходимости данного ряда является интервал
(-4; -2).
Замечание. В некоторых случаях функциональный ряд можно при помощи замены переменой привести к виду степенного ряда, для нахождения области сходимости которого можно воспользоваться формулами радиуса сходимости.
studfiles.net
Степенные ряды
Частным случаем функциональных рядов являются степенные ряды.
Определение
Степенным рядом называется функциональный ряд
, (15)
члены
которого являются произведениями
постоянных 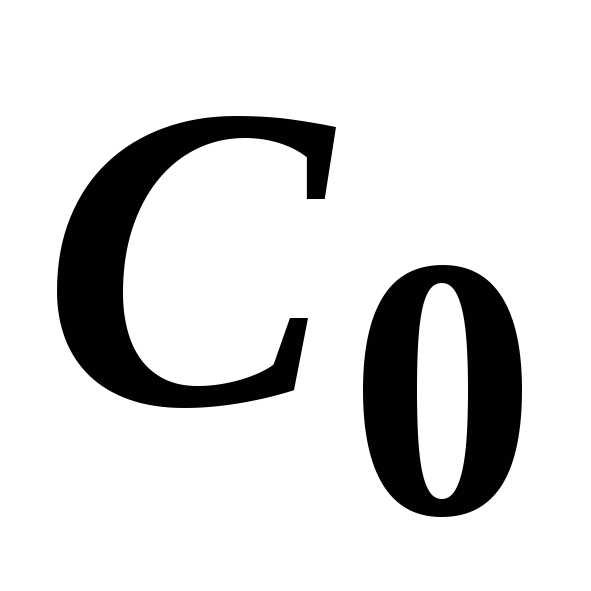 ,
, ,
…,
,
…,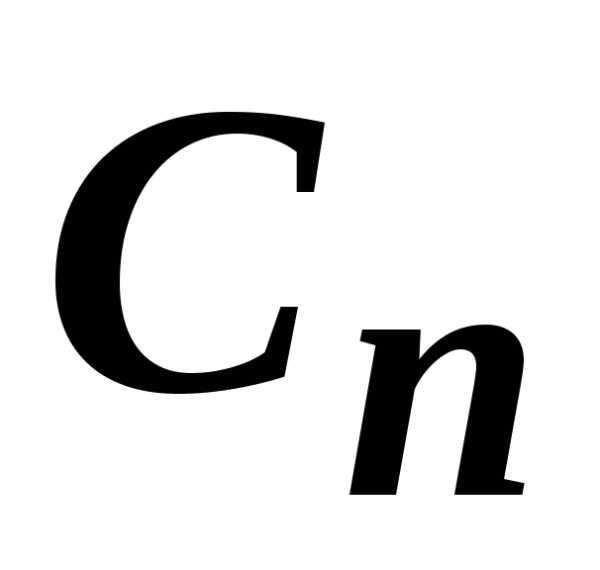 ,…
на степенные функции от разности
,…
на степенные функции от разности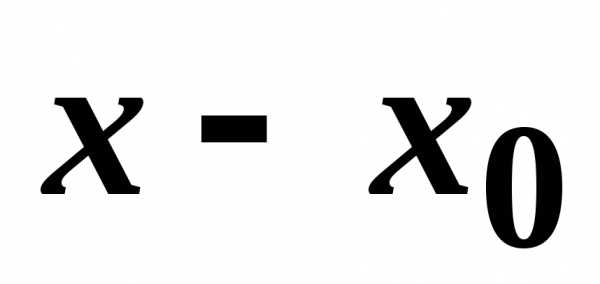 с целыми неотрицательными показателями
степеней.
с целыми неотрицательными показателями
степеней.
Точка x0 называется центром степенного ряда.
Пример 20
Ряд
– степенной ряд с центром в точке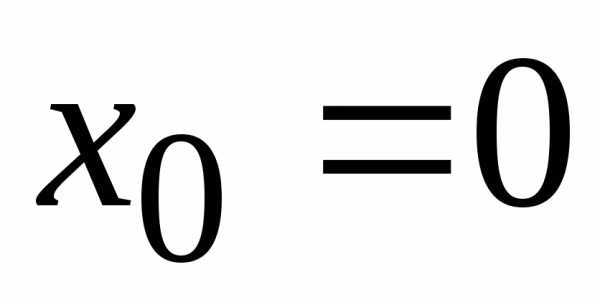 .
.
Ряд
– степенной ряд с центром в точке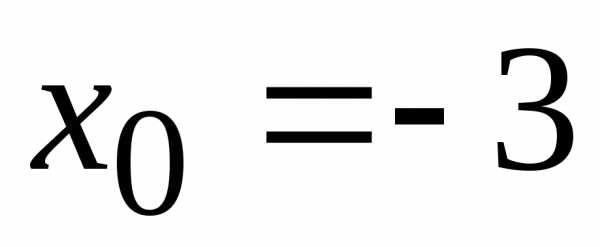 .
.
Ряд – функциональный ряд.
Исследование степенного ряда на сходимость, а именно нахождение области сходимости степенного ряда, является важной задачей теории рядов. Ее решение основано на теореме Абеля.
ТЕОРЕМА 11 (Теорема Абеля)
Если степенной ряд сходится при
 ,
то он сходится, и притом абсолютно, для
всех
,
то он сходится, и притом абсолютно, для
всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
.
Если степенной ряд расходится при
 ,
то он расходится для всех
,
то он расходится для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
.
Доказательство
1)
Введем замену
.
Тогда получаем степенной ряд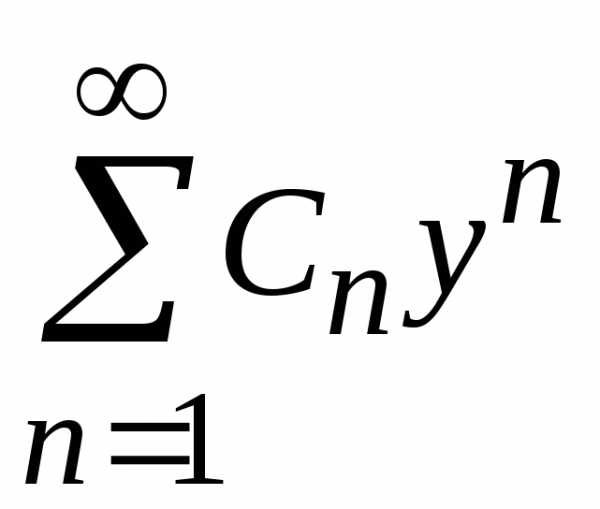 ,
точка сходимости которого,
а неравенство, описывающее область
сходимости, примет вид
,
точка сходимости которого,
а неравенство, описывающее область
сходимости, примет вид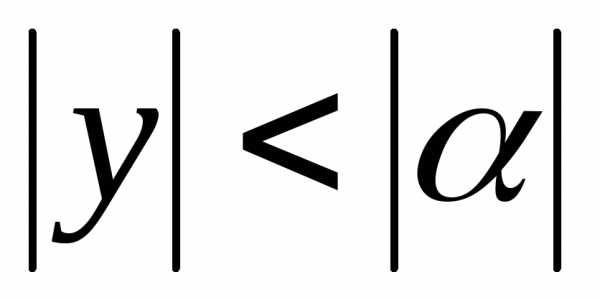 .
.
По
условию числовой
ряд 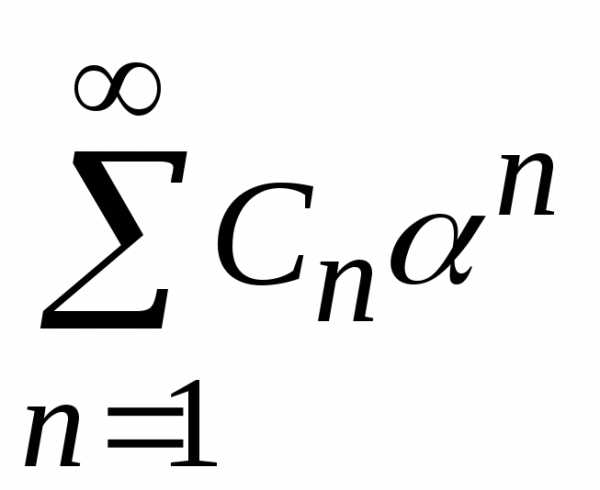 сходится,
следовательно общий член
сходится,
следовательно общий член 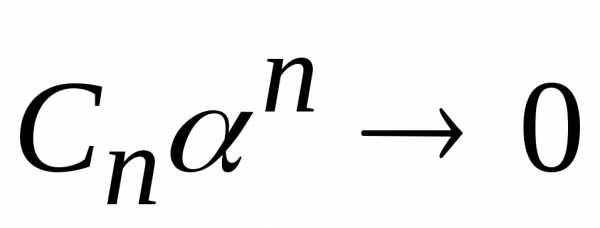 при,
но любая последовательность, имеющая
предел ограничена, т.е. существует такое
при,
но любая последовательность, имеющая
предел ограничена, т.е. существует такое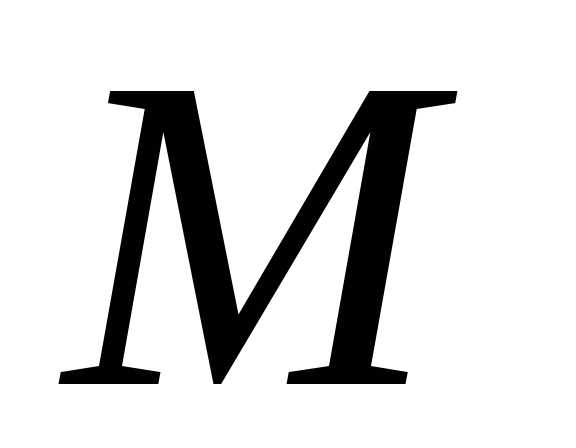 ,
что
,
что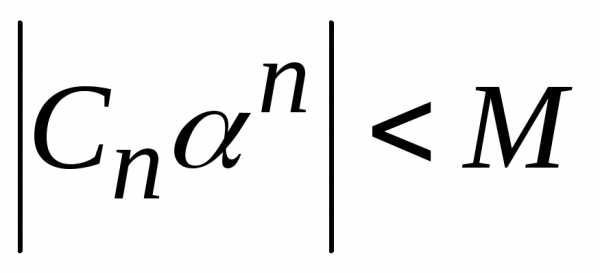 для всех
для всех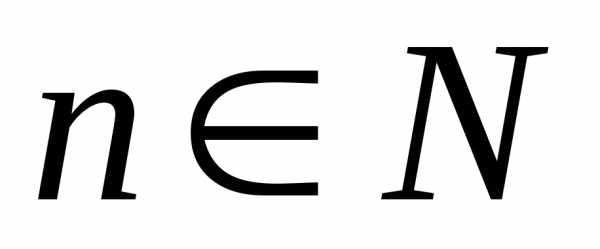 .
.
Рассмотрим
общий член степенного ряда 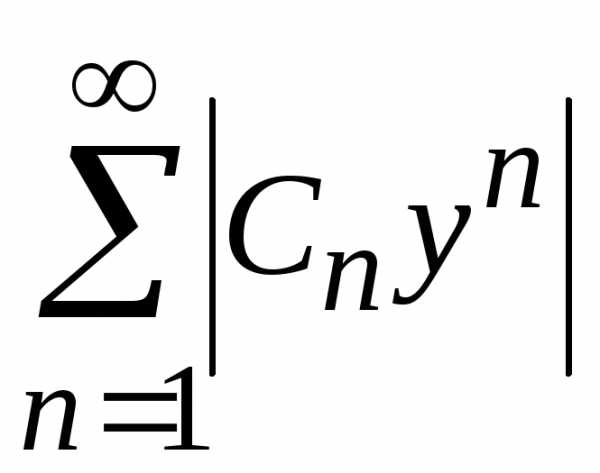 .
.
,
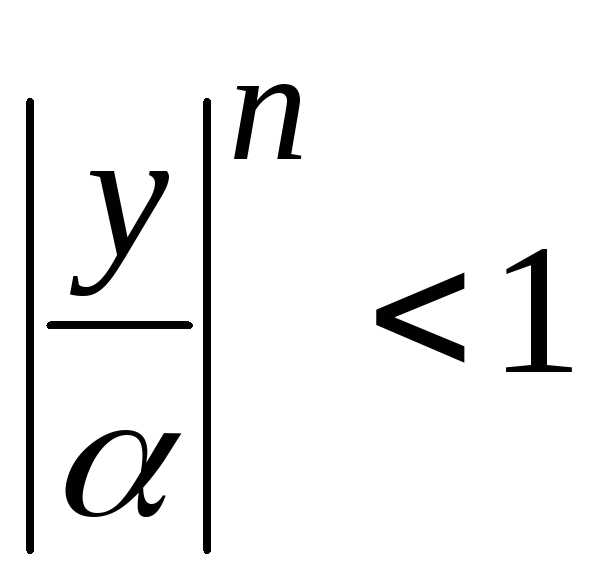 ,
так как
,
так как 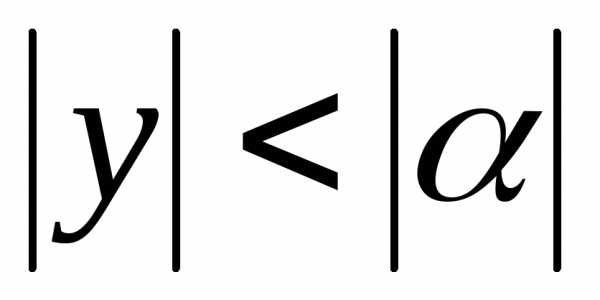 .
.
Получили
новый ряд 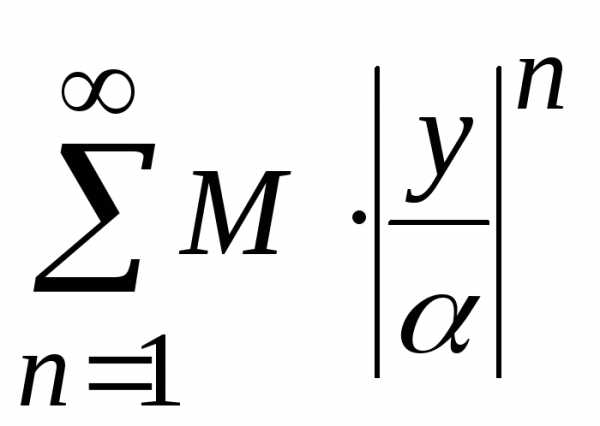 ,
который является геометрической
прогрессией со знаменателем
,
который является геометрической
прогрессией со знаменателем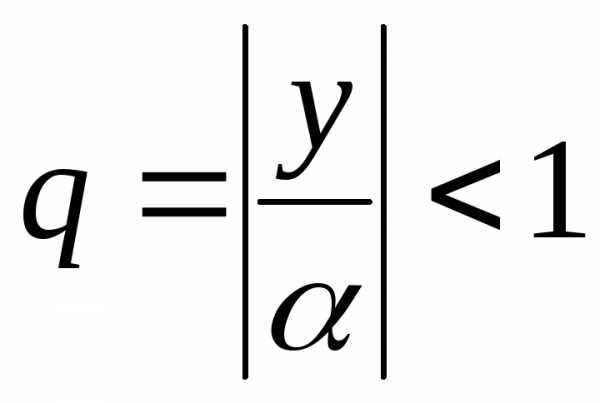 ,
следовательно, он сходится. Так как
,
следовательно, он сходится. Так как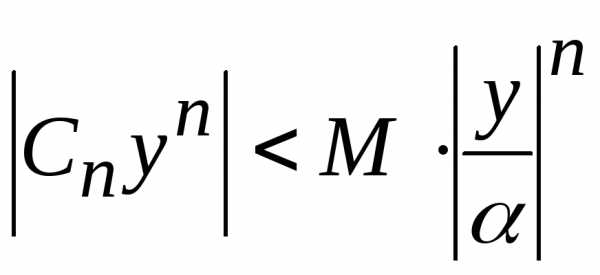 ,
то из первого признака сравнения следует
абсолютная сходимость исходного
степенного ряда.
,
то из первого признака сравнения следует
абсолютная сходимость исходного
степенного ряда.
2) Вторую часть теоремы можно доказать аналогично.
Геометрическая интерпретация этой теоремы
Если
ряд (1) сходится в точке 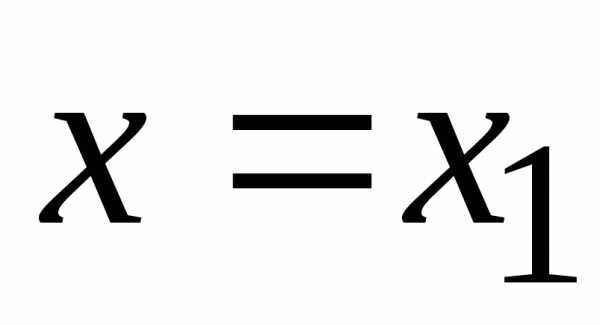 ,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда
,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда 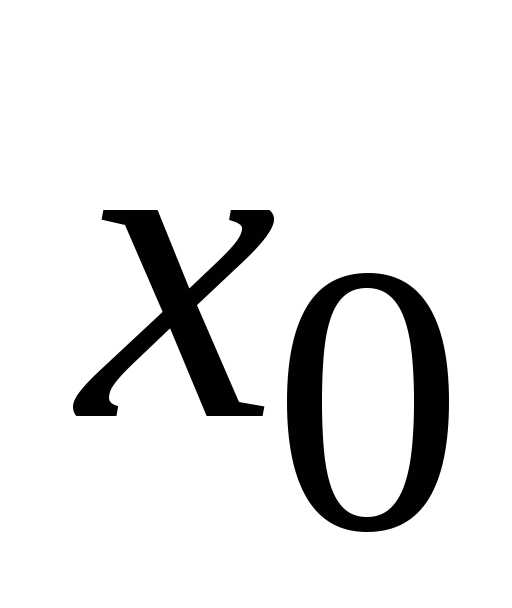 ,
чем
,
чем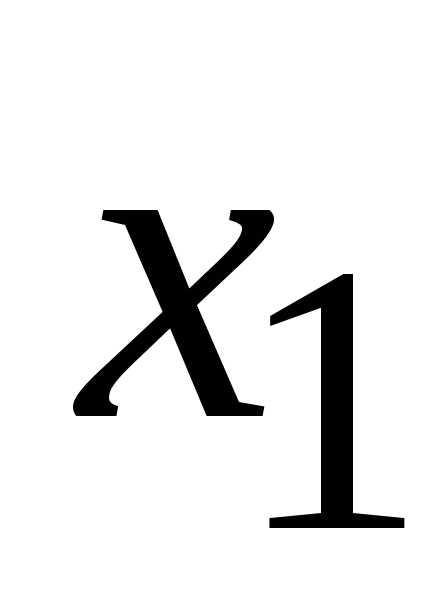 .
Если же ряд расходится при
.
Если же ряд расходится при 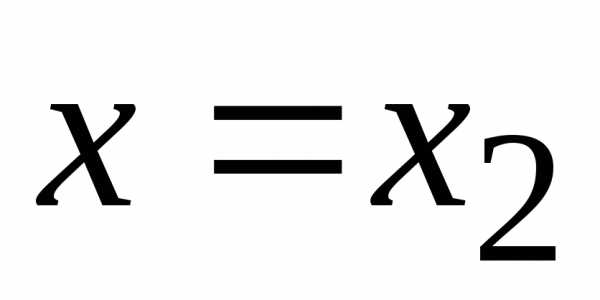 ,
то он расходится и во всех более удаленных
от центра ряда точках.
,
то он расходится и во всех более удаленных
от центра ряда точках.
Опираясь
на теорему Абеля, можно доказать, что
существует такое положительное число  ,
что для всех
,
что для всех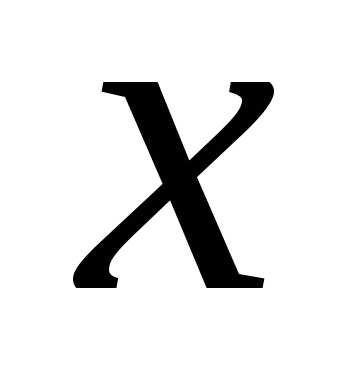 ,
удовлетворяющих неравенству ,
ряд сходится абсолютно и расходится
при всех
,
удовлетворяющих неравенству ,
ряд сходится абсолютно и расходится
при всех 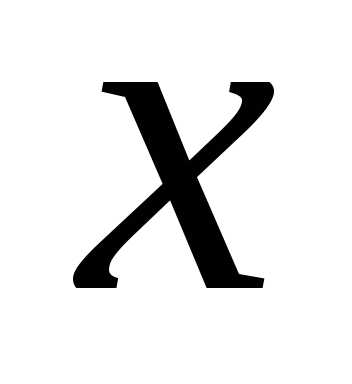 ,
для которых .
,
для которых .
Число  называетсярадиусом
сходимости ряда
называетсярадиусом
сходимости ряда 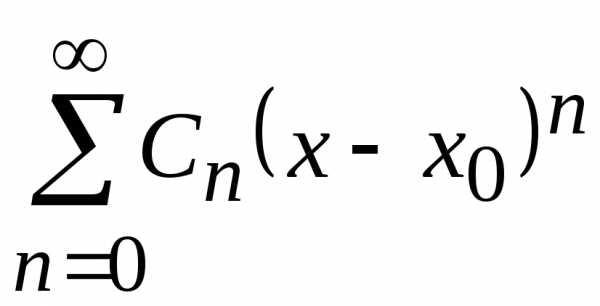 ,
а интервал
–интервалом
сходимости.
,
а интервал
–интервалом
сходимости.
В
частном случае интервал сходимости
степенного ряда может совпадать со всей
числовой осью (в этом случае 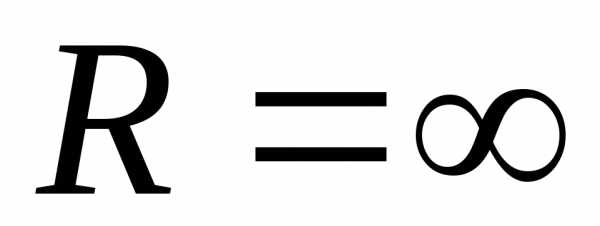 )
или может превращаться в точку (в этом
случае
)
или может превращаться в точку (в этом
случае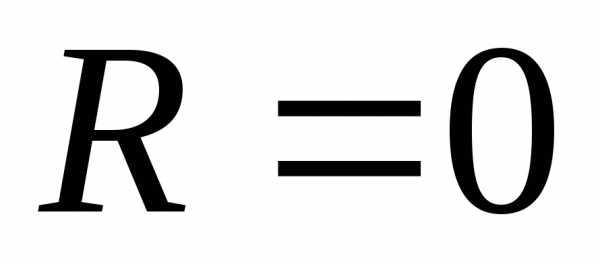 ).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
Пример 21. Найти интервал сходимости степенного ряда
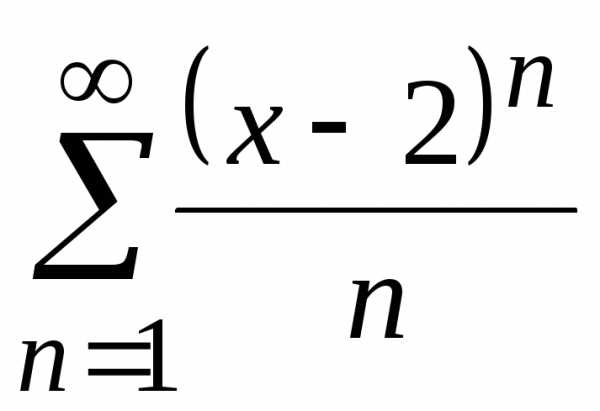 .
.
Решение
Первый способ решения
Рассмотрим
ряд, составленный из абсолютных величин
членов данного ряда: 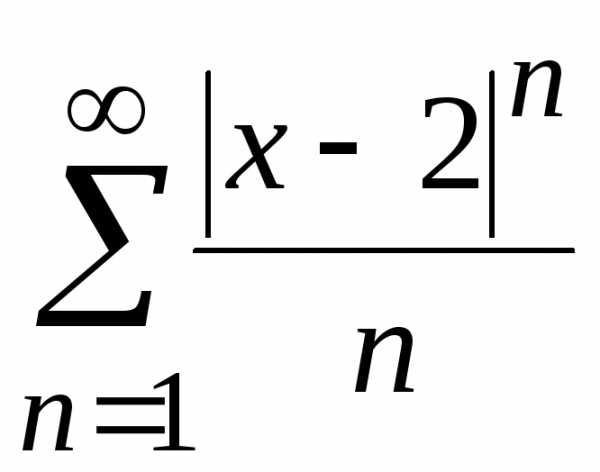 .
Применим признак Даламбера:
.
Применим признак Даламбера:
.
Если 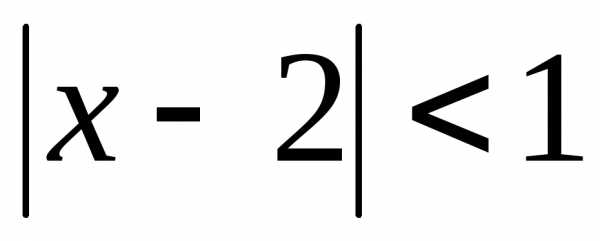 ,
то ряд сходится. Итак,,–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках
,
то ряд сходится. Итак,,–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точках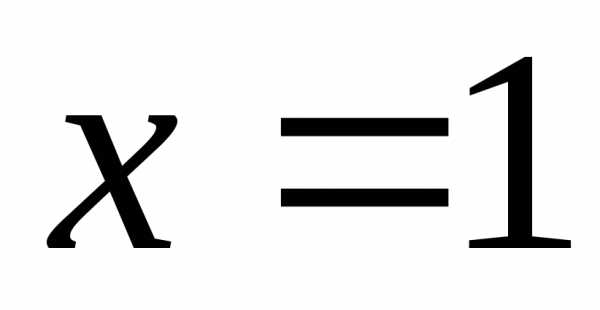 и
и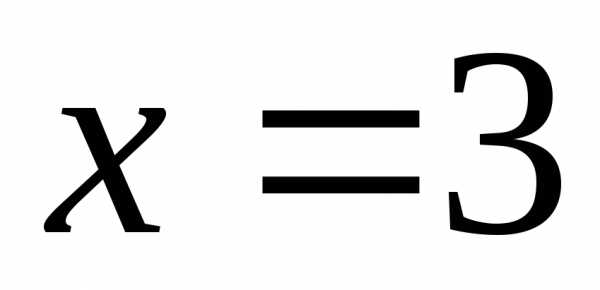 ,
исследуется отдельно.
,
исследуется отдельно.
При 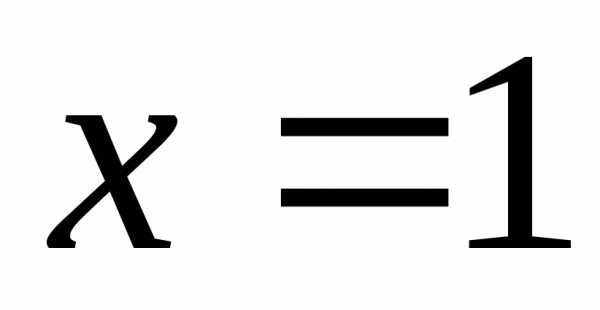 из данного ряда получаем ряд
из данного ряда получаем ряд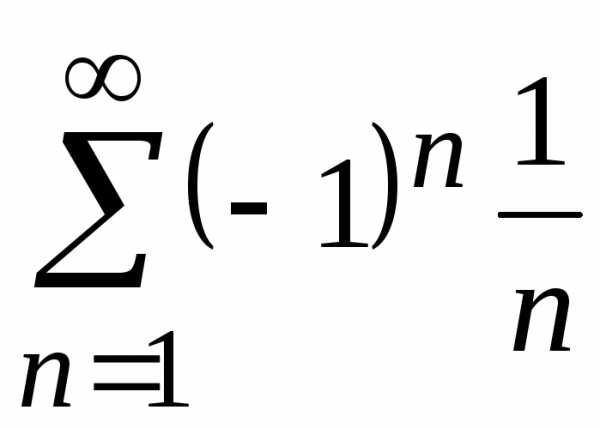 ,
который условно сходится.
,
который условно сходится.
При 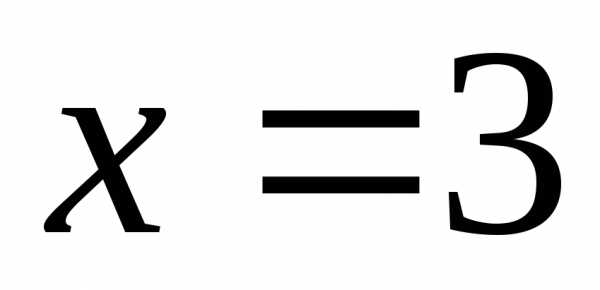 получаем гармонический ряд
получаем гармонический ряд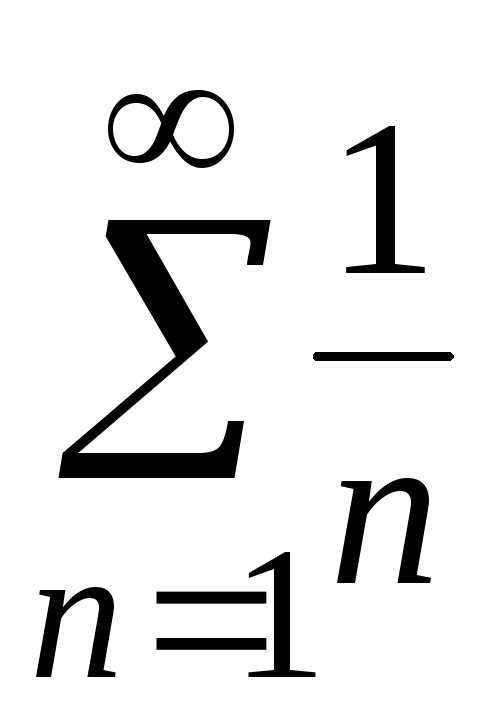 ,
который расходится.
,
который расходится.
Второй способ решения
Если
для степенного ряда (2) существует 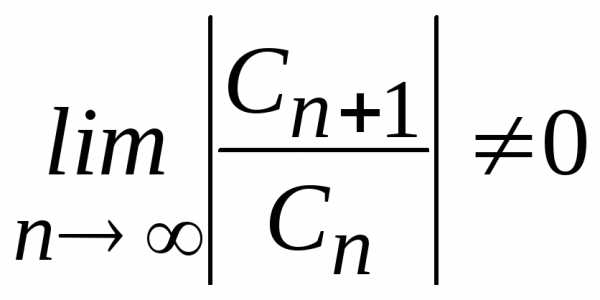 ,
то радиус сходимости степенного ряда
можно вычислить по формуле
,
то радиус сходимости степенного ряда
можно вычислить по формуле
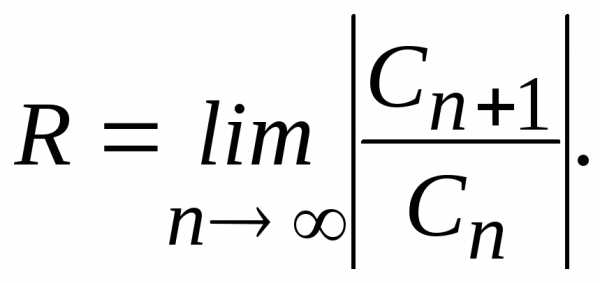
В
нашем случае 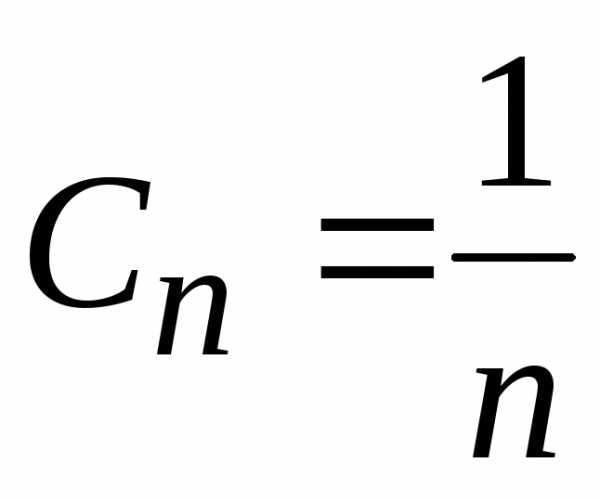 и
и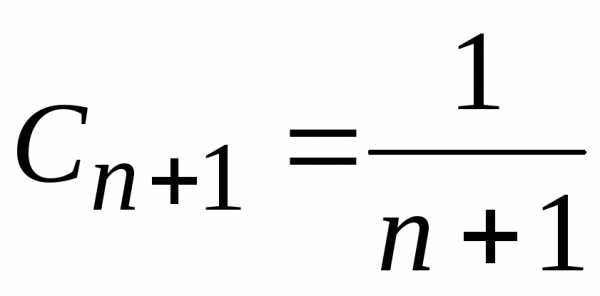 ,
поэтому
,
поэтому
.
Так
как 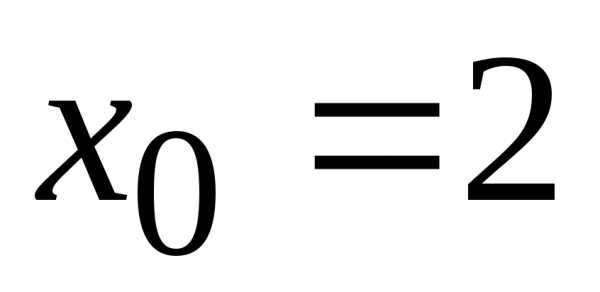 – центр степенного ряда, то– интервал сходимости данного ряда.
– центр степенного ряда, то– интервал сходимости данного ряда.
Сходимость ряда на концах интервала сходимости исследована выше.
Итак,
данный ряд сходится абсолютно при
и условно при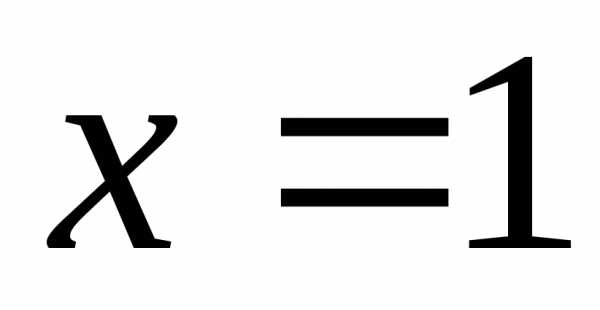 .
.
studfiles.net
Метод нахождения интервала сходимости степенного ряда
1) Дан , фиксируем х, получаем числовой ряд, и применим к ряду из модулей (для знакоположительности) признак Даламбера.
2) По признаку Даламбера вычисляем
— чтобы ряд сходился по признаку Даламбера.
3) Рассмотрим неравенство
<1|:
— интервал сходимости.
4) На концах интервала сходимости, в точках инужно провести дополнительное исследование.
Замечание: Частным случаем может оказаться, что , тогда интервал сходимости вырождается в точку х=0точка сходимости.степенной ряд сходится на всей числовой оси и интервал сходимости
Примеры:
1)
2)
3)
4)
Равномерная сходимость степенного ряда
Теорема: равномерно сходится на любом отрезке от целиком лежащем внутри интервала сходимости.
Доказательство:
Степенной ряд сходится в точкесходится числовой ряд
Возьмем степенной рядмажорируется насходящимся числовым рядомпо признаку Вейерштрасса о равномерной сходимости степенного ряда, равномерносходится на
Конец доказательства.
Следствия:
1) Т.к члены степенного ряда являются непрерывными функциями, то внутри интервала сходимости сумма ряда тоже будет тоже непрерывной функцией.
2)Степенной ряд можно почленно интегрировать на любом лежащем внутри интервала сходимости.
3) Степенной ряд можно почленно дифференцировать внутри интервала сходимости, т.к интервал сходимости ряда из производных будет точно таким же.
Доказательство:
— степенной ряд.
— ряд из производных.
<1 у ряда из производных тот же интервал сходимости.
Конец доказательства.
Степенной ряд по степеням х-а
Рассмотрим
Сделаем замену: x-a=X
Найдём интервал сходимости полученного ряда, -R<x<R, сделаем обратную замену: -R<x-a<R|+a, a-R<x<a+R
Интервал сходимости полученного ряда имеет центр в точке А.
Пример:
Ряды Тейлора
На I курсе рассматривалась формула Тейлора для функции f(x) n+1 раз дифференцируемая в окрестности точки .
где
Если f(x) любое число раз дифференцируема в окрестности точки переходя к пределув формуле Тейлора получим:
ряд стоящий в правой части равенства называется рядом Тейлора для функции f(x) по степеням , а сама формула называетсяразложением функции f(x) в ряд Тейлора.
Формально ряд Тейлора может быть получен для любой функции, но сходится к этой функции он будет только тогда, когда
Если этот предел , то ряд либо расходится, либо сходится к совсем другой функции.
Единственность разложения функции в ряд Тейлора
Теорема: Если функция f(x) разлагается в степенной ряд по степеням , то это обязательно ряд Тейлора.
Доказательство:
Пусть функция разлагается в степенной ряд вида:
Найдём коэффициенты степенного ряда, Подставим
Продифференцируем 1 раз
Подставим
Продифференцируем 2 раз
Подставим
Продифференцируем 3 раз
Подставим
Аналогично покажем
Коэффициенты степенного ряда совпадают с коэффициентами рядами Тейлора.
Конец доказательства.
Условия разложимости функции в ряд Тейлора
Определение: Семейство функций называетсяравномерно ограниченным на множестве D, если существует число M>0, что сразу для всех функций семейства и любого.
Теорема:Пусть функция -любое количество раз дифференцируема в окрестности точкии семейство ее производных любого порядка равномерно ограничено в окрестности точки,то функциюможно разложить в ряд Тэйлора в окрестности точки.
Покажем что
Остаточный член
, где M>0 (т.к семейство производных равномерно ограничено)
Рассмотрим
Можно показать по признаку Даламбера, что ряд сходится при любом х.
По необходимому признаку сходимости
Рассмотрим
Конец доказательства.
studfiles.net
Интервал сходимости степенного ряда и его нахождение.
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Лекция 8
Тема: Степенные ряд. Теорема Абеля. Интервал сходимости степенного ряда и его нахождение.
Степенные ряды. Теорема Абеля
Функциональный ряд вида:
называется степенным рядом c0,c1,…,cn,…-коэффициенты ряда. Коэффициенты ряда будем считать действительными числами
Теорема Абеля. Если степенной ряд сходится в точке x1, , то он сходится и при том абсолютно в интервале .
Доказательство. По условию степенной ряд сходится в точке , т.е. сходится ряд . По необходимому признаку сходимости общий член последнего ряда стремится к нулю, т.е. . Отсюда следует, что выполняется неравенство . Теперь рассмотрим ряд , составленный из модулей членов данного степенного ряда. Имеем:
Так как по условию , то . Ряд является рядом из членов геометрической прогрессии со знаменателем , поэтому он сходится. По теореме сравнения сходится и ряд . Следовательно, удовлетворяющего неравенству ряд сходится и притом абсолютно. ▼
Интервал сходимости степенного ряда и его нахождение.
Рассмотрим степенной ряд . Отметим, что степенной ряд всегда сходится в точке x=x0 . При фиксированном x x0 ряд будет числовым и к ряду , составленному из модулей членов данного ряда, можно применить либо признак Даламбера, либо признак Коши.
1) Применим признак Даламбера к ряду
. получается из заменой n на n+1.
.
Мы предположим, что существует предел .По признаку Даламбера при ряд сходится, а при расходится.
Следовательно, при ряд сходится, а при ряд расходится.
В концевых точках интервала ряд может сходиться, а может и расходиться.
Интервал ) называется интервалом сходимости степенного ряда, R-радиус сходимости степенного ряда.
2) Применим признак Коши к ряду
Предположим, что существует предел . По признаку Коши при ряд сходится, а при расходится.
Отметим, что в каждой точке интервала сходимости ряд сходится, а вне интервала сходимости ряд расходится. В концевых точках интервала сходимости ряд может сходиться, а может и расходиться, в этом случае следует проводить дополнительные исследования.
Пример 1. Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости.
Решение. Рассмотрим ряд, составленный из модулей членов данного ряда, т.е. ряд , который является знакоположительным рядом и к нему можно применить признак Даламбера.
,
– интервал сходимости, R=2.
Исследуем сходимость данного ряда на концах интервала сходимости.
1) x=-1. Рассмотрим ряд из модулей , который является рядом Дирихле при s=2>1, он сходится. Следовательно ряд сходится абсолютно.
2) x=3. = – сходится.
Пример 2. Найти интервал сходимости ряда .
Решение. Рассмотрим ряд и применим признак Коши:
. Следовательно, данный ряд сходится в одной точке x=3, R=0.
Пример 3. Найти интервал сходимости ряда
Решение. Рассмотрим ряд и применим признак Даламбера.
, . =
. Следовательно, ряд сходится на всей числовой оси, R= .
Теорема 1. Сумма степенного ряда есть функция непрерывная в интервале сходимости степенного ряда.
Теорема 2. Степенной ряд можно почленно дифференцировать в интервале сходимости и справедливо равенство:
При этом интервал сходимости продифференцированного ряда тот же, что и данного ряда.
Теорема 3. Степенной ряд можно почленно интегрировать в интервале сходимости и справедливо равенство:
, .
Проинтегрированный степенной ряд имеет тот же интервал сходимости, что и данный ряд.
megapredmet.ru
Степенные ряды.
Степенные
ряды 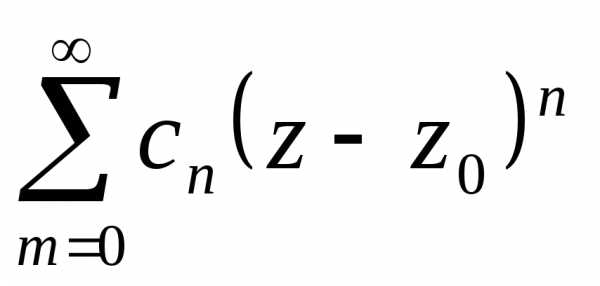 — это частный случай функциональных
рядов, в котором члены ряда представляют
собой степени отклонения переменной
— это частный случай функциональных
рядов, в котором члены ряда представляют
собой степени отклонения переменной от некоторой фиксированной точки
плоскости
от некоторой фиксированной точки
плоскости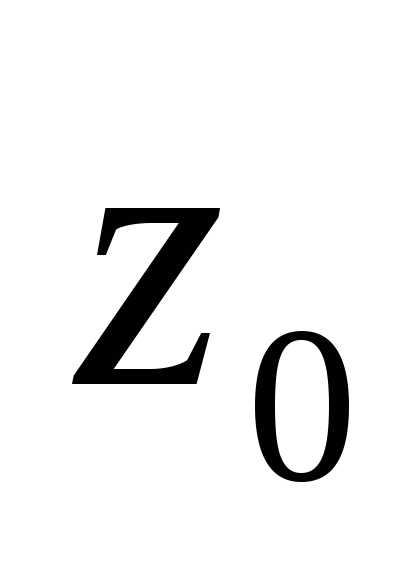 (центра сходимости ряда). Степенные ряды
действительной переменной сходятся в
интервале
(центра сходимости ряда). Степенные ряды
действительной переменной сходятся в
интервале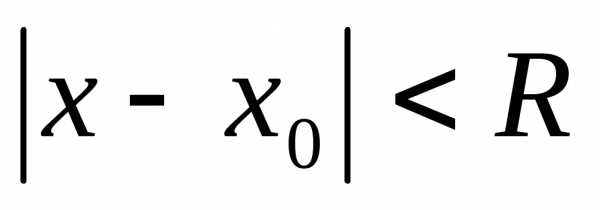 ,
где
,
где 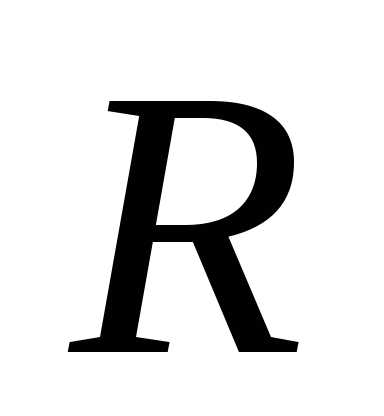 —
радиус сходимости ряда. Точно так же
степенной ряд комплексной переменной
сходится на множестве
—
радиус сходимости ряда. Точно так же
степенной ряд комплексной переменной
сходится на множестве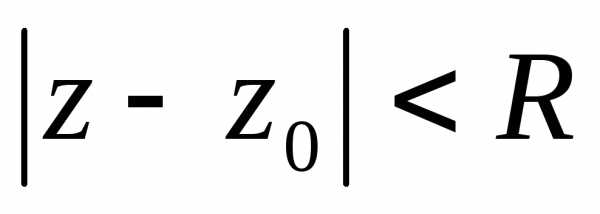 ,
только в комплексных числах это множество
представляет собой круг без границы.
Сходимость ряда на границе исследуется
отдельно.
,
только в комплексных числах это множество
представляет собой круг без границы.
Сходимость ряда на границе исследуется
отдельно.
Теорема Абеля.Если степенной ряд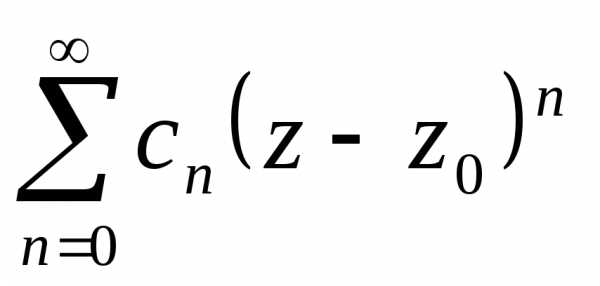 сходится в точке
сходится в точке ,
то он абсолютно сходится в круге.
Если степенной ряд
,
то он абсолютно сходится в круге.
Если степенной ряд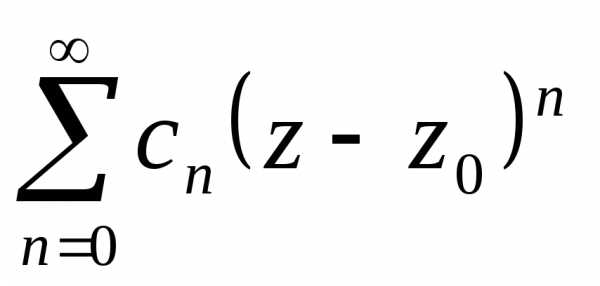 расходится в точке
расходится в точке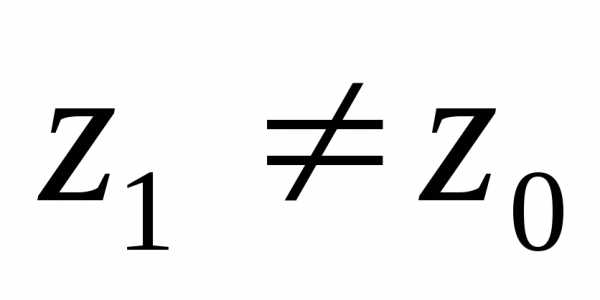 ,
то он расходится во внешности круга.
,
то он расходится во внешности круга.
Доказательство(аналогично случаю действительной переменной).
Пусть ряд сходится в точке
 и.
и.
Так как ряд
сходится в точке 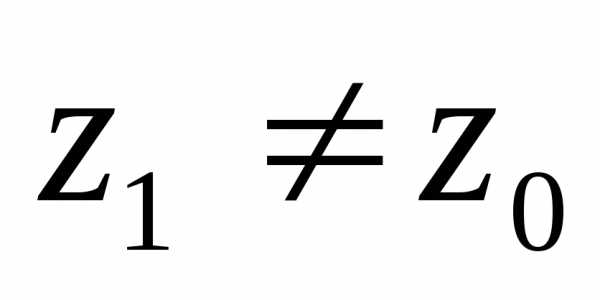 ,
то по необходимому признаку сходимости
ряда.
,
то по необходимому признаку сходимости
ряда.
Тогда .
Исследуем
степенной ряд на абсолютную сходимость.
Рассмотрим ряд из модулей членов ряда. 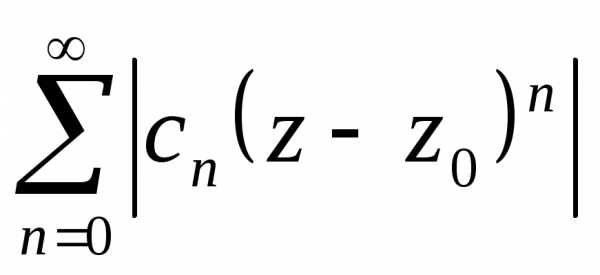 Оценим
общий член ряда из модулей.
Оценим
общий член ряда из модулей.
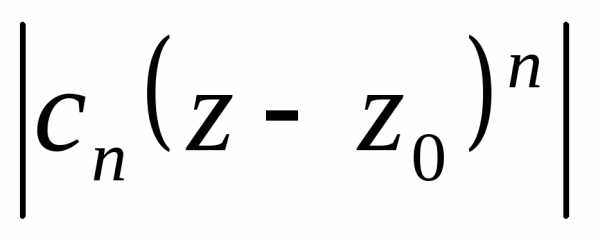 .
.
Ряд из модулей исходного ряда
сходится по первому признаку сравнения
числовых рядов (ряд сравнения – сходящаяся
бесконечно убывающая геометрическая
прогрессия 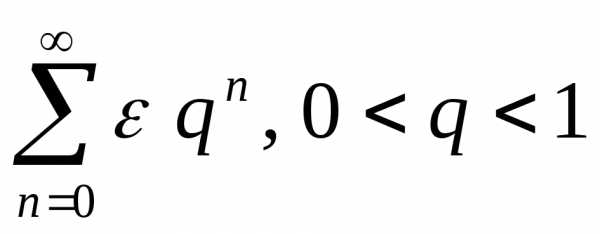 ).
Следовательно, исходный ряд в областисходится абсолютно.
).
Следовательно, исходный ряд в областисходится абсолютно.
Замечание.Казалось бы, что из признака Вейерштрасса
в областиследует равномерная сходимость исходного
ряда, но здесь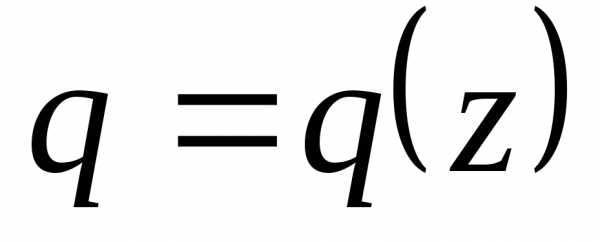 ,
а в признаке Вейерштрасса требуется
указать один мажорирующий ряд для всех
точек
,
а в признаке Вейерштрасса требуется
указать один мажорирующий ряд для всех
точек рассматриваемой
области, то есть
рассматриваемой
области, то есть не
должно зависеть от
не
должно зависеть от .
Поэтому равномерную сходимость ряда в
областиутверждать нельзя. Однако если взять
.
Поэтому равномерную сходимость ряда в
областиутверждать нельзя. Однако если взять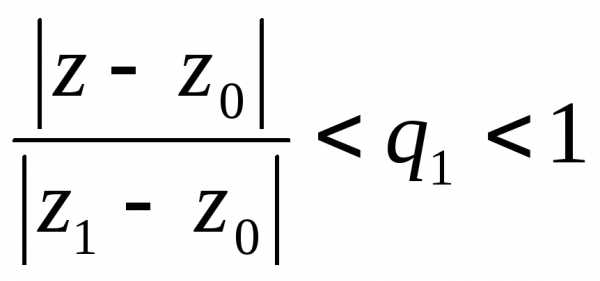 (
(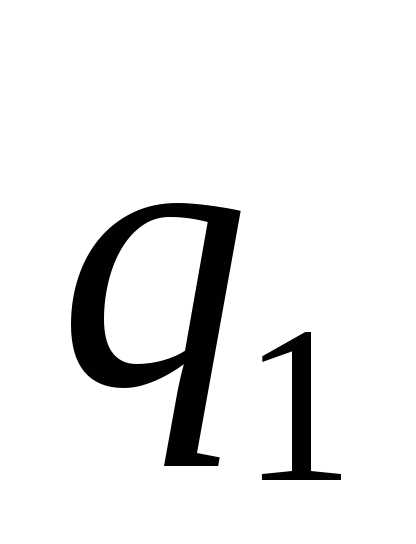 не зависит от
не зависит от ),
то в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса.
),
то в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса.
Пусть ряд расходится в точке
 и.
и.
Если ряд сходится
в точке  ,
то по доказанному в пункте 1), он должен
абсолютно сходиться в точке
,
то по доказанному в пункте 1), он должен
абсолютно сходиться в точке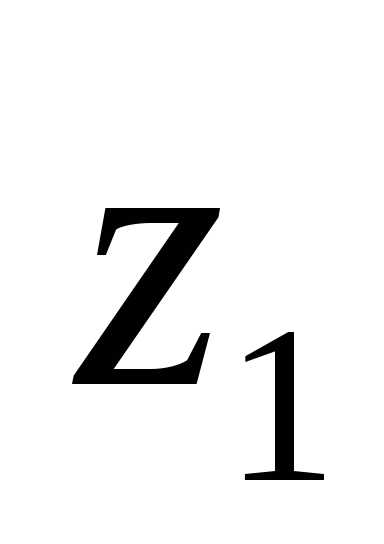 ,
следовательно, сходиться в точке
,
следовательно, сходиться в точке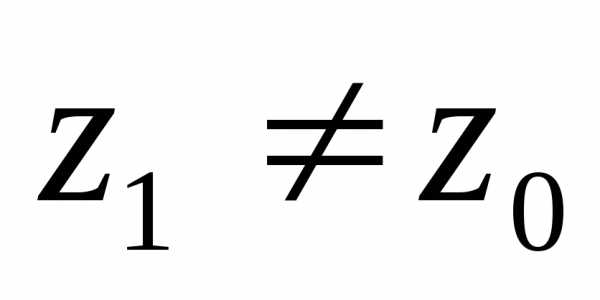 .
Это противоречит тому, что исходный ряд
расходится в точке
.
Это противоречит тому, что исходный ряд
расходится в точке ,
следовательно исходный ряд расходится
в области.
,
следовательно исходный ряд расходится
в области.
Определение радиуса сходимости и исследование сходимости ряда на границе круга сходимости.
Рассмотрим монотонноубывающуюпоследовательность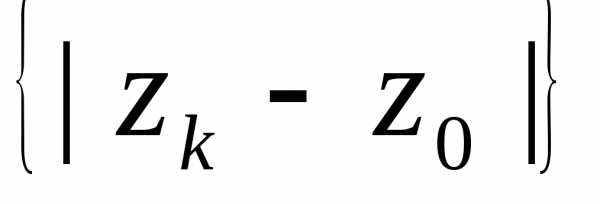 ,
такую, что в точке
,
такую, что в точке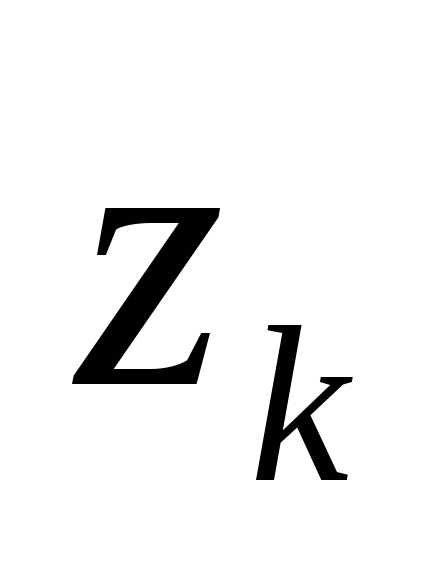 степенной
ряд
степенной
ряд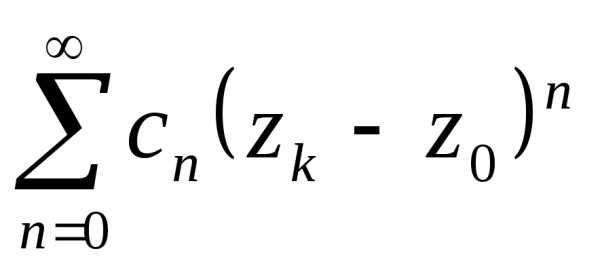 расходится.
Если выбрать
расходится.
Если выбрать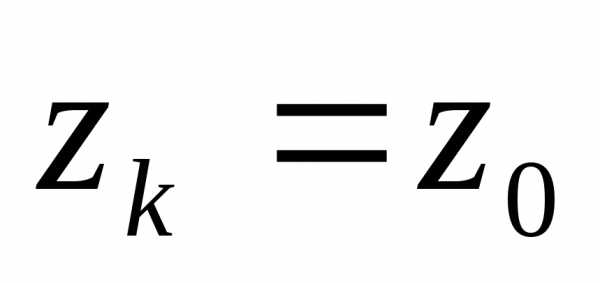 ,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
,
то степенной ряд будет сходиться (ряд
из нулей), поэтому рассматриваемая
последовательность ограничена снизу
нулем. По теореме Вейерштрасса монотонно
убывающая, ограниченная снизу числовая
последовательность имеет предел. То
есть.
Такое число 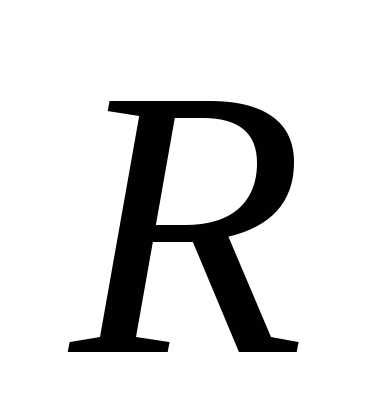 называетсярадиусом сходимости
степенного ряда.Следовательно,степенной ряд абсолютно сходится в
круге
называетсярадиусом сходимости
степенного ряда.Следовательно,степенной ряд абсолютно сходится в
круге 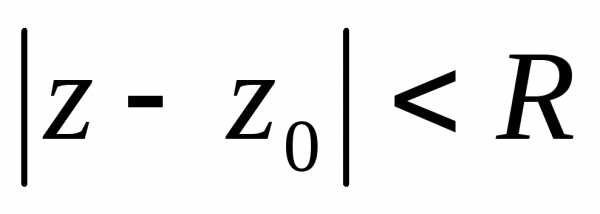 сходимости степенного ряда.
сходимости степенного ряда.
Теорема. Степенной ряд равномерно сходится внутри круга сходимости.
Доказательство. Пусть.
Выберем,
например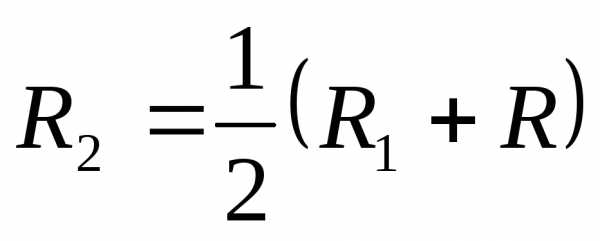 .
На окружностистепенной ряд сходится абсолютно, так
как эта окружность лежит внутри круга
сходимости. Тогда
.
На окружностистепенной ряд сходится абсолютно, так
как эта окружность лежит внутри круга
сходимости. Тогда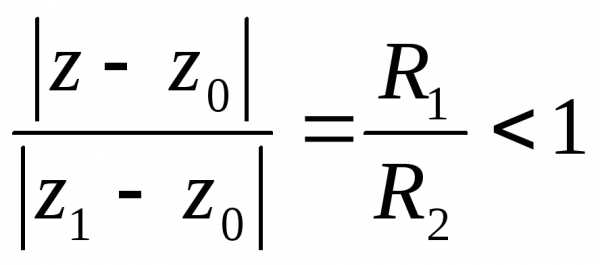 (
(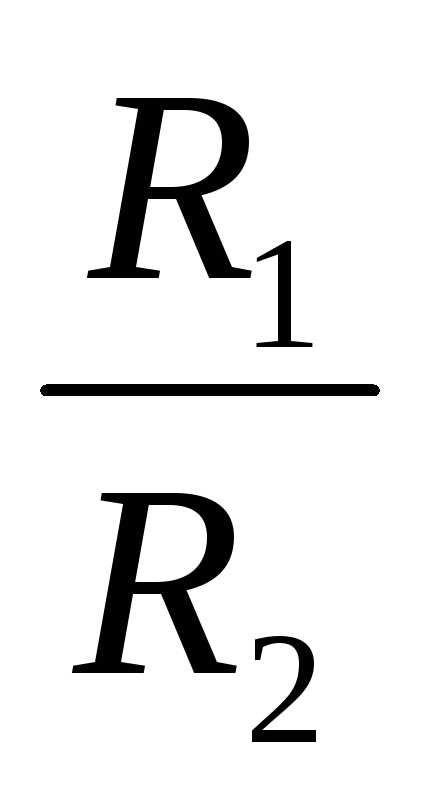 не зависит от
не зависит от ),
тогда в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса (замечание в
доказательстве теоремы Абеля).
),
тогда в областистепенной ряд будет сходиться равномерно
по признаку Вейерштрасса (замечание в
доказательстве теоремы Абеля).
Следствие. Внутри круга сходимости справедливы теоремы о непрерывности суммы ряда, о почленном интегрировании (по любой кусочно-гладкой дуге, принадлежащей кругу сходимости) и дифференцировании ряда.
Теорема. При почленном дифференцировании и интегрировании степенного ряда его радиус сходимости не меняется.
Доказательство. Рассмотрим ряд из модулей членов степенного ряда (это – знакоположительный числовой ряд в конкретной точке) и определим радиус сходимости по признаку Даламбера.
.
Продифференцируем
почленно степенной ряд 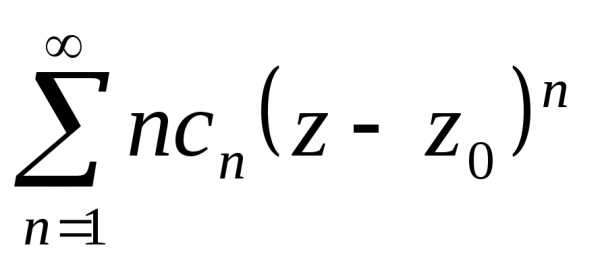 ,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
,
перейдем к ряду из модулей и найдем
радиус сходимости по признаку Даламбера.
.
Таким образом, при почленном дифференцировании радиус сходимости степенного ряда не меняется. Он не меняется и при почленном интегрировании, иначе он изменился бы при почленном дифференцировании.
Исследуем сходимость степенного ряда на границе круга сходимости.
Рассмотрим ряд
из модулей на границе круга сходимости 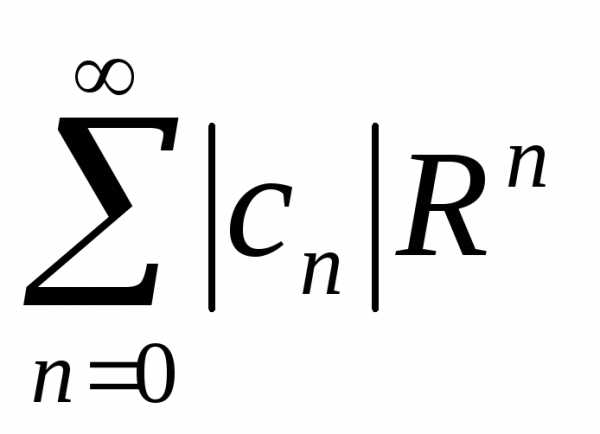 .
.
Если ряд из модулей на границе круга сходимости сходится, то исходный степенной ряд абсолютно сходится на всей границе.
В самом деле этот ряд является мажорантным для степенного ряда в любой точке границы.
Если , то исходный степенной ряд расходится на всей границе.
В этом случае , и не выполняется необходимый признак сходимости для исходного степенного ряда на всей границе круга сходимости. Поэтомуисходный степенной ряд расходится на всей границе.
Если ряд из модулей на границе круга сходимости расходится, но ,то исходный степенной ряд сходится в одних точках границе и расходится в других. В этом случае для того, чтобы исследовать сходимость в точке границы, надо подставить ее в качестве
 в степенной ряд и исследовать сходимость
полученного числового ряда.
в степенной ряд и исследовать сходимость
полученного числового ряда.
Приведенные
выше примеры 3, 4, 5 (после критерия Коши):
ряд 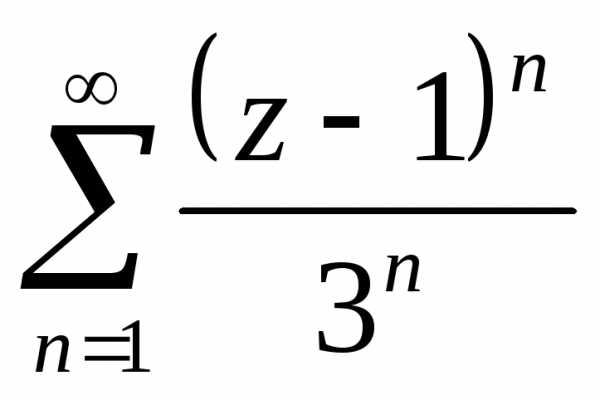 ,
ряд
,
ряд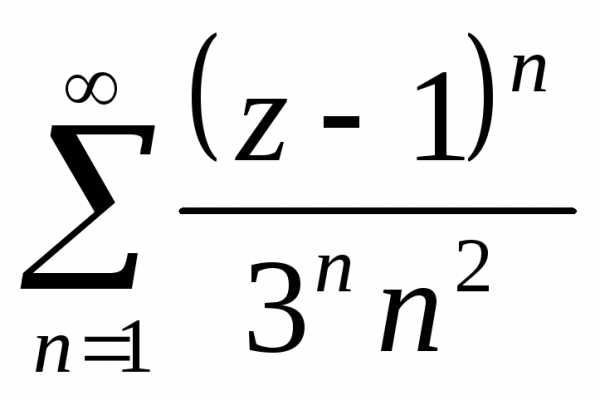 ,
ряд
,
ряд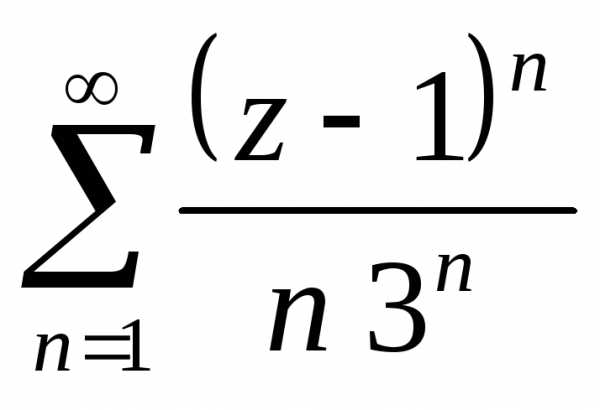 иллюстрируют все три случая. Первый ряд
расходится на всей границе
иллюстрируют все три случая. Первый ряд
расходится на всей границе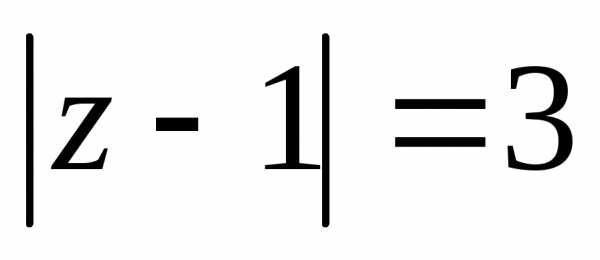 ,
так как на ней не выполняется необходимый
признак сходимости ряда. Второй ряд
сходится на всей границе, третий ряд
сходится в одних точках границы и
расходится в других.
,
так как на ней не выполняется необходимый
признак сходимости ряда. Второй ряд
сходится на всей границе, третий ряд
сходится в одних точках границы и
расходится в других.
Теорема. Сумма степенного ряда является аналитической функцией в его круге сходимости (без доказательства).
Ряд Тейлора.
Рядом Тейлораназывается степенной ряд вида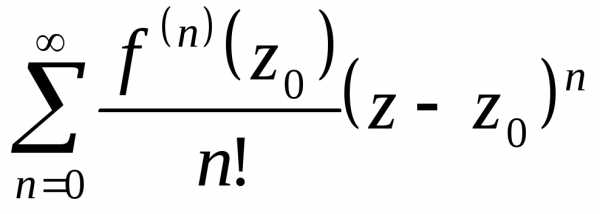 (предполагается,
что функция
(предполагается,
что функция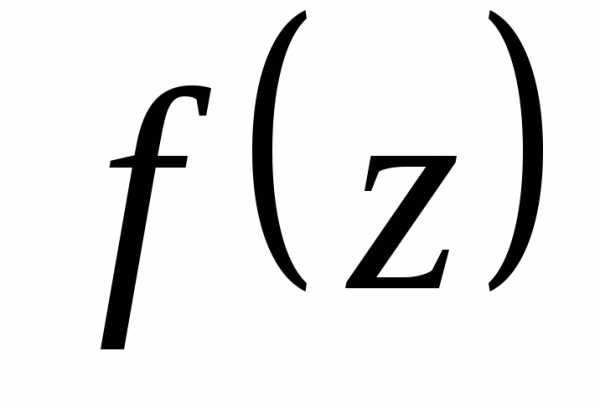 является бесконечно дифференцируемой).
является бесконечно дифференцируемой).
Рядом Маклорена называется ряд Тейлора при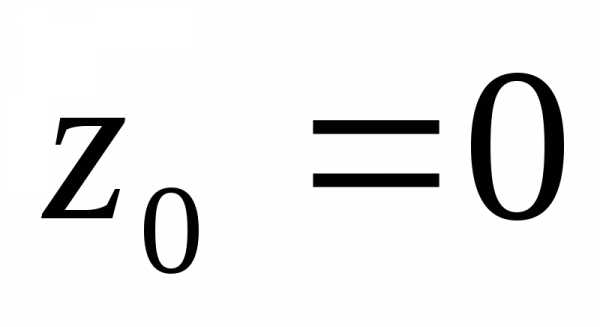 ,
то есть ряд
,
то есть ряд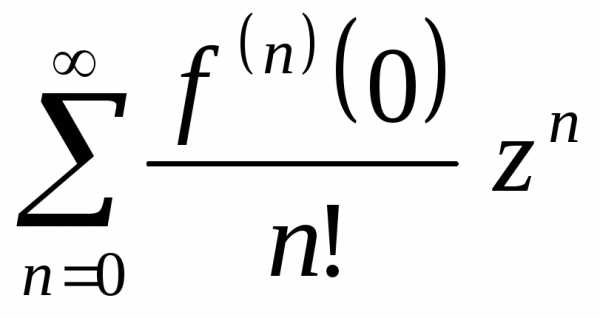 .
.
Теорема. Степенной ряд является рядом Тейлора для своей суммы.
Доказательство.Пустьи
степенной ряд сходится в круге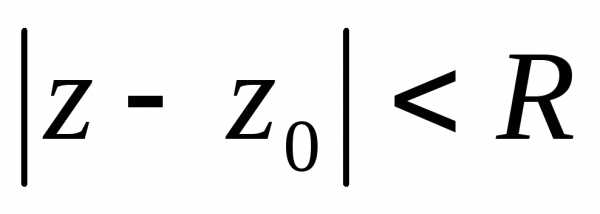 .
Подставим в разложение
.
Подставим в разложение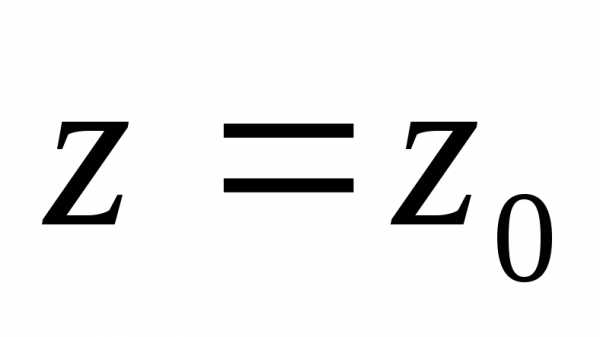 ,
получим
,
получим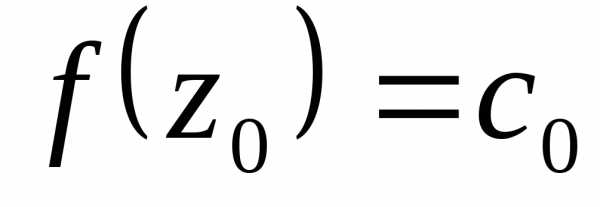 .
.
Так как сумма
степенного ряда – функция аналитическая,
мы можем дифференцировать функцию, а
так как степенной ряд сходится равномерно
внутри круга сходимости, мы можем его
дифференцировать почленно. Полученный
ряд будет сходиться в том же круге, так
как радиус сходимости при дифференцировании
не меняется. Поэтому сумма этого ряда
будет
фунцией аналитической в том же круге.
Ее вновь можно дифференцировать,
дифференцируя почленно степенной ряд
и т.д. Отсюда следует, что если аналитическая функция является суммой
степенного ряда (это будет показано
позже), то она является бесконечно
дифференцируемой функцией. Вычислим
коэффициенты в степенных рядах, полученных
почленным дифференцированием.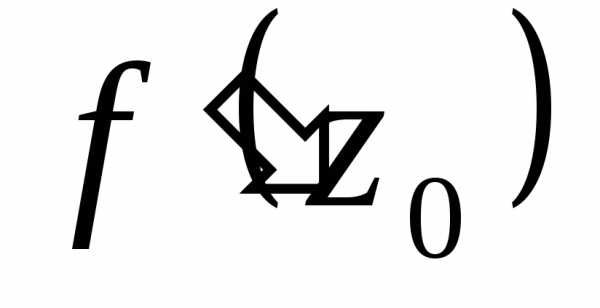 =
=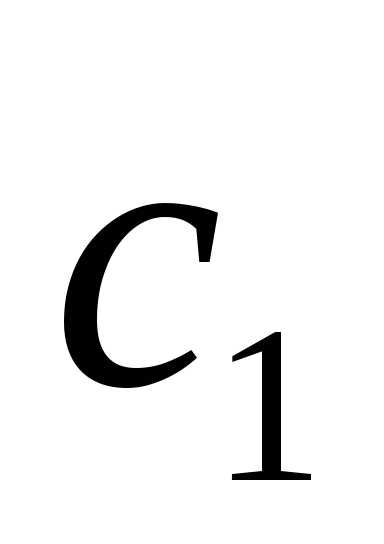 ,
,
,,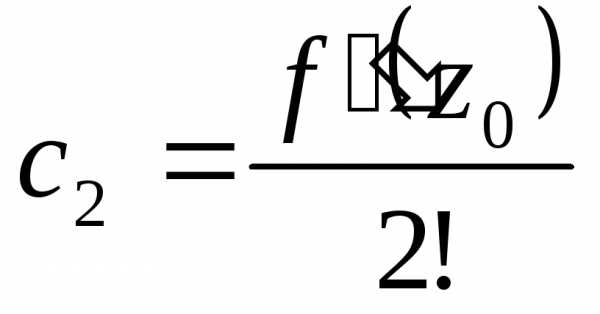 ,
,
,,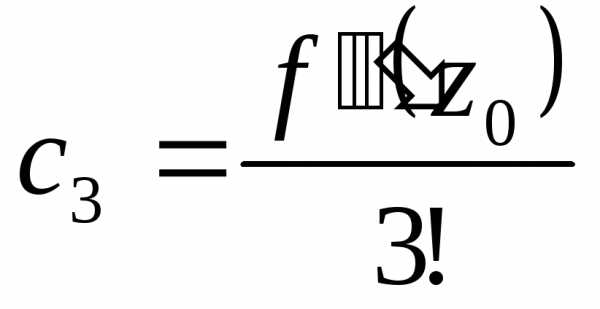 ,
,
Продолжая этот
процесс, получим 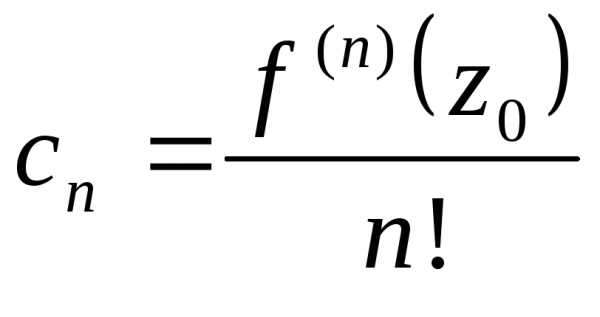 .
Это – коэффициенты ряда Тейлора.
.
Это – коэффициенты ряда Тейлора.
Запишем разложения в ряд Маклорена основных элементарных функций.
Так как эти формулы справедливы на всей действительной оси, то по теореме Абеля они справедливы и на всей комплексной плоскости (в круге с началом координат бесконечного радиуса).
, 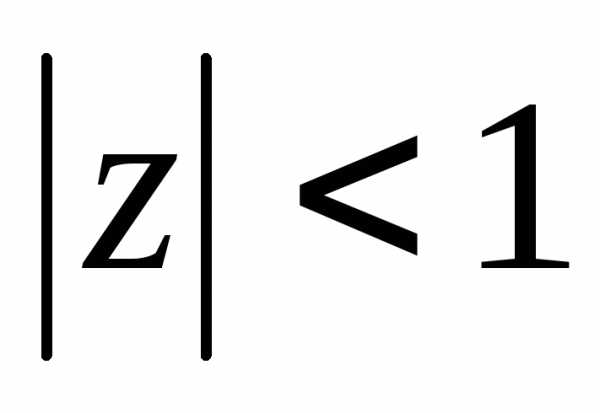 .
.
,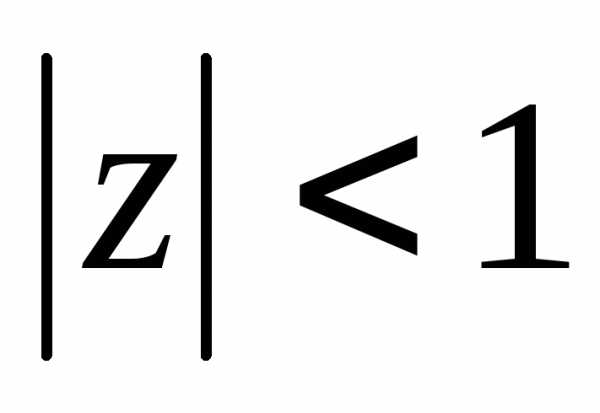 .
.
( интегрируя предыдущую формулу)
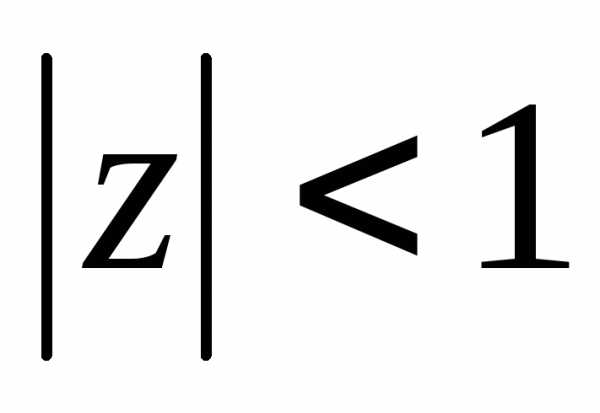 ,
,
studfiles.net
2. Найти области сходимости степенных рядов
Решение
Найдём интервал сходимости ряда ,
Тогда или , .
Ряд сходится абсолютно на интервале (-2;2)
Исследуем поведение ряда на концах интервала сходимости:
При x=2 ряд примет вид , данный ряд расходится, так как не выполняется необходимый признак сходимости рядаов
При х=-2 ряд примет вид . Как мы убедились выше этот ряд расходится.
Значит степенной ряд имеет интервал сходимости:
Решение
Найдём интервал сходимости ряда Тогда или , .
Ряд сходится абсолютно на интервале (-4;-2)
Исследуем поведение ряда на концах интервала сходимости:
При x=-4 ряд примет вид , данный ряд является знакопеременным, исследуем его на абсолютную сходимость:
Воспользуемся вторым признаком сравнения: , , . Следовательно и сходятся или расходятся одновременно, а так как ряд сходится (Так как ряд Дирихле сходится при р>1), то ряд тоже сходится абсолютно.
При х=-2 ряд примет вид . Как мы убедились выше этот ряд сходится.
Значит степенной ряд имеет интервал сходимости:
3. Вычислить приближённое значение интеграла с точностью до 0,001 разлогая подынтегральную функцию в ряд Тейлора.
Решение
Приведём интеграл к виду
Воспользуемся разложением функции в ряд Маклорена
, при
Тогда
Имеем
Получен знакочередующийся ряд, слагаемое меньше чем 0.001. Отбрасывая это слагаемое, получим приближённое значение интеграла с заданной точностью
4. Проинтегрировать приближенно с помощью ряда Тейлора дифференциальное уравнение. Найти четыре первых (отличных от нуля) члена разложения. ,
Решение
Будем искать частное решение уравнения в виде ряда:
(1)
Непосредственно из уравнения найдем: .
Дифференцируя последовательно обе части уравнения получим
И полагая X=0 в полученных равенствах, будем иметь:
Подставляя в ряд (1) найденные значения получим: .
| < Предыдущая | Следующая > |
|---|
matica.org.ua

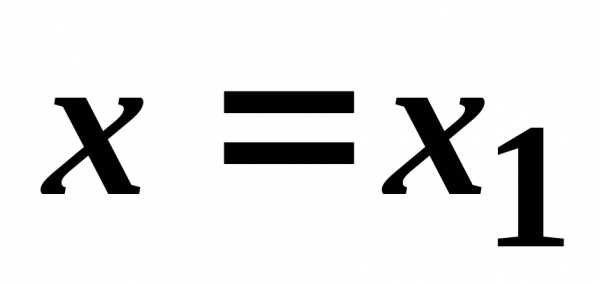 ,
то он сходится, и притом абсолютно, для
всех
,
то он сходится, и притом абсолютно, для
всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ,
то он расходится для всех
,
то он расходится для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству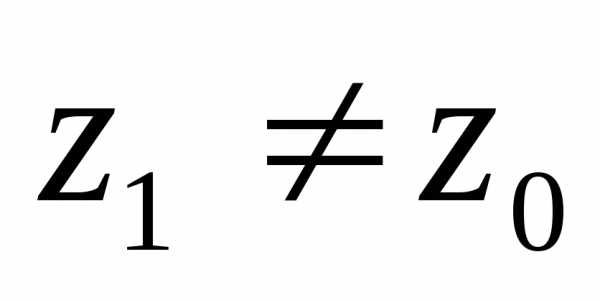 и.
и.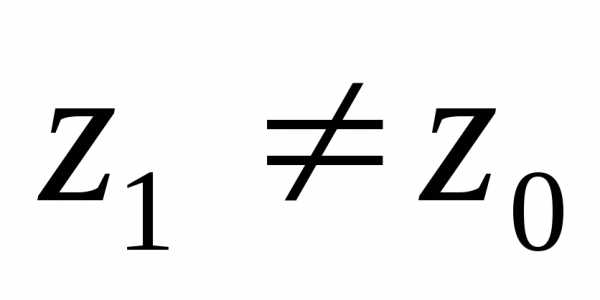 и.
и. в степенной ряд и исследовать сходимость
полученного числового ряда.
в степенной ряд и исследовать сходимость
полученного числового ряда.