Найти матрицу 2а – Матричный калькулятор

Произведение двух матриц: формула, решения, свойства

Определение. Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.

Из этого определения следует формула элемента матрицы C:

Произведение матрицы А на матрицу В обозначается АВ.

Пример 1. Найти произведение двух матриц А и B, если

,

.

Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:

На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B, произведения которых складываются для получения элемента матрицы C.

В результате получаем элементы произведения матриц:

 

Теперь у нас есть всё, чтобы записать произведение двух матриц:

.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы

В .

Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:

Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:

В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .

Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:

а) 2 Х 10 и 10 Х 5;

б) 10 Х 2 и 2 Х 5;

в) 4 Х 4 и 4 Х 10.

Решение:

а) 2 Х 5;

б) 10 Х 5;

в) 4 Х 10.

Далее — примеры на нахождение произведения двух матриц различной размерности.

Пример 3. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 2, число столбцов в матрице B — 2. Следовательно, размерность матрицы C = AB — 2 X 2.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

Найти произведение матриц самостоятельно, а затем посмотреть решение

---

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 5. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 2, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 2 X 1.

Вычисляем элементы матрицы C = AB.

Произведение матриц запишется в виде матрицы-столбца: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 6. Найти произведение матриц A и B, если:

.

Решение. Число строк в матрице A — 3, число столбцов в матрице B — 3. Следовательно, размерность матрицы C = AB — 3 X 3.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 7. Найти произведение матриц

A и B, если:

.

Решение. Число строк в матрице A — 1, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 1 X 1.

Вычисляем элемент матрицы C = AB.

Произведение матриц является матрицей из одного элемента: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».

Возведение матрицы в степень

Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы.

n-ая степень матрицы путём умножения матрицы на саму себя n раз:

Пример 8. Дана матрица . Найти A² и A³.

Решение:

Найти произведение матриц самостоятельно, а затем посмотреть решение

Пример 9. Дана матрица

Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.

Правильное решение и ответ.

Свойства произведения двух матриц

Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .              

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где

—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

                                                                                               

Получается, что АЕ = А .

Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения

С = ЕА :

Доказано: ЕА = А .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.

Свойство 3. Произведение матриц некоммутативно:
.

Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.

Пример 11. Найти произведения матриц АВ и ВА, если

,

,

и убедиться в том, что эти произведения не равны друг другу:

.

Решение. Находим:

И действительно, найденные произведения не равны:
.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .

Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .

Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то

.

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

function-x.ru

Решение матриц онлайн

Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, при этом сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придет многофункциональный математический калькулятор. В его арсенал входит решение матриц онлайн, в нашем калькуляторе можно выполнить все основные операции над матрицами!

Матрица — это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трех строк и пяти столбцов.

Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.

Как решать матрицы в онлайн калькуляторе?

Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.

Кнопка, открывающая калькулятор матриц:

Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.

Кнопки калькулятора, выполняющие основные действия над матрицами:

Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами.

Вычисление матриц онлайн с помощью формы быстрого ввода:

Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».

Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.

Вектор столбец

Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3, 4 или 5 строк соответственно.

Кнопки калькулятора для ввода вектора:

Вектор-столбец из 3-х строк:

(2, 6, 8)

Квадратная матрица

Матрица называется квадратной, если число ее строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.

Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки калькулятора.

Кнопки калькулятора для ввода квадратных матриц:

Пример квадратной матрицы 4 порядка:

[[8, 4, 1, 8][7, 1, 8, 8][8, 4, 1, 6][4, 8, 3, 1]]

Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.

Пример симметричной матрицы:

[[1, 2, 8, 11][2, 3, 24, 5][8, 24, 6, 4][11, 5, 4, 9]]

Есть еще такие виды матриц в математике.

Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.

Пример единичной матрицы:

[[1, 0, 0, 0][0, 1, 0, 0][0, 0, 1, 0][0, 0, 0, 1]]

Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.

Пример нулевой матрицы:

[[0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0]]

Сложение и вычитание матриц онлайн

С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, то-есть число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.

Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.

Сложение матриц примеры

Сложение двух матриц:

[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]

Сумма двух матриц:

[[2, 7][4, 5]]+[[2, 10][6, 8]]

Векторное произведение матриц

Для выполнения этой операции используйте клавишу Cross Product.

Пример произведения векторов:

(2, 6, 4)#(8, 2, 5)

Умножение матриц

Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.

Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.

Умножение матриц пример:

[[2, 8][4, 2]]*[[8, 8][7, 1]]

Умножение матрицы на число онлайн:

[[5, 6][7, 8]]*9

Решение матричных уравнений

Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. Решение матричных уравнений осуществляется с помощью кнопки Solve Ecuation System.

Пример решения системы уравнений матриц:

[[6, 1, 8],[7, 5, 3],[2, 9, 4]]*x=(1, 2, 3)

Транспонирование матрицы

Используйте клавишу Matrix Transponent, когда нужно выполнить транспонирование матрицы — действие, в котором строки со столбцами меняются местами. Таким образом, транспонированная матрица получается путем замены строк на столбы в исходной матрице.

Использовать калькулятор матриц, чтобы транспонировать матрицу онлайн, очень просто. Нужно заполнить данные исходной матрицы и нажать кнопку Matrix Transponent. Нахождение транспонированной матрицы ^Т также можно выбрать из выпадающего меню в поле выбора действия с матрицами.

Найти транспонированную матрицу можно у любой матрицы вне зависимости от количества ее строк и столбцов (не забывайте, калькулятор матриц имеет ограничение на размер матрицы — максимум 5 x 5).

Транспонирование матрицы онлайн калькулятором:

[[2, 3, 4][1, 5, 8][7, 1, 4]]^T

Решение обратной матрицы

Обратной матрицей называют таблицу, при умножении на которую исходная матрица принимает вид единичной матрицы (применимо только к квадратным видам матриц).

Нахождение обратной матрицы осуществляется с помощью кнопки Matrix Inverse.

Пример нахождения обратной матрицы:

[[2, 4][2, 2]]^-1

Нахождение определителя матрицы

В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).

Пример, как найти определитель матрицы онлайн:

det([[-2, 2, -3],[-1, 1, 3],[2, 0, -1]])

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Решение матриц онлайн was last modified: Март 3rd, 2016 by Admin

compuzilla.ru

«Понятие матрицы. Определитель матрицы. Действия над матрицами. Обратная матрица.»

Типовой расчет №1

По теме: «Понятие матрицы. Определитель матрицы. Действия над матрицами. Обратная матрица.»

Даны матрицы:

Найти:

№1 Вычислить определители матриц A и C

№2 Найти транспонированные матрицы A^т, С^т, D^т

№3 Выполнить действия над матрицами 3А–2В; 3С–С^т

№4 Найти произведения матриц: В∙А, А∙D, D∙C

№5 Найти обратные матрицы для A и C

№ варианта (№ по списку в журнале)	i	j	k
1	1	2	3
2	5	4	-2
3	4	8	-3
4	2	6	4
5	3	7	5
6	6	5	6
7	8	4	1
8	-1	2	0
9	5	3	-1
10	8	-3	2
11	9	-2	4
12	6	1	5
13	7	-1	0
14	4	6	-2
15	6	5	-3
16	8	-4	6
17	-2	-3	4
18	3	2	5
19	-1	0	6
20	0	7	-8
21	4	-5	2
22	-2	4	-3
23	-3	3	-1
24	7	2	1
25	5	1	0
26	3	2	7
27	1	5	-2
28	0	-2	4
29	3	-1	-2
30	-7	2	4

Образец решения:

Даны матрицы:

№1 Вычислить определители матриц A и C

№2 Найти транспонированные матрицы: A^т, С^т, D^т

№3 Выполнить действия над матрицами: 2А–3В; С^т – 2С

№4 Найти произведения матриц: B∙A, А∙D, D∙C

№5 Найти обратные матрицы для A и C

Решение:

№1 Вычислить определители матриц A и C.

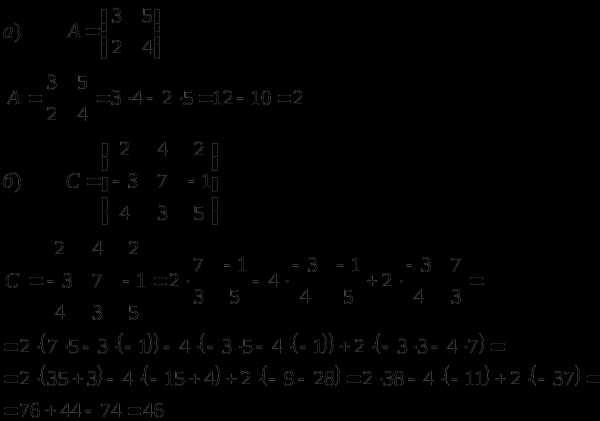
№2 Найдем транспонированные матрицы: A^т, С^т, D^т

№3 Выполнить действия над матрицами: 2А–3В; 3С–С^т

№4 Найти произведения матриц: А∙В, А∙D, D∙C

№5 Найти обратные матрицы для A и C

а) Обратная матрица да квадратной матрицы второго порядка находится по формуле:

б) Обратная матрица да квадратной матрицы третьего порядка находится по формуле:

(рассчитано в №1)

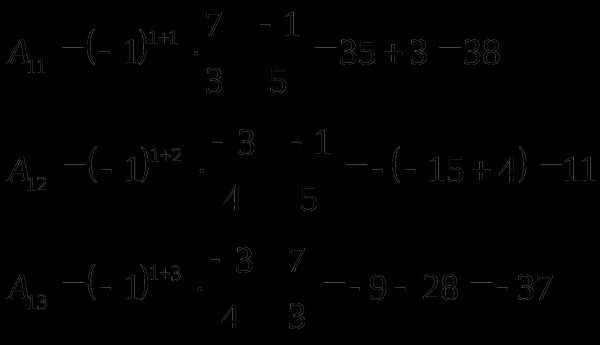
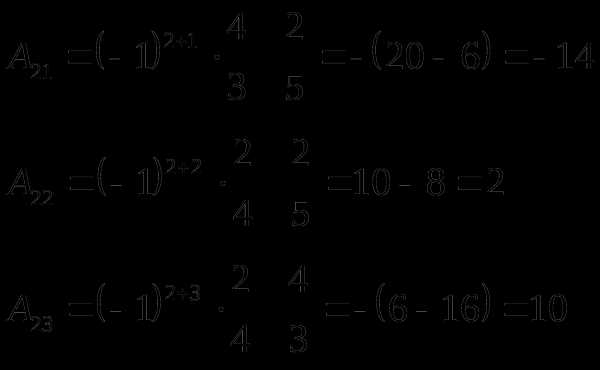
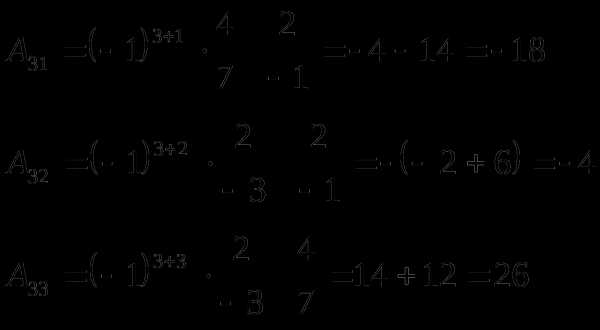
gigabaza.ru

1.1.4. Произведение матриц | Решение задач по математике и другим предме

Умножение матрицы А = ||Aij|| размера на матрицу В = ||Bij|| размера определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т. е. когда N=L. В этом случае произведение матриц определяется следующим образом:

Произведением матриц АВ называется матрица С = ||СIj|| размера , у которой ,

Иначе говоря, элемент Cij равен сумме произведений элементов I-ой строки матрицы А на соответствующий элемент J-ого столбца матрицы В. С помощью знака суммирования можно записать это так:

Пример 2.

Найти произведение матриц

и .

Имеем

.

Отметим, что произведение матриц некоммутативно, т. е. в общем случае АВ Не равно ВА. В приведённом выше примере матрицу В просто нельзя даже умножить на матрицу А. Но, даже если А и В – квадратные матрицы одного порядка (тогда существуют произведения АВ и ВА), то, как показывает следующий пример, произведения АВ и ВА могут не совпадать.

Пример 3.

Пусть , .

Тогда ,

.

Единичной матрицей называется квадратная матрица вида

.

Упражнение 5.

Доказать, что для любой квадратной матрицы А

АЕ=ЕА=А,

Где Е – единичная матрица того же порядка, что и А.

Доказательство.

Пусть А и Е – квадратные матрицы П-го порядка, В = АЕ.

Тогда Bij = Ai1E1J + Ai2E2J + … + Aijejj + … + Ainenj.

Но Eij = 0 при I, не равном J, a Ejj = 1. Следовательно, Bij = Aij·1 = Aij. Таким образом, все элементы матрицы В равны соответствующим элементам матрицы А, то есть В = А.

Если матрица С = ЕА, то СIj = еI1А1J + еI2А2J + … + ЕIiАIj + … + ЕInАNj = 1·Aij = Aij

(учитываем, что Eii = 1, Eij = 0 при I, не равном J). Значит, С = А. Утверждение доказано.

Приведём ряд свойств произведений матриц.

Доказательство.

Пусть размер матрицы A = ||Aij|| матрицы B = ||Bij|| — а матрицы

C = ||Cij|| Имеем AB = ||AIj||, где

Тогда (AB)C = ||GIj||, где

Где — элемент матрицы ВС. Тем самым, если обозначить элемент матрицы А(ВС) через G’Ij, будем иметь

2. А(В+С)=АВ+АС, (В+С)А=ВА+СА

Доказательство.

Пусть матрица A = ||Aij|| имеет размер а матрицы B = ||Bij|| и C = ||Cij|| имеют размер Тогда для элементов матрицы А(В+С)= ||GIj|| имеем

Из определения произведения матриц вытекает, что АВ= ||AIj||, а АС= ||BIj||, т. е. А(В+С)=АВ+АС. Аналогично доказываем, что (В+С)А=ВА+СА.

Упражнение 1.6.

Пусть А и В – квадратные матрицы одного порядка. Вывести формулу для (А+В)2 (при натуральном П Под СN Понимается произведение С·С·…·С).

Решение.

Используем свойства сложения и умножения матриц:

(А + В)2 = (А + В)(А + В) = (А + В)А + (А + В)В = А·А + В·А + А·В +В·В =

= А2 + В·А + А·В +В2.

Заметьте, что результат может совпасть с Формулой сокращенного умножения (А + В)2 = А2 + 2АВ + В2 Только в том случае, если АВ = ВА. В общем случае это неверно!

Ответ: (А + В)2 = А2 + В·А + А·В +В2.

Упражнение7.

Пусть А и В – квадратные матрицы одного порядка. Разложить на множители выражение АВ+2В.

Решение.

Используем свойство единичной матрицы (см. упражнение 5):

Следовательно, В = ЕВ. Тогда АВ + 2В = АВ + (2Е)В = (А + 2Е)В

(использовано свойство 2 произведения матриц).

Ответ: АВ + 2В = (А + 2Е)В.

Упражнение 8.

Пусть А,В и С – квадратные матрицы одного порядка. Разложить на множители выражение А2С +АС 2.

Решение.

Поскольку А2 = А·А, С2 = С·С, запишем заданный матричный многочлен в виде: А2С +АС 2 = А·А·С +А·С·С и воспользуемся свойствами произведения матриц:

А·А·С +А·С·С = А(А·С +С·С) = А((А + С)С) = А(А + С)С.

Ответ: А2С +АС 2 = А(А + С)С.

Упражнение 9.

Найти АВ и ВА.

Решение.

Определим размеры матрицы А: и В: Следовательно, существуют оба произведения: и АВ, и ВА, причем размер матрицы С = АВ: а матрицы D = BA:

Вычислим элементы матрицы С:

Таким образом, матрица С имеет вид:

.

Матрица D состоит из единственного элемента:

Тогда .

Ответ: , .

< Предыдущая		Следующая >

matica.org.ua