Правила нахождения производных, формулы и примеры
Рассмотрим функции и которые являются дифференцируемыми в точке (то есть имеют производную в этой точке). Тогда для нахождения производных используют следующие правила.
1. Производная произведения константы на некоторую функцию равна произведению этой константы на производную от заданной функции, то есть константа выносится за знак производной:
2. Производная суммы/разности двух функций равна сумме/разности производных от каждой их них:
Замечание. Это свойство справедливо и для большего, чем два, числа функций.
Замечание. Первые два правила можно объединить в одно свойство линейности:
3. Производная произведения двух функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй:
4. Производная частного двух функций равна отношению разности произведений производной числителя на знаменатель и числителя на производную знаменателя и квадрата исходного знаменателя, то есть
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Производная частного | Математика
При дифференцировании функций нахождение производной частного обычно вызывает наибольшие затруднения. Лучший способ разобраться и понять, как находится производная частного, — рассмотреть конкретные примеры с подробными пояснениями.
Именно этим мы сейчас и займемся. Для дифференцирования нам понадобится таблица производных. Напишем еще раз правило, по которому берется производная частного:
(Поначалу неплохо его выписать на листочек и держать перед глазами). В отличие от производной произведения, затруднений с определением, где здесь u, а где — v, в производной частного нет: понятно, что все, что вверху, в числителе — это u, а все что внизу, в знаменателе — v. Если u и v — табличные функции, производная частного может быть найдена легко: достаточно расписать все по формуле, найти каждую из производных, и упростить.
Пример. Найти производную частного:
Здесь u=2-4x, v=3x+7
Производную линейной функции полезно помнить: (kx+b)’=k, где k и b — числа, причем k — число, стоящее перех x. А можно найти как производную суммы: (kx+b)’=k·x’+b’=k·1+0=k. Таким образом, (2-4x)’=-4, (3x+7)’=3, и знак умножения перед скобкой и перед буквой обычно не пишется
Общий множитель в числителе выносим за скобку, затем дробь сокращаем:
u=2x³+7x-5, v=6x-8. Расписываем по формуле производной частного:
здесь числитель представляет собой сумму и разность функций. Как находить производную суммы и разности, мы уже знаем.
Здесь u=2lnx+1, v=2√x. Значит, производная частного равна
Примеры для самопроверки. Найти производную частного:
Показать решение
1) u=5x²-8x, v=7-x. Теперь ищем производную частного:
Пока что мы рассмотрели только самые простые примеры на производную частного. В более сложных примерах числитель и знаменатель дроби могут быть сложными функциями, либо являться, в свою очередь, производными произведения и частного. Такие примеры мы обсудим чуть позже.
www.matematika.uznateshe.ru
Производная произведения и частного функции
Формула производной произведения функции имеет вид .
Формула производной частного функции имеет вид .
Однако было бы наивно надеяться, что на контрольной или экзамене Вам обязательно попадётся пример на нахождение производной такого частного: , где легко подставить простенькое выражение в формулу и выдать правильное решение.
В реальных задачах требуется найти производную таких произведений и частных, в которые вкрались тригонометрические выражения и логарифмы, не говоря уже о множителях (константах), и вообще о том, что может содержать произведение или частное функции. Поэтому примеры нахождения производной произведения и частного функций вынесены в эту отдельную статью.
Пример 1.Найти производную функции
.
Решение. От нас требуется найти производную произведения функций. Прежде всего вынесем множитель 2 за знак производной:
.
Теперь применяем формулу дифференцирования произведения:
Приводим слагаемые в скобках к общему знаменателю:

В числителе первого слагаемого можно заметить знакомое по школьной математике выражение двойного угла:
Существует также известное из школьной математики тождество:
.
Подставляем его в наш промежуточный результат и получаем:
.
Производная данного произведения найдена.
Найти производную произведения функций самостоятельно, а затем посмотреть решение
Пример 2.Найти производную функции
.
Пример 4.Найти производную функции
Решение. Перед нами сумма частных. Следовательно, каждое слагаемое будет дифференцировано как частное. Применяем правило дифференцирования частного, не забывая, чему равны производные числа(константы) и самой переменной x:
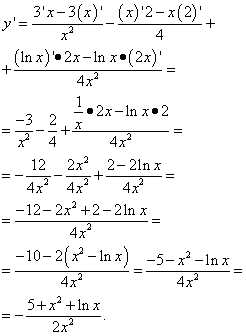
Пример 5.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Находим производную произведения в числителе:
Шаг 3. Находим производную суммы:
Шаг 4. Находим производную функции:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на x:
Найти производную частного функций самостоятельно, а затем посмотреть решение
.
Пример 8.Найти производную функции
Шаг 1. Применим правило дифференцирования произведения:
Шаг 2. Найдём производную частного, помня, что производная константы равна нулю, а корень из константы является также константой:
Шаг 3. Находим производную арктангенса (формула 12 в таблице производных):
Искомая производная:
Пример 9.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Дифференцируем по правилам для произведения и показательной функции (формула 17 в таблице производных):

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Вновь настоятельно рекомендуем изучить производную сложной функции.
Поделиться с друзьями
Весь блок «Производная»
function-x.ru
Частные производные, примеры решений
Теория по частным производным
Пусть функция двух переменных – непрерывна и дифференцируема. Частной производной по называется производная от этой функции по при условии, что – константа. Частной производной по называется производная от этой функции по при условии, что – константа.
Полный дифференциал функции , находится по формуле
Частные производные второго порядка находят дифференцированием производных первого порядка:
При нахождении частных производных, правила и таблица производных элементарных функций справедливы и применимы для любой переменной, по которой ведется дифференцирование.
Примеры
ПРИМЕР 4| Задание | Найти все производные второго порядка для функции |
| Решение | Сначала отыщем все производные первого порядка. При нахождения производной , дифференцируем исходную функцию по ; считается константой. Учитывая свойство линейности производной и формулу для вычисления степенной функции, получим
При нахождения производной , дифференцируем по , а считаем константой, получим:
Теперь перейдем к вычислению производных второго порядка. По определению, вторая производная по равна . Следовательно, от первой производной нужно взять производную по , при этом считаем константой:
Аналогично вычислим частную производную второго порядка по :
Вычислим смешанные производные второго порядка. По определению, смешанная производная равна , то есть от первой производной нужно взять производную по , при этом считаем константой:
Производная , то есть от первой производной берем производную по , а переменную считаем константой:
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Производная произведения функций — доказательство
Пусть функции и определены в некоторой окрестности точки и имеют в точке производные. Тогда их произведение имеет в точке производную, которая определяется по формуле:
Доказательство
Введем обозначения:
;
.
Здесь и являются функциями от переменных и . Но для простоты записи мы будем опускать обозначения их аргументов.
Далее замечаем, что
;
.
По условию функции и имеют производные в точке , которые являются следующими пределами:
;
.
Из существования производных следует, что функции и непрерывны в точке . Поэтому
;
.
Рассмотрим функцию y от переменной x, которая является произведением функций и :
.
Рассмотрим приращение этой функции в точке :
.
Теперь находим производную:
.
Итак,
.
Правило доказано.
Вместо переменной можно использовать любую другую переменную. Обозначим ее как x. Тогда если существуют производные и , то производная произведения двух функций определяется по формуле:
.
Или в более короткой записи
(1) .
Следствие
Пусть являются функциями от независимой переменной x. Тогда
;
;
и т. д. …
Докажем первую формулу. Вначале применим формулу производной произведения (1) для функций и , а затем – для функций и :
.
Аналогично доказываются другие подобные формулы.
Примеры
Пример 1
Найдите производную
.
Решение
Применяем правило дифференцирования произведения двух функций
(1) .
.
Из таблицы производных находим:
;
.
Тогда
.
Окончательно имеем:
.
Ответ
.
Пример 2
Найти производную функции от переменной x
.
Решение
Применяем формулу производной произведения двух функций:
(1) .
.
Применяем формулу производной суммы и разности функций:
.
.
Применяем правила дифференцирования постоянных:
;
.
;
.
Из таблицы производных находим:
;
.
Тогда
;
;
.
Окончательно имеем:
.
Ответ
.
Пример 3
Найти производную функции
.
Решение
Последовательно применяем правила дифференцирования.
;
;
;
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Производная первого порядка, все формулы и примеры
Производная первого порядка функции , заданной явно, находится с помощью таблицы производных

а также правил дифференцирования (нахождения производных):
- Константу можно выносить за знак производной:
- Производная суммы/разности:
- Производная произведения:
- Производная частного двух функций:
| Задание | Найти производную функции, заданной явно
|
| Решение | Искомая производная
Производная суммы/разности функций равна сумме/разности их производных, то есть:
Производную первого слагаемого находим по таблице производных как производную степенной функции тогда
Во втором слагаемом, согласно свойствам производных, вначале вынесем константу 3 за знак производной:
А затем производную найдем по выше предложенной формуле производной степенной функции:
Производную третьего слагаемого находим как производную частного по формуле . Для будем иметь:
А таким образом, для заданной функции имеем:
|
| Ответ |
Производная первого порядка параметрической функции
В случае если функция задана параметрически в виде – параметр, то первая производная такой функции находится по формуле:
Производная первого порядка неявной функции
Если функция задана неявно равнение или то для нахождения первой производной поступают следующим образом:
- дифференцируют левую и правую части заданного равенства:
или
- находят производные от каждой из частей равенства, используя таблицу производных и правила дифференцирования, а также учитывают, что – сложная функция;
- из полученного равенства выражают .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Полная производная функции, формула и примеры
Функция где называется сложной функцией переменных и
В случае, когда функции и зависят только от переменной то есть то производная рассматриваемой функции по независимой переменной задается соотношением:
Если же а то формула (1) принимает вид:
В формулах (1), (2) выражение называется полной производной функции
ПРИМЕР 1| Задание | Найти полную производную функции если |
| Решение | Находим частные производные:
Тогда, согласно формуле (1), имеем:
|
| Ответ |
| Задание | Найти полную производную функции если |
| Решение | Искомую производную будем находить по следующей формуле:
Находим частные производные:
Итак, имеем:
|
| Ответ |
ru.solverbook.com
