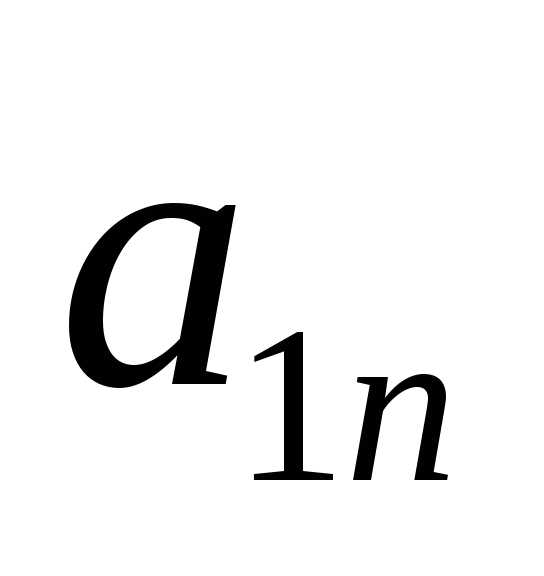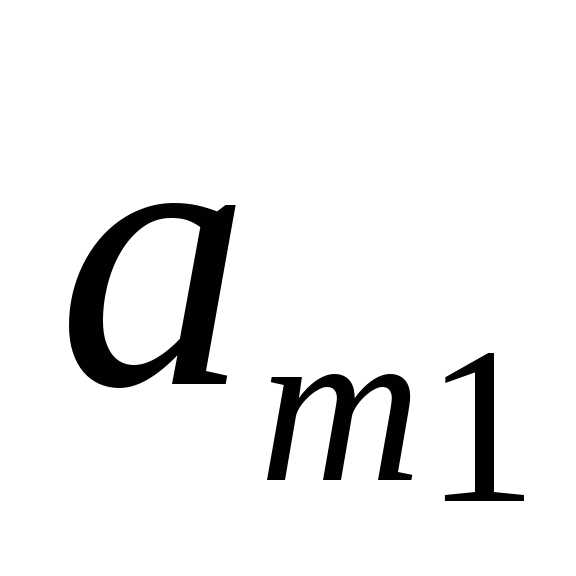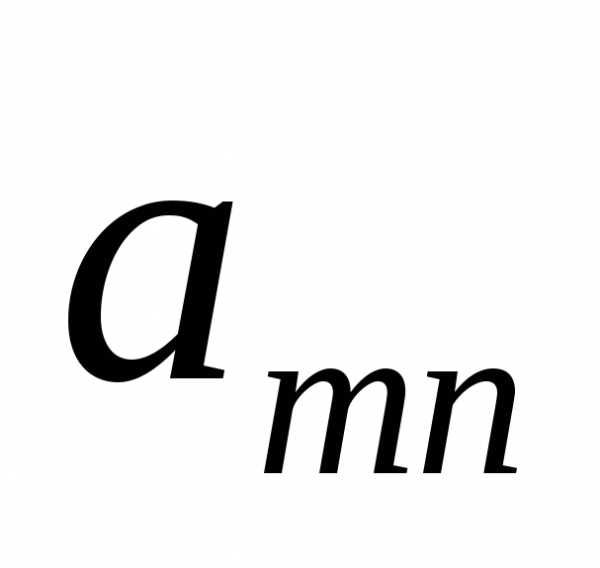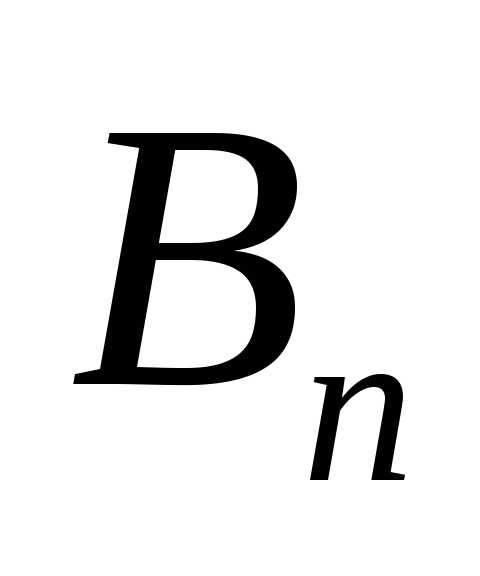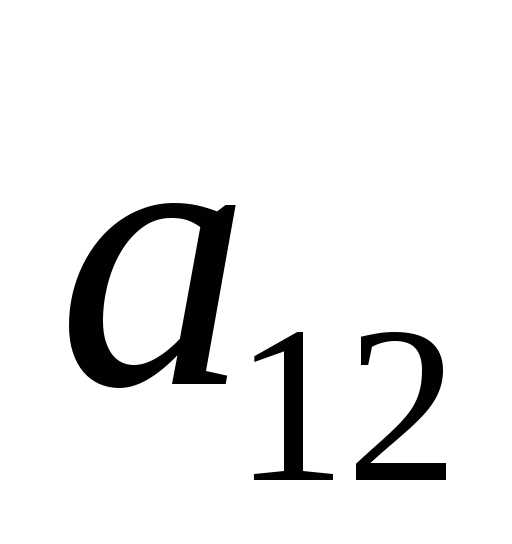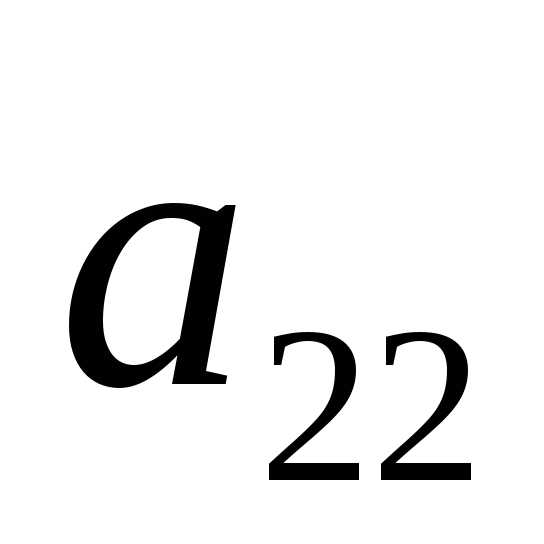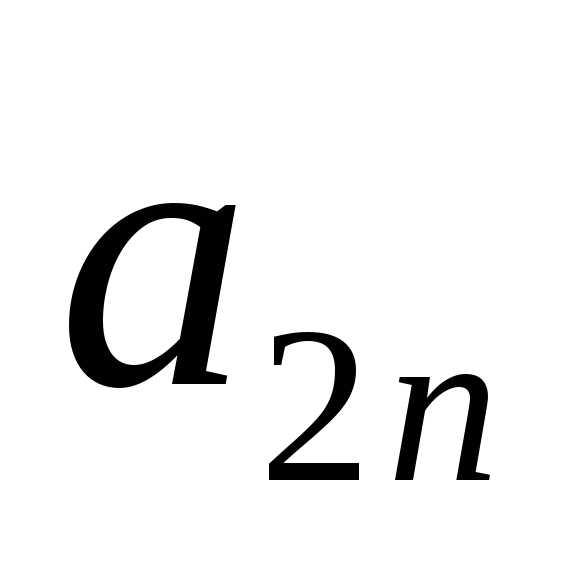Нижняя и верхняя цена игры — Мегаобучалка
Определим стратегию игрока , которая обеспечила бы ему наибольший из возможных выигрышей вне зависимости от того как поведет себя игрок В. Выбирая стратегию, мы должны руководствоваться тем, что наш противник действует разумно и на любую нашу стратегию отвечает той стратегией из числа имеющихся у него, которая обеспечивает нам минимальный выигрыш.
То есть, если мы воспользуемся стратегией , то при разумных действиях противника наш выигрыш будет равен . Обозначим, через наибольшее значение из всех : . Величина называется нижней ценой игрыили максиминным выигрышем (максимином). Число лежит в определенной строке матрицы; та стратегия игрока , которая соответствует этой строке, называется максиминной стратегией. Очевидно, если игрок будет придерживаться максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш, во всяком случае, не меньший .
Нижняя цена игры – гарантированный выигрыш игрока при любой стратегии противника
Очевидно, аналогичные рассуждения можно провести и за противника . Выдвигая стратегию , противник понимает, что мы ответим на эту стратегию той стратегией из всех возможных, которая даст нам максимальный выигрыш равный . Обозначим через наименьшее значение из всех : . Величина называется верхней ценой игры (минимаксом). Соответствующая минимаксному выигрышу стратегия противника называется его минимаксной стратегией. Придерживаясь своей наиболее осторожной минимаксной стратегии, игрок может гарантировать себе проигрыш не более , вне зависимости от того, как поступит игрок .
Верхняя цена игры — гарантированный проигрыш игрока при любой стратегии противника (это тот минимальный проигрыш, который может себе обеспечить игрок , действуя наиболее осторожно).
Принцип осторожности, диктующий игрокам выбор соответствующих стратегий в теории игр в ее приложениях, часто называют принципом минимакса.
Задача № 6.1.
Игроки и одновременно и независимо друг от друга пишут одно из трех чисел: 1, 2 или 3. Если сумма написанных чисел четная, то платит эту сумму в рублях; если она нечетная, то, наоборот, платит эту сумму. Требуется проанализировать игру; составить ее матрицу; найти нижнюю и верхнюю цены игры.
Решение.
Игра состоит из двух ходов (ход игрока и ход игрока ), оба хода личные. У игрока три стратегии: — написать число 1; – написать число 2; – написать число 3. У противника (игрока ) тоже три стратегии. Игра представляет собой игру 3 3 с матрицей, приведенной ниже.
Нижняя цена игры ; верхняя цена игры . Максиминная стратегия игрока это стратегия; применяя ее систематически, игрок может твердо рассчитывать на выигрыш не менее, чем «-3», т.е. его проигрыш не составит более, чем 3 рубля в каждой игре. Аналогично, применяя стратегии
Задача №6.2.
В распоряжении игрока имеются три вида вооружения: , , . У противника имеется три вида самолетов , , . Задача игрока поразить самолет; задача противника (игрока ) – сохранить его. При применении вооружения самолеты , , поражаются соответственно с вероятностями: 0,9; 0,4; 0,2. При применении вооружения самолеты поражаются с вероятностями: 0,3; 0,6; 0,8, а при применении вооружения – 0,5; 0,7; 0,2.
Сформулировать ситуацию в терминах теории игры. Определить верхнюю и нижнюю цены игры.Решение.
Ситуация может рассматриваться как игра 3 3 с двумя личными ходами и одним случайным. Личный ход игрока – выбор типа вооружения. Личный ход игрока – выбор вида самолета. Случайный ход — действие вооружения; этот ход может окончиться поражением или не поражением самолета. Выигрыш игрока равен единице, если самолет поражен, и равен нулю в противном случае. Стратегиями игрока являются три варианта вооружения; стратегиями игрока являются три варианта самолетов. Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения данного самолета данным оружием. Ниже приводится матрица игры:
| 0,9 | 0,4 | 0,2 | 0,2 | |
| 0,3 | 0,6 | 0,8 | 0,3 | |
| 0,5 | 0,7 | 0,2 | 0,2 | |
| 0,9 | 0,7 | 0,8 | 0,7 0,3 |
Нижняя цена игры =0,3; верхняя цена игры =0,7. Наиболее осторожная (максиминная) стратегия игрока – это стратегия ; пользуясь вооружением , игрок гарантирует себе, что будет поражать самолеты в среднем не менее, чем с частотой 0,3. Наиболее осторожной (минимаксной) стратегией игрока будет стратегия . Выбирая второй вид самолетов, игрок может быть уверен, что он будет поражаться не более чем с частотой 0,7.
Продемонстрируем на данном примере свойство неустойчивости минимаксных стратегий.До тех пор пока оба игрока придерживаются своих наиболее осторожных стратегий, средний выигрыш игрока равен 0,6. Это число больше, чем нижняя цена игры =0,3, но меньше, чем верхняя цена игры =0,7. Теперь допустим, что игроку стало известно, что игрок применяет стратегию , он немедленно применит стратегию , чем сведет выигрыш игрока к 0,3. В свою очередь, на стратегию игрок может ответить стратегией , дающей выигрыш 0,9 и т.д.
Таким образом, положение, при котором оба игрока пользуются своими минимаксными стратегиями, является неустойчивым и может быть нарушено поступившими сведениями о стратегии противоположной стороны.
Однако существуют некоторые игры, для которых минимаксные стратегии являются устойчивыми. Это те игры, для которых нижняя цена игры равна верхней: .
Если нижняя цена игры равна верхней, то их общее значение называется чистой ценой игры
Задача №6.3
Пусть игра задана платежной матрицей 4 4:
| 0,4 | 0,5 | 0,9 | 0.3 | 0,3 | |
| 0,8 | 0,4 | 0,3 | 0.7 | 0,3 | |
| 0,7 | 0,6 | 0,8 | 0.9 | 0,6 | |
| 0.7 | 0.2 | 0.4 | 0.6 | 0.2 | |
| 0,8 | 0,6 | 0,8 | 0.9 | 0.6 0.6 |
Найдем нижнюю цену игры: =0,6. Найдем верхнюю цену игры: =0,6. Они оказались равными. Следовательно, у игры есть чистая цена , равная .
Элемент 0,6, выделенный в платежной матрице, является одновременно минимальным в своей строке и максимальным в своем столбце. В геометрии точку на поверхности, обладающую аналогичным свойством, называют седловой точкой; по аналогии этот термин применяется и в теории игр. Элемент матрицы, обладающий этим свойством, называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
Седловая точка – платеж, который одновременно является наибольшим в своем столбце и наименьшим в своей строке.
Стратегии, соответствующие седловой точке, называют оптимальными стратегиями (в данном примере , ), а их совокупность называют решением игры.
Решение игры обладает замечательным свойством. Если один из игроков придерживается своей оптимальной стратегии, а другой игрок будет любым способом отклоняться от своей оптимальной стратегии, то для игрока допустившего отклонение, это никогда не может оказаться выгодным: в лучшем случае выигрыш его останется неизменным, в худшем случае его выигрыш уменьшится (проигрыш увеличится).
Это утверждение легко проверить на примере рассматриваемой игры с седловой точкой. Мы видим, что в случае игры с седловой точкой минимаксные стратегии обладают своеобразной «устойчивостью»: если одна сторона придерживается своей минимаксной стратегии, то для другой невыгодно отклоняться от своей минимаксной стратегии. В данном случае, даже если у игроков имеются сведения о том, что противник избрал свою оптимальную стратегию, это не изменит поведения игроков. Пара оптимальных стратегий в игре с седловой точкой является как бы «положением равновесия»: любое отклонение от оптимальной стратегии приводит отклоняющегося игрока к невыгодным последствиям, вынуждающим его вернуться в исходное положение.
megaobuchalka.ru
Матричные игры — платежная матрица, стратегии, седловая точка, цена игры
В общем случае матричная игра задается прямоугольной матрицей размерности . Номер строки матрицы соответствует номеру стратегии , применяемой игроком . Номер столбца соответствует стратегии , применяемой игроком . Описанная игра однозначно определяется матрицей
Каждый элемент матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую игроком игроку , если выбирает стратегию, соответствующую -й строке, а выбирает стратегию, соответствующую -му столбцу.
Матричную игру часто записывают в развернутой форме в виде таблицы, называемой платежной матрицей.
Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый игрок стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, тогда как второй игрок выбирает стратегию, приводящую его к минимальному проигрышу. В этой связи вводят понятия нижней и верхней чистой цены игры.
Нижней чистой ценой игры (максимином) называется число , определяемое по формуле:
Верхней чистой ценой игры (минимаксом) называется число , определяемое по формуле:
Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными).
Различают стратегии чистые и смешанные. Чистая стратегия первого игрока (чистая стратегия второго игрока) – это возможный ход первого (второго) игрока, выбранный им с вероятностью, равной 1.
В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, то есть .
Если для чистых стратегий , игроков и соответственно имеет место равенство , то пару чистых стратегий называют седловой точкой матричной игры, элемент матрицы, стоящий на пересечении i-й строки и -го столбца – седловым элементом платежной матрицы, а число – чистой ценой игры.
100task.ru
Матричные игры: примеры решения задач
Матричной игрой в математической теории игр называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой — выигрыши первого игрока, которые являются также проигрышами второго игрока.
Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.
Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.
Теперь обо всём по порядку и подробно.
В матричной игре её правила определяет платёжная матрица.
Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока — n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и есть проигрыши.
В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.
Составим платёжную матрицу:
.
Если первый игрок выбирает i-ю чистую стратегию, а второй игрок — j-ю чистую стратегию, то выигрыш первого игрока составит aij единиц, а проигрыш второго игрока — также aij единиц.
Так как aij + (- aij) = 0, то описанная игра является матричной игрой с нулевой суммой.
Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает «орёл» или «решка». Если одновременно выпали «орёл» и «орёл» или «решка» или «решка», то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:
.
Задача теории игр — определить выбор стратегии первого игрока, которая гарантировала бы ему максимальный средний выигрыш, а также выбор стратегии второго игрока, которая гарантировала бы ему максимальный средний проигрыш.
Как происходит выбор стратегии в матричной игре?
Вновь посмотрим на платёжную матрицу:
.
Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.
При решении задач на цену игры и определение стратегии для этих величин у первого игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и уже из них выбрать максимальный. Таким образом, выигрыш первого игрока будет максимальным из минимальных. Отсюда и название — максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии, которую выбирает первый игрок.
Теперь определим величину проигрыша второго игрока, если он использует j-ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v2, называется минимаксным проигрышем или верхней ценой игры.
При решении задач на цену игры и определение стратегии для определения этих величин у второго игрока следует поступать следующим образом. Из каждого столбца выписать значение максимального элемента и уже из них выбрать минимальный. Таким образом, проигрыш второго игрока будет минимальным из максимальных. Отсюда и название — минимаксный выигрыш. Номер столбца этого элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует «минимакс», то независимо от выбора стратегии первым игроком, он проиграет не более v2 единиц.
Пример 1. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк — 2, это нижняя цена игры, ей соответствует первая строка, следовательно, максиминная стратегия первого игрока первая. Наименьший из наибольших элементов столбцов — 5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго игрока — вторая.
Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.
Итак, гарантированный выигрыш первого игрока:
.
Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:
.
Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так:
.
Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:
.
Ещё пример из этой же серии.
Пример 2. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк — 3, это нижняя цена игры, ей соответствует вторая строка, следовательно, максиминная стратегия первого игрока вторая. Наименьший из наибольших элементов столбцов — 5, это верхняя цена игры, ей соответствует первый столбец, следовательно, минимаксная стратегия второго игрока — первая.
Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.
Таким образом, если , то — оптимальная чистая стратегия первого игрока, а — оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены игры достигаются на одной и той же паре стратегий.
В этом случае матричная игра имеет решение в чистых стратегиях.
Пример 3. Дана матричная игра с платёжной матрицей
.
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Нижняя цена игры совпадает с верхней ценой игры. Таким образом, цена игры равна 5. То есть . Цена игры равна значению седловой точки . Максиминная стратегия первого игрока — вторая чистая стратегия, а минимаксная стратегия второго игрока — третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
Решить задачу на матричную игру самостоятельно, а затем посмотреть решение
Пример 4. Дана матричная игра с платёжной матрицей
.
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Правильное решение и ответ.
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.
Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.
Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.
Если первый игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией первого игрока. Иначе говоря, это «смесь» чистых стратегий. При этом сумма этих вероятностей равна единице:
.
Если второй игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией второго игрока. При этом сумма этих вероятностей равна единице:
.
Если первый игрок использует смешанную стратегию p, а второй игрок — смешанную стратегию q, то имеет смысл математическое ожидание выигрыша первого игрока (проигрыша второго игрока). Чтобы его найти, нужно перемножить вектор смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор смешанной стратегии второго игрока (который будет матрицей из одного столбца):
.
Пример 5. Дана матричная игра с платёжной матрицей
.
Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока), если смешанная стратегия первого игрока , а смешанная стратегия второго игрока .
Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока) оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора смешанной стратегии второго игрока:
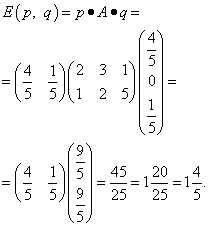
Оптимальной смешанной стратегией первого игрока называется такая смешанная стратегия , которая обеспечивала бы ему максимальный средний выигрыш , если игра повторяется достаточное число раз.
Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия , которая обеспечивала бы ему минимальный средний проигрыш , если игра повторяется достаточное число раз.
По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):
,
.
В таком случае для функции E существует седловая точка, что означает равенство .
Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования, то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.
Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.
Функция цели в прямой задаче линейного программирования:
.
Система ограничений в прямой задаче линейного программирования:
Функция цели в двойственной задаче:
.
Система ограничений в двойственной задаче:
Оптимальный план прямой задачи линейного программирования обозначим
,
а оптимальный план двойственной задачи обозначим
Линейные формы для соответствующих оптимальных планов обозначим и ,
а находить их нужно как суммы соответствующих координат оптимальных планов.
В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:
,
.
Математики-теоретики доказали, что цена игры следующим образом выражается через линейные формы оптимальных планов:
,
то есть является величиной, обратной суммам координат оптимальных планов.
Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:
,
,
в которых вторые сомножители — векторы. Оптимальные смешанные стратегии также, как мы уже определили в предыдущем параграфе, являются векторами. Поэтому, умножив число (цену игры) на вектор (с координатами оптимальных планов) получим также вектор.
Пример 6. Дана матричная игра с платёжной матрицей
.
Найти цену игры V и оптимальные смешанные стратегии и .
Решение. Составляем соответствующую данной матричной игре задачу линейного программирования:
Приводим задачу к канонической форме и решаем задачу и двойственную ей задачу симплекс-методом.
Получаем решение прямой задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Получаем решение двойственной задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Находим цену игры:
.
Находим оптимальную смешанную стратегию первого игрока:
.
Находим оптимальную смешанную стратегию второго игрока:
.
Пусть дана игра с платёжной матрицей
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях, как показано в параграфах 1 и 2.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:
.
Формула для нахождения оптимальной смешанной стратегии второго игрока:
.
Формула для нахождения цены игры:
.
Пример 7. Дана матричная игра с платёжной матрицей
.
Найти оптимальные смешанные стратегии игроков и цену игры.
Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:
.
Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:
.
Цена игры:
.
Матричная игра, седловая точка, чистые стратегии, смешанные стратегии… А для чего всё это? Рассмотрим на примере, как с помощью матричных игр решаются экономические задачи.
Пример 8. Составить матричную игру для следующей задачи.
Предприятие может выпускать три вида продукции (A1, A2, A3), получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний (B1, B2, B3, B4). Дана матрица, элементы которой aij характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м состоянием спроса.
| B1 | B2 | B3 | B1 | |
| A1 | 3 | 3 | 6 | 8 |
| A2 | 9 | 10 | 4 | 2 |
| A3 | 7 | 7 | 5 | 4 |
Решение. Задача сводится к матричной игре предприятия A против спроса B.
Прежде чем решать задачу, можно упростить игру, проведя анализ платёжной матрицы и отбросив стратегии, заведомо невыгодные или дублирующие. Вторая стратегия (второй столбец матрицы) является явно невыгодной для игрока B по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока B — уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить. Получим следующую матрицу:
.
Далее составляется и решается задача линейного программирования. Это мы уже умеем.
Поделиться с друзьями
Материалы по векторам и матрицам
Линейное программирование
function-x.ru
Верхняя и нижняя цена игры
Верхняя и нижняя цена игры [c.91]Как находится верхняя и нижняя цена игры для вполне определенной матричной антагонистической игры двух лиц [c.244]
Выписываем справа минимумы строк и из них выбираем наибольший а, = 0,4 (отмечен звездочкой). Это нижняя цена игры, или максимин. Затем выписываем внизу максимумы столбцов и из них выбираем наименьший р, = 0,8 (отмечен звездочкой). Это верхняя цена игры, или минимакс. [c.151]
При равновесной цене РЕ объем спроса составит X, что значительно превышает фиксированный объем предложения ХЕ-Дефицит приведет к образованию очереди, на место в которой будут претендовать все покупатели, цены спроса которых выше или равны равновесной цене, рР > РЕ- Как видно из нижней части рис. 5.6, товар удастся купить лишь тем из них, кто согласен расплатиться за него помимо денег частью своего свободного времени, Ti >TE. Результаты распределения по очереди приведены в табл. 5.2. Из нее видно, что очередь здесь играет роль дополнительного фильтра для покупателей, чьи индивидуальные цены спроса превышают равновесную цену. Через этот фильтр пройдут лишь те из них, кто согласится пожертвовать сравнительно большой долей своего свободного времени. Сравнив положение покупателей А и В в верхней и нижней частях рис.5.6, можем заметить, что и здесь возможна перепродажа купленного по оче- [c.207]
Еще одно отличие товарной биржи от фондовой заключается в том, что на товарных биржах существуют лимиты. Если стоимость акций Дженерал моторе или 50К может меняться каждый день в зависимости только от настроения и причуд свободного рынка, то на товарные операции ежедневно устанавливаются верхние и нижние границы. Возьмите, например, лимиты на сою на бирже Чикаго борд оф трейд . Они устанавливаются в пределах сорока центов за бушель в обе стороны от средней цены, сложившейся на конец предыдущего дня торгов. Средняя цена есть среднее значение между ценой продажи и ценой покупки. Сорок центов кажутся не очень большой суммой, но сою продают бушелями и каждый контракт — это пять тысяч бушелей. Таким образом, сорок центов выливаются в две тысячи долларов. При неустойчивом рынке не редкость, когда этот лимит исчерпывается за первые несколько минут торгов. У того, кто захочет выйти из игры, может просто не хватить времени. Как и у того, кто захочет вступить в игру. Причем зто может продолжаться несколько дней подряд. А теперь представьте себе, как в такой ситуации чувствует себя тот, у кого на руках сто контрактов, от которых он хотел бы отделаться. [c.85]
Если считать, что между согласием и пониманием существует конфликт, то на основе принципа минимакса для матрицы В находим нижнюю цену игры а = 10, которая гарантирует наличие согласия 10 сотрудников и верхнюю цену игры /3=15, которая показывает, что в худшем случае 15 сотрудников неверно понимают миссию. Матрица Б имеет седловую точку а = /3 = 1 50, а это показывает, что согласие и верное понимание являются для данного опроса оптимальным. [c.154]
На разных этапах жизненного цикла товара управление конкурентоспособностью имеет свою специфику, которая в условиях кризиса носит обостренный (жесткий) характер. На первом этапе — увеличения объема продаж — конкуренция носит ограниченный характер, разница в уровне цен верхнего и нижнего пределов по фирмам-конкурентам сокращается, что создает предпосылки для начала ценового соперничества. Последнее, однако, играет второстепенную роль, оставляя главным фактором конкурентоспособности эксплуатационные качества изделия. На этом этапе производитель имеет возможность и должен вести разработку новых модификаций изделий, дифференцируя потребительский спрос. Это могут быть незначительные усовершенствования с точки зрения удобства пользования изделием, его функционального назначения и т.п. Конверсионная фирма должна стремиться выявить те сегменты рынка, где ее изделия будут выступать в роли специали- [c.316]
Если р = а, т. е. верхняя цена равна нижней цене игры, то соответствующие чистые стратегии называются оптимальными, а про игру говорят, что она имеет седловую точку. Седловая точка является минимальным элементом соответствующей строки и максимальным элементом соответствующего столбца. Эта точка есть точка равновесия игры, определяющая однозначно оптимальные стратегии. Оптимальность здесь означает, что ни один игрок не стремится изменить свою стратегию, так как его противник может на это ответить выбором другой стратегии, дающей худший для первого игрока результат. [c.331]
Один из Десяти принципов экономике (гл. 1) утверждает, что рынок обычно являет собой хороший способ организации экономической деятельности. Вот почему экономисты почти всегда выступают против установления верхних и нижних пределов цен. По мнению экономистов, цена отнюдь не является результатом случайного процесса. Они утверждают, что цены — итог принятия компаниями и потребителями миллионов решений, определяющих кривые спроса и предложения. Цены играют важнейшую роль в достижении равновесия спроса и предложения и, следовательно, координации экономической деятельности. Законодательное установление цен игнорирует сигналы, детерминирующие распределение ресурсов общества. [c.143]
До недавнего времени западные биржевики использовали три типа графиков для отслеживания цен столбики, линейные и крестики-нолики. Столбиковый, или штриховой график давно стал самым популярным. Биржевик начинает с того, что выбирает масштаб времени, в котором хочет работать — в зависимости от его выбора штрих может отражать неделю, месяц, час или только несколько минут биржевой игры. Верхняя точка штриха отражает максимальную силу быков за избранный период, нижняя точка — максимальную силу медведей, а штришки слева и справа — цены открытия и закрытия. Линейные графики отражают только цены закрытия, а крестики-нолики также только цены закрытия, но лишь те, что отличаются от предыдущих не менее, чем на предустановленную величину. [c.314]
Общее значение нижней и верхней цены игры а. = р = v называется чистой ценой игры. [c.148]
Вполне определенной игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство [c.92]
Среди конечных игр, имеющих практическое значение, сравнительно редко встречаются игры с седловой точкой. Более типичным является случай, когда нижняя и верхняя цены игры не совпадают (а Ф / ), причем, нетрудно показать, что тогда а [c.93]
Из основной теоремы следует, что каждая конечная игра имеет цену и она лежит между нижней и верхней ценами игры [c.95]
Рассмотрим матрицу игры (2.2.1). Соотношениям отыскания нижней а и верхней /3 цены игры можно поставить в соответствие эквивалентные им задачи [c.96]
Нижняя и верхняя цена игры [c.162]
Цена игры заключена между нижней и верхней ценами, т. е. а [c.334]
Ее и верхняя цена игры равна нижней, т. е. [c.239]
Обычные разрывы не дают хороших возможностей для игрока, но если вы вынуждены играть, то играйте против них. Если цены поднялись, продавайте как только рынок перестанет давать новые максимумы и поставьте меры предосторожности над максимумом за прошедшие несколько дней. Закрывайте позицию на понижение и извлекайте прибыль на нижнем краю разрыва. Если цены прыгнули вниз, закупайте как только рынок перестанет давать новые минимумы и поставьте меры предосторожности под минимумом за последние несколько дней. Дайте указание продавать и извлекайте прибыль на верхнем краю разрыва. [c.60]
Если вы намерены покупать при прорыве вверх, поместите свой заказ выше верхней границы треугольника и понижайте его по мере того, как треугольник становится уже. Если вы хотите продавать при прорыве вниз, поместите заказ на продажу ниже нижней границы треугольника. По мере того, как треугольник становится уже, повышайте его. Когда вы в игре, поместите предохранительную остановку немного внутри треугольника. Цены могут вернуться к границе, но, при истинном прорыве, они не проникнут глубоко внутрь. [c.68]
В этом разделе верхняя и нижняя цены платежного обязательства вычислены в простейшем примере. Эти числа имеют наглядную интерпретацию как свойства графика функции, определяющей доход от этой ценной бумаги. Вводится и поясняется понятие мартингальных мер, которые играют ключевую роль в исследовании свойств безарбитражности и полноты рынков. [c.25]
Верхняя и нижняя границы торгового канала (см. рисунок 5.13.) называются линиями поддержки (support) и сопротивления (resistan e). Верхние точки (пики) графика лежат на уровне цен, при которых котором давление со стороны продавцов на валютном рынке превосходит давление со стороны покупателей, из-за чего цена не может расти, иначе говоря создается уровень сопротивления росту цен. Точно так же нижние точки графика представляют уровень, на котором давление со стороны продавцов уступает давлению покупателей, и цена не может понизиться, т.е. создается уровень поддержки цены. Чем дольше график цены остается в пределах торгового канала, касаясь его границ, тем более надежными являются эти линии. При этом важную роль играет также торговый объем, особенно когда речь идет о событиях, происходящих вблизи линий поддержки и сопротивления. Если цена отскакивает от этих линий при большом объеме, надежность тренда возрастает. Подлинность прорыва проверяется по правилу изменения цены после прорыва на 3% от предыдущей цены закрытия. [c.64]
На рисунках 3.4—3.7 представлены некоторые наиболее часто встречающиеся типы свечей. На рисунке 3.4 показана длинная черная свеча, которая соответствует медвежьему периоду развития рынка, когда цена открытия близка к максимальной цене, а цена закрытия опускается почти до минимальной цены. Свеча на рисунке 3.5 является полной противоположностью указанной выше и соответствует бычьему периоду развития рынка. Цены колеблются в широком диапазоне рынок открылся вблизи минимальной цены, а закрылся — вблизи максимальной цены торговой сессии. На рисунке 3.6 показаны свечи с малым размером тела, что соответствует упорной схватке между быками и медведями. Такие свечи называют волчками (spinning tops) они, как правило, нейтральны, когда возникают в пределах узкого торгового коридора. Как будет показано далее в разделе о звездах и моделях харами , волчки начинают играть важную роль при образовании определенных графических моделей. Волчки могут быть как черными, так и белыми. На рисунке 3.6 свечи имеют небольшие верхнюю и нижнюю тени, но в данном случае размер теней не играет важной роли. Главной отличительной чертой волчка является маленькое тело. На рисунке 3.7 показаны варианты свечей, у которых вообще нет тела. Оно превратилось в горизонтальную линию. Такие свечи носят название Дожи (doji). [c.20]
Длинноногий дожи играет особо важную роль, если он появляется на вершине. У дожи, показанного на рисунке 8.2, — длинные верхняя и нижняя тени, что явно свидетельствует о периоде нерешительности на рынке. В течение торговой сессии рынок быстро поднимался, а затем резко упал (или наоборот). Затем цена закрытия сравнялась с ценой открытия (или приблизилась к ней вплотную). Если цены открытия и закрытия находятся в центре ценового диапазона сессии, такую свечу называют рикшей . Если свеча не является дожи, но обладает очень длинной верхней и/или нижней тенью и маленьким телом, ее назьюают высокой волной (high-wave). Группа высоких волн является сигналом разворота тенденции. Японские аналитики говорят о свечах с очень длинными тенями, что они сбились с пути . [c.159]
Довольно распространенный способ использования линии тренда линейной регрессии заключается в построении каналов. Канал линейной регрессии — его разработал Гилберт Рафф (Gilbert Raff) — состоит из двух параллельных линий, равноудаленных вверх и вниз от линии тренда линейной регрессии. Расстояние между границами канала и линией регрессии равно величине максимального отклонения цены закрытия от линии регрессии. Все ценовые изменения происходят в границах регрессионного канала, где нижняя граница играет роль линии поддержки, а верхняя — линии сопротивления. Обычно цены выходят за границы канала лишь на короткое время. Если же они остаются за пределами канала дольше обычного, то это предвещает возможность разворота тенденции. [c.110]
Стратегии игроков, определяемые по правилам максими-на и минимакса, будут удовлетворять принципу равновесия, если реализуемая при этом ситуация (а, Ь ) обеспечивает равенство нижней и верхней цены игры, т. е. v(a, Ъ ) = v = v. В этом случае говорят, что игра имеет ситуацию равновесия в чистых стратегиях. От равновесной ситуации невыгодно отклоняться ни одному из игроков, так как она сформирована из стратегий, доставляющих наибольший гарантированный результат каждому из них. Именно равновесная ситуация может рассматриваться в качестве решения игры. [c.242]
Японские подсвечники, в отличие от западных биржевых чартов, очень большое внимание уделяют связи между ценами открытия и закрытия. Подсвечники показывают эту связь совершенно уникальным образом. Расстояние между ценой открытия и закрытия формируют тело подсвечника, причем если рынок закрылся выше по сравнению с открытием, то тело подсвечника оставлено белым, наоборот, при падающем рынке тело подсвечника заполняется черным цветом. Тонкие линии выше и ниже реального тела, подобно биржевому чарту, отражают максимальную и минимальную цены за период. Они известны как тени. Если верхняя тень отсутствует, т. е. максимальная цена равна цене открытия или закрытия, то верхняя часть называется бритым верхом и соответственно для равенства минимальной цены ценам открытия либо закрытия нижняя часть — бритым даем. Подсвечник, где цены открытия и закрытия очень близки или равны, в результате чего он не имеет тела, называется доджи. Он играет очень важную роль в анализе, поскольку практически всегда характеризует нерешительность на рынке и отсутствие преобладающих тенденций. Многие из образцов подсвечни- [c.245]
Некоторые трейдеры используют колебания цен внутри «торгового коридора» для биржевой игры. Они покупают на спадах, когда цены оказываются у нижней границы, и продают на оживлениях при достижении ценами верхней границы «коридора». Благодаря четко определенным границам «коридора», подобная тактика дает трейдеру некоторые преимущества, позволяя получать прибыль в условиях неопределенного рынка. Поскольку при такой игре позиции открываются вблизи известных границ «коридора», рискованность сделок относительно невилика и легко просчитывается. Пока границы «торгового коридора» не нарушены, данный подход (позволяющий получать прибыль без учета тенденции рынка) может оказаться довольно успешным. При прорыве границ «коридора» трейдер не только немедленно закрывает последнюю убыточную позицию, он также может заключить новую сделку в направлении возникшей тенденции. При застое рынка особенно полезна такая разновидность индикаторов, как осциллятор, но после прорыва линии тренда (по причинам, которые мы обсудим ниже, в главе 10) его эффективность несколько снижается. [c.147]
Играя в пределах прямоугольника, покупайте на нижней границе и продавайте на верхней. Осциляторы помогут вам решить, когда цены готовы развернуться в пределах прямоугольника. Стохастика (Sto hasti ), индекс относительной силы (RSI) и %R Вильямса (Wm%R) (см. главу 4), указывают на изменение движения цен в прямоугольнике, когда они доходят до своих ключевых уровней меняют направление движения. [c.65]
economy-ru.info
|
ТОП 10: |
Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности mxn . Пусть игрок А выбирает некоторую стратегию Аi, тогда в наихудшем случае он получит выигрыш, равный . Предвидя такую возможность, игрок А должен выбирать такую стратегию, чтобы максимизировать свой минимальный выигрыш :
Величина -гарантированный выигрыш игрока А –нижняя цена игры. Стратегия, обеспечивающая получение называется максиминной. Игрок В, выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии Вj его проигрыш не превосходит максимального из значений элементов j-го столбца матрицы, т.е. меньше или равен . Поэтому игрок В, очевидно, выберет такое значение j, при котором его максимальный проигрыш минимизируется:
Величина называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) – минимаксной. Нижняя цена игры всегда не превосходит верхней цены игры. Если , то число v называется ценой игры. Игра, для которой , называется игрой с седловой точкой. Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными. Седловая точка соответствует оптимальным стратегиям игроков . Доказательство теоремы о существовании в любой конечной матричной игре нижней и верхней цен игры в смешанных стратегиях. Так как функция α (P) по лемме H (P,Q): (P,Q)Î x , где P= , Q=( ) непрерывна на компакте , то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях: =max(PÎ α(P) Аналогичным образом обосновывается существование верхней цены игры в смешанных стратегиях =min(QÎ β(Q)
27. Понятие стратегии, оптимальной во множестве смешанных стратегий. Основная теорема матричных игр Дж.Фон Неймана. • игра без седловой точки; • игроки используют случайную смесь чистых стратегий с заданными вероятностями; • игра многократно повторяется в сходных условиях; • при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком; • допускается осреднение результатов игр. 2) Для матричной игры с любой матрицей А величины
Доказательство критерия оптимальности смешанной стратегии игрока А в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока В. В определении равновесной ситуации в чистых стратегиях ( , учитывая, что( =a , гдеF – функция выигрыша, неравенство можно переписать в виде неравенства max (1≤i≤m)F( =F( которое соответствует неравенству, а равенство в виде равенства соответствующего равенству. Это означает по данному определению седловой точки функции, что равновесная ситуация в чистых стратегиях ( является седловой точкой функции выигрышаF. Вместе с тем значение F =a , также называют седловой точкой матрицы игры. В общем случае седловые точки произвольных функций двух векторных аргументов также обладают свойствами равнозначности и взаимозаменяемости, доказанными для частного случая седловых точек матриц игры.
29. Доказательство критерия оптимальности смешанной стратегии игрока в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества смешанных стратегий игрока А. Теорема. Для того, чтобы стратегия Qo игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство H(P,Qo)≤V для любого РϵSB, т.е. выбор игроком В одной из своих оптимальных стратегий Qoгарантирует ему проигрыш, не большей цены игры V, при любой стратегии Р игрока А. Доказательство. Пусть Qo – оптимальная стратегия игрока В. Тогда по основной теореме матричных игр фон Неймана показатель эффективности β(Qo) стратегии Qo равен цене игры V: V= β(Qo). Рассматривая β(Qo) как показатель эффективности β(Qo, SA) стратегии Qo относительно множества SA смешанных стратегий игрока А, будем иметь по определению β(Qo, SA)=maxH(P,Qo). Следовательно, V= β(Qo)= β(Qo, SA)=maxH(P,Qo), откуда получаем неравенство H(P,Qo)≤V. Но V= V¾=min β(Q)≤ β(Qo). Получаем β(Qo)=V, которое в силу теоремы фон Неймана означает, что стратегия Qo являеься оптимальной. 30. Доказательство критерия оптимальности смешанной стратегии игрока в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока . Теорема. Пусть V- цена игра, H(P0,Q) – функция выигрыша, SCB={B1,…,Bn} – множество чистых стратегий игрока В. Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы Н(Р0,Bj)≥V, j=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P0, Q)≥V и Н(Р0,Bj)≥V. Докажем эквивалентность. Пусть справедливо неравенство H(P0, Q)≥V. Так как это неравенство имеет место для любой стратегии QϵSB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Bjϵ SCB, j=1,…,n , т.е. неравенство Н(Р0,Bj)≥V имеет место. Таким образом импликация H(P0, Q)≥V на Н(Р0,Bj)≥V доказана. Теперь пусть имеет место неравенство Н(Р0,Bj)≥V, j=1,…,n. Тогда по формуле с учетом того, что =1, получим, , QϵSB, т.е. доказано неравенство H(P0, Q)≥V. Таким образом, справедлива импликация Н(Р0,Bj)≥V на H(P0, Q)≥V и, следовательно, эквивалентность H(P0, Q)≥V и Н(Р0,Bj)≥V.
31. Доказательство критерия оптимальности смешанной стратегии игрока в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции в смешанных стратегиях и множества чистых стратегий игрока . Теорема. Пусть V- цена игра, H(P,Q0) – функция выигрыша, SCA={A1,…,An} – множество чистых стратегий игрока A. Для того чтобы стратегия Q0 игрока В была оптимальной, необходимо и достаточно, чтобы Н(Ai,Q0)≤V, i=1,…,n. Доказательство. Достаточно установить эквивалентность неравенств H(P,Qo)≤V и Н(Ai,Q0)≤V. Докажем эквивалентность. Пусть справедливо неравенство H(P,Qo)≤V. Так как это неравенство имеет место для любой стратегии PϵSA игрока A, то оно, в частности, будет справедливым и для его чистых стратегий Aiϵ SCA, i=1,…,n , т.е. неравенство H(P,Qo)≤V имеет место. Таким образом импликация H(P,Qo)≤V на Н(Ai,Q0)≤V доказана. Теперь пусть имеет место неравенство Н(Ai,Q0)≤V, i=1,…,n. Тогда по формуле с учетом того, что =1, получим, , PϵSA, т.е. доказано неравенство H(P,Qo)≤V. Таким образом, справедлива импликация Н(Ai,Q0)≤V на H(P,Qo)≤V и, следовательно, эквивалентность H(P,Qo)≤V и Н(Ai,Q0)≤V.
32. Доказательство теоремы о геометрической интерпретации множества стратегий игрока , оптимальных во множестве смешанных стратегий. Следствие. Множество SOA оптимальных стратегий игрока А является выпуклым многогранником (политопом), содержащимся в симплексе SA всех смешанных стратегий игрока А. Доказательство. Для каждой оптимальной стратегии Р0=(р01,…,р0m) игрока А справедливо неравенство Н(Р0,Bj)≥V, j=1,…,n, которое можно переписать следующим образом: , j=1,…,n. Множество точек Р0=(р01,…,р0m) m-мерного пространства Rm, координаты p0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Р0=(р01,…,p0m), координаты p0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока А SOA ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то SOA является выпуклым многогранником.
33. Доказательство теоремы о геометрической интерпретации множества стратегий игрока , оптимальных во множестве смешанных стратегий. Следствие. Множество SOВ оптимальных стратегий игрока В является выпуклым многогранником (политопом), содержащимся в симплексе SВ всех смешанных стратегий игрока В. Доказательство. Для каждой оптимальной стратегии Q0=(q01,…,q0m) игрока А справедливо неравенство Н(Ai,Q0)≤V, i=1,…,m, которое можно переписать следующим образом: , j=1,…,m. Множество точек Q0=(q01,…,q0m) m-мерного пространства Rm, координаты q0i, i=1,…,m, которых удовлетворяет этому неравенству для фиксированного jϵ{1,…,n}, является замкнутым полупростанством, а множество точек Q0=(q01,…,q0m), координаты q0i, i=1,…,m, которых удовлетворяют этому неравенству для всех j=1,…,n, является пересечением конечного числа n замкнутых полупростанств и называется выпуклым замкнутым полиэдром. Так как к тому же множество оптимальных оптимальных стратегий игрока B SOB ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SB, то SOB является выпуклым многогранником.
34. Доказательство в терминах множеств смешанных стратегий игроков и критерия того, что число — цена игры в смешанных стратегиях, а и — стратегии, оптимальные во множестве смешанных стратегий соответственно игроков и . Теорема. Для того чтобы V было ценой игры, а Р0 и Q0 – оптимальными стратегиями соответственно игроков А и В, другими словами, для того, чтобы {P0,Q0,V} было решеннием игры, необходимо и достаточно выполнение двойного неравенства H(P,Q0)≤V≤H(P0,Q) для любых PϵSA и QϵSB. Доказательство. Необходимость. Пусть V – цена игры и P0, Q0 – оптимальные стратегии. Тогда неравенства H(P,Qo)≤V и H(P0, Q)≥V справедливы и их можно записать в неравенство H(P,Q0)≤V≤H(P0,Q). Достаточность. Пусть для некоторого числа V и некоторых стратегий Р0 игрока А и Q0 игрока В выполняется двойное неравенство (P,Q0)≤V≤H(P0,Q). Так как это неравенство верно для любых PϵSA и QϵSB, то в частности оно будет справедливо и для Р= P0, Q= Q0: H(P0,Q0)≤V≤H(P0,Q0), т.е. V=H(P0,Q0). Тогда получим: H(P,Q0)≤ H(P0,Q0)≤H(P0,Q), PϵSA и QϵSB. max(PϵSA)H(P,Q0)≤ H(P0,Q0)≤min(QϵSB)H(P0,Q) или β(Qo)≤ H(P0,Q0)≤α(Р0). Отсюда по определению верхней и нижней цен игры получим: V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. Из H(P0,Q0)≤V≤H(P0,Q0) и V¾=min(QϵSB)β(Q)≤ β(Qo)≤ H(P0,Q0)≤α(Р0)≤ max(PϵSA) α(Р)=V¾. следует, что V – цена игры, а также справедливость равенства V= α(Р0)= β(Qo)= H(P0,Q0), которое по определению оптимальных стратегий, означает, что P0,Q0 – оптимальные стратегии соответственно игроков А и В.
35. Доказательство в терминах множеств чистых стратегий игроков и критерия того, что число — цена игры в смешанных стратегиях, а и — стратегии, оптимальные во множестве смешанных стратегий соответственно игроков и . Теорема. Для того, чтобы V была ценой игры, а P0,Q0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства Н(Ai,Q0)≤V≤ Н(Р0,Bj), i=1,…,m, j=1,…,n. Доказательство. Достаточно доказать эквивалентность неравенств H(P,Q0)≤V≤H(P0,Q) и Н(Ai,Q0)≤V≤ Н(Р0,Bj). Пусть справедливо неравенство H(P,Q0)≤V≤H(P0,Q). Так как оно имеет место для любых стратегий PϵSA и QϵSB, то, в частности, оно справедливо и для любых чистых стратегий P=Ai, i=1,…,m, и Q=Bj, j=1,…,n, т.е. справедливо двойное неравенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Докажем обратное. Пусть имеет равенство Н(Ai,Q0)≤V≤ Н(Р0,Bj). Тогда из него, допустив получим: = =1, получим: , PϵSA и QϵSB, т.е. справедливо неравенство H(P,Q0)≤V≤H(P0,Q).
36. Доказательство в терминах седловых точек выигрыш-функции критерия того, что число — цена игры в смешанных стратегиях, а PO и QO — стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и B. Для того чтобы V было ценой игры, а Р° и Qo — оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно, чтобы (Р°, Q°) была седловой точкой выигрыш-функции Н(Р, Q) и Н(Р°, Q°) = V. Множество номеров i ∈ {1,2,…,m}, для которых pi> 0, называется спектром смешанной стратегии Р={р1,р2,…, рm) и обозначается supp Р. Таким образом, suppР = {i∈{1,2,…, m):рi>0} Чистая стратегия Ai— называется пассивной или активной относительно смешанной оптимальной стратегии Р° = (р1O,р2O,…, рmO)в зависимости от того, i не ∈supp Р° или i∈supp Р°, т.е. в зависимости от того, pi0 = 0 или рi0> 0. |
infopedia.su
Нижняя и верхняя цена игры
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
|
… | … | … | … | … | |
|
|
| … |
|
|
|
|
| … |
|
В таблице приведены числа  —
минимально возможный выигрыш игрока
А, применяющего стратегию
—
минимально возможный выигрыш игрока
А, применяющего стратегию (
(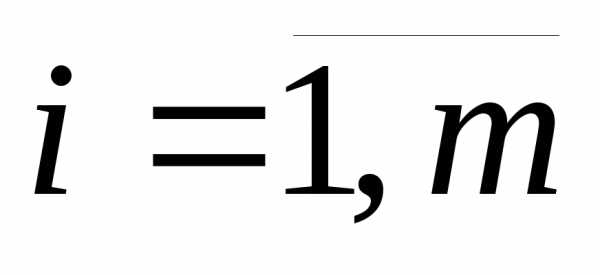 )
и
)
и — максимально возможный проигрыш игрока
В, если он пользуется стратегией
— максимально возможный проигрыш игрока
В, если он пользуется стратегией (
(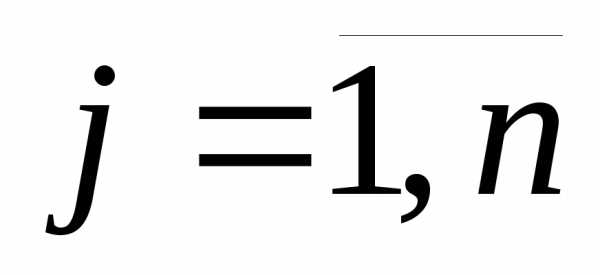 ).
).
Число называютнижней чистойценой игры(максимином), а соответствующую ему чистую стратегию – максиминной.
Число  показывает, какой минимальный
гарантированный выигрыш может получить
игрок А, правильно применяя свои чистые
стратегии при любых действиях игрока
В.
показывает, какой минимальный
гарантированный выигрыш может получить
игрок А, правильно применяя свои чистые
стратегии при любых действиях игрока
В.
Число называютверхней чистой ценой игры(минимаксом), а соответствующую чистую стратегию минимаксной.
Число  показывает, какой минимальный
гарантированный проигрыш может быть у
игрока В, при правильном выборе им своих
чистых стратегий независимо от действий
игрока А.
показывает, какой минимальный
гарантированный проигрыш может быть у
игрока В, при правильном выборе им своих
чистых стратегий независимо от действий
игрока А.
Ясно, что  .
.
Если 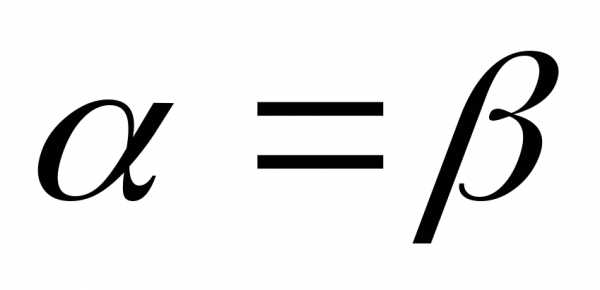 ,
то говорят, что игра имеет седловую
точку в чистых стратегиях и чистую цену
игры.
Стратегии образующие седловую точку,
являются оптимальными. Тройку (
,
то говорят, что игра имеет седловую
точку в чистых стратегиях и чистую цену
игры.
Стратегии образующие седловую точку,
являются оптимальными. Тройку (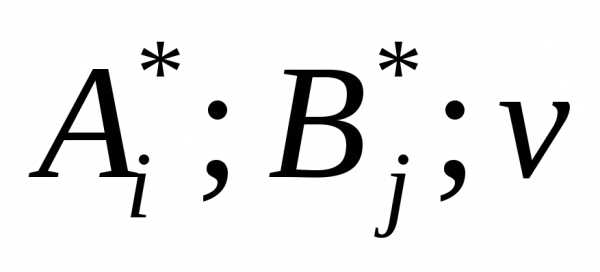 )
называют решением игры.
)
называют решением игры.
Пример
Проверим наличие седловой точки.
1
4
9
16
1
16
9
4
1
1
10
10
10
15
10
16
10
10
16
Для игрока А: Max (1, 1, 10) = 10
Для игрока В: min(16, 10, 10, 16) = 10
Седловые точки — (3, 2) и (3, 4). Цена игры = 10; оптимальный выбор для игрока 1 — третий, для игрока 2 равнозначны второй и третий
Смешанные стратегии
Для игр без седловых точек оптимальные стратегии игроков находятся в области смешанных стратегий.
Смешанной стратегией игрока А называют вектор , компоненты которого удовлетворяют условиям.
Смешанной стратегией игрока В называют вектор , компоненты которого удовлетворяют условиям.
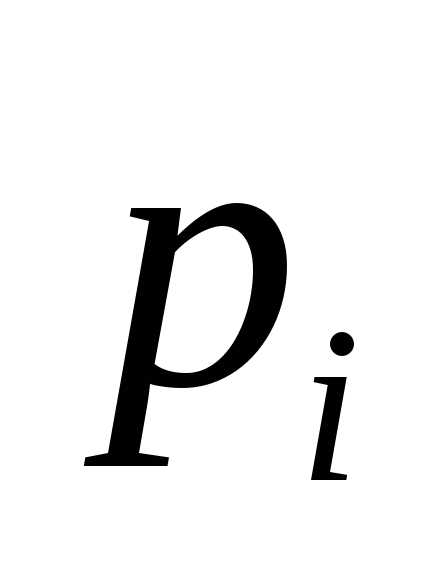 и
и — вероятности, с которыми игроки А и В
выбирают свои чистые стратегии
— вероятности, с которыми игроки А и В
выбирают свои чистые стратегии и
и в ходе игры.
в ходе игры.
При использовании смешанных стратегий
игра приобретает случайный характер,
случайной становится и величина выигрыша
игрока А (проигрыша игрока В). Эта величина
является функцией смешанных стратегий  и
и и определяется по формуле.
и определяется по формуле.
Функцию 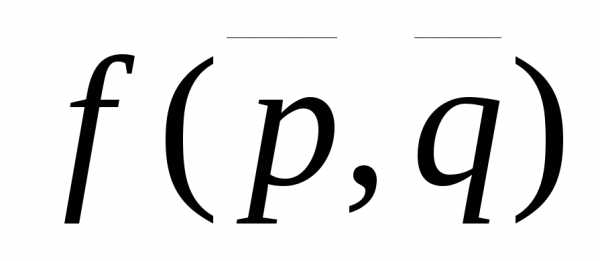 называют функцией выигрыша или платежной
функцией.
называют функцией выигрыша или платежной
функцией.
Смешанные стратегии называются
оптимальными, если они образуют седловую
точку для платежной функции 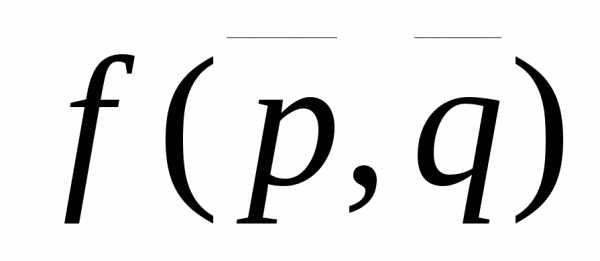 ,
т.е. если они удовлетворяют неравенству.
,
т.е. если они удовлетворяют неравенству.
Величину называют ценой игры.
Поиск оптимальных смешанных стратегий
начинают с упрощения платежной матрицы.
Если в платежной матрице элементы k-й
строки не меньше соответствующих
элементовs-й строки, т. е.,
то говорят, что стратегия доминирует над стратегией
доминирует над стратегией .
Аналогично, если элементыl-го
столбца не превосходят соответствующих
элементовr-го столбца, т. е.,
то говорят, что стратегия
.
Аналогично, если элементыl-го
столбца не превосходят соответствующих
элементовr-го столбца, т. е.,
то говорят, что стратегия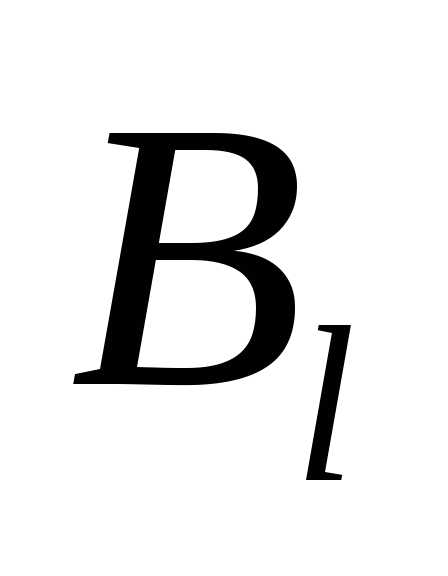 доминирует над стратегией
доминирует над стратегией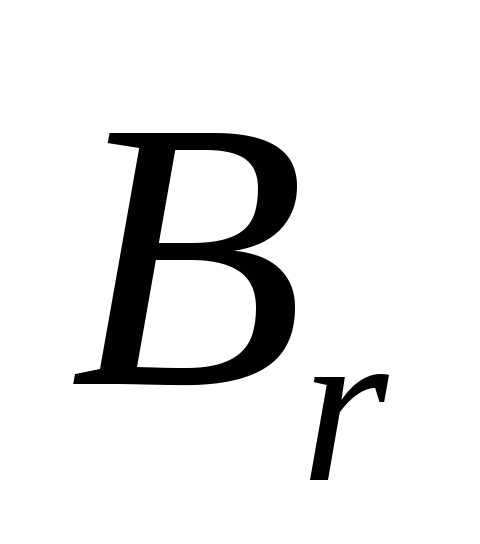 .
Частным случаем доминирования стратегий
является дублирование стратегий, когдаили.
Исключение из платежной матрицы
доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно)
позволяет уменьшить ее размерность, а
это упрощает решение игры. Вероятность
применения доминируемых стратегий
равна нулю.
.
Частным случаем доминирования стратегий
является дублирование стратегий, когдаили.
Исключение из платежной матрицы
доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно)
позволяет уменьшить ее размерность, а
это упрощает решение игры. Вероятность
применения доминируемых стратегий
равна нулю.
Оптимальные смешанные стратегии  и
и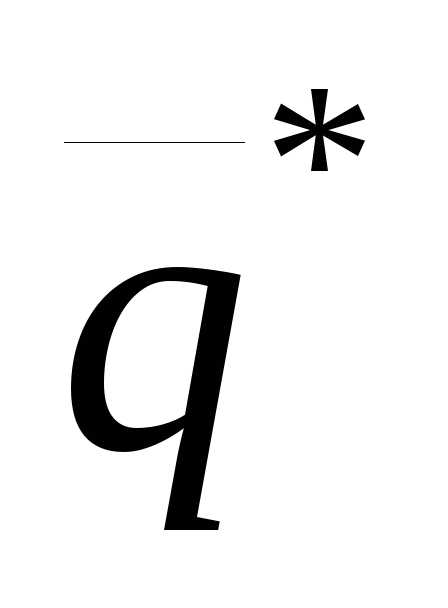 в игре с платежной матрицей
в игре с платежной матрицей и
ценойvостаются оптимальными и для
игры с платежной матрицей(гдеb> 0) и ценойbv
+ с. На этом основании платежную матрицу
можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными
числами, а это упрощает расчеты.
и
ценойvостаются оптимальными и для
игры с платежной матрицей(гдеb> 0) и ценойbv
+ с. На этом основании платежную матрицу
можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными
числами, а это упрощает расчеты.
Пример
Упростить следующую платежную матрицу.
Методы решения матричных игр. Решение матричной игры сведением к задаче линейного программирования
Пусть игра задана платежной матрицей.
| | | … | |
| | | … | |
| | | … | |
… | … | … | … | |
| | | … | |
Оптимальные смешанные стратегии иигроков А и В могут быть найдены в результате решения пары двойственных задач линейного программрования.
Для игрока А:
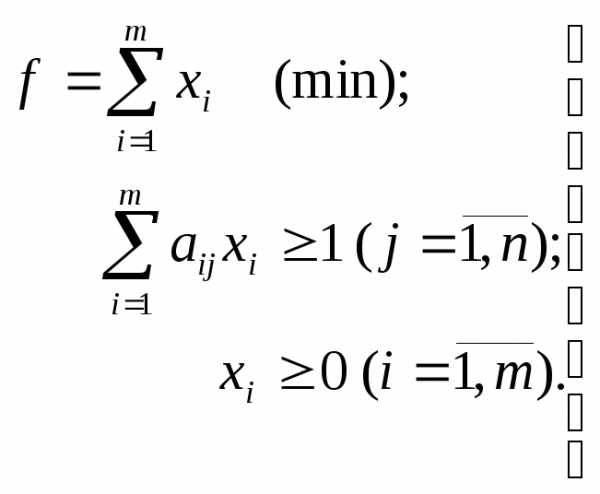
В результате решения задачи находятся
оптимальный вектор
и ,
а затем.
,
а затем.
Для игрока В:
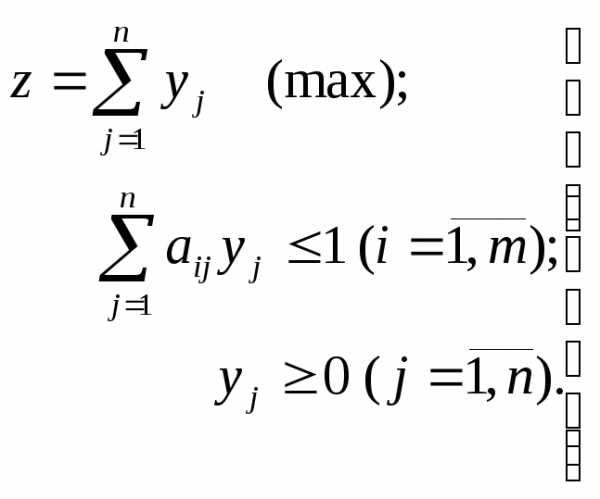
Решая задачу , находят оптимальный
вектор
и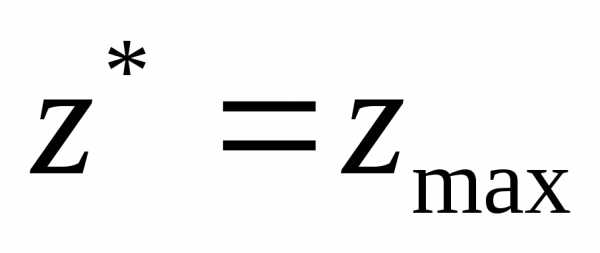 ,
а затем.
,
а затем.
Пример
1 | 3 | 5 | 7 | 1 |
7 | 4 | 3 | 1 | 1 |
4 | 4 | 4 | 3 | 3 |
7 | 4 | 5 | 7 |
Проверим наличие седловой точки.
Для игрока А: Max(1, 1, 3) = 3
Для игрока В: min(7, 4, 5, 7) = 4
Так как значения не совпадаю, Седловой точки нет, а цена игры Vнаходится в промежутке [3; 4].
Решим задачу в смешанных стратегиях. Для этого составим пару двойственных задач.

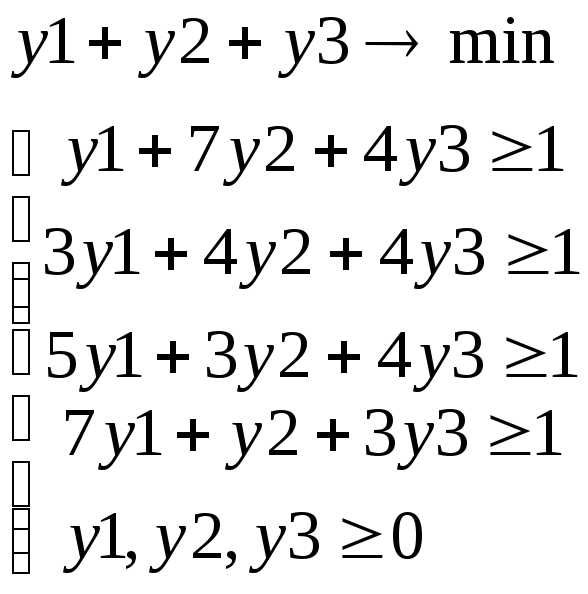
Решая задачи, находим, что
X={0.05, 0.15, 0, 0.07}
Y={0.07, 0.05, 0.15}
F=0.27
Отсюда находим цену игры и вероятности применения стратегий
V=1/0.27=3.7
P={0.19, 0.56, 0.26}
Q={0.26, 0.19, 0.56}
studfiles.net
2. Нижняя и верхняя цена игры. Принцип минимакса
Рассмотрим конечную
игру
размерностиm×n.
Решим задачу: определить оптимальные
стратегии игроков. Проанализируем
каждую из стратегий первого игрока.
Выбирая стратегию 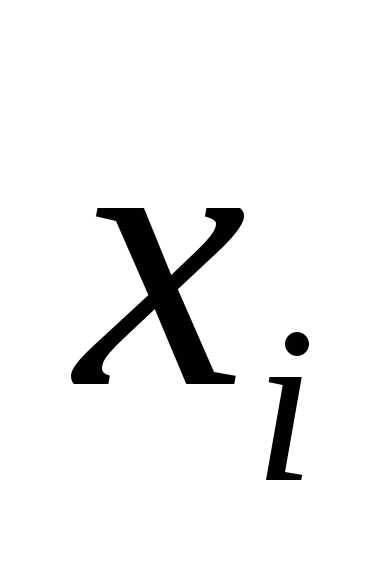 ,
он должен рассчитывать на то, что второй
игрок ответит на нее той из своих
стратегий
,
он должен рассчитывать на то, что второй
игрок ответит на нее той из своих
стратегий ,
для которой выигрыш первого игрока
,
для которой выигрыш первого игрока минимален. Обозначим это значение
выигрыша
минимален. Обозначим это значение
выигрыша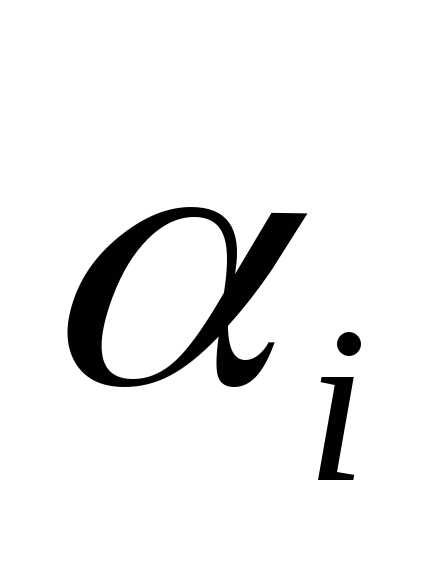 :
:
(1) 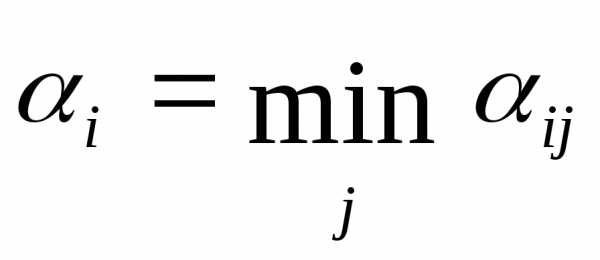 .
.
Здесь знаком  обозначено
минимальное значение параметра
обозначено
минимальное значение параметра  при всех возможных
при всех возможных .
.
Выбирая какую–либо
стратегию 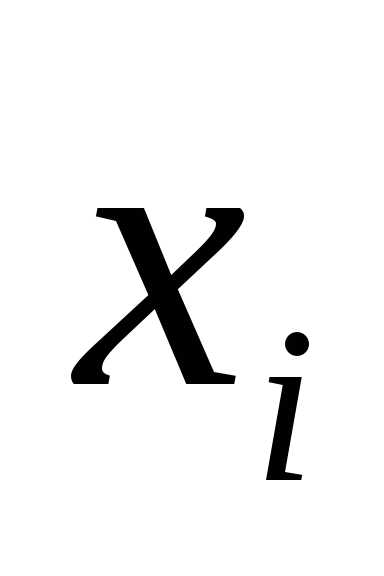 ,
первый игрок должен понимать, что в
результате разумных действий противника
он не выиграет больше, чем
,
первый игрок должен понимать, что в
результате разумных действий противника
он не выиграет больше, чем .
Действуя осторожно и избегая всякого
риска, он должен выбрать ту стратегию
.
Действуя осторожно и избегая всякого
риска, он должен выбрать ту стратегию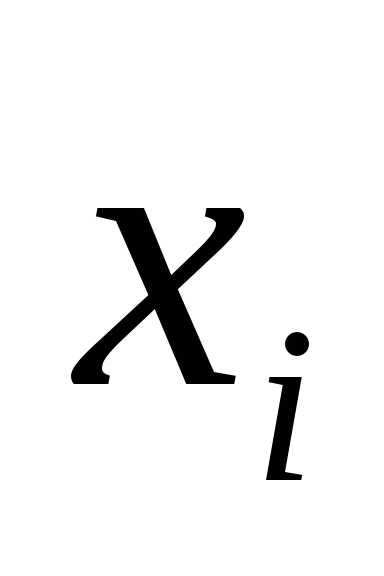 ,
для которой число
,
для которой число является максимальным. Обозначим это
максимальное значение
является максимальным. Обозначим это
максимальное значение :
:
 , или ,учитывая
формулу (1),
, или ,учитывая
формулу (1),
(2) .
Величина  называется нижней ценой игры или
максиминным выигрышем (максимином)
первого игрока.
называется нижней ценой игры или
максиминным выигрышем (максимином)
первого игрока.
Число  лежит в определенной строке платежной
матрицы. Соответствующая этой строке
стратегия первого игрока называется
максиминной стратегией. Если он будет
придерживаться максиминной стратегии,
то ему при любом поведении противника
гарантирован выигрыш не меньший
лежит в определенной строке платежной
матрицы. Соответствующая этой строке
стратегия первого игрока называется
максиминной стратегией. Если он будет
придерживаться максиминной стратегии,
то ему при любом поведении противника
гарантирован выигрыш не меньший .
Это его гарантированный выигрыш, если
он придерживается наиболее осторожной
максиминной стратегии.
.
Это его гарантированный выигрыш, если
он придерживается наиболее осторожной
максиминной стратегии.
Аналогичное
рассуждение можно провести за второго
игрока. Так как он заинтересован в том,
чтобы выигрыш первого игрока был
минимальным, то он должен просмотреть
каждую свою j–тую
стратегию ( столбец чисел 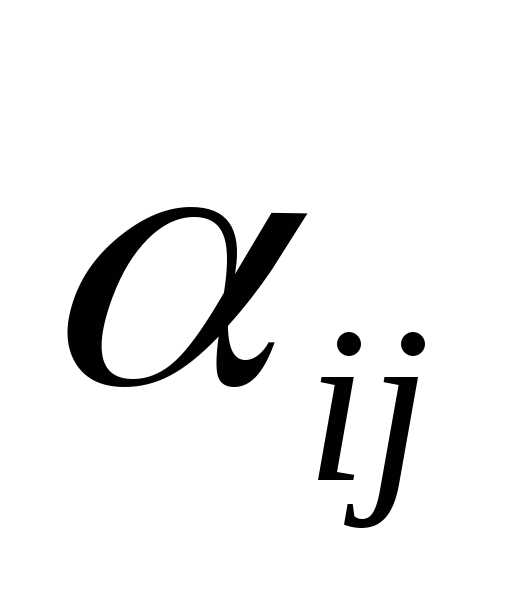 ) и определить максимальный выигрыш
первого игрока при этой стратегии.
Обозначим это значение выигрыша
) и определить максимальный выигрыш
первого игрока при этой стратегии.
Обозначим это значение выигрыша :
:
(3)  .
.
Выбирая какую–либо
стратегию 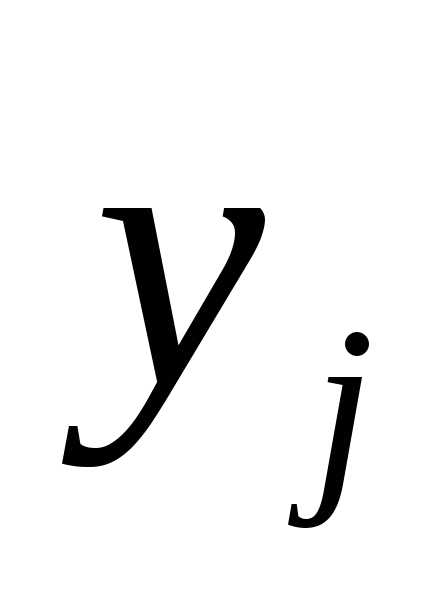 ,
второй игрок должен понимать, что в
результате разумных действий противника
он не проиграет больше, чем
,
второй игрок должен понимать, что в
результате разумных действий противника
он не проиграет больше, чем .
Действуя осторожно и избегая всякого
риска, он должен выбрать ту стратегию
.
Действуя осторожно и избегая всякого
риска, он должен выбрать ту стратегию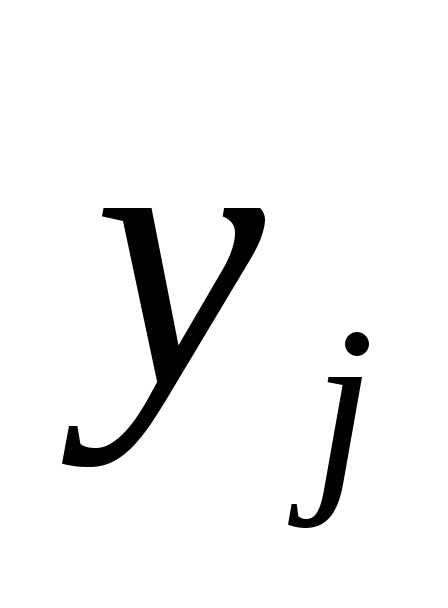 ,
для которой число
,
для которой число является минимальным. Обозначим это
минимальное значение
является минимальным. Обозначим это
минимальное значение :
:
(4) 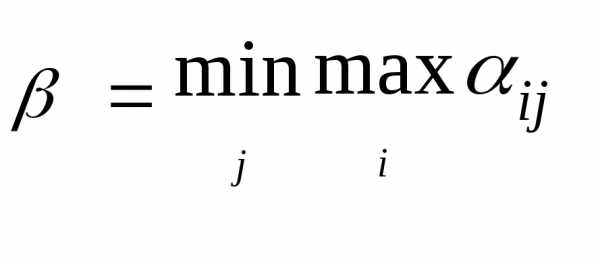
Величина  называется верхней ценой игры или
минимаксным выигрышем (минимаксом)
второго игрока.
называется верхней ценой игры или
минимаксным выигрышем (минимаксом)
второго игрока.
Соответствующая
столбцу с числом  стратегия второго игрока называется
его минимаксной стратегией. Если он
будет придерживаться своей минимаксной
стратегии, то ему при любом поведении
первого игрока гарантирован проигрыш
не больший
стратегия второго игрока называется
его минимаксной стратегией. Если он
будет придерживаться своей минимаксной
стратегии, то ему при любом поведении
первого игрока гарантирован проигрыш
не больший .
.
Принцип осторожности, диктующий игрокам выбор своих наиболее осторожных стратегий (максиминной для первого и минимаксной для второго игроков) в теории игр называется «принципом минимакса». Максиминную и минимаксную стратегии игроков обозначают общим термином «минимаксные стратегии».
В качестве примеров определим нижнюю и верхнюю цену игры и минимаксные стратегии для примеров 1, 2 из предыдущего раздела.
Пример 1. Игра Ани
и Бори. Добавим к платежной матрице игры
справа столбец чисел 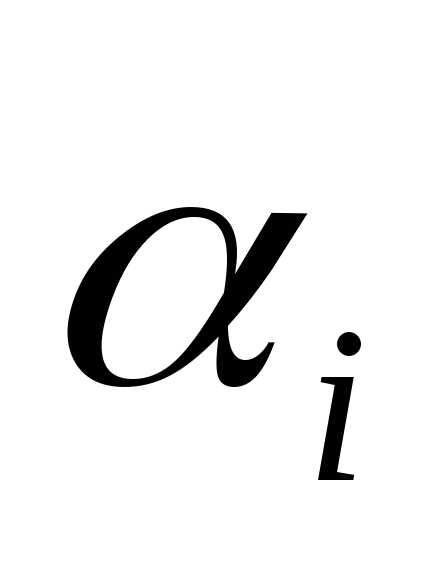 и снизу строку чисел
и снизу строку чисел :
:
Боря
Аня
Б0
Ч1

Б1
1
0
0
Ч1
–1
0
–1

1
0
Вычисляем нижнюю
цену игры по формуле (2):  =
0, верхнюю цену игры по формуле (4):
=
0, верхнюю цену игры по формуле (4):
 = 0. Они оказались одинаковыми.
= 0. Они оказались одинаковыми.
Элемент 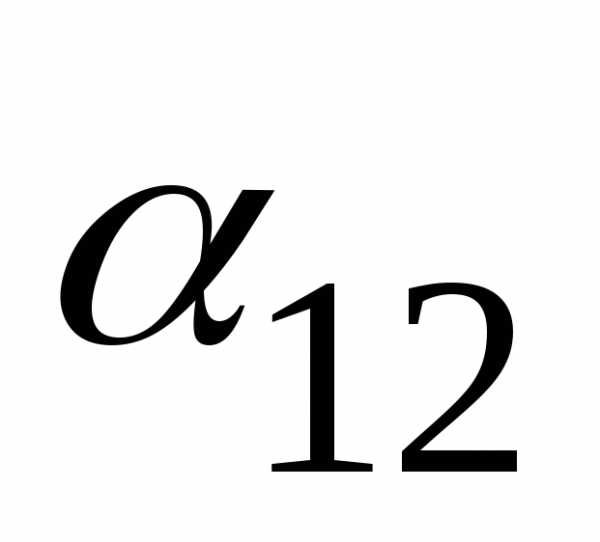 =
0, выделенный в платежной матрице,
является одновременно минимальным в
строке и максимальным в столбце. В
геометрии точку на поверхности, обладающую
свойством: аппликата точки минимальна
по одной координате и максимальна по
другой, называют седловой точкой. По
аналогии этот термин применяется в
теории игр: элемент платежной матрицы
с указанным свойством называется
седловой точкой матрицы, а про игру
говорят, что она имеет седловую точку.
=
0, выделенный в платежной матрице,
является одновременно минимальным в
строке и максимальным в столбце. В
геометрии точку на поверхности, обладающую
свойством: аппликата точки минимальна
по одной координате и максимальна по
другой, называют седловой точкой. По
аналогии этот термин применяется в
теории игр: элемент платежной матрицы
с указанным свойством называется
седловой точкой матрицы, а про игру
говорят, что она имеет седловую точку.
Если нижняя цена игры равна верхней, то их общее значение называется ценой игры (иногда – чистой ценой игры).
Седловой точке
соответствует пара минимаксных стратегий.
В примере 1 – это стратегии 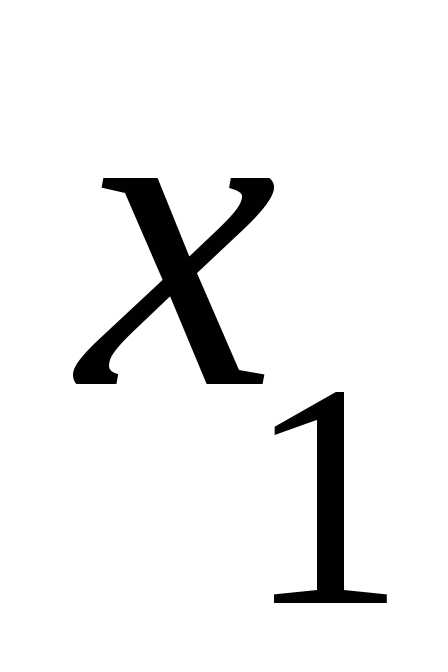 и
и 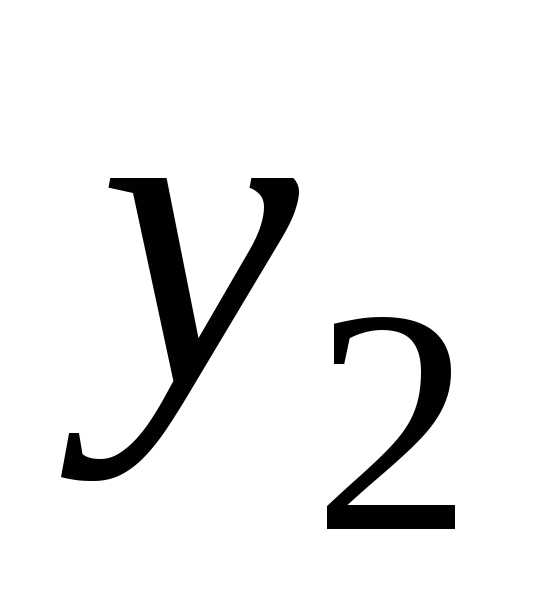 .
Они являются оптимальными стратегиями
игроков. Если один из игроков, например,
Боря, отклонится от своей оптимальной
второй стратегии, а Аня будет придерживаться
своей первой оптимальной стратегии, то
Боря проиграет 1 рубль. Таким образом,
решением игры Ани и Бори является пара
их минимаксных стратегий.
.
Они являются оптимальными стратегиями
игроков. Если один из игроков, например,
Боря, отклонится от своей оптимальной
второй стратегии, а Аня будет придерживаться
своей первой оптимальной стратегии, то
Боря проиграет 1 рубль. Таким образом,
решением игры Ани и Бори является пара
их минимаксных стратегий.
Для каждой игры с
седловой точкой существует решение –
пара минимаксных стратегий игроков,
являющиеся оптимальными стратегиями
игроков , а цена игры v
равна общему значению нижней и верхней
цены игры: v
=  =
= .
Это решение обладает свойством:
.
Это решение обладает свойством:
Если один из игроков придерживается своей оптимальной стратегии, а другой отклоняется от своей оптимальной стратегии, то от этого он может только потерять и ни в коем случае не увеличить свой выигрыш.
Пример 2. Игра
Эдварда и Фионы. Снова добавим к платежной
матрице игры справа столбец чисел  и снизу строку чисел
и снизу строку чисел .
Вычисляем нижнюю цену игры по формуле
(2):
.
Вычисляем нижнюю цену игры по формуле
(2): =
–3 , верхнюю цену игры по формуле
(4):
=
–3 , верхнюю цену игры по формуле
(4):
 = 2. Они оказались неодинаковыми. Заметим,
что
= 2. Они оказались неодинаковыми. Заметим,
что
 , игра не
имеет седловой точки.
, игра не
имеет седловой точки.
Фиона
Эдвард
1
2

1
2
–3
–3
2
–3
4
–3


2
4
Теорема. Для любой конечной игры выполняется неравенство:


Доказательство.
Пусть  =
=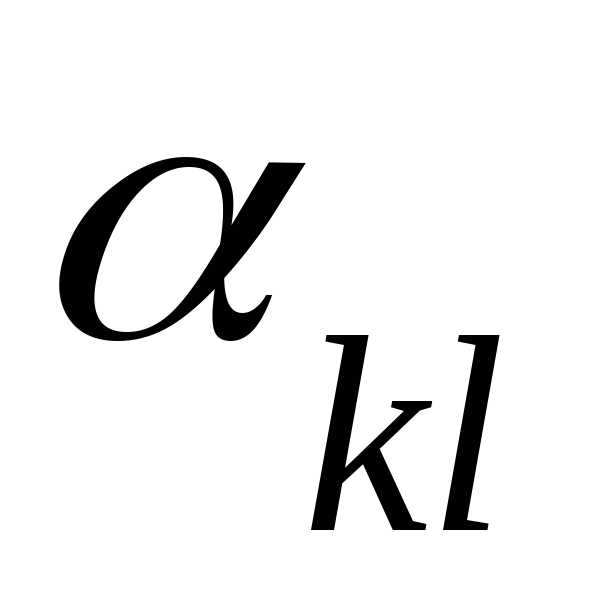 ,
, =
=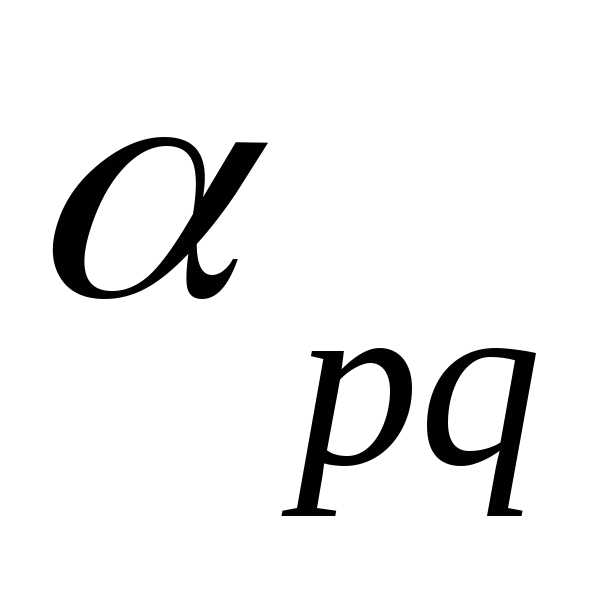 По определению чисел
По определению чисел и
и имеем:
имеем:
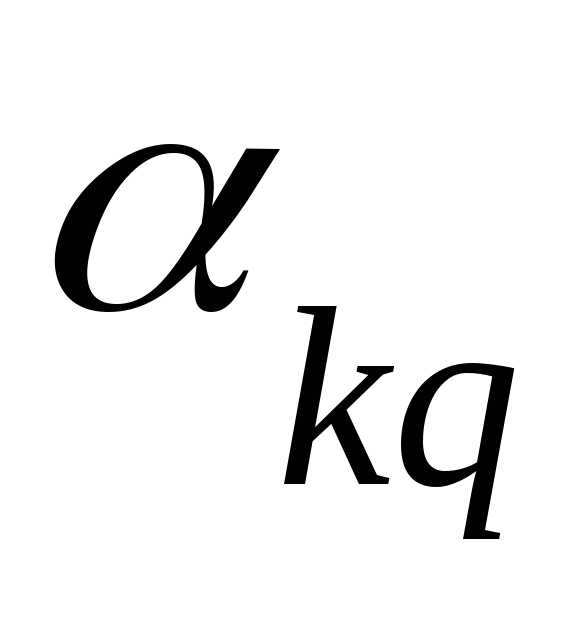 ,
,
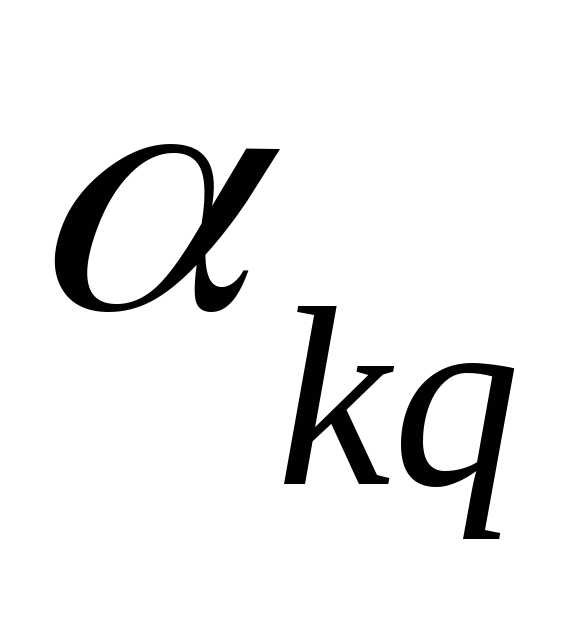 ,
следовательно,
,
следовательно,
 .
.
Для первого игрока в примере 2 любая стратегия является максиминной, для второго игрока минимаксной стратегией является его первая стратегия.
В случае 
 ,
как в примере 2, минимаксные стратегии
игроков являются неустойчивыми. В самом
деле, пусть первый игрок применяет свою
первую максиминную стратегию, а второй
– свою минимаксную первую стратегию.
До тех пор, пока оба игрока придерживаются
этих стратегий, выигрыш первого игрока
равен 2. Но если второму игроку станет
известно, что первый игрок применяет
первую стратегию, то он применит свою
вторую стратегию и сведет выигрыш
противника к –3. Наоборот, если первому
игроку станет известно, что второй игрок
применяет вторую стратегию, то он
применит тоже вторую стратегию и
увеличит свой выигрыш до 4. Поэтому
минимаксные стратегии игроков в игре
без седловой точки не являются
оптимальными.
,
как в примере 2, минимаксные стратегии
игроков являются неустойчивыми. В самом
деле, пусть первый игрок применяет свою
первую максиминную стратегию, а второй
– свою минимаксную первую стратегию.
До тех пор, пока оба игрока придерживаются
этих стратегий, выигрыш первого игрока
равен 2. Но если второму игроку станет
известно, что первый игрок применяет
первую стратегию, то он применит свою
вторую стратегию и сведет выигрыш
противника к –3. Наоборот, если первому
игроку станет известно, что второй игрок
применяет вторую стратегию, то он
применит тоже вторую стратегию и
увеличит свой выигрыш до 4. Поэтому
минимаксные стратегии игроков в игре
без седловой точки не являются
оптимальными.
В случае игры без седловой точки неясно, как находить цену игры и как определять оптимальные стратегии. Для этого необходимо обобщить понятие стратегии, определив понятие смешанной стратегии, предложенной Д. Бернулли в 1732 году.
studfiles.net